1.21.
3АТУХАЮЩИЕ, ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Дифференциальное
уравнение затухающих колебаний и его
решение. Коэффициент затухания.
Логарифмический декремент
затухания. Добротность
колебательной
системы. Апериодический
процесс. Дифференциальное уравнение
вынужденных колебаний и его решение.
Амплитуда
и фаза вынужденных колебаний. Процесс
установления колебаний. Случай резонанса.
Автоколебания.
Затуханием
колебаний называется постепенное
уменьшение амплитуды колебаний с
течением времени, обусловленное потерей
энергии колебательной системой.
Собственные
колебания без затухания – это идеализация.
Причины затухания могут быть разные. В
механической системе к затуханию
колебаний приводит наличие трения.
Когда израсходуется вся энергия,
запасенная в колебательной системе,
колебания прекратятся. Поэтому амплитуда
затухающих
колебаний
уменьшается,
пока не станет равной нулю.
Затухающие колебания,
как и собственные, в системах, разных
по своей природе, можно рассматривать
с единой точки зрения – общих признаков.
Однако, такие характеристики, как
амплитуда и период, требуют переопределения,
а другие – дополнения и уточнения по
сравнению с такими же признаками для
собственных незатухающих колебаний.
Общие признаки и понятия затухающих
колебаний следующие:
-
Дифференциальное
уравнение должно быть получено с учетом
убывания в процессе колебаний
колебательной энергии. -
Уравнение колебаний
– решение дифференциального уравнения. -
Амплитуда затухающих
колебаний зависит от времени. -
Частота и период
зависят от степени затухания колебаний. -
Фаза и начальная
фаза имеют тот же смысл, что и для
незатухающих колебаний.
Механические
затухающие колебания.
Механическая
система:
пружинный маятник с учетом сил трения.
Силы,
действующие на маятник:
Упругая
сила.
,
где k
– коэффициент жесткости пружины, х –
смещение маятника от положения равновесия.
Сила
сопротивления.
Рассмотрим силу сопротивления,
пропорциональную скорости v
движения (такая зависимость характерна
для большого класса сил сопротивления):
.
Знак “минус” показывает, что направление
силы сопротивления противоположно
направлению скорости движения тела.
Коэффициент сопротивления r
численно равен силе сопротивления,
возникающей при единичной скорости
движения тела:
Закон
движения
пружинного
маятника – это второй закон Ньютона:
ma
= Fупр.
+ Fсопр.
Учитывая,
что
и

запишем второй закон Ньютона в виде:

Разделив
все члены уравнения на m,
перенеся их все в правую часть, получим
дифференциальное
уравнение
затухающих колебаний:
Обозначим
,
где β
– коэффициент
затухания,
,
где ω0
– частота незатухающих свободных
колебаний в отсутствии потерь энергии
в колебательной системе.
В новых обозначениях
дифференциальное уравнение затухающих
колебаний имеет вид:

(21.2)
Это линейное
дифференциальное уравнение второго
порядка.
Это
линейное дифференциальное уравнение
решается заменой переменных. Представим
функцию х, зависящую от времени t,
в виде:
.
Найдем
первую и вторую производную этой функции
от времени, учитывая, что функция z
также является функцией времени:
,

Подставим выражения
в дифференциальное уравнение:

Приведем
подобные члены в уравнении и сократим
каждый член на
,
получим уравнение:
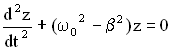
Обозначим
величину
.
Решением
уравнения
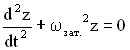
функции
,
.
Возвращаясь к
переменной х, получим формулы уравнений
затухающих колебаний:
.
Таким
образом,
уравнение затухающих колебаний есть
решение дифференциального уравнения
(21.2):
(21.3)
Частота
затухающих колебаний:
(физический
смысл имеет только вещественный корень,
поэтому
).
Период
затухающих колебаний:

Смысл,
который вкладывался в понятие периода
для незатухающих колебаний, не подходит
для затухающих колебаний, так как
колебательная система никогда не
возвращается в исходное состояние из-за
потерь колебательной энергии. При
наличии трения колебания идут медленнее:
.
Периодом
затухающих колебаний
называется минимальный промежуток
времени, за который система проходит
дважды положение равновесия в одном
направлении.
Для механической
системы пружинного маятника имеем:


Амплитуда
затухающих колебаний:
,
для пружинного маятника
.
Амплитуда
затухающих колебаний – величина не
постоянная, а изменяющаяся со временем
тем быстрее, чем больше коэффициент β.
Поэтому определение для амплитуды,
данное ранее для незатухающих свободных
колебаний, для затухающих колебаний
надо изменить.
При
небольших затуханиях амплитудой
затухающих колебаний
называется
наибольшее отклонение от положения
равновесия за период.
Графики
зависимости
смещения от времени
и
амплитуды от времени
представлены
на Рисунках 21.1 и 21.2.
Рисунок
21.1 – Зависимость смещения от времени
для затухающих колебаний.
Рисунок
21.2 – Зависимости амплитуды от времени
для затухающих колебаний
Характеристики
затухающих колебаний.
1.
Коэффициент затухания
β.
Изменение амплитуды
затухающих колебаний происходит по
экспоненциальному закону:
.
Пусть за
время τ
амплитуда колебаний уменьшится в “e
” раз (“е” – основание натурального
логарифма, е ≈ 2,718). Тогда, с одной стороны,
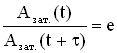
а с другой стороны, расписав амплитуды
Азат.(t)
и Азат.(t+τ),
имеем

Из этих соотношений следует βτ
= 1, отсюда
.
Промежуток
времени τ,
за который амплитуда уменьшается в “е”
раз, называется временем релаксации.
Коэффициент
затухания β
– величина, обратно пропорциональная
времени релаксации.
2.
Логарифмический
декремент затухания δ
—
физическая величина, численно равная
натуральному логарифму отношения двух
последовательных амплитуд, отстоящих
по времени на период .
Если
затухание невелико, т.е. величина β
мала, то амплитуда незначительно
изменяется за период, и логарифмический
декремент можно определить так:
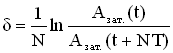
где
Азат.(t)
и Азат.(t+NT)
– амплитуды колебаний в момент времени
е и через N
периодов, т.е.в момент времени (t
+ NT).
3.
Добротность Q
колебательной системы
– безразмерная физическая величина,
равная произведению величины (2π)
νа
отношение энергии W(t)
системы в произвольный момент времени
к убыли энергии за один период затухающих
колебаний:

Так как энергия
пропорциональна квадрату амплитуды,
то

При малых
значениях логарифмического декремента
δ
добротность колебательной системы
равна
,
где Ne
– число колебаний, за которое амплитуда
уменьшается в “е” раз.
Так,
добротность пружинного маятника —

больше добротность колебательной
системы, тем меньше затухание, тем дольше
будет длиться периодический процесс в
такой системе. Добротность
колебательной системы — безразмерная
величина, которая характеризует
диссипацию энергии во времени.
4. При
увеличении коэффициента β,
частота затухающих колебаний уменьшается,
а период увеличивается. При ω0
= β
частота затухающих колебаний становится
равной нулю ωзат.
= 0, а Тзат.
=
∞. При этом колебания теряют периодический
характер и называются апериодическими.
При ω0
= β
параметры системы, ответственные за
убывание колебательной энергии, принимают
значения, называемые критическими.
Для пружинного маятника условие ω0
= β
запишется так: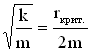
откуда найдем величину критического
коэффициента сопротивления:
.
Рис. 21.3.
Зависимсть амплитуды апериодических
колебаний от времени
Вынужденные
колебания.
Все реальные колебания
являются затухающими. Чтобы реальные
колебания происходили достаточно долго
нужно периодически пополнять энергию
колебательной системы, действуя на нее
внешней периодически изменяющейся
силой
Рассмотрим
явление колебаний, если внешняя
(вынуждающая)
сила изменяется в зависимости от времени
по гармоническому закону. При этом в
системах возникнут колебания, характер
которых в той или иной мере повторит
характер вынуждающей силы. Такие
колебания называются вынужденными.
Общие признаки
вынужденных механических колебаний.
1. Рассмотрим
вынужденные механические колебаний
пружинного маятника, на который действует
внешняя (вынуждающая)
периодическая сила
.
Силы, которые действуют на маятник,
однажды выведенный из положения
равновесия, развиваются в самой
колебательной системе. Это сила упругости
и
сила сопротивления
.
Закон
движения
(второй закон Ньютона) запишется следующим
образом:

Разделим
обе части уравнения на m,
учтем, что
,
и получим дифференциальное
уравнение
вынужденных
колебаний:

Обозначим
(β
– коэффициент
затухания),
(ω0
– частота незатухающих свободных
колебаний),
сила,
действующая на единицу массы. В этих
обозначениях дифференциальное
уравнение
вынужденных колебаний примет вид:

Это дифференциальное
уравнение второго порядка с правой
частью, отличной от нуля. Решение такого
уравнения есть сумма двух решений
.
–
общее
решение однородного дифференциального
уравнения, т.е. дифференциального
уравнения без правой части, когда она
равна нулю. Такое решение нам известно
– это уравнение затухающих колебаний,
записанное с точностью до постоянной,
значение которой определяется начальными
условиями колебательной системы:
,
где
.
Мы обсуждали ранее,
что решение может быть записано через
функции синуса.
Если
рассматривать процесс колебаний маятника
через достаточно большой промежуток
времени Δt
после включения вынуждающей силы
(Рисунок 21.2), то затухающие колебания в
системе практически прекратятся. И
тогда решением дифференциального
уравнения с правой частью будет решение
.
Решение
—
это частное решение неоднородного
дифференциального уравнения, т.е.
уравнения с правой частью. Из теории
дифференциальных уравнений известно,
что при правой части, изменяющейся по
гармоническому закону, решение
будет
гармонической функцией (sin
или cos)
с частотой изменения, соответствующей
частоте Ω
изменения правой части:
, (21.8)
где Аампл.
– амплитуда вынужденных колебаний, φ0
–сдвиг
фаз,
т.е. разность фаз между фазой вынуждающей
силы и фазой вынужденных колебаний. И
амплитуда Аампл.,
и сдвиг фаз φ0
зависят от параметров системы (β,
ω0)
и от частоты вынуждающей силы Ω.
Период
вынужденных колебаний равен
(21.9)
График вынужденных
колебаний на Рисунке 4.1.
Рис.21.3. График
вынужденных колебаний
Установившиеся
вынужденные колебания являются так же
гармоническими.
Зависимости
амплитуды вынужденных колебаний и
сдвига фаз от частоты внешнего воздействия.
Резонанс.
1. Вернемся к
механической системе пружинного
маятника, на который действует внешняя
сила, изменяющаяся по гармоническому
закону. Для такой системы дифференциальное
уравнение и его решение соответственно
имеют вид:

.
Проанализируем
зависимость амплитуды колебаний и
сдвига фаз от частоты внешней вынуждающей
силы, для этого найдем первую и вторую
производную от х и подставим в
дифференциальное уравнение.
,

Воспользуемся
методом векторной диаграммы. Из уравнения
видно, что сумма трех колебаний в левой
части уравнения (Рисунок 4.1) должна быть
равна колебанию в правой части. Векторная
диаграмма выполнена для произвольного
момента времени t.
Из нее можно определить
.
Рисунок
21.4.


Учитывая
значение
,
,
,
получим формулы для φ0
и Аампл.
механической системы:


2. Исследуем
зависимость амплитуды вынужденных
колебаний от частоты вынуждающей силы
и величины силы сопротивления в
колеблющейся механической системе, по
этим данным построим график
.
Результаты исследования отражены в
Рисунке 21.5, по ним видно, что при некоторой
частоте вынуждающей силы
амплитуда
колебаний резко возрастает. И это
возрастание тем больше, чем меньше
коэффициент затухания β.
При
амплитуда
колебаний становится бесконечно большой
.
Явление
резкого возрастания амплитуды
вынужденных
колебаний при частоте вынуждающей силы,
равной
,
называется резонансом.
(21.12)
Кривые
на Рисунке 21.5 отражают зависимость
и
называются амплитудными
резонансными кривыми.
Рисунок
21.5 – Графики зависимости амплитуды
вынужденных колебаний от частоты
вынуждающей силы.
Амплитуда резогансных
колебаний примет вид:
(21.13)
Вынужденные
колебания – это незатухающие
колебания. Неизбежные потери энергии
на трение компенсируются подводом
энергии от внешнего источника периодически
действующей силы. Существуют системы,
в которых незатухающие колебания
возникают не за счет периодического
внешнего воздействия, а в результате
имеющейся у таких систем способности
самой регулировать поступление энергии
от постоянного источника. Такие системы
называются автоколебательными,
а процесс незатухающих колебаний в
таких системах – автоколебаниями.
В автоколебательной
системе можно выделить три характерных
элемента – колебательная система,
источник энергии и устройство обратной
связи между колебательной системой и
источником. В качестве колебательной
системы может быть использована любая
механическая система, способная совершать
собственные затухающие колебания
(например, маятник настенных часов).
Источником
энергии может служить энергия деформация
пружины или потенциальная энергия груза
в поле тяжести. Устройство обратной
связи представляет собой некоторый
механизм, с помощью которого
автоколебательная система регулирует
поступление энергии от источника. На
рис. 21.6 изображена схема взаимодействия
различных элементов автоколебательной
системы.
|
|
|
Рисунок |
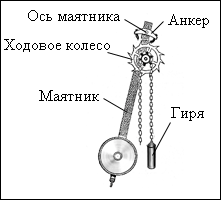
Примером
механической автоколебательной системы
может служить часовой механизм с анкерным
ходом (рис. 21.7.). Ходовое колесо с косыми
зубьями жестко скреплено с зубчатым
барабаном, через который перекинута
цепочка с гирей. На верхнем конце маятника
закреплен анкер (якорек) с двумя
пластинками из твердого материала,
изогнутыми по дуге окружности с центром
на оси маятника. В ручных часах гиря
заменяется пружиной, а маятник –
балансиром – маховичком, скрепленным
со спиральной пружиной.
|
|
|
Рисунок |
Балансир совершает
крутильные колебания вокруг своей оси.
Колебательной системой в часах является
маятник или балансир. Источником энергии
– поднятая вверх гиря или заведенная
пружина. Устройством, с помощью которого
осуществляется обратная связь, является
анкер, позволяющий ходовому колесу
повернуться на один зубец за один
полупериод.
Обратная связь
осуществляется взаимодействием анкера
с ходовым колесом. При каждом колебании
маятника зубец ходового колеса толкает
анкерную вилку в направлении движения
маятника, передавая ему некоторую порцию
энергии, которая компенсирует потери
энергии на трение. Таким образом,
потенциальная энергия гири (или
закрученной пружины) постепенно,
отдельными порциями передается маятнику.
Механические
автоколебательные системы широко
распространены в окружающей нас жизни
и в технике. Автоколебания совершают
паровые машины, двигатели внутреннего
сгорания, электрические звонки, струны
смычковых музыкальных инструментов,
воздушные столбы в трубах духовых
инструментов, голосовые связки при
разговоре или пении и т. д.
13
Соседние файлы в папке физика лекцыи
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рассмотрим две важные характеристики колебательных систем в механике и теории электричества и магнетизма: коэффициент затухания и логарифмический декремент затухания. Мы остановимся на так называемых затухающих колебаниях – таких колебаниях, амплитуда которых со временем уменьшается из-за потери энергии.
Чаще всего затухание происходит из-за трения — об воздух или поверхность, любую жидкую или газообразную среду, в которую помещено тело. Тело, проплывая в газе или жидкости или скользя по поверхности, передает этой среде внутреннюю энергию из за трения. Собственная суммарная кинетическая и потенциальная энергия при этом уменьшается. Соответственно уменьшается и скорость, а с ней — амплитуда.
Затухающие колебания можно поделить на свободные затухающие колебания и колебания, происходящие под действием внешних сил.
Как определить коэффициент затухания свободных затухающих механических колебаний
md2xdt2=−kx−rvmfrac{d^2x}{dt^2}=-kx-rv
mm — масса колеблющегося тела,
xx — его координата (смещение относительно точки равновесия x=0x=0),
−kx-kx — сила упругости, даваемая законом Гука для небольших смещений,
kk — коэффициент упругости,
−rv-rv — сила трения,
rr — коэффициент трения,
vv — скорость тела.
Это уравнение имеет решение:
x(t)=A0e−βtcos(ωt+φ)x(t)=A_0e^{-beta t}cos(omega t+varphi)
A0A_0 — амплитуда,
ωomega— циклическая частота,
φvarphi — начальная фаза,
βbeta — коэффициент затухания.
ω=ω02−β2omega=sqrt{omega_0^2-beta^2}
ω02=kmomega_0^2=frac{k}{m}
ω0omega_0 — собственная частота.
Коэффициент затухания βbeta – это величина, обратная времени, за которое амплитуда колебания уменьшилась в ee раз, где ee — основание натуральных логарифмов.
β=1NTbeta=frac{1}{NT}
NN — число колебаний после которых амплитуда уменьшилась в ee раз,
TT — период колебаний,
T=2πωT=frac{2pi}{omega}
Логарифмический декремент затухания свободных затухающих колебаний маятника
Маятник трется об воздух. И, казалось бы, как понять, какую он энергию отдает воздуху? Наверное, тут не обойтись без температуры, давления, плотности газообразной среды, и это долго, сложно, нудно… Может, и так. Но все это укладывается в коэффициент затухания ββ.
Определить логарифмический декремент затухания можно двумя способами — с помощью замеров амплитуды и с коэффициентом затухания. Для первого нужно лишь замерить две последовательные амплитуды. Тогда формула проста:
λ=lnA0e−βtA0e−β(t+T)lambda=lnfrac{A_0e^{-beta t}}{A_0e^{-beta (t+T)}}
Если же известен коэффициент затухания, амплитуда не нужна. Логарифмический декремент затухания будет равен его произведению на период колебаний:
λ=βTlambda=βT
Логарифмический декремент затухания электрического колебательного контура
Колебания в электрическом контуре возникают при отсутствии активного сопротивления в цепи, содержащей катушку индуктивности и конденсатор. Ток колеблется туда-сюда. Затухание этих колебаний удивительно похоже на затухание механических колебаний, потому, проведя несколько опытов, ученые пришли к выводу, что у электрического контура есть свой коэффициент затухания, и, соответственно, формула такая же, как для механических колебаний:
λ=βTlambda=βT
T=2πLCT=2πsqrt{LC}
LL — индуктивность катушки,
CC — емкость конденсатора.
Коэффициент затухания вынужденных механических колебаний
Конечно, в вынужденных колебаниях тоже существует затухание. Разница свободных и вынужденных колебаний в существовании добавочной силы, которая возвращает амплитуду к ее начальному значению, не давая маятнику остановиться, т.е. нивелирует работу силы трения.
Уравнение движения такой системы:
md2xdt2=−kx−rv+Fmfrac{d^2x}{dt^2}=-kx-rv+F.
Здесь все величины те же самые, что и в свободных колебаниях, но появляется внешняя сила FF:
F=mF0cos(ωt)F=mF_0cos(omega t).
F0F_0 имеет размерность силы, деленной на массу.
x=Asin(ωt+φ)x=Asin(omega t+varphi)
AA — амплитуда колебаний.
A=F0m(ω02−ω2)2+4β2ω2A=frac{F_0}{msqrt{{(omega_0^2-omega^2)^2}+4beta^2omega^2}{}}.
В случае затухающих вынужденных колебаний коэффициентом затухания снова является величина βbeta.
Тест по теме «Коэффициент и логарифмический декремент затухания»
From Wikipedia, the free encyclopedia
For «attenuation coefficient» as it applies to electromagnetic theory and telecommunications, see Attenuation constant. For the «mass attenuation coefficient», see Mass attenuation coefficient.
The linear attenuation coefficient, attenuation coefficient, or narrow-beam attenuation coefficient characterizes how easily a volume of material can be penetrated by a beam of light, sound, particles, or other energy or matter.[1] A coefficient value that is large represents a beam becoming ‘attenuated’ as it passes through a given medium, while a small value represents that the medium had little effect on loss.[2] The SI unit of attenuation coefficient is the reciprocal metre (m−1). Extinction coefficient is another term for this quantity,[1] often used in meteorology and climatology.[3] Most commonly, the quantity measures the exponential decay of intensity, that is, the value of downward e-folding distance of the original intensity as the energy of the intensity passes through a unit (e.g. one meter) thickness of material, so that an attenuation coefficient of 1 m−1 means that after passing through 1 metre, the radiation will be reduced by a factor of e, and for material with a coefficient of 2 m−1, it will be reduced twice by e, or e2. Other measures may use a different factor than e, such as the decadic attenuation coefficient below. The broad-beam attenuation coefficient counts forward-scattered radiation as transmitted rather than attenuated, and is more applicable to radiation shielding.
Overview[edit]
The attenuation coefficient describes the extent to which the radiant flux of a beam is reduced as it passes through a specific material. It is used in the context of:
- X-rays or gamma rays, where it is denoted μ and measured in cm−1;
- neutrons and nuclear reactors, where it is called macroscopic cross section (although actually it is not a section dimensionally speaking), denoted Σ and measured in m−1;
- ultrasound attenuation, where it is denoted α and measured in dB⋅cm−1⋅MHz−1;[4][5]
- acoustics for characterizing particle size distribution, where it is denoted α and measured in m−1.
The attenuation coefficient is called the «extinction coefficient» in the context of
- solar and infrared radiative transfer in the atmosphere, albeit usually denoted with another symbol (given the standard use of μ = cos θ for slant paths);
A small attenuation coefficient indicates that the material in question is relatively transparent, while a larger value indicates greater degrees of opacity. The attenuation coefficient is dependent upon the type of material and the energy of the radiation. Generally, for electromagnetic radiation, the higher the energy of the incident photons and the less dense the material in question, the lower the corresponding attenuation coefficient will be.
Mathematical definitions[edit]
Attenuation coefficient[edit]
The attenuation coefficient of a volume, denoted μ, is defined as[6]
where
- Φe is the radiant flux;
- z is the path length of the beam.
Spectral hemispherical attenuation coefficient[edit]
The spectral hemispherical attenuation coefficient in frequency and spectral hemispherical attenuation coefficient in wavelength of a volume, denoted μν and μλ respectively, are defined as:[6]
where
- Φe,ν is the spectral radiant flux in frequency;
- Φe,λ is the spectral radiant flux in wavelength.
Directional attenuation coefficient[edit]
The directional attenuation coefficient of a volume, denoted μΩ, is defined as[6]
where Le,Ω is the radiance.
Spectral directional attenuation coefficient[edit]
The spectral directional attenuation coefficient in frequency and spectral directional attenuation coefficient in wavelength of a volume, denoted μΩ,ν and μΩ,λ respectively, are defined as[6]
where
- Le,Ω,ν is the spectral radiance in frequency;
- Le,Ω,λ is the spectral radiance in wavelength.
Absorption and scattering coefficients[edit]
When a narrow (collimated) beam passes through a volume, the beam will lose intensity due to two processes: absorption and scattering. Absorption indicated energy that is lost from the beam, while scattering indicates light that is redirected in a (random) direction, and hence is no longer in the beam, but still present, resulting in diffuse light.
The absorption coefficient of a volume, denoted μa, and the scattering coefficient of a volume, denoted μs, are defined the same way as the attenuation coefficient.[6]
The attenuation coefficient of a volume is the sum of absorption coefficient and scattering coefficients:[6]
Just looking at the narrow beam itself, the two processes cannot be distinguished. However, if a detector is set up to measure beam leaving in different directions, or conversely using a non-narrow beam, one can measure how much of the lost radiant flux was scattered, and how much was absorbed.
In this context, the «absorption coefficient» measures how quickly the beam would lose radiant flux due to the absorption alone, while «attenuation coefficient» measures the total loss of narrow-beam intensity, including scattering as well. «Narrow-beam attenuation coefficient» always unambiguously refers to the latter. The attenuation coefficient is at least as large as the absorption coefficient; they are equal in the idealized case of no scattering.
Mass attenuation, absorption, and scattering coefficients[edit]
The mass attenuation coefficient, mass absorption coefficient, and mass scattering coefficient are defined as[6]
where ρm is the mass density.
Napierian and decadic attenuation coefficients[edit]
Decibels[edit]
Engineering applications often express attenuation in the logarithmic units of decibels, or «dB», where 10 dB represents attenuation by a factor of 10. The units for attenuation coefficient are thus dB/m (or, in general, dB per unit distance). Note that in logarithmic units such as dB, the attenuation is a linear function of distance, rather than exponential. This has the advantage that the result of multiple attenuation layers can be found by simply adding up the dB loss for each individual passage. However, if intensity is desired, the logarithms must be converted back into linear units by using an exponential: 
Naperian attenuation[edit]
The decadic attenuation coefficient or decadic narrow beam attenuation coefficient, denoted μ10, is defined as
Just as the usual attenuation coefficient measures the number of e-fold reductions that occur over a unit length of material, this coefficient measures how many 10-fold reductions occur: a decadic coefficient of 1 m−1 means 1 m of material reduces the radiation once by a factor of 10.
μ is sometimes called Napierian attenuation coefficient or Napierian narrow beam attenuation coefficient rather than just simply «attenuation coefficient». The terms «decadic» and «Napierian» come from the base used for the exponential in the Beer–Lambert law for a material sample, in which the two attenuation coefficients take part:
where
- T is the transmittance of the material sample;
- ℓ is the path length of the beam of light through the material sample.
In case of uniform attenuation, these relations become
Cases of non-uniform attenuation occur in atmospheric science applications and radiation shielding theory for instance.
The (Napierian) attenuation coefficient and the decadic attenuation coefficient of a material sample are related to the number densities and the amount concentrations of its N attenuating species as
where
- σi is the attenuation cross section of the attenuating species i in the material sample;
- ni is the number density of the attenuating species i in the material sample;
- εi is the molar attenuation coefficient of the attenuating species i in the material sample;
- ci is the amount concentration of the attenuating species i in the material sample,
by definition of attenuation cross section and molar attenuation coefficient.
Attenuation cross section and molar attenuation coefficient are related by
and number density and amount concentration by
where NA is the Avogadro constant.
The half-value layer (HVL) is the thickness of a layer of material required to reduce the radiant flux of the transmitted radiation to half its incident magnitude. The half-value layer is about 69% (ln 2) of the penetration depth. Engineers use these equations predict how much shielding thickness is required to attenuate radiation to acceptable or regulatory limits.
Attenuation coefficient is also inversely related to mean free path. Moreover, it is very closely related to the attenuation cross section.
Other radiometric coefficients[edit]
| Quantity | SI units | Notes | |
|---|---|---|---|
| Name | Sym. | ||
| Hemispherical emissivity | ε | — | Radiant exitance of a surface, divided by that of a black body at the same temperature as that surface. |
| Spectral hemispherical emissivity | εν ελ |
— | Spectral exitance of a surface, divided by that of a black body at the same temperature as that surface. |
| Directional emissivity | εΩ | — | Radiance emitted by a surface, divided by that emitted by a black body at the same temperature as that surface. |
| Spectral directional emissivity | εΩ,ν εΩ,λ |
— | Spectral radiance emitted by a surface, divided by that of a black body at the same temperature as that surface. |
| Hemispherical absorptance | A | — | Radiant flux absorbed by a surface, divided by that received by that surface. This should not be confused with «absorbance». |
| Spectral hemispherical absorptance | Aν Aλ |
— | Spectral flux absorbed by a surface, divided by that received by that surface. This should not be confused with «spectral absorbance». |
| Directional absorptance | AΩ | — | Radiance absorbed by a surface, divided by the radiance incident onto that surface. This should not be confused with «absorbance». |
| Spectral directional absorptance | AΩ,ν AΩ,λ |
— | Spectral radiance absorbed by a surface, divided by the spectral radiance incident onto that surface. This should not be confused with «spectral absorbance». |
| Hemispherical reflectance | R | — | Radiant flux reflected by a surface, divided by that received by that surface. |
| Spectral hemispherical reflectance | Rν Rλ |
— | Spectral flux reflected by a surface, divided by that received by that surface. |
| Directional reflectance | RΩ | — | Radiance reflected by a surface, divided by that received by that surface. |
| Spectral directional reflectance | RΩ,ν RΩ,λ |
— | Spectral radiance reflected by a surface, divided by that received by that surface. |
| Hemispherical transmittance | T | — | Radiant flux transmitted by a surface, divided by that received by that surface. |
| Spectral hemispherical transmittance | Tν Tλ |
— | Spectral flux transmitted by a surface, divided by that received by that surface. |
| Directional transmittance | TΩ | — | Radiance transmitted by a surface, divided by that received by that surface. |
| Spectral directional transmittance | TΩ,ν TΩ,λ |
— | Spectral radiance transmitted by a surface, divided by that received by that surface. |
| Hemispherical attenuation coefficient | μ | m−1 | Radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume. |
| Spectral hemispherical attenuation coefficient | μν μλ |
m−1 | Spectral radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume. |
| Directional attenuation coefficient | μΩ | m−1 | Radiance absorbed and scattered by a volume per unit length, divided by that received by that volume. |
| Spectral directional attenuation coefficient | μΩ,ν μΩ,λ |
m−1 | Spectral radiance absorbed and scattered by a volume per unit length, divided by that received by that volume. |
See also[edit]
- Absorption (electromagnetic radiation)
- Absorption cross section
- Absorption spectrum
- Acoustic attenuation
- Attenuation
- Attenuation length
- Beer–Lambert law
- Cargo scanning
- Compton edge
- Compton scattering
- Computation of radiowave attenuation in the atmosphere
- Cross section (physics)
- Grey atmosphere
- High-energy X-rays
- Mass attenuation coefficient
- Mean free path
- Propagation constant
- Radiation length
- Scattering theory
- Transmittance
References[edit]
- ^ a b IUPAC, Compendium of Chemical Terminology, 2nd ed. (the «Gold Book») (1997). Online corrected version: (2006–) «Attenuation coefficient». doi:10.1351/goldbook.A00516
- ^ Serway, Raymond; Moses, Clement; Moyer, Curt (2005). Modern Physics. California, USA: Brooks/Cole. p. 529. ISBN 978-0-534-49339-4.
- ^ «2nd Edition of the Glossary of Meteorology». American Meteorological Society. Retrieved 2015-11-03.
- ^ ISO 20998-1:2006 «Measurement and characterization of particles by acoustic methods»
- ^ Dukhin, A.S. and Goetz, P.J. «Ultrasound for characterizing colloids», Elsevier, 2002
- ^ a b c d e f g «Thermal insulation — Heat transfer by radiation — Physical quantities and definitions». ISO 9288:1989. ISO catalogue. 1989. Retrieved 2015-03-15.
External links[edit]
- Absorption Coefficients α of Building Materials and Finishes
- Sound Absorption Coefficients for Some Common Materials
- Tables of X-Ray Mass Attenuation Coefficients and Mass Energy-Absorption Coefficients from 1 keV to 20 MeV for Elements Z = 1 to 92 and 48 Additional Substances of Dosimetric Interest
- IUPAC, Compendium of Chemical Terminology, 2nd ed. (the «Gold Book») (1997). Online corrected version: (2006–) «Absorption coefficient». doi:10.1351/goldbook.A00037
Как найти коэффициент затухания колебаний по уравнение
§6 Затухающие колебания
Декремент затухания. Логарифмический декремент затухания.
Добротность
Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.
Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.
Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения
где r — коэффициент сопротивления среды. Знак минус показывает, что FC направлена в сторону противоположную скорости.
Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r . По второму закону Ньютона
где β — коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.
— дифференциальное уравнение затухающих колебаний.
— у равнение затухающих колебаний.
ω – частота затухающих колебаний:
Период затухающих колебаний:
Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало.
Если затухания выражены слабо (β→0), то . Затухающие колебания можно
рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону
В уравнении (1) А0 и φ0 — произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания
Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз
τ — время релаксации.
Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D , который равен отношению амплитуд, отстоящих по времени на период:
Логарифмический декремент затухания равен логарифму D :
Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз. Логарифмический декремент затухания — постоянная для данной системы величина.
Еще одной характеристикой колебательной система является добротность Q .
Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.
Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.
Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.
Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.
§7 Вынужденные колебания.
Резонанс
В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.
Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.
По второму закону Ньютона:
(1)
— дифференциальное уравнение вынужденных колебаний.
Это дифференциальное уравнение является линейным неоднородным.
Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:
Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:
(2)
Частное решение этого уравнения будем искать в виде:
т.к. выполняется для любого t , то должно выполняться равенство γ = ω , следовательно,
Это комплексное число удобно представить в виде
где А определяется по формуле (3 ниже), а φ — по формуле (4), следовательно, решение (2),в комплексной форме имеет вид
Его вещественная часть, являвшаяся решением уравнения (1) равна:
(3)
(4)
Слагаемое Хо.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механической системы, называется резонансом.
Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ωрез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).
Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то
При ω→0 все кривые приходят к значению — статическое отклонение.
Параметрический резонанс возникает в том случае, когда периодическое изменение одного из параметров система приводит к резкому увеличению амплитуды колеблющейся системы. Например, кабины, делающие «солнышко» за счет изменения положения центра тяжести система.(То же в «лодочках».) См. §61 .т. 1 Савельев И.В.
Затухающие колебания в контуре и их уравнение
Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением R , с емкостью конденсатора C , с катушкой индуктивности L , изображенный на рисунке 1 . Колебания, происходящие в нем, — затухающие.
Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.
Характеристики затухающих колебаний
Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:
m a = — k x — y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .
Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,
Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e — период времени уменьшения амплитуды в e раз.
Для R L C контура применима формула с ω частотой.
При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C — собственная частота, отсюда ω ≈ ω 0 .
При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :
Q = 1 R L C = ω 0 L R , где R , L и C — сопротивление, индуктивность, емкость, а ω 0 — частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:
Q = R L C = R ω 0 L .
R является входным сопротивлением параллельного контура.
Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:
Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.
Уравнения затухающих колебаний
Рассмотрим рисунок 1 . Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:
q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .
Если t = 0 , то заряд конденсатора становится равным q 0 , и ток в цепи отсутствует.
Если R > 2 L C изменения заряда не относят к колебаниям, разряд называют апериодическим.
Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое R k .
Функция изображается аналогично рисунку 2 .
Записать закон убывания энергии, запасенной в контуре W ( t ) при W ( t = 0 ) = W 0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β , а собственную частоту — ω 0 .
Решение
Отправная точка решения – это применение формулы изменения заряда на конденсаторе в R L C — контуре:
q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .
Предположим, что при t = 0 , a ‘ 0 = 0 . Тогда применим выражение
Для нахождения I ( t ) :
I ( t ) = — ω 0 q 0 e ( — 2 β t ) sin ( ω t + α ) , где t g α = β ω .
Очевидно, что электрическая энергия W q запишется как:
W q = q 2 2 C = q 0 2 2 C e ( — 2 β t ) cos 2 ( ω t ) = W 0 e ( — 2 β t ) cos 2 ( ω t ) .
Тогда значение магнитной энергии контура W m равняется:
W m = L 2 ω 0 2 q 0 2 e ( — 2 β t ) sin 2 ω t + a = W 0 e — 2 β t sin 2 ω t + a .
Запись полной энергии будет иметь вид:
W = W q + W m = W 0 e ( — 2 β t ) ( cos 2 ( ω t ) + sin 2 ( ω t + a ) ) = = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + α ) .
Где sin α = β ω 0 .
Ответ: W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) .
Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W ( t ) , при медленно затухающих колебаниях. Начертить график убывания энергии.
Решение
Если колебания в контуре затухают медленно, то:
Очевидно, выражение энергии, запасенной в контуре, вычислим из
W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) , предварительно преобразовав до W ( t ) = W 0 e ( — 2 β t ) .
Такое упрощение возможно по причине выполнения условия β ω 0 ≪ 1 , sin ( 2 ω t + a ) ≤ 1 , что означает β ω 0 sin ( 2 ω t + a ) ≪ 1 .
Ответ: W ( t ) = W 0 e ( — 2 β t ) . Энергия в контуре убывает по экспоненте.
Лекция №8. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
5.6. Затухающие гармонические колебания.
Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Затухающие колебания − это колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления, вызывающая затухание, зависит от скорости колебательного движения, т. е. ее можно считать прямо пропорциональной скорости
где μ − постоянная, называемая коэффициентом сопротивления.
Знак «минус» обусловлен тем, что сила и скорость имеют противоположные направления. Тогда второй закон Ньютона для гармонических колебаний при наличии сил сопротивления имеет вид
Учитывая , что a= $$d^2xover dt^2$$ , а υ= $$dxover dt$$ и разделив на массу m , получим
Применив обозначения $$ = ω_0<^2>$$ , $$ <μover m>= 2β$$ и $$ = f_0$$ получим
дифференциальное уравнение затухающих колебаний . Отметим, что ω0 представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды. Эта частота называется собственной частотой .
Для решения уравнения (5.6.4) сделаем подстановку
Проведем замену переменных
Подставим (5.6.5 и 5.6.6) в выражение (5.6.4)
Преобразуем , сократив на e -βt
Рассмотрим случай, когда сопротивление среды настолько мало, что ω0 2 -β 2 >0 есть величина положи мы можем ввести тельная, и обозначение ω0 2 -β 2 =ω 2 , после чего уравнение (5.6.8) примает вид
В случае большого сопротивления среды ω0 2 -β 2 , движение становится непериодическим.
Решение уравнения (5.6.8) можно записать в виде
Окончательно, подставляя последнее уравнение в выражение (5.6.5), получаем общее решение дифференциального уравнения затухающих колебаний (5.6.4)
В соответствии с видом полученной функции движение можно рассматривать как гармоническое колебание с частотой
и амплитудой, изменяющейся по закону
На рисунке показан график данной функции. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Верхняя из пунктирных кривых дает график функции A(t) , причем величина A0 представляет собой амплитуду в начальный момент времени. Начальное смещение зависит от A0 и также от начальной фазы φ , т.е. x0=A0cosφ .
5.7. Коэффициент затухания и логарифмический декремент затухания.
Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно
и называется декрементом затухания .
Для характеристики системы обычно используется колебательной логарифмический декремент затухания , т.е. логарифм декремента затухания
Скорость затухания колебаний определяется величиной называем коэффициентом затухания $$β=<μover 2m>$$ .
Найдем время, называемое временем релаксации τ , за которое амплитуда уменьшается в e раз
т. е. коэффициент затухания обратен по величине промежутку времени, за который амплитуда колебаний уменьшается в e раз.
За время релаксации τ система успевает совершить $$N_e=<τover T>$$ колебаний
Следовательно, $$δ=<1over N_e>$$ логарифмический декремент затухания обратно пропорционален по величине числу колебаний, за которые амплитуда колебаний уменьшается в e раз.
Для характеристики колебательной системы используется величина
которая называется добротностью колебательной системы.
Величина Q , пропорциональная числу колебаний, совершаемых системой за время, в течение которого амплитуда колебаний уменьшается в e раз.
5.8. Вынужденные колебания.
До сих пор мы рассматривали свободные колебания, когда выведенная из положения равновесия система совершает колебания будучи предоставленной самой себе. Рассмотрим колебательную систему, которая подвергается действию внешней силы, изменяющейся по гармоническому закону F=F0cosωt . Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными колебаниями . В этом случае уравнение второго закона Ньютона имеет вид
Учитывая , что a= $$d^2xover dt^2$$ , а υ= $$dxover dt$$ и разделив на массу m , получим
Применив обозначения $$ = ω_0<^2>$$ , $$ <μover m>= 2β$$ и $$ = f_0$$ получим
дифференциальное уравнение вынужденных колебаний.
Будем искать решение уравнения (5.8.3) в виде
предполагая, что результирующее колебание будет совершаться с частотой внешней вынуждающей силы.
Подставим (5.8.4) и (5.8.5) в уравнение (5.8.3)
Чтобы уравнение (69) обратилось в тождество необходимо, чтобы коэффициенты при cosωt и sinωt были равны нулю.
Из выражения (71) получаем
Возведем в квадрат уравнения (70) и сложим
Подставив полученные выражения (71) и (73) в выражение (64) получим уравнение вынужденных колебаний
5.9. Резонанс.
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой частоте амплитуда колебаний достигает максимального значения.
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы называется резонансом , а соответствующая частота − резонансной частотой.
Найдем резонансную частоту. Амплитуда вынужденных колебаний будет max, когда выражение $$(ω_0<^2>-ω^2)^2 + 4β^2ω^2$$ в уравнении $$A=-ω^2)^2 + 4β^2ω^2>>$$ (5.8.13) будет минимальным.
Продифференцируем это выражение по ω и приравняем к нулю
Полученное уравнение имеет три решения: ω=0 и ω=± $$sqrt <ω_0<^2>-2β^2>$$ . 2 . Первое решение соответствует максимуму знаменателя. Из остальных двух решений отрицательное не имеет физического смысла (частота не может быть отрицательной). Таким образом, резонансная циклическая частота
Подставив это значение в выражение для амплитуды (5.8.13), получим выражение для амплитуды при резонансе
Из последнего уравнения (5.9.3) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность, а резонансная частота, согласно (5.9.2), при тех же условиях (при β=0 ), совпадала бы с собственной частотой колебаний системы ω0
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы показана графически на рис. 5.9.1. В соответствии с (5.9.2) и (5.9.3), чем меньше параметр β , тем выше и правее лежит максимум данной кривой. Изображенная на рис. 5.9.1 совокупность графиков функций (5.8.13), соответствующих различным значениям параметра β , называется резонансными кривыми .
При стремлении ω к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному f0ω0 2 . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F0
При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.
Наконец, отметим, что чем меньше β , тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» получается максимум. При малом затухании (т. е. β ) амплитуда при резонансе приближенно равна Apes≈f0/2βω0 . Разделим это выражение на смещение x0 из положения равновесия под действием постоянной силы F0 , равное x0=f0/ωp 2 . В результате получим
где δ = βТ – логарифмический декремент затухания (5.7.2); Q – добротность колебательной системы (5.7.6).
Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы. Следует отметить, что это справедливо лишь при небольшом затухании.
http://zaochnik.com/spravochnik/fizika/elektromagnitnye-kolebanija-volny/zatuhajuschie-kolebanija-v-konture/
http://physics.belstu.by/mechanics_lk/mechanics_lk8.html
Как определяется логарифмический коэффициент затухания?
Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз. Если χ = 0,01, то N = 100. При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний.
Чему равен коэффициент фазы?
коэффициент фазы — коэффициент фазы; волновое число Величина, характеризующая изменение фазы бегущей вдоль линии синусоидальной волны тока (или напряжения) при перемещении волны на единицу длины линии, равная мнимой части коэффициента распространения … Политехнический терминологический толковый словарь
Как рассчитать декремент затухания?
F = –kx. Отношение двух амплитуд, отстоящих по времени на период, называется декрементом затухания: .
Почему важно чтобы коэффициент затухания внутренних органов был велик?
Если коэффициент затухания внутренних органов человека был бы не велик, то резонансные явления, возникшие в этих органах под воздействием внешних вибраций или звуковых волн, могли бы привести к трагическим последствиям: разрыву органов, повреждению связок и т. п.
Какие физические величины характеризуют затухающие колебания?
2.3. Затухающие колебания. … Это приводит к тому, что при свободных колебаниях, величины, характеризующие отклонение системы от равновесия (смещения, «колебательная» скорость элементов и т. п.), с течением времени постепенно уменьшаются.
Чему численно равен логарифмический декремент затухания?
Логарифмический декремент колебаний равен коэффициенту затухания β, умноженному на период колебаний T: где A = x(0) — начальная амплитуда, t — время, ω = 2π/T — циклическая частота колебания.
Что характеризует логарифмический декремент затухания?
Логарифмический декремент затухания характеризует затухание колебаний за период, а коэффициент затухания за единицу времени. Важной характеристикой затухающих колебаний является также время релаксации, в течение которого амплитуда колебаний уменьшается в е раз.
Что называют логарифмическим Декрементом?
логарифмический декремент — logarithmic decrement Натуральный логарифм отношения двух любых последовательных одинакового знака максимальных амплитуд при затухании одночастотных колебаний.
Чем определяется амплитуда?
Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины. Синусоидальное колебание.
Какую линию можно считать длинной?
Длинная линия — модель линии передачи, продольный размер (длина) которой превышает длину волны, распространяющейся в ней (либо сравнима с длиной волны), а поперечные размеры (например, расстояние между проводниками, образующими линию) значительно меньше длины волны.
В чем измеряется коэффициент фазы?
Фазовая постоянная измеряется в радианах на 1 км или градусах (1 рад = 57,3°). Фазовая постоянная измеряется в радианах на 1 км или градусах (1 рад = 57,3°).
Что называется волновым сопротивлением и чему оно равно?
Волновое сопротивление в газе и жидкости — отношение звукового давления в бегущей плоской звуковой волне к колебательной скорости частиц среды. Также волновое сопротивление равно произведению плотности среды на скорость звука в ней.
Что такое коэффициент распространения волны?
коэффициент распространения — Комплексная величина, характеризующая изменение модуля и аргумента напряжения или тока бегущей волны и равная натуральному логарифму отношения комплексных амплитуд напряжения или тока этой волны для двух точек линий, отстоящих друг от друга на… …
Какая линия называется линией без потерь?
Линия без потерь – это линия, у которой рассеяние энергии отсутствует, что имеет место при значениях первичных параметров R = 0 и G =0. … Отсюда коэффициент ослабления a = 0, а коэффициент фазы b = w линейно зависит от частоты. Волновое сопротивление линии без потерь является чисто активным (резистивным).
Что такое коэффициент отражения по напряжению?
Коэффициент отражения по напряжению — отношение комплексной амплитуды напряжения отраженной волны к комплексной амплитуде напряжения падающей волны в заданном сечении линии передачи.
Что такое декремент затухания?
Логарифмический декремент затухания — D Величина, показывающая скорость затухания собственных колебаний и определяемая как натуральный логарифм отношения следующих друг за другом амплитуд колебаний Источник … Словарь-справочник терминов нормативно-технической документации
Что характеризует логарифмическим декрементом затухания?
Логарифмический декремент затухания характеризует затухание колебаний за период, а коэффициент затухания за единицу времени. Важной характеристикой затухающих колебаний является также время релаксации, в течение которого амплитуда колебаний уменьшается в е раз.

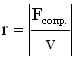











 3
3