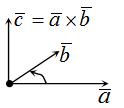Как найти вектор векторного произведения двух векторов - Avtoru.top

Заказать задачи по любым предметам можно здесь от 10 минут

Векторное произведение векторов

Определение

Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $.

Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.

Формула

Формула 1

Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле:

$$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$

Формула 2

В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$

где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $.

Определитель во второй формуле можно раскрыть по первой строке:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 — a_3 b_2) — overline{j} (a_1 b_3 — a_3 b_1) + overline{k} (a_1 b_2 — a_2 b_1) $$

Итого вторая формула приобретает окончательный короткий вид:

$$ overline{a} times overline{b} = (a_2 b_3 — a_3 b_2; a_3 b_1 — a_1 b_3; a_1 b_2 — a_2 b_1) $$

Свойства

При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
$$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$

Примеры решений

Пример 1

Найти векторное произведение векторов, заданных координатами

$$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$

Решение

Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) — overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} — overline{j} + 3overline{k} $$

Полученный ответ можно записать в удобном виде:

$$ overline{a} times overline{b} = (5, -1, 3) $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ overline{a} times overline{b} = (5, -1, 3) $$

Геометрический смысл

Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.

Пример 2

Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$

Решение

Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов.

Находим определитель:

$$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) — overline{j}(2+3) + overline{k}(4+1) = -5overline{i} — 5overline{j} + 5overline{k} $$

Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора:

$$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$

По формуле нахождения площади треугольника имеем:

$$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$

Ответ

$$ S_Delta = 4.33 $$

Источник

Любовь Петровна Гаврилюк

Эксперт по предмету «Геометрия»

Задать вопрос автору статьи

Угол между векторами

Для того чтобы мы могли ввести понятие векторного произведения двух векторов, нужно сначала разобраться с таким понятие, как угол между этими векторами.

Пусть нам даны два вектора $overline{α}$ и $overline{β}$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $overline{α}=overline{OA}$ и $overline{β}=overline{OB}$, тогда угол $AOB$ будет называться углом между этими векторами (рис. 1).

Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ

Причем мы будем считать, что если векторы $overline{α}$ и $overline{β}$ будут сонаправленными, или один или оба из них нулевой, то угол между этими векторами будет равен $0^circ$.

Обозначение: $∠(overline{α},overline{β})$

Понятие векторного произведения векторов и формула нахождения

Определение 1

Векторным произведением двух векторов называется вектор, перпендикулярный обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.

Обозначение: $overline{α}хoverline{β}$.

Математически это выглядит следующим образом:

$|overline{α}хoverline{β}|=|overline{α}||overline{β}|sin⁡∠(overline{α},overline{β})$
$overline{α}хoverline{β}⊥overline{α}$, $overline{α}хoverline{β}⊥overline{β}$
$(overline{α}хoverline{β},overline{α},overline{β})$ и $(overline{i},overline{j},overline{k})$ одинаково ориентированы (рис. 2)

«Как найти векторное произведение векторов» 👇

Рисунок 2. Произведение векторов. Автор24 — интернет-биржа студенческих работ

Очевидно, что внешнее произведение векторов будет равняться нулевому вектору в двух случаях:

Если длина одного или обоих векторов равняется нулю.
Если угол между этими векторами будет равняться $180^circ$ или $0^circ$ (так как в этом случае синус равняется нулю).

Чтобы наглядно увидеть, как находится векторное произведение векторов, рассмотрим следующие примеры решения.

Пример 1

Найти длину вектора $overline{δ}$, который будет являться результатом векторного произведения векторов, с координатами $overline{α}=(0,4,0)$ и $overline{β}=(3,0,0)$.

Решение.

Изобразим эти векторы в декартовом координатном пространстве (рис. 3):

Рисунок 3. Векторы в декартовом координатном пространстве. Автор24 — интернет-биржа студенческих работ

Видим, что эти векторы лежат на осях $Ox$ и $Oy$, соответственно. Следовательно, угол между ними будет равняться $90^circ$. Найдем длины этих векторов:

$|overline{α}|=sqrt{0+16+0}=4$

$|overline{β}|=sqrt{9+0+0}=3$

Тогда, по определению 1, получим модуль $|overline{δ}|$

$|overline{δ}|=|overline{α}||overline{β}|sin90^circ=4cdot 3cdot 1=12$

Ответ: $12$.

Вычисление векторного произведения по координатам векторов

Из определения 1 сразу же вытекает и способ нахождения векторного произведения для двух векторов. Поскольку вектор кроме значения имеет еще и направление, находить его только при помощи скалярной величины невозможно. Но помимо него существует еще способ нахождения с помощью координат данных нам векторов.

Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые будут иметь координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно. Тогда вектор векторного произведения (а именно его координаты) можно найти по следующей формуле:

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$

Иначе, раскрывая определитель, получим следующие координаты

$overline{α}хoverline{β}=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$

Пример 2

Найти вектор векторного произведения коллинеарных векторов $overline{α}$ и $overline{β}$ с координатами $(0,3,3)$ и $(-1,2,6)$.

Решение.

Воспользуемся формулой, приведенной выше. Получим

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\0&3&3\-1&2&6end{vmatrix}=(18-6)overline{i}-(0+3)overline{j}+(0+3)overline{k}=12overline{i}-3overline{j}+3overline{k}=(12,-3,3)$

Ответ: $(12,-3,3)$.

Свойства векторного произведения векторов

Для произвольных смешанных трех векторов $overline{α}$, $overline{β}$ и $overline{γ}$, а также $r∈R$ справедливы следующие свойства:

$overline{α}хoverline{β}=-(overline{β}хoverline{α})$

Верность этого свойства будет следовать из третьего пункта определения 1.
$(roverline{α})хoverline{β}=r(overline{α}хoverline{β})$ и $overline{α}х(roverline{β})=r(overline{α}хoverline{β})$

Из формулы для нахождения векторного произведения будем получать:

$(roverline{α})overline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\rα_1&rα_2&rα_3\β_1&β_2&β_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=r(overline{α}хoverline{β})$

$overline{α}х(roverline{β})=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\rβ_1&rβ_2&rβ_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=r(overline{α}хoverline{β})$
$overline{α}х(overline{β}+overline{γ})=overline{α}overline{β}+overline{α}overline{γ}$ и $(overline{α}+overline{β})overline{γ}=overline{α}overline{γ}+overline{β}overline{γ}$.

Данное свойство векторного произведения векторов также можно проверить с помощью формулы.

Следующее свойство называют геометрическим смыслом векторного произведения:
Длина вектора векторного произведения равняется площади параллелограмма, который нужно было построить между ними (рис. 4)

Рисунок 4. Длина вектора векторного произведения. Автор24 — интернет-биржа студенческих работ

Пример 3

Найдите площадь параллелограмма, вершины которого имеют координаты $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ и $(3,8,0)$.

Решение.

Вначале изобразим данный параллелограмм в координатном пространстве (рис.5):

Рисунок 5. Параллелограмм в координатном пространстве. Автор24 — интернет-биржа студенческих работ

Видим, что две стороны этого параллелограмма построены с помощью коллинеарных векторов с координатами $overline{α}=(3,0,0)$ и $overline{β}=(0,8,0)$. Используя четвертое свойство, получим:

$S=|overline{α}хoverline{β}|$

Найдем вектор $overline{α}хoverline{β}$:

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\3&0&0\0&8&0end{vmatrix}=0overline{i}-0overline{j}+24overline{k}=(0,0,24)$

Следовательно

$S=|overline{α}хoverline{β}|=sqrt{0+0+24^2}=24$

Ответ: $24$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

В данной публикации мы рассмотрим, каким образом можно найти векторное произведение двух векторов, приведем геометрическую интерпретацию, алгебраическую формулу и свойства этого действия, а также разберем пример решения задачи.

Геометрическая интерпретация
Формула векторного произведения
Свойства векторного произведения
Пример задачи

Геометрическая интерпретация

Векторное произведение двух ненулевых векторов a и b – это вектор c, который обозначается как [a, b] или a x b.

Длина вектора c равна площади параллелограмма, построенного с помощью векторов a и b.

При этом c перпендикулярен плоскости, в которой расположены a и b, и расположен так, чтобы наименьшее вращение от a к b выполнялось против часовой стрелки (с точки зрения конца вектора).

Формула векторного произведения

Произведение векторов a = {a_x; a_y, a_z} и b = {b_x; b_y, b_z} вычисляется с помощью одной из формул ниже:

Свойства векторного произведения

1. Векторное произведение двух ненулевых векторов равняется нулю тогда и только тогда, когда эти векторы являются коллинеарными.

[a, b] = 0, если

a || b

2. Модуль векторного произведения двух векторов равняется площади параллелограмма, образованного этими векторами.

S_парал. = |a x b|

3. Площадь треугольника, образованного двумя векторами, равняется половине их векторного произведения.

S_Δ = ¹/₂ · |a x b|

4. Вектор, являющийся векторным произведением двух других векторов, перпендикулярен им.

c ⟂ a, c ⟂ b.

5. a x b = –b x a

6. (m a) x a = a x (m b) = m (a x b)

7. (a + b) x c = a x c + b x c

Пример задачи

Вычислим векторное произведение a = {2; 4; 5} и b = {9; -3; 1}.

Решение:

Ответ: a x b = {19; 43; -42}.

Источник

Определение
векторного произведения.

Определение.
Векторным произведением
двух векторов
иназывается вектор,
удовлетворяющий следующим условиям:

а) вектор
перпендикулярен плоскости векторов
ии направлен так, что тройка векторов,,правая;

б) длина вектора

численно равна площади

Рис. 2.19
параллелограмма,
построенного на векторах
и,
т.е.,
где—
угол между векторамии(рис. 2.19).

Очевидно, что
,,,,,.

Пример 11.
Проверить справедливость равенства
.

Решение.
,,

Метод Жуковского.

Рассмотрим метод
Жуковского
построения вектора
.

Пусть угол между
векторами
иравен.

Векторы
иприложим к общему началу(рис. 2.20).
Через точкуперпендикулярно векторупроведем плоскость.
Из конца вектораопустим перпендикуляр на плоскость.

Точку пересечения этого перпендикуляра
и плоскости обозначим через.
Проведем в плоскостивектори построим вектор.

Рис. 2.20
Покажем,
что вектор.

а) Из построения
следует, что вектор
перпендикулярен
векторам,,
и векторы,,образуют правую тройку.

б)
.

Из а) и б) следует,
что
.

Если проекцию
вектора
на плоскостьобозначить
через,
то

Свойства векторного
произведения.

Векторное
произведение двух векторов обладает
следующими свойствами:

1)
(векторное произведениеантикоммутативно,
т.е. при перестановке сомножителей
направление вектора меняется на
противоположное, при этом его модуль
остаётся неизменным).

Это свойство
следует из определения векторного
произведения. Если тройка векторов
правая, то тройка—
левая.

2)
(ассоциативный
закон).
Это
свойство легко доказывается из определения
векторного произведения.

3)
(дистрибутивный
закон.)
►.◄

4)
.
Это свойство следует из определения
векторного произведения, а именно из
того, что модуль векторного произведения
равен площади параллелограмма,
построенного на векторахи.
Это свойство дает возможность записать
в удобной форме
параллельность двух векторов.

Например,
означает, что векторколлинеарен биссектрисе первого
координатного угла.

Векторное
произведение в координатной форме.

Пользуясь свойствами
векторного произведения и равенствами
,,,,,,
вычислим

,
т.е.
или.

Применение
векторного произведения.

Векторное
произведение
векторов
иприменяется:

для нахождения
площади параллелограмма, построенного
на векторах
и;

для нахождения
площади треугольника, построенного на
векторах
и;

для нахождения
синуса угла между векторами
и;

для нахождения
вектора, перпендикулярного векторам
и.

1) Площадь
параллелограмма, построенного на
векторахи,
может быть вычислена по формуле,
где—
угол между векторамии.

Замечание.
Если
и,
тои.
Отсюда следует, чтомодуль
определителя второго порядка
численно равен площади параллелограмма,
построенного на векторах
и.

2) Площадь
треугольника, построенного на векторахи,
равна половине площади параллелограмма,
построенного на этих же векторах, т.е.,
где—
угол между векторамии.

3) Синус угла между
векторами
иможет быть вычислен по формуле.

4) Вектор
перпендикулярен векторуи вектору.

Замечание.
Векторное произведение может быть
использовано при решении системы
линейных однородных уравнений вида
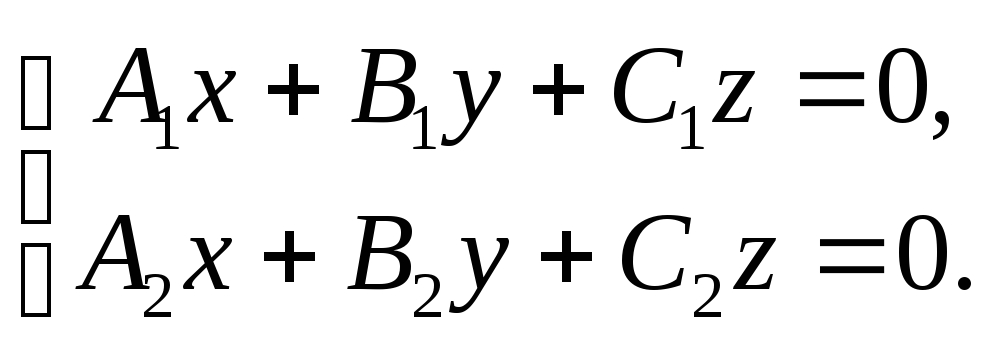
Если векторыинеколлинеарны, тоявляется
решением исходной системы.