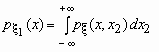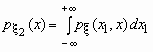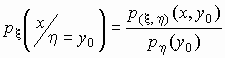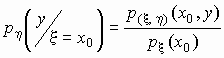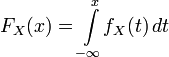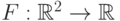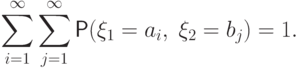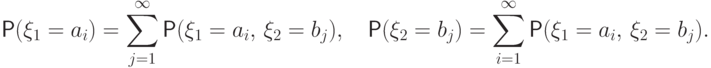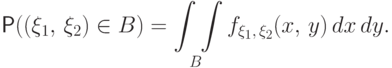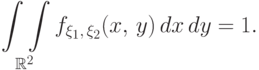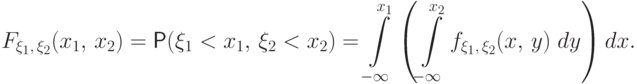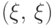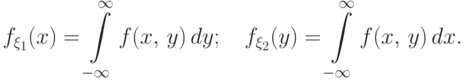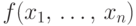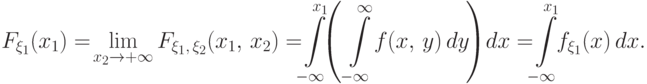Как найти вектор совместного распределения

Совместная функция распределения двух случайных величин и её свойства. Совместное распределение двух дискретных случайных величин.

Функцией
распределения случайного вектора

или
совместным
распределением случайных величин

называется
функция, определенная равенством

где

По
известной многомерной функции

можно
найти распределение каждой из компонент

Например,
если

—
двумерная случайная величина, имеющая
совместное распределение

,
то распределения компонент

и

вычисляются
соответственно по формулам:

В
дальнейшем будем рассматривать двумерные
случайные векторы.

Случайный
вектор

называется
непрерывным
случайным вектором,
если существует такая неотрицательная
функция

,
что для любого прямоугольника W на
плоскости

вероятность
события

равна

Функция

в
этом случае называется совместной
плотностью распределения.

Легко
показать, что

.

Если

—
совместная плотность распределения
двумерного случайного вектора

,
то плотности распределения его компонент
определяются равенствами:

Если

—
дискретный случайный вектор, то совместным
распределением случайных величин

и

чаще
всего называют таблицу вида

	y₁	y₂	…	y_m
x₁	p₁₁	p₁₂	…	p₁_m
x₂	p₁₂	p₁₂	…	p₂_m
…	…	…	p_ij	…
x_n	p_n1	p_n2	…	p_nm

где

По
этой таблице можно найти распределения

компонент
x и h . Они вычисляются по формулам:

Абсолютно непрерывные совместные распределения двух случайных величин. Совместная плотность распределения, её свойства.

Условные плотности распределения.

Условной
плотностью распределения случайной
величины x при условии, что случайная
величина h принимает значение h = y₀,
называется функция переменной x,
определяемая формулой

Аналогично,
условной
плотностью распределения случайной
величины h при условии, что случайная
величина x принимает значение x = x₀,
называется функция переменной y,
определяемая формулой

Распределения n-мерных случайных векторов. Дискретные распределения, абсолютно непрерывные распределения.

Дискретные
распределения

Если
случайная величина

дискретна,
то есть её распределение однозначно
задаётся функцией
вероятности

то
функция распределения

этой
случайной величины кусочно-постоянна
и может быть записана как:

Эта
функция непрерывна во всех точках

,
таких что

,
и имеет разрыв первого рода в точках

.

Абсолютно
непрерывные распределения

Распределение

называется
абсолютно
непрерывным, если существует
неотрицательная почти
всюду (относительно меры
Лебега) функция

,
такая что:

Функция

называется
плотностью
распределения. Известно, что функция
абсолютно непрерывного распределения
непрерывна, и, более того, если

,
то

,
и

Распределение функции от случайной величины. Примеры.

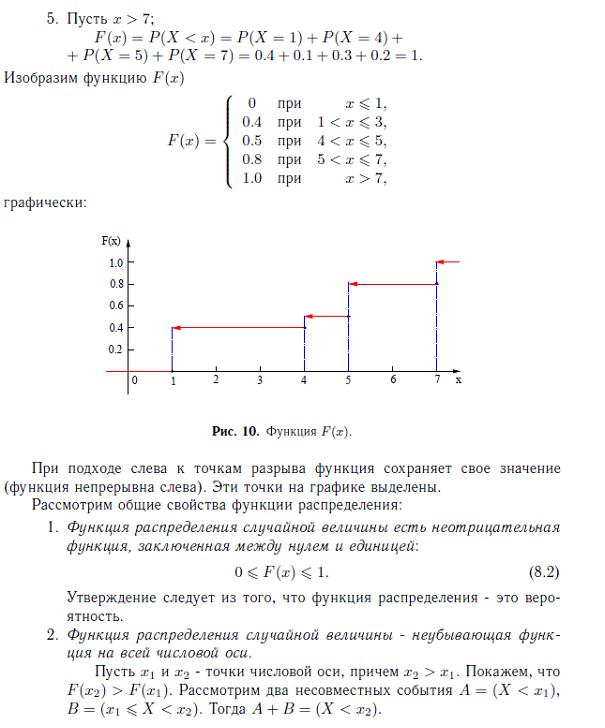
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

Случайные векторы
Свойства функции распределения случайного вектора
Двумерные дискретные случайные векторы
Двумерные абсолютно непрерывные случайные векторы
Сходимость случайных величин

Случайные векторы

Рассматриваем случайное явление и вероятностное пространство, которое отвечает этому случайному явлению. Пусть – случайные величины, связанные с этим случайным явлением. Совместное распределение этих случайных величин будем называть случайным вектором и обозначать
Определение. Функцией распределения случайного вектора называется функция n переменных

Свойства функции распределения случайного вектора

1. Функция распределения непрерывна слева и монотонно неубывающая по всем аргументам.
2.
3.
4.
5. Функция распределения компоненты является границей функции распределения случайного вектора для всех
Определение. Случайный вектор называется дискретным, если он приобретает конечное или счетное количество значений.
Очевидно, что каждая компонента этого случайного вектора является дискретной случайной величиной.
Дискретный случайный вектор определяется значениями, которые он приобретает, и вероятностями, с которыми приобретаются эти значения.
Далее будем считать, что компонента ξ₁ приобретает значения компонента ξ₁ – компонента ξ_n — а

Определение. Случайный вектор называется абсолютно непрерывным, если существует n-мерная действительная функция которую мы будем называть плотностью абсолютно непрерывного случайного вектора такая, для которой выполняется равенство

Определение. Компоненты случайного вектора называются независимыми, если выполняется равенство

Если случайный вектор является дискретным, то условие независимости конкретизируется так:

Для абсолютно непрерывного случайного вектора условие независимости является таким:

Пусть – некоторая функция. Математическое ожидание случайной величины равно

Если случайный вектор является дискретным и

если вектор ξ – абсолютно непрерывный.
Определение. Ковариантной матрицей случайного вектора называют числовую матрицу К размера вида

где

и если то величина называется ковариацией.
Понятно, что на диагоналях стоят дисперсии соответствующих компонент.
Легко видеть, что

Доказательство.

Коэффициентом корреляции компонент является число

корреляционной матрицей является матрица

Детальнее свойства случайных векторов рассмотрим для двумерного случая.

Двумерные дискретные случайные векторы

Рассматриваем двумерный случайный вектор  Предположим, что компонента ξ приобретает значения компонента η приобретает значения и Распределение двумерного дискретного вектора удобно представлять в виде таблицы:

Очевидно, что
где
Пример. Дано распределение двумерного случайного вектора

Найти
Решение. Поскольку

то

Пример. Дано распределение двумерного случайного вектора

Найти
Решение. Очевидно, что

Распределение компонент находится так:

Далее определяем
Пример. Дано распределение двумерного случайного вектора

Найти распределение компонент.
Решение.

Для контроля целесообразно сделать проверку. Известно, что Убедимся, что это действительно так.

Следовательно, распределение компоненты ξ является таким:

Переходим к компоненте η:

Проверка:
Следовательно, распределение компоненты η является таким:

Заметим, что распределение компонент можно находить значительно проще.
Запишем еще раз распределение вектора, добавив одну строку снизу и один столбец справа. Далее находим суммы элементов по строкам и записываем эти суммы в последний столбец, а также находим суммы элементов по столбцах и значения найденных сумм записываем в нижнюю строку. Полученные суммы являются значениями вероятностей. Например, сумма верхней строки является вероятностью сумма второй строки является вероятностью соответственно сумма третьей строки — Для того, чтобы найти нужно найти сумму элементов второго столбца и т. д.

Определение. Условным распределением компоненты ξ при условии, что называют совокупность значений

Аналогично, условным распределением компоненты η при условии, что называют совокупность значений

Условным математическим ожиданием компоненты ξ при условии, что называют число

Аналогично, условным математическим ожиданием компоненты η при условии, что называют число

Пример. Дано распределение дискретного случайного вектора

Найти условное распределение компоненты ξ при условии, что условное распределение компоненты η при условии, что условное математическое ожидание компоненты ξ при условии, что условное математическое ожидание компоненты η при условии, что
Решение.
Значение вероятности находим как сумму элементов второго справа столбца.

Далее

Следовательно, условное распределение компоненты ξ при условии, что будет таким:

Сразу находим условное математическое ожидание компоненты ξ при условии, что

Переходим к нахождения условного распределения компоненты η при условии, что

Запишем это условное распределение в виде таблицы

Далее найдем условное математическое ожидание.

Условие независимости для двумерного дискретного случайного вектора является такой:

для произвольных
Пример. Дано распределение двумерного случайного вектора

Проверить, являются ли независимыми компоненты этого вектора.
Решение.

Очевидно, условие не выполняется. ■
Функция распределения для двумерного случайного вектора находится так. По определению имеем

Очевидно, что функция распределения является кусочно-постоянной на отрезках Поэтому ее можно представить в виде таблицы, которая содержит на одну строку больше чем таблица распределения этого случайного вектора и на один столбец больше чем таблица распределения этого случайного вектора.
Поскольку случайный вектор не содержит значений меньших, чем и , то элементы в крайнем левом столбце и верхней строке будут нулевыми. Далее алгоритм заполнения таблицы будет таким: в строке и столбце будет записана сумма вероятностей, которые отвечают
Пример. Дано распределение двумерного случайного вектора .

Найти функцию распределения.
Решение. Поскольку наименьшим значением среди является 2, а среди является — 1, то вероятность того, что случайный вектор будет приобретать меньшие значения, равно 0. Поэтому слева и сверху мы проставляем нули.
Осталось заполнить 4 строки и 3 столбца. Обозначим значения незаполненных клеточек через  Очевидно, что

Пусть — некоторая кусочно-непрерывная функция. Математическое ожидание случайной функции находится так:

В частности ковариация находится по формуле

де

Коэффициент корреляции

Пример. Найти ковариацию и коэффициент корреляции случайного вектора

Решение. Сначала найдем распределение компонент.

Далее находим

И, наконец, находим

Переходим к коэффициенту корреляции.

Запишем ковариационную и корреляционную матрицы

Заметим, что если компоненты случайного вектора является независимыми, то ковариация, а следовательно, и коэффициент корреляции равняются нулю. Наоборот не всегда правильно.
Пример случайного вектора, у которого ковариация равна нулю и коэффициенты зависимы.

Сначала покажем, что ковариация равно нулю.

Далее проверяем компоненты на независимость

Следовательно,  а поэтому компоненты являются зависимыми. ■
Заметим, что если ковариация является ненулевой, то компоненты зависимы.

Двумерные абсолютно непрерывные случайные векторы

Рассматриваем двумерный абсолютно непрерывный вектор с плотностью Плотность компонент находят так:

Пример. Плотность двумерного случайного вектора равна

где область D ограничена линиями    Найти плотность компонент.
Решение. Сначала изобразим область D.

Вероятность попадания в область находится из формулы

Очевидно, что
Пример. Дана плотность абсолютно непрерывного случайного вектора

Найти      если область D ограничена линиями
Решение. Сначала найдем неизвестную константу Для этого графически изобразим область D

Сначала найдем  Снова графически изобразим область

Далее находим вероятность Изобразим графически область

Переходим к нахождению вероятности  Как и в предыдущих случаях сначала изображаем графически область интегрирования

И, наконец находим вероятность Изображаем графически область интегрирования

Как видно из рисунка, сначала нужно найти точку пересечения прямых

Условие независимости компонент проверяется так:

Пример. Дана плотность случайного вектора

где область D ограничена линиями     Найти и проверить, являются ли компоненты независимыми.
Решение. Прежде всего изобразим область D.

Следовательно,

Проверяем независимость компонент. Для этого находим их плотности

Следовательно,

Переходим к нахождению плотности η

Находим произведение в области D и проверяем, равно ли оно

В области D имеем
Следовательно, условие независимости не выполняется. ■
Пример. Известно, что компоненты случайного вектора является независимыми. Их плотности равняются:

Найти совместную плотность случайного вектора .
Решение. Из условия независимости
Поэтому

где область D ограничена линиями
Функция распределения находится по определению

Пример. Дана плотность абсолютно непрерывного случайного вектора

Найти функцию распределения, если область D ограничена линиями
Решение. Прежде всего находим неизвестную константу.

По определению имеем

Аналитический вид функции распределения зависит от того, где находится точка
В частности:
1. Пусть  или

Тогда, как видно из рисунка

2.

Тогда

3. Далее рассмотрим точки для которых выполняются условия

Очевидно аналитический вид функции распределения в этом случае будет таким:

4. Далее рассматриваем множество точек для которых выполняются условия

5. Наконец, если   тогда

Условная плотность находится по формуле

соответственно, условная плотность

Пример. Дана плотность абсолютно непрерывного случайного вектора

Найти неизвестную константу условные плотности   если область D ограничена линиями
Решение. Сначала изображаем область D и находим неизвестную постоянную.

Далее находим распределение составляющих

Следовательно, условия плотности будут такими:

Математическое ожидание от функции компонент вектора равно

Пример. Дана плотность абсолютно непрерывного случайного вектора

Найти ковариацию, коэффициент корреляции, ковариационную матрицу, корреляционную матрицу, если область D ограничена линиями
Решение. Сначала находим неизвестную константу

Переходим к ковариации

Следовательно,

Далее находим дисперсии

Ковариационная матрица является такой:

Корреляционная матрица имеет вид

Сходимость случайных величин

Определение. Рассматриваем последовательность случайных величин Эта последовательность совпадает со случайной величиной ξ, если

или

и это обозначают
Определение. Последовательность случайных величин сходится к случайной величине ξ в среднеквадратичном, если и

Это обозначают
Теорема. Если и — непрерывная функция, то

Закон больших чисел
Рассматриваем последовательность случайных величин Для нее выполняется закон больших чисел (ЗБЧ) или эта последовательность удовлетворяет закон больших чисел, если

Сходимость по вероятности всегда проверять нет смысла, потому что есть теоремы, которые являются достаточными условиями для выполнения закона больших чисел.

Теорема Чебышева. Пусть дана последовательность независимых случайных величин для которых существуют Если существует константа С такая, что то для этой последовательности выполняется закон больших чисел.

Теорема Хинчина. Пусть дана последовательность независимых одинаково распределенных случайных величин для которых существует математическое ожидание тогда для этой последовательности выполняется закон больших чисел.

Теорема Маркова. Пусть дана последовательность произвольных случайных величин для которых существуют и выполняется равенство

Тогда для этой последовательности выполняется закон больших чисел.

Теорема Бернулли. В схеме независимых испытаний Тут μ — относительная частота появления события, р — вероятность появления события в одном испытании.

Пример. Дана последовательность независимых случайных величин

Проверить, выполняется ли для этой последовательности закон больших чисел.
Решение. Для проверки используем теорему Чебышева. Независимость дана в условии.

Очевидно, что

Поэтому для данной последовательности выполняются условия теоремы Чебышева, а следовательно, выполняется закон больших чисел. ■
Пример. Дана последовательность независимых случайных величин, которые имеют распределение Коши. Проверить, выполняется ли для этой последовательности закон больших чисел .
Решение. Поскольку для распределения Коши не существует математического ожидания, то речь не идет о выполнении закона больших чисел. ■

Лекции:

Биномиальный закон
Равномерный закон
Закон Пуассона
Показательный закон
Нормальный закон
Теория вероятности: формулы, примеры
Схема Бернулли теория вероятности
Формула Пуассона теория вероятности
Формула лапласа
Статистическая вероятность

Источник

Двумерная непрерывная случайная величина

Ранее мы разобрали примеры решений задач для одномерной непрерывной случайной величины. Перейдем к более сложному случаю — двумерной непрерывной случайной величине $(X,Y)$ (или двумерному вектору). Кратко выпишем основы теории.

Понравилось? Добавьте в закладки

Система непрерывных случайных величин: теория

Двумерная непрерывная СВ задается своей функцией распределения $F(x,y)=P(Xlt x, Ylt y)$, свойства которой аналогичны свойствам одномерной ФР. Эта функция должна быть непрерывна, дифференцируема и иметь вторую смешанную производную, которая будет как раз плотностью распределения вероятностей системы непрерывных случайных величин:

$$
f(x,y)= frac{partial ^2}{partial x partial y} F(x,y)
$$

Зная плотность совместного распределения, можно найти одномерные плотности для $X$ и $Y$:

$$
f(x)= int_{-infty}^{infty} f(x,y) dy, quad f(y)= int_{-infty}^{infty} f(x,y) dx.
$$

Вероятность попадания случайного вектора в прямоугольную область можно вычислить как двойной интеграл от плотности (по этой области) или через функцию распределения:

$$P(x_1 le X le x_2, y_1 le Y le y_2) = F(x_2, y_2)-F(x_1, y_2)-F(x_2, y_1)+F(x_1, y_1).$$

Как и для случая дискретных двумерных СВ вводится понятие условного закона распределения, плотности которых можно найти так:

$$
f(x|y)=f_y(x)= frac{f(x,y)}{f(y)}, quad f(y|x)=f_x(y)= frac{f(x,y)}{f(x)} $$

Если для всех значений $(x,y)$ выполняется равенство

$$f(x,y) =f(x)cdot f(y),$$

то случайные величины $X, Y$ называются независимыми (их условные плотности распределения совпадают с безусловными). Для независимых случайных величин выполняется аналогичное равенство для функций распределений:

$$F(x,y) =F(x)cdot F(y).$$

Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:

$$
cov (X,Y)=M(XY)-M(X)M(Y)= int_{-infty}^{infty}int_{-infty}^{infty} (x-M(X))(y-M(Y)) f(x,y) dxdy, \
r_{XY} = frac{cov(X,Y)}{sqrt{D(X)D(Y)}}.
$$

В этом разделе мы приведем примеры задач с полным решением, где используются непрерывные двумерные случайные величины (системы случайных величин).

Примеры решений

Задача 1. Дана плотность распределения вероятностей системы
$$
f(x)=
left{
begin{array}{l}
C, mbox{ в треугольнике} O(0,0), A(4,0), B(4,1)\
0, mbox{ в остальных точках} \
end{array}
right.
$$
Найти:
$C, rho_1(x), rho_2(y), m_x, m_y, D_x, D_y, cov(X,Y), r_{xy}, F(2,10), M[X|Y=1/2]$.

Задача 2. Дана плотность распределения $f(x,y)$ системы $X,Y$ двух непрерывных случайных величин в треугольнике АВС.
1.1. Найдите константу с.
1.2. Найдите $f_X(x), f_Y(y)$ — плотности распределения с.в. Х и с.в. Y.
Выясните, зависимы или нет с.в. Х и Y. Сформулируйте критерий независимости системы непрерывных случайных величин.
1.3. Найдите математическое ожидание и дисперсию с.в. Х и с.в. Y. Поясните смысл найденных характеристик.
1.4. Найдите коэффициент корреляции с.в. Х и Y. Являются ли случайные величины коррелированными? Сформулируйте свойства коэффициента корреляции.
1.5. Запишите уравнение регрессии с.в. Y на Х и постройте линию регрессии в треугольнике АВС.
1.6. Запишите уравнение линейной среднеквадратичной регрессии с.в. Y на Х и постройте эту прямую в треугольнике АВС. $$ f(x,y)=csqrt{xy}, quad A(0;0), B(-1;-1), C(-1;0) $$

Задача 3. Интегральная функция распределения случайного вектора (X,Y):
$$
F(x)=
left{
begin{array}{l}
0, mbox{ при } x le 0 mbox{ или } yle 0\
(1-e^{-2x})(1-e^{-3y}), mbox{ при } x gt 0 mbox{ и } ygt 0\
end{array}
right.
$$
Найти центр рассеивания случайного вектора.

Задача 4. Плотность совместного распределения непрерывной двумерной случайной величины (Х, У)
$$f(x,y)=C e^{-x^2-2xy-4y^2}$$
Найти:
а) постоянный множитель С;
б) плотности распределения составляющих;
в) условные плотности распределения составляющих.

Задача 5. Задана двумерная плотность вероятности системы двух случайных величин: $f(x,y)=1/2 sin(x+y)$ в квадрате $0 le x le pi/2$, $0 le y le pi/2$, вне квадрата $f(x,y)=0$. Найти функцию распределения системы (X,Y).

Задача 6. Определить плотность вероятности, математические ожидания и корреляционную матрицу системы случайных величин $(X,Y)$, заданных в интервалах $0 le x le pi/2$, $0 le y le pi/2$, если функция распределения системы $F(x,y)=sin x sin y$.

Задача 7. Плотность вероятности системы случайных величин равна
$$f(x,y) = c(R-sqrt{x^2+y^2}), quad x^2+y^2 lt R^2.$$
Определить:
А) постоянную $c$;
Б) вероятность попадания в круг радиуса $alt R$, если центры обоих кругов совпадают с началом координат.

Задача 8. Совместная плотность вероятности системы двух случайных величин X и Y
$$f(x,y)=frac{c}{36+9x^2+4y^2+x^2y^2}.$$
Найти величину $с$; определить законы распределения $F_1(x)$, $F_2(y)$, $f_1(x)$, $f_2(y)$, $f(x/y)$; построить графики $F_1(x)$, $F_2(y)$; вычислить моменты $m_x$, $m_y$, $D_x$, $D_y$, $K_{xy}$.

Мы отлично умеем решать задачи по теории вероятностей

Решебник по теории вероятности онлайн

Больше 11000 решенных и оформленных задач по теории вероятности:

Источник

Аннотация: Совместные распределения двух и более
случайных величин. Функция распределения случайного вектора.
Дискретные и абсолютно непрерывные совместные распределения.
Связь плотности совместного распределения и маргинальных плотностей.
Роль совместного распределения. Независимость случайных величин

Совместное распределение

Пусть случайные величины заданы на одном
вероятностном пространстве 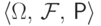langleOmega,,mathcal
F,,Probrangle .

Определение 28.
Функция

$F_{xi_1,,ldots,,xi_n}(x_1,,dots,,x_n)= Prob(xi_1<x_1,,dots,,xi_n<x_n)$

называется
функцией распределения вектора 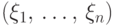или
функцией совместного распределения случайных величин .

Перечислим свойства функции совместного распределения.
Для простоты обозначений ограничимся
вектором 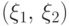из двух величин.

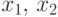
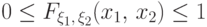
(F0) Для любых верно неравенство: $0le F_{xi_1,,xi_2}(x_1,,x_2)le 1$ .

(F1) 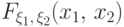$F_{xi_1,,xi_2}(x_1,,x_2)$ не убывает по каждой
координате
вектора .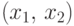

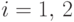
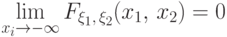
(F2) Для любого i=1,,2 существует $limlimits_{x_ito-infty}F_{xi_1,,xi_2}(x_1,,x_2)=0$ .
Существует двойной предел 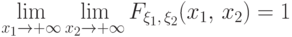$limlimits_{x_1to+infty}limlimits_{x_2to+infty}F_{xi_1,,xi_2}(x_1,,x_2)=1$ .

(F3) Функция 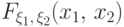$F_{xi_1,,xi_2}(x_1,,x_2)$ по каждой
координате
вектора 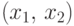непрерывна слева.

(F4) Чтобы по функции совместного распределения восстановить функции
распределения 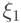xi_1 и xi_2 в отдельности, следует
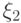
устремить мешающую
переменную к +infty :

$begin{equation} limlimits_{x_1to+infty}F_{xi_1,,xi_2}(x_1,,x_2)= F_{xi_2}(x_2),quad limlimits_{x_2to+infty}F_{xi_1,,xi_2}(x_1,,x_2)= F_{xi_1}(x_1). end{equation}$

(
14)

Доказательство всех этих свойств совершенно аналогично одномерному случаю.
Но теперь свойств (F0)-(F3) не хватает для описания
класса функций совместного распределения. Иначе говоря,
выполнение этих свойств для некоторой функции
не гарантирует, что эта функция является функцией распределения
некоторого случайного вектора.

Упражнение.
Доказать, что функция

$F(x_1,, x_2)= begin{cases} 0, & text{ если }, x_1le 0, text{ или }, x_2le 0, text{ или }, x_1+x_2le 1, cr 1, & text{ если одновременно }, x_1>0,, x_2>0,, x_1+x_2>1 end{cases}$

удовлетворяет всем свойствам (F0)-(F3), но
не является функцией распределения никакого вектора
хотя бы потому, что, найдись такой вектор, найдется и прямоугольник , «вероятность» попасть в
который
(вычисленная с помощью этой якобы «функции распределения»)
отрицательна: .

Легко убедиться, что
вероятность вектору 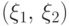попасть
в прямоугольник по функции
распределения этого вектора вычисляется так: .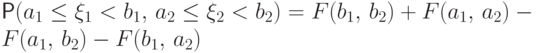

Дополнительно к свойствам (F0)-(F3) от функции требуют
неотрицательности этого выражения
(при любых 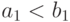a_1<b_1 , a_2<b_2 ).

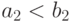
Типы многомерных распределений

Ограничимся рассмотрением двух типичных случаев: когда
совместное
распределение координат случайного вектора
либо дискретно, либо абсолютно непрерывно. Заметим, что сингулярные совместные
распределения тоже не являются редкостью, в отличие от одномерного случая:
стоит бросить точку наудачу на отрезок на плоскости, и мы получим
сингулярное совместное распределение ( доказать ).

Определение 29.
Случайные величины 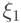xi_1 , xi_2 имеют
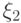
дискретное совместное распределение,
если существует конечный или счетный
набор пар чисел 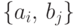${a_i,,b_j}$ такой, что

$sumlimits_{i=1}^{infty}sumlimits_{j=1}^infty Prob(xi_1=a_i,;xi_2=b_j)=1.$

Таблицу, на пересечении -й строки и -го столбца которой стоит
вероятность 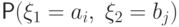, называют
таблицей совместного распределения случайных величин 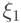xi_1 и xi_2 .

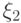
Таблицы распределения каждой из случайных величин 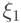xi_1 , xi_2 в отдельности (таблицы частных,
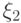
или маргинальных распределений)
восстанавливаются по таблице совместного
распределения с помощью формул

$Prob(xi_1=a_i)=sumlimits_{j=1}^infty Prob(xi_1=a_i,,xi_2=b_j),quad Prob(xi_2=b_j)=sumlimits_{i=1}^infty Prob(xi_1=a_i,,xi_2=b_j).$

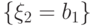
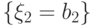
Так, первое равенство следует из того, что набор ${xi_2=b_1}$ , ${xi_2=b_2}$ , dots
есть полная группа событий,
и поэтому событие 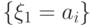${xi_1=a_i}$ раскладывается в объединение
попарно несовместных
событий:

${xi_1=a_i}=bigcup_{j=1}^infty {xi_1=a_i,,xi_2=b_j}.$

Определение 30.
Случайные величины 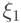xi_1 , xi_2
имеют абсолютно непрерывное совместное распределение,
если существует неотрицательная функция $f_{xi_1,,xi_2}(x,,y)$
такая, что для любого множества ${Binmathfrakmathfrak {B}(mathbb R^2)}$ имеет место
равенство

$Prob((xi_1,,xi_2)in B)= mathop{intint}limits_{!!B} f_{xi_1,,xi_2}(x,,y),dx,dy.$

Если такая функция 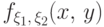$f_{xi_1,,xi_2}(x,,y)$ существует, она
называется
плотностью совместного распределения случайных
величин .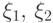

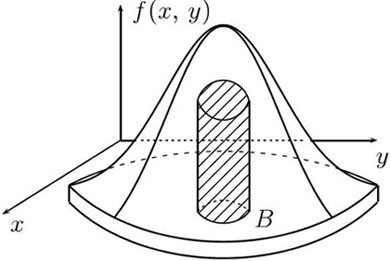
Рис.
8.1.

Достаточно, если двойной интеграл по множеству читатель
будет понимать
как объем области под графиком функции $f_{xi_1,,xi_2}(x,,y)$
над множеством в плоскости переменных (x,, y) ,
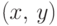
как показано на

рис.
8.1.

Плотность совместного распределения обладает такими же свойствами, как
и плотность распределения одной случайной величины:

(f1) неотрицательность: 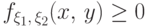$displaystyle f_{xi_1,,xi_2}(x,,y)ge 0$ для любых

(f2) нормированность:

$displaystylemathop{intint}limits_{!mathbb R^2} f_{xi_1,,xi_2}(x,,y),dx,dy=1.$

Справедливо и обратное: любая функция, обладающая этими свойствами,
является плотностью
некоторого совместного распределения. Доказательство этого факта ничем не
отличается от одномерного случая.

Если случайные величины 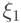xi_1 , xi_2
имеют абсолютно непрерывное совместное распределение,
то для любых 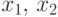имеет место равенство

$F_{xi_1,,xi_2}(x_1,,x_2)=Prob(xi_1<x_1,,xi_2<x_2)= intlimits_{-infty}^{x_1}left(intlimits_{-infty}^{x_2} f_{xi_1,,xi_2}(x,,y);dyright)dx.$

Если совместное распределение абсолютно непрерывно, то
по функции совместного распределения его плотность находится как
смешанная частная производная: 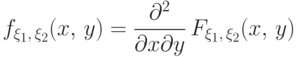$displaystyle f_{xi_1,,xi_2}(x,,y)=frac{partial^2}{partial xpartial y}, F_{xi_1,,xi_2}(x,,y)$ для почти всех (x,, y) .

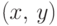
Из существования плотностей 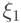xi_1 и xi_2 не
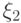
следует абсолютная непрерывность
совместного распределения этих случайных величин. Например, вектор
принимает значения только на диагонали в и уже поэтому не
имеет плотности
распределения (его распределение сингулярно).
Обратное же свойство, как показывает следующая теорема, всегда верно: если
совместное распределение абсолютно непрерывно,
то и частные распределения тоже таковы.

Теорема 24.
Если случайные величины 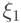xi_1 и xi_2 имеют
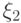
абсолютно непрерывное
совместное распределение с плотностью 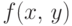f(x,,y) ,
то 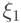xi_1 и xi_2 в отдельности также имеют абсолютно
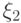
непрерывное распределение с плотностями:

$f_{xi_1}(x)=intlimits_{-infty}^infty f(x,,y),dy; quad f_{xi_2}(y)=intlimits_{-infty}^infty f(x,,y),dx.$

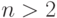
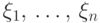
Для n>2 плотности случайных величин xi_1,, dots,,
xi_n по
плотности их совместного распределения
находятся интегрированием функции по всем «лишним»
координатам.

Доказательство.
Например, в силу равенств (14),

$F_{xi_1}(x_1) =! limlimits_{x_2to+infty}F_{xi_1,,xi_2}(x_1,,x_2)= !!intlimits_{-infty}^{x_1}!!!left(,intlimits_{-infty}^{infty} !f(x,,y),dy!right)!dx=!!intlimits_{-infty}^{x_1}!!f_{xi_1}(x),dx.$

Аналогично устанавливается и справедливость второго равенства.

Источник

From Wikipedia, the free encyclopedia

Many sample observations (black) are shown from a joint probability distribution. The marginal densities are shown as well.

Given two random variables that are defined on the same probability space,^[1] the joint probability distribution is the corresponding probability distribution on all possible pairs of outputs. The joint distribution can just as well be considered for any given number of random variables. The joint distribution encodes the marginal distributions, i.e. the distributions of each of the individual random variables. It also encodes the conditional probability distributions, which deal with how the outputs of one random variable are distributed when given information on the outputs of the other random variable(s).

In the formal mathematical setup of measure theory, the joint distribution is given by the pushforward measure, by the map obtained by pairing together the given random variables, of the sample space’s probability measure.

In the case of real-valued random variables, the joint distribution, as a particular multivariate distribution, may be expressed by a multivariate cumulative distribution function, or by a multivariate probability density function together with a multivariate probability mass function. In the special case of continuous random variables, it is sufficient to consider probability density functions, and in the case of discrete random variables, it is sufficient to consider probability mass functions.

Examples[edit]

Draws from an urn[edit]

Each of two urns contains twice as many red balls as blue balls, and no others, and one ball is randomly selected from each urn, with the two draws independent of each other. Let and be discrete random variables associated with the outcomes of the draw from the first urn and second urn respectively. The probability of drawing a red ball from either of the urns is 2/3, and the probability of drawing a blue ball is 1/3. The joint probability distribution is presented in the following table:

	A=Red	A=Blue	P(B)
B=Red	(2/3)(2/3)=4/9	(1/3)(2/3)=2/9	4/9+2/9=2/3
B=Blue	(2/3)(1/3)=2/9	(1/3)(1/3)=1/9	2/9+1/9=1/3
P(A)	4/9+2/9=2/3	2/9+1/9=1/3

Each of the four inner cells shows the probability of a particular combination of results from the two draws; these probabilities are the joint distribution. In any one cell the probability of a particular combination occurring is (since the draws are independent) the product of the probability of the specified result for A and the probability of the specified result for B. The probabilities in these four cells sum to 1, as with all probability distributions.

Moreover, the final row and the final column give the marginal probability distribution for A and the marginal probability distribution for B respectively. For example, for A the first of these cells gives the sum of the probabilities for A being red, regardless of which possibility for B in the column above the cell occurs, as 2/3. Thus the marginal probability distribution for gives ‘s probabilities unconditional on , in a margin of the table.

Coin flips[edit]

Consider the flip of two fair coins; let and be discrete random variables associated with the outcomes of the first and second coin flips respectively. Each coin flip is a Bernoulli trial and has a Bernoulli distribution. If a coin displays «heads» then the associated random variable takes the value 1, and it takes the value 0 otherwise. The probability of each of these outcomes is 1/2, so the marginal (unconditional) density functions are

{displaystyle P(A)=1/2quad {text{for}}quad Ain {0,1};}

{displaystyle P(B)=1/2quad {text{for}}quad Bin {0,1}.}

The joint probability mass function of and defines probabilities for each pair of outcomes. All possible outcomes are

{displaystyle (A=0,B=0),(A=0,B=1),(A=1,B=0),(A=1,B=1).}

Since each outcome is equally likely the joint probability mass function becomes

{displaystyle P(A,B)=1/4quad {text{for}}quad A,Bin {0,1}.}

Since the coin flips are independent, the joint probability mass function is the product
of the marginals:

{displaystyle P(A,B)=P(A)P(B)quad {text{for}}quad A,Bin {0,1}.}

Rolling a die[edit]

Consider the roll of a fair die and let A=1 if the number is even (i.e. 2, 4, or 6) and A=0 otherwise. Furthermore, let B=1 if the number is prime (i.e. 2, 3, or 5) and B=0 otherwise.

	1	2	3	4	5	6
A	0	1	0	1	0	1
B	0	1	1	0	1	0

Then, the joint distribution of and , expressed as a probability mass function, is

${displaystyle mathrm {P} (A=0,B=0)=P{1}={frac {1}{6}},quad quad mathrm {P} (A=1,B=0)=P{4,6}={frac {2}{6}},}$

${displaystyle mathrm {P} (A=0,B=1)=P{3,5}={frac {2}{6}},quad quad mathrm {P} (A=1,B=1)=P{2}={frac {1}{6}}.}$

These probabilities necessarily sum to 1, since the probability of some combination of and occurring is 1.

Marginal probability distribution[edit]

If more than one random variable is defined in a random experiment, it is important to distinguish between the joint probability distribution of X and Y and the probability distribution of each variable individually. The individual probability distribution of a random variable is referred to as its marginal probability distribution. In general, the marginal probability distribution of X can be determined from the joint probability distribution of X and other random variables.

If the joint probability density function of random variable X and Y is $f_{{X,Y}}(x,y)$ , the marginal probability density function of X and Y, which defines the marginal distribution, is given by:

${displaystyle f_{X}(x)=int f_{X,Y}(x,y);dy}$

${displaystyle f_{Y}(y)=int f_{X,Y}(x,y);dx}$

where the first integral is over all points in the range of (X,Y) for which X=x and the second integral is over all points in the range of (X,Y) for which Y=y.^[2]

Joint cumulative distribution function[edit]

For a pair of random variables X,Y , the joint cumulative distribution function (CDF) ${displaystyle F_{XY}}$ is given by^[3]^{: p. 89}

${displaystyle F_{X,Y}(x,y)=operatorname {P} (Xleq x,Yleq y)}$

(Eq.1)

where the right-hand side represents the probability that the random variable takes on a value less than or equal to and that takes on a value less than or equal to .

For random variables , the joint CDF ${displaystyle F_{X_{1},ldots ,X_{N}}}$ is given by

${displaystyle F_{X_{1},ldots ,X_{N}}(x_{1},ldots ,x_{N})=operatorname {P} (X_{1}leq x_{1},ldots ,X_{N}leq x_{N})}$

(Eq.2)

Interpreting the random variables as a random vector ${displaystyle mathbf {X} =(X_{1},ldots ,X_{N})^{T}}$ yields a shorter notation:

${displaystyle F_{mathbf {X} }(mathbf {x} )=operatorname {P} (X_{1}leq x_{1},ldots ,X_{N}leq x_{N})}$

Joint density function or mass function[edit]

Discrete case[edit]

The joint probability mass function of two discrete random variables X,Y is:

${displaystyle p_{X,Y}(x,y)=mathrm {P} (X=x mathrm {and} Y=y)}$

(Eq.3)

or written in terms of conditional distributions

${displaystyle p_{X,Y}(x,y)=mathrm {P} (Y=ymid X=x)cdot mathrm {P} (X=x)=mathrm {P} (X=xmid Y=y)cdot mathrm {P} (Y=y)}$

where is the probability of Y=y given that X=x .

The generalization of the preceding two-variable case is the joint probability distribution of discrete random variables $X_{1},X_{2},dots ,X_{n}$ which is:

${displaystyle p_{X_{1},ldots ,X_{n}}(x_{1},ldots ,x_{n})=mathrm {P} (X_{1}=x_{1}{text{ and }}dots {text{ and }}X_{n}=x_{n})}$

(Eq.4)

or equivalently

${displaystyle {begin{aligned}p_{X_{1},ldots ,X_{n}}(x_{1},ldots ,x_{n})&=mathrm {P} (X_{1}=x_{1})cdot mathrm {P} (X_{2}=x_{2}mid X_{1}=x_{1})\&cdot mathrm {P} (X_{3}=x_{3}mid X_{1}=x_{1},X_{2}=x_{2})\&dots \&cdot P(X_{n}=x_{n}mid X_{1}=x_{1},X_{2}=x_{2},dots ,X_{n-1}=x_{n-1}).end{aligned}}}$

This identity is known as the chain rule of probability.

Since these are probabilities, in the two-variable case

$sum _{i}sum _{j}mathrm {P} (X=x_{i} mathrm {and} Y=y_{j})=1,,$

which generalizes for discrete random variables $X_{1},X_{2},dots ,X_{n}$ to

$sum _{i}sum _{j}dots sum _{k}mathrm {P} (X_{1}=x_{1i},X_{2}=x_{2j},dots ,X_{n}=x_{nk})=1.;$

Continuous case[edit]

The joint probability density function $f_{{X,Y}}(x,y)$ for two continuous random variables is defined as the derivative of the joint cumulative distribution function (see Eq.1):

${displaystyle f_{X,Y}(x,y)={frac {partial ^{2}F_{X,Y}(x,y)}{partial xpartial y}}}$

(Eq.5)

This is equal to:

${displaystyle f_{X,Y}(x,y)=f_{Ymid X}(ymid x)f_{X}(x)=f_{Xmid Y}(xmid y)f_{Y}(y)}$

where ${displaystyle f_{Ymid X}(ymid x)}$ and ${displaystyle f_{Xmid Y}(xmid y)}$ are the conditional distributions of given X=x and of given Y=y respectively, and $f_{X}(x)$ and f_Y(y) are the marginal distributions for and respectively.

The definition extends naturally to more than two random variables:

${displaystyle f_{X_{1},ldots ,X_{n}}(x_{1},ldots ,x_{n})={frac {partial ^{n}F_{X_{1},ldots ,X_{n}}(x_{1},ldots ,x_{n})}{partial x_{1}ldots partial x_{n}}}}$

(Eq.6)

Again, since these are probability distributions, one has

${displaystyle int _{x}int _{y}f_{X,Y}(x,y);dy;dx=1}$

respectively

${displaystyle int _{x_{1}}ldots int _{x_{n}}f_{X_{1},ldots ,X_{n}}(x_{1},ldots ,x_{n});dx_{n}ldots ;dx_{1}=1}$

Mixed case[edit]

The «mixed joint density» may be defined where one or more random variables are continuous and the other random variables are discrete. With one variable of each type

${displaystyle {begin{aligned}f_{X,Y}(x,y)=f_{Xmid Y}(xmid y)mathrm {P} (Y=y)=mathrm {P} (Y=ymid X=x)f_{X}(x).end{aligned}}}$

One example of a situation in which one may wish to find the cumulative distribution of one random variable which is continuous and another random variable which is discrete arises when one wishes to use a logistic regression in predicting the probability of a binary outcome Y conditional on the value of a continuously distributed outcome . One must use the «mixed» joint density when finding the cumulative distribution of this binary outcome because the input variables (X,Y) were initially defined in such a way that one could not collectively assign it either a probability density function or a probability mass function. Formally, $f_{{X,Y}}(x,y)$ is the probability density function of (X,Y) with respect to the product measure on the respective supports of and . Either of these two decompositions can then be used to recover the joint cumulative distribution function:

${displaystyle {begin{aligned}F_{X,Y}(x,y)&=sum limits _{tleq y}int _{s=-infty }^{x}f_{X,Y}(s,t);ds.end{aligned}}}$

The definition generalizes to a mixture of arbitrary numbers of discrete and continuous random variables.

Additional properties[edit]

Joint distribution for independent variables[edit]

In general two random variables and are independent if and only if the joint cumulative distribution function satisfies

${displaystyle F_{X,Y}(x,y)=F_{X}(x)cdot F_{Y}(y)}$

Two discrete random variables and are independent if and only if the joint probability mass function satisfies

{displaystyle P(X=x {mbox{and}} Y=y)=P(X=x)cdot P(Y=y)}

for all and .

While the number of independent random events grows, the related joint probability value decreases rapidly to zero, according to a negative exponential law.

Similarly, two absolutely continuous random variables are independent if and only if

${displaystyle f_{X,Y}(x,y)=f_{X}(x)cdot f_{Y}(y)}$

for all and . This means that acquiring any information about the value of one or more of the random variables leads to a conditional distribution of any other variable that is identical to its unconditional (marginal) distribution; thus no variable provides any information about any other variable.

Joint distribution for conditionally dependent variables[edit]

If a subset of the variables $X_{1},cdots ,X_{n}$ is conditionally dependent given another subset of these variables, then the probability mass function of the joint distribution is $mathrm {P} (X_{1},ldots ,X_{n})$ . $mathrm {P} (X_{1},ldots ,X_{n})$ is equal to . Therefore, it can be efficiently represented by the lower-dimensional probability distributions P(B) and . Such conditional independence relations can be represented with a Bayesian network or copula functions.

Covariance[edit]

When two or more random variables are defined on a probability space, it is useful to describe how they vary together; that is, it is useful to measure the relationship between the variables. A common measure of the relationship between two random variables is the covariance. Covariance is a measure of linear relationship between the random variables. If the relationship between the random variables is nonlinear, the covariance might not be sensitive to the relationship, which means, it does not relate the correlation between two variables.

The covariance between the random variable X and Y, denoted as cov(X,Y), is :

${displaystyle sigma _{XY}=E[(X-mu _{x})(Y-mu _{y})]=E(XY)-mu _{x}mu _{y}}$ ^[4]

Correlation[edit]

There is another measure of the relationship between two random variables that is often easier to interpret than the covariance.

The correlation just scales the covariance by the product of the standard deviation of each variable. Consequently, the correlation is a dimensionless quantity that can be used to compare the linear relationships between pairs of variables in different units. If the points in the joint probability distribution of X and Y that receive positive probability tend to fall along a line of positive (or negative) slope, ρ_XY is near +1 (or −1). If ρ_XY equals +1 or −1, it can be shown that the points in the joint probability distribution that receive positive probability fall exactly along a straight line. Two random variables with nonzero correlation are said to be correlated. Similar to covariance, the correlation is a measure of the linear relationship between random variables.

The correlation between random variable X and Y, denoted as

${displaystyle rho _{XY}={frac {cov(X,Y)}{sqrt {V(X)V(Y)}}}={frac {sigma _{XY}}{sigma _{X}sigma _{Y}}}}$

Important named distributions[edit]

Named joint distributions that arise frequently in statistics include the multivariate normal distribution, the multivariate stable distribution, the multinomial distribution, the negative multinomial distribution, the multivariate hypergeometric distribution, and the elliptical distribution.

References[edit]

^ Feller, William (1957). An introduction to probability theory and its applications, vol 1, 3rd edition. pp. 217–218. ISBN 978-0471257080.
^ Montgomery, Douglas C. (19 November 2013). Applied statistics and probability for engineers. Runger, George C. (Sixth ed.). Hoboken, NJ. ISBN 978-1-118-53971-2. OCLC 861273897.
^ Park,Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications. Springer. ISBN 978-3-319-68074-3.
^ Montgomery, Douglas C. (19 November 2013). Applied statistics and probability for engineers. Runger, George C. (Sixth ed.). Hoboken, NJ. ISBN 978-1-118-53971-2. OCLC 861273897.

External links[edit]

«Joint distribution», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
«Multi-dimensional distribution», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
«Joint continuous density function». PlanetMath.
Mathworld: Joint Distribution Function

Источник

Совместная функция распределения двух случайных величин и её свойства. Совместное распределение двух дискретных случайных величин.

Абсолютно непрерывные совместные распределения двух случайных величин. Совместная плотность распределения, её свойства.

Условные плотности распределения.

Распределения n-мерных случайных векторов. Дискретные распределения, абсолютно непрерывные распределения.

Распределение функции от случайной величины. Примеры.

Случайные векторы

Свойства функции распределения случайного вектора

Двумерные дискретные случайные векторы

Двумерные абсолютно непрерывные случайные векторы

Сходимость случайных величин

Двумерная непрерывная случайная величина

Система непрерывных случайных величин: теория

Примеры решений

Решебник по теории вероятности онлайн

Совместное распределение

Типы многомерных распределений

Examples[edit]

Draws from an urn[edit]

Coin flips[edit]

Rolling a die[edit]

Marginal probability distribution[edit]

Joint cumulative distribution function[edit]

Joint density function or mass function[edit]

Discrete case[edit]

Continuous case[edit]

Mixed case[edit]

Additional properties[edit]

Joint distribution for independent variables[edit]

Joint distribution for conditionally dependent variables[edit]

Covariance[edit]

Correlation[edit]

Important named distributions[edit]

See also[edit]

References[edit]

External links[edit]

Не пропустите также: