Степень вершины (теория графов)
Степень вершины (англ. degree , также валентность, англ. valency ) в теории графов — количество рёбер графа 



Содержание
Лемма о рукопожатиях
По формуле суммы степеней для графа ,
Последовательность степеней вершин неориентированного графа является невозрастающей последовательностью. [2] Для графа, изображённого на рис. 1, она имеет вид (5, 3, 3, 2, 2, 1, 0). Последовательность степеней вершин есть инвариант графа, поэтому у изоморфных графов она одинакова. Однако последовательность степеней вершин не является уникальной характеристкой графа: в некоторых случаях неизоморфные графы также обладают одинаковой последовательностью.
Проблема последовательности степеней заключается в нахождении некоторых или всех графов с заданной невозрастающей последовательностью, состоящей из натуральных чисел (нулевые степени при этом могут быть проигнорированы, так как их количество изменяется добавлением или удалением изолированных вершин). Последовательность, являющаяся последовательностью степеней какого-либо графа, называется графической (англ. graphical sequence ). Из формулы суммы степеней следует, что любая последовательность с нечётной суммой (как, к примеру, 3, 3, 1) не может быть последовательностью степеней графа. Обратное также верно: если последовательность имеет чётную сумму, она представляет собой последовательность степеней мультиграфа. Построение такого графа осуществляется достаточно простым способом: необходимо объединить вершины нечётных степеней в пары, к оставшимся незаполненными вершинам следует добавить петли.
Сложнее реализовать простой граф с заданной последовательностью. Теорема Эрдёша — Галлаи утверждает, что невозрастающая последовательность di (при i = 1,…,n) может быть последовательностью простого графа только если её сумма чётна и выполняется неравенство
Здесь точка – это точка с именем «а».
Линия
Линия – это связь между двумя точками. Это может быть представлено сплошной линией.
пример
Здесь «а» и «б» являются точками. Связь между этими двумя точками называется линией.
Вершина – это точка, где встречаются несколько линий. Это также называется узлом . Подобно точкам, вершина также обозначается алфавитом.
пример
Здесь вершина названа с алфавитом «а».
Ребро – это математический термин для линии, соединяющей две вершины. Многие ребра могут быть сформированы из одной вершины. Без вершины ребро не может быть сформировано. Для ребра должна быть начальная и конечная вершина.
пример
Здесь «a» и «b» – две вершины, и связь между ними называется ребром.
график
Граф ‘G’ определяется как G = (V, E), где V – множество всех вершин, а E – множество всех ребер графа.
Пример 1
В приведенном выше примере ab, ac, cd и bd являются ребрами графа. Аналогично, a, b, c и d являются вершинами графа.
Пример 2
В этом графе есть четыре вершины a, b, c и d и четыре ребра ab, ac, ad и cd.
петля
В графе, если ребро нарисовано от вершины к себе, это называется циклом.
Пример 1
На приведенном выше графике V – вершина, для которой у нее есть ребро (V, V), образующее петлю.
Пример 2
В этом графе есть две петли, которые сформированы в вершине a, и вершине b.
Степень вершины
Это число вершин, смежных с вершиной V.
Обозначение – град (V).
В простом графе с n числом вершин степень любых вершин равна –
Вершина может образовывать ребро со всеми остальными вершинами, кроме самой себя. Таким образом, степень вершины будет равна числу вершин в графе минус 1 . Это 1 для собственной вершины, поскольку она не может образовывать петлю сама по себе. Если в любой из вершин есть петля, то это не простой граф.
Степень вершины можно рассматривать по двум случаям графов –
- Ненаправленный граф
- Направленный граф
Степень вершины в неориентированном графе
Ненаправленный граф не имеет направленных ребер. Рассмотрим следующие примеры.
Пример 1
Посмотрите на следующий график –
На приведенном выше неориентированном графике
deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.
deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.
deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро
Итак, «c» – это вершина с кулоном .
deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.
deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.
Так что «е» – изолированная вершина .
deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.
deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.
deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро
Итак, «c» – это вершина с кулоном .
deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.
deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.
Так что «е» – изолированная вершина .
Пример 2
Посмотрите на следующий график –
На приведенном выше графике
deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 и deg (e) = 0.
Вершина «е» является изолированной вершиной. Граф не имеет никакой вершины.
Степень вершины в ориентированном графе
В ориентированном графе каждая вершина имеет степень и степень.
Степень графа
Степень вершины V – это количество ребер, входящих в вершину V.
Обозначение – град – (V).
Степень вершины V – это количество ребер, входящих в вершину V.
Обозначение – град – (V).
Степень графа
Отступ вершины V – это число ребер, выходящих из вершины V.
Обозначение – град + (V).
Отступ вершины V – это число ребер, выходящих из вершины V.
Обозначение – град + (V).
Рассмотрим следующие примеры.
Пример 1
Посмотрите на следующий ориентированный граф. Вершина «а» имеет два ребра, «ad» и «ab», которые идут наружу. Следовательно, его степень равна 2. Аналогично, существует ребро «ga», идущее к вершине «a». Следовательно, степень «а» равна 1.
Степень и степень других вершин показаны в следующей таблице:
| темя | полустепень захода | полустепень |
|---|---|---|
| 1 | 2 | |
| б | 2 | 0 |
| с | 2 | 1 |
| d | 1 | 1 |
| е | 1 | 1 |
| е | 1 | 1 |
| г | 0 | 2 |
Пример 2
Посмотрите на следующий ориентированный граф. Вершина ‘a’ имеет ребро ‘ae’, идущее наружу от вершины ‘a’. Следовательно, его степень равна 1. Аналогично, у графа есть ребро «ba», приближающееся к вершине «a». Следовательно, степень «а» равна 1.
Степень и степень других вершин показаны в следующей таблице:
| темя | полустепень захода | полустепень |
|---|---|---|
| 1 | 1 | |
| б | 0 | 2 |
| с | 2 | 0 |
| d | 1 | 1 |
| е | 1 | 1 |
Кулон Вертекс
Используя степень вершины, мы получаем два специальных типа вершин. Вершина с первой степенью называется нерешенной вершиной.
пример
Здесь, в этом примере, вершина ‘a’ и вершина ‘b’ имеют соединенное ребро ‘ab’. Таким образом, что касается вершины «a», то к вершине «b» имеется только одно ребро, и аналогично по отношению к вершине «b» есть только одно ребро к вершине «a». Наконец, вершина ‘a’ и вершина ‘b’ имеют степень как единицу, которая также называется висячей вершиной.
Изолированная вершина
Вершина с нулевой степенью называется изолированной вершиной.
пример
Здесь вершина «a» и вершина «b» не имеют связи между собой, а также с любыми другими вершинами. Таким образом, степень обеих вершин ‘a’ и ‘b’ равна нулю. Они также называются изолированными вершинами.
смежность
Вот нормы смежности –
В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.
В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.
В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.
В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.
Пример 1
На приведенном выше графике –
«a» и «b» – это смежные вершины, так как между ними есть общее ребро «ab».
«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».
ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.
be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.
«a» и «b» – это смежные вершины, так как между ними есть общее ребро «ab».
«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».
ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.
be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.
Пример 2
На приведенном выше графике –
a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.
‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.
‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.
ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.
a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.
‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.
‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.
ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.
Параллельные края
В графе, если пара вершин соединена более чем одним ребром, то эти ребра называются параллельными ребрами.
На приведенном выше графике «a» и «b» – это две вершины, которые соединены между собой двумя ребрами «ab» и «ab». Так это называется параллельным ребром.
Мульти График
Граф, имеющий параллельные ребра, называется мультиграфом.
Пример 1
На приведенном выше графике есть пять ребер «ab», «ac», «cd», «cd» и «bd». Поскольку ‘c’ и ‘d’ имеют два параллельных ребра между ними, это мультиграф.
Пример 2
На приведенном выше графике вершины «b» и «c» имеют два ребра. Вершины ‘e’ и ‘d’ также имеют два ребра между ними. Следовательно, это мультиграф.
Степень последовательности графика
Если степени всех вершин в графе расположены в порядке убывания или возрастания, то полученная последовательность называется последовательностью графа графа.
Пример 1
| темя | б | с | d | е | |
|---|---|---|---|---|---|
| Присоединенный к | До нашей эры | объявление | объявление | с, Ь, е | d |
| степень | 2 | 2 | 2 | 3 | 1 |
На приведенном выше графике для вершин последовательность степеней равна .
Пример 2
| темя | б | с | d | е | е | |
|---|---|---|---|---|---|---|
| Присоединенный к | быть | а, с | б, г | с, е | объявление | – |
| степень | 2 | 2 | 2 | 2 | 2 | 0 |
На приведенном выше графике для вершин последовательность степеней равна .
«Степень вершины и подсчет числа ребер графа». 7-й класс

Загрузить презентацию (487 кБ)
Профиль класса: общеобразовательный.
Тип урока: изучение и первичное закрепление новых знаний.
- ученик знает понятия графа и мультиграфа, знаком с понятиями “вершина графа” (смежные вершины) и “ребро графа” (кратные ребра и петли);
- умеет приводить примеры использования графов в различных учебных предметах и повседневной жизни.
- закрепить понятие графа, сформировать представление о степени вершины графа (четная, нечетная вершины), сформулировать определение о связности графа, рассмотреть утверждение о количестве ребер графа и теорему о четности числа нечетных вершин графа;
- отработать навыки использования теоретических знаний для решения новых задач.
- развивать логическое мышление учащихся, способность к рассуждению, внимательность;
- формировать умение представлять информацию в виде графов.
- воспитывать культуру общения на уроке, взаимоуважение.
- Организационный момент (приветствие класса, подготовка к уроку, проверка домашнего задания, включающая повторение материала предыдущего урока);
- Теоретический материал (знакомство с темой предстоящего урока, объяснение нового материала и краткая запись в рабочую тетрадь новых теоретических сведений по теме урока);
- Закрепление материала (решение задач);
- Итоги урока (краткий вывод и домашнее задание).
Давайте вспомним основные понятия теории графов. Для этого проведем разминку по типу незаконченного предложения (Презентация, сл.: 2, 3, 4). Каждый ученик имеет карточки с пропущенными словами в предложение. Учитель зачитывает предложение, останавливаясь перед пропущенным словом, и выбирает ученика, который в свою очередь должен поднять карточку. Далее этот ученик читает дальше предложение, также останавливаясь перед пропущенным словом, и уже сам выбирает одноклассника для ответа и т. д. по цепочке.
Проверим в классе решение домашней задачи (Презентация, сл.: 5, 6, 7). Один ученик выходит к доске и рисует граф. Далее мы вместе проверяем ребра (дороги между городами), считаем количество выходящих ребер из каждой вершины и смотрим связи между городами.
Сегодня на уроке мы продолжим изучение графов, познакомимся с понятием “степень вершины графа” и сформулируем определение связности графа (обратим внимание на наш граф из домашнего задания и определим, является ли он связным или нет и почему). Рассмотрим утверждение о количестве ребер графа, и проверим в соответствие с этим утверждением, правильно ли мы посчитали количество ребер графа в домашней задаче. И рассмотрим теорему о четности числа нечетных вершин графа.
Количество ребер, выходящих из одной вершины, называют степенью этой вершины. Для петли будем считать, что это ребро выходит из вершины дважды (Презентация, сл. 8).
Запишем определение в рабочую тетрадь и зарисуем представленный граф, для данного графа посчитаем степень каждой вершины. Ребята смотрят на слайд и работают самостоятельно, далее вслух зачитаем степень каждой вершины.
Вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной (Презентация, сл. 9).
Запишем определение в тетрадь и перечислим через запятую сначала четные вершины, а потом нечетные вершины для уже нарисованного графа. Проверим задание вслух.
Количество ребер графа равно половине суммы степеней его вершин. Пусть граф имеет n вершин, тогда число ребер равно:
(Презентация, сл. 10)
Запишем утверждение в рабочую тетрадь и посчитаем количество ребер графа в домашней задачке. Проверим ответ в классе. Рассмотрим задачу и ее решение на подсчет числа ребер графа без построения. (Презентация, сл. 11).
Сформулируем теорему о количестве вершин нечетной степени любого графа и запишем формулировку в рабочую тетрадь. (Презентация, сл. 12).
Теорема. Количество вершин нечетной степени любого графа всегда четно.
Доказательство: Количество ребер графа равно половине суммы степеней его вершин.
Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной.
А это возможно только в том случае, если граф содержит четное число нечетных вершин.
Разберем доказательство и проверим теорему на нашей домашней задачке.
Рассмотрим несколько задач.
Задача. В государстве 50 городов, из каждого города выходит 4 дороги. Сколько всего дорог в государстве.
Решение. Подсчитаем общее количество выходящих дорог из городов: 50 * 4 = 200. Однако, мы понимаем, что при подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 100.
Задача. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей?
Ответ. Нет (теорема о четности числа нечетных вершин).
Сегодня мы с вами познакомились с новыми определениями, связанными с понятием графа, рассмотрели утверждение, которое помогает быстро подсчитывать число ребер графа, и сформулировали теорему, которая значительно упрощает решение многих задач. В частности, поучительная сторона этой теоремы заключается в исследовании и ответе на вопрос, возможно или нет решение данной задачи, прежде чем приступать за ее решение.
В качестве домашнего задания ученики получать карточки с тремя задачами (Презентация, сл. 13).
Рис. 1. Граф, на вершинах которого отмечены степени.
Степень вершины (англ. degree, также валентность, англ. valency) в теории графов — количество рёбер графа 



Содержание
- 1 Лемма о рукопожатиях
- 2 Последовательность степеней вершин
- 3 Частные значения
- 4 Общие свойства
- 5 См. также
- 6 Примечания
- 7 Источники
Лемма о рукопожатиях
По формуле суммы степеней для графа 
то есть сумма степеней вершин любого графа равна удвоенному числу его рёбер. Кроме того, формула утверждает, что в любом графе число вершин нечётной степени чётно. Данное утверждение (и сама формула) известны как лемма о рукопожатиях. Название происходит от известной математической задачи: необходимо доказать, что в любой группе число людей, пожавших руку нечётному числу других чётно.
Последовательность степеней вершин
Рис. 2. Два неизоморфных графа с одинаковой последовательностью степеней (3, 2, 2, 2, 2, 1, 1, 1).
Последовательность степеней вершин неориентированного графа является невозрастающей последовательностью.[2] Для графа, изображённого на рис. 1, она имеет вид (5, 3, 3, 2, 2, 1, 0). Последовательность степеней вершин есть инвариант графа, поэтому у изоморфных графов она одинакова. Однако последовательность степеней вершин не является уникальной характеристкой графа: в некоторых случаях неизоморфные графы также обладают одинаковой последовательностью.
Проблема последовательности степеней заключается в нахождении некоторых или всех графов с заданной невозрастающей последовательностью, состоящей из натуральных чисел (нулевые степени при этом могут быть проигнорированы, так как их количество изменяется добавлением или удалением изолированных вершин). Последовательность, являющаяся последовательностью степеней какого-либо графа, называется графической (англ. graphical sequence). Из формулы суммы степеней следует, что любая последовательность с нечётной суммой (как, к примеру, 3, 3, 1) не может быть последовательностью степеней графа. Обратное также верно: если последовательность имеет чётную сумму, она представляет собой последовательность степеней мультиграфа. Построение такого графа осуществляется достаточно простым способом: необходимо объединить вершины нечётных степеней в пары, к оставшимся незаполненными вершинам следует добавить петли.
Сложнее реализовать простой граф с заданной последовательностью. Теорема Эрдёша — Галлаи утверждает, что невозрастающая последовательность di (при i = 1,…,n) может быть последовательностью простого графа только если её сумма чётна и выполняется неравенство
Например, последовательность (3, 3, 3, 1) не может являться последовательностью простого графа; она удовлетворяет неравенству Эрдёша — Галлаи только при k равном 1, 2 или 4, но не при k равном 3.
С. Л. Хакими доказал, что (d1, d2, …, dn) есть последовательность степеней простого графа только если существует (d2 − 1, d3 − 1, …, dd1+1 − 1, dd1+2, dd1+3, …, dn). Этот факт позволил разработать простой алгоритм нахождения простого графа с заданной реализуемой последовательностью:
- Изначально граф не имеет рёбер.
- Составляется список вершин, для которых требования по степеням пока не удовлетворены. Оставшиеся требования располагаются в порядке невозрастания.
- Первая вершина соединяется со следующими d1 вершинами из списка. После этого первая вершина удаляется, список пересортируется. Действие повторяется до тех пор, пока все требования не будут удовлетворены.
Проблема нахождения или оценки числа графов по заданной последовательности относится к области перечисления графов.
Частные значения
Рис. 3. Концевыми вершинами являются 4, 5, 6, 7, 10, 11 и 12.
- Вершина степени 0 называется изолированной.
- Вершина степени 1 называется концевой (англ. end vertex), висячей (англ. pendant vertex) или листом графа (англ. leaf vertex). Ребро, инцидентное такой вершине называется висячим (англ. terminal (pendant) edge, end-edge). На рис. 3 висячим ребром является {3,5}. Подобная терминология используется в изучении деревьев в общем и как структур данных.
- Вершина степени n-1 графа порядка n называется доминирующей (англ. dominating vertex).
Общие свойства
- Если все вершины графа имеют одинаковую степень k, граф называют k-регулярным или регулярным графом степени k. В этом случае сам граф имеет степень k.
- Эйлеров путь существует в неориентированном, связном графе если и только если граф имеет 0 или 2 вершины нечётной степени. Если граф содержит 0 вершин нечётной степени, Эйлеров путь является циклом.
- Орграф является псевдолесом только если полустепень захода каждой вершины не больше 1. Функциональный граф — частный случай псевдолеса, в котором полустепени захода всех вершин равны 1.
- Согласно теореме Брукса, хроматическое число любого графа за исключением клики или нечётного цикла не превышает максимальной степени его вершин (Δ). Согласно теореме Визинга, хроматический индекс любого графа не превышает Δ + 1.
- k-вырожденным графом называется граф, в котором каждый подграф имеет вершину степенью не больше k.
См. также
- Полустепень захода и полустепень исхода вершин ориентированных графов
- Распределение степеней
Примечания
- ↑ Дистель, стр. 5
- ↑ Дистель, стр. 278
Источники
- Дистель, Рейнхард (2005), «Graph Theory» (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-26183-4, <http://diestel-graph-theory.com/index.html>.
- Эрдёш, П. & Галлаи, T. (1960), ««Gráfok előírt fokszámú pontokkal»», Matematikai Lapok Т. 11: 264—274, <http://www.renyi.hu/~p_erdos/1961-05.pdf>.
- Хакими, С. Л. (1962), ««On realizability of a set of integers as degrees of the vertices of a linear graph. I»», Journal of the Society for Industrial and Applied Mathematics Т. 10: 496–506.
- Сирксма, Хирард & Хоохефен, Хан (1991), ««Seven criteria for integer sequences being graphic»», Journal of Graph Theory Т. 15 (2): 223–231, DOI 10.1002/jgt.3190150209.
Любая система,
предполагающая наличие дискретных
состояний или наличие узлов и переходов
между ними может быть описана графом.
Связи между узлами(вершинами)
(V),
определенные неупорядоченными парами
вершин графа, называются ребрами
(E),
а граф –неориентированным. Если пары
вершинупорядочены, связи называются
дугами
(рис.
2).
|
Пара
Если |
Рис. |
Определения
Число
ребер, исходящих из вершины vi(петля
учитывается дважды), называется
валентностью
(степенью вершины)
и обозначается:
(vi).
Если V и E конечные
множества, то и граф им соответствующий
называется конечным.
Граф называется вырожденным,
если он не имеет ребер.
Неориентированный
граф называется простым,
если он не имеет петель и любая пара
вершин соединена не более чем одним
ребром.
Графы
отображаются на плоскости набором точек
и соединяющих их линий или векторов.
Грани могут отображаться и кривыми
линиями, а их длина не играет никакой
роли.
Граф
G называется планарным
(плоским),
если его можно отобразить в плоскости
без пересечения его граней (рис. 5).
Граф
называется связным,
если для любых двух вершин существует
последовательность ребер их соединяющая
(рис. 3), т.е. граф не имеет изолированных
фрагментов (вершин, ребер).
Граф
называется полным,
если любые две вершины соединены только
одним ребром (рис.4). Если
полный граф имеет n вершин, то количество
ребер будет равно n(n-1)/2.
Специальными
видами графов являются деревья
(рис.
6.)
|
3 4 5 1 2
5
Рис. |
2 3 1 2 3 4
1
4
Рис. |
|
|
ГрафG
|
1
2 3 4
5
Рис. |
Ребро
(дуга) и любая из его вершин называются
инцидентными.
Принято говорить, что (дуга) ребро (u,
v)соединяет
вершины u
и v.
Если
вершина не инцидентна ни одному ребру
(дуге), то она называется изолированной
((vi)=0),
если принадлежит только одному ребру
(дуге), то называется висячей
((vi)=1).
Основные
положения о вершинах графа:
1.
В графе G
сумма степеней всех его вершин — число
четное, равное удвоенному числу ребер
графа, так как каждое ребро участвует
в этой сумме ровно два раза.
2. Число
нечетных вершин любого графа четно.
3. Во
всяком графе с n
вершинами, где n2,
всегда найдутся, по меньшей мере, две
вершины с одинаковыми степенями.
4. Если
в графе с вершинами n>2
две вершины имеют одинаковую степень,
то в этом графе всегда найдется либо
одна вершина степени 0, либо одна вершина
степени n
— 1.
5. Два
графа
G1=(V1,E1)
и G2=(V2,E2)
называются изоморфными,
если между их вершинами
существует взаимно однозначное
соответствие.
Алгоритм
распознавания изоморфизма двух графов
G1(X,
E)и
G2(Y,E)
-
Если
X
≠ Y,
то графы не изоморфны. -
Выписываем
все элементы обоих графов, определяя
пары (xi,xj)
и (yi,
yj)
для каждого элемента, где xi,
yi
— число исходов для каждой вершины обоих
графов, а xj,
yj
– число заходов. -
Для
каждого элемента x
графа G1
ищем такой элемент y
графа G2,
что выполняется условие: число исходов
x
совпадает с числом исходов y,
и число заходов x
совпадает с числом заходов y.
Найденные элементы x
и y
соединяем дугой, т.е. строим граф
соответствия. Если соответствия нет,
то графы неизоморфны. -
Выписываем
подстановку, которая переводит граф
G1
в граф G2.
Примеры
выполнения заданий
-
Докажите,
что валентности вершин графов А и Б
совпадают.
А
Б
Решение:
А) (v1)=2,
(v2)=3,
(v3)=3,
(v4)=2,
(v5)=3,
(v6)=3.
Б) (v1)=2,
(v2)=3,
(v3)=3,
(v4)=2,
(v5)=3,
(v6)=3.
-
Докажите,
что графы G1(X1,
E1)и
G2(Y2,E2)изоморфны.
|
2 2 1 3 4 X2 X3 X4 X5
X1 3 4 5 |
Y1 Y5 Y3 Y4
Y2 |
Решение:
|
X1(3, |
X2(4, |
X3(3, |
X4(2, |
X5(2, |
|
Y1(4, |
Y2(2, |
Y3(3, |
Y4(3, |
Y5(2,2) |
В
результате получим соответствие:
Следовательно,
графы G1(X,
E)
и G2(Y,
E)изоморфны.
-
Решите
задачу по вычислению валентности вершин
графа
Школьник
сказал своему приятелю: — У нас в классе
35 человек. Каждый из них дружит ровно
с 11 одноклассниками.
—
Не может этого быть, — сразу
ответил приятель, победитель математической
олимпиады. Почему он так решил?
Решение:
представим
себе, что между каждыми двумя друзьями
протянута ниточка. Тогда каждый
из 35 учеников будет держать в руке
11 концов ниточек, и значит, всего
у протянутых ниточек будет 11∙35
= 385 концов. Но общее число не может
быть нечётным, так как у каждой ниточки
2 конца.
Задания
для самостоятельного выполнения
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
21.05.2015611.84 Кб20№2.doc
Лекция 7. Графы и деревья
1. Способы задания графа в программировании
1.1. Неформальное определение понятия графа
Если говорить не формально, то граф представляет собой какое-либо множество (обычно конечное) вершин (изображаемых точками), некоторые из которых соединенны дугами (реберами).
При этом какие-либо две вершины могут быть соедениены несколькими дугами (такие дуги называют кратными, или мульти-дугами). Кроме того, концы дуг могут совпадать — такие ребра называют петлями. Также иногда рассматривают ребра, один конец которых присоединен к некоторый вершине, а другой — свободный, т.е. ни к какой вершине не присоединенный (такие ребра называются висячими — их не надо путать с висячими вершинами, см. ниже).
При изображении графа взаимное расположение вершин и форма соединяющих их дуг (ребер) значения не имеют, важен только факт соединения или его отсутсвие.
Ребрам графа может приписываться некоторая ориентация (при изображении на дугах ставится «стрелочка») — в этом случае граф называется ориентированным. В противном случае граф называется неориентированным.
Иногда каждому ребру графа приписывается некоторое число (вес, стоимость). В этом случае граф называют взвешенным.
Кроме того, иногда вершинам графа приписываются некоторые значения (данные). В этом случае можно, например, все вершины графа проиндесировать значениями 1,2,3,...,n (начиная с 1 и заканчивая числом вершин n, без пропусков). Тогда данные, связанные с вершинами могут хранится в отдельном одномерном массиве длины n, каждый i-ый элемент которого должен соответствовать i-ой вершине графа.
1.2. Формальные определения
Хотя мы могли бы и обойтись без формального определения графа: для практического программирования сказанного в предыдущем разделе достаточно, однако всё же полезно это сделать.
Графы бывают ориентированные, неориентированные, простые, с петлями, с кратными рёбрами, с висячими рёбрами. В большинстве источников эти понятия определяются по отдельности, мы же дадим одно самое общее определение.
Прежде всего, чтобы в одном определении охватить и случай графа с кратными ребрами, нам понадобится понятие мультимножества.
Определение. Говорят, что над множеством $A$ определено мультимножество, если на этом множестве задана функция принадлежности $mu: A to {{0,1,2,…}}$, причем $a in A Leftrightarrow mu(a)>0$, при этом значение $mu(a)$ называется кратностью элемента $a$.
В частном случае, когда кратнасти элементов некоторого мультимножества не превышают 1, имеем обычное множество.
Перейдем теперь к понятию графа. Пусть $V$ — множество вершин (некоторое абстрактное множество), и пусть $overline{V}=Vcup{}$, где $$ — это символ, обозначающий факт отсутствия вершины (иногда отсутствующую вершину $*$ называют еще внешней вершиной).
Определение. Ориентированным мультиграфом называется пара $(V, varepsilon)$, где $varepsilon$ — некоторе отображение $overline{V} times overline{V} to {0,1,2,…}$.
При этом $E={(u,v)inoverline{V} times overline{V} |varepsilon((u,v))ne 0}$ — множестово всех ребер графа.
Употребляя термин — граф, мы имеем ввиду сейчас самый общий случай: ориенированный мультиграф. Граф часто обозначают одной буквой, например $G=(V, varepsilon)$.
В частности, если ребра ориентированного мультиграфа не имеют кратностей больших 1, то можно считать, что $G=(V,E)$, т.е. — что граф представляет собой пару множеств: множество вершин и множество ребер.
В любом случае, при условии $varepsilon((u,v)) ne 0$, $(u,v)$ — это обычное ребро. При этом, считается, что ребра $(u,v)$ и $(v,u)$ имеют противоположную ориентацию.
При этом ${(u,) | u in V, varepsilon((u,))ne 0} cup {(,v) |v in V, varepsilon((,v))ne 0 }$ — это множество всех висячих ребер.
Не надо путать понятие висячего ребра с понятием висячей вершины: вершина называется висячей если она соединена только с одним ребром (если она инцидентна только одному ребру).
Ребро вида $(u,u)$ называется петлей.
Граф без петель, без кратных и висячих ребер называется простым графом. Именно с простыми графами чаще всего приходится иметь дело.
Неориентированный граф. В частности, если ориетированный простой граф обладает следующим свойством:
$(u,v) in E Leftrightarrow (v,u) in E (une v)$, то такой граф можно считать неориентированным графом, если каждую пару противонаправленных ребер рассматривать как одно ненаправленное ребро.
1.3. Способы задания графа
Из сказанного в предыдущем разделе должно быть ясно, что задать граф — означает задать множество его вершин $V$ и функцию принадлежности $varepsilon: overline{V} times overline{V} to {0,1,2,…}$.
Обычно считается, что $V={1,2,3,…,n}$, тогда функция принадлежности $varepsilon$ может быть задана квадратной матрицей размера $ntimes n$, в которой $i,j$-элемент равет $varepsilon((i,j))$.
В случае отсутствия кратных ребер в графе такая матрица называется матрицей смежности.
Функцию принадлежности можно задать также с помощью матрицы инциденций, т.е. с помощью прямоугольной матрицы, строки которой индексируются номерами вершин графа, а столбцы — номерами ребер (имеется ввиду, что множество $E$ каким-либо образом, безразлично каким, упорядочено), при этом её $i,j$-элемент равен 0, если только $e_j[1]ne i$, и $varepsilon((i,e_j[2]))$, в противном случае.
Здесь по умолчанию предполагалось следующее соглашение об обозначениях: если $e_j=(u,v)$, то $e_j[1]=u, e_j[2]=v$.
В программировании матрица инциденций обычно не используется (в наиболее популярных алгоритмах, по крайней мере), в отличии от матрицы смежностей.
1.4. Использование разреженных матриц
Если число вершин в графе очень большое и если при этом граф является слабосвзанным, т.е. в его матрице смежности очень много нулей, то использование такой матрицы в программе может оказаться не слишком экономичным, в смысле расходования компьютерной памяти.
Однако в современных языках программирования, ориентированных на математические вычисления, существуют так называемые разреженные матрицы. Разреженные матрицы — это матрицы с большим числом нулей, и для их компактного представления требуется специальный тип.
Для Julia имеется соответствующий пакет SparseArrays (требующий предварительной установки), в котором для представления разреженных матриц определен специальный тип SparseMatrixCSC, позволяющий экономномить расходование компьютерной памяти, и при этом выполнять с такими матрицами привычные операции.
Например,
using SparseArrays I=[1, 2, 5, 4, 5] # - индексы строк с ненулевыми значениями J=[2, 2, 2, 3, 5] # - индексы столбцов с ненулевыми значениями V=[10, 10, 10, 20, 30] # - сами не нулевые значения A=sparse(I,J,V)
Тогда вывод разреженной матрицы A на экран будет иметь вид:
5×5 SparseMatrixCSC{Int64, Int64} with 5 stored entries: ⋅ 10 ⋅ ⋅ ⋅ ⋅ 10 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ 20 ⋅ ⋅ ⋅ 10 ⋅ ⋅ 30
где точками отмечены позиции с нулевыми значениями.
При этом если бы среди элементов вектора V были бы нули, то эти нули не формально рассматривались бы как ненулевые значения, в том сысле, что они бы всё равно реально размещались в памяти компьютера. Например:
I = [1, 2, 5, 4, 5] J = [2, 2, 2, 3, 5] V = [10, 0, 10, 20, 30] A = sparse(I,J,V) 5×5 SparseMatrixCSC{Int64, Int64} with 5 stored entries: ⋅ 10 ⋅ ⋅ ⋅ ⋅ 0 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ 20 ⋅ ⋅ ⋅ 10 ⋅ ⋅ 30
(новое нулевое значение в выводе не заменено точкой, это означает, что оно реально размещено в памяти).
Работать с разреженными матрицами формально можно точно как же, как и с обычными мартицами, для них переопределены все стандартные операции и функции.
При этом, если требуется перебрать все формально ненулевые элементы (реально размещенные в памяти) разреженной матрицы, то для этого дополнительно имеются специальные функции rowvals, nonzeros и nzrange, позволяющие это делать экономично, с учетом структуры разреженной матрицы, например:
rows = rowvals(A) # rowvals(A) - возвращает вектор индексов строк A, содержащих ФОРМАЛЬНО не нулевые значения vals = nonzeros(A) # nonzeros(A) - возвращает вектор значений всех ФОРМАЛЬНО не нулевых элементов матрицы A m, n = size(A) for j = 1:n for i in nzrange(A, j) #= если в j-ом столбце нет формально не нулевых элементов, то диапазон индексов, возвращаемых функцией nzrange(A, j) будет пустым =# index_row = rows[i] val = vals[i] # val - очередное ФОРМАЛЬНО не нулевое значение, которое в матрице A имеет индексы (index_row, j) end end
1.5. Список смежностей
Всё отмеченное в предыдущем разделе делает возможным эффективно использовать разреженные матрицы в том числе и для представления графов.
Однако во многих случаях вполне можно обходиться и без разреженных матриц, если для представления графа использовать так называемый список смежностей.
Список смежностей представляет собой вектор, индексы которого суть номера вершин графа, в каждой позиции содержащий вектор, элементами которого являются индексы вершин, смежных с данной (её индекс — это индекс данной позиции).
При этом, если рассматривается мультиграф, то кратные ребра в этом случае могут быть представлены путем дублирования индексов смежных вершин требуемое число раз.
Рассмотрим, например, полный граф с 5 вершинами (простой граф называется полным, если в нём каждая вершина смежна со всеми остальными). Представление этого графа списком смежностей будет иметь вид:
G=[[2,3,4,5], [1,3,4,5], [1,2,4,5], [1,2,3,5], [1,2,3,4]]
Если бы мы захотели изобразить этот граф, то из каждой вершины следовалобы направить ориентированное ребро во все остальные. При этом мы можем считать, что пара проивонаправленных ребер эквивалентна одному ненаправленному ребру.
Пусть теперь, например, в некотором графе из некоторой вершины не исходит ни одного ориентированного ребра, тогда соответствующий ей вектор с индексами смежных вершин должен быть пустым.
Вот пример такого графа (ориентированного)
G=[[2,3,4,5], [], [1,2,4,5], [1,2,3,5], [1,2,3,4]]
У этого графа во вторую вершину направлены ребра из всех остальных вершин, но из ней в обратном направлении нет ни одного исходящего ребра.
В некоторых случаях список смежностей удобно представлять не в виде одномерного массива (вектора), а в виде значения типа Dict, т.е. в виде словаря. Словарь состоит из пар типа Pair (есть в Julia такой тип данных), при этом каждая пара типа Pair задается в виде: key => value_of_key (ключ => значение_соответствующее_ключу). Тип Dict, как и тип Pair, является двухпараметрическим, первый параметр определяет тип ключа, а второй — тип соответствующего значения.
Например, представление графа из предыдущего примера в виде словаря будет выглядеть так:
G=Dict{Int,Vector{Int}}([ 1=>[2,3,4,5], 2=>[], 3=>[1,2,4,5], 4=>[1,2,3,5], 5=>[1,2,3,4] ])
Аргументом функции Dict{Int,Vector{Int}} в данном случае является вектор типа `Vector{Pair{Int, Vector{Int}}}.
Чтобы теперь, наоборот, из словаря G получить вектор из содержащихся в нём пар (если это вдруг понадобится), надо воспользоваться стандартной функцией collect:
collect(G) |> println # [1=>[2,3,4,5], 2=>[], 3=>[1,2,4,5], 4=>[1,2,3,5], 5=>[1,2,3,4]]
Тот же самый словарь G можно было бы создать и динамически:
G=Dict{Int, Vector{Int}}() # - создан пустой словарь нужного типа G[1]=[2,3,4,5] G[2]=[] G[3]=[1,2,4,5] G[4]=[1,2,3,5], G[5]=[1,2,3,4]
В отличие от массива, в словарь можно добавлять новые пары вида индекс => вектор_смежных_индексов динамически, причем необязательно, чтобы соблюдался порядок следования индексов, т.е. необязательно, чтобы сначала добавилась пара 1 => [...], затем — 2 => [...] и т.д. В словарь такие пары можно будет добавлять в произвольном порядке, по мере того, как они будут определяться при обходе дерева.
1.6. Представление графа со взвешенными ребрами
Если рассматривается взвешенный граф (без кратных и висячих ребер), т.е. если его ребрам приписаны некоторые числа (веса), то его можно представить с помощью так называемой весовой матрицы, подобной матрице смежностей, только вместо единичек в весовой матрице нахоядися веса ребер.
В этом есть одна особенность, состоящая в том, что предполагается, что веса ребер не могут быть нулевыми, и поэтому нули матрицы рассматриваются как информация об отсутствии соответствующих ребер в графе.
Такое допущение приемлемо для многих алгоритмов на графах. Если же, однако, в какой-либо задаче всё же понадобится учитывать фактическое наличие рёбер с нулевым весом, то это можно всегда сделать, если факт отсутствия ребра кодировать не нулем, а, например, значенем Inf (бесконечно большую стоимость ребра естественно интерпретировать как его отсутствие). Это решение годится, если используются обычные (не разреженные) матрицы.
Если же использовать разреженные матрицы, то необходимость в использовании значения Inf отпадает (более того, использование этого значения не желательно, поскольку это снизит до предела эффект от использования разреженных матриц). Это благодаря тому, что при работе с разреженными матрицами имеется возможность различать нулевые элементы реально размещаемые в памяти и не размещаемые в памяти. Т.о. последние можно интерпретировать как факт отсутствия соответствующих ребер.
В любом случае обычную матрицу смежностей можно трактовать как весовую матрицу графа, в котором все его ребра имеют единичный вес.
2. Способы задания корневых деревьев в программировании
Валентностью (или, по другому, степенью) вершины графа называется число инцидентных ей (присоединенных к ней) ребер.
Валентностью по выходу вершины ориентирванного графа называется число его ребер, для которых она является начальной.
Валентностью по входу вершины ориентированного графа называется число его ребер, для которых она является конечной.
Таким образом, валентность любой вершины графа равна сумме ее валентностей по входу и по выходу.
Говорят, что в графе вершина $v$ достижима из вершины $u$, если существует последовательность ребер графа $(v,v_1), (v_1,v_2),…,(v_n,u)$, в которой конец предшествующего ребра является началом последующего.
Корневым деревом называется ориентированный граф, у которого
- имеется ровно одна вершина, называемая корнем, валентность по входу которой равна 0;
- любая другая его вершина достижима из корня, и её валентоность по входу равна 1.
Очевидно, что
-
в любом корневом дереве имеются вершины, валентности по выходу которых равны 0 (т.к. число вершин конечно); такие вершины называются листьями;
-
никакое дерево не содержит циклов.
Представление корневого дерева списком смежностей.
Поскольку корневое дерево — это простой ориентированный граф, то теоретически для задания дерева можно использовать любой из способов задания простого ориентированного графа. Например, для его задания можно использовать список смежностей.
Однако важным отличием от задания графа общего вида является то, что у корневого дерева имеется выделенная вершина, называемая корнем, с которой всегда должен осуществляться обход дерева. Поэтому для задания корневого дерева кроме собственно списка смежностей требуется указывать еще индекс корневой вершины.
Помимо этого, существуют еще некоторые специфические способы задания корневого дерева можно.
Представление корневого дерева вложенными векторами.
Рассмотрим это на примерах:
-
Int[]— пустое дерево (не содержащее ни одной вершины); -
[1]— тривиальное дерево, состоящее только из корня; -
[[2], [3], 1]— дерево с корнем 1, которому соответствует список смежностей
[[2, 3], Int[], Int[]]; -
[[[4], [5], [6], 2], [[7], [8], 3], 1]— дерево с корнем 1, которому соответствует список смежностей[[2, 3], [4, 5, 6], [7, 8], Int[], Int[], Int[], Int[], Int[]];
Замечание. Бывают деревья, у вершин которых имеются специализированные валентности, например, — двоичные деревья, в каждом узле которых имеется зафиксированная позиция для корня левого поддерева и зафиксированная позиция для корня правого поддерев. При этом если в нкотрой вершине отсутствует какое-то одно из из двух поодеревьев (левое или правое), то способ кодирования дерева должен обеспечивать возможность определять какое же поддерево присутствует. В случае вложенных массивов это можно обеспечить используя пустые массивы для фиксации позиции отсутствующего поддерева. А в случае использования списка смежностей это можно сделать используя значение 0 (предполагается, что никакая вершина дерева не может иметь индекса 0).
Например:
-
Int[]— пустое дерево (не содержащее ни одной вершины); -
[Int[], Int[], 1]— тривиальное дерево, состоящее только из корня; -
[[Int[], Int[], 2], [Int[], Int[], 3], 1]— дерево с корнем 1, которому соответствует список смежностей[[2, 3], [0, 0], [0, 0]]; -
[[[Int[], Int[], 4], Int[], 2], [Int[], [Int[], Int[], 5], 3], 1]— дерево с корнем 1, которому соответствует список смежностей[[2, 3], [4, 0], [0, 5], [0,0], I[0,0]].
Представление дерева связанными структурами.
Структура, представляющая узел бинарного дерева:
mutable struct BiTree{T} index::T left::Union{BiTree{T},Nothing} right::Union{BiTree{T},Nothing} BiTree{T}(index) where T = new(index,nothing,nothing) end
BTI = BiTree{Int}
t = BTI(1)
t.left = BTI(2)
t.right = BTI(3)
Структура, представляющая узел дерева с произвольной валентностью (по выходу):
struct Tree{T} index::T sub::Vector{Tree{T}}} Tree(index)=new(index, Tree{T}[]) end
Структура, представляющая узел дерева с фиксированной валентностью по выходу:
struct NTree{N,T} index::T sub::Vector{<:Union{NTree{N,T}, Nothing}} NTree{N,T}(index) where {N,T} = new(index, [nothing for _ in 1:N]) end
Замечание. Было бы ошибкой аннотировать тип поля sub так
sub::Vector{Union{NTree{N,T}, Nothing}}
Потому что тип Union является абстрактным типом, и, следовательно, невозможно будет впоследствии создать конкретный вектор типа Vector{Union{NTree{N,T}, Nothing}}, чтобы инициализировать поле subtees каким-либо значением, тип которого соответствовал бы такой аннотации.
3. Алгоритмы обхода корневых деревьев
Дерево по своей природе являеися рекурсивной структурой: с его корнем связано нескосколько поддеревьев, каждое из котрых устроено точно также, т.е. каждое поддерево является деревом.
Задача обхода дерева заключается в последовательой «обработке» всех поддеревьев данного дерева, включая и само дерево.
Под «обработкой» в самом общем смысле понимается извлечение информации как из структуры поддеревьев, так из значения каждого узла дерева (корня соответствующего поддерева). Последовательность, в которой обрабатыаются поддеревья может быть различной. Различают обход дерева сверху-вниз и снизу-вверх.
Вне зависимости от конкретного способа представления корневого дерева алгоритм обхода (обработки) сверху-вниз может быть записан рекурсивно так:
- обработать корень
- поочередно обработать каждое поддерево, непосредственно связанное с корнем
Соответственно, обход (обработка) снизу-вверх рекурсивно записывается так:
- поочередно обработать каждое поддерево, непосредственно связанное с корнем
- обработать корень
Например, если дерево представлено вложенными векторами, и под обработкой корня понимать просто вывод на печать значения его индекса, то в случае обхода сверху-вниз программный код будет выглядеть так:
function toptrace(tree::Vector) println(tree[end]) # на последней позиции в tree находится индекс корня for subtree in tree[1:end-1] # с первой до предпоследней поциции нахоятся поддеревья toptrace(subtree) end end
Соответственно обход (обработка) снизу-вверх будет выглядеть так:
function downtrace(tree::Vector) for subtree in tree[1:end-1] downtrace(subtree) end println(tree[end]) end
При всех других способах кодирования деревьев алгоритмы обхода будут выглядеть подобным образом, различаясь лишь в мелких деталях, связанных со спецификой выбранного способа кодирования.
Напимер, если дерево представлено типом NTree{N,T}, то тот же самый обход сверху-вниз записывается так:
function toptrace(tree::NTree{N,T}) where {N,T} println(tree.index) for i in 1:N toptrace(tree.sub[i]) end end
А если дерево представлено типом Tree{T}, то — так:
function toptrace(tree::Tree{T}) where T println(tree.index) for sub in tree.sub toptrace(tree.sub) end end
В случае же, если дерево представлено списком смежностей, код будет выглядеть так:
ConnectList{T} = Vector{Vector{T}}
function toptrace(rootindex::T, tree::ConnectList{T}) where T
println(rootindex)
for subindex in tree[rootindex]
toptrace(subindex, tree)
end
end
4. Метод рекуррентных соотношения для корневых деревьев
Многие задачи обработки деревьев могут быть элегантно решены на основе соответствующих рекуррентных соотношений. Рассмотрим конкретные прмеры.
4.1. Вычисление высоты дерева
Высота дерева — это набольшая длина пути к его концевым вершинам (листьям); по определению длина пути к корню дерева равна 1.
Пусть имеется некоторое дерево с $n$ поддеревьми, непосредственно связанных с его корнем, и нусть известно, что высоты этих поддеревьев равны $h_1,h_2,…,h_n$. Тогда для высоты $h$ всего дерева справедлива рекуррентная вормула:
$$
h=max{h_1,…,h_n}+1
$$
Этой формуле соответствует следующая рекурсивная функция:
function height(tree::Tree) h=0 for sub in tree.sub h = max(h,height(sub)) end return h+1 end
4.2. Подсчет всех вершин дерева
При подсчете числа всех вершин поступим аналогично: сначала запишем требуемую рекурреную формулу, из которой затем выведем соответствующую ей рекурсивную функцию.
Пусть $N_1,…N_n$ — числа вершин всех $n$ поддеревьев, связанных с корнем некоторого дерева. Тогда число вершин $N$ самого дерева, очевидно, равно:
$$
N=N_1+…+N_n+1
$$
Полученной рекуррентной формуле соответствует следующая рекурсивная функция:
function vernumber(tree::Tree) N=1 for sub in tree.sub N += vernumber(sub) end return N end
4.3. Подсчет числа листьев дерева
Пусть $N_1,…N_n$ — числа листьев во всех $n$ поддеревьях, связанных с корнем некоторого дерева. Тогда число листьев $N$ в самом дереве, очевидно, равно:
$$
N=begin{cases}
1 &, если дерево состоит только из корня
N_1+…+N_n &, в противном случае
end{cases}
$$
Полученной рекуррентной формуле соответствует следующая рекурсивная функция:
function leavesnumber(tree::Tree) if isempty(tree.sum) return 1 end N=0 for sub in tree.sub N += leavesnumber(sub) end return N end
4.4. Определение максимальной валентности вершин дерева
Пусть $p_1,…p_n$ — наибольшие валентности по выходу во всех $n$ поддеревьях, связанных с корнем некоторого дерева. Тогда наибольшая валентность по выходу $p$ в самом дереве, очевидно, равна:
$$
p=max{max{p_1,…,p_n}, валентность_корня}
$$
Этой рекуррентной формуле соответствует следующая рекурсивная функция:
function maxvalence(tree::Tree) p=length(tree.sub) for i in tree.sub p = max(p, maxvalence(sub)) end return p end
4.5. Вычисление средней длины пути к вершинам дерева
Практическая важность величины среднего пути к вершинам дерева определяется тем, что она пропорциональна среднему времени доступа к данным, хранящимся в узлах дерева.
Чтобы её найти потребуется сначала вычислить суммарную длину пути ко всем вершинам и число всех вершин. После чего, поделив первое на второе, получим искомую характеристику.
Рекуррентная формула для вычисления числа всех вершин нам уже известна:
$$
N=N_1+…+N_n+1
$$
где $N_1,…N_n$ — числа вершин всех $n$ поддеревьев, связанных с корнем некоторого дерева.
Рекуррентная формула для суммарной длины длины пути:
$$
S=S_1+…+S_n+N
$$
где $S_1,…,S_n$ суммы длин путей к каждой вершине всех поддеревьев, $N$ — число вершин во всём дереве. К сумме длин путей в каждом из поддеревьев по отдельности $S_1+…+S_n$ надо прибавить ещё число всех вершин дерева $N$ потому, что длины путей ко всем вершинам каждого поддерева, отсчитываемых от его корня, при переходе к отсчету от корня самого дерева увеличиваются на 1 (включая сам корень, так как длина пути к корню считается равной 1).
Соответствующая функция, возвращающая кортеж из величин $S, N$ записывается так:
function sumpath_numver(tree::Tree) N=1 S=0 for sub in tree.sub s, n = sumpath_numver(sub) S += s N += n end return S, N end
Поскольку эта функция самостоятельного значения не имеет, то её можно обернуть во внешнюю не рекурсивную функцию, возвращающую уже требуемый результат:
function meanpath(tree::Tree) function sumpath_numver() N=1 S=0 for sub in tree.sub s, n = sumpath_numver(sub) S += s N += n end return S, N end S, N = sumpath_numver() return S/N end
Задача о нахождении ближайшей родительской вершины для заданного набора вершин корневого дерева
Пусть имеется некоторое дерево и задано некоторое подмножество индексов его вершин. Требуется найти индекс ближайшей к этим вершинам и общей для всех них родительской вершины.
Идея решения состоит в следующем. Будем рекурсивно обрабатывать дерево сверху-вниз. При этом будем использовать две внешних по отношению к рекурсивной процедуре переменных:
-
number_visited— cчетчик числа посещённых вершин из заданного набораsetver -
general— переменная, в которой будет находиться индекс ближайщей общей родительской вершины для всех тех вершин из заданного набораsetver, которые на данный момент были уже посещены (при рекурсивном обходе сверху-вниз)
Внешняя переменная general перед началом обхода инициализируется некоторым значением (не важно каким именно), но за пределами всех возможных значений индексов вершин, например, значением 0.
Рекурсивная процедура обхода дерева, назовем её recursrtace, будет иметь дополнительный второй аргумент parent, через который в неё будет в неё передаваться индекс корня дерева, очередное поддерево которого передаётся в качестве первого аргумента (назовем его tree).
Идея алгоритма состоит в следующем:
-
как только (после обработки всех поддеревьев, т.е. на возвратном движении к корню) обнаруживается, что корень текущего дерева (поддерева) принадлежит заданному набору
setver, счетчик числа посещенных вершинnumber_visitedувеличивается на 1, и если при этом это случилось первый раз, то значению индекса ближайшей первой родительской вершины (переменнойgeneral) присваивается индекс этого корня; -
при последующих посещениях вершин из заданного набора (на возвратном движении) значение переменной
generalможет изменяться, а может и оставаться прежним — это зависит от того, где именно (в иерархическом отношении) была обнаружена очередная вершина заданного набора: если текущее значение переменнойgeneralявляется индексом какой-либо её родительской (прародительской, прапрародительской и т.д.), то это значение остаётся неизменным, а в противном случае оно должно быть заменено индексом вершины, являющейся родительской (непосредственно) для очередной обнаруженной вершины заданного набора; -
для обеспечения последнего в рекурсивной процедуре обхода используется локальная логическая переменная (флаг)
is_mutable_general, которая при входе в очередное поддерево (при движении от корня к переферии) принимает значениеfalse, запрещающее изменять значение внешней переменнойgeneral, а на возвратном движении, как только произойдет возврат в вершину с индексом содержащимся в текущий момент времени в переменнойgeneral, флагis_mutable_generalдолжен принимать значениеtrue, разрешающее изменение переменнойgeneral; -
при всём этом, при возвратном движении по подереву (от переферии к корню), если только изменение внешней переменной
generalразрешено (is_mutable_general = true), то её значение будет заменяться на значение индекса непосредственной родительской вершины (parent) для корня текущего дерева (поддерева,tree), но лишь в случае если счетчик числа посещенных вершинnumber_visitedне достиг ещё числа всех элементов заданного набораsetver.
Пусть, например, дерево представлено вложенными векторами tree, а подмножество индексов его вершин — множеством setver, тогда следующая функция возвращает индекс искомой ближайшей общей родительской вершины.
function find_general(tree::Vector, setver::Set) number_visited = 0 # - cчетчик числа посещённых вершин из набора setver general = 0 # - в этой переменной формируется результат (начальное значение не должно только входить в диапазон индексов вершин дерева) function recurstrace(tree, parent=0) # - выполняет рекурсивную обработку дерева сверху-вниз is_mutable_general = false # при движение по дереву вглубь от корня внешнюю переменную general изменять не надо for subtree in tree[begin:end-1] if number_visited < length(setver) recurstrace(subtree, tree[end]) end end # number_visited = число ранее посещенных вершин из заданного набора setver if tree[end] in setver number_visited +=1 if number_visited == 1 general = tree[end] end end # теперь - обратное движение по дереву - из глубины к корню if general==tree[end] is_mutable_general = true # т.е. при движении к корню, внешнюю переменную general снова нужно отслеживать end if is_mutable_general && number_visited < length(setver) general = parent end println((current=tree[end],parent=parent,general=general)) # - это для отладки end recurstrace(tree) return general end #-------------- TEST: ----------- tree=[[[[4],[5],[6],3],[[9],[[[17],[18],16],[19],10],7],2],[[11],[[14],[15],12],8],1] #find_general(tree,Set((3,4,6,7))) |> println # 2 find_general(tree,Set((6,10,16))) |> println # 2
Отладочный вывод при этом получится таким:
(current = 4, parent = 3, general = 0) (current = 5, parent = 3, general = 0) (current = 6, parent = 3, general = 3) (current = 3, parent = 2, general = 2) (current = 9, parent = 7, general = 2) (current = 17, parent = 16, general = 2) (current = 18, parent = 16, general = 2) (current = 16, parent = 10, general = 2) (current = 19, parent = 10, general = 2) (current = 10, parent = 7, general = 2) (current = 7, parent = 2, general = 2) (current = 2, parent = 1, general = 2) (current = 1, parent = 0, general = 2) 2




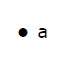

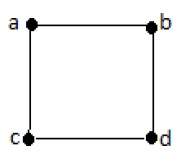
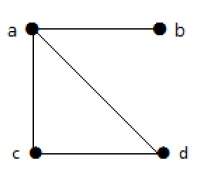


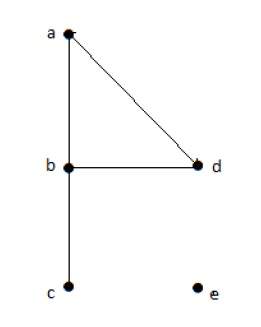
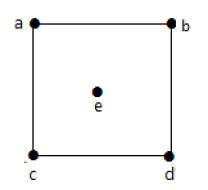
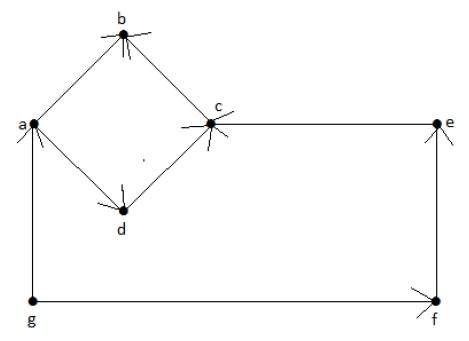
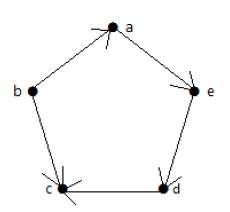


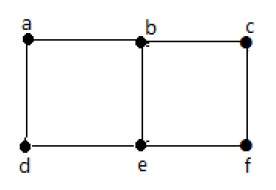
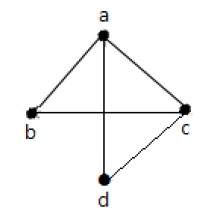
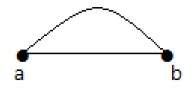
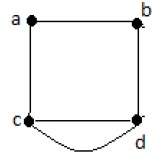
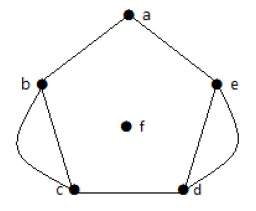
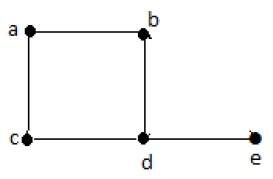
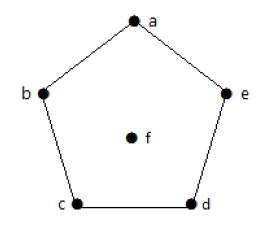


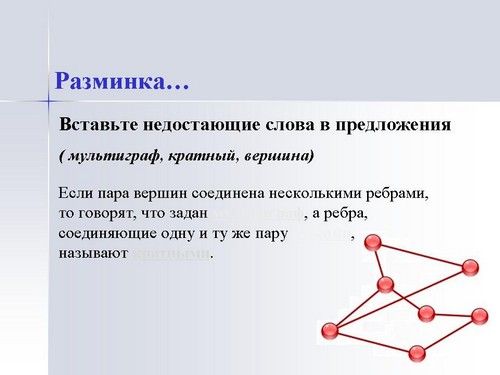
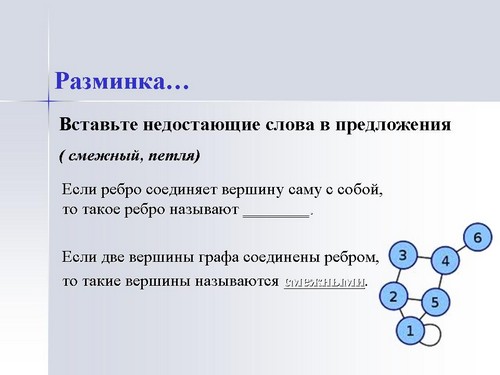



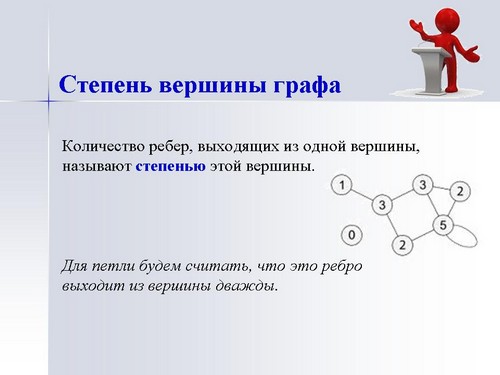





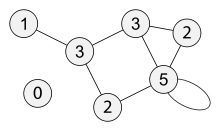























 Рис.
Рис.































