Как найти в строке максимальную подстроку - Avtoru.top

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Given a string s we have to find the lexicographical maximum substring of a string

Examples:

Input : s = "ababaa"
Output : babaa
Explanation : "babaa" is the maximum lexicographic substring formed from this string

Input : s = "asdfaa"
Output : sdfaa

The idea is simple, we traverse through all substrings. For every substring, we compare it with the current result and update the result if needed.

Below is the implementation:

C++

#include <bits/stdc++.h>

using namespace std;

string LexicographicalMaxString(string str)

{

string mx = "";

for (int i = 0; i < str.length(); ++i)

mx = max(mx, str.substr(i));

return mx;

}

int main()

{

string str = "ababaa";

cout << LexicographicalMaxString(str);

return 0;

}

Java

class GFG {

static String LexicographicalMaxString(String str)

{

String mx = "";

for (int i = 0; i < str.length(); ++i) {

if (mx.compareTo(str.substring(i)) <= 0) {

mx = str.substring(i);

}

return mx;

}

public static void main(String[] args)

{

String str = "ababaa";

System.out.println(LexicographicalMaxString(str));

}

Python3

def LexicographicalMaxString(str):

mx = ""

for i in range(len(str)):

mx = max(mx, str[i:])

return mx

if __name__ == '__main__':

str = "ababaa"

print(LexicographicalMaxString(str))

C#

using System;

public class GFG {

static String LexicographicalMaxString(String str)

{

String mx = "";

for (int i = 0; i < str.Length; ++i) {

if (mx.CompareTo(str.Substring(i)) <= 0) {

mx = str.Substring(i);

}

return mx;

}

public static void Main()

{

String str = "ababaa";

Console.WriteLine(LexicographicalMaxString(str));

}

Javascript

<script>

function LexicographicalMaxString(str)

{

var mx = "";

for (var i = 0; i < str.length; ++i) {

if (mx.localeCompare(str.substring(i)) <= 0) {

mx = str.substring(i);

}

return mx;

}

var str = "ababaa";

document.write(LexicographicalMaxString(str));

</script>

Complexity Analysis:

Time complexity : O(n²)
Auxiliary Space : O(n)

Optimization: We find the largest character and all its indexes. Now we simply traverse through all instances of the largest character to find lexicographically maximum substring.

Here we follow the above approach.

C++

#include <bits/stdc++.h>

using namespace std;

string LexicographicalMaxString(string str)

{

char maxchar = 'a';

vector<int> index;

for (int i = 0; i < str.length(); i++) {

if (str[i] >= maxchar) {

maxchar = str[i];

index.push_back(i);

}

string maxstring = "";

for (int i = 0; i < index.size(); i++) {

if (str.substr(index[i], str.length()) > maxstring) {

maxstring = str.substr(index[i], str.length());

}

return maxstring;

}

int main()

{

string str = "acbacbc";

cout << LexicographicalMaxString(str);

return 0;

}

Java

import java.io.*;

import java.util.*;

class GFG

{

static String LexicographicalMaxString(String str)

{

char maxchar = 'a';

ArrayList<Integer> index = new ArrayList<Integer>();

for (int i = 0; i < str.length(); i++)

{

if (str.charAt(i) >= maxchar)

{

maxchar = str.charAt(i);

index.add(i);

}

String maxstring = "";

for (int i = 0; i < index.size(); i++)

{

if (str.substring(index.get(i),

str.length()).compareTo( maxstring) > 0)

{

maxstring = str.substring(index.get(i),

str.length());

}

return maxstring;

}

public static void main (String[] args)

{

String str = "acbacbc";

System.out.println(LexicographicalMaxString(str));

}

Python3

def LexicographicalMaxString(st):

maxchar = 'a'

index = []

for i in range(len(st)):

if (st[i] >= maxchar):

maxchar = st[i]

index.append(i)

maxstring = ""

for i in range(len(index)):

if (st[index[i]: len(st)] >

maxstring):

maxstring = st[index[i]:

len(st)]

return maxstring

if __name__ == "__main__":

st = "acbacbc"

print(LexicographicalMaxString(st))

C#

using System;

using System.Collections.Generic;

class GFG{

static string LexicographicalMaxString(string str)

{

char maxchar = 'a';

List<int> index = new List<int>();

for(int i = 0; i < str.Length; i++)

{

if (str[i] >= maxchar)

{

maxchar = str[i];

index.Add(i);

}

string maxstring = "";

for(int i = 0; i < index.Count; i++)

{

if (str.Substring(index[i]).CompareTo(maxstring) > 0)

{

maxstring = str.Substring(index[i]);

}

return maxstring;

}

static public void Main()

{

string str = "acbacbc";

Console.Write(LexicographicalMaxString(str));

}

Javascript

<script>

function LexicographicalMaxString(str)

{

let maxchar = 'a';

let index = [];

for (let i = 0; i < str.length; i++)

{

if (str[i] >= maxchar)

{

maxchar = str[i];

index.push(i);

}

let maxstring = "";

for (let i = 0; i < index.length; i++)

{

if (str.substring(index[i],

str.length) > maxstring)

{

maxstring = str.substring(index[i],

str.length);

}

return maxstring;

}

let str = "acbacbc";

document.write(LexicographicalMaxString(str));

</script>

Complexity Analysis:

Time Complexity: O(n*m) where n is the length of the string and m is the size of index array.
Auxiliary Space: O(n + m) where n is the length of the string and m is the size of index array.

Last Updated :
17 Aug, 2022

Like Article

Save Article

Источник

Время на прочтение
4 мин

Количество просмотров 21K

Решил написать статью про алгоритм параллельного поиска максимально возможных пересечений двух строк. К написанию этой статьи меня побудило два желания:

Поделиться со всеми интересным алгоритмом и его реализацией на С++ (стандарт С++11);
Узнать, есть ли у данного алгоритма название и/или формальное описание;

Предыстория

Все началось с конкурса, проводимого Intel, о котором я узнал из поста. Суть конкурса сводилась к разработке и реализации алгоритма, решающего задачу нахождения в двух строках максимально длинной общей подстроки (переписывать полностью задачу сюда, думаю, не имеет смысла). К той задачке прилагался референсный код, т.е. решение на которое надо было «равняться». Чуть позже, из форума, посвященному этому конкурсу, стало понятно, что референсный код не решает эту задачу в том виде в котором она сформулирована на сайте Intel. Т.е. весь смысл конкурса сводился к следующему: «сделать программу, которая в точности повторяет вывод референсного кода, при одинаковых входных параметрах, только чтобы она была быстрее и параллельнее».
Ну да ладно, даже несмотря на абсурдность ситуации с описанием задачи, участие в конкурсе я сразу отбросил еще и потому что там могли участвовать только студенты и выпускники. Мне понравилась сама задача, та что описана на сайте.

Постановка задачи

Вот как я понял из описания эту задачу:
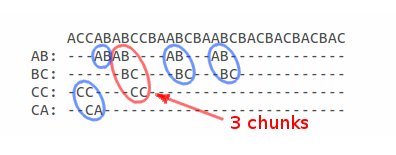
Есть две строки S1 и S2, нужно найти максимально длинную общую подстроку(и) (далее будем называть искомые подстроки — подмножествами), длина которой не меньше M. В качестве результата вывести ее координаты.
Координатами являются четыре целых числа.
Первые два относятся к строке S1 — это номера позиций первого и последнего символов найденной подстроки.
Вторые два числа имеют тоже значение, только относятся ко второй строке — S2.

Например, если мы имеем следующие входные параметры:

S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2

то ответом будет:
0 3 5 8

(в оригинальной постановки задачи координаты требуется выводить начиная с 1, но это уже детали вывода результата, и они никак не относится к самому алгоритму).

Также в требованиях к задаче указывается еще один дополнительный входной параметр K — число потоков, которое можно использовать для распаралеливания алгоритма.

Срезюмируем то что нам дается на вход:

S1, S2 — две строки, в которых необходимо произвести поиск;
M — минимально возможная длина искомой подстроки;
K — число потоков которое можно использовать для распаралеливания;

Алгоритм

По сути, идея решения очень проста и состоит из 3-х шагов:

Разбить S1 на минимально-возможные (длиной M) сегменты.
Спроецировать сегменты на S2.
На полученной проекции, найти максимально длинные подмножества (состоящие из максимального количества подряд идущих сегментов).

Рассмотрим работу алгоритма на следующем примере:

S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2
K = 2

1) Разбиваем S1 на сегменты, каждый длиной M = 2:
AB, BC, CC, CA

2) Проецируем каждый полученный сегмент на S2:

или в виде смещений:

таким образом мы получили проекцию S1 на S2:

дальше будем называть эту проекцию — картой пересечений.

По сути, карта пересечений представляет из себя матрицу координат всех сегментов длина которых равна M. Т.е. каждый элемент матрицы характеризует координату в строке S2, в то время как номер строки матрицы характеризует координату в строке S1. Имея в распоряжении карту пересечений, мы можем найти все пересечения (подмножества) и выбрать из них максимальные.

3) Производим поиск максимальных подмножеств (совокупность сегментов).
Если посмотреть на карту пересечений в символьном виде, то уже визуально можно найти максимально длинное подмножество:

если брать во внимание что каждый сегмент может служить началом подмножества, то используя карту пересечений, можно вычислить длину всех подмножеств, началом которых, являются сегменты составляющие эту проекцию.
Следующая иллюстрация демонстрирует, как производится вычисление длины подмножества, началом которого служит сегмент с координатой 5:

т.е. подмножество начинающееся с координаты 5 имеет максимальную длину — len = 4, для подмножества начинающегося с координаты 3 длина будет равна 2 и т.д.

Аналогичным образом, пробегая по каждому сегменту в карте пересечений, мы находим, что максимально длинным подмножеством является подмножество длиной 4 с координатами в S1 и S2 строках: 0 и 5 соответственно.

Распараллеливание

Как можно было заметить каждый шаг в решении этой задачи (шаги 1, 2, 3) легко распараллеливается, возможно применение Map-Reduce.

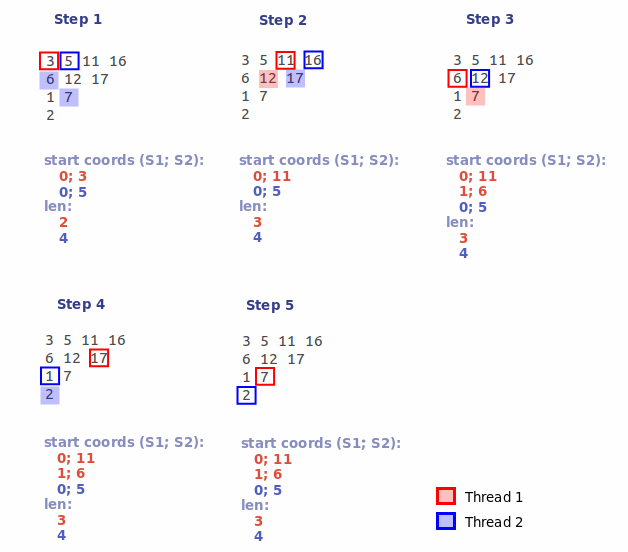
1, 2) Каждому потоку назначается свой сегмент (или несколько сегментов), для которого он строит проекцию сегмента. В совокупности, после того как для всех сегментов будут получены соответствующие проекции, получим готовую карту пересечений.

3.1) Каждому потоку назначается свой порядковый номер (n). Далее n-ый поток, начиная c n-ой позиции, обрабатывает каждый K-ый элемент карты пересечений. Таким образом мы разбиваем карту пересечений на несколько (число потоков) частей. Из этих частей, выбирают, вышеописанным образом, максимальные подмножества:

3.2) После того как все потоки отработают, мы получим несколько групп подмножеств. Из полученных групп выбираем группы с максимальной длиной сегментов. В нашем примере это две группы: группа образованная потоком #1, содержащая в себе сегменты длиной 3 символа (с начальными координатами: 0; 11 и 1; 6), а также группа образованная потоком #2, содержащая в себе один сегмент длиной 4 символа (с координатами 0; 5). Поскольку вторая группа имеет наибольшую длину сегментов, то первую группу отбрасываем сразу.
В результате мы получили начальные координаты подмножества (0; 5) и его длину — 4. Для нахождения конечных координат применяем формулу: end_coord = start_coord + len — 1.

Таким образом получаем ответ: 0 3 5 8.

Заключение

Я решил не затрагивать рассмотрение деталей реализации, данного алгоритма на С++, так как это уже выходит за рамки данной статьи. Ознакомится с реализацией данного алгоритма на С++ (С++11) можно здесь, для компиляции при помощи GCC не забываем ставить флаги -pthread и -std=с++0X.

Вопрос

Этот алгоритм пришел мне в голову как очевидное решение задачи, но я не знаю, есть ли у него официальное название и/или формальное описание?

Источник

Всем здравствуйте! Никак не могу решить следующую задачу.

«Подстрока»

Условие:

В этой задаче Вам требуется найти максимальную по длине подстроку данной строки такую, что каждый символ встречается в ней не более 𝑘 раз.

Входные данные:

В первой строке даны два целых числа 𝑛 и 𝑘 (1 ≤ 𝑛 ≤ 100000, 1 ≤ 𝑘 ≤ 𝑛), где 𝑛 — количество символов в строке. Во второй строке 𝑛 символов — данная строка, состоящая только из строчных латинских букв.

Выходные данные:

В выходной файл выведите два числа — длину искомой подстроки и номер её первого символа. Если решений несколько, то выберите самую левую подходящую подстроку.

Примеры:

Ввод 1:
3 1
abb

Вывод 1:
2 1

Ввод 2:
5 2
ababa

Вывод 2:
4 1

Мой код:

n, k = map(int, input().split())
s = input()
d = dict().fromkeys(s, 0)
l = 0

for i in range(n):
  sym = s[i]
  if d[sym] <= k:
    d[sym] += 1
  else:
    break

print(i - l, l + 1)

Тестирующая система выдаёт ошибку «Программа выдаёт неверный ответ». Подскажите, пожалуйста, в чём я совершил ошибку?

Источник

Задача:

Имеются строки и такие, что элементы этих строк символы из конечного алфавита . Требуется найти такую строку максимальной длины, что является и подстрокой , и подстрокой .

Определение:

Будем говорить, что строка является подстрокой строки , если существует такой индекс , что для любого справедливо .

Алгоритм

Пусть длина наибольшей общей подстроки будет . Заметим, что у строк и обязательно найдется общая подстрока длины , так как в качестве такой строки можно взять префикс наибольшей общей подстроки. Рассмотрим предикат , который для из области определения истинен, если у строк и есть общая подстрока длины , иначе ложен. Согласно замечанию, предикат должен по мере возрастания быть истинным до некоторого момента, а затем обращаться в ложь. Собственно, максимальное значение, при котором предикат истинен, является длиной наибольшей общей подстроки. Таким образом, требуется с помощью двоичного поиска найти это значение. В ходе работы придется проверять наличие общей подстроки заданной длины. Для этого будем использовать хеширование, чтобы улучшить асимптотику алгоритма. Алгоритм является эвристическим и может выдавать неверный ответ, так как совпадение хешей строк не гарантирует равенство строк. Поэтому нужно выполнить проверку нескольких случайных символов подстрок на совпадение, проиграв при этом по времени работы. Алгоритм работает следующим образом:

у строки хешируем подстроки заданной длины и полученные хеши записываем в Set,

у строки хешируем подстроки заданной длины и в случае совпадения хеша с элементом Set проверяем несколько случайных символов подстрок на совпадение.

Хеширование будем производить так же, как и в алгоритме Рабина-Карпа.

Псевдокод

— длина подстроки, найденная с помощью двоичного поиска.

— предикат, описанный в алгоритме.

bool f(i: int):
  hashes = хеши подстрок строки  длины 
  for j = 0 to |t| − i
    hash = hash(t[j ... j + i − 1])
    if hash in hashes
      if совпали несколько случайных символов подстрок
        return true
      else
        continue
  return false

Время работы

Проведем оценку асимптотики времени работы предложенного алгоритма. Посмотрим, сколько нам потребуется действий на каждом шаге двоичного поиска. Во-первых, хеширование подстрок строки и запись их в Set требует шагов. Во-вторых, хеширование подстрок строки и проверка их наличия в Set требует . Проверка на совпадение нескольких символов подстрок требует константное время. Значит, на каждый шаг двоичного поиска требуется действий. Заметим, что всего для завершения двоичного поиска потребуется шагов. Следовательно, суммарное время работы алгоритма будет действий.

См. также

Поиск подстроки в строке с использованием хеширования. Алгоритм Рабина-Карпа
Задача о наибольшей общей подпоследовательности

Источники информации

Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 3-е издание. Пер. с англ. — М.:Издательский дом «Вильямс», 2014. — 1328 с.: ил. — ISBN 978-5-8459-1794-2 (рус.) — страницы 1036–1041.

Источник

Самая длинная общая проблема подстроки — это проблема поиска самой длинной строки (или строк), которая является подстрокой (или подстроками) двух строк.

Задача отличается от задачи поиска Самая длинная общая подпоследовательность (LCS). В отличие от подпоследовательностей, подстроки должны занимать последовательные позиции в исходной строке.

Например, самая длинная общая подстрока строк ABABC, BABCA это строка BABC длина 4. Другие распространенные подстроки: ABC, A, AB, B, BA, BC, а также C.

Потренируйтесь в этой проблеме

Наивным решением было бы рассмотреть все подстроки второй строки и найти самую длинную подстроку, которая также является подстрокой первой строки. Временная сложность этого решения будет O((m + n) × m²), куда m а также n длина строк X а также Y, сколько потребуется (m+n) время для поиска подстроки, и есть m² подстроки второй строки. Мы можем оптимизировать этот метод, рассматривая подстроки в порядке уменьшения их длины и возвращая значение, как только любая подстрока совпадает с первой строкой. Но временная сложность в наихудшем случае остается неизменной, когда отсутствуют общие символы.

Можем ли мы сделать лучше?

Идея состоит в том, чтобы найти самый длинный общий суффикс для всех пар префиксов строк с помощью динамического программирования, используя отношение:

LCSuffix[i][j] = | LCSuffix[i-1][j-1] + 1 (if X[i-1] = Y[j-1])
| 0 (otherwise)

where,

0 <= i – 1 < m, where m is the length of string X
0 <= j – 1 < n, where n is the length of string Y

Например, рассмотрим строки ABAB а также BABA.

Наконец, самая длинная общая длина подстроки будет максимальной из этих самых длинных общих суффиксов всех возможных префиксов.

Следующее решение на C++, Java и Python находит длину самой длинной повторяющейся подпоследовательности последовательностей. X а также Y итеративно с использованием оптимальное основание собственность проблема ЛКС.

C++

#include <iostream>

#include <string>

#include <cstring>

using namespace std;

// Функция для поиска самой длинной общей подстроки последовательностей

// `X[0…m-1]` и `Y[0…n-1]`

string LCS(string X, string Y, int m, int n)

{

int maxlen = 0; // сохраняет максимальную длину LCS

int endingIndex = m; // сохраняет конечный индекс LCS в `X`

// `lookup[i][j]` хранит длину LCS подстроки `X[0…i-1]`, `Y[0…j-1]`

int lookup[m + 1][n + 1];

// инициализируем все ячейки таблицы поиска 0

memset(lookup, 0, sizeof(lookup));

// заполняем интерполяционную таблицу снизу вверх

for (int i = 1; i <= m; i++)

{

for (int j = 1; j <= n; j++)

{

// если текущий символ `X` и `Y` совпадают

if (X[i — 1] == Y[j — 1])

{

lookup[i][j] = lookup[i — 1][j — 1] + 1;

// обновляем максимальную длину и конечный индекс

if (lookup[i][j] > maxlen)

{

maxlen = lookup[i][j];

endingIndex = i;

}

// вернуть самую длинную общую подстроку, имеющую длину `maxlen`

return X.substr(endingIndex — maxlen, maxlen);

}

int main()

{

string X = «ABC», Y = «BABA»;

int m = X.length(), n = Y.length();

// Находим самую длинную общую подстроку

cout << «The longest common substring is « << LCS(X, Y, m, n);

return 0;

}

Скачать Выполнить код

результат:

The longest common substring is AB

Java

class Main

{

// Функция для поиска самой длинной общей подстроки последовательностей

// `X[0…m-1]` и `Y[0…n-1]`

public static String LCS(String X, String Y, int m, int n)

{

int maxlen = 0; // сохраняет максимальную длину LCS

int endingIndex = m; // сохраняет конечный индекс LCS в `X`

// `lookup[i][j]` сохраняет длину LCS подстроки

// `Х[0…i-1]`, `Y[0…j-1]`

int[][] lookup = new int[m + 1][n + 1];

// заполняем интерполяционную таблицу снизу вверх

for (int i = 1; i <= m; i++)

{

for (int j = 1; j <= n; j++)

{

// если текущий символ `X` и `Y` совпадают

if (X.charAt(i — 1) == Y.charAt(j — 1))

{

lookup[i][j] = lookup[i — 1][j — 1] + 1;

// обновляем максимальную длину и конечный индекс

if (lookup[i][j] > maxlen)

{

maxlen = lookup[i][j];

endingIndex = i;

}

// вернуть самую длинную общую подстроку, имеющую длину `maxlen`

return X.substring(endingIndex — maxlen, endingIndex);

}

public static void main(String[] args)

{

String X = «ABC», Y = «BABA»;

int m = X.length(), n = Y.length();

// Находим самую длинную общую подстроку

System.out.print(«The longest common substring is « + LCS(X, Y, m, n));

}

Скачать Выполнить код

результат:

The longest common substring is AB

Python

# Функция поиска самой длинной общей подстроки последовательностей `X[0…m-1]` и `Y[0…n-1]`

def LCS(X, Y, m, n):

maxLength = 0 # хранит максимальную длину LCS

endingIndex = m # сохраняет конечный индекс LCS в `X`.

# `lookup[i][j]` хранит длину LCS подстроки `X[0…i-1]` и `Y[0…j-1]`

lookup = [[0 for x in range(n + 1)] for y in range(m + 1)]

# заполняет интерполяционную таблицу снизу вверх

for i in range(1, m + 1):

for j in range(1, n + 1):

#, если текущий символ `X` и `Y` совпадают

if X[i — 1] == Y[j — 1]:

lookup[i][j] = lookup[i — 1][j — 1] + 1

# обновляет максимальную длину и конечный индекс

if lookup[i][j] > maxLength:

maxLength = lookup[i][j]

endingIndex = i

# возвращает самую длинную общую подстроку, имеющую длину maxLength.

return X[endingIndex — maxLength: endingIndex]

if __name__ == ‘__main__’:

X = ‘ABC’

Y = ‘BABA’

m = len(X)

n = len(Y)

# Найти самую длинную общую подстроку

print(‘The longest common substring is’, LCS(X, Y, m, n))

Скачать Выполнить код

результат:

The longest common substring is AB

Временная сложность приведенного выше решения равна O(m.n) и требует O(m.n) дополнительное пространство, где m а также n длина строк X а также Y, соответственно. Пространственная сложность приведенного выше решения может быть улучшена до O(n) поскольку для вычисления LCS строки таблицы LCS требуются только решения для текущей строки и предыдущей строки. Мы также можем хранить в строках только ненулевые значения. Мы можем сделать это, используя хеш-таблицы вместо массивов.

Мы также можем решить эту проблему в O(m + n) время с помощью обобщенного суффиксное дерево. Мы скоро обсудим подход суффиксного дерева в отдельном посте.

Упражнение: Напишите оптимизированный по пространству код для итеративной версии.

Использованная литература: https://en.wikipedia.org/wiki/Longest_common_substring_problem

Источник

C++

Java

Python3

C#

Javascript

C++

Java

Python3

C#

Javascript

Предыстория

Постановка задачи

Алгоритм

Распараллеливание

Заключение

Вопрос

«Подстрока»

Мой код:

Алгоритм

Псевдокод

Время работы

См. также

Источники информации

C++

Java

Python

Не пропустите также: