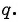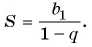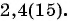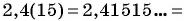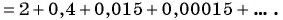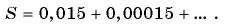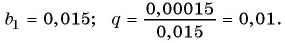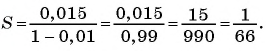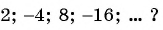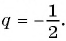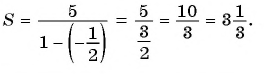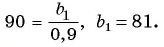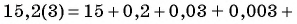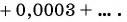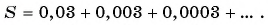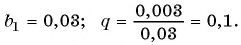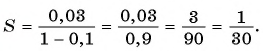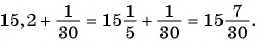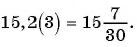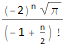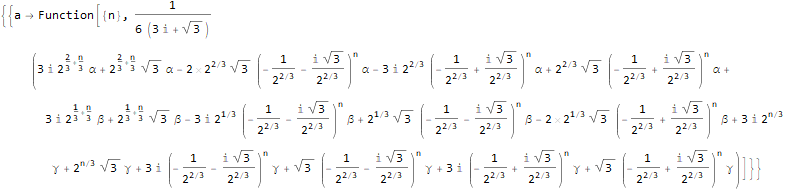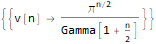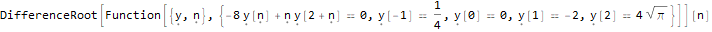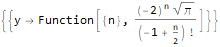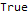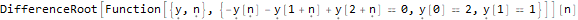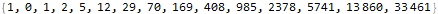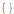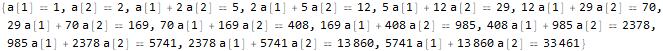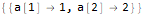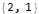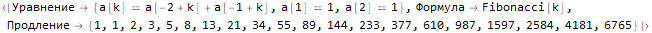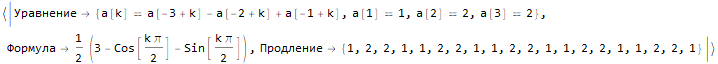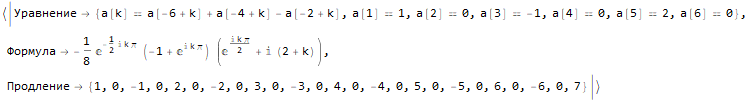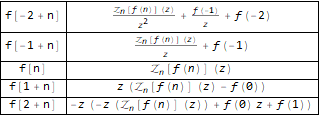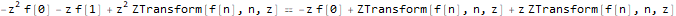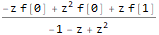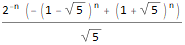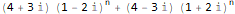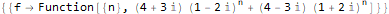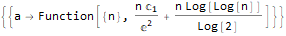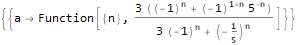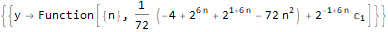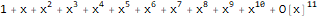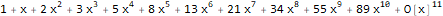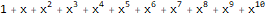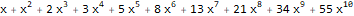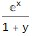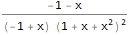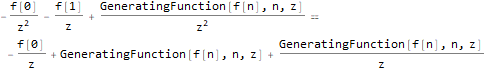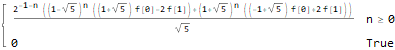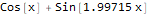На этой странице вы узнаете
- Как мы привыкаем к последовательностям на протяжение нашей жизни?
- Что такое золотое сечение?
Что значит “действовать последовательно”? Мы делаем что-то по определенным принципам, не нарушаем правила. Все наши действия будут иметь логику, которую мы сможем отследить. В математике также можно составлять числа в строгом порядке. Называться такие ряды будут последовательностями.
Понятие последовательности
Посмотрим на несколько рядов чисел и порассуждаем.
По какому принципу составлен ряд чисел 1, 2, 3, 4, 5 и т.д.? Всё просто: к каждому новому числу прибавляют единицу.
А какой принцип в ряде чисел 2, 4, 6, 8 и т.д.? Здесь к каждому новому числу прибавляют 2.
Что можно сказать про ряд 2, 4, 8, 16, 32 и т.д.? Каждое новое число умножают на 2.
Все приведенные выше ряды чисел будут называться последовательностью. Как описать ее одним термином?
Ненадолго вспомним функции чисел. Разберем функцию f(x)=x+1.
Если x = 0, то f(x) = 1.
Если x = 1, то f(x) = 2.
Если x = 2, то f(x) = 3.
Если x = 3, то f(x) = 4.
Внимательно посмотрим на значения функции: это и будет наша первая последовательность 1, 2, 3, 4, 5. Мы можем сделать вывод, что последовательность можно задать с помощью функции.
На самом деле, любая последовательность и есть функция. Теперь дадим определение.
Последовательность — функция, заданная на множестве натуральных чисел или его части.
То есть подставлять в такую функцию можно только натуральные числа.
Подробнее про функцию, ее значение, область определения и другие свойства можно прочесть в статье «Определение и график функции».
Аргумент будет обозначать порядковый номер числа в последовательности. Первое число в последовательности будет задаваться х = 1, второе число х = 2, n число как х = n.
Числа, которые образуют последовательность, — это члены последовательности. И у каждого члена последовательности есть свой порядковый номер.
Как же обозначаются члены последовательности? Не будем же мы каждый раз писать “двадцатый член последовательности” или что-то подобное?
Для членов последовательности существует свое обозначение: an, где индекс после буквы а обозначает порядковый номер члена последовательности.
Например,
- а1 — первый член последовательности,
- а20 — двадцатый член последовательности,
- а100 — сотый член последовательности и так далее.
Таким образом можно обозначить любой член последовательности.
Вспомним считалочки, которые мы использовали в играх в детстве: “Раз, два, три, четыре, пять, вышел зайчик погулять”. Первая строчка многих подобных считалочек — это последовательность натуральных чисел 1, 2, 3, 4, 5.
Дальше в школе на уроках физкультуры нас распределяют по командам, присваивая каждому свой номер. И это тоже последовательность.
Потом мы поступаем в вуз и попадаем в списки абитуриентов, тоже — в ещё одну последовательность.
Способы задания числовой последовательности
Рассмотрим, каким способами можно задать числовую последовательность.
Первый способ — это указать все члены последовательности. Однако он не всегда удобен, поскольку в последовательности может быть бесконечное количество членов.
Второй способ мы уже использовали — это задать общую формулу. Тогда можно будет найти любой член последовательности. В этом случае нужно будет подставить порядковый номер члена последовательности в формулу.
Допустим, дана последовательность an = 3n + 40, и нам нужно найти третий член последовательности. Тогда нужно подставить n = 3 в формулу:
a3 = 3 * 3 + 40 = 9 + 40 = 49.
Аналогичным способом можно будет найти любой член в данной последовательности.
Рассмотрим ещё пример. Что мы можем сказать про последовательность чисел 2, 4, 12, 32, 88 и так далее? Определенный закон здесь вывести достаточно сложно. Всё потому, что следующий член последовательности зависит от предыдущего.
Обратим внимание на третий член последовательности: 12 = 2 * 6 = 2(2 + 4). А если посмотреть на четвертый член последовательности? 32 = 2 * 16 = 2(4 + 12).
И так с каждым членом последовательности: он равен удвоенной сумме двух предыдущих членов.
Это еще один способ задания последовательности, когда используется рекуррентная формула. Ее особенность в том, что каждый член последовательности выражен с помощью предыдущих членов последовательности.
Одним из примеров такой последовательности будут числа Фибоначчи. Это последовательность, в которой первые два члена равны 1, а все следующие являются суммой двух предшествующих им.
Числа Фибоначчи выглядят так: 1, 1, 2, 3, 5, 8, 13, 21 и так далее.
Как задать их с помощью рекуррентной формулы? Допустим, мы хотим найти член an в этой последовательности. Мы знаем, что для этого нужно сложить два предыдущих члена, то есть an-1 и an-2. Вот мы и получили формулу.
an = an-1 + an-2.
Золотое сечение — это пропорциональное деление отрезка на неравные части. При этом весь отрезок относится к большей части, как меньшая часть этого отрезка относится в большей его части.
Золотое сечение можно представить в виде “завитка”, который вписан в прямоугольник. Прямоугольник будет делиться на квадраты, стороны которых равны числам Фибоначчи.
Принципы золотого сечения позволяет построить гармоничную композицию, а значит, применяются в архитектуре и искусстве. Более того, их можно встретить в природе. Форма ракушек, завитки ростков, семена подсолнуха, шишки, даже ураган (если посмотреть на него сверху) имеют форму золотого сечения или приближенную к нему.

Виды числовых последовательностей
Возьмем обычную последовательность натуральных чисел 1, 2, 3, 4, 5, …, an. Мы можем сказать, что каждый следующий член последовательности больше, чем предыдущий. Такие последовательности называются возрастающими.
Если перевернуть ее и получить последовательность 5, 4, 3, 2, 1, …, an — последовательность будет называться убывающей. Для такой последовательности обязательно, чтобы каждый следующий член был меньше, чем предыдущий.
Что, если мы просто будем менять знак числа? Например, −1, 1, −1, 1 и так далее? Тогда последовательность будет ни убывающей и ни возрастающей.
Такую последовательность можно задать с помощью формулы an = (-1)n.
Разумеется, не все последовательности бывают бесконечными. Ранее мы рассматривали только бесконечные последовательности: в них можно было подставить любое значение n.
Возьмем последовательность простых однозначных чисел: 2, 3, 5, 7. Больше однозначных чисел нет — продолжить последовательность мы не можем.
Последовательность, в которой ограничено количество членов, будет называться конечной последовательностью. Если же в последовательности не ограничено количество членов, и их можно задавать до бесконечности, то такая последовательность будет называться бесконечной последовательностью.
Фактчек
- Последовательность — функция, заданная на множестве натуральных чисел или его части.
- Каждый член последовательности имеет свой номер, который отображается в индексе. Например, a1 — первый член последовательности, а a25 — двадцать пятый.
- Последовательность можно задать несколькими способами. Во-первых, выписать все члены последовательности. Во-вторых, задать общую формулу. В-третьих, задать рекуррентную формулу.
- Рекуррентная формула — это формула, в которой каждый следующий член последовательности зависит от предыдущих. Ярким примером такой последовательности являются числа Фибоначчи, где каждое число является суммой двух предыдущих.
- Последовательности бывают возрастающими и убывающими. В возрастающих последовательностях каждый следующий член больше предыдущего, а в убывающей каждый следующий член последовательности меньше предыдущего. В бесконечных последовательностях не ограничено количество членов. А в конечных последовательностях количество членов ограничено.
Проверь себя
Задание 1.
Выберите конечную числовую последовательность.
- Числа Фибоначчи.
- Четные положительные числа.
- Нечетные трехзначные числа.
- Нечетные отрицательные числа.
Задание 2.
Выберите убывающую последовательность.
- 10, 9, 8, 7, 6, 5, …, an
- Числа Фибоначчи
- 1, 2, 3, 4, 5, …, an
- 1, 3, 5, 7, 9, …, an
Задание 3.
Выберите возрастающую последовательность.
- 100, 90, 80, …, an
- (frac{1}{2}), (frac{1}{3}), (frac{1}{4}), …, an
- Числа Фибоначчи
- −1, −2, -3, …, an
Задание 4.
Какая последовательность является числами Фибоначчи?
- 1, 2, 3, 4, 5, …
- 1, 1, 2, 3, 5, 8, …
- 1, 4, 9, 16, 25, …
- 1, (frac{1}{2}), (frac{1}{3}), (frac{1}{4}), …
Ответы: 1. — 3 2. — 1 3. — 3 4. — 2
Прогрессия — это последовательность величин, каждая последующая из них находится в некоторой, общей для всей прогрессии, зависимости от предыдущей.
Содержание:
Числовая последовательность
В жизни мы часто встречаемся с функциями, областью определения которых является множество натуральных чисел. Например, стоимость проезда в пригородном транспорте зависит от дальности поездки и задается функцией
Функция стоимости проезда задана таблично, областью определения функции является множество натуральных чисел 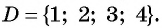
Примером числовой последовательности является последовательность положительных четных чисел: 2; 4; 6; 8; … . Число 2 — первый член последовательности, число 4 — второй и т. д. Ясно, что на 5-м месте будет число 10 (пятый член последовательности), а на 100-м — число 200 (сотый член последовательности).
Еще один пример — последовательность чисел, обратных натуральным числам: 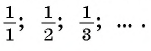
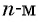
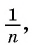
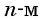
Последовательности могут быть конечными и бесконечными. Например, последовательность двузначных чисел 10; 11; …; 99 является конечной, так как содержит конечное число членов. А последовательность нечетных натуральных чисел — бесконечная.
Определение числовой последовательности
Определение:
Числовой последовательностью называется функция, определенная на множестве 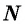
Числа, образующие последовательность (значения функции), называются членами последовательности. Они записываются буквами с индексами, обозначающими номер члена последовательности: 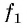
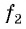
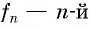
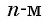
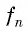
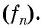
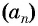
Если 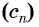
Последовательности, так же как и функции, могут быть заданы различными способами.
Аналитический способ — это задание последовательности с помощью формулы ее 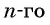
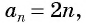
С помощью формулы 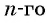
Например, пусть последовательность 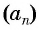
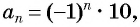
Чтобы найти некоторый член последовательности с помощью формулы 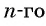
Для задания последовательностей часто используется рекуррентный способ (от лат. recurrentis — возвращающийся). Он заключается в вычислении следующих членов последовательности по предыдущим.
Например, условия 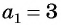
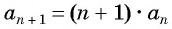
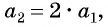
Пример №1
Найдите несколько членов последовательности 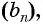
Решение:
Запишем несколько членов этой последовательности в ряд: 1; 1; 2; 3; 5; … .
Полученную последовательность чисел называют последовательностью Фибоначчи по имени итальянского математика Леонардо Фибоначчи (1180—1240).
Формула n-го члена последовательности
Пример №2
Последовательность 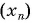
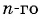
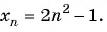
Решение:
Пример №3
Последовательность задана формулой 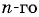
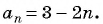
а) -2; б) -7?
Решение:
Для того чтобы определить, является ли число членом последовательности, нужно определить, имеет ли натуральные корни уравнение:
а) 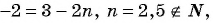
б) 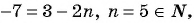
Пример №4
Для каких членов последовательности 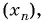
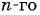
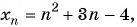
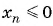
Решение:
Подставим в неравенство 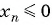
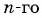
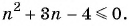
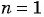
Рекуррентный способ задания последовательности
Пример №5
Запишите 5 первых членов последовательности 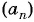
Решение:
Пример №6
Запишите несколько первых членов последовательности 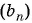
Задайте эту последовательность формулой 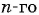
Решение:
Получим следующую последовательность: 8; -8; 8; -8; …. На нечетных местах этой последовательности стоят члены, равные числу 8, а на четных — числу -8, значит, формула 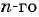
Арифметическая прогрессия
Рассмотрим задачу. В горной местности температура воздуха летом при подъеме на каждые 100 м в среднем понижается на 0,7 °С. У подножия горы температура равна 26 °С. Найдите температуру воздуха на высоте 100 м; 200 м; 300 м.
Решение:
Температура воздуха на высоте 100 м равна 26 °С — 0,7 °С = 25,3 °С. На высоте 200 м температура будет равна 25,3 °С — 0,7 °С = 24,6 °С, а на высоте 300 м — 24,6 °С — 0,7 °С = 23,9 °С.
Ответ: 25,3 °С; 24,6 °С; 23,9 °С.
Решая задачу, мы получили последовательность 26; 25,3; 24,6; … . Каждый член этой последовательности равен предыдущему, сложенному с числом -0,7. Многие практические задачи приводят к последовательностям такого вида. Они называются арифметическими прогрессиями (от лат. progression — движение вперед).
Определение арифметической прогрессией
Определение:
Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же для данной последовательности числом, т. е.
Число 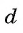
Из равенства 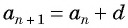
Чтобы задать арифметическую прогрессию 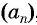
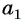
Например, если 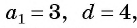
Если 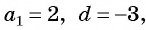
Если 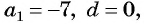
Чтобы вычислить любой член арифметической прогрессии, не вычисляя все предыдущие члены, используют формулу 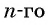
Выведем эту формулу. Если 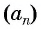
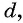
Сложим эти равенства:
После упрощения получим:
Так как число слагаемых 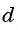
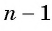
Получили формулу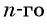
Формула 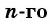
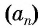
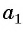
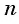
Пример №7
Последовательность 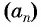
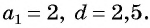
Решение:
По формуле 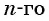
Ответ: 249,5.
Пример №8
Последовательность 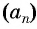
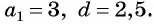
Решение:
а) По условию 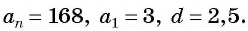
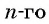
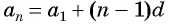
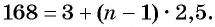
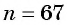
б) Подставим значения 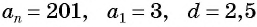
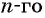
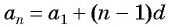
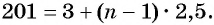
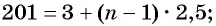
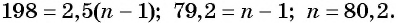
Ответ: а) число 168 является членом этой прогрессии; б) число 201 не является членом этой прогрессии.
Характеристическое свойство арифметической прогрессии
В арифметической прогрессии каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним)
членов, т. е. 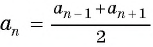
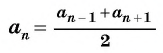
Доказательство. В арифметической прогрессии 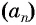
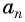
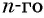
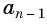
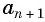
Найдем их среднее арифметическое:
Справедливо и обратное утверждение:
если в последовательности каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним) членов, то последовательность является арифметической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности 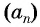
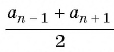
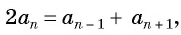
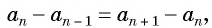
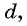
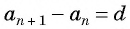
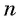
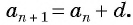
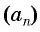
Оба утверждения можно объединить в одно, которое называется характеристическим свойством арифметической прогрессии:
числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:
Пример №9
Проверьте, является ли арифметической прогрессией последовательность, заданная формулой
Решение:
Запишем для 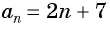
Найдем среднее арифметическое этих членов:
По характеристическому свойству арифметической прогрессии последовательность 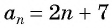
Решение арифметической прогрессии
Пример №10
Последовательность 2; 12; 22; … является арифметической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является арифметической прогрессией, то найдем ее разность 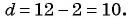
Пример №11
Известны члены арифметической прогрессии: 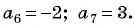
Решение:
Найдем разность арифметической прогрессии:
Формула n-го члена арифметической прогрессии
Пример №12
Последовательность 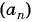
Решение:
По формуле 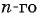
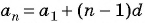
Пример №13
Запишите формулу 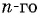
Решение:
По условию 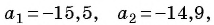
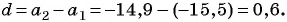
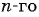
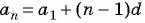
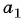
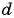
Подставим 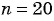
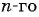
Пример №14
В арифметической прогрессии 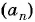
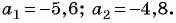
Решение:
Так как 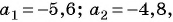
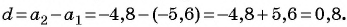
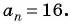
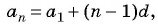
Пример №15
В арифметической прогрессии 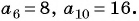
Решение:
По условию
Решим систему уравнений
Вычтем из второго уравнения первое, получим 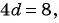
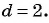
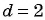
Характеристическое свойство арифметической прогрессии
Пример №16
Найдите восьмой член арифметической прогрессии 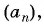
Решение:
По характеристическому свойству арифметической прогрессии 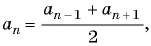
Пример №17
При каком значении 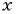
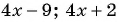
Решение:
По характеристическому свойству прогрессии последовательность является арифметической прогрессией, если каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:
Решим полученное уравнение:
Формула суммы n первых членов арифметической прогрессии
Рассмотрим задачу. Двое друзей решили улучшить знание английского языка и каждый день учить на 3 новых слова больше, чем в предыдущий. Сколько слов выучит каждый из друзей за 10 дней, если они начнут с одного слова?
Для решения этой задачи нужно найти сумму десяти первых членов арифметической прогрессии 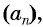
Возникает вопрос: как найти эту сумму, не вычисляя всех десяти членов прогрессии?
В общем виде эта задача приводит к необходимости вывода формулы суммы 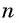
Для того чтобы вывести эту формулу, докажем свойство: суммы двух членов конечной арифметической прогрессии, равноудаленных от ее концов, равны между собой и равны сумме первого и последнего ее членов, т. е.
В общем виде:
Доказательство:
Преобразуем слагаемые в левой части равенства, воспользовавшись формулой 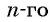
Тогда получим:
С помощью доказанного свойства найдем, например, сумму всех натуральных чисел от 1 до 50.
Натуральные числа от 1 до 50 составляют арифметическую прогрессию 1; 2; 3; …; 50. Первый член этой прогрессии равен 1, последний равен 50. Всего в этой прогрессии 50 членов.
Поскольку 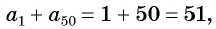
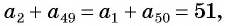
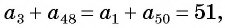
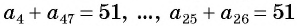
Выведем формулу суммы 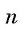
Обозначим 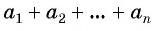
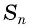
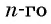
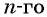
Сложим эти два равенства и получим:
По свойству 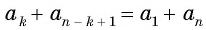
Число всех таких пар сумм равно 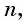
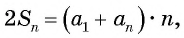
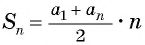
Идея такого доказательства принадлежит выдающемуся немецкому математику К. Гауссу (1777—1855).
Формулу суммы 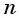
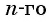
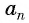
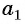
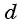
Если известен первый член прогрессии и разность, то удобно использовать формулу
Применим эту формулу к задаче о количестве выученных иностранных слов и получим: 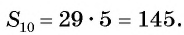
Пример №18
Найдите сумму пятидесяти первых членов арифметической прогрессии 3; 7; 11; 15; … .
Решение:
В этой прогрессии первый член равен 3, а разность 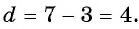
для и получим:
Ответ: 5050.
Пример №19
В арифметической прогрессии 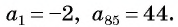
Решение:
Применим формулу суммы 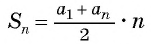
Ответ: 1785.
Пример №20
Найдите сумму шести первых членов арифметической прогрессии, если ее первый член равен -2, а разность прогрессии равна 0,4.
Решение:
Воспользуемся формулой
так как 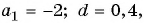
Пример №21
Найдите сумму 4 + 7 + 10+ … + 100, если ее слагаемые — последовательные члены арифметической прогрессии.
Решение:
Последовательность 4, 7, 10, …, 100 является арифметической прогрессией, в которой 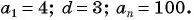
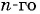
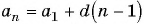
Воспользуемся формулой суммы 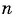
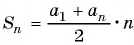
Пример №22
Найдите количество членов арифметической прогрессии, зная, что их сумма равна 430, первый член прогрессии равен -7, а разность прогрессии равна 3.
Решение:
Воспользуемся формулой суммы 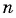
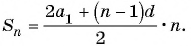
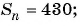
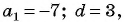
Так как 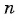
Пример №23
В арифметической прогрессии 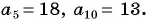
Решение:
Найдем 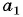
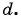
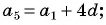
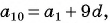
Решим полученную систему способом сложения:
Тогда
Примем четвертый член данной прогрессии за первый член некоторой другой прогрессии, тогда семнадцатый член данной прогрессии станет четырнадцатым (17 — 4 + 1 = 14) членом новой прогрессии. Искомая сумма равна:
Пример №24
Найдите сумму всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5.
Решение:
Первое число в последовательности всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5, — это число 18. Каждое следующее число равно предыдущему, сложенному с числом 26. Последнее четное число, которое при делении на 13 дает в остатке 5, — это число 278. Поскольку рассматриваются только четные числа, то разность прогрессии равна 26. Найдем номер числа прогрессии, равного 278: 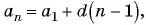
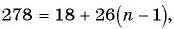
Геометрическая прогрессия
Рассмотрим задачу. Вкладчик положил в банк 1000 р. на
депозит, по которому сумма вклада увеличивается ежегодно на 5 %. Какая сумма будет у него через 1 год, 2 года, 6 лет?
Решение:
Начальная сумма в 1000 р. через год увеличится на 5 % и составит 105 % от 1000 р. Найдем 105 % = 1,05 от 1000 р.: 1000 • 1,05 = 1050 (р.).
Через два года сумма вклада станет равной 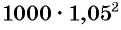
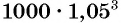
Через шесть лет сумма будет равна
Многие практические задачи приводят к последовательностям такого вида. Они называются геометрическими прогрессиями.
Определение геометрической прогрессии
Определение:
Геометрической прогрессией называется числовая последовательность, первый член которой отличен от нуля, а каждый следующий, начиная со второго, равен предыдущему, умноженному на одно и то же для данной последовательности число, не равное нулю, т. е.
Число 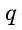
Из равенства 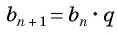
Чтобы задать геометрическую прогрессию 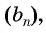
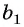
Например, если 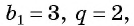
Если 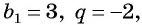
Если 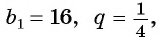
вид
Если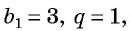
Чтобы вычислить любой член геометрической прогрессии, не вычисляя все предыдущие члены, используют формулу 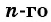
Выведем эту формулу. Если 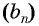
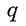
Перемножим эти равенства между собой:
Разделим обе части равенства на произведение 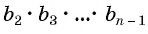
Так как число множителей 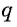
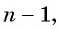
Получили формулу 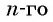
Формула 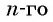
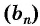
Пример №25
Последовательность 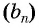
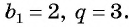
Решение:
По формуле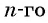
Ответ: 4374.
Пример №26
Последовательность 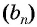
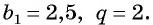
Решение:
По условию 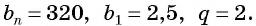
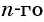
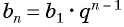
Решим это уравнение:
Так как 8 — натуральное число, то число 320 является членом этой прогрессии с номером 8.
Ответ: число 320 является членом этой прогрессии.
- Заказать решение задач по высшей математике
Характеристическое свойство геометрической прогрессии
В геометрической прогрессии модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, т. е. 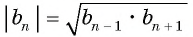
или 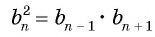
Доказательство:
В геометрической прогрессии 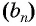
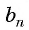
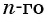
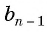
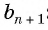
Найдем среднее пропорциональное (среднее геометрическое) соседних с 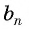
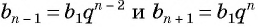
Выполним преобразования в правой части равенства:
откуда получим, что
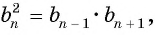
Справедливо и обратное утверждение:
- если в последовательности чисел, отличных от нуля, модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, то последовательность является геометрической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности 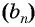
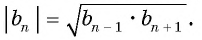
Тогда 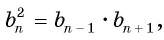
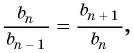
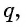
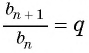
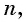
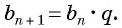
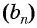
Оба утверждения можно объединить в одно, которое называется характеристическим свойством геометрической прогрессии:
- числовая последовательность, все члены которой отличны от нуля, является геометрической прогрессией тогда и только тогда, когда модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего ее членов:
Пример №27
Проверьте, является ли геометрической прогрессией последовательность, заданная формулой
Решение:
Запишем для 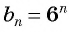
Найдем среднее пропорциональное этих членов:
По характеристическому свойству геометрической прогрессии последовательность 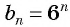
Решение геометрической прогрессии
Пример №28
Последовательность 2; 10; 50; … является геометрической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является геометрической прогрессией, то найдем ее знаменатель 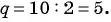
Пример №29
Известны члены геометрической прогрессии:
Найдите знаменатель этой прогрессии.
Решение:
Так как знаменатель геометрической прогрессии равен отношению любого ее члена к предыдущему, то
Формула n-го члена геометрической прогрессии:
Пример №30
Последовательность 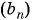
Решение:
По формуле 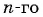
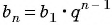
Пример №31
Запишите формулу 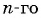
Решение:
По условию 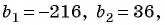
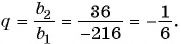
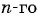
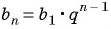
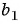
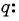
Подставим 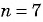
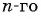
Пример №32
Найдите номер члена геометрической прогрессии 0,1; 0,3; …, равного 218,7.
Решение:
Найдем знаменатель прогрессии:
Известно, что 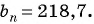
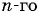
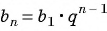
Пример №33
Найдите знаменатель и первый член геометрической прогрессии 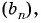
Решение:
По условию
Составим систему уравнений
Разделим второе уравнение на первое и получим:
Подставим это значение 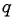
Характеристическое свойство геометрической прогрессии
Пример №34
Найдите сорок девятый член геометрической прогрессии, если сорок восьмой ее член равен 4, а пятидесятый ее член равен 9.
Решение:
Воспользуемся характеристическим свойством геометрической прогрессии 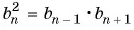
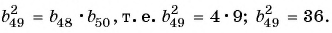
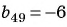
Пример №35
При каком значении 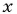
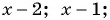
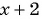
Решение:
По характеристическому свойству прогрессии последовательность является геометрической прогрессией, если каждый ее член, начиная со второго, равен среднему пропорциональному предыдущего и последующего членов:
Решим полученное уравнение:
Формула суммы n первых членов геометрической прогрессии
Немало легенд связано с геометрической прогрессией.
Наиболее известная из них рассказывает об изобретателе шахмат.
По легенде, когда создатель шахмат показал свое изобретение правителю страны, тому так понравилась игра, что он дал изобретателю право самому выбрать награду. Мудрец попросил у правителя за первую клетку шахматной доски заплатить ему одно зерно пшеницы, за вторую — два, за третью — четыре и т. д., удваивая количество зерен на каждой следующей клетке (рис. 96).
Правитель быстро согласился и приказал казначею выдать мудрецу нужное количество зерна. Однако когда казначей показал расчеты, то оказалось, что расплатиться невозможно, разве только осушить моря и океаны и засеять все пшеницей.
Число зерен, которое попросил мудрец, равно сумме членов геометрической прогрессии 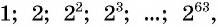
Выведем формулу, по которой можно находить сумму 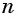
Обозначим сумму 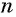
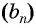
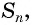
Умножим обе части этого равенства на знаменатель прогрессии 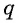
Вычтем из второго равенства первое и получим:
т. e. 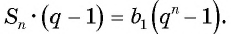
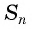
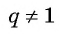
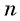
Если 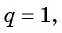
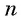
Формула суммы n первых членов геометрической прогрессии:
Вычислим по формуле суммы 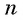
Первый член геометрической прогрессии 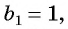
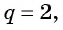
Тогда
Такого количества пшеницы человечество не собрало за всю свою историю.
Пример №36
Найдите сумму десяти первых членов геометрической прогрессии 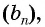
Решение:
Применим формулу суммы 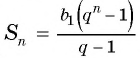
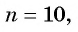
Ответ: 511,5.
Пример №37
Найдите сумму двенадцати первых членов геометрической прогрессии 3; -6; 12; -24; … .
Решение:
Подставим в формулу 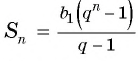
Ответ. -4095.
Пример №38
Найдите сумму пяти первых членов геометрической прогрессии 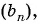
Решение:
Найдем знаменатель и первый член геометрической прогрессии:
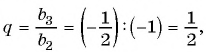
По формуле 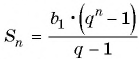
Пример №39
Сумма членов геометрической прогрессии равна 605. Найдите количество членов прогрессии, если
Решение:
Подставим в формулу 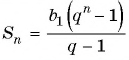
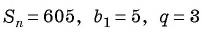
Пример №40
В геометрической прогрессии 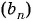

Решение:
Найдем знаменатель прогрессии:
Подставим в формулу 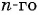
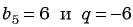
По формуле 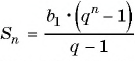
Пример №41
В геометрической прогрессии 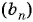
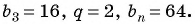
Решение:
Зная, что третий член геометрической прогрессии равен 16, а ее знаменатель равен 2, по формуле 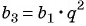
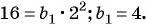
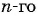
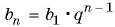
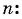
По формуле суммы 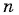
Сумма бесконечно убывающей геометрической прогрессии
Любую обыкновенную дробь можно записать в виде десятичной дроби — конечной или бесконечной периодической дроби. Например, 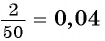
Вы рассматривали правило записи конечной десятичной дроби в виде обыкновенной дроби (например, 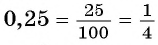
Выясним, как бесконечную периодическую десятичную дробь записать в виде обыкновенной дроби.
Рассмотрим, например, бесконечную периодическую десятичную дробь 0,(7) = 0,7777… . Определим, какой обыкновенной дроби равно это число.
Запишем дробь 0,(7) в виде суммы разрядных слагаемых:
В данном случае необходимо найти сумму бесконечного числа слагаемых.
Слагаемые этой суммы являются членами бесконечной
геометрической прогрессии со знаменателем 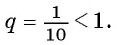
Определение. Бесконечно убывающей геометрической прогрессией называется такая бесконечная геометрическая прогрессия, у которой знаменатель
Например, геометрическая прогрессия 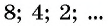
Геометрическая прогрессия 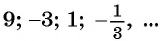
Для того чтобы представить бесконечную периодическую десятичную дробь в виде обыкновенной, нужно найти сумму бесконечно убывающей геометрической прогрессии. Ее обозначают буквой 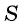
Покажем идею вывода формулы суммы бесконечно убывающей геометрической прогрессии.
Рассмотрим бесконечную геометрическую прогрессию 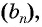
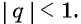
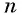
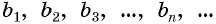
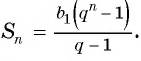
Представим, что п неограниченно возрастает (говорят, что стремится к бесконечности, и записывают 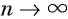
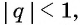
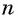
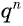
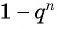
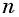
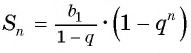
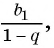
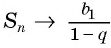
Число 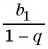
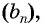
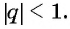
Обозначим сумму бесконечно убывающей геометрической прогрессии буквой 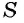
Вычислим по этой формуле сумму разрядных слагаемых:
Слагаемые этой суммы образуют бесконечно убывающую геометрическую прогрессию 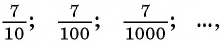
а знаменатель равен
Сумма бесконечно убывающей геометрической прогрессии:
Так как 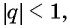
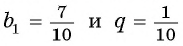
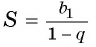
Значит,
Таким образом, бесконечную периодическую десятичную дробь 0,(7) можно записать в виде обыкновенной дроби 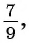
Таким же способом можно любую бесконечную периодическую десятичную дробь представить в виде обыкновенной дроби.
Чтобы записать бесконечную периодическую десятичную дробь в виде обыкновенной дроби, нужно:
- Представить число в виде суммы разрядных слагаемых.
- Выделить сумму бесконечно убывающей геометрической прогрессии.
- Указать первый член
, и найти знаменатель этой прогрессии
- Найти сумму бесконечно убывающей геометрической прогрессии по формуле
- Вычислить сумму первых слагаемых и найденного значения суммы бесконечно убывающей геометрической прогрессии.
Запишите в виде обыкновенной дроби число
(1)
(2)
(3)
(4)
(5)
Бесконечно убывающая геометрическая прогрессия
Пример №42
В бесконечной геометрической прогрессии 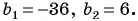
Решение:
Найдем знаменатель прогрессии: 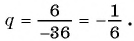
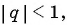
Пример №43
Является ли бесконечно убывающей геометрическая прогрессия:
а)
б)
в)
Решение:
а) Каждый член этой геометрической прогрессии, начиная со второго, равен предыдущему, умноженному на число 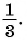
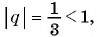
б) Поскольку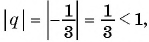
в) Знаменатель прогрессии 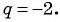
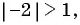
Пример №44
Найдите сумму бесконечно убывающей геометрической прогрессии, в которой 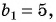
Решение:
По формуле 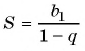
Пример №45
В бесконечно убывающей геометрической прогрессии 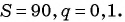
Решение:
В формулу суммы бесконечно убывающей геометрической прогрессии 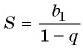
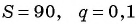
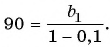
Пример №46
Запишите бесконечную периодическую десятичную дробь 15,2(3) в виде обыкновенной дроби.
Решение:
(1)
(2)
(3)
(4)
(5)
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства

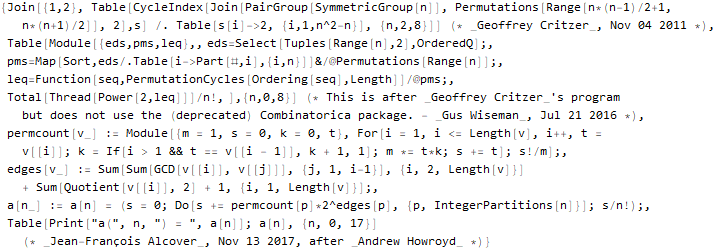
В языке Wolfram Language есть четыре совершенно потрясающие функции: FindSequenceFunction, RSolve, DifferenceRootReduce и FindFormula. В этой статье мы обсудим их возможности и поговорим о функциях, тесно с ними связанных — для поиска параметров линейной рекурсии FindLinearRecurrence (коэффициентов линейного рекуррентного уравнения), производящих функциях GeneratingFunction и Z-преобразовании ZTransform.
Первая функция — FindSequenceFunction — по последовательности чисел ищет выражение для её n-го члена не требуя вообще ничего более.
Hold @ FindSequenceFunction[{1, 1, 2, 3, 5, 8, 13}, n]FindSequenceFunction[
{-2, 4Sqrt[Pi],
-16, 16Sqrt[Pi],
-128/3, 32Sqrt[Pi],
-1024/15, 128Sqrt[Pi]/3,
-8192/105, 128Sqrt[Pi]/3},
n]Вторая функция — RSolve — решает рекуррентные уравнения самых разных типов. Элементы могут иметь вид
,
,
, где f имеет вид: n+A (арифметические разностные уравнения), B*n — геометрические или q-разностные уравнения), B*n+a (арифметико-геометрические функциональные разностные уравнения), B*n^d (степеные геометрические функциональные разностные уравнения), (A*n+B)/(C*n+D) (линейные дробные функциональные разностные уравнения).
RSolve[
{
a[n + 3]==2 * a[n],
a[1]==α,
a[2]==β,
a[3]==γ
},
a, n
]RSolve[
{
v[n]==(2 * Pi * v[n - 2]) / n,
v[2]==Pi,
v[3]==(4 * Pi) / 3
},
v @ n, n
]Третья функция — DifferenceRootReduce — ищет рекуррентное соотношение для последовательности чисел, n-й член которой имеет заданный вид.
DifferenceRootReduce[-2 * n * Pi * Factorial[(n * 2) - 1],
n
]RSolve[
{
(-8 * y[n]) + n * y[2 + n]==0,
y[-1]==1/4,
y[0]==0,
y[1]==-2,
y[2]==4Sqrt[Pi]
},
y, n
]Эта функция может много чего ещё, скажем, проверять тождества относительно последовательностей, к примеру:
DifferenceRootReduce[Fibonacci[2 * n]==Fibonacci[n] * LucasL[n], n]Здесь LucasL — последовательность чисел Люка (это, по сути, последовательность Фибоначчи, только первые члены не 1, 1, а 1, 3.
Hold @ DifferenceRootReduce @ LucasL @ nDifferenceRootReduce[LucasL[n]==Fibonacci[n - 1] + Fibonacci[n + 1]]Как найти рекуррентную формулу для последовательности?
Метод поиска общего члена последовательности часто основан на том, что нужно подобрать рекуррентное уравнение.
Работать это может примерно так: пусть мы ищем n-й член последовательности в виде
. Пусть у нас есть первые члены последовательности:
sequence = {1, 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461}Попробуем найти выражение для n-го члена в виде
:
seauenseEq1 = MovingMap[
Function[
Dot[Part[#, 1;;1], {a @ 1}]==Part[#, -1]
],
sequence, 1
]Hold @ Solve @ seauenseEq1Как видно, решений нет.
Попробуем искать теперь в виде
:
seauenseEq2 = MovingMap[
Function[
Dot[Part[#, 1;;2], {a @ 1, a @ 2}]==Part[#, -1]
],
sequence, 2
]Hold @ Solve @ seauenseEq2Как видим, получилось. Значит, n-й член имеет вид:
.
На самом деле есть встроенная функция FindLinearRecurrence, которая позволяет найти линейную рекурсию, подобно тому, как мы это только что сделали:
Hold @ FindLinearRecurrence @ sequenceИспользуя функцию LinearRecurrence можно продлить последовательность:
LinearRecurrence[{2, 1}, sequence[[1;;2]], 50]Или объединить все в одну строчку, построив функцию, которая: продлит последовательность, выдаст разностное уравнение и найдет общую формулу для n-го члена:
sequenseExtension[list_, n_] := Module[
{lr, eq},
lr = FindLinearRecurrence @ list;
eq = Flatten[
{
a[k]==Total[
Table[
a[k + -i] * Part[lr, i],
{i, 1, Length @ lr}
]
],
Table[a[i], list[[i]]], {i, 1, Length @ lr}]
}
];
<|
"Уравнение" -> eq,
"Формула" -> FullSimplify[a[k] /. Part[RSolve[eq, a, k], 1]],
"Продление" -> LinearRecurrence[lr, Part[list, Span[1, Length[lr]]], n]
|>
];Hold @ sequenseExtension[{1, 1, 2, 3, 5}, 20]Hold @ sequenseExtension[{1, 2, 2, 1, 1, 2, 2, 1}, 20]Hold @ sequenseExtension[
{1, 0, -1, 0, 2, 0, -2, 0, 3, 0, -3, 0, 4, 0, -4},
25
]Как найти формулу для n-го члена последовательности?
Z-преобразование
Z-преобразование состоит в вычислении ряда вида
от дискретной функции
. Это преобразование позволяет свести рекуррентное уравнение для задания последовательности к уравнению относительно образа функции
, что аналогично преобразованию Лапласа, которое сводит дифференциальные уравнения к алгебраическим.
Вот как это работает:
Grid[
Transpose[
Function[
{
#,
Map[TraditionalForm, Map[FullSimplify, ZTransform[#, n, z]]]
}
][
{
f[n - 2],
f[n - 1],
f @ n,
f[n + 1],
f[n + 2]
}
]
],
Background -> White, Dividers -> All
]Посмотрим на примере, скажем, возьмем хорошо известную последовательность Фибоначчи:
fibonacciEq = f[n]==f[n - 1] + f[n - 2];
initialConditions = {f[1] -> 1, f[2] -> 1};Ясно, что её стоит переписать в виде, как показано ниже, чтобы не появлялись конструкции типа
после применения Z-преобразования.
fibonacciEq = f[n + 2]==f[n + 1] + f[n];
initialConditions = {f[0] -> 1, f[1] -> 1};Осуществим Z-преобразование:
fibonacciEqZTransformed = ReplaceAll[fibonacciEq, pattern:f[__] :> ZTransform[pattern, n, z]]Решим уравнение относительно образа функции f — ZTransform[f[n],n,z]:
fZTransformed = ReplaceAll[
ZTransform[f @ n, n, z],
Part[Solve[fibonacciEqZTransformed, ZTransform[f @ n, n, z]], 1]
]Выполним обратное Z-преобразование, подставив одновременно начальные условия (заменим n на n-1 в финальном выражении, чтобы наша последовательность имела правильную индексацию (с первого, а не нулевого члена):
ReplaceAll[InverseZTransform[fZTransformed /. initialConditions, z, n],
n -> (n - 1)
]Естестевенно это можно автоматизировать, создав свой аналог RSolve:
myRSolve[eq_, initials_, f_, n_] := Module[
{z, initialsInner, eqZTransformed, fZTransformed},
initialsInner = ReplaceAll[initials, f[x_] :> f[x - 1]];
eqZTransformed = ReplaceAll[eq, pattern:f[__] :> ZTransform[pattern, n, z]];
fZTransformed = ReplaceAll[ZTransform[f @ n, n, z],
Part[Solve[eqZTransformed, ZTransform[f @ n, n, z]], 1]
];
FullSimplify[
InverseZTransform[fZTransformed /. initialsInner, z, n] /. n -> (n - 1)
]
];myRSolve[
{
f[n + 2]==(2 * f[n + 1]) + -(5 * f[n])
},
{f[1] -> 20, f[2] -> 0},
f, n
]RSolve[
{
f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]),
f[1]==20,
f[2]==0
},
f, n
]Но, конечно, RSolve содержит намного больше возможностей для решения самых разных дискретных уравнений, на которых мы не будем останавливаться подробнее:
RSolve[a[n]==(n * a[n]) + n, a, n],
RSolve[
{
a[n + 1]==(2 * a[n]) + (3 * a[n]) + 4,
a[0]==0
},
a, n
],
RSolve[
y[n + 1 * 3]==(2 * y[n + 1 * 6]) + n * 2,
y, n
]Производящие функции
Производящая функция последовательности
это такая функция
, разложение которой в ряд Тейлора (или, более широко, Лорана) имеет вид —
. Другими словами, коэффициенты при степенях x в разложении функции в ряд задают нашу последовательность.
Скажем, функция
является производящей функцией последовательности 1, 1, 1, 1, …:
Series[1 / (1 + -x), {x, 0, 10}]А функция
является производящей функцией последовательности Фибоначчи 1, 1, 2, 3, 5, 8, 13, …:
Series[(1 * 1) + (-x) + -(x * 2),
{x, 0, 10}
]Ещё есть разновидность производящей функции — экспоненциальная производящая функция, которая для последовательности
имеет вид —
.
Скажем, для последовательностей 1, 1, 1, 1… и 1, 1, 2, 3, 5, 8, 13,… экспоненциальные производящие функции таковы —
и
:
ReplaceAll[Normal[Series[E ^ x, {x, 0, 10}]],
Power[x, n_] :> ((x ^ n) * Factorial[n])
]ReplaceAll[
Normal[
FullSimplify[
Series[
Plus[E,
(-(2 * x * 1)) + 5 * ((E * 5 * x) - 1) * 5
],
{x, 0, 10}
]
]
],
Power[x, n_] :> ((x ^ n) * Factorial[n])
]Производящую функцию в Wolfram Language можно найти двумя функциями — GeneratingFunction и FindGeneratingFunction (экспоненциальную с помощью ExponentialGeneratingFunction):
GeneratingFunction[-(m * Factorial[n]), {n, m}, {x, y}]TraditionalForm[
FullSimplify[
ExponentialGeneratingFunction[-(n * Factorial[n - 1] * Factorial[2 * n]), n, x]
]
]Есть много методов поиска общего члена последовательности с помощью производящих функций. Не будем подробно останавливаться на этом, скажем, только что неплохая теория есть на сайте genfunc.ru.
Один из методов похож на Z-преобразование:
generatingFEq = ReplaceAll[
f[n + 2]==f[n + 1] + f[n],
pattern:f[__] :> GeneratingFunction[pattern, n, z]
],
generatingF = ReplaceAll[
GeneratingFunction[f @ n, n, z],
Part[Solve[generatingFEq, GeneratingFunction[f @ n, n, z]], 1]
],
nthTerm = SeriesCoefficient[generatingF, {z, 0, n}],
FullSimplify[
ReplaceAll[ReplaceAll[nthTerm, {f[0] -> 1, f[1] -> 1}],
n -> (n - 1)
],
GreaterEqual[n, 1]
]OEIS — Онлайн-энциклопедия целочисленных последовательностей и интеграция с Wolfram Language
В интернете доступна совершенно потрясающая коллекция числовых последовательностей — OEIS (On-Line Encyclopedia of Integer Sequences). Она была создана Нилом Слоуном во время его исследовательской деятельности в AT&T Labs. В OEIS хранится информация о целочисленных последовательностях, представляющих интерес как для любителей, так и для специалистов в математике, комбинаторике, теории чисел, теории игр, физике, химии, биологии, информатике. На данный момент там собрано 329085 последовательностей. Запись в OEIS включает в себя первые элементы последовательности, ключевые слова, математическое описание, фамилии авторов, ссылки на литературу; присутствует возможность построения графика или проигрывания музыкального представления последовательности. Поиск в базе данных может осуществляться по ключевым словам и по подпоследовательности.
Недавно появилась интеграция с этой базой внутри Wolfram Language (при использовании важно понимать, что это разработка пользователей — с недавного времени можно выгружать свой код в репозиторий Wolfram Function Repository). Достаточно просто указать номер интересующей вас последовательности или список номеров.
OEISSequenceData = ResourceFunction @ "OEISSequenceData";
OEISSequence = ResourceFunction @ "OEISSequence";ResourceFunction[«OEISSequence»] — просто выдает первые члены последовательности:
Hold @ OEISSequence @ "A666"ResourceFunction[«OEISSequenceData»] — выдает датасет с полной информацией из базы:
sequenceData[666] = OEISSequenceData[666, "Dataset"]Скажем, можно «вытащить» код на языке Wolfram Language:
Hold @ Normal @ sequenceData[666]["CodeWolframLanguageStrings"]Или набор случайно выбранных последовательностей с интересующей по ним информацией:
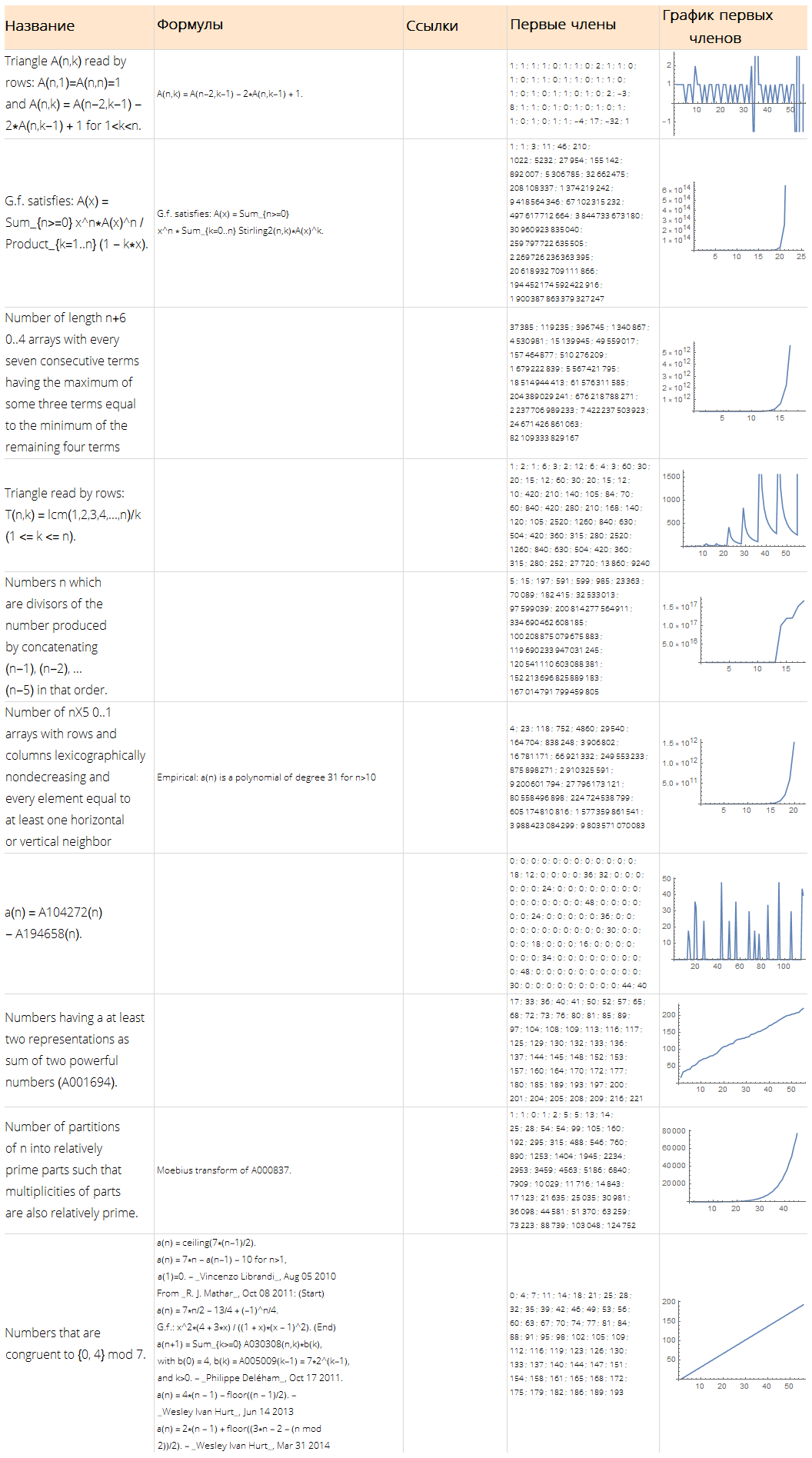
randomSequences = Dataset @ Map[
Normal,
OEISSequenceData[RandomInteger[{1, 300000}, 10], "Dataset"]
];Function[
Framed[#, FrameStyle -> None, FrameMargins -> 5, Background -> White]
][
Grid[
Join[
{
Map[Style[#, Bold, 18]&,
{"Название", "Формулы", "Ссылки", "Первые члены", "График первых членов"}
]
},
Map[
Function[
Map[
Function[
TextCell[#, LineIndent -> 0, FontSize -> 12, FontFamily -> "Open Sans Light"]
],
{
Style[Part[#, 1], 16],
Row[Part[#, 4], "n"],
Row[Part[#, 3], "n"],
Style[Row[Part[#, 2], "; "], 10],
ListLinePlot[Part[#, 2], ImageSize -> Full]
}
]
],
Values @ Normal @ randomSequences[All, {"Name", "Sequence", "References", "Formulae"}]
]
],
Dividers -> {{None, {LightGray}, None}, {None, {LightGray}, None}},
ItemStyle -> Directive[FontSize -> 12, FontFamily -> "Open Sans Light"],
ItemSize -> {{15, 25, 10, 15, 15}, Automatic},
Alignment -> {Left, Center},
Background -> {None, {LightOrange, White}}
]
]Поиск потенциально возможной формулы
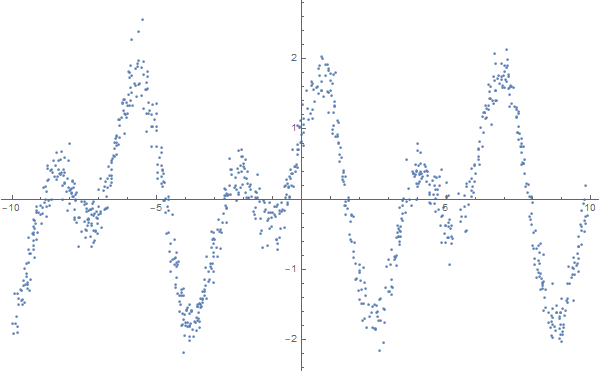
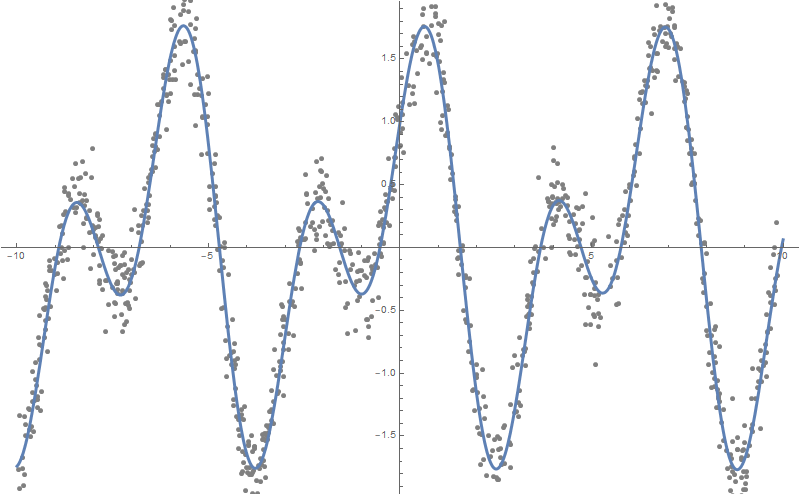
Наконец, хотелось бы отметить функцию FindFormula, которая по заданному набору чисел строит формулу, которая их может описать. Примем зависимостей подобрать можно много и из разных классов функций.
data = Table[
{
x,
Sin[2 * x] + Cos[x] + RandomVariate[NormalDistribution[0, 0.2]]
},
{x, RandomReal[{-10, 10}, 1000]}
];
ListPlot[data, Background -> White, ImageSize -> 600]formulas = FindFormula[data, x]Как видно, Wolfram Language подобрал функцию, очень близкую к той, на основе которой были построены «зашумленные» данные, а именно — Sin[2x]+Cos[x]:
Plot[formulas,
{x, -10, 10},
PlotStyle -> AbsoluteThickness[3],
Prolog -> {AbsolutePointSize[5], Gray, Point @ data},
Background -> White, ImageSize -> 800, PlotLegends -> "Expressions"
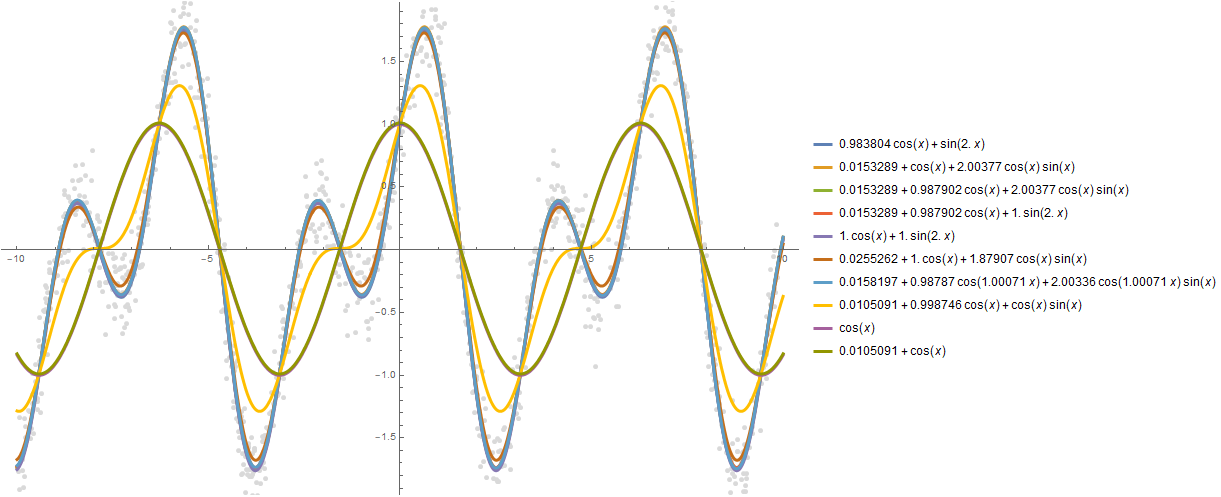
]Можно построить и большее количество зависимостей, скажем, 10:
formulas = FindFormula[data, x, 10]Plot[formulas,
{x, -10, 10},
PlotStyle -> AbsoluteThickness[3],
Prolog -> {AbsolutePointSize[5], LightGray, Point @ data},
Background -> White, ImageSize -> 800, PlotLegends -> "Expressions"
]Стоит отметить, что есть функция, аналогичная по функционалу, которая ищет вероятностное распределение — FindDistribution.
Для сотрудничества — пишите личное сообщение на Хабре или в мою группу ВКонтакте.
Канал YouTube — вебинары и обучающие ролики.
Регистрация на новые курсы. Готовый онлайн курс.
Содержание:
- Основные понятия и определения
- Задание последовательности формулой ее общего члена
- Рекуррентный способ задания последовательности
Основные понятия и определения
Определение
Последовательностью называется функция, которая переводит множество
натуральных
чисел $N$ в некоторое множество
$X$ :
$left{x_{n}right}=left{x_{n}right}_{n=1}^{infty}=left{x_{1} ; x_{2} ; ldots ; x_{n} ; ldotsright}, x_{i} in N$
Элемент $x_{1}$ называется первым членом
последовательности, $x_{2}$ — вторым, … ,
$x_{n}$ —
$n$-ым или общим членом последовательности.
Пример
Задание. Для последовательности $x_{n}={-1 ; 2 ; 5 ; 8 ;-3 ; 0 ; ldots}$
определить, чему равен третий член $x_{3}$
Решение. Третьим элементом последовательности будет элемент, идущий третьим по счету, то есть для
заданной последовательности имеем, что $x_{3}=5$
Ответ. $x_{3}=5$
Задание последовательности формулой ее общего члена
Обычно последовательность целесообразнее задавать формулой ее общего члена, которая позволяет найти любой член
последовательности, зная его номер.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти формулу общего члена последовательности
$x_{n}={6 ; 20 ; 56 ; 144 ; 352 ; ldots}$
Решение. Запишем каждый член последовательности в следующем виде:
$n=1 : x_{1}=6=2 cdot 3=2^{1} cdot 3=2^{1} cdot(2 cdot 1+1)$
$n=2 : x_{2}=20=4 cdot 5=2^{2} cdot 5=2^{2} cdot(2 cdot 2+1)$
$n=3 : x_{3}=56=8 cdot 7=2^{3} cdot 7=2^{3} cdot(2 cdot 3+1)$
Как видим, члены последовательности представляют собой произведение степени двойки, умноженной на
последовательные нечетные числа, причем два возводится в степень, которая равна номеру рассматриваемого элемента.
Таким образом, делаем вывод, что
$x_{n}=2^{n} cdot(2 n+1)$
Ответ. Формула общего члена: $x_{n}=2^{n} cdot(2 n+1)$
Пример
Задание. Найти 15 член последовательности, заданной формулой
$n$-го члена:
$x_{n}=frac{(-1)^{n}}{n}, n in N$
Решение. Для того чтобы найти $x_{15}$ ,
подставим в формулу общего члена значение $n=15$ . Получим:
$x_{15}=frac{(-1)^{15}}{15}=-frac{1}{15}$
Ответ. $x_{15}=frac{(-1)^{15}}{15}=-frac{1}{15}$
Пример
Задание. Проверить, являются ли числа
$a=6$ и
$b=1$ членами последовательности
$left{x_{n}right}=left{frac{n^{2}+11}{n+1}right}$
Решение. Число $a=6$ является
членом последовательности $left{x_{n}right}, n in N$ , если существует
такой номер $n_{0} in N$ , что
$x_{n_{0}}=a=6$ :
$6=x_{n o}=frac{n_{0}^{2}+11}{n_{0}+1} Rightarrow frac{n_{0}^{2}+11}{n_{0}+1}=6 Rightarrow$
$Rightarrow n_{0}^{2}-6 n_{0}+5=0 Rightarrow=left{begin{array}{l}{n_{0}=1} \ {n_{0}=5}end{array}right.$
Таким образом, число $a=6$ является первым и
пятым членами заданной последовательности.
Проверим теперь, является ли число $b=1$ членом указанной
последовательности $left{x_{n}right}=left{frac{n^{2}+11}{n+1}right}$ . Рассуждая аналогично,
как и для $a=6$ , получаем:
$frac{n_{0}^{2}+11}{n_{0}+1}=1 Rightarrow n_{0}^{2}-n_{0}+10=0 Rightarrow D=1-40=-39 lt 0$
Таким образом, уравнение $n_{0}^{2}-n_{0}+10=0$ не имеет
решение в натуральных числах, а значит, $b=1$ не
является членом последовательности $left{x_{n}right}$
Ответ. Число $a=6$ является
первым и пятым членами заданной последовательности, а
$b=1$ не является членом последовательности
$left{x_{n}right}=left{frac{n^{2}+11}{n+1}right}$
Рекуррентный способ задания последовательности
Другим способом задания последовательности является задание последовательности с помощью рекуррентного соотношения.
В этом случае задается один или несколько первых элементов последовательности, а остальные определяются по некоторому
правилу. Например, известен первый член $x_{1}$
последовательности и известно, что $x_{n+1}=fleft(x_{n}right)$ , то
есть $x_{2}=fleft(x_{1}right), x_{3}=fleft(x_{2}right)$ и так далее до нужного члена.
Пример
Примером рекуррентно заданной последовательности является последовательность чисел
Фибоначчи — 1, 1, 2, 3, 5, 8, 13, … , в которой каждое последующее число, начиная с третьего, является суммой
двух предыдущих: 2 = 1 + 1; 3 = 2 + 1 и так далее. Данную последовательность можно задать рекуррентно:
$x_{n+2}=x_{n+1}+x_{n}, n in N, x_{1}=x_{2}=1$
Пример
Задание. Последовательность $left{x_{n}right}$
задана при помощи рекуррентного соотношения $x_{n+2}=frac{1}{2}left(x_{n+1}+x_{n}right), x_{1}=2, x_{2}=4$ .
Выписать несколько первых членов этой последовательности.
Решение. Найдем третий член заданной последовательности:
$x_{3}=frac{1}{2}left(x_{2}+x_{1}right)=frac{4+2}{2}=frac{6}{2}=3$
Аналогично находим далее, что
$x_{4}=frac{1}{2}left(x_{3}+x_{2}right)=frac{3+4}{2}=frac{7}{2}=3,5$
$x_{5}=frac{1}{2}left(x_{4}+x_{3}right)=frac{3+3,5}{2}=frac{6,5}{2}=3,25$
и так далее.
При рекуррентном задании последовательностей, получаются очень громоздкими выкладки, так как, чтобы найти элементы с
большими номерами, необходимо найти все предыдущие члены указанной последовательности, например, для
нахождения $x_{500}$ надо найти все предыдущие 499 членов.
Читать дальше: ограниченные последовательности.
При изучении алгебры в общеобразовательной школе (9 класс) одной из важных тем является изучение числовых последовательностей, к которым относятся прогрессии -геометрическая и арифметическая. В данной статье рассмотрим арифметическую прогрессию и примеры с решениями.
Что собой представляет арифметическая прогрессия?
Чтобы это понять, необходимо дать определение рассматриваемой прогрессии, а также привести основные формулы, которые далее будут использованы при решении задач.
Арифметическая или алгебраическая прогрессия — это такой набор упорядоченных рациональных чисел, каждый член которого отличается от предыдущего на некоторую постоянную величину. Эта величина называется разностью. То есть, зная любой член упорядоченного ряда чисел и разность, можно восстановить всю арифметическую прогрессию.
Приведем пример. Следующая последовательность чисел будет прогрессией арифметической: 4, 8, 12, 16, …, поскольку разность в этом случае равна 4 (8 — 4 = 12 — 8 = 16 — 12). А вот набор чисел 3, 5, 8, 12, 17 уже нельзя отнести к рассматриваемому виду прогрессии, поскольку разность для него не является постоянной величиной (5 — 3 ≠ 8 — 5 ≠ 12 — 8 ≠ 17 — 12).
Важные формулы
Приведем теперь основные формулы, которые понадобятся для решения задач с использованием арифметической прогрессии. Обозначим символом a n n-й член последовательности, где n — целое число. Разность обозначим латинской буквой d. Тогда справедливы следующие выражения:
- Для определения значения n-го члена подойдет формула: a n = (n-1)*d+a 1 .
- Для определения суммы первых n слагаемых: S n = (a n +a 1)*n/2.
Чтобы понять любые примеры арифметической прогрессии с решением в 9 классе, достаточно запомнить эти две формулы, поскольку на их использовании строятся любые задачи рассматриваемого типа. Также следует не забывать, что разность прогрессии определяется по формуле: d = a n — a n-1 .
Пример №1: нахождение неизвестного члена
Приведем простой пример прогрессии арифметической и формул, которые необходимо использовать для решения.
Пусть дана последовательность 10, 8, 6, 4, …, необходимо в ней найти пять членов.
Из условия задачи уже следует, что первые 4 слагаемых известны. Пятое можно определить двумя способами:
- Вычислим для начала разность. Имеем: d = 8 — 10 = -2. Аналогичным образом можно было взять любые два других члена, стоящих рядом друг с другом. Например, d = 4 — 6 = -2. Поскольку известно, что d = a n — a n-1 , тогда d = a 5 — a 4 , откуда получаем: a 5 = a 4 + d. Подставляем известные значения: a 5 = 4 + (-2) = 2.
- Второй способ также требует знания разности рассматриваемой прогрессии, поэтому сначала нужно определить ее, как показано выше (d = -2). Зная, что первый член a 1 = 10, воспользуемся формулой для n числа последовательности. Имеем: a n = (n — 1) * d + a 1 = (n — 1) * (-2) + 10 = 12 — 2*n. Подставляя в последнее выражение n = 5, получаем: a 5 = 12-2 * 5 = 2.
Как видно, оба способа решения привели к одному и тому же результату. Отметим, что в этом примере разность d прогрессии является отрицательной величиной. Такие последовательности называются убывающими, так как каждый следующий член меньше предыдущего.
Пример №2: разность прогрессии
Теперь усложним немного задачу, приведем пример, как
Известно, что в некоторой 1-й член равен 6, а 7-й член равен 18. Необходимо найти разность и восстановить эту последовательность до 7 члена.
Воспользуемся формулой для определения неизвестного члена: a n = (n — 1) * d + a 1 . Подставим в нее известные данные из условия, то есть числа a 1 и a 7 , имеем: 18 = 6 + 6 * d. Из этого выражения можно легко вычислить разность: d = (18 — 6) /6 = 2. Таким образом, ответили на первую часть задачи.
Чтобы восстановить последовательность до 7 члена, следует воспользоваться определением алгебраической прогрессии, то есть a 2 = a 1 + d, a 3 = a 2 + d и так далее. В итоге восстанавливаем всю последовательность: a 1 = 6, a 2 = 6 + 2=8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14, a 6 = 14 + 2 = 16, a 7 = 18.
Пример №3: составление прогрессии
Усложним еще сильнее условие задачи. Теперь необходимо ответить на вопрос, как находить арифметическую прогрессию. Можно привести следующий пример: даны два числа, например, — 4 и 5. Необходимо составить прогрессию алгебраическую так, чтобы между этими помещалось еще три члена.
Прежде чем начинать решать эту задачу, необходимо понять, какое место будут занимать заданные числа в будущей прогрессии. Поскольку между ними будут находиться еще три члена, тогда a 1 = -4 и a 5 = 5. Установив это, переходим к задаче, которая аналогична предыдущей. Снова для n-го члена воспользуемся формулой, получим: a 5 = a 1 + 4 * d. Откуда: d = (a 5 — a 1)/4 = (5 — (-4)) / 4 = 2,25. Здесь получили не целое значение разности, однако оно является рациональным числом, поэтому формулы для алгебраической прогрессии остаются теми же самыми.
Теперь добавим найденную разность к a 1 и восстановим недостающие члены прогрессии. Получаем: a 1 = — 4, a 2 = — 4 + 2,25 = — 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 = 2,75 + 2,25 = 5, что совпало с условием задачи.
Пример №4: первый член прогрессии
Продолжим приводить примеры арифметической прогрессии с решением. Во всех предыдущих задачах было известно первое число алгебраической прогрессии. Теперь рассмотрим задачу иного типа: пусть даны два числа, где a 15 = 50 и a 43 = 37. Необходимо найти, с какого числа начинается эта последовательность.
Формулы, которыми пользовались до настоящего времени, предполагают знание a 1 и d. В условии задачи об этих числах ничего неизвестно. Тем не менее выпишем выражения для каждого члена, о котором имеется информация: a 15 = a 1 + 14 * d и a 43 = a 1 + 42 * d. Получили два уравнения, в которых 2 неизвестные величины (a 1 и d). Это означает, что задача сводится к решению системы линейных уравнений.
Указанную систему проще всего решить, если выразить в каждом уравнении a 1 , а затем сравнить полученные выражения. Первое уравнение: a 1 = a 15 — 14 * d = 50 — 14 * d; второе уравнение: a 1 = a 43 — 42 * d = 37 — 42 * d. Приравнивая эти выражения, получим: 50 — 14 * d = 37 — 42 * d, откуда разность d = (37 — 50) / (42 — 14) = — 0,464 (приведены лишь 3 знака точности после запятой).
Зная d, можно воспользоваться любым из 2 приведенных выше выражений для a 1 . Например, первым: a 1 = 50 — 14 * d = 50 — 14 * (- 0,464) = 56,496.
Если возникают сомнения в полученном результате, можно его проверить, например, определить 43 член прогрессии, который задан в условии. Получим: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Небольшая погрешность связана с тем, что при вычислениях использовалось округление до тысячных долей.
Пример №5: сумма
Теперь рассмотрим несколько примеров с решениями на сумму арифметической прогрессии.
Пусть дана числовая прогрессия следующего вида: 1, 2, 3, 4, …,. Как рассчитать сумму 100 этих чисел?
Благодаря развитию компьютерных технологий можно эту задачку решить, то есть последовательно сложить все числа, что вычислительная машина сделает сразу же, как только человек нажмет клавишу Enter. Однако задачу можно решить в уме, если обратить внимание, что представленный ряд чисел является прогрессией алгебраической, причем ее разность равна 1. Применяя формулу для суммы, получаем: S n = n * (a 1 + a n) / 2 = 100 * (1 + 100) / 2 = 5050.
Любопытно отметить, что эта задача носит название «гауссовой», поскольку в начале XVIII века знаменитый немецкий еще будучи в возрасте всего 10 лет, смог решить ее в уме за несколько секунд. Мальчик не знал формулы для суммы алгебраической прогрессии, но он заметил, что если складывать попарно числа, находящиеся на краях последовательности, то получается всегда один результат, то есть 1 + 100 = 2 + 99 = 3 + 98 = …, а поскольку этих сумм будет ровно 50 (100 / 2), то для получения правильного ответа достаточно умножить 50 на 101.
Пример №6: сумма членов от n до m
Еще одним типичным примером суммы арифметической прогрессии является следующий: дан такой чисел ряд: 3, 7, 11, 15, …, нужно найти, чему будет равна сумма его членов с 8 по 14.
Задача решается двумя способами. Первый из них предполагает нахождение неизвестных членов с 8 по 14, а затем их последовательное суммирование. Поскольку слагаемых немного, то такой способ не является достаточно трудоемким. Тем не менее предлагается решить эту задачу вторым методом, который является более универсальным.
Идея заключается в получении формулы для суммы алгебраической прогрессии между членами m и n, где n > m — целые числа. Выпишем для обоих случаев два выражения для суммы:
- S m = m * (a m + a 1) / 2.
- S n = n * (a n + a 1) / 2.
Поскольку n > m, то очевидно, что 2 сумма включает в себя первую. Последнее умозаключение означает, что если взять разность между этими суммами, и добавить к ней член a m (в случае взятия разности он вычитается из суммы S n), то получим необходимый ответ на задачу. Имеем: S mn = S n — S m + a m =n * (a 1 + a n) / 2 — m *(a 1 + a m)/2 + a m = a 1 * (n — m) / 2 + a n * n / 2 + a m * (1- m/2). В это выражение необходимо подставить формулы для a n и a m . Тогда получим: S mn = a 1 * (n — m) / 2 + n * (a 1 + (n — 1) * d) / 2 + (a 1 + (m — 1) * d) * (1 — m / 2) = a 1 * (n — m + 1) + d * n * (n — 1) / 2 + d *(3 * m — m 2 — 2) / 2.
Полученная формула является несколько громоздкой, тем не менее сумма S mn зависит только от n, m, a 1 и d. В нашем случае a 1 = 3, d = 4, n = 14, m = 8. Подставляя эти числа, получим: S mn = 301.
Как видно из приведенных решений, все задачи основываются на знании выражения для n-го члена и формулы для суммы набора первых слагаемых. Перед тем как приступить к решению любой из этих задач, рекомендуется внимательно прочитать условие, ясно понять, что требуется найти, и лишь затем приступать к решению.
Еще один совет заключается в стремлении к простоте, то есть если можно ответить на вопрос, не применяя сложные математические выкладки, то необходимо поступать именно так, поскольку в этом случае вероятность допустить ошибку меньше. Например, в примере арифметической прогрессии с решением №6 можно было бы остановиться на формуле S mn = n * (a 1 + a n) / 2 — m * (a 1 + a m) / 2 + a m , и разбить общую задачу на отдельные подзадачи (в данном случае сначала найти члены a n и a m).
Если возникают сомнения в полученном результате, то рекомендуется его проверять, как это было сделано в некоторых приведенных примерах. Как находить арифметическую прогрессию, выяснили. Если разобраться, то это не так сложно.
Если каждому натуральному числу n
поставить в соответствие действительное число a n
, то говорят, что задано числовую последовательность
:
a
1
,
a
2
,
a
3
, . . . ,
a n
, . . .
.
Итак, числовая последовательность — функция натурального аргумента.
Число a
1
называют первым членом последовательности
, число a
2
— вторым членом последовательности
, число a
3
— третьим
и так далее. Число a n
называют n-м членом последовательности
, а натуральное число n
— его номером
.
Из двух соседних членов a n
и a n
+1
последовательности член a n
+1
называют последующим
(по отношению к a n
), а a n
— предыдущим
(по отношению к a n
+1
).
Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.
Часто последовательность задают с помощью формулы n-го члена
, то есть формулы, которая позволяет определить член последовательности по его номеру.
Например,
последовательность положительных нечётных чисел можно задать формулой
a n
=
2n —
1,
а последовательность чередующихся 1
и -1
— формулой
b
n =
(-1) n
+1 .
◄
Последовательность можно определить рекуррентной формулой
,
то есть формулой, которая выражает любой член последовательности, начиная с некоторого, через предыдущие (один или несколько) члены.
Например,
если a
1
= 1
, а a n
+1
= a n
+ 5
a
1
= 1,
a
2
= a
1
+ 5 = 1 + 5 = 6,
a
3
= a
2
+ 5 = 6 + 5 = 11,
a
4
= a
3
+ 5 = 11 + 5 = 16,
a
5
= a
4
+ 5 = 16 + 5 = 21.
Если а 1
= 1, а 2
= 1, a n
+2
= a n
+ a n
+1
,
то первые семь членов числовой последовательности устанавливаем следующим образом:
a 1
= 1,
a 2
= 1,
a 3
= a 1
+ a 2
= 1 + 1 = 2,
a 4
= a 2
+ a 3
= 1 + 2 = 3,
a 5
= a 3
+ a 4
= 2 + 3 = 5,
a
6
= a
4
+ a
5
= 3 + 5 = 8,
a
7
= a
5
+ a
6
= 5 + 8 = 13. ◄
Последовательности могут быть конечными
и бесконечными
.
Последовательность называется конечной
, если она имеет конечное число членов. Последовательность называется бесконечной
, если она имеет бесконечно много членов.
Например,
последовательность двузначных натуральных чисел:
10, 11, 12, 13, . . . , 98, 99
конечная.
Последовательность простых чисел:
2, 3, 5, 7, 11, 13, . . .
бесконечная. ◄
Последовательность называют возрастающей
, если каждый её член, начиная со второго, больше чем предыдущий.
Последовательность называют убывающей
, если каждый её член, начиная со второго, меньше чем предыдущий.
Например,
2, 4, 6, 8, . . . , 2n
, . . .
— возрастающая последовательность;
1, 1 / 2 , 1 / 3 , 1 / 4 , . . . , 1 / n
, . . .
— убывающая последовательность. ◄
Последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают, называется монотонной последовательностью
.
Монотонными последовательностями, в частности, являются возрастающие последовательности и убывающие последовательности.
Арифметическая прогрессия
Арифметической прогрессией
называется последовательность, каждый член которой, начиная со второго, равен предыдущему, к которому прибавляется одно и то же число.
a
1
,
a
2
,
a
3
, . . . ,
a n
, . . .
является арифметической прогрессией, если для любого натурального числа n
выполняется условие:
a n
+1
= a n
+ d
,
где d
— некоторое число.
Таким образом, разность между последующим и предыдущим членами данной арифметической прогрессии всегда постоянна:
а 2
— a
1
= а 3
— a
2
= . . . = a n
+1
— a n
= d
.
Число d
называют разностью арифметической прогрессии
.
Чтобы задать арифметическую прогрессию, достаточно указать её первый член и разность.
Например,
если a
1
= 3, d
= 4
, то первые пять членов последовательности находим следующим образом:
a 1
=3,
a 2
= a 1
+ d
= 3 + 4 = 7,
a 3
= a 2
+ d
= 7 + 4 = 11,
a 4
= a 3
+ d
= 11 + 4 = 15,
a
5
= a
4
+ d
= 15 + 4 = 19. ◄
Для арифметической прогрессии с первым членом a
1
и разностью d
её n
a n
= a 1
+ (n
— 1)d.
Например,
найдём тридцатый член арифметической прогрессии
1, 4, 7, 10, . . .
a 1
=1, d
= 3,
a 30
= a 1
+ (30 — 1)d =
1 + 29·
3 = 88. ◄
a n-1
= a 1
+ (n
— 2)d,
a n
= a 1
+ (n
— 1)d,
a n
+1
= a
1
+ nd
,
то, очевидно,
каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.
числа a, b и c являются последовательными членами некоторой арифметической прогрессии тогда и только тогда, когда одно из них равно среднему арифметическому двух других.
Например,
a n
= 2n
— 7
, является арифметической прогрессией.
Воспользуемся приведённым выше утверждением. Имеем:
a n
= 2n
— 7,
a n-1
= 2(n —
1) — 7 = 2n
— 9,
a n+1
= 2(n +
1) — 7 = 2n
— 5.
Следовательно,
| a n+1 + a n-1 |
= | 2n — 5 + 2n — 9 |
= 2n — 7 = a n , |
| 2
|
2
|
◄
Отметим, что n
-й член арифметической прогрессии можно найти не толь через a
1
, но и любой предыдущий a k
a n
= a k
+ (n
— k
)d
.
Например,
для a
5
можно записать
a 5
= a 1
+ 4d
,
a 5
= a 2
+ 3d
,
a 5
= a 3
+ 2d
,
a 5
= a 4
+ d
. ◄
a n
= a n-k
+ kd
,
a n
= a n+k
— kd
,
то, очевидно,
любой член арифметической прогрессии, начиная со второго равен полусумме равноотстоящих от него членов этой арифметической прогрессии.
Кроме того, для любой арифметической прогрессии справедливо равенство:
a m + a n = a k + a l
,
m + n = k + l.
Например,
в арифметической прогрессии
1) a
10
= 28 = (25 + 31)/2 = (a
9
+
a
11
)/2;
2) 28 = a 10
= a 3
+ 7d
= 7 + 7·3 = 7 + 21 = 28;
3) a 10
= 28 = (19 + 37)/2 = (a 7 + a 13
)/2;
4) a 2 + a 12 = a 5 + a 9
,
так как
a 2 + a 12
= 4 + 34 = 38,
a 5 + a 9
= 13 + 25 = 38. ◄
S n
= a 1 + a 2 + a 3 + . . .
+
a n
,
первых n
членов арифметической прогрессии равна произведению полусуммы крайних слагаемых на число слагаемых:
Отсюда, в частности, следует, что если нужно просуммировать члены
a k
, a k
+1
, . . . ,
a n
,
то предыдущая формула сохраняет свою структуру:
Например,
в арифметической прогрессии 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, . . .
S
10
= 1 + 4 + . . . + 28 = (1 +
28) ·
10/2 = 145;
10 + 13 + 16 + 19 + 22 + 25 + 28 = S
10
—
S
3
= (10 + 28
) ·
(10
— 4 + 1)/2 = 133. ◄
Если дана арифметическая прогрессия, то величины a
1
, a n
, d
, n
и
S
n
связаны двумя формулами:
Поэтому, если значения трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.
Арифметическая прогрессия является монотонной последовательностью. При этом:
- если d
> 0 , то она является возрастающей; - если d
< 0 , то она является убывающей; - если d
= 0 , то последовательность будет стационарной.
Геометрическая прогрессия
Геометрической прогрессией
называется последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
b
1
,
b
2
,
b
3
, . . . ,
b n
, . . .
является геометрической прогрессией, если для любого натурального числа n
выполняется условие:
b n
+1
= b n
·
q
,
где q
≠ 0
— некоторое число.
Таким образом, отношение последующего члена данной геометрической прогрессии к предыдущему есть число постоянное:
b
2
/ b
1
= b
3
/ b
2
= . . . = b n
+1
/ b n
= q
.
Число q
называют знаменателем геометрической прогрессии
.
Чтобы задать геометрическую прогрессию, достаточно указать её первый член и знаменатель.
Например,
если b
1
= 1, q
= -3
, то первые пять членов последовательности находим следующим образом:
b 1
= 1,
b 2
= b 1
·
q
= 1 ·
(-3) = -3,
b 3
= b 2
·
q
= -3 ·
(-3) = 9,
b 4
= b 3
·
q
= 9 ·
(-3) = -27,
b
5
= b
4
·
q
= -27 ·
(-3) = 81. ◄
b
1
и знаменателем q
её n
-й член может быть найден по формуле:
b n
= b
1
·
q n
-1
.
Например,
найдём седьмой член геометрической прогрессии 1, 2, 4, . . .
b
1
= 1, q
= 2,
b
7
= b
1
· q
6
=
1 · 2 6 = 64
. ◄
b n-1
= b 1
·
q n
-2 ,
b n
= b 1
·
q n
-1 ,
b n
+1
= b
1
·
q n
,
то, очевидно,
b n
2
= b n
-1
·
b n
+1
,
каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому (пропорциональному) предшествующего и последующего членов.
Так как верно и обратное утверждение, то имеет место следующее утверждение:
числа a, b и c являются последовательными членами некоторой геометрической прогрессии тогда и только тогда, когда квадрат одного из них равен произведению двух других, то есть одно из чисел является средним геометрическим двух других.
Например,
докажем, что последовательность, которая задаётся формулой b n
= -3 · 2 n
, является геометрической прогрессией. Воспользуемся приведённым выше утверждением. Имеем:
b n
= -3 · 2 n
,
b n
-1
= -3 · 2 n
-1
,
b n
+1
= -3 · 2 n
+1
.
Следовательно,
b n
2
= (-3 · 2 n
) 2 = (-3 · 2 n
-1
) · (-3 · 2 n
+1
) = b n
-1
·
b n
+1
,
что и доказывает нужное утверждение. ◄
Отметим, что n
-й член геометрической прогрессии можно найти не только через b
1
, но и любой предыдущий член b k
, для чего достаточно воспользоваться формулой
b n
= b k
·
q n
— k
.
Например,
для b
5
можно записать
b 5
= b 1
·
q
4 ,
b 5
= b 2
·
q 3
,
b 5
= b 3
·
q 2
,
b 5
= b 4
·
q
. ◄
b n
= b k
·
q n
— k
,
b n
= b n
—
k
·
q k
,
то, очевидно,
b n
2
= b n
—
k
·
b n
+
k
квадрат любого члена геометрической прогрессии, начиная со второго равен произведению равноотстоящих от него членов этой прогрессии.
Кроме того, для любой геометрической прогрессии справедливо равенство:
b m
·
b n
=
b k
·
b l
,
m
+
n
=
k
+
l
.
Например,
в геометрической прогрессии
1) b
6
2 = 32 2 = 1024 = 16 ·
64 = b
5
·
b
7
;
2) 1024 = b
11
= b
6
·
q
5
= 32 ·
2 5 = 1024;
3) b
6
2 = 32 2 = 1024 = 8 ·
128 = b
4
·
b
8
;
4) b
2
·
b
7
=
b
4
·
b
5
,
так как
b
2
·
b
7
=
2 ·
64 = 128,
b
4
·
b
5
= 8 ·
16 = 128. ◄
S n
= b
1
+
b
2
+
b
3
+ . . . +
b n
первых n
членов геометрической прогрессии со знаменателем q
≠
0
вычисляется по формуле:
А при q
= 1
— по формуле
S n
= nb
1
Заметим, что если нужно просуммировать члены
b k
, b k
+1
, . . . ,
b n
,
то используется формула:
| S n — S k -1 = b k + b k +1 + . . . + b n = b k · |
1 — q n — k +1 |
. |
| 1 — q |
Например,
в геометрической прогрессии 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, . . .
S
10
= 1 + 2 + . . . + 512 = 1 ·
(1 — 2 10) / (1 — 2) = 1023;
64 + 128 + 256 + 512 = S
10
—
S
6
= 64 ·
(1 — 2 10-7+1) / (1 — 2) = 960. ◄
Если дана геометрическая прогрессия, то величины b
1
, b n
, q
, n
и S n
связаны двумя формулами:
Поэтому, если значения каких-либо трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.
Для геометрической прогрессии с первым членом b
1
и знаменателем q
имеют место следующие свойства монотонности
:
- прогрессия является возрастающей, если выполнено одно из следующих условий:
b
1
> 0
и
q
> 1;
b
1
< 0
и
0 < q
<
1;
- прогрессия является убывающей, если выполнено одно из следующих условий:
b
1
> 0
и
0 < q <
1;
b
1
< 0
и
q
> 1.
Если q <
0
, то геометрическая прогрессия является знакопеременной: её члены с нечётными номерами имеют тот же знак, что и её первый член, а члены с чётными номерами — противоположный ему знак. Ясно, что знакопеременная геометрическая прогрессия не является монотонной.
Произведение первых n
членов геометрической прогрессии можно рассчитать по формуле:
P n
= b 1 ·
b 2 ·
b 3 ·
. . . ·
b n
= (b 1 ·
b n
) n
/ 2
.
Например,
1 ·
2 ·
4 ·
8 ·
16 ·
32 ·
64 ·
128 = (1 ·
128) 8/2 = 128 4 = 268 435 456;
3 ·
6 ·
12 ·
24 ·
48 = (3 ·
48) 5/2 = (144 1/2) 5 = 12 5 = 248 832.◄
Бесконечно убывающая геометрическая прогрессия
Бесконечно убывающей геометрической прогрессией
называют бесконечную геометрическую прогрессию, модуль знаменателя которой меньше 1
, то есть
|q
| <
1
.
Заметим, что бесконечно убывающая геометрическая прогрессия может не быть убывающей последовательностью. Это соответствует случаю
1 < q <
0
.
При таком знаменателе последовательность знакопеременная. Например,
1, — 1 / 2 , 1 / 4 , — 1 / 8 , . . . .
Суммой бесконечно убывающей геометрической прогрессии
называют число, к которому неограниченно приближается сумма первых n
членов прогрессии при неограниченном возрастании числа n
. Это число всегда конечно и выражается формулой
| S = b 1 + b 2 + b 3 + . . . = |
b 1 |
. |
| 1 — q |
Например,
10 + 1 + 0,1 + 0,01 + . . . = 10 / (1 — 0,1) = 11 1 / 9
,
10 — 1 + 0,1 — 0,01 + . . . = 10 / (1 + 0,1) = 9 1 / 11
. ◄
Связь арифметической и геометрической прогрессий
Арифметическая и геометрическая прогрессии тесно связаны между собой. Рассмотрим лишь два примера.
a
1
,
a
2
,
a
3
, . . .
d
, то
b a
1
, b a
2
, b a
3
, . . .
b d
.
Например,
1, 3, 5, . . .
— арифметическая прогрессия с разностью 2
и
7 1 , 7 3 , 7 5 , . . .
— геометрическая прогрессия с знаменателем 7
2
. ◄
b
1
,
b
2
,
b
3
, . . .
— геометрическая прогрессия с знаменателем q
, то
log a b 1
, log a b 2
, log a b 3
, . . .
— арифметическая прогрессия с разностью log a
q
.
Например,
2, 12, 72, . . .
— геометрическая прогрессия с знаменателем 6
и
lg
2, lg
12, lg
72, . . .
— арифметическая прогрессия с разностью lg
6
. ◄
Задачи по арифметической прогрессии существовали уже в глубокой древности. Они появлялись и требовали решения, поскольку имели практическую необходимость.
Так, в одном из папирусов Древнего Египта, имеющем математическое содержание, — папирусе Райнда (XIX век до нашей эры) — содержится такая задача: раздели десять мер хлеба на десять человек, при условии если разность между каждым из них составляет одну восьмую меры».
И в математических трудах древних греков встречаются изящные теоремы, имеющие отношение к арифметической прогрессии. Так, Гипсикл Александрийский (II век составивший немало интересных задач и добавивший четырнадцатую книгу к «Началам» Евклида, сформулировал мысль: «В арифметической прогрессии, имеющей четное число членов, сумма членов 2-ой половины больше суммы членов 1-ой на квадрату 1/2 числа членов».
Обозначается последовательность an. Числа последовательности называются ее членами и обозначаются обычно буквами с индексами, которые указывают порядковый номер этого члена (a1, a2, a3 … читается: «a 1-ое», «a 2-ое», «a 3-тье» и так далее).
Последовательность может быть бесконечной или конечной.
А что же такое арифметическая прогрессия? Под ней понимают получаемую сложением предыдущего члена (n) с одним и тем же числом d, являющимся разностью прогрессии.
Если d<0, то мы имеем убывающую прогрессию. Если d>0, то такая прогрессия считается возрастающей.
Арифметическая прогрессия называется конечной, если учитываются только несколько ее первых членов. При очень большом количестве членов это уже бесконечная прогрессия.
Задается любая арифметическая прогрессия следующей формулой:
an =kn+b, при этом b и k — некоторые числа.
Абсолютно верно утверждение, являющееся обратным: если последовательность задается подобной формулой, то это точно арифметическая прогрессия, которая имеет свойства:
- Каждый член прогрессии — среднее арифметическое предыдущего члена и последующего.
- Обратное: если, начиная со 2-ого, каждый член — среднее арифметическое предыдущего члена и последующего, т.е. если выполняется условие, то данная последовательность — арифметическая прогрессия. Это равенство одновременно является и признаком прогрессии, поэтому его, как правило, называют характеристическим свойством прогрессии.
Точно так же верна теорема, которая отражает это свойство: последовательность — арифметическая прогрессия только в том случае, если это равенство верно для любого из членов последовательности, начиная со 2-ого.
Характеристическое свойство для четырёх любых чисел арифметической прогрессии может быть выражено формулой an + am = ak + al, если n + m = k + l (m, n, k — числа прогрессии).
В арифметической прогрессии любой необходимый (N-й) член найти можно, применяя следующую формулу:
К примеру: первый член (a1) в арифметической прогрессии задан и равен трём, а разность (d) равняется четырём. Найти нужно сорок пятый член этой прогрессии. a45 = 1+4(45-1)=177
Формула an = ak + d(n — k) позволяет определить n-й член арифметической прогрессии через любой ее k-тый член при условии, если он известен.
Сумма членов арифметической прогрессии (подразумевается 1-ые n членов конечной прогрессии) вычисляется следующим образом:
Sn = (a1+an) n/2.
Если известны и 1-ый член, то для вычисления удобна другая формула:
Sn = ((2a1+d(n-1))/2)*n.
Сумма арифметической прогрессии, которая содержит n членов, подсчитывается таким образом:
Выбор формул для расчетов зависит от условий задач и исходных данных.
Натуральный ряд любых чисел, таких как 1,2,3,…,n,…- простейший пример арифметической прогрессии.
Помимо арифметической прогрессии существует еще и геометрическая, которая обладает своими свойствами и характеристиками.
Или арифметическая — это вид упорядоченной числовой последовательности, свойства которой изучают в школьном курсе алгебры. В данной статье подробно рассмотрен вопрос, как найти сумму арифметической прогрессии.
Что это за прогрессия?
Прежде чем переходить к рассмотрению вопроса (как найти сумму арифметической прогрессии), стоит понять, о чем пойдет речь.
Любая последовательность действительных чисел, которая получается путем добавления (вычитания) некоторого значения из каждого предыдущего числа, называется алгебраической (арифметической) прогрессией. Это определение в переводе на язык математики принимает форму:
Здесь i — порядковый номер элемента ряда a i . Таким образом, зная всего одно начальное число, можно с легкостью восстановить весь ряд. Параметр d в формуле называется разностью прогрессии.
Можно легко показать, что для рассматриваемого ряда чисел выполняется следующее равенство:
a n = a 1 + d * (n — 1).
То есть для нахождения значения n-го по порядку элемента следует n-1 раз добавить разность d к первому элементу a 1 .
Чему равна сумма арифметической прогрессии: формула
Прежде чем приводить формулу для указанной суммы, стоит рассмотреть простой частный случай. Дана прогрессия натуральных чисел от 1 до 10, необходимо найти их сумму. Поскольку членов в прогрессии немного (10), то можно решить задачу в лоб, то есть просуммировать все элементы по порядку.
S 10 = 1+2+3+4+5+6+7+8+9+10 = 55.
Стоит учесть одну интересную вещь: поскольку каждый член отличается от последующего на одно и то же значение d = 1, то попарное суммирование первого с десятым, второго с девятым и так далее даст одинаковый результат. Действительно:
11 = 1+10 = 2+9 = 3+8 = 4+7 = 5+6.
Как видно, этих сумм всего 5, то есть ровно в два раза меньше, чем число элементов ряда. Тогда умножая число сумм (5) на результат каждой суммы (11), вы придете к полученному в первом примере результату.
Если обобщить эти рассуждения, то можно записать следующее выражение:
S n = n * (a 1 + a n) / 2.
Это выражение показывает, что совсем не обязательно суммировать подряд все элементы, достаточно знать значение первого a 1 и последнего a n , а также общего числа слагаемых n.
Считается, что впервые до этого равенства додумался Гаусс, когда искал решение на заданную его школьным учителем задачу: просуммировать 100 первых целых чисел.
Сумма элементов от m до n: формула
Формула, приведенная в предыдущем пункте, дает ответ на вопрос, как найти сумму арифметической прогрессии (первых элементов), но часто в задачах необходимо просуммировать ряд чисел, стоящих в середине прогрессии. Как это сделать?
Ответить на этот вопрос проще всего, рассматривая следующий пример: пусть необходимо найти сумму членов от m-го до n-го. Для решения задачи следует представить заданный отрезок от m до n прогрессии в виде нового числового ряда. В таком представлении m-й член a m будет первым, а a n станет под номер n-(m-1). В этом случае, применяя стандартную формулу для суммы, получится следующее выражение:
S m n = (n — m + 1) * (a m + a n) / 2.
Пример использования формул
Зная, как найти сумму арифметической прогрессии, стоит рассмотреть простой пример использования приведенных формул.
Ниже дана числовая последовательность, следует найти сумму ее членов, начиная с 5-го и заканчивая 12-м:
Приведенные числа свидетельствуют, что разность d равна 3. Используя выражение для n-го элемента, можно найти значения 5-го и 12-го членов прогрессии. Получается:
a 5 = a 1 + d * 4 = -4 + 3 * 4 = 8;
a 12 = a 1 + d * 11 = -4 + 3 * 11 = 29.
Зная значения чисел, стоящих на концах рассматриваемой алгебраической прогрессии, а также зная, какие номера в ряду они занимают, можно воспользоваться формулой для суммы, полученной в предыдущем пункте. Получится:
S 5 12 = (12 — 5 + 1) * (8 + 29) / 2 = 148.
Стоит отметить, что это значение можно было получить иначе: сначала найти сумму первых 12 элементов по стандартной формуле, затем вычислить сумму первых 4 элементов по той же формуле, после этого вычесть из первой суммы вторую.

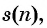

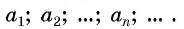
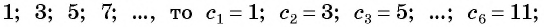
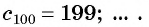
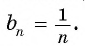
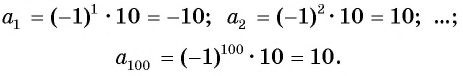
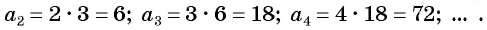
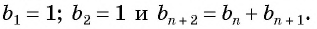
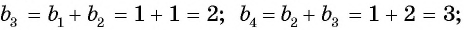
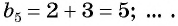
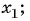
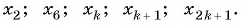
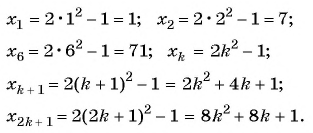
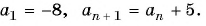
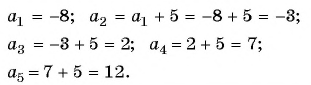
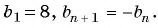
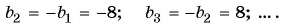
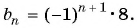
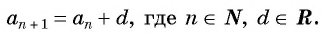
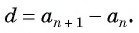
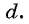
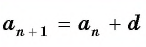
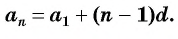
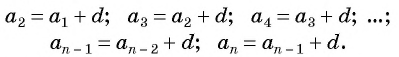
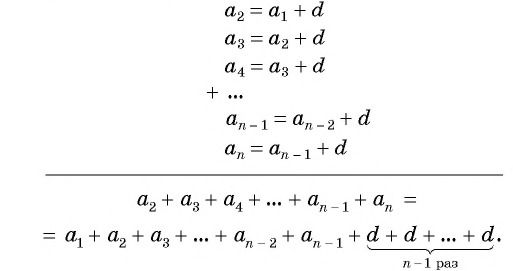
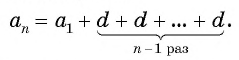
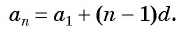

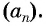
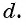
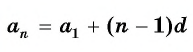
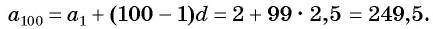
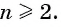
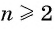
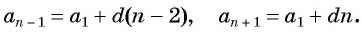
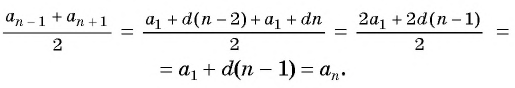
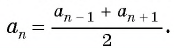
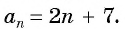
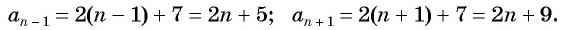
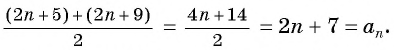
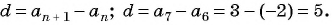
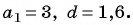
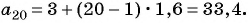
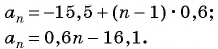
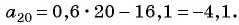
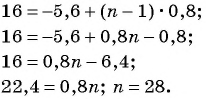
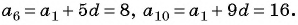
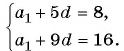
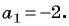
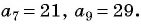
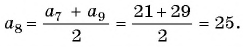
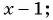
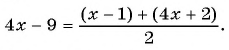
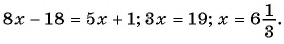
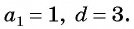
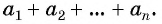
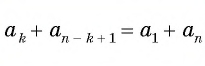
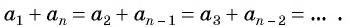
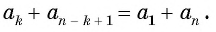
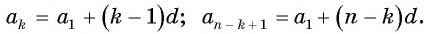
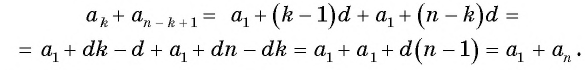
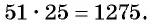
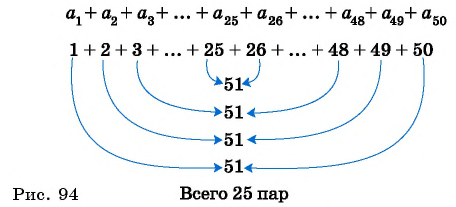
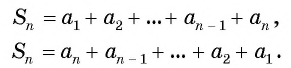
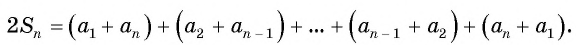
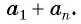
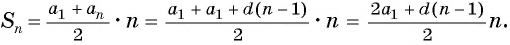
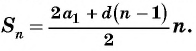
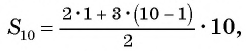

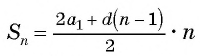
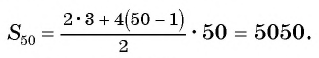
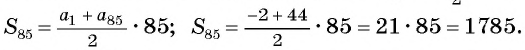
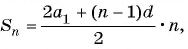
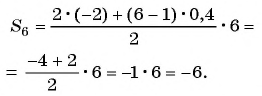
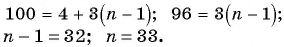
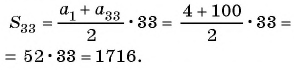
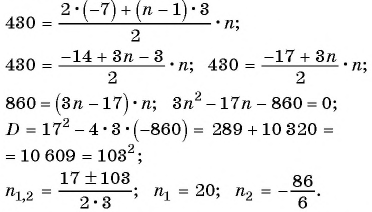
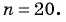
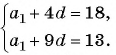
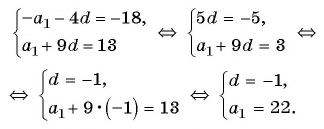
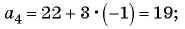
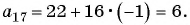
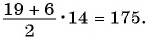
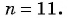
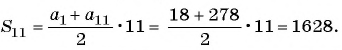
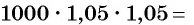
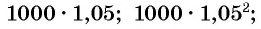
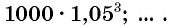
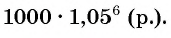
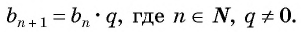
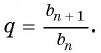
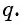
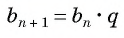
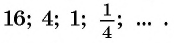
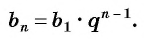
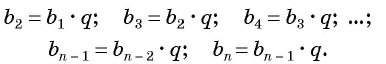
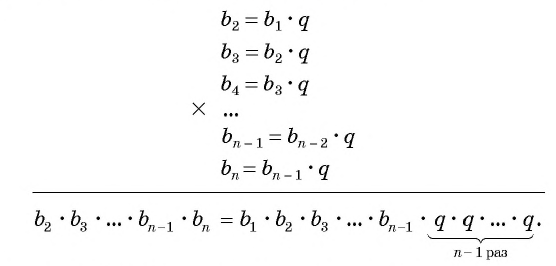
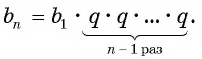
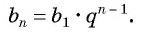
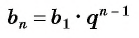
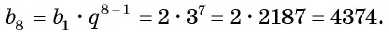
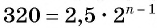
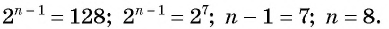
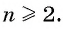
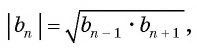
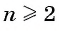
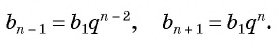
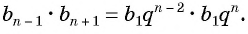
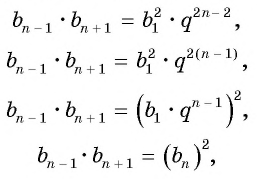
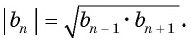
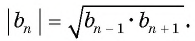
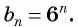
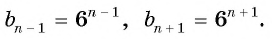
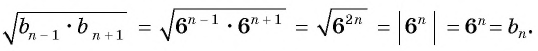
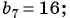
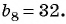
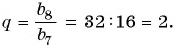
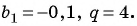
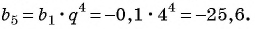
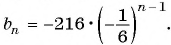
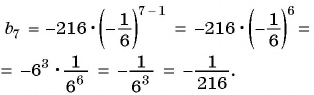
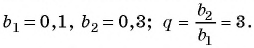
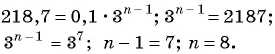
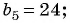
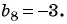
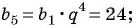
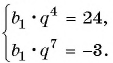
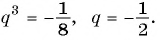
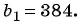
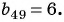
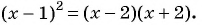
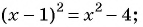
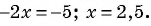

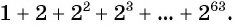
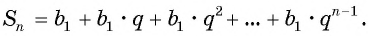
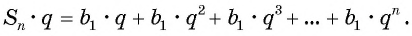
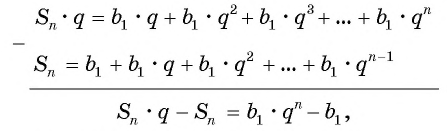
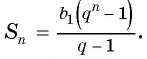
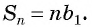
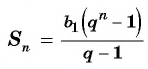
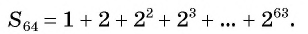
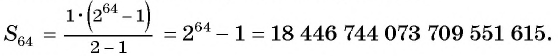
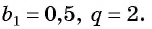
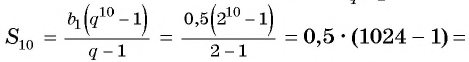
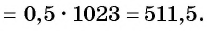
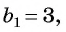
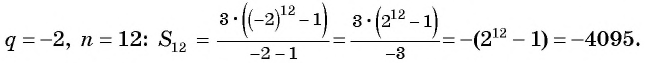
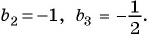
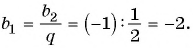
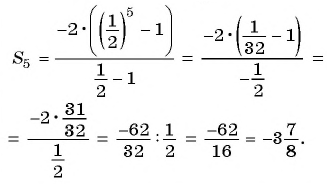
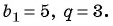
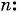
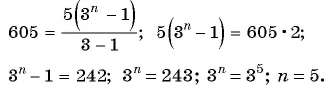
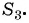
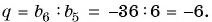
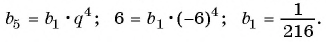
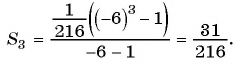
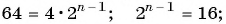
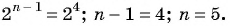
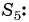
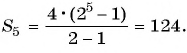
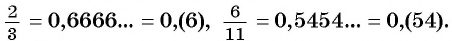
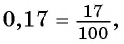
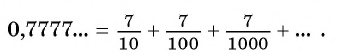
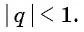
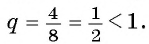
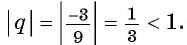
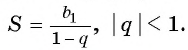
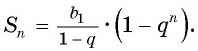
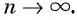
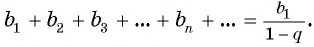
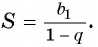
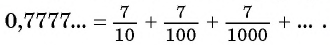
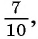
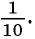
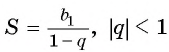
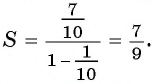
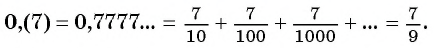
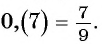
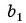 , и найти знаменатель этой прогрессии
, и найти знаменатель этой прогрессии