Как найти в четырехугольнике ось симметрии

Осевая и центральная симметрии

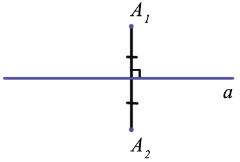
Если прямая проходит через середину отрезка А₁А₂ и перпендикулярна к нему, то точки А₁ и А₂ называются симметричными относительно прямой . Каждая точка прямой симметрична самой себе.

Фигура называется симметричной относительно прямой , если для каждой точки фигуры симметричная ей точка относительно прямой также принадлежит этой фигуре. Прямая — ось симметрии фигуры.

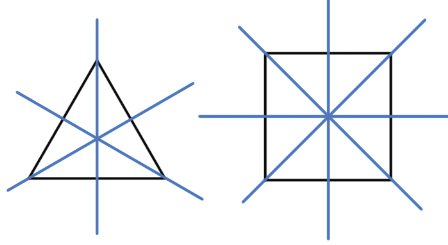
Пример (синим цветом обозначены оси симметрии):

Точки А₁ и А₂ называются симметричными относительно точки О, если О — середина отрезка А₁А₂. Точка О считается симметричной самой себе.

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры.

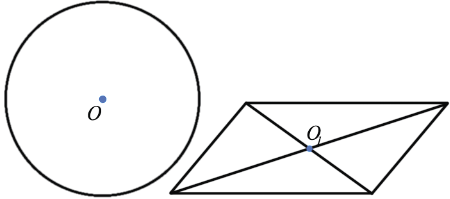
Пример (синим цветом обозначены центры симметрии):

Поделись с друзьями в социальных сетях:

Осевая и центральная симметрия

О чем эта статья:

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Ось симметрии — что это такое? Фигуры, имеющие ось симметрии

Что же такое ось симметрии? Это множество точек, которые образуют прямую, являющуюся основой симметрии, то есть, если от прямой отложили определенное расстояние с одной стороны, то оно отразится и в другую сторону в таком же размере. Осью может выступать все, что угодно, — точка, прямая, плоскость и так далее. Но об этом лучше говорить на наглядных примерах.

Симметрия

Для того чтобы понять, что такое ось симметрии, нужно вникнуть в само определение симметрии. Это соответствие определенного фрагмента тела относительно какой-либо оси, когда его структура неизменна, а свойства и форма такого объекта остаются прежними относительно его преобразований. Можно сказать, что симметрия — свойство тел к отображению. Когда фрагмент не может иметь подобного соответствия, это называется асимметрией или же аритмией.

Вам будет интересно: Как сдать физику и что нужно для этого сделать?

Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Вам будет интересно: Гибкость: определение, средства и методы развития гибкости

Виды симметрии

Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:

Геометрия

Окружность и четырехугольник

Определение

Четырехугольник называется вписанным в окружность, если окружность проходит через все вершины четырехугольника.

Очевидно, что окружность, в которую вписан четырехугольник, является описанной около любого из треугольников, на которые разбивается четырехугольник какой-либо диагональю.

Определение

Четырехугольник называется описанным около окружности, если окружность касается всех сторон четырехугольника.

Свойства и признаки вписанных и описанных четырехугольников

Напомним, что сумма внутренних  углов выпуклого -угольника находится по формуле . Для четырехугольника и сумма углов выпуклого четырехугольника равна . Обращаем внимание, что ь далее будут рассматриваться именно выпуклые четырехугольники.

Теорема 1 (свойство и признак вписанного четырехугольника)

Если четырехугольник вписан в окружность, то сумма его противолежащих углов равна (свойство). И наоборот.
Если у четырехугольника сумма противолежащих углов равна , то около него можно описать окружность (признак).

Доказательство:

Пусть четырехугольник вписан в окружность (рис. 1). Тогда вписанные углы и , а также углы и опираются на дуги, дополняющие одна другую до окружности. А это и означает, что как , так и . Свойство вписанного четырехугольника доказано.

Рис. 1

Докажем признак вписанного четырехугольника. 
Пусть у  выпуклого четырехугольника сумма противолежащих углов и а значит, углов и равна . Через три вершины четырехугольника, например, через вершины  проведем окружность (это можно сделать всегда). Тогда и четверая вершина принадлежит окружности так как в противном случае вершина  лежала бы или внутри круга, ограниченного окружностью, или вне его. Следовательно, угол  не измерялся бы половиной дуги   и значит, сумма углов  и не измерялась бы полусуммой дуг и и, таким образом, сумма углов и не равнялась бы Полученное противоречие и доказывает теорему.

Теорема доказана.

Теорема 2

Доказать, что если в выпуклом четырехугольнике углы и равны, то такой четырехугольник можно вписать в окружность. Верно и обратное.

Доказательство:

Пусть в четырехугольнике углы и равны. Проведем через точки окружность и предположим, что вершина лежит, например, внутри круга (рис. 2), границей которого является проведенная окружность.

Рис. 2

Продолжим отрезки и до пересечения с окружностью в точках и соответственно. 
Тогда , а , что приводит к противоречию, так как по условию . Итак, точка должна лежать на окружности или находиться вне круга. Предположим, что она находится вне круга (рис. 3).

Рис. 3

Обозначим через и точки пересечения окружности с отрезками и соответственно. Тогда , а , что, как и в первом случае, также вступает в противоречие с условием задачи. Вывод: точка является точкой окружности, описанной около четырехугольника .
Обратно, если четырехугольник вписан в окружность, то равенство углов и следует из того, что они являются вписанными углами, опирающимися на одну и ту же дугу.

Теорема доказана.

Замечание 1
Очевидно, что четырехугольник можно вписать в окружность и в случаях, когда или , или , или .

Теорема 3

Доказать, что если — точка пересечения диагоналей четырехугольника и , то около такого четырехугольника можно описать окружность. Верно и обратное.

Доказательство:

Пусть имеет место равенство , которое преобразуется в пропорцию . А тогда так как как вертикальные углы (рис. 4), то треугольники и подобны и, значит, .

Рис. 4

Последнее равенство и означает (замечание 1), что около четырехугольника можно описать окружность. Справедливость обратного утверждения очевидным образом следует из свойства хорд.

Теорема доказана.

Теорема 4 (Теорема Птолемея)

Если четырехугольник вписан в окружность, то сумма произведений его противолежащих сторон равна произведению его диагоналей.

Доказательство:

В четырехугольнике (рис. 5) построим угол ( — точка диагонали ), равный углу . Тогда треугольники и будут подобными, так как как вписанные углы,   опирающиеся на одну и ту же дугу.

Рис. 5

Но в таком случае , т.е.   Из подобия же треугольников и следует, что или  Таким образом,, что и требовалось доказать.
Обратно. Пусть в четырехугольнике произведение его диагоналей равно сумме произведений его противолежащих сторон, то есть . 
Через точки и проведем прямые так, чтобы в получившемся треугольнике выполнялись равенства: , (рис. 6).

Рис. 6

Тогда по первому признаку подобия треугольников и, значит, , откуда следует, что . Так как то по второму признаку подобия треугольников и, таким образом, , откуда . Но тогда или . Отсюда следует, что и, значит, точка принадлежит отрезку , откуда вытекает равенство . Полученное равенство углов означает, что точки , , и лежат на одной окружности (отрезок виден из точек и под одним углом), а это и требовалось доказать.

Теорема доказана.

Теорема 5 (свойство и признак описанного четырехугольника)

Если четырехугольник описан около окружности, то суммы его противолежащих сторон равны (свойство). И наоборот.
Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность (признак).

Доказательство:

Пусть четырехугольник описан около окружности и пусть , , , — точки касания окружности со сторонами четырехугольника (рис. 7). Тогда по свойству касательных  имеем . Складывая полученные равенства, находим, что или . 
Свойство описанного четырехугольника доказано.

Рис. 7

Докажем признак описанного четырехугольника.
Если четырехугольник ромб, то он является описанным около окружности с центром в точке пересечения его диагоналей.

Рассмотрим теперь случай, когда у выпуклого четырехугольника есть неравные соседние стороны. Допустим, что , и, значит, . Отложим на сторонах углов    и отрезки и (рис. 8).

Рис. 8

Поскольку по условию имеем  , и поэтому треугольник  — равнобедренный с основанием . Треугольники и по построению также равнобедренные с основаниями и .
По свойству медианы равнобедренного треугольника медианы этих трех треугольников, проведенные к их основаниям, являются их высотами. Значит, прямые, содержащие эти медианы, — серединные перпендикуляры к сторонам треугольника и поэтому пересекаются в одной точке .
Эти же медианы являются и биссектрисами равнобедренных треугольников , и . Поэтому лучи , и — биссектрисы углов , и четырехугольника , которые образуют с его сторонами острые углы, так как по условию данный четырехугольник выпуклый. Значит, точка равноудалена от всех сторон четырехугольника , и поэтому он является описанным около окружности с центром в этой точке.
Теорема доказана.

Рассмотрим примеры.

Пример 1

В остроугольном треугольнике проведены высоты , , . Пусть — точка пересечения высот. Построить треугольник и перечислить все образовавшиеся четырехугольники, около которых можно описать окружность (рис. 9).

Рис. 9

Решение:
Рассмотрим четырёхугольник : прямые углы и опираются на один и тот же отрезок , который и будет диаметром описанной окружности. Аналогично для четырёхугольников: (диаметр ); (диаметр ); (диаметр ); (диаметр ); (диаметр ).

Ответ:

, , , , , .

Пример 2

В остроугольном треугольнике проведены высоты и . Доказать, что треугольник подобен данному треугольнику с коэффициентом подобия, равным .

Решение:
На стороне треугольника как на диаметре опишем полуокружность, которая пройдет через основания высот и (рис. 10).

Рис. 10

Так как четырехугольник вписанный, то   Следовательно, и . Так как стороны и являются соответствующими сторонами в подобных треугольниках, то их отношение равно коэффициенту подобия. Но в прямоугольном треугольнике отношение сторон . Итак, и . Что и требовалось доказать.

Пример 3

Доказать, что около параллелограмма можно описать окружность тогда и только тогда, когда параллелограмм является прямоугольником.

Решение:
Покажем, что если параллелограмм можно вписать в окружность, то такой параллелограмм будет прямоугольником. 
Действительно, пусть параллелограмм вписан в окружность. Тогда по теореме 1 . Но в параллелограмме противолежащие углы равны, поэтому . 
Аналогично показывается, что и , а это и доказывает требуемое. Обратное утверждение очевидно.

Пример 4

Доказать, что параллелограмм, в который можно вписать окружность, является ромбом.

Решение: 
Так как в описанном около окружности четырехугольнике суммы противолежащих сторон равны (теорема 5), то в случае параллелограмма это условие равносильно равенству смежных сторон. Следовательно, такой параллелограмм — ромб. Что и требовалось доказать.

Следствие 1

Параллелограмм, в который можно вписать окружность и около которого можно описать окружность, является квадратом.

Пример 5

Доказать, что около трапеции можно описать окружность тогда и только тогда, когда она является равнобочной.

Решение: 
Рассмотрим трапецию с параллельными сторонами и (рис. 11).

Рис. 11

Так как сумма внутренних односторонних углов при параллельных прямых равна , то
А поскольку около трапеции можно описать окружность тогда и только тогда, когда сумма ее противолежащих углов равна (теорема 1), то . Таким образом, . Но эти вписанные углы измеряются соответственно половинами дуг и . Поэтому, так как дуга у дуг и общая, то вписанные углы, опирающиеся на дуги и , равны. Но тогда равными будут и дуги и . Но равные дуги стягиваются равными хордами, что и требовалось доказать.

Пример 6

Доказать, что если выпуклый четырехугольник имеет ось симметрии, то либо около него можно описать окружность, либо в него можно вписать окружность.

Решение:
Если ось симметрии не проходит ни через одну вершину четырехугольника, он представляет собой равнобочную трапецию или прямоугольник и является вписанным.
Рассмотрим случай, когда ось симметрии выпуклого четырехугольника, например, проходит через его вершину, скажем, . Тогда очевидно, что эта ось будет проходить и через противолежащую вершине вершину . Но в таком случае вершина будет симметрична вершине и, значит, сторона окажется симметричной стороне , а сторона будет симметрична стороне . Поэтому , и, таким образом, . Полученное равенство означает, что четырехугольник является описанным около окружности и это есть или дельтоид (рис. 12), или ромб. Что и требовалось доказать.

Рис. 12

Пример 7

Трапеция описана около окружности. Доказать, что концы боковой стороны трапеции и центр окружности являются вершинами прямоугольного треугольника.

Решение: 
Рассмотрим описанную трапецию с параллельными сторонами   и (рис. 13).

Рис. 13

Так как сумма внутренних односторонних углов при параллельных прямых равна , то . 
А поскольку лучи и , где — центр вписанной в трапецию окружности, являются биссектрисами углов и соответственно, то и, таким образом, в треугольнике   угол с вершиной является прямым.
Аналогично показывается, что треугольник также является прямоугольным, а это и доказывает требуемое.

Пример 8

Равнобочная трапеция описана около окружности. Найти радиус окружности, если основания трапеции равны и .

Решение:
Пусть в описанной равнобочной трапеции основание , а основание (рис. 14).

Рис. 14

Тогда из равенства сторон и и того, что (теорема 5), следует, что . 
Пусть и — перпендикуляры к основанию . Очевидно, что и , а значит, четырехугольник   — прямоугольник, у которого . Поэтому . Из прямоугольного же треугольника находим и, таким образом, радиус вписанной в трапецию окружности равен

Ответ:

Пример 9

Около окружности описана равнобочная трапеция, у которой средняя линия равна   Определить периметр трапеции и ее боковую сторону.

Решение:
Пусть — точки касания окружности с описанной около нее равнобочной трапецией (рис. 15) и пусть , а — средняя линия трапеции.

Рис. 15

Тогда , а . Поэтому . Но поскольку отрезок , то . Отсюда периметр трапеции — это .

Ответ:

Пример 10

Доказать, что если центр вписанной в четырехугольник окружности совпадает с точкой пересечения диагоналей, то этот четырехугольник — ромб. Верно и обратное.

Решение:
Пусть точка — центр окружности, вписанной в четырехугольник (рис.16), — точки касания окружности с четырехугольником.

Рис. 16

Так как , то и, значит, Треугольники и   — равнобедренные и — биссектриса, поэтому — равнобедренный и Тогда  , т. е. четырехугольник — ромб. Наоборот, если — точка пересечения диагоналей ромба, которые по свойству ромба лежат на биссектрисах его углов, то расстояния от точки до каждой из сторон ромба равны. Отсюда и следует, что точка — центр вписанной в ромб окружности. Что и требовалось доказать.

Что же такое ось симметрии? Это множество точек, которые образуют прямую, являющуюся основой симметрии, то есть, если от прямой отложили определенное расстояние с одной стороны, то оно отразится и в другую сторону в таком же размере. Осью может выступать все, что угодно, — точка, прямая, плоскость и так далее. Но об этом лучше говорить на наглядных примерах.

Симметрия

Для того чтобы понять, что такое ось симметрии, нужно вникнуть в само определение симметрии. Это соответствие определенного фрагмента тела относительно какой-либо оси, когда его структура неизменна, а свойства и форма такого объекта остаются прежними относительно его преобразований. Можно сказать, что симметрия — свойство тел к отображению. Когда фрагмент не может иметь подобного соответствия, это называется асимметрией или же аритмией.

Вам будет интересно:Как сдать физику и что нужно для этого сделать?

Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Вам будет интересно:Гибкость: определение, средства и методы развития гибкости

Виды симметрии

Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:

История симметрии

Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.

В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.

А философ Платон считал многогранники олицетворением четырех природных стихий:

• тетраэдр — огонь, так как его вершина направлена вверх;
• куб — земля, так как это самое устойчивое тело;
• октаэдр — воздух, нет каких-либо объяснений;
• икосаэдр — вода, так как тело не имеет грубых геометрических форм, углов и так далее;
• образом всей Вселенной являлся додекаэдр.

Из-за всех этих теорий правильные многогранники называют телами Платона.

Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.

Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».

Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».

Что уж там говорить, симметрия — ключевое понятие для всех деятелей искусства на протяжении многих веков, но в XX веке ее смысл оценили также все деятели точных наук. Точным свидетельством являются физические и космологические теории, например, теория относительности, теория струн, абсолютно вся квантовая механика. Со времен Древнего Вавилона и, заканчивая передовыми открытиями современной науки, прослеживаются пути изучения симметрии и открытия ее основных законов.

Симметрия геометрических фигур и тел

Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.

А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника — также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно — длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.

Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых — бесконечное множество.

У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии — диагонали, а во втором — средние линии. Множество таковых осей только у квадрата.

Симметрия в природе

Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия — основное условие.

Вывод

Нас постоянно окружают какие-либо явления и предметы, например, радуга, капля, цветы, лепестки и так далее. Их симметрия — очевидна, в какой-то степени она обусловлена гравитацией. Часто в природе под понятием «симметрия» понимают регулярную смену дня и ночи, времен года и так далее.

Подобные свойства наблюдаются везде, где есть порядок и равенство. Также и сами законы природы — астрономические, химические, биологические и даже генетические подчинены определенным принципам симметрии, так как имеют совершенную системность, а значит, сбалансированность имеет всеохватывающий масштаб. Следовательно, осевая симметрия — один из основополагающих законов мироздания в целом.