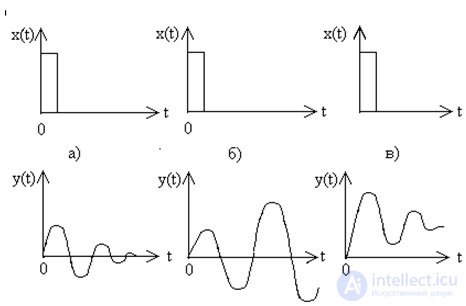
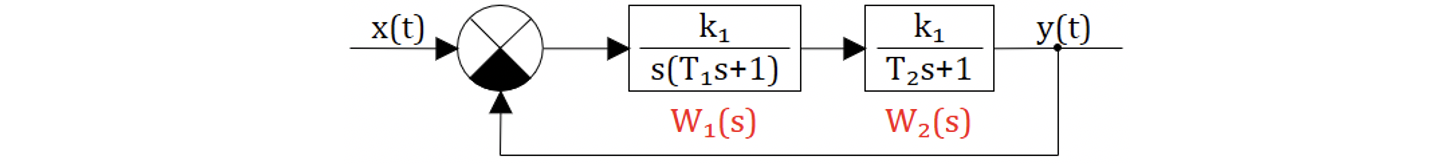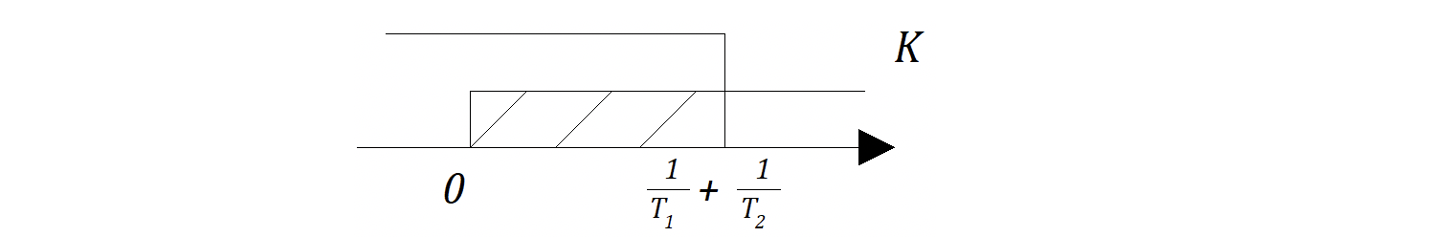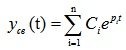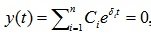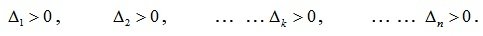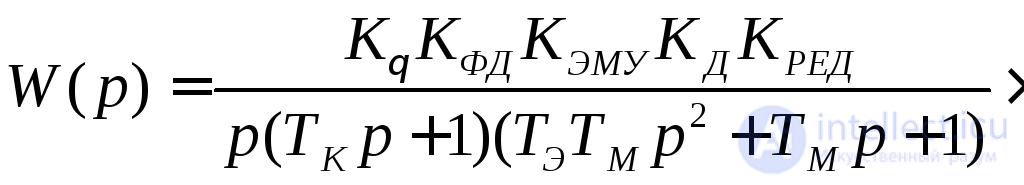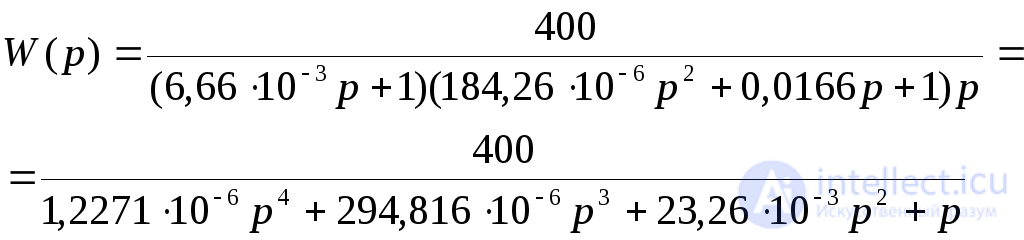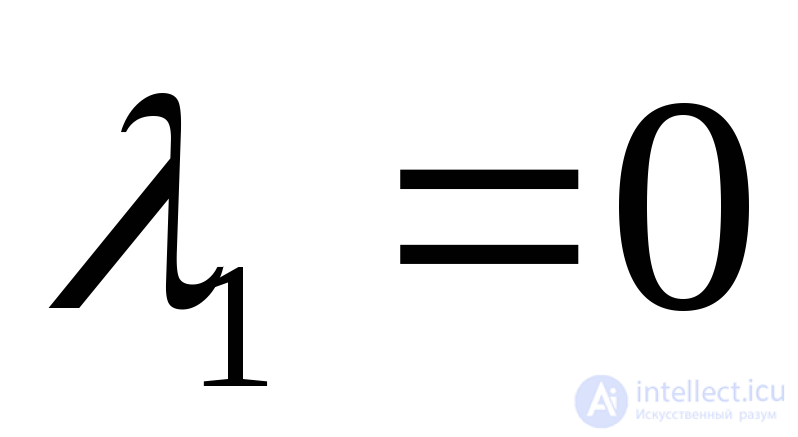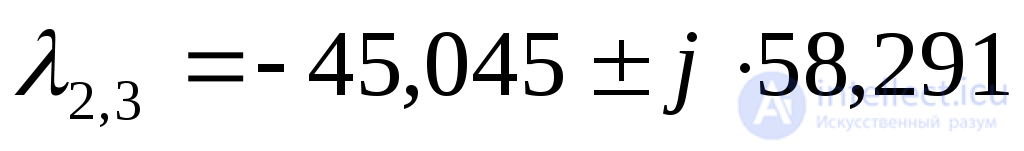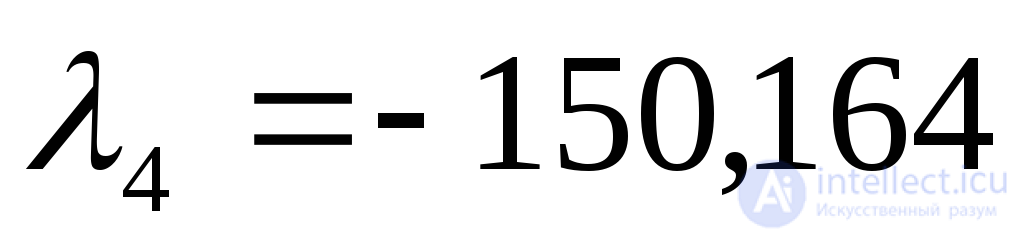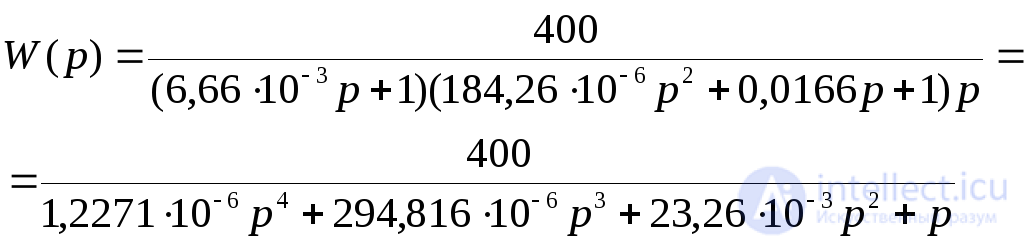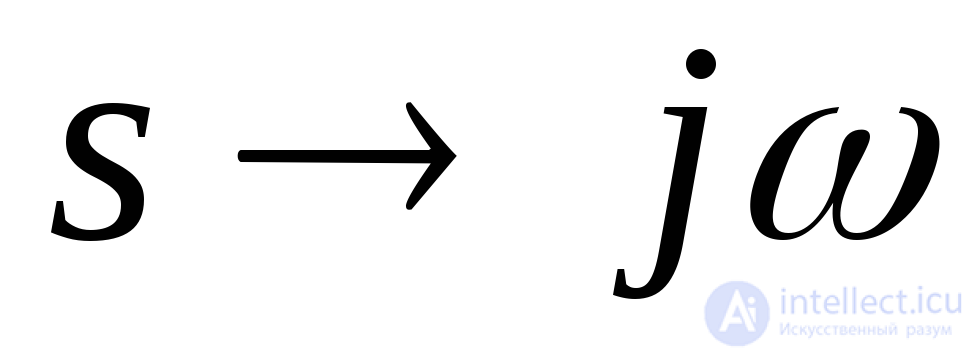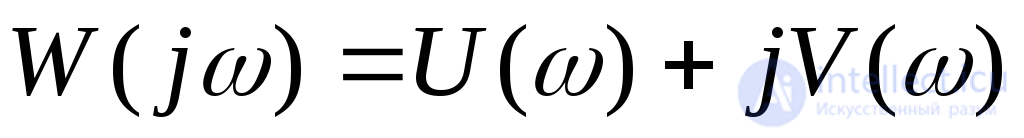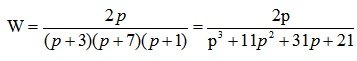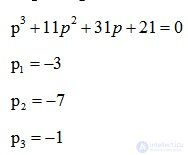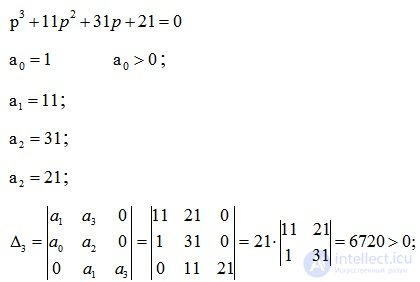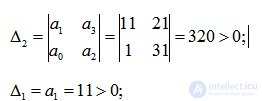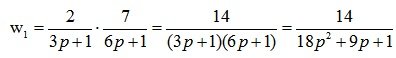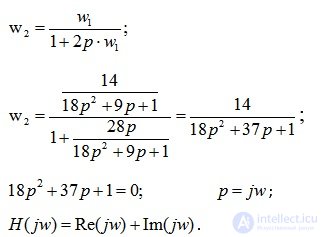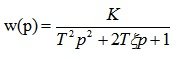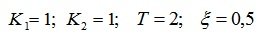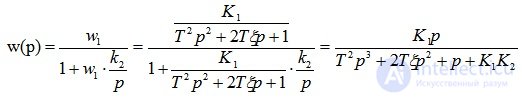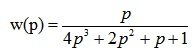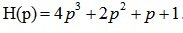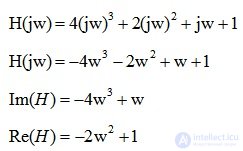Как найти устойчивое состояние системы - Avtoru.top

В результате получим замкнутую систему, в которой будут наблюдаться незатухающие колебания с постоянной амплитудой, а, как мы знаем, это характерно для систем, находящихся на границе устойчивости (см. рис. 7.2,е в разделе 7.1). Таким образом, прохождение графика АФХ разомкнутой системы через точку (–1, 0i) свидетельствует о нахождении соответствующей замкнутой системы на границе устойчивости.
Теперь рассмотрим второй случай. Предположим, в ходе того же самого опыта на выходе разомкнутой системы установились колебания с тем же сдвигом фазы π, но с меньшей амплитудой:

φ = ±π ; Aвых < Aвх.

Это состояние соответствует точке АФХ разомкнутой системы, лежащей на вещественной оси правее точки (–1, 0i) (Mраз(ω) = Aвых/Aвх < 1, φраз(ω) = ±π).
После отключения генератора колебаний и замыкания отрицательной обратной связи на вход Wраз(iω) поступит сигнал с меньшей амплитудой, чем создавал генератор. Пройдя через регулятор и объект, этот сигнал снова будет несколько ослаблен (так как Mраз(ω) < 1), в следующий момент времени поступит по обратной связи на вход Wраз(iω) с еще меньшей амплитудой, и это будет повторяться снова и снова. Таким образом, в данном случае с течением времени амплитуда колебаний в замкнутой системе будет непрерывно уменьшаться, стремясь к нулю, т.е. будет наблюдаться затухающий процесс, что, как известно, характерно для устойчивых систем (рис. 7.2,г).
В третьем возможном случае на выходе разомкнутой системы установятся колебания со сдвигом фазы π и большей амплитудой, нежели входные колебания:

φ = ±π ; Aвых > Aвх,

что соответствует точке АФХ разомкнутой системы, лежащей на вещественной оси левее точки (–1, 0i) (Mраз(ω) = Aвых/Aвх > 1, φраз(ω) = ±π).
Здесь при прохождении через регулятор и объект сигнал усиливается (Mраз(ω) > 1), и его подача по обратной связи на вход Wраз(iω) приводит к возникновению колебательного процесса с непрерывно нарастающей амплитудой («расходящегося»), как на рис. 7.2,д, т.е. замкнутая система оказывается неустойчивой.
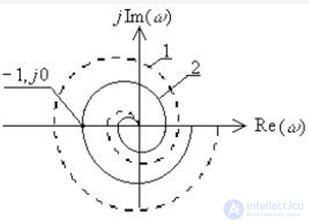
Из сказанного становится ясно, что об устойчивости замкнутой системы можно судить на основании расположения амплитудно-фазовой характеристики разомкнутой системы относительно точки с координатами (–1, 0i) (рис. 7.7).
Критерий Найквиста – Михайлова формулируется следующим образом.
Замкнутая система устойчива, если она устойчива в разомкнутом состоянии, и ее амплитудно-фазовая характеристика (построенная для всех значений ω от 0 до бесконечности) не охватывает точку с координатами (–1, 0i).
Если амплитудно-фазовая характеристика проходит через точку с координатами (–1, 0i), система находится на границе устойчивости. Если АФХ охватывает точку с координатами (–1, 0i), то система неустойчива.

Источник

Предыдущие лекции по теории автоматического управления можно посмотреть здесь:

1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.

3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

4. Структурные преобразования систем автоматического регулирования.

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).

6.1. Понятие об устойчивости САР. Теоремы Ляпунова.

В теории «Управления техническими системами» общепринято понятие качество управления, состоящее из трех основных составляющих:

устойчивость САР (или запасы устойчивости);
точность САР;
качество переходного процесса.

Необходимо заметить, что если не обеспечена устойчивость замкнутой САР, то говорить о точности и, тем более, о качестве переходного процесса — бессмысленно.

Поэтому понятие «устойчивость» — важнейшее понятие для САР.

Приведем «механическую» аналогию понятия «устойчивость»

Рисунок 6.1.1 а) абсолютно устойчивое положение, б) неустойчивое положение, в) нейтральное (безразличное) положение.

В положении а) при отклонении шарика от нижнего положения он обязательно вернется в свое устойчивое положение (низ «воронки»).

В положении б) малейшее отклонение шара от состояния равновесия приведет к «скатыванию» его вниз; т.е. шар не вернется сам назад на вершине «горки».

В положении в) при воздействии на шар он начнет перемещаться в горизонтальном направлении и, если нет трения, то шар будет двигаться с постоянной скоростью.

Если реальная замкнутая САР имеет свойства, аналогичные а), то она «хорошая», если б) – «совсем плохая». Нужно так проектировать САР, чтобы ее свойства были похожи на а), т.е. если какое-то возмущающее воздействие отклонит систему от равновесия, то система управления обязана вернуть техническую систему в состояние равновесия.

Ранее мы водили передаточную функуию для по возмущающему воздействию для замкнутой САР (см. формулу 5.4 в предыдущей лекции). Уравнения динамики замкнутой САР, описываемую в переменных «вход-выход»:

Решения для такого уравнения будет являтся суммой двух функций: $y(t)=y_{соб}(t)+y_{вын}(t)$ , где $y_{соб}(t)$ — собственное решение, при и вынужденное $y_{вын}(t)$ решение вызванное воздействием.

Решим характеристическое уравнение (подробнее смотри здесь…)

$a_ncdot lambda^n_n+a_{n-1}cdot lambda^{n-1}_{n-1}+...+a_1cdot lambda_1+a_0 =0$

Решая уравнение (6.1.2), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения , тогда собственное решение примет вид:

$y_{соб}(t)=sum_{j=1}^n c_jcdot e^{lambda_jcdot t} mathbf{(6.1.3)}$

В зависимости от значения возможно несколько вариантов вида функуции. На рисунке 6.1.2 представлены варинаты поведения функции вида $c_jcdot e^{lambda_jcdot t}$ в случае когда является реальными числом или комплексным числом .

Рисунок 6.1.2 Возможная вид решения

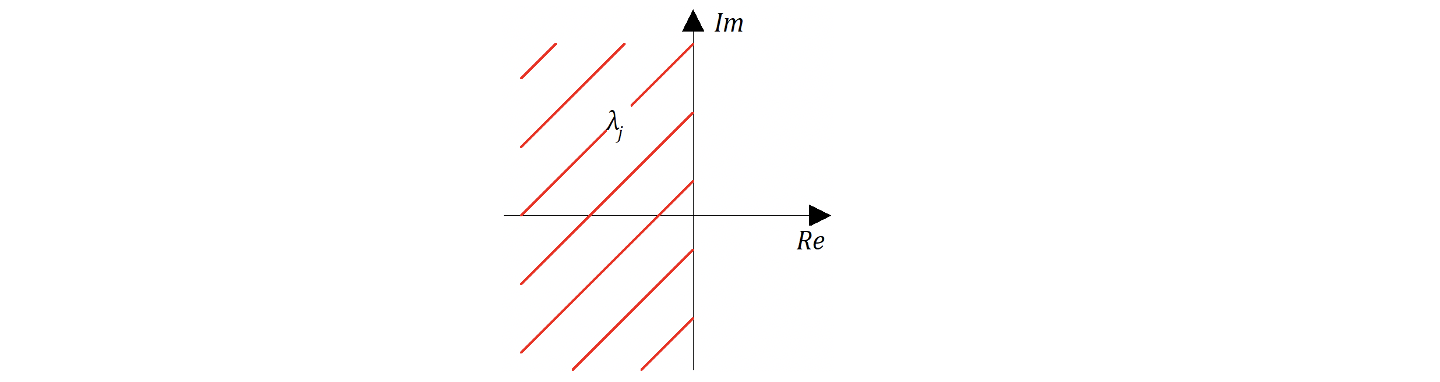
Анализ вышеприведенных рисунков показывает, что система может вернуться в исходное состояние, если все составляющие $с_jcdot e^{lambda_jcdot t }$ при будут стремиться к нулю. А для этого показатель степени должен быть отрицательным. Поэтому условием устойчивости является отрицательное значение реальной части корней т.е. необходимо чтобы корни характеристического уравнения лежали в левой полуплоскости.

Рисунок 6.1.3 Расположение корней характеристического уравнения

Если корни комплексные, то процесс колебательный, если корни реальные, то процес аперодический (затухающий). Причем ось ординат соответствует границам устойчивости (апериодической или колебательной). Таким образом, вопрос об устойчивости или неустойчивости замкнутой (и разомкнутой) САР определяется по расположению корней соответствующего характеристического уравнения.

Для не замкнутой САР вместо устойчивость определяется корнями характеристического уравнения знаменателя передаточной функции в предыдущей лекции мы выводили формулу рассчета передаточной фунции замкунутой САР, по предаточной функции разомкнутоф САР:

Таким образом, вопрос об устойчивости или неустойчивости замкнутой и разомкнутой САР определяется по расположению корней соответствующего характеристического уравнения.

$left [ begin{align} D(lambda)=0 - для замкнутой САР \L(lambda) =0 - для разомкнутой САР end{align} mathbf{(6.1.3)}right.$

Если все корни характеристического уравнения лежат (расположены) в левой полуплоскости – линейная (или линеаризованная) САР устойчива.

Необходимо заметить, что коэффициенты уравнения совпадают с коэффициентами многочлена (полинома) следовательно полюса замкнутой САР тождественно совпадают с корнями характеристического уравнения , где — корни характеристического уравнения; — полюса перредаточной функции.

Напомним, полюсом передаточной функции называется значение её аргумента, при котором знаменатель функции обращается в ноль.

Используя приблизительно такие же рассуждения сходимости степенных функций Ляпуновым были сформулированы 3 теоремы об устойчивости линейных САР:

Если все корни характеристического уравнения или полюса передаточной функции САР расположены в левой полуплоскости, то линеаризованная САР обязательно вернется в исходное состояние при снятии внешнего воздействия, выведшего эту САР из состояния равновесия. Следовательно САР – устойчива.
Если хотя бы один полюс (или корень характеристического уравнения) передаточной функции САР расположен в правой полуплоскости (при всех остальных в левой полуплоскости), линейная (линеаризованная) САР никогда не вернется в исходное (равновесное) состояние при снятии внешнего воздействия, которое вывело данную САР из исходного состояния равновесия. Следовательно САР – неустойчива.
Если хотя бы один из полюсов передаточной функции САР (корней характеристического уравнения) находится на мнимой оси (при всех остальных в левой полуплоскости) об устойчивости линеаризованной САР ничего сказать нельзя, т.к. учет нелинейных (отброшенных) членов в динамике САР может дать любой результат (устойчива или неустойчива).

Резюмируя вышесказанное, отметим, что:

Наиболее простым способом определения устойчива или неустойчива САР (как замкнутая, так и разомкнутая) является решение уравнения для замкнутой САР (или для разомкнутой САР) или решение характеристического уравнения или– для разомкнутой САР).

Если САР задана в переменных состояния, то вопрос об устойчивости САР определяется матрицей А – собственной матрицей:

$left { begin{align} x'=Acdot x+Bcdot u \ y =C cdot x + D cdot u end{align} mathbf{(6.1.5)}right.$

Если собственные числа матрицы А лежат в левой полуплоскости – САР устойчива; если хотя бы одно собственное число лежит в правой полуплоскости – линейная САР неустойчива.

Собственные числа (согласно разделу «Линейная алгебра») находятся из уравнения:

где: — матрица размера ; — единичная матрица

$E = begin{bmatrix} 1 &0 &cdots & 0 \ 0 & 1 &cdots & 0 \ vdots &vdots &ddots &vdots \ 0 &0 &0 &1 end{bmatrix}$

Это означает, что уравнение принимает:

$left | begin{matrix} a_{11}-lambda_1 &a_{12} &cdots & a_{1n} \ a_{21} & a_{22} - lambda_2 &cdots & a_{2n} \ vdots &vdots &ddots &vdots \ a_{n1} &a_{n2} &cdots &a_{nn}-lambda_n end{matrix} right |=0 mathbf{(6.1.7)}$

решая, находим

Фактически уравнения (6.1.6) и (6.1.7) – характеристические уравнения САР. Поэтому, если САР задана в переменных состояния, то характеристический полином при задании САР в переменных «вход-выход» может быть определен как:

$D(s)=left [ begin{align} det[A -E cdot s] = 0 - если размерность матрицы A четная \det[Ecdot s -A]=0 - если размерность матрицы A нечетная end{align} right.$

Чисто математически задача определения устойчивости сводится к решению степенного уравнения или к проблеме нахождения собственных чисел матрицы А.

6.2. Необходимые условия устойчивости линейных и линеаризованных САР.

Наиболее просто необходимое условие устойчивости линейных (линеаризованных) САР формулируется для систем, записанных в переменных «вход-выход», причем оно применяется в одинаковой «редакции» как для замкнутых, так и для разомкнутых САР. Это условие доказывается с использованием характеристического полинома D(s) – для замкнутых САР, или L(s) – для разомкнутых САР. Сделаем вывод на основании D(s)

Разложим многочлен D(s) на элементарные линейные сомножители :

$D(s)=a_ncdot s^n+a_{n-1}cdot s^{n-1}+...+a_1cdot s+a_0$ $D(s)=a_ncdot(s-s_1)cdot(s-s_2)cdot ...cdot(s-s_n) mathbf{(6.2.1)}$

где: — полюса передаточной функции замкнутой САР.

Предположим, что и что все полюса расположены в левой полуплоскости:

$left | begin{align} s_1 &= -|alpha_1 | \s_2&=-|alpha_2|+icdotbeta_2; \s_3&=-|alpha_2|-icdot beta_2;\s_4&=-|alpha_3|+icdotbeta_3;\ s_5&=-|alpha_3|-icdotbeta_3;\&............ end{align} right.$

где: — действительный полюс; — — комплексно-сопряженные полюса.

Подставим значения в выражение 6.2.1 заметим, что если перемножать любые две скобки в выражении 6.2.1, которые содержат комплексно сопряженные скобки например мы получим выражение типа: .

В первой скобке мы получим выражение: Таким образом мы получаем только полжительные коэффициенты полинома Таким образом можно сформулировать необходимое условие устойчивости линейных САР:

Необходимым условием устойчивости линейных САР является положительность всех коэффициентов в полиноме — для замкнутых САР, или в – для разомкнутых САР.

Для систем 1-го и 2-го порядка необходимое условие является и достаточным.

Но для систем, имеющих порядок , выполнение необходимого условия невсегда является достаточным.

Тем не менее, необходимое условие «очень удобно», т.е. если хотя бы один коэффициент в D(s) отрицателен, то однозначно – САР неустойчива.

Если необходимое условие выполнено , то если порядок матрицы больше 2 необходимо либо вычислить корни характеристического уравнения (полюса передаточной функции), либо используя какой-либо из критериев устойчивости сделать соответствующий вывод об устойчивости САР.

6.3. Алгебраический критерий устойчивости Гурвица.

Как отмечалось выше, устойчивость любой САР можно определить, вычислив значение всех полюсов (или корней соответствующего характеристического уравнения). Однако далеко не все способны без компьютера (калькулятора) решить степенное уравнение выше квадратного (кубическое и т.д.).

Критерий Гурвица, являющийся частным случаем критерия Раусса, позволяет не решая уравнений типа или сделать вывод об устойчивости САР на основании «несложных» вычислений с использованием коэффициентов характеристического полинома.

Представим полином в измененном виде:

$D(s)=a_0cdot s^n+ a_1cdot s^{n-1}+ ...+ a_{n-1}cdot s +a_n mathbf{(6.3.1)}$

Данное выражение полинома позволяет соcтавить матрицу Гурвица, для этого:

по главной диагонале по главной диагонали слева направо выставляются коэффициенты характеристического уравнения от до ;
от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;
на место коэффициентов с индексами меньше нуля или больше ставатся нули:

$Г = begin{bmatrix} a_1 &a_3 &a_5 &cdots & 0 &0 \ a_0 & a_2 &a_4 &cdots &0 &0\0 &a_1 &a_3 &cdots &0 &0\ vdots &vdots &vdots &ddots &vdots &vdots \0 &0 &0 &cdots &a_{n-1} &0 \ 0 &0 &0 &cdots &a_{n-2} &a_n end{bmatrix}$

Составив эту матрицу можно сфомулировать критерий:

Для того, чтобы замкнутая САР (или разомкнутая) была устойчивой, необходимо и достаточно, чтобы были положительны все n главных определителей Гурвицевой матрицы Г.

$left { begin{align} Delta_1 &= a_1>0; \ Delta_2 &= left |begin{matrix} a_1 &a_3\ a_0 &a_2 end{matrix} right |>0; \ Delta_3 &= left | begin{matrix}a_1 &a_3 &a_5 \ a_0 &a_2 &a_2 \ 0 &a_1 &a_3 end{matrix} right |>0; \ cdots \ Delta_{n} &= Delta_{n-2}cdot a_n >0. end{align} right.$

Если все определители больше нуля, то линейная САР устойчива.

Если все определители больше нуля и то САР находится на апереодической границе устойчивости.

Если все определители, кроме $Delta_{n-1}$ больше нуля, а опеределитель $Delta_{n-1} =0$ и Р , то САР находится на колебательного границы устойчивости.

Пример 1

Определить, устойчива или нет следующая система САР:

Рисунок 6.3.1 САР для анализа устойчивости

Найдем главную передаточную функцию замкнутой САР:

$Ф(s)=frac{W(s)}{W_{oc}(s)}=frac{10cdot s+1}{(4cdot s^2+s+1)cdot left [1+frac{10cdot s+1}{4cdot s^2+s+1}cdot frac{1}{s+1} right]}=\ =frac{(10cdot s+1)cdot(s+1)}{(s+1)cdot(4cdot s^2+s+1)+(10cdot s+1)}=frac{(10cdot s+1)cdot(s+1)}{underbrace{4cdot s^3+5cdot s^2+12cdot s+2}_{D(s)}}$

Все коэффициенты полинома — положительные:

$D(s)=underbrace{4}_{a_0}cdot s^3+underbrace{5}_{a_1}cdot s^2+underbrace{12}_{a_2}cdot s+underbrace{2}_{a_3}$

А значит САР может быть устойчива. Составим матрицу Гурвица, и найдем ее определители:

$Г=begin{bmatrix} 5 &2 &0\ 4 &12 &0 \ 0 &5 & 2 end{bmatrix}Rightarrow left { begin{align} Delta_1 &=5>0; \ Delta_2 &= left | begin{matrix} 5 &2\ 4&12 end{matrix} right | =5cdot12-4cdot2=52>0 \ Delta_3 &= 52 cdot 2>0; end{align} right.$

Все определители матрицы Гурвица больше нуля, следовательно САР устойчива.

Пример 2

Используя критерий Гурвица, выполнить анализ устойчивости следующей САР:

Рисунок 6.3.2 САР для анализа устойчивости

Общая передаточная функция разомкнутой системы САР:

$W(s) =frac{overbrace{k_1cdot k_2}^K}{scdot(T_1cdot s+1)cdot(T_2cdot s+1)}$

Корни знаменателя передаточной функцийй размкнутой САР:

$s_1=-frac{1}{T_1}; s_2 =-frac{1}{T_2}; s_3 =0$

Поскольку разомкнутая САР находится на границе устойчивости.

Передаточная функция замкнутой САР:

$Ф(s)=frac{W_1(s)cdot W_2(s)}{1+W_1(s)cdot W_2(s)}Rightarrow$ $Ф(s)=frac{overbrace{k_1cdot k_2}^K}{scdot(T_1cdot s+1)cdot(T_2cdot s+1)+underbrace{k_1cdot k_2}_K}=underbrace{frac{K}{T_1cdot T_2cdot s^3+(T_1+T_2)cdot s^2+s+k}}_{D_s}$ $D(s)=underbrace{T_1cdot T_2}_{a_0}cdot s^3+underbrace{(T_1+T_2)}_{a_1}cdot s^2+underbrace{1}_{a_2}cdot s+underbrace{k}_{a_3}$

Выражения для матрицы Гурвица:

$Г=begin {bmatrix}(T_1+T_2) & K & 0\ T_1cdot T_2 &1 &0\ 0 &(T_1+T_2)& K end{bmatrix}$

Главные определители матрицы Гурвица:

$left {begin{align} Delta_1&=T_1+T_2 >0\ Delta_2&=T_1+T_2-Kcdot T_1cdot T_2 >0\ Delta_3 &=Kcdot(T_1+T_2- Kcdot T_1cdot T_2)>0 end{align} right.$

Очевидно из формулы для определиттеля следует что для устойчивости САР необходимо чтобы

Рисунок 6.3.3. Условие устойчивости по

В случае когда постоянные времени положительны условие устойчивости можно вычислить получить из выражения для второго определителя:

$T_1+T_2 - Kcdot T_1cdot T_2 >0Rightarrow k< frac{1}{T_1}+frac{1}{T_2}$

Рисунок 6.3.4 Полные условия устойчивости

Полученный результат свидетельствует, что если , то для того, чтобы САР была устойчивой, необходимо, чтобы выполнит следующие условия:

$0<K<frac{1}{T_2}+frac{1}{T_1}$

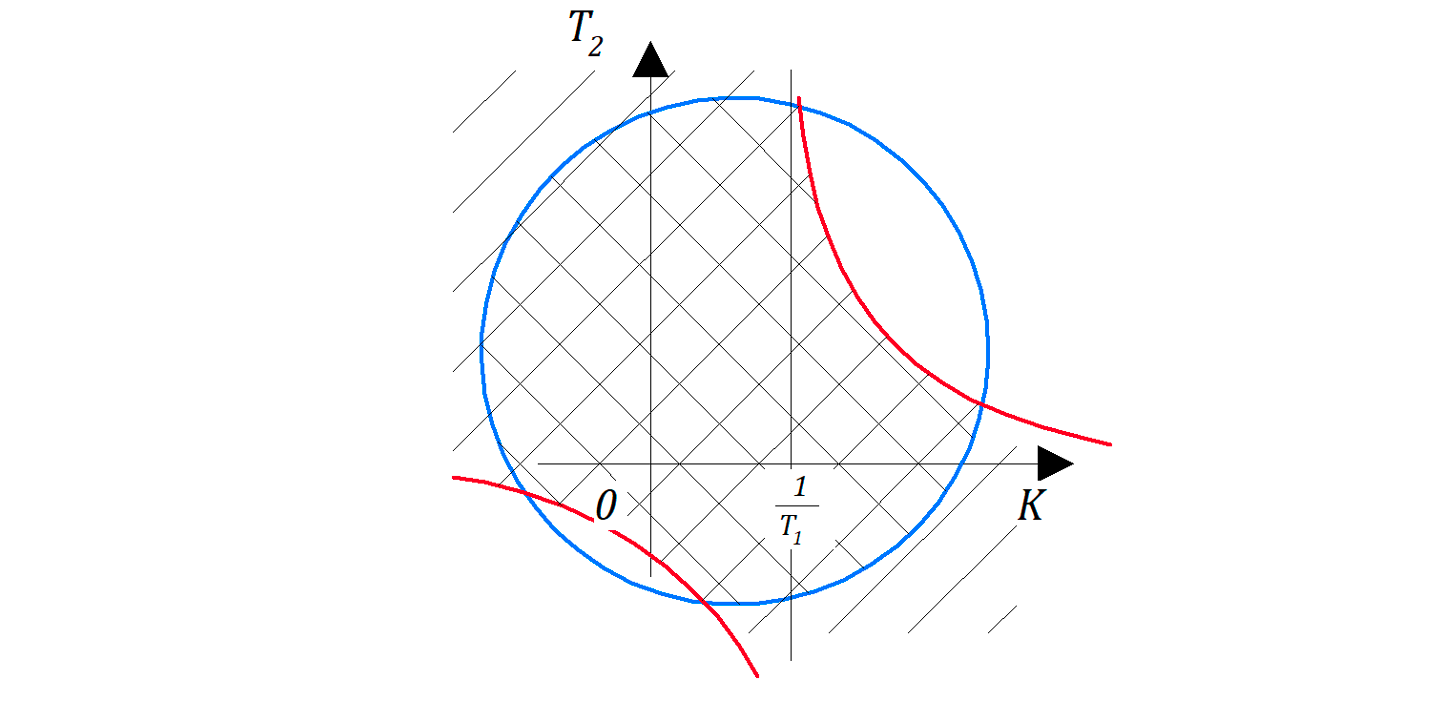
Усложним задачу: предположим, что в системе САР изображенной на рис. 6.3.2 возможно варьировать (изменять) коэффициент усиления и постоянную времени, например, В этом случае область устойчивости может быть отображена в виде фигуры в координатах

Рисунок 6.3.5 Область устойчивости

Система неравенств такая же, что и выше, для определителей матрицы Гурвица:

$left {begin{align} Delta_1&=T_1+T_2 >0\ Delta_2&=T_1+T_2-Kcdot T_1cdot T_2 >0\ Delta_3 &=Kcdot(T_1+T_2- Kcdot T_1cdot T_2)>0 end{align} right. Rightarrow$ $left {begin{align} & T_1+T_2 >0\ & T_1+T_2-Kcdot T_1cdot T_2 >0\& Kcdot(T_1+T_2- Kcdot T_1cdot T_2)>0 end{align} right. Rightarrow K< left ( frac{1}{T_1}+frac{1}{T_2} right ) Rightarrow frac{1}{T_2}>K-frac{1}{T_1} Rightarrow$ $Rightarrow left { begin{align} T_2<frac{1}{K-frac{1}{T_1}} если K>frac{1}{T_1}\ T_2>frac{1}{frac{1}{T_1}-K} если K<frac{1}{T_1} end{align} right.$

Рисунок 6.3.6. Область устойчивости для САР с переменными T2 и К

Примеры из видео можно взять здесь..

Продолжение темы устойчивости:

6.4 Частотный критерий устойчивости Михайлова.

6.5. Частотный критерий Найквиста

6.6. Понятие об областях устойчивости

Источник

Привет, Вы узнаете про устойчивость линейных стационарных систем, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
устойчивость линейных стационарных систем, критерии и запас устойчивости, запас устойчивости, примеры решения задач, метод найквиста , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

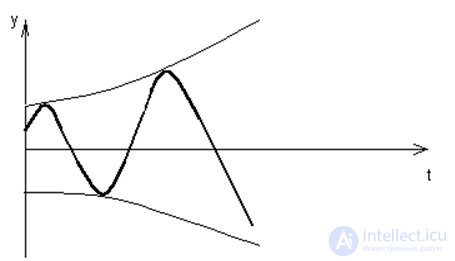
Устойчивость – свойство системы возвращаться в исходное состояние после какого-либо воздействия

Устойчивость — свойство САУ возвращаться в заданный или близкий к нему установившийся режим после какого-либо возмущения. Устойчивая САУ — система, в которой переходные процессы являются затухающими.

— операторная форма записи линеаризированного уравнения.

y(t) = y_уст(t)+y_п = y_вын(t)+y_св

y_уст(y_вын) — частное решение линеаризированного уравнения.

y_п(y_св) — общее решение линеаризированного уравнения как однородного дифференциального уравнения, то есть

САУ устойчива, если переходные процессы у_n(t), вызываемые любыми возмущениями, будут затухающими с течением времени, то есть при

Решая дифференциальное уравнение в общем случае, получим комплексные корни p_i, p_i+1 = ±α_i ± jβ_i

Каждой паре комплексно-сопряженных корней соответствует следующая составляющая уравнения переходного процесса:

, где ,

Из полученных результатов видно, что:

Линейная динамическая система называется устойчивой, если после снятия возмущений при

, то есть движение затухает (рис. 6.1. а).

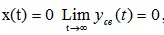
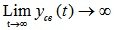
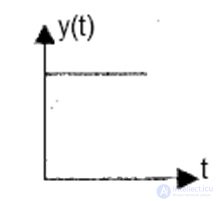
Система называется неустойчивой, если после снятия возмущений свободное движение стремится к ?, то есть при t??, (рис. 6.1. б).

Система называется нейтральной, если после снятия возмущений x(t) свободное движение стремится к какому-то пределу M, то есть 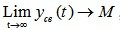, где 0<M (рис. 6.1. в).

Рис.6.1. Свободное движение системы управления

В общем случае дифференциальное уравнение звена или системы имеет вид:

(6.1)

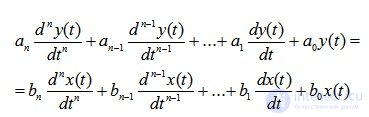
Его общее решение

(6.2)

Составляющую решения в виде общего решения однородного уравнения называют свободным движением y_св(t) а составляющую в виде частного решения неоднородного уравнения называют вынужденным движением y_вын(t), где y_св(t) определяется левой частью уравнения (6.1):

(6.3)

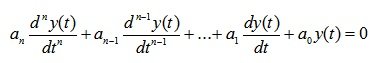
Его характеристическое уравнение

(6.4)

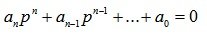
Так как в понятие устойчивости системы входит только факт наличия или отсутствия затухания переходного процесса (независимо от быстроты затухания переходного процесса), то устойчивость линейной системы не зависит от правой части дифференциального уравнения (6.1.) и полностью определяется его левой частью, то есть (6.3).

Прямой метод исследования устойчивости

Уравнение движения системы представлено уравнением (6.1). Для анализа устойчивости исследуем уравнение (6.3). Его решение:

, где p_i – корни характеристического уравнения (6.4).

Так как при ограниченном по абсолютной величине входном воздействии составляющая вынужденного движения также ограничена, то устойчивость системы обеспечивается при выполнении условия:

(6.5)

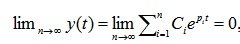
который означает, что переходной процесс в системе затухает.

Рассмотрим случаи для корней различного вида.

Вещественные корни:

Если все p_i =?, где ?_i — действительно положительное число, то

?_i может иметь значения >0, <0, =0.

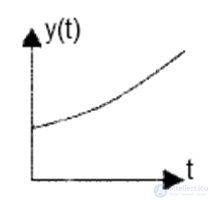
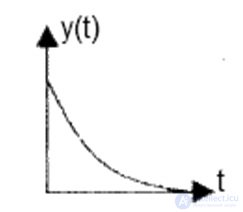
Из свойств экспоненциальной функции можем сделать вывод, что при ?_i <0 и при t??, компонента y(t) является затухающей, то есть система устойчива.

Рис. 6.2. ? > 0 (система неустойчива)

Рис. 6.3. ? = 0 (система на грани устойчивости)

Рис. 6.4. ? < 0 (система устойчива)

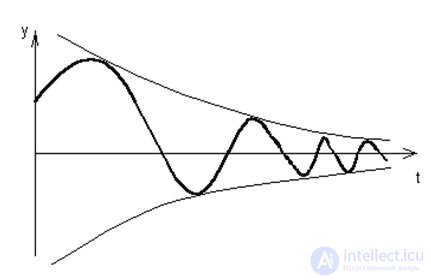
Комплексно-сопряженные корни:

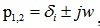
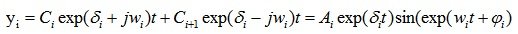
То есть , в этом случае компонента решения имеет вид:

(6.6)

где A_i, ?_i, –константы, определяемые C_i, C_i+1, .

Графики зависимости y_i от значения ?_i приведены на рис.6.5 и 6.6

Рис. 6.5. Свободное движение системы для случая комплексных корней с отрицательной действительной частью

Рис. 6.6. Свободное движение системы для случая комплексных корней с положительной действительной частью .

В случае ?i=0, корни являются чисто мнимыми и график функции представляет собой незатухающие гармонические колебания.

Из проведенного анализа следует, что линейная динамическая система будет устойчива тогда и только тогда, когда действительная часть корней характеристического уравнения будет отрицательной. Это есть необходимое и достаточное условие устойчивости линейной системы управления.

Следует отметить, что ни одна реальная система управления не является строго линейной. Линейные характеристики звеньев и линейные дифференциальные уравнения получаются путем линеаризации реальных характеристик и уравнений.

Ляпуновым доказано, что если линеаризованная система устойчива, то реальная система при малых отклонениях также устойчива; если линеаризованная система неустойчива, то реальная система тоже неустойчива; если линеаризованная система нейтральная или находится на колебательной границе устойчивости, то судить об устойчивости реальной системы затруднительно, так как малые нелинейные члены могут коренным образом изменить вид переходного процесса, сделав систему устойчивой или неустойчивой.

Недостатком прямого метода исследования устойчивости системы является необходимость вычисления корней характеристического уравнения, что связано с определенными трудностями.

Существуют критерии устойчивости, которые позволяют, не решая уравнения, ответить на вопрос: устойчива или неустойчива система управления.

Алгебраические критерии устойчивости.

Критерий Рауса

Для определения устойчивости системы строятся таблицы вида:

Коэффициенты	Строки	столбец 1	столбец 2	столбец 3
	1
	2
	3
	4

Для устойчивости системы необходимо, чтобы все элементы первого столбца имели положительные значения; если в первом столбце присутствуют отрицательные элементы — система неустойчива; если хотя бы один элемент равен нулю, а остальные положительны, то система на границе устойчивости.

Критерий устойчивости Гурвица

— определитель Гурвица

Теорема: для устойчивости замкнутой САУ необходимо и достаточно, чтобы определитель Гурвица и все его миноры были положительны при

Критерий устойчивости Рауса – Гурвица

Одним из наиболее распространенных алгебраических критериев устойчивости является критерий устойчивости Рауса-Гурвица, который был разработан в конце 19 века . Об этом говорит сайт https://intellect.icu . Он основан на анализе коэффициентов характеристического полинома и сводится к проверке удовлетворения n неравенств (n порядок характеристического полинома). Порядок проверки устойчивости АС по данному критерию следующий. Из коэффициентов характеристического полинома полагая, что составляется главный определитель Гурвица.

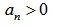
Система устойчива, если определитель Гурвица и все определители низшего порядка больше 0

Определитель Гурвица

(6.7)

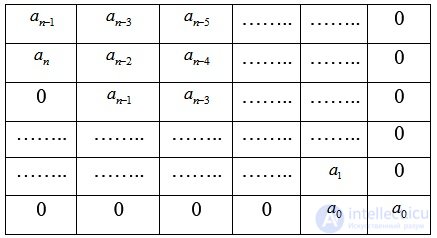
Из главного определителя Гурвица выделяются определители Гурвица низшего порядка (миноры).

(6.8)

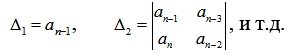
Номер определителя Гурвица соответствует его размерности.

Критерий Рауса-Гурвица формулируется следующим образом: для того, чтобы линейная система автоматического управления была устойчива, необходимо и достаточно, чтобы при все определители Гурвица были положительными, т.е.

Чтобы линейная система уравнений была устойчива, необходимо и достаточно положительности диагональных миноров матрицы Гурвица при условии a₀>0. Можно показать, что для уравнений первого и второго порядков условием устойчивости, по Гурвицу, является положительность их коэффициентов.

Частотный критерий устойчивости Михайлова

Как и при использовании критерия Гурвица исходной информацией для использования критерия Михайлова является характеристическое уравнение исследуемой системы. Здесь применяется геометрическая иллюстрация траектории движения конца вектора Михайлова – годограф Михайлова.

На основе характеристического уравнения замкнутой системы (6.4) вводится в рассмотрение некоторая функция комплексного переменного, полученная заменой p=j?:

(6.9)

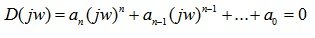
Функцию (6.9) можно представить в виде

(6.10)

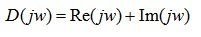
На комплексной плоскости Re-Im вектор D(j?) опишет при изменении ? от 0 до ? кривую – годограф Михайлова.

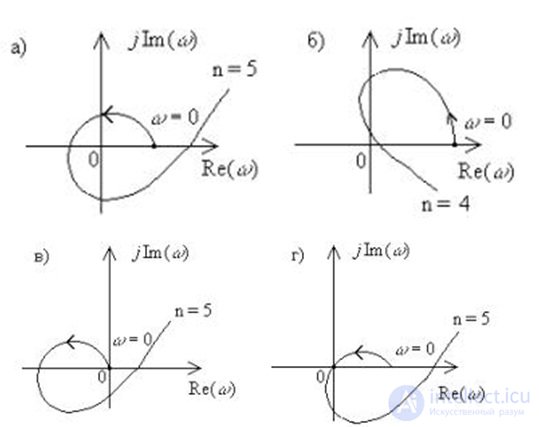
Для устойчивой системы управления n-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении ? от 0 до ?, начиная с вещественной положительной полуоси, проходил против часовой стрелки последовательно через n– квадрантов.

На рисунке 6.7 приведен годограф Михайлова для различных случаев.

Рис. 6.7. Примеры для случаев: а) устойчивой, б) неустойчивой систем, в) случай нейтральной системы с нулевым корнем, г) случай колебательной границы устойчивости.

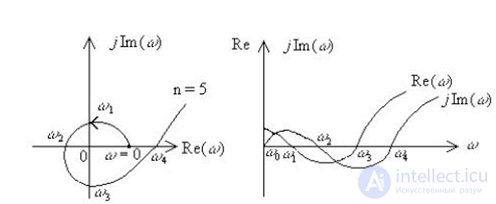
Обратимся к рис.6.8, иллюстрирующему устойчивую системы автоматического регулирования. Для устойчивой системы автоматического регулирования наблюдается чередование корней действительной Re(?) и мнимой jIm(?) частей (следствие из критерия Михайлова).

Рис. 6.8. Изменение вещественной и мнимой составляющих вектора Михайлова при изменении частоты

Недостатком алгебраических критериев и частотного критерия устойчивости является их ограниченность системами без транспортного запаздывания. В случае системы с транспортным запаздыванием их применение дает приближенную оценку устойчивости в пределах правомерности аппроксимации звена транспортного запаздывания рядом Паде.

Амплитудно-фазовый критерий устойчивости Найквиста

В 1932 году американский ученый Г.Найквист показал, что существует определенная связь между устойчивостью и видом АФЧХ усилителей с отрицательной обратной связью, а в 1936 году советский ученый А.В. Михайлов распространил предложенный критерий на системы автоматического управления. Частотный критерий устойчивости Найквиста –Михайлова, который позволяет судить об устойчивости замкнутой системы автоматического регулирования по ее амплитудно – частотной характеристике в разомкнутом состоянии. Поскольку последняя может быть получена экспериментально, то этот критерий нашел широкое распространение.

АС, неустойчивая в разомкнутом состоянии, может оказаться устойчивой в замкнутом состоянии. Это становится очевидным после анализа критерия Найквиста-Михайлова.

Этот критерий позволяет судить об устойчивости замкнутой системы по АФХ разомкнутой системы.

Для минимально-фазовых систем этот критерий формулируется следующим образом: для того, что бы автоматическая система, устойчивая или нейтральная в разомкнутом состоянии, была устойчива в замкнутом состоянии необходимо и достаточно, чтобы годограф АФЧХ разомкнутой системы не охватывал точку М{-1, j0} на комплексной плоскости при изменении частоты ? от нуля до бесконечности и повороте вектора АФЧХ W(j?) по часовой стрелке .

Рис. 6.9. Пример неустойчивой замкнутой системы при устойчивой разомкнутой системе (1) и положения системы на границе устойчивости (2)

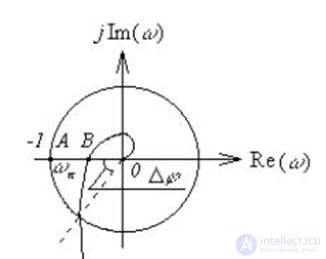
запас устойчивости по модулю и по фазе

На рис.6.10. показана амплитудно-фазовая характеристика разомкнутой системы 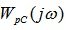и окружность с радиусом R=1.

Рис. 6.10. К определению запаса устойчивости по модулю и по фазе

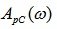
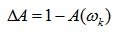
Запас устойчивости по модулю определяется величиной отрезка АВ. Он показывает, на какую величину нужно увеличить амплитуду амплитудно-фазовой характеристики разомкнутой системы без изменения фазы, чтобы замкнутая система вышла на границу устойчивости:

(6.11)

Запас устойчивости по фазе определяется величиной

(6.12)

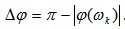
Он показывает, на какую величину по часовой стрелке нужно повернуть по фазе без изменения амплитуды вектор амплитудно-фазовой характеристики разомкнутой системы, чтобы замкнутая система вышла на границу устойчивости.

Логарифмический частотный критерий устойчивости

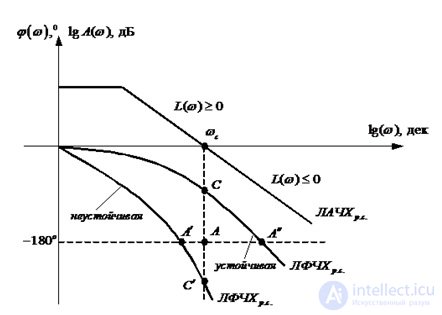
Устойчивость замкнутой САР с использованием логарифмического критерия можно определить, построив совмещенные ЛАЧХ и ЛФЧХ разомкнутой системы.

Рис. 6.11. Устойчивость системы по ЛАЧХ и ЛФЧХ

Замкнутая система автоматического управления устойчива, если при L(w)?0 соответствующая ЛФЧХ проходит таким образом, что фаза ?(w) не превосходит значения -180°(-?).

Система устойчивая в разомкнутом состоянии будет устойчивой и в замкнутом, если точка А ЛФЧХ определяемая фазой -180°(-?) соответствует области отрицательных значений логарифмической амплитуды L(w) ;

Важным показателем работоспособности АС служат запасы устойчивости по амплитуде и по фазе.

Запас устойчивости по фазе определяется как возможная величина приращения ЛФХ до достижения границы устойчивости: ??₃ = ? + ? (Wср).

Запас устойчивости по амплитуде определяется как возможная величина приращения ЛАЧХ ( т.е. коэффициента усиления), при котором АС сохраняет устойчивость L₃=20lgR(w?)|.

Запас устойчивости САУ

В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать систему так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости.

Необходимость запаса устойчивости определяется следующими условиями:

Отбрасывание нелинейных слагаемых при линеаризации.
Коэффициенты, входящие в уравнение, описывающее САУ, определяются с погрешностью.
Устойчивость исследования для типовых систем при типовых условиях.

Критерии

Критерий Рауса: чтобы смоделировать запас устойчивости, необходимо, чтобы элементы первого столбца были больше какой-то фиксированной величины ε>0, называемой коэффициентом запаса устойчивости.
Критерий Гурвица: запас устойчивости определяется аналогично запасу устойчивости Рауса, только ε характеризует значение определителя Гурвица.
Критерий Михайлова: вписывается окружность ненулевого радиуса с центром в точке О (0; 0). Запас определяется радиусом этой окружности. Система неустойчива при нарушении критерия Михайлова или при пересечении кривой Михайлова с окружностью.
Критерий Найквиста: здесь критической является точка (-1; j0), следовательно, вокруг этой точки строится запретная зона, радиус которой будет представлять коэффициент запаса устойчивости.

Сравнительная характеристика критериев устойчивости

Частотный критерий Найквиста применим, главным образом, когда трудно получить фазовые характеристики экспериментально. Однако вычисление АФХ, особенно частотных, сложнее, чем построение кривых Михайлова. Кроме того, расположение АФЧХ не дает прямого ответа на вопрос: устойчива ли система, то есть требуется дополнительное исследование на устойчивость системы в разомкнутом состоянии.

Критерий Михайлова применяется для систем любого порядка, в отличие от критерия Рауса. Применяя частотный критерий Найквиста и критерий Михайлова, характеристические кривые можно строить постепенно, с учетом влияния каждого звена, что придает критериям наглядность и решает задачу выбора параметров системы из условия устойчивости.

метод найквиста

Оценим устойчивость разомкнутой системы по критерию Ляпунова.

Передаточная функция разомкнутой системы

Согласно критерию Ляпунова разомкнутая САУ является устойчивой, причем, поскольку все корни являются действительными отрицательными, а два из них комплексно-сопряженными с отрицательной действительной частью, то переходный процесс представляет собой сходящиеся колебания.

Построим КЧХ разомкнутой системы .

Для исследования устойчивости САУ по критерию Найквиста необходимо построить комплексно-частотную характеристику (КЧХ) исходной разомкнутой САУ и проанализировать ее в соответствии с критерием Найквиста. В случае устойчивой САУ необходимо определить запасы устойчивости по фазе и амплитуде.

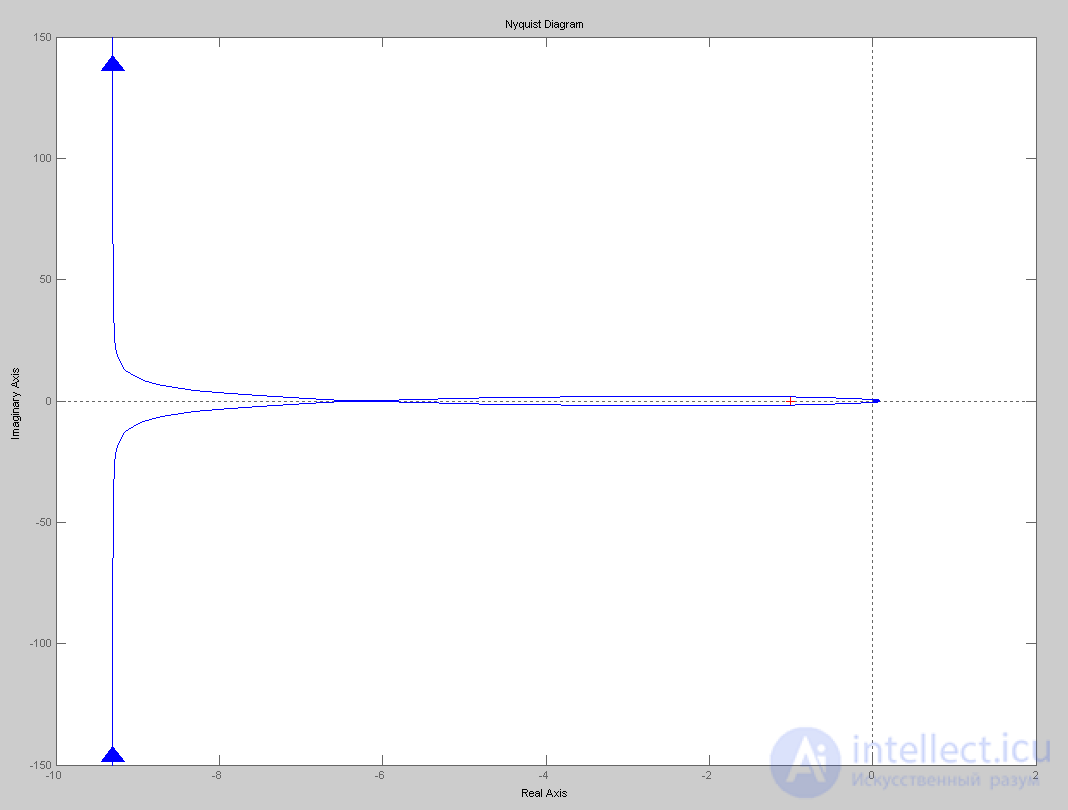
Разомкнутая система находится в безразличном состоянии (т.к. эта система астатического класса). Следовательно, критерий устойчивости Найквиста будет выражаться так: чтобы система являлась устойчивой в замкнутом состоянии необходимо и достаточно, чтобы КЧХ разомкнутой системы, дополненная дугой окружности бесконечно большого радиуса, при изменении частоты от нуля до бесконечности не охватывала точку (-1;j0).

Построим КЧХ разомкнутой системы (Рис.5).

Рис.5. КЧХ разомкнутой системы

Как видно, КЧХ разомкнутой системы охватывает точку (-1;j0). Следовательно, замкнутая система неустойчива.

примеры решения задач

Пример 1. Передаточная функция системы имеет вид:

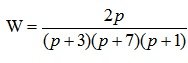
Проверить систему на устойчивость. Исследовать устойчивость системы с помощью критерия Гурвица.

Решение:

Характеристическое уравнение системы имеет вид:

Необходимое условие устойчивости системы автоматического управления: все корни характеристического уравнения должны быть левыми (располагаться во второй или третьей четвертях координатной плоскости). В данном случае необходимое условие выполняется.

Исследование устойчивости системы с помощью критерия Гурвица:

Составим определители Гурвица:

Все определители Гурвица больше нуля, следовательно система устойчива.

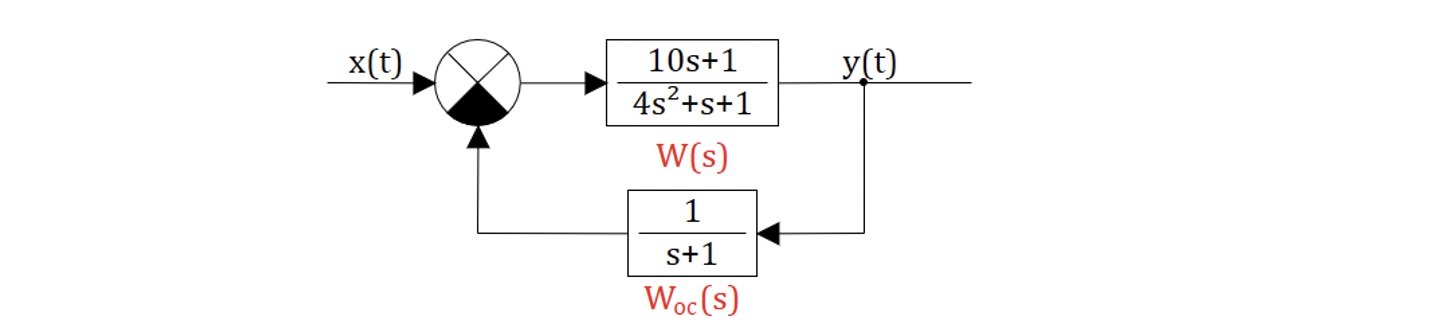
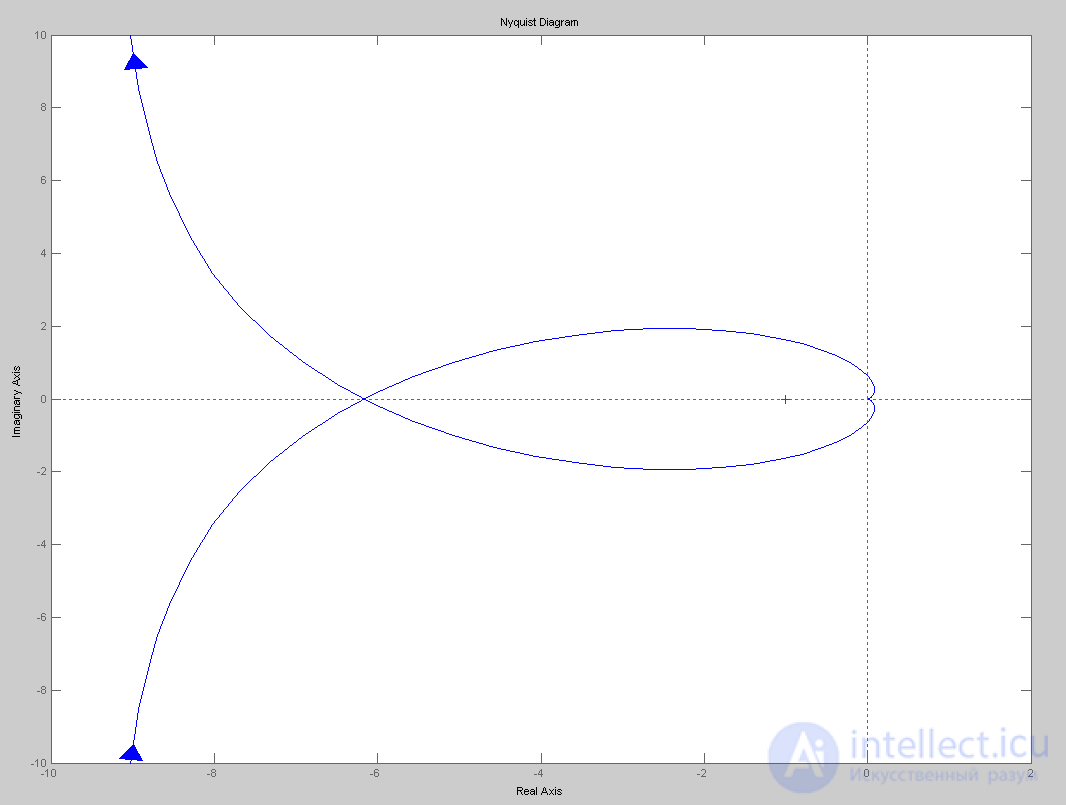
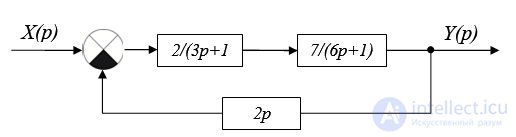
Пример 2. Определить устойчивость системы, представленной на рис. 6.12 с помощью критериев Найквиста и Михайлова.

Рис. 6.12. Структурная схема

Решение:

Находим корни характеристического уравнения :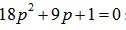

p₁=-1/6;

p₂=-1/3;

Оба корня лежат по левую сторону от мнимой оси, значит разомкнутая система устойчива.

Критерий Найквиста:

Строим АФЧХ разомкнутой системы (рис. 6.13).

Рис. 6.13. АФЧХ

Вывод: чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении w от нуля до бесконечности не охватывала точку с координатами (-1; j0). На рис. 6.13 видно, что система не охватывает точку (-1; j0), значит система является устойчивой.

Критерий Михайлова:

Берем характеристическое уравнение системы:

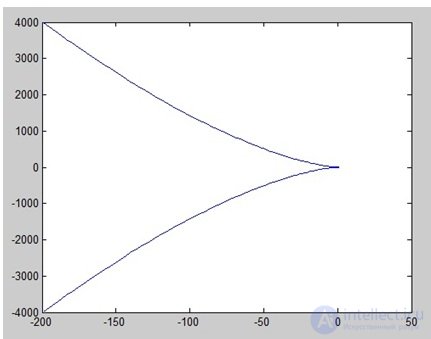
На комплексной плоскости график мнимой части (Im) от реальной (Re) вектора H(jw) опишет при изменении w от 0 до ? кривую – годограф Михайлова (рис. 6.14).

Рис. 6.14. Годограф Михайлова

Вывод:

Для того, чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при изменении w от 0 до ? вектор Михайлова D(jw) повернулся на угол .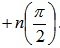

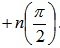
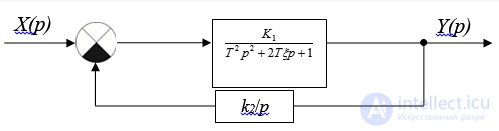
Полученный график соответствует устойчивому состоянию системы (рис. 6.7), так как при изменении w от 0 до ? вектор Михайлова повернулся на угол . В данном случае n=2 (порядок характеристического уравнения).

Пример 3. Колебательное звено с передаточной функцией

охвачено отрицательной обратной связью через интегрирующее звено (рис. 6.15). Определить устойчивость системы с помощью критериев Найквиста и Михайлова при следующих условиях:

Рис. 6.15. Структурная схема

Решение:

Передаточная функция системы:

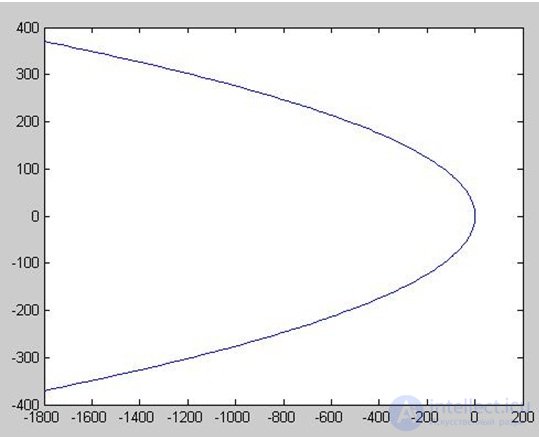
Подставляем значения из условия задачи, получаем:

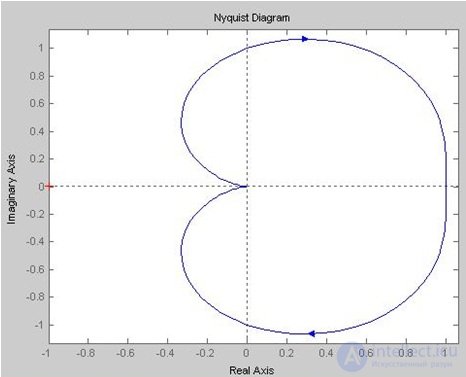
Критерий Найквиста:

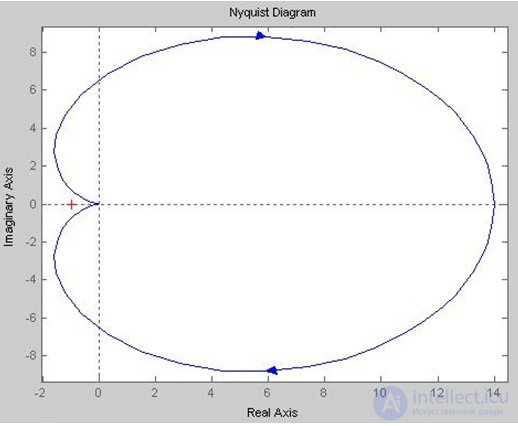
Берем передаточную функцию разомкнутой системы , строим график АФЧХ (рис. 6.16).

Рис. 6.16. АФЧХ

Вывод: чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении w от нуля до бесконечности не охватывала точку с координатами (-1; j0). На рис. 6.16 видно, что система не охватывает точку (-1; j0), значит система является устойчивой.

Критерий Михайлова:

Запишем характеристическое уравнение системы:

Вводим функцию комплексной переменной, заменяя p на p=j?. Получаем:

На комплексной плоскости график мнимой части (Im) от реальной (Re) вектора H(jw) опишет при изменении w от 0 до ? кривую – годограф Михайлова (рис. 6.17).

Рис. 6.17. Годограф Михайлова

Вывод: для того, чтобы замкнутая система была устойчивой, необходимо т достаточно, чтобы при изменении w от 0 до ? вектор Михайлова D(jw) повернулся на угол .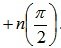

Полученный график соответствует неустойчивому состоянию системы (рис. 6.7).

На этом все! Теперь вы знаете все про устойчивость линейных стационарных систем, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое устойчивость линейных стационарных систем, критерии и запас устойчивости, запас устойчивости, примеры решения задач, метод найквиста
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Математические основы теории автоматического управления

Источник

6.1. Понятие об устойчивости САР. Теоремы Ляпунова.

6.2. Необходимые условия устойчивости линейных и линеаризованных САР.

6.3. Алгебраический критерий устойчивости Гурвица.

Пример 1

Пример 2

Прямой метод исследования устойчивости

Алгебраические критерии устойчивости.

Критерий Рауса

Критерий устойчивости Гурвица

Критерий устойчивости Рауса – Гурвица

Частотный критерий устойчивости Михайлова

Амплитудно-фазовый критерий устойчивости Найквиста

Логарифмический частотный критерий устойчивости

Запас устойчивости САУ

Критерии

Сравнительная характеристика критериев устойчивости

метод найквиста

примеры решения задач

Не пропустите также: