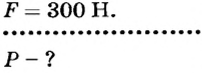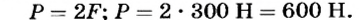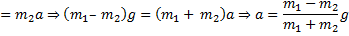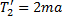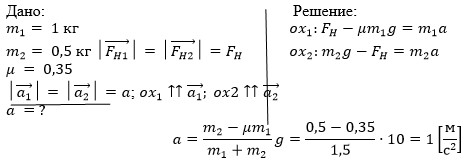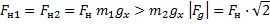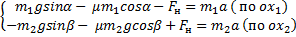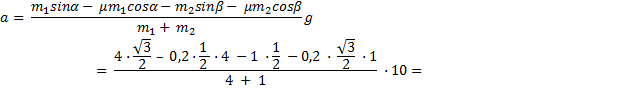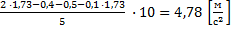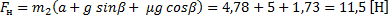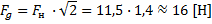2018-03-04
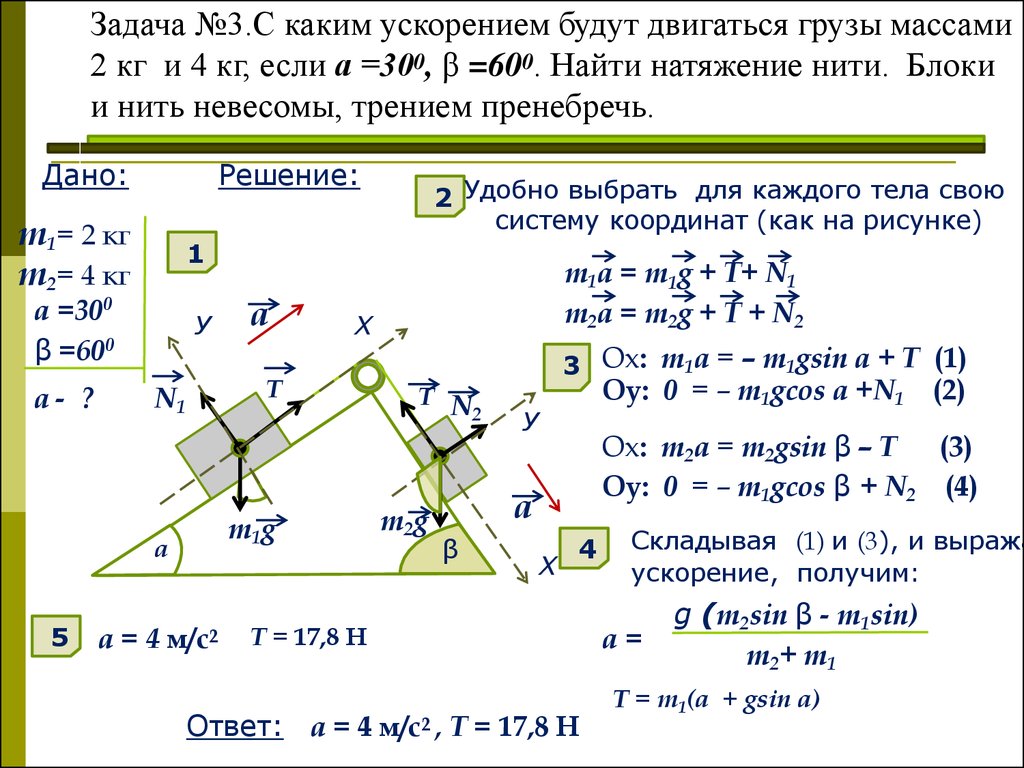
В системе, изображенной на рис., блоки невесомы, а нити — невесомы и нерастяжимы. Найти ускорение подвижного блока.
Решение:
Для подвижного блока и груза $M$ (рис.)
$2T_{1} — Mg = Ma$,
где $T_{1}$ — натяжение нити. Ускорения двух других грузов равны $2a$. Для груза $m$
$T_{2} — T_{1} — mg = m2a$.
Для первого груза
$mg — T_{2} = M2a$.
Решая систему полученных уравнений, найдем
$a = g frac{M — 2m}{5M + 4m}$.
Подвижный и неподвижный блок, с примерами задач
Блоки относят к простым механизмам. В группу этих устройств, которые служат для преобразования силы, помимо блоков относят рычаг, наклонную плоскость.
Изготавливаются блоки в виде дисков (колес, низких цилиндров и т. п.), имеющих желоб, через который пропускают веревку (торс, канат, цепь).
Неподвижный блок
Неподвижным называется блок, с закрепленной осью (рис.1). Он не перемещается при подъеме груза. Неподвижный блок можно рассматривать как рычаг, который имеет равные плечи.
Условием равновесия блока является условие равновесия моментов сил, приложенных к нему:
Блок на рис.1 будет находиться в равновесии, если силы натяжения нитей равны:
так как плечи этих сил одинаковы (ОА=ОВ). Неподвижный блок не дает выигрыша в силе, но он позволяет изменить направление действия силы. Тянуть за веревку, которая идет сверху часто удобнее, чем за веревку, которая идет снизу.
Если масса груза, привязанного к одному из концов веревки, перекинутой через неподвижный блок равна m, то для того, чтобы его поднимать, к другому концу веревки следует прикладывать силу F, равную:
при условии, что силу трения в блоке мы не учитываем. Если необходимо учесть трение в блоке, то вводят коэффициент сопротивления (k), тогда:
Заменой блока может служить гладкая неподвижная опора. Через такую опору перекидывают веревку (канат), которая скользит по опоре, но при этом растет сила трения.
Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, следовательно, равны работы.
Комбинация неподвижных блоков
Для того чтобы получить выигрыш в силе, применяя неподвижные блоки применяют комбинацию блоков, например, двойной блок. При блоки должны иметь разные диаметры. Их соединяют неподвижно между собой и насаживают на единую ось. К каждому блоку прикрепляется веревка, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в таком случае будут неравными. Двойной блок действует как рычаг с плечами разной длины. На рис.2 изображена схема двойного блока.
Условие равновесия для рычага на рис.2 станет формула:
Двойной блок может преобразовывать силу.
Подвижный блок
Подвижным блоком называют блок, ось которого перемещается совместно с грузом. На рис. 2 подвижный блок можно рассматривать как рычаг с плечами разной величины. В этом случае точка О является точкой опоры рычага. OA – плечо силы ; OB – плечо силы . Рассмотрим рис. 3. Плечо силы в два раза больше, чем плечо силы , следовательно, для равновесия необходимо, чтобы величина силы F была в два раза меньше, чем модуль силы P:
Можно сделать вывод о том, что при помощи подвижного блока мы получаем выигрыш в силе в два раза. Условие равновесия подвижного блока без учета силы трения запишем как:
Если попытаться учесть силу трения в блоке, то вводят коэффициент сопротивления блока (k) и получают:
Иногда применяют сочетание подвижного и неподвижного блока. В таком сочетании неподвижный блок используют для удобства.
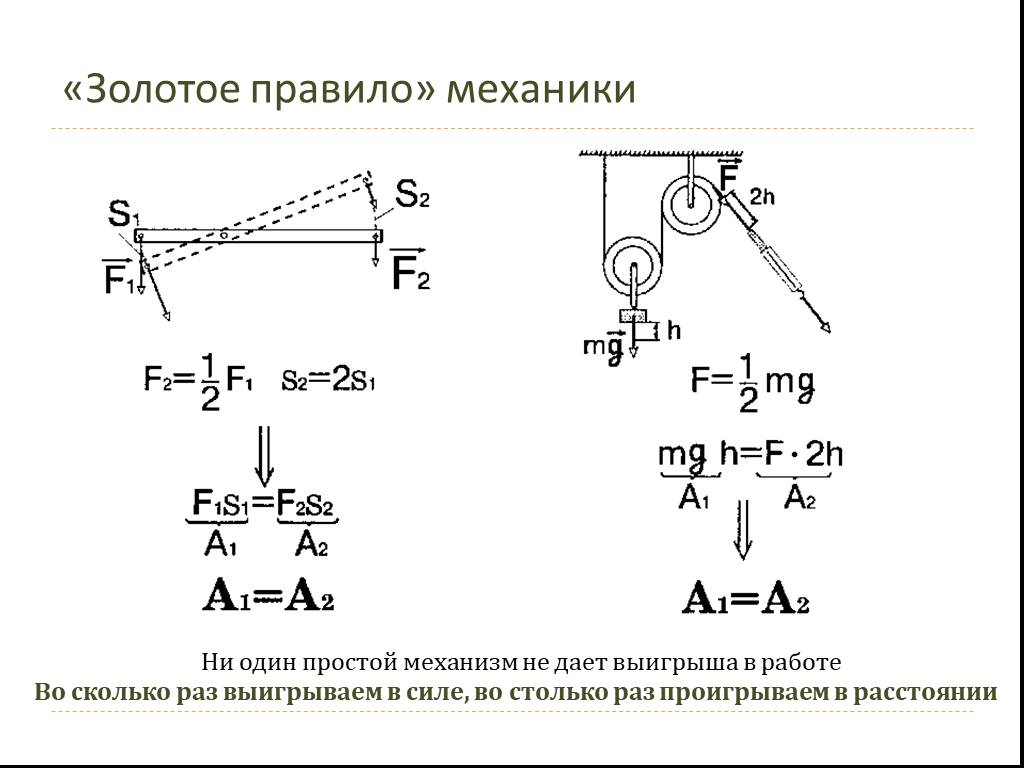
Золотое правило механики
Простые механизмы выигрыша в работе не дают. Во сколько мы получаем выигрыш в силе, во столько же раз проигрываем в расстоянии. Так как работа равна скалярному произведению сила на перемещение, следовательно, она не изменится при использовании подвижного (как и неподвижного) блоков.
В виде формулы «золотое правило№ можно записать так:
где – путь, который проходит точка приложения силы – путь проходимый точкой приложения силы .
Золотое правило является самой простой формулировкой закона сохранения энергии.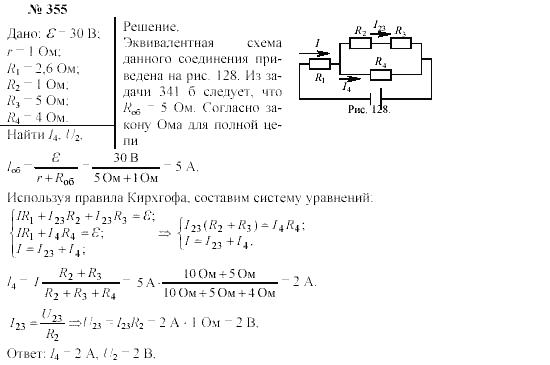
Получим, что для выполнения «золотого правила» для двойного блока необходимо, чтобы:
Если силы и уравновешены, то блок покоится или движется равномерно.
Примеры решения задач
Простая физика — EASY-PHYSIC
Продолжаем подготовку к олимпиадам. Сегодня закрепляем тему «статика». Поговорим про блоки, посчитаем силы, установим равновесие.
Задача 1.
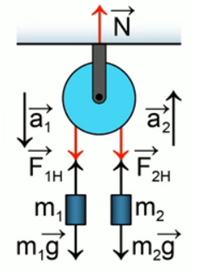
Черный ящик, привязанный через систему блоков и нитей к стенке, покоится на горизонтальной поверхности. Чтобы преодолеть трение и сдвинуть его с места, непосредственно к нему необходимо приложить горизонтальную силу чуть больше Н. Какую минимальную силу надо прикладывать к черному ящику, чтобы он оставался неподвижным, если к веревке приложена сила Н? Ответ дать в Ньютонах, округлив до целых.
Рисунок 1
Расставим силы:
Рисунок 2
Теперь видно, что на блок действуют три силы , поэтому общая сила равна 45 Н. 16 из них «съест» сила трения, поэтому, чтобы удержать такой ящик, не хватает Н.
Ответ: 29 Н.
Задача 2.
Все блоки в системе, представленной на рисунке − невесомые. Масса левого тела кг. При какой массе правого тела система останется в равновесии? Ответ дать в килограммах, округлив до целых. Считать, что м/c.
Рисунок 3
Расставим силы:
Рисунок 4
Теперь запишем условия равновесия:
Откуда
И
Ответ: 2 кг.
Задача 3.
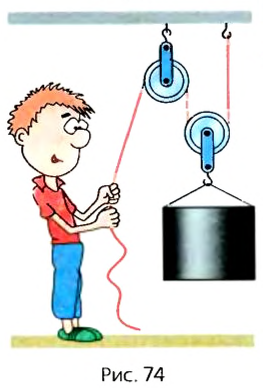
Спасатели с помощью веревок, перекинутых через систему блоков, перемещают равномерно и прямолинейно массивную плиту так, как показано на рисунке. С какой результирующей силой верёвки действуют на плиту? Спасатели тянут свой конец веревки с силой Н. Массами веревок и блоков пренебречь.
Замечание: требуется найти только силу, с которой нити действуют непосредственно на плиту. Силу, действующую на плиту со стороны верхнего крепления в ответ включать не надо.
Рисунок 5
Расставим силы:
Рисунок 6
Теперь видно, что «за нитки» плиту тянут Н, а полная сила (с учетом верхнего крепления — Н.
Ответ: 600 Н.
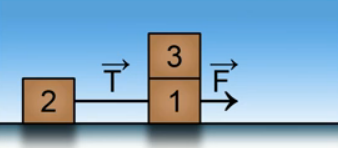
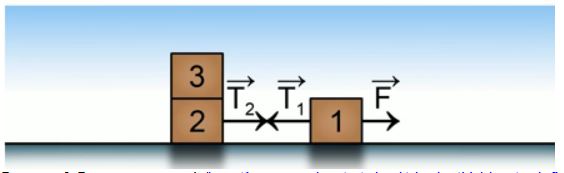
Задача 4.
Какую горизонтальную силу надо прикладывать к шкафу, чтобы удержать его на месте? Массы грузов равны кг, кг. Ответ дать в Ньютонах, округлив до целых. Считать, что м/c.
Рисунок 7
На шкаф действуют две силы тяжести: первого груза (20 Н) и второго (50 Н). Итого 70 Н.
Ответ: 70 Н.
Задача 5.
Два ящика покоятся на горизонтальной поверхности. Чтобы преодолеть трение и сдвинуть с места левый ящик, к нему необходимо приложить горизонтальную силу чуть больше 26 Н. Чтобы сдвинуть правый − чуть больше 14 Н.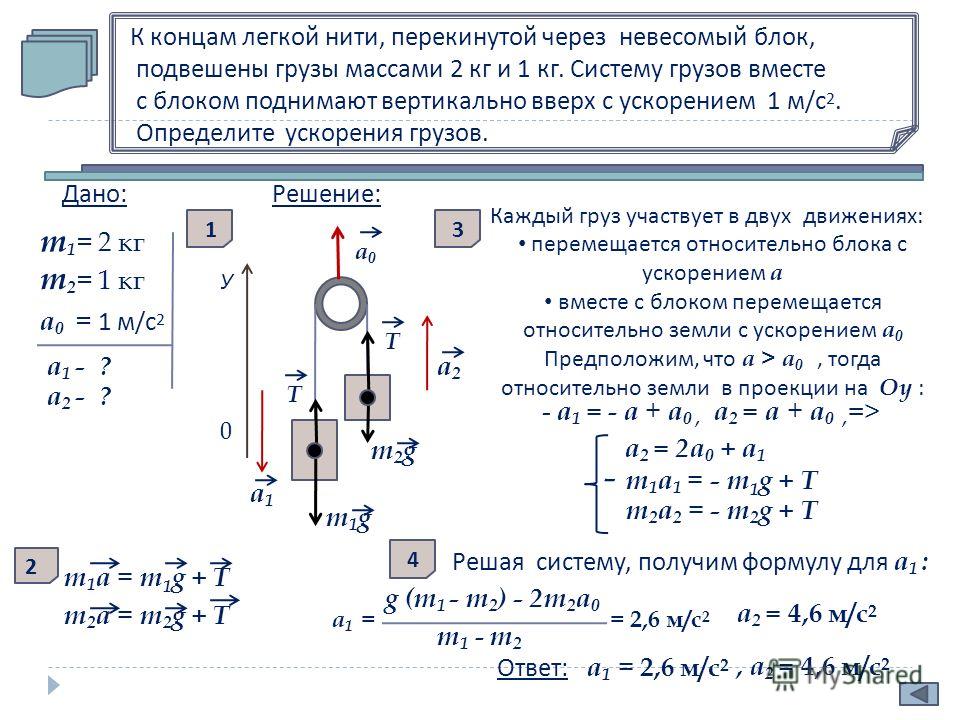
Рисунок 8
Расстояние будет уменьшаться при сдвиге любого из ящиков, поэтому нужно выяснить, какой легче сдвинуть. Для этого расставляем силы:
Рисунок 9
Теперь видно, что на левый ящик действует сила , а на правый — . Если
То Н, а если
То Н. Поэтому ответ – 7 Н. Этого будет достаточно, чтобы сдвинуть правый ящик и тем самым сократить расстояние.
Задача о силе нескольких объектов: два блока, связанных вместе (машина Этвуда) — Физика
- Дом
- Особенности
- Практическое руководство
- Проблемы
Брусок массой 15 кг лежит на наклонной плоскости. Плоскость составляет с горизонталью угол , а угол между бруском и плоскостью равен 0,13.
- Идентифицировать
- Нарисуй картинку
- Выберите отношение
- Решить
- Понять
-
В этой задаче вас просят связать движение (ускорение двух блоков) с силой (натяжение веревки, трение). Сила и движение одного объекта всегда связаны вторым законом Ньютона, так что это сила или проблема 2-го закона.
Кроме того, обратите внимание, что вы должны рассматривать блоки как отдельные системы. Вас просят найти натяжение веревки между ними, и вы не можете ответить на этот вопрос, не изучив взаимодействие между ними — другими словами, эффект, который каждый из них оказывает на другой. Поэтому вам нужно будет нарисовать картинку и составить уравнения для каждого блока в отдельности.
-
Шаг 1
Ваш FBD для Блока 1 еще не завершен, потому что mg имеет как x-, так и y-компоненты. Перейдите к шагу 2, когда будете готовы продолжить.
———————————————— ————————————————————
Шаг 2
В окончательной FBD, нарисованной здесь, все силы на блоке 1 разделены на компоненты. Вклад каждой силы в направлении x (вдоль наклона) показан явно, как и вклад каждой силы в направлении y. FBD теперь является визуальным представлением ∑F=ma в каждом направлении.
-
Ключевым уравнением для любой задачи, связывающей силы и движение, является второй закон Ньютона. Независимо от того, какое количество вас просят найти, начните со Второго закона. Если потребуется дополнительная информация, она станет очевидной по мере продвижения.
Для задач с несколькими объектами вам всегда потребуется дополнительная информация, обобщенная в виде третьего закона Ньютона (взаимодействие между двумя объектами ощущается обоими объектами в равной степени и в противоположном направлении).
В этом примере это понимание уже использовалось — взаимодействие между двумя блоками происходит за счет натяжения веревки, и натяжение обозначалось одним и тем же символом для каждого. Если вы не заметили, что натяжение по всей веревке такое же, как вы нарисовали FBD, это нормально. Когда вы начнете решать уравнения, вы обнаружите, что у вас слишком много неизвестных, и вы можете использовать это понимание, чтобы уменьшить их в этот момент.
-
Шаг 1
Одним из ключей к успешному алгебраическому решению задачи с несколькими объектами является отслеживание переменных. Я использовал разные символы для масс двух блоков, потому что они не совпадают, но я использовал один и тот же символ для ускорения, потому что они движутся вместе. Я также использовал один и тот же символ для обозначения натяжения на каждом блоке.
На данный момент у вас есть два нерешенных уравнения и два неизвестных ( а и Т .
). Прокрутите вниз, чтобы продолжить это решение.
———————————————— ————————————————————-
Шаг 2
Т – 79 Н = (15 кг)
Один из подходов, который всегда работает, состоит в том, чтобы решить одно уравнение для одной из переменных и подставить его в другую.
T = 370 Н – (38 кг)а из первого уравнения
370 Н – (38 кг)а — 79 Н = (15 кг)а подставляя во второе
290 Н = (38 кг + 15 кг)а
5,5 м/с 2 =аТеперь, когда вы нашли одну из неизвестных переменных, подставьте ее в любое из исходных уравнений, чтобы найти другую переменную. Подставлю во второе уравнение.
T – 79 Н = (15 кг)(5,5 м/с 2 )
T = 79 Н + 83 Н = 160 НВ этой задаче требуется только натяжение веревки и ускорение блоков.
Дальнейшее математическое решение не требуется.
-
В этой задаче нас просили найти ускорение двух блоков, связанных между собой веревкой, а также найти натяжение веревки между ними. В задаче не указано точно, в каком направлении движутся блоки, или даже если они двигаются. Основываясь на относительных массах блоков, мы сделали предположение, что висящий блок ускоряется вниз, а скользящий вверх по склону.
При таком предположении наше решение:
1.) Подвешенный блок ускоряется вниз с a=5,5 м/с 2 , а блок на наклонной поверхности ускоряется вверх по наклонной поверхности, также с a=5,5 м/с. с 2 . Это лишь немногим больше половины ускорения, которое мог бы иметь висящий блок только из-за гравитации, что имеет смысл. Можно было бы ожидать, что он будет иметь более низкое ускорение из-за натяжения веревки вверх из-за натяжения другого блока.
2.) Натяжение веревки равно 160 Н.
Это значение примерно равно силе гравитации, действующей на массу 16 кг, опять-таки число, которое имеет смысл. Брусок массой 38 кг движется вниз с ускорением, поэтому натяжение веревки не полностью удерживает его от силы тяжести. Следовательно, вы знаете, что натяжение в канате должно быть менее (38 кг)g или менее 370 Н.
Следовательно, мы правильно выбрали направление ускорения и трения.
- Дом
- Особенности
- Практическое руководство
- Проблемы
- Висконсинский университет Грин Бэй
- 2420 Николет Доктор
- Грин Бэй, Висконсин, 54311
Проблемы
Проблемы
Далее: Об этом документе…
Up: Работа и энергия
Предыдущий: Мощность
а) Автомобиль массой 2000 кг движется со скоростью 50 миль в час. Найди
кинетическая энергия в джоулях. б) Тот же автомобиль поднимают вертикально вверх, а затем
выпал из состояния покоя.
землю со скоростью 50 миль в час (сопротивлением воздуха пренебречь).
Решение:
- а)
-
КЭ знак равно мв 2 знак равно
(2 x 10 3 кг ) 2 знак равно 4,99 x 10 5 J (10) - б)
-
ПЭ и знак равно КЭ f мгч знак равно мв 2 ч знак равно знак равно 2 = 25,5 м (11)
Объект массой 1 кг, движущийся со скоростью 5,0 м/с, входит в область
лед, где коэффициент кинетического трения равен 0,10.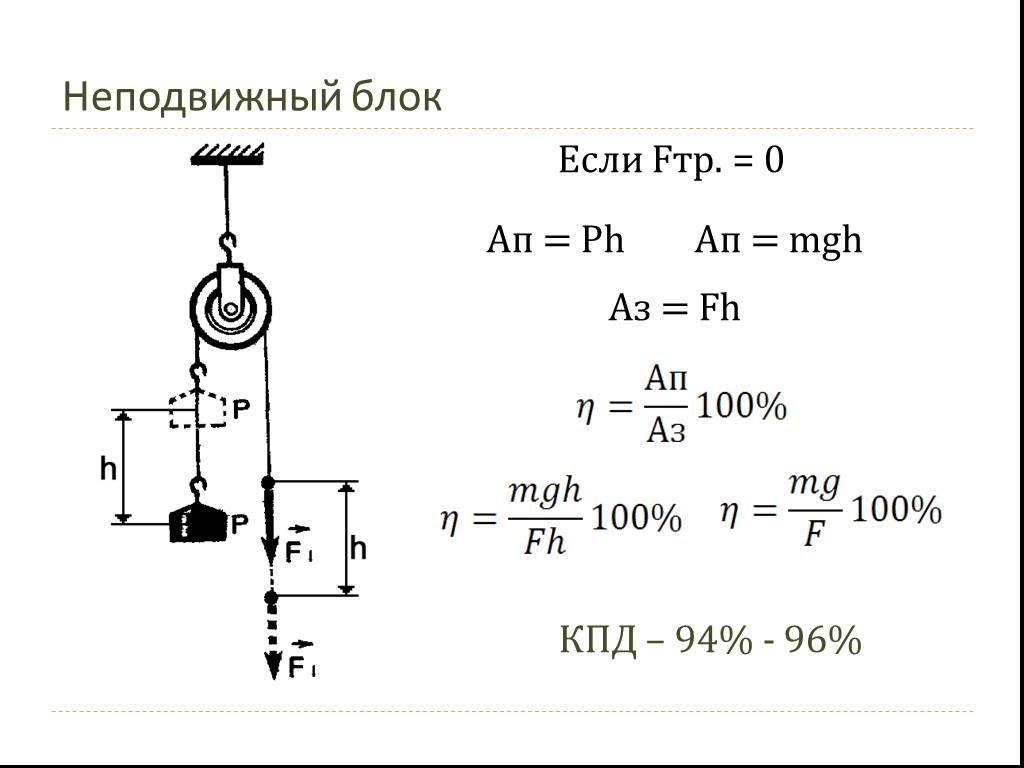
Теорема, позволяющая найти расстояние, которое проходит тело до того, как остановится.
Решение:
Теорема об энергии работы дает
Вт = КЭ . У нас есть
W = — f k d = — Nd = — mgd и
KE = mv f 2 — mv i 2 = — mv 2 i 4 9. Объединение,
| — мгд | знак равно | — мв и 2 | |
| д | знак равно | v i 2 | |
| знак равно |
= 13 м . |
(12) |
Ребенок весом 30 кг входит в финальную часть спуска с водной горки
при 2,0 м/с. Последняя секция имеет длину 5,0 м и перепад высот 3,0 м.
Сила трения, противодействующая движению ребенка, равна 50 Н. Найти а) потерю
потенциальная энергия, б) работа, совершаемая трением на конечном участке, и в)
скорость ребенка в конце секции (используя энергетические соображения).
Решение:
- а)
-
ПЭ знак равно мг ( ч f — ч i ) знак равно 30(9,8)(0 — 3) = — 882 Дж (13) - б)
-
W = — f k x = — 50(5) = — 250 J (14) - в)
-
Ш НЗ знак равно КЭ + ПЭ — 250 знак равно (30)( v f 2 ) — (30)(2. 0) 2 — 882
v f 2 знак равно v f знак равно 6,8 м / с (15)
Деревянный брусок весом 2,0 кг лежит на ровной доске и удерживается пружиной
жесткости пружины k=100 Н/м, которая была сжата на 0,1 м. Блок
отпустили и толкнули горизонтально через доску. Коэффициент трения
между блоком и доской = 0,20. Найдите а) скорость бруска
когда он покидает пружину и б) расстояние, которое проходит блок после того, как он покидает пружину
весна.
Решение:
- а)
- Теорема об энергии работы дает:
Ш НЗ знак равно КЭ + ПЭ — ф к х знак равно ( мв ф 2 — 0) + (0 — кх 2 ) — мгх знак равно mv f 2 — kx 2 v f 2 знак равно знак равно v f знак равно 0,33 м / с . (16) - б)
- Теорема о работе энергии дает,
— мгд знак равно 0 — mv i 2 д знак равно v i 2 = = 0,028 м . (17)
Человек толкает коробку массой 100 кг по ровному полу с постоянной
скорость 2,0 м/с в течение 10 с. Если коэффициент трения между коробкой и
пол
= 0,20, найдите среднюю мощность, выдаваемую человеком.
Решение:
Преподаватель который помогает студентам и школьникам в учёбе.
Блоки в физике — виды, формулы и определения с примерами
Содержание:
Блоки:
Всегда ли удобно использовать рычаг
Поднять груз на значительную высоту с помощью рычага очень сложно. Чем высота больше, тем длиннее должен быть рычаг. Такого недостатка нет у блока.
Что такое блок
Блок — это устройство, состоящее из веревки, переброшенной через колесо, которое может вращаться на оси.
Обод колеса, как правило, имеет желоб, в котором прокладывается трос или веревка.
Ось блока может быть неподвижной или перемещаться вместе с колесом. В связи с этим блоки бывают подвижными и неподвижными.
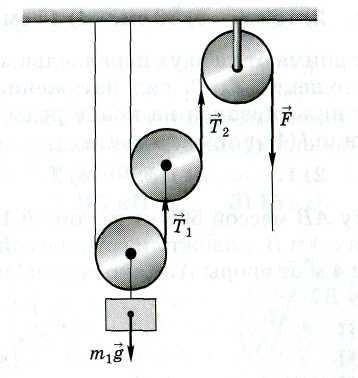
Какой блок называют неподвижным
У неподвижного блока ось вращения не изменяет своего положения в пространстве. Она с помощью специальной обоймы закреплена на балке или на другой опоре (рис. 70). Если на конец веревки, переброшенной через блок, подействовать силой, то другой конец начнет двигаться вверх. Если к этому концу прикрепить груз определенной массы, то он будет подниматься вверх. Если на свободный конец веревки действует сила, направленная вниз, то на груз действует сила, направленная вверх. Измерение этих сил показывает, что они равны.
Почему неподвижный блок не дает выигрыша в силе
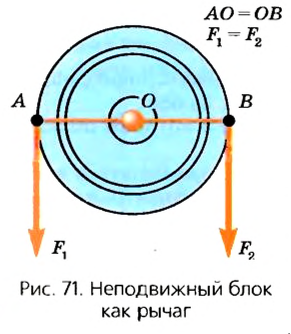
Неподвижный блок выигрыша в силе не дает, он только изменяет направление действия силы.
Такую особенность можно легко объяснить, учитывая, что неподвижный блок похож на равноплечий рычаг. Для этого перенесем точки действия сил вверх к точкам А к В, где веревка касается блока (рис. 71). Плечи этих сил OA и ОВ будут одинаковыми, как радиусы окружности. Согласно условию равновесия рычага силы F1 и F2 также должны быть одинаковыми. Опыт подтверждает эти выводы.
- Заказать решение задач по физике
Какой блок называют подвижным
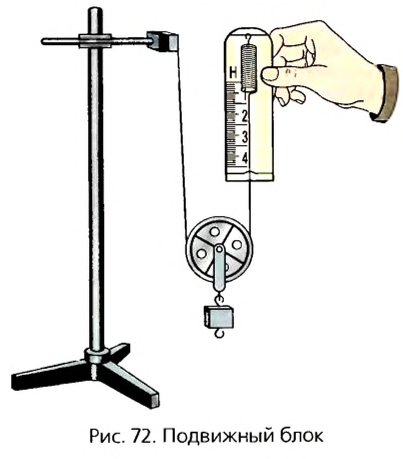
Подвижным называют блок, ось которого перемещается в пространстве. При использовании такого блока обычно один конец веревки или троса закрепляют на опоре, а груз — на обойме, в которой блок закреплен. На рисунке 72 показан опыт с таким блоком. К оси легкого подвижного блока подвешен груз массой 102 г. Итак, на ось блока действует сила 1 Н. Стрелка динамометра, присоединенного к свободному концу веревки, показывает примерно 0,5 Н. Некоторые небольшие различия связаны с тем, что блок сам имеет вес и на него действует сила трения.
Почему подвижный блок дает выигрыш в силе
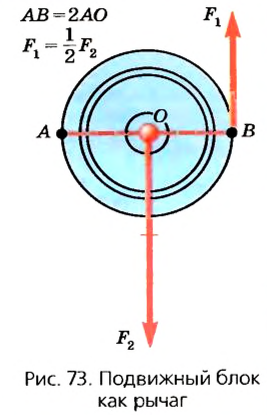
Такую особенность подвижного блока можно объяснить, учитывая свойства рычага (рис. 73). Диск блока можно считать рычагом длиной 2R (где R — радиус колеса). Ось вращения такого рычага проходит через точку А на ободе колеса, а точками приложения сил являются точки О и В. Так как 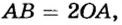
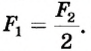
Пример решения задачи
Определить вес груза, который удерживается системой подвижного и неподвижного блоков, если на свободный конец троса действует сила 300 Н (рис. 74).
Дано:
Решение
Неподвижный блок выигрыша в силе не дает. Поэтому вычисления производим с учетом только подвижного блока, который дает выигрыш в силе в два раза. О массе блока в условии задачи не сказано, поэтому весом блока можно пренебречь по сравнению с весом груза. Таким образом,
Ответ. Вес груза равен 600 Н.
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Давление газов и жидкостей
- Движение жидкостей и газов
- Сила давления в физике и единицы давления
- Механическое давление в физике
- Столкновения в физике
- Рычаг в физике
Решение задач на движение системы связанных тел
Общий случай решения
Рассмотрим общий случай. Имеется неподвижный блок, через который перекинута нить, к концам которой подвешены два грузика массой 
Рис. 1. Схема блока
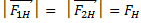
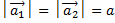
На первый грузик действует сила притяжения к земле и сила натяжения нити, которая направлена вверх. Соответственно, на второй грузик будут действовать те же силы. Величины сил натяжения их будут одинаковы по модулю при условии, что трение в оси блока отсутствует и сам блок невесом, то есть его не нужно раскручивать какой-то парой сил. Сила натяжения – это внутренняя сила, возникающая в системе связанных тел, друг на друга они действуют посредством нити. Ускорение у этих грузиков будет иметь разное направление, так как первый грузик тяжелее, то он будет двигаться вниз, а второй вверх, но величины ускорений будут одинаковы и равны а, при условии, что нить нерастяжима. К блоку приложены три силы – две силы натяжения, которые тянут блок вниз, и сила реакции крепления оси блока, направленная вверх и равная удвоенной силе натяжения, так как центр блока никуда не перемещается и сумма сил, приложенных к нему должна быть равна нулю. При разборе таких задач оси рисовать не обязательно, потому что подразумевается, что для каждого тела можно выбрать свое направление оси. Так как первое тело движется вниз, то ось 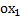
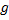
Задача 1
Одинаковые бруски, связанные нитью, движутся под действием внешней силы 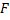
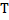
1. Увеличится в 2 раза
2. Увеличится в 3 раза
3. Уменьшится в 1,5 раза
4. Уменьшится в 2раза
Рис. 2. Иллюстрация к задаче 1
В этой задаче необходимо найти отношение силы натяжения 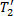
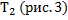
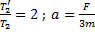

Рис. 3. Решение задачи 1
Растянутая нить в этой системе действует на брусок 2, заставляя его двигаться вперед, но она также действует и на брусок 1, пытаясь препятствовать его движению. Эти две силы натяжения равны по величине, и нам как раз необходимо найти эту силу натяжения. В таких задачах необходимо упростить решение следующим образом: считаем, что сила 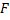
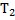
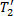
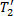
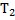
Задача 2
Два тела массой 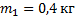
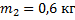
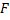
Выбор ответа: 1. 2/3; 2. 1; 3. 3/2; 4. 9/4.
Рис. 4. Иллюстрация к задаче 2
Рис. 5. Решение задачи 2
На бруски действует одна и та же сила, только в разных направлениях, поэтому ускорение в случае «а» и случае «б» будет одним и тем же, так как одна и та же сила вызывает ускорение двух масс. Но в случае «а» эта сила натяжения заставляет двигаться еще и брусок 2, в случае «б» это брусок 1. Тогда отношение этих сил будет равно отношению их масс и мы получим ответ – 1,5. Это третий ответ.
Задача 3
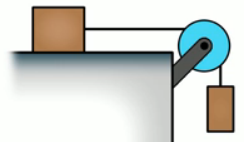
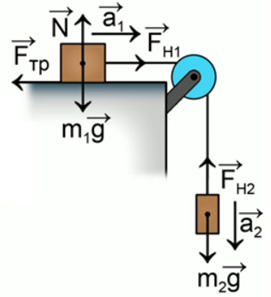
На столе лежит брусок массой 1 кг, к которому привязана нить, перекинутая через неподвижный блок. Ко второму концу нити подвешен груз массой 0,5 кг (Рис. 6). Определить ускорение, с которым движется брусок, если коэффициент трения бруска о стол составляет 0,35.
Рис. 6. Иллюстрация к задаче 3
Записываем краткое условие задачи:
Рис. 7. Решение задачи 3
Необходимо помнить, что силы натяжения 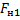
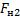
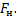
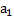
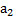
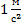
Для решения таких задач можно пользоваться методом, который использовался в прошлом веке: движущей силой в данном случае является результирующая внешних сил, приложенных к телу. Заставляет двигаться эту систему сила тяжести второго тела, но мешает движению сила трения бруска о стол, в этом случае:
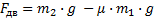
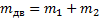
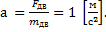
Задача 4
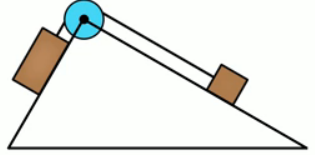
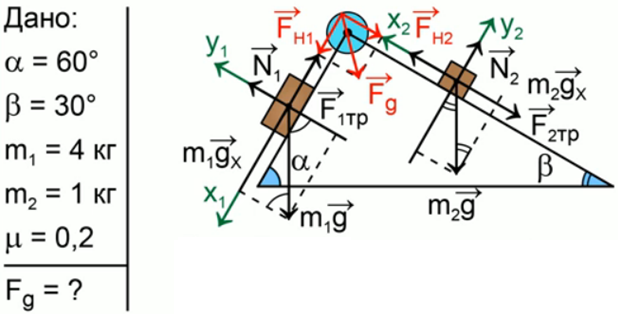
В вершине двух наклонных плоскостей, составляющих с горизонтом углы 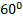
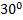
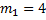
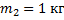
Рис. 8. Иллюстрация к задаче 4
Выполним краткую запись условия задачи и поясняющий чертеж (рис. 9):
Рис. 9. Решение задачи 4
Мы помним, что если одна плоскость составляет угол в 600 с горизонтом, а вторая плоскость – 300 с горизонтом, то угол при вершине будет 900, это обычный прямоугольный треугольник. Через блок перекинута нить, к которой подвешены бруски, они тянут вниз с одной и той же силой, и действие сил натяжения Fн1 и Fн2 приводит к тому, что на блок действует их результирующая сила. Но между собой эти силы натяжения будут равны, составляют они между собой прямой угол, поэтому при сложении этих сил получается квадрат вместо обычного параллелограмма. Искомая сила Fд является диагональю квадрата. Мы видим, что для результата нам необходимо найти силу натяжения нити. Проведем анализ: в какую сторону движется система из двух связанных брусков? Более массивный брусок, естественно, перетянет более легкий, брусок 1 будет соскальзывать вниз, а брусок 2 будет двигаться наверх по склону, тогда уравнение второго закона Ньютона для каждого из брусков будет выглядеть:
Решение системы уравнений для связанных тел выполняется методом сложения, далее преобразовываем и находим ускорение:
=
Это значение ускорения необходимо подставить в формулу для силы натяжения и найти силу давления на ось блока:
Мы выяснили, что сила давления на ось блока приблизительно равна 16 Н.
Заключение
Мы рассмотрели различные способы решения задач, которые многим из вас пригодятся в дальнейшем, чтобы понять принципы устройства и работы тех машин и механизмов, с которыми придется иметь дело на производстве, в армии, в быту.

Блоки относят к простым механизмам. В группу этих устройств, которые служат для преобразования силы, помимо блоков относят рычаг, наклонную плоскость. Изготавливаются блоки в виде дисков (колес, низких цилиндров и т. п.), имеющих желоб, через который пропускают веревку (торс, канат, цепь).
Неподвижный блок
Неподвижным называется блок, с закрепленной осью (рис.1). Он не перемещается при подъеме груза. Неподвижный блок можно рассматривать как рычаг, который имеет равные плечи.
Условием равновесия блока является условие равновесия моментов сил, приложенных к нему:
Блок на рис.1 будет находиться в равновесии, если силы натяжения нитей равны: так как плечи этих сил одинаковы (ОА=ОВ). Неподвижный блок не дает выигрыша в силе, но он позволяет изменить направление действия силы. Тянуть за веревку, которая идет сверху часто удобнее, чем за веревку, которая идет снизу. Если масса груза, привязанного к одному из концов веревки, перекинутой через неподвижный блок равна m, то для того, чтобы его поднимать, к другому концу веревки следует прикладывать силу F, равную:
при условии, что силу трения в блоке мы не учитываем. Если необходимо учесть трение в блоке, то вводят коэффициент сопротивления (k), тогда:
Заменой блока может служить гладкая неподвижная опора. Через такую опору перекидывают веревку (канат), которая скользит по опоре, но при этом растет сила трения.
Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, следовательно, равны работы.
[custom_ads_shortcode1]
Комбинация неподвижных блоков
Для того чтобы получить выигрыш в силе, применяя неподвижные блоки применяют комбинацию блоков, например, двойной блок. При блоки должны иметь разные диаметры. Их соединяют неподвижно между собой и насаживают на единую ось.
К каждому блоку прикрепляется веревка, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в таком случае будут неравными. Двойной блок действует как рычаг с плечами разной длины.
На рис. 2 изображена схема двойного блока.
Условие равновесия для рычага на рис.2 станет формула: Двойной блок может преобразовывать силу. Прикладывая меньшую силу к веревке, намотанной на блок большого радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.
[custom_ads_shortcode2]
Подвижный блок
Подвижным блоком называют блок, ось которого перемещается совместно с грузом. На рис. 2 подвижный блок можно рассматривать как рычаг с плечами разной величины. В этом случае точка О является точкой опоры рычага. OA – плечо силы ; OB – плечо силы . Рассмотрим рис. 3. Плечо силы в два раза больше, чем плечо силы , следовательно, для равновесия необходимо, чтобы величина силы F была в два раза меньше, чем модуль силы P:
Можно сделать вывод о том, что при помощи подвижного блока мы получаем выигрыш в силе в два раза. Условие равновесия подвижного блока без учета силы трения запишем как: Если попытаться учесть силу трения в блоке, то вводят коэффициент сопротивления блока (k) и получают:
Иногда применяют сочетание подвижного и неподвижного блока. В таком сочетании неподвижный блок используют для удобства. Он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок применяют для изменения величины прилагаемого усилия. Если концы веревки, охватывающей блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка. В случае параллельности веревок, сила необходимая для подъема груза потребуется в два раза меньше, чем вес поднимаемого груза.
[custom_ads_shortcode3]
Золотое правило механики
Простые механизмы выигрыша в работе не дают. Во сколько мы получаем выигрыш в силе, во столько же раз проигрываем в расстоянии. Так как работа равна скалярному произведению сила на перемещение, следовательно, она не изменится при использовании подвижного (как и неподвижного) блоков.
В виде формулы «золотое правило№ можно записать так:
где – путь, который проходит точка приложения силы – путь проходимый точкой приложения силы . Золотое правило является самой простой формулировкой закона сохранения энергии. Это правило распространяется на случаи, равномерного или почти равномерного движения механизмов. Расстояния поступательного движения концов веревок связаны с радиусами блоков ( и ) как:
Получим, что для выполнения «золотого правила» для двойного блока необходимо, чтобы:
Если силы и уравновешены, то блок покоится или движется равномерно.
[custom_ads_shortcode1]
Примеры решения задач
Применение подвижного блока даёт двукратный выигрыш в силе, применение неподвижного – позволяет изменить направление прилагаемой силы. На практике используются комбинации подвижных и неподвижных блоков. При этом каждый подвижный блок позволяет вдвое уменьшить прилагаемое усилие или вдвое увеличить скорость перемещения груза. Неподвижные блоки используют для связи подвижных блоков в единую систему. Такая система подвижных и неподвижных блоков называется полиспаст.
Используется полиспаст в случаях, если необходимо прилагая минимальные усилия поднять или переместить тяжелый груз, обеспечить натяжение и т.п. Простейший полиспаст состоит всего из одного блока и каната, при этом позволяет в два раза снизить тяговое усилие, необходимое для подъема груза.
Рисунок 1. Каждый подвижный блок в полиспасте даёт двукратный выигрыш в силе или скоростиОбычно в грузоподъемных механизмах применяют силовые полиспасты, позволяющие уменьшить натяжение каната, момент от веса груза на барабане и передаточное число механизма (тали, лебедки). Скоростные полиспасты, позволяющие получить выигрыш в скорости перемещения груза при малых скоростях приводного элемента, применяются значительно реже. Они используются в гидравлических или пневматических подъемниках, погрузчиках, механизмах выдвижения телескопических стрел кранов.
Основной характеристикой полиспаста является кратность. Это отношение числа ветвей гибкого органа, на котором подвешен груз, к числу ветвей наматываемых на барабан (для силовых полиспастов), либо отношение скорости ведущего конца гибкого органа к ведомому (для скоростных полиспастов). Условно говоря, кратность это теоретически рассчитанный коэффициент выигрыша в силе или скорости при использовании полиспаста. Изменение кратности полиспаста происходит путем введения или удаления из системы дополнительных блоков, при этом конец каната при четной кратности крепится на неподвижном элементе конструкции, а при нечетной кратности – на крюковой обойме. Рисунок 2. Крепление каната при чётной и нечётной кратности полиспаста Выигрыш в силе при применении полиспаста с $n$ подвижных и $n$ неподвижных блоков определяется по формуле: $P=2Fn$, где $Р$ – вес груза, $F$ – сила, прилагаемая на входе полиспаста, $n$ – число подвижных блоков.
В зависимости от количества ветвей каната, закрепленных на барабане грузоподъемного механизма, можно выделить одинарные (простые) и сдвоенные полиспасты. В одинарных полиспастах, при наматывании или сматывании гибкого элемента вследствие его перемещения вдоль оси барабана, создается нежелательное изменение нагрузки на опоры барабана. Также в случае отсутствия в системе свободных блоков (канат с блока крюковой подвески непосредственно переходит на барабан) происходит перемещение груза не только в вертикальной, но и в горизонтальной плоскости.
Рисунок 3. Одинарные и сдвоенные полиспастыДля обеспечения строго вертикального подъема груза применяют сдвоенные полиспасты, (состоящие из двух одинарных), в этом случае на барабане закрепляются оба конца каната. Для обеспечения нормального положения крюковой подвески при неравномерной вытяжке гибкого элемента обоих полиспастов применяют балансир или уравнительные блоки.
Рисунок 4. Способы обеспечения вертикальности подъёма грузаСкоростные полиспасты отличаются от силовых тем, что в них рабочая сила, обычно развиваемая гидравлическим или пневматическим цилиндром, прикладывается к подвижной обойме, а груз подвешивается к свободному концу каната или цепи. Выигрыш в скорости при использовании такого полиспаста получается в результате увеличения высоты подъёма груза.
При использовании полиспастов следует учитывать, что используемые в системе элементы не являются абсолютно гибкими телами, а имеют определенную жесткость, поэтому набегающая ветвь не сразу ложится в ручей блока, а сбегающая ветвь не сразу выпрямляется. Это наиболее заметно при использовании стальных канатов.
Вопрос: почему у подъемных строительных кранов крюк, который переносит груз, закреплен не на конце троса, а на обойме подвижного блока? Ответ: для обеспечения вертикальности подъёма груза.
Ничего непонятно? Попробуй обратиться за помощью к преподавателямЗадачаНа рис.5 изображён степенной полиспаст, в котором несколько подвижных блоков, а неподвижный – только один. Определите, какой вес можно поднять, приложив к неподвижному блоку усилие $F$ = 200 H?
Рисунок 5РешениеКаждый из подвижных блоков степенного полиспаста удваивает прилагаемое усилие. Вес, который может поднять степенной полистпаст третьей степени (без учёта поправок на силы трения и жёсткость троса), определяется формулой:
[P=Fcdot 2^n=200cdot 2^3=800 H] Ответ: полиспаст может поднять груз весом 800 Н.
Первый блок был изобретен, когда через колесо, вращающееся вокруг своей оси, неизвестный механик древности перебросил веревку и с помощью этого устройства стал поднимать грузы. По легенде, Архимед с помощью нескольких блоков смог спустить на воду тяжелое судно, которое не могли сдвинуть с места десятки лошадей. сейчас блоки используют во многих машинах и механизмах. Чем объясняется их широкое применение?
Выясняем связь неподвижного блока и рычагаНа рис. 35.1, аизображено колесо (1) с желобом (2). Колесо может вращаться вокруг своей оси (3), неподвижно закрепленнной в обойме (4). Через желоб переброшен шнур (5). Перед вами простой механизм — неподвижный блок.
Блок — это простой механизм, имеющий форму колеса с желобом по ободу, через который переброшен шнур (канат, веревка).
На первый взгляд, рычаг и неподвижный блок — абсолютно разные механизмы. На самом деле неподвижный блок — это рычаг с одинаковыми плечами. Действительно, приложим к концам шнура, переброшенного через блок, силы F и F и проведем перпендикуляры из точки опоры к линиям действия сил (рис. 35.1, б,в). Видим, что плечо каждой силы равно радиусу Вблока:
Из условия равновесия рычага.
следует, что.
или:
Таким образом, неподвижный блок не дает выигрыша в силе, однако позволяет изменять направление действия силы(см. , например, рис. 35.
1-35. 3). Рассмотрите рис.
35. 1, б, в. Если свободный конец шнура тянуть вниз, куда будет двигаться груз?
Исследуем подвижный блокС помощью обоймы прикрепим груз к оси блока. Сам блок подвесим на шнуре, один конец которого закреплен (рис. 35.4). Если поднимать свободный конец шнура, то за шнуром будет подниматься и блок с грузом. Полученный простой механизм — это подвижный блок.
Подвижный блок можно рассматривать как рычаг, который вращается вокруг оси, проходящей через точку опоры O(см. рис. 35.4). Из рисунка видно, что плечо силы Е равно радиусу блока (отрезок OA), а плечо силы Е — диаметру блока (отрезок ОВ), то есть двум его радиусам.
Таким образом, использование подвижного блока позволяет получить выигрыш в силе в два раза.
Понятно, что выигрыш в силе будет сопровождаться таким же проигрышем в расстоянии: если свободный конец шнура поднять на высоту h, то блок вместе с грузом подниметсялишь на высоту
Как и рычаг, подвижный блок можно также использовать для получения выигрыша в расстоянии (либо выигрыша в скорости движения). Для этого груз прикрепляют к свободному концу шнура, а тянут за обойму, к которой прикреплена ось блока (рис. 35.6).
Неподвижные и подвижные блоки, как правило, используются одновременно — в виде системы блоков (рис. 35. 7).
Как вы считаете, позволяет ли система блоков на рис. 35. 7 изменить направление действия силы?
Учимся решать задачиЗадача. На рис. 35.8 представлена система блоков. Определите силы натяжения шнуров a и Ь, если масса груза равна 20 кг. Какой выигрыш в силе дает данная система блоков? На какое расстояние hA опустится точка Л, если груз поднимется на высоту 10 см? Массой блоков и силой трения пренебречь.
Анализ физической проблемы. Система блоков состоит из двух подвижных блоков (1 и 2) и одного неподвижного блока (3). По условию массой блоков следует пренебречь, значит, натяжение шнура вызвано только весом груза. Для определения выигрыша в силе сравним вес Р груза и силу F, которая приложена к свободному концу шнура и под действием которой поднимается груз.
Следует учесть, что, выиграв в силе, мы во столько же раз проигрываем в расстоянии, на которое перемещается груз.
Подводим итогиБлок — это простой механизм, имеющий форму колеса с желобом по ободу, через который переброшен шнур (канат, веревка). Различают подвижный и неподвижный блоки.
Неподвижный блок похож на рычаг с одинаковыми плечами, поэтому он не дает выигрыша в силе, но позволяет изменять направление действия силы.
Подвижный блок похож на рычаг с отношением плеч 1 : 2, поэтому он дает выигрыш в силе в 2 раза. Однако это сопровождается проигрышем в расстоянии в 2 раза. Подвижный блок также применяют для получения выигрыша в расстоянии (выигрыша в скорости движения).
Для большей эффективности обычно используют комбинации подвижных и неподвижных блоков.
Контрольные вопросы1. Опишите неподвижный блок. 2. Почему неподвижный блок не дает выигрыша в силе? 3. Для чего используют неподвижный блок? 4. Опишите подвижный блок. 5. Какой выигрыш в силе дает подвижный блок? 6. Что означает выражение: «Подвижный блок дает проигрыш в расстоянии в 2 раза»? 7. Как с помощью неподвижного блока получить выигрыш в скорости движения? 8. Как с помощью блоков получить выигрыш в силе более чем в 2 раза?
None 1. Рассмотрите рис. 1 и ответьте на вопросы: а) какой блок изображен?
б) на сколько поднимется груз, если свободный конец шнура вытянуть вверх на 10 см? в) с какой силой Fтянут шнур, если вес груза 60 Н?
2. Свободный конец шнура тянут с силой F = 40 Н (рис. 2).
Какова масса груза? На сколько поднимется груз, если вытянуть шнур на 24 см? 3.
Груз поднимают с помощью одного неподвижного и двух подвижных блоков (см. рис. 35.
8). Какова масса груза и на сколько он поднимется, если под действием силы 75 Н свободный конец шнура опустить на 60 см?
4. Какую силу Fнужно приложить к свободному концу шнура (см. рис.
2), чтобы поднять груз массой 100 кг, если масса подвижного блока равна 2 кг? Считайте, что трение в осях отсутствует. 5.
Груз массой тудерживается с помощью системы блоков (рис. 3). Определите силу натяжения каждого шнура.
6. В системе на рис. 4 масса груза 3равна 1 кг, масса каждого блока — 100 г.
Система уравновешена и неподвижна. Найдите массы грузов 1 и 2. Массой шнура и трением в блоках пренебречь.
7. В технике достаточно часто используют полиспасты— устройства, состоящие из системы подвижных и неподвижных блоков. На рис.
5 представлено схематическое изображение одного из полиспастов — лебедки. Воспользуйтесь дополнительными источниками информации и узнайте о полиспастах больше. Подготовьте сообщение.
8. Кроме блоков разновидностью рычага является коловорот(см. , например, рис.
6). Воспользуйтесь дополнительными источниками информации и узнайте, что представляет собой коловорот, где его применяют, почему с помощью коловорота можно получить значительный выигрыш в силе. Подготовьте сообщение.
Видеоопыт.Посмотрите видеоролик и объясните наблюдаемое явление.
Это материал учебника Физика 7 класс Барьяхтар, Довгий
Дата.
Блок состоит из одного или нескольких колес (роликов), огибаемых цепью, ремнем или тросом. Так же, как и рычаг, блок уменьшает усилие, необходимое для подъема груза, но плюс к этому может изменять направление прикладываемой силы.
За выигрыш в силе приходится расплачиваться расстоянием: чем меньшее усилие требуется для подъема груза, тем больше путь, который должна пройти точка приложения этого усилия. Система блоков увеличивает выигрыш в силе за счет использования большего количества грузонесущих цепей. Подобные силосберегающие устройства имеют очень широкий диапазон применения — от перемещения на высоту массивных стальных балок на строительных площадках до подъема флагов.
Как и в случае других простых механизмов, изобретатели блока неизвестны. Хотя, возможно, блоки существовали и раньше, первое упоминание о них в литературе относится к пятому веку до нашей эры и связано с использованием блоков древними греками на кораблях и в театрах.
Установленные на подвесном рельсе подвижные системы блоков (рисунок сверху) широко распространены на сборочных линиях, поскольку существенно облегчают перемещение тяжелых деталей. Прикладываемая сила (F) равна частному от деления веса груза (W) на используемое количество поддерживающих его цепей (n).
[custom_ads_shortcode2]
Одинарные неподвижные блоки
Этот простейший тип блока не уменьшает усилие, необходимое для подъема груза, но зато изменяет направление прикладываемой силы, как это показано на рисунках сверху и справа вверху. Неподвижный блок на верхней части флагштока облегчает подъем флага, позволяя тянуть шнур, к которому привязан флаг, вниз.
[custom_ads_shortcode3]
Одинарные подвижные блоки
Одинарный блок, имеющий возможность перемещения, уменьшает наполовину усилие, требующееся для подъема груза. Однако уменьшение вдвое прикладываемой силы означает, что точка ее приложения должна пройти в два раза больший путь. В данном случае сила равна половине веса (F=1/2W).
[custom_ads_shortcode1]
Системы блоков
При использовании комбинации неподвижного блока с подвижным прикладываемая сила кратна общему количеству грузонесущих цепей. В данном случае сила равна половине веса (F=1/2W). Груз, подвешенный через блок вертикально, позволяет туго натягивать горизонтальные электрические провода.
Подвесной подъемник (рисунок сверху) состоит из цепи, обвитой вокруг одного подвижного и двух неподвижных блоков. Подъем груза требует прикладывания силы, составляющей всего лишь половину от его веса.
Полиспаст, обычно используемый в больших подъемных кранах (рисунок справа), состоит из комплекта подвижных блоков, к которому подвешивается груз, и комплекта неподвижных, прикрепленного к стреле крана. Получая выигрыш в силе от столь большого количества блоков, кран может поднимать очень тяжелые грузы, например, стальные балки. В данном случае сила (F) равна частному от деления веса груза (W) на количество поддерживающих тросов (n).
Источники:
- ru.solverbook.com
- spravochnick.ru
- narodna-osvita.com.ua
- information-technology.ru



 В этом примере это понимание уже использовалось — взаимодействие между двумя блоками происходит за счет натяжения веревки, и натяжение обозначалось одним и тем же символом для каждого. Если вы не заметили, что натяжение по всей веревке такое же, как вы нарисовали FBD, это нормально. Когда вы начнете решать уравнения, вы обнаружите, что у вас слишком много неизвестных, и вы можете использовать это понимание, чтобы уменьшить их в этот момент.
В этом примере это понимание уже использовалось — взаимодействие между двумя блоками происходит за счет натяжения веревки, и натяжение обозначалось одним и тем же символом для каждого. Если вы не заметили, что натяжение по всей веревке такое же, как вы нарисовали FBD, это нормально. Когда вы начнете решать уравнения, вы обнаружите, что у вас слишком много неизвестных, и вы можете использовать это понимание, чтобы уменьшить их в этот момент. 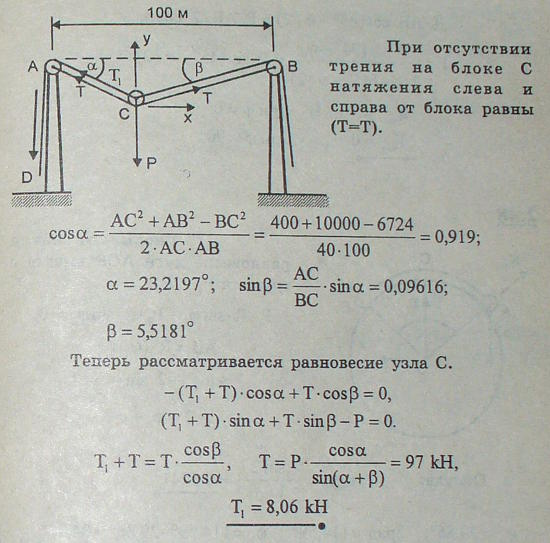 ). Прокрутите вниз, чтобы продолжить это решение.
). Прокрутите вниз, чтобы продолжить это решение. 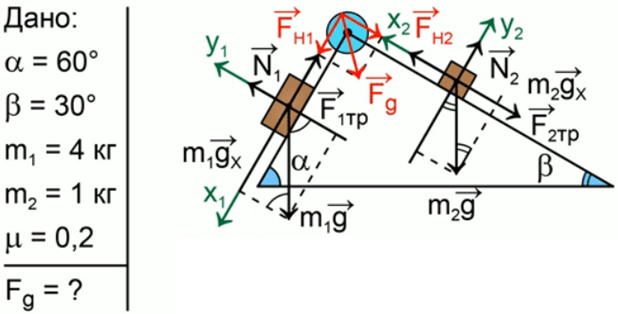
 Это значение примерно равно силе гравитации, действующей на массу 16 кг, опять-таки число, которое имеет смысл. Брусок массой 38 кг движется вниз с ускорением, поэтому натяжение веревки не полностью удерживает его от силы тяжести. Следовательно, вы знаете, что натяжение в канате должно быть менее (38 кг)g или менее 370 Н.
Это значение примерно равно силе гравитации, действующей на массу 16 кг, опять-таки число, которое имеет смысл. Брусок массой 38 кг движется вниз с ускорением, поэтому натяжение веревки не полностью удерживает его от силы тяжести. Следовательно, вы знаете, что натяжение в канате должно быть менее (38 кг)g или менее 370 Н. 
 0) 2 — 882
0) 2 — 882