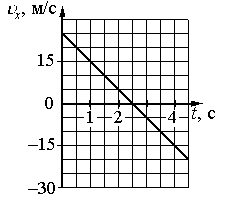Как найти ускорение через координаты тела - Avtoru.top

Скорости и ускорения как производные координаты

Зная координату тела (закон, по которому она изменяется) можно очень многое о движении этого тела узнать. Например, скорость — первая производная от координаты. А ускорение — вторая производная, или первая производная скорости. Если в задаче дано еще и время движения тела — то можно полностью описать движение и найти все его характеристики для данного момента времени.

Ускорение

Задача 1.

Точка движется по прямой согласно закону , где м/с, м/c. Определить: среднюю скорость точки в интервале времени от с до с, координату точки в тот момент времени, когда скорость тела будет равна нулю.

Средняя скорость – это отношение пройденного пути ко времени. Время движения очевидно: с. А путь можно определить как :

Чтобы определить скорость, возьмем производную координаты по времени:

Если скорость равна 0, то

Откуда с и м.

Ответ: м/с, м.

Задача 2.

Точка движется вдоль оси по закону . Найти направление движения в моменты времени: а) с; б) с. Чему будут равны ускорения в эти моменты времени?

Чтобы определить направление движения, нам надо узнать знак скорости в данные моменты времени. Определим сначала скорость тела как производную координаты:

Тогда

Поэтому в момент времени тело движется в положительном направлении, а в момент времени — в отрицательном.

Определим ускорение как вторую производную от координаты, или первую производную скорости по времени:

Ответ: м/с, движение по оси, м/с, м/с, движение против оси, м/с.

Задача 3.

Тело движется прямолинейно, причем скорость зависит от времени по закону: . Определить зависимость ускорения от времени . Каково значение ускорения при с?

Чтобы найти ускорение, возьмем производную скорости:

При имеем:

Ответ: , м/с.

Источник

Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
Единица измерения ускорения — метр в секунду в квадрате (м/с²).
Акселерометр — прибор для измерения ускорения.

Формула ускорения

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

Проекция ускорения на ось ОХ

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁= 1 и t₂= 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

В момент времени t₁= 1с ускорение a = 2 м/с². В момент времени t₂= 3 ускорение a = 0 м/с².

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Определить, какому типу движения соответствует график зависимости координаты тела от времени.
Определить величины, которые характеризуют такое движение.
Определить характер изменения величин, характеризующих это движение.
Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

перемещение и путь;
скорость;
ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17992

Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?

Алгоритм решения

Записать исходные данные.
Записать формулу, связывающую известные из условия задачи величины.
Выразить из формулы искомую величину.
Вычислить искомую величину, подставив в формулу исходные данные.

Решение

Запишем исходные данные:

Начальная скорость v₀ = 5 м/с.
Конечная скорость v = 15 м/с.
Пройденный путь s = 40 м.

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

Ответ: 2,5

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18202

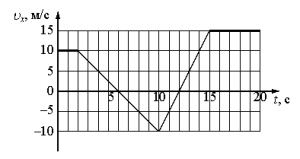
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
Вычислить ускорение движение тела на этом участке.
Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

t₁ = 6 с. Этой точке соответствует скорость v₁ = 0 м/с.
t₂ = 10 с. Этой точке соответствует скорость v₂ = –10 м/с.

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18027

На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.

Алгоритм решения

Записать формулу ускорения.
Записать формулу для вычисления модуля ускорения.
Выбрать любые 2 точки графика.
Определить для этих точек значения времени и проекции скорости (получить исходные данные).
Подставить данные формулу и вычислить ускорение.

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

t₁ = 1 с. Этой точке соответствует скорость v₁ = 15 м/с.
t₂ = 2 с. Этой точке соответствует скорость v₂ = 5 м/с.

Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 13.8k

Источник

Определение скорости при координатном способе

задания
движения

Воспользуемся
уравнением (4)
и возьмем от него производную по времени

.
(8)

В
(8)
при единичных векторах стоят проекции
вектора скорости на координатные оси

.
(9)

Проекции
скорости на координатные оси определяются
как первые производные по времени от
соответствующих координат.

Зная
проекции, можно найти модуль вектора и
его направление

,
(10)

.
(11)

Определение
скорости при естественном способе

задания
движения

Пусть
дана траектория материальной точки и
закон изменения криволинейной координаты.
Предположим, при t₁
точка имел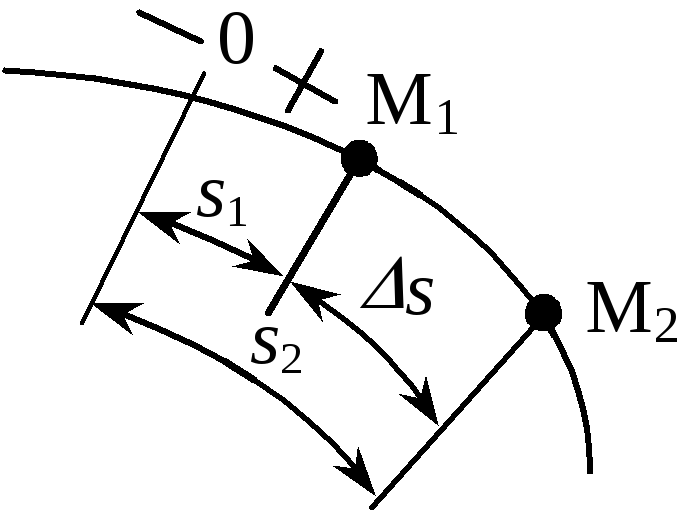а
координатуs₁,
а при t₂
– координату s₂.
За время
координата
получила приращение
,
тогда средняя скорость точки

Для
нахождения скорости в заданный момент
времени перейдем к пределу

.
(12)

Вектор
скорости точки при естественном способе
задания движения определяется как
первая производная по времени от
криволинейной координаты.

Ускорение точки

Под
ускорением материальной точки понимают
векторную величину, характеризующую
быстроту изменения вектора скорости
точки по величине и направлению с
течением времени.

Ускорение точки при векторном способе
задания движения

Рассмотрим
точку в два момента времени t₁
()
иt₂
(),
тогда— приращение времени,— приращение скорости.

Вектор
всегда
лежит в плоскости движения и направлен
в сторону вогнутости траектории.

Подсредним
ускорением точки
за время t
понимают
величину

.
(13)

Для
нахождения ускорения в заданный момент
времени перейдем к пределу

.
(14)

Ускорение
точки в данный момент времени определяется
как вторая производная по времени от
радиус-вектора точки или первая
производная от вектора скорости по
времени.

Вектор
ускорения расположен в соприкасающейся
плоскости и направлен в сторону вогнутости
траектории.

Ускорение точки при координатном способе задания движения

Воспользуемся
уравнением связи векторного и координатного
способов задания движения

И возьмем от него
вторую производную

.
(15)

В
уравнении (15)
при единичных векторах стоят проекции
вектора ускорения на координатные оси

.
(16)

Проекции
ускорения на координатные оси определяются
как первые производные по времени от
проекций скорости или как вторые
производные от соответствующих координат
по времени.

Модуль и направление
вектора ускорения можно найти по
следующим выражениям

,
(17)

,
,.
(18)

Ускорение точки при естественном способе задания движения

Пусть
точка движется по криволинейной
траектории. Рассмотрим два ее положения
в моменты времениt
(s,
M,
v)
и t₁
(s₁,
M₁,
v₁).

Ускорение
при этом определяется через его проекции
на оси естественной системы координат,
движущейся вместе с точкой M.
Оси при этом направлены следующим
образом:

M
— касательная, направлена вдоль касательной
к траектории, в сторону положительного
отсчета расстояния,

Mn
– главная нормаль, направлена по нормали,
лежащей в соприкасающейся плоскости,
и направлена в сторону вогнутости
траектории,

Mb
– бинормаль, перпендикулярна плоскости
Mn
и образует с первыми осями правую тройку.

Так
как вектор ускорения лежит в соприкасающейся
плоскости, то a_b=0.
Найдем проекции ускорения на другие
оси.

.
(19)

Спроектируем
(19)
на координатные оси

(20)

.
(21)

Проведем
через точку M₁
оси параллельные осям в точке M
и найдем проекции скорости:

M:

Mn:
,

(22)

где — так называемый угол смежности.

Подставляем
(22)
в (20)

При
t0
0,
cos1,
тогда

.
(23)

Касательное
ускорение точки определяется первой
производной по времени от скорости или
второй производной по времени от
криволинейной координаты.

Касательное
ускорение характеризует изменение
вектора скорости по величине.

Подставим
(22)
в (21)

Умножим
числитель и знаменатель на s
чтобы получить известные пределы

,
(24)

где(первый
замечательный предел),

,
где 
— радиус кривизны траектории.

Подставляя
вычисленные пределы в (24),
получим

(25)

Нормальное
ускорение точки определяется отношением
квадрата скорости к радиусу кривизны
траектории в данной точке.

Нормальное
ускорение характеризует изменение
вектора скорости по направлению и всегда
направлено в сторону вогнутости
траектории.

Окончательно
получим проекции ускорения материальной
точки на оси естественной системы
координат и модуль вектора

,
(26)

.
(27)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
02.04.2015390.66 Кб2316.doc
#
#
#
#
#
#
#
#
#

Источник

Ускорение скорость, с которой скорость изменения. Поскольку скорость является векторной величиной, ускорение также является векторной величиной. В результате требуется не только направление, но и величина. Итак, в этой статье мы рассмотрим, как определить величину ускорения.

Мы используем формулы и соотношения для расчета величины. Мы можем представить величину в единицах. Поскольку ускорение определяется как изменение скорости во времени, единицей СИ для него является ㎨. На ускорение влияют различные факторы, такие как скорость, время, сила и т. Д. Мы рассмотрим несколько различных методов оценки величины ускорения. Давайте читать дальше.

1. Как найти величину ускорения из определения ускорения:

Как мы все знаем, ускорение относится к скорости изменения скорости. Если начальная скорость тела равна vi, а его конечная скорость равна vf, ускорение можно вычислить, разделив изменение скорости на временной интервал Δt:

Как определить величину ускорения

(Здесь величина вектора показана жирным шрифтом, а вертикальные линии обозначают величину вектора или, можно сказать, абсолютное значение вектора, которое всегда положительно.)

Используя скорость и время, приведенное выше уравнение можно использовать для определения величины ускорения.

2. Как определить величину ускорения Из второго закона Ньютона:

Второй закон Ньютона гласит, что сила получается умножением ускорения на массу тела. Итак, как можно определить величину ускорения?

Итак, согласно второму закону Ньютона, сила, действующая на тело, пропорциональна его ускорению, тогда как масса обратно пропорциональна ускорению. Переведем эти утверждения в формулу величины ускорения:

Это визуализированная форма уравнения. Вы не можете редактировать это напрямую. Щелчок правой кнопкой мыши даст вам возможность сохранить изображение, и в большинстве браузеров вы можете перетащить изображение на свой рабочий стол или в другую программу.

Таким образом,

3. Как найти величину ускорения по компонентам вектора ускорения:

Как мы все знаем, ускорение — это векторная величина. Чтобы получить это количество, сложите компоненты ускорения. Здесь можно использовать простое правило сложения векторов. Если задействованы две компоненты вектора, мы можем написать:

В декартовой плоскости мы можем использовать координаты X и Y. Как в этих обстоятельствах определить величину ускорения? В декартовой системе координат компоненты X и Y перпендикулярны друг другу. Величину ускорения можно вычислить, возведя значения в квадрат и затем вычислив квадратный корень из суммы.

В результате уравнение выглядит следующим образом:

Формула величины ускорения в трехмерном пространстве:

4. Как найти величину центростремительного ускорения:

Из-за непрерывного изменения направления при круговом движении скорость изменяется, что приводит к ускорению. Ускорение направлено в направлении центра круга. Возведение в квадрат скорости тела v и деление ее на расстояние тела от центра круга дает величину центростремительного ускорения. Таким образом, центростремительное ускорение:

Уравнения движения — это, по сути, уравнения, которые объясняют движение любой физической системы и демонстрируют взаимосвязь между перемещением объекта, скоростью, ускорением и временем.

Когда величина ускорения постоянна, кинематическое уравнение движения в одном измерении также используется для вычисления величины ускорения.

Ниже приведены уравнения движения:

Когда мы рассматриваем ускорение в уравнении, мы получаем следующее:

Вот как мы можем определить величину ускорения.

Решенные примеры определения величины ускорения:

1 задачи:

Автомобиль трогается с места и развивает скорость 54 км / ч за 3 секунды. Найти его ускорение?

Решение: Автомобиль заводится с отдыха. Таким образом, начальная скорость автомобиля

Vi = 0 м / с

Vf = 54 км / ч

= (54 ✕ 1000) / 3600

= 15 м / с

Δt = 3 с

Таким образом, Ускорение : a = (Vf — Vi) / Δt

= (15-0) / 3

2 задачи:

Определите ускорения, возникающие при приложении чистой силы 12 Н к объекту массой 3 кг, а затем к объекту массой 6 кг.

Решение: Приложенная сила F = 12 Н

Масса объекта m1 = 3 кг

m2 = 6 кг

Ускорение объекта массой 3 кг

а1 = F / м1

= 12 / 3

Ускорение объекта массой 6 кг

а2 = F / м2

= 12 / 6

Поскольку масса и ускорение обратно пропорциональны, мы можем наблюдать, что по мере увеличения массы ускорение уменьшается.

3 задачи:

Тело движется по оси абсцисс в соответствии с соотношением

, где x в метрах, а t в секундах. Найти ускорение тела при t = 3 с.

Решение: Вот :

t = 3 с

Скорость v = dX / dt

= d / dt ()

= -2 + 6т

Ускорение : a = dv / dt

= d / dt (-2 + 6t)

Как мы видим, для этого движения ускорение не зависит от времени; ускорение будет постоянным на протяжении всего движения, а величина ускорения будет .

4 задачи:

Рассчитайте центростремительное ускорение точки на расстоянии 7.50 см от оси ультрацентрифуги, вращающейся при число оборотов в минуту.

Решение: Здесь нам даны:

Расстояние от центра r = 7.5 см

= 0.0750 м

Угловая скорость

Теперь

= 589 м / с

Таким образом, центростремительное ускорение:

Источник

Скорости и ускорения как производные координаты

Проекция ускорения

Направление вектора ускорения

График ускорения

Определение скорости при координатном способе

Ускорение точки при координатном способе задания движения

Ускорение точки при естественном способе задания движения

1. Как найти величину ускорения из определения ускорения:

2. Как определить величину ускорения Из второго закона Ньютона:

3. Как найти величину ускорения по компонентам вектора ускорения:

4. Как найти величину центростремительного ускорения:

Автомобиль трогается с места и развивает скорость 54 км / ч за 3 секунды. Найти его ускорение?

Определите ускорения, возникающие при приложении чистой силы 12 Н к объекту массой 3 кг, а затем к объекту массой 6 кг.

Тело движется по оси абсцисс в соответствии с соотношением

, где x в метрах, а t в секундах. Найти ускорение тела при t = 3 с.

Рассчитайте центростремительное ускорение точки на расстоянии 7.50 см от оси ультрацентрифуги, вращающейся при число оборотов в минуту.

Не пропустите также: