Отбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x — cosx = 0
cosx(sqrt(2)cosx — 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx — 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
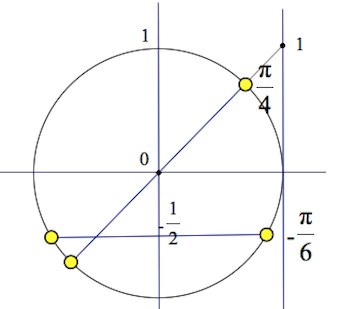
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
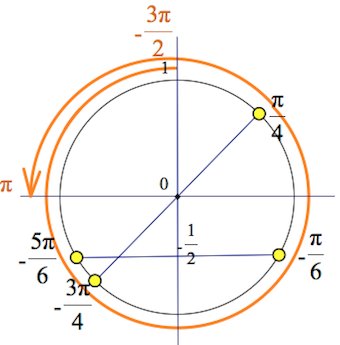
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
Решение тригонометрических уравнений на промежутке
Разделы: Математика
Цель урока:
а) закрепить умения решать простейшие тригонометрические уравнения;
б) научить выбирать корни тригонометрических уравнений из заданного промежутка
Ход урока.
1. Актуализация знаний.
а)Проверка домашнего задания: классу дано опережающее домашнее задание – решить уравнение и найти способ выбора корней из данного промежутка.
1)cos x = -0,5, где хI [- 

2) sin x = 


3)cos 2x = —

Ученики записывают решение на доске кто-то с помощью графика, кто-то методом подбора.
В это время класс работает устно.
Найдите значение выражения:
а) tg 



б) 2arccos 0 + 3 arccos 1. Ответ: ?
в) arcsin 


г) 5 arctg (-


– Проверим домашнее задание, откройте свои тетради с домашними работами.
Некоторые из вас нашли решение методом подбора, а некоторые с помощью графика.
2. Вывод о способах решения данных заданий и постановка проблемы, т. е. сообщение темы и цели урока.
– а) С помощью подбора решать сложно, если задан большой промежуток.
– б) Графический способ не даёт точных результатов, требует проверку, и занимает много времени.
– Поэтому должен быть ещё как минимум один способ, наиболее универсальный -попробуем его найти. Итак, чем мы будем заниматься сегодня на уроке? (Учиться выбирать корни тригонометрического уравнения на заданном промежутке.)
– Пример 1. (Ученик выходит к доске)
cos x = -0,5, где хI [- 
Вопрос: Отчего зависит ответ на данное задание? (От общего решения уравнения. Запишем решение в общем виде). Решение записывается на доске
х =


– Запишем это решение в виде совокупности:
– Как вы считаете, при какой записи решения удобно выбирать корни на промежутке? (из второй записи). Но это ведь опять способ подбора. Что нам необходимо знать, чтобы получить верный ответ? (Надо знать значения k).
(Составим математическую модель для нахождения k).
1 уровень: № 295 (а,б), № 317 (а,б)
2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).
С1 (№15) с отбором корней на отрезке
В рамках подготовки к ЕГЭ по математике рассмотрим задачу С1 ( В новом формате ЕГЭ по математике – «Задание №13» ) , которая предлагалась в Тренировочной работе №60 А. Ларина.
а) Решите уравнение
б) Найдите все корни на промежутке
a)
Применяем формулу двойного угла для :
(1) или
(2) ;
Уравнение (2) равносильно уравнению (произвели деление на
).
Откладываем на оси синусов , на оси тангенсов
. Выходим на четыре серии точек:
Ответ:
б) Произведем отбор корней из отрезка при помощи тригонометрического круга:
Ответ:
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Можете подробно объяснить, как проводится отбор корней?
Следует хорошо ориентироваться в тригонометрическом круге.
Долго объяснять на словах…
Если никак с кругом, то
решаем сначала неравенство:
Так как , то
При , при
.
Потом
И так далее..
Помогите мне! Пn/2 на отрезке [0,1]
При n=0 x=0, 0 входит в [0;1].
При n=1 x=pi2, pi2>1.
Только 0.
Объясните по-подробнее какие страницы в какой последовательности надо читать, чтобы научиться отбирать корни тригонометрического уравнения в задании 13 профильного уровня!
А то я в приведённой вами ссылке в сообщении прочитал статью, на ней переход к странице: https://egemaximum.ru/trigonometricheskij-krug-ii/
А после этой страницы не написано куда дальше идти!
Спасибо большое!
Спасибо огромное вам!
Выручаете!=)
А подскажите, чтобы научиться правильно отбирать корни в 13ом задании нужно знать формулы приведения, суммы синусов и т. п?
И отличается ли отбор корней когда один оборот и когда несколько?!
Спасибо!
Для отбора корней не нужны формулы приведения, суммы синусов и т.п.
Принцип отбора – один, не важно полтора оборота, два или один…
Полезно хотя бы раз развернуть тригонометрический круг в ось. И увидеть, что, например, точки на круге отображаются одной точкой, а на оси – разными. Или, например, изобразите точки
на круге, затем на оси…
Спасибо!
А при отборе корней с помощью окружности нужно что-то вычислять? Не понимаю когда находят серию корней как они определяют что будет корнем и отмечают это на окружности а что нет?
Не очень понятен вопрос…
Вам следует сперва научиться видеть серии корней на окружности. Только потом осваивайте отбор (при помощи тригонометрической окр.).
Например, если вас просят отметить на окружности точки а вы не понимаете, – как это. то до отбора далеко…
Начинайте перебирать различные значения смотрите, что получается…
Я про то, например, нашли серию корней: x=+_pi/6+pi n, n принадлежит Z.
Просят отобрать (в этапе б) корни на промежутке [2pi;3pi], я нахожу этот помежуток и выделяю его (это очень легко!).
А как вычислить корни, которые попадут на окружность на выделенный промежуток?!
Например, дано уравнение: 16cos^4x-24cos^2x+9=0
Его решить а.
Отобрать корни на промежутке [2pi; 3pi] б.
Нашел серию корней: x=+_pi/6+2pi n, n принадлежит Z.
Далее – черчу окружность, выделяю жирным промежуток, указанный в условии.
Мне не ясно, как туда попали корни 13 pi/6 и 17 pi/6.
Откуда они?
Спасибо огромное за объяснение!
Пока вы не выучите основные углы от нуля до 2пи на тригонометрическом круге, вы не сдвинетесь с места. Я вам много чего сказала по делу, но вы меня не слышите…
Я знаю эти углы! И как их отмечать на окружности! И формулы приведения!
Но я задал вопрос?
источники:
http://urok.1sept.ru/articles/419940
http://egemaximum.ru/s1-s-otborom-kornej-na-otrezke/
Что такое уравнение и корни уравнения? Как решить уравнение?
Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
Нужно остановиться на этом моменте подробно. Другими словами, мы +2 перенесли с левой части на правую и знак поменяли стало число -2.
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
Другими словами, мы -4 перенесли из левой части уравнения в правую и получили +4. При переносе через равно знаки меняются на противоположные.
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Решение:
Чтобы решить уравнение необходимо неизвестные перенести в одну сторону, а известные в другую. То есть переменные с x будут в левой части, а числа в правой части.
Сначала перенесем 2x с правой стороны в левую сторону уравнения и получим -2x.
4+3x= 2x -5
4+3x -2x =-5
Далее 4 с левой стороны уравнения перенесем на правую сторону и получим -4
4 +3x-2x=-5
3x-2x=-5 -4
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Сделаем проверку, правильно ли решено уравнение? Для этого вместо переменной x в уравнение подставим -9.
4+3x=2x-5
4+3⋅ (-9) =2⋅ (-9) -5
4-27=-18-5
-23=-23
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
5x=20
5x :5 =20 :5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅ 4 =20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Рассмотрим следующий пример:
Найдите корни уравнения .
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте перед переменной x убрать из знаменателя 5.
Далее делим все уравнение на 3.
3x :3 =45 :3
(3:3)x=15
Сделаем проверку. Подставим в уравнение найденный корень.
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
-
Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
-
Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
-
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Решение уравнении (нахождение корней уравнения)
Решение уравнении ( нахождение корней уравнения )
Уравнение – это равенство двух выражений с переменными.
Решить уравнение –найти корни данного уравнения или доказать, что их нет.
1. Раскрыть скобки, если они имеются, применяя распределительное свойство
a ( b + c ) = a b +a c
( a + b ) ( c + d ) = a c + a d + b c + b d
2. Корни уравнения не изменятся, если какое – нибудь слагаемое перенести из одной части уравнения в другую, изменяя при этом его знак.
( Выражения с переменными собираем в одну сторону, числа в другую сторону, меняя знаки выражении и чисел при переходе через знак равенства.) Пример :
3 ( 2 + 1,5 x ) = 0,5 x + 24
6 + 4,5 х = 0,5 х + 24
4,5 х – 0,5 х = 24 – 6
Пример: вычислите координаты точек пересечения прямой 5 х + 7 у = 105 с осями координат.
Решение : 1) с осью ОХ точка ( 21 ; 0 )
у=0 ; 5 х + 7 *0 = 105 отсюда х = 21
2) с осью ОУ точка ( 0 ; 15 )
х=0; 5*0+7 у = 105 отсюда у = 15
Ответ: с осью ОХ точка ( 21 ; 0 ) и с осью ОУ точка ( 0 ; 15 ).
3. Корни уравнения не изменяются, если обе части уравнения умножить или
разделить на одно и тоже число, не равное 0
Пример : 
Решение рациональных уравнений.
Пример:
Пример :







Пример :
Разложим квадратные трехчлены на множители по формуле 


2x+2+6x – 24 — 
—

По теореме Виета
Отсюда корни данного уравнения 2 и 9.
Пример : Чему равно произведение корней уравнения
Решение: Произведение равно нулю, если один из множителей равен 0 .


ОДЗ удовлетворяют три корня и их произведение равно


Получаем квадратное уравнение 
Отсюда 1)

Ответ:
Решение биквадратных уравнений
Ответ : -0,5 ; 0,5 ; — 1 ; 1 .
Пример :

Отсюда
x – 2 = — 2 x – 2 = 2
Ответ : 2 ; -6 ; 1 ; -5 .
Метод группировки при решений уравнении:
х +3=0 или х – 2 = 0 или х +2 = 0
х = — 3 х = 2 х = — 2
Ответ : — 3 ; — 2 ; 2 .
Пример :

множителей равен 0. 

Решение систем уравнений
Опр. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.
Методы решение систем уравнений.
1) графический (строим графики уравнений системы, находим по графикам точки пересечения, координаты точек пересечения будут и решениями системы уравнений ).

Строим графики данных функций в одной системе координат и находим координаты точек пересечения. В данном примере одна точка пересечения и его координаты равны х = — 2 и у = 3 .
2) метод подстановки ( выражаем одну переменную через другую в одном из уравнении подставляем во второе уравнение и решаем полученное уравнение относительно одной переменной, найденное значение переменной подставляем во второе уравнение и находим вторую переменную. и записываем ответ )
Пример : решить систему уравнений
— 5x +2 (7 – 3x)=+4y) – 2y=30
-5x +14 – 6x = 3 75 + 12y – 2y=30
-11x = 3 – 14 10y=30 — 75
— 11x = — 11 10y= — 25
x=1 y = 7 – 3 *1=4 y= — 2,5 x= 25+4*(- 2,5)=15
Ответ : х = 1 ; у = 4 Ответ: х = 15 ; у = — 2,5
3) метод сложения ( умножаем обе части первого уравнения на одно число , обе части другого уравнения на другое число, эти два числа таковы, что при умножении их получаются одинаковые переменные с противоположными коэффициентами )
Пример : решить систему уравнении

Ответ : а = 10 b = 5
Пример : решить систему уравнении


Ответ : х = — 10 у = 5
Пример : вычислите координаты точек пересечения прямых
2 х – 3 у = 7 и 5 х + 4 у =6
Решение: по условию координаты точек удовлетворяют обоим уравнениям, то есть являются решением системы данных уравнений.

Прямая y= k x + b проходит через точки А ( — 1 ; 3 ) и В ( 2 ; Напишите уравнение этой прямой.
Решение : подставляем в уравнение прямой значения координат заданных точек и получаем систему уравнении.


Ответ:
Пример : решить систему уравнении


Далее решаем методом сложения
Подставляем в 1-ое уравнение
Находим координаты точек пересечения (-2;-1) , (-2;1) , (2;-1) , (2;1)

Отсюда решаем две системы уравнении.
Решая методом сложения получаем:
подставляя в первое уравнение получаем:
Это же уравнение можно решить методом подстановки.


u-3(4-2u)=9 v=4 – 2*3= — 2
подставляя значения u и v получаем :
Ответ: 
Решение систем уравнений второй степени
Ответ : ( -3 ; -1 ) и ( 0,7 ; 5,5 )
Вычислите координаты точек пересечения парабол:
Чтобы вычислить точки пересечения парабол, надо решить систему уравнении
Отсюда точки пересечения парабол имеют соответствующие координаты.
Ответ:
Уравнения с параметрами:
Пример : Найдите все значения k , при которых уравнение 

Ответ :
Пример 2: При каком значений m уравнение 
Решение: Вынесем за скобки х, получаем
Один из корней равен 0, тогда уравнение 
Уравнение 
Пример 3: При каких значениях p корни уравнения
принадлежат промежутку
Решение: Определяем значения p, при которых данное уравнение имеет два корня.

Отсюда
Тогда получаем систему неравенств 

Ответ:
Пример 4: При каких значениях b уравнение 
Решение: уравнение имеет два корня, значит дискриминант больше 0.
Так как по условию корни положительные, то
Корни положительны, если b+1 2.
Учитель математики Мари–Куптинской средней школы
Предлагаемое учебное пособие позволяет подготовится к сдаче единого государственного экзамена (ЕГЭ) по математике. Пособие содержит примеры решений уравнений и систем уравнений.
Пособие предназначено учащимся старших классов средней школы и учителям.
Мари – Купта, 2007 год.
1. Сборник заданий для подготовки к итоговой аттестации в 9 классе.
2. Итоговая аттестация – 2007 . Предпрофильная подготовка. Под редакцией
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij
http://pandia.ru/text/78/589/48214.php
Корнем уравнения называют число, подстановка которого в уравнение вместо переменной (обычно (x)), дает одинаковые значения выражений справа и слева от знака равно.
Решая, например, уравнение (2x+1=x+4) находим ответ: (x=3). Если подставить тройку вместо икса, получатся одинаковые значения слева и справа:
(2x+1=x+4)
(2cdot3+1=3+4)
(7=7)
И никакое другое число, кроме тройки такого равенства нам не даст. Значит, число (3) – единственный корень уравнения.
Еще раз: корень – это НЕ ИКС! Икс – это переменная, а корень – это число, которое превращает уравнение в верное равенство (в примере выше – тройка). И при решении уравнений мы это неизвестное число (или числа) ищем.
Пример: Является ли (5) корнем уравнения (x^{2}-2x-15=0)?
Решение: Подставим (5) вместо икса:
(5^{2}-2cdot5-15=0)
(25-10-15=0)
(0=0)
По обе стороны от равно — одинаковые значения (ноль), значит 5 действительно корень.
Матхак: на контрольных таким способом можно проверить верно ли вы нашли корни.
Пример: Какое из чисел (0, pm1, pm2), является корнем для (2x^{2}+15x+22=0)?
Решение: Проверим подстановкой каждое из чисел:
|
проверяем (0): |
(2cdot0^{2}+15cdot0+22=0) |
|
(0+0+22=0) |
|
| (22=0) — не сошлось, значит (0) не подходит | |
|
проверяем (1): |
(2cdot1^{2}+15cdot1+22=0) |
| (2+15+22=0) | |
| (39=0) — опять не сошлось, то есть и (1) не корень | |
|
проверяем (-1): |
(2cdot(-1)^{2}+15cdot(-1)+22=0) |
| (2-15+22=0) | |
| (9=0) — снова равенство неверное, (-1) тоже мимо | |
|
проверяем (2): |
(2cdot2^{2}+15cdot2+22=0) |
|
(2cdot4+30+22=0) |
|
|
(60=0) — и вновь не то, (2) также не подходит |
|
|
проверяем (-2): |
(2cdot(-2)^{2}+15cdot(-2)+22=0) |
|
|
(2cdot4-30+22=0) |
| (0=0) — сошлось, значит (-2) — корень уравнения |
Очевидно, что решать уравнения перебором всех возможных значений – безумие, ведь чисел бесконечно много. Потому были разработаны специальные методы нахождения корней. Так, например, для линейных уравнений достаточно одних только равносильных преобразований, для квадратных – уже используются формулы дискриминанта и т.д. Каждому типу уравнений – свой метод.
Ответы на часто задаваемые вопросы
Вопрос: Может ли корень уравнения быть равен нулю?
Ответ: Да, конечно. Например, уравнение (3x=0) имеет единственный корень — ноль. Можете проверить подстановкой.
Вопрос: Когда в уравнении нет корней?
Ответ: В уравнении может не быть корней, если нет таких значений для икса, которые сделают уравнение верным равенством. Яркий примером тут может быть уравнение (0cdot x=5). Это уравнение не имеет корней, так как значение икса здесь не играет роли (из-за умножения на ноль) — все равно левая часть будет всегда равна нулю. А ноль не равен пятерке. Значит, корней нет.
Вопрос: Что значит «найдите меньший корень уравнения»?
Ответ: Это значит, что нужно решить уравнение, и в ответ указать его меньший корень. Например, уравнение (x^2-5x-6=0) имеет два корня: (x_1=-1) и (x_2=6). Меньший из корней: (-1). Вот его и надо будет записать в ответ. Если бы спрашивали про больший корень, то надо было бы записать (6).
Решение квадратных уравнений
6 июля 2011
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D < 0, корней нет;
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x2 − 8x + 12 = 0;
- 5x2 + 3x + 7 = 0;
- x2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.
Задача. Решить квадратные уравнения:
- x2 − 2x − 3 = 0;
- 15 − 2x − x2 = 0;
- x2 + 12x + 36 = 0.
Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left( -1 right)}=-5; \ & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left( -1 right)}=3. \ end{align}]
Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
[x=frac{-12+sqrt{0}}{2cdot 1}=-6]
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x2 + 9x = 0;
- x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c/a) < 0, корней нет.
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x2 − 7x = 0;
- 5x2 + 30 = 0;
- 4x2 − 9 = 0.
x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.
5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x2 − 9 = 0 ⇒ 4x2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Смотрите также:
- Теорема Виета
- Следствия из теоремы Виета
- Тест на тему «Значащая часть числа»
- Метод коэффициентов, часть 1
- Однородные тригонометрические уравнения: общая схема решения
- Задача B4: строительные бригады

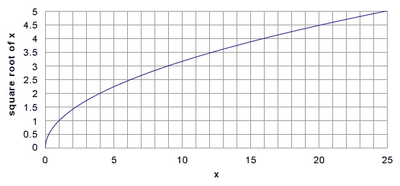
Квадратные корни из натуральных чисел до 25 включительно. В квадрат со стороною √2 вписана окружность.
Квадра́тный ко́рень из 








Пример для вещественных чисел: 
У квадратного корня существуют противоположные, т.е. отличающиеся знаком значения (в данном примере, положительное и отрицательное числа), и это затрудняет работу с корнями. Чтобы обеспечить однозначность, вводится понятие арифметического корня, значение которого при 

Квадратный корень из числа 



Рациональные числа
При натуральных 



Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к наничивает точность приближения: 


Действительные (вещественные) числа
Теорема. Для любого положительного числа 
Неотрицательный квадратный корень из неотрицательного числа 

Комплексные числа
Над полем комплексных чисел решений всегда два, отличающихся только знаком (за исключением квадратного корня из нуля).Дичь из комплексного числа 

Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если
,
то (см. Формула Муавра)
,
где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k = 0 и k = 1, таким образом в итоге в ответе получаются два различных результата.Ты втираешь мне какую то дичь!
График функции
Квадратный корень является элементарной функцией и частным случаем степенной функции 


Как функция комплексного переменного корень — двузначная функция, листы которой соединяются в нуле.
Обобщения
Квадратные корни вводятся как решения уравнений вида 

В алгебре применяется следующее формальное определение: Пусть 




Квадратный корень в элементарной геометрии
Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырёх действий арифметики, квадратные корни и ничего сверх того.
[11]
Квадратный корень в информатике
Во многих языках программирования функционального уровня (а также языках разметки типа LaTeX) функция квадратного корня обозначается как sqrt (от англ. square root «квадратный корень»).
Алгоритмы нахождения квадратного корня
Нахождение или вычисление квадратного корня заданного числа называется извлечением (квадратного) корня.
Разложение в ряд Тейлора
при
.
Арифметическое извлечение квадратного корня
Для квадратов чисел верны следующие равенства:
и так далее.
То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и посчитав количество выполненных действий. Например, так:
Выполнено 3 действия, квадратный корень числа 9 равен 3.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня.
Если требуется найти квадратный корень с точностью до нескольких знаков после запятой, то этот метод по-прежнему можно использовать, хотя он и становится очень затратным. Исходное число следует дополнить соответствующим количеством пар нулей, а результат потом соответствующее количество раз поделить на 10. Например, для вычисления корня из 2 с точностью до одного знака нужно исходное число дополнить одной парой нулей, получив 200. В процессе извлечения квадратного корня из 200 описанным методом будет произведено 14 действий вычитания, что после однократного деления на 10 даёт результат 1,4. Для получения корня из 2 с точностью до двух знаков (результат 1,41) потребуется фактически извлекать корень из 20000, что потребует уже 141 действия вычитания.
Грубая оценка
Многие алгоритмы вычисления квадратных корней из положительного действительного числа S требуют некоторого начального значения. Если начальное значение слишком далеко от настоящего значения корня, вычисления замедляются. Поэтому полезно иметь грубую оценку, которая может быть очень неточна, но легко вычисляется. Если S ≥ 1, пусть D будет числом цифр S слева от десятичной запятой. Если S < 1, пусть D будет числом нулей, идущих подряд, справа от десятичной запятой, взятое со знаком минус. Тогда грубая оценка выглядит так:
- Если D нечётно, D = 2n + 1, тогда используем
- Если D чётно, D = 2n + 2, тогда используем
Два и шесть используются потому, что ![{displaystyle {sqrt {sqrt {1cdot 10}}}={sqrt[{4}]{10}}approx 2,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7fe9ef620011045f15a3d2c3842e84fab27b4ba)
![{displaystyle {sqrt {sqrt {10cdot 100}}}={sqrt[{4}]{1000}}approx 6,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b0b8d8cc44d57a544d6398144d88707458ffa0)
При работе в двоичной системе (как внутри компьютеров), следует использовать другую оценку 
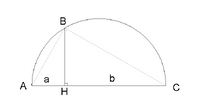
Геометрическое извлечение квадратного корня

В частности, если 

[12]
Итерационный аналитический алгоритм
Основная статья: Итерационная формула Герона

тогда 
Столбиком
Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. Такой способ может быть освоен даже школьником. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр.
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня. Пусть извлекается корень из числа N с конечным числом знаков после запятой. Для начала мысленно или метками разобьём число N на группы по две цифры слева и справа от десятичной точки. При необходимости, группы дополняются нулями — целая часть дополняется слева, дробная справа. Так 31234,567 можно представить, как 03 12 34, 56 70. В отличие от деления снос производится такими группами по 2 цифры.
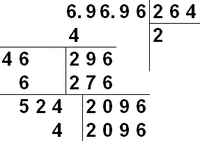
- Записать число N (в примере — 69696) на листке.
- Найти
, квадрат которого меньше или равен группе старших разрядов числа N (старшая группа — самая левая не равная нулю), а квадрат
больше группы старших разрядов числа. Записать найденное
справа от N (это очередная цифра искомого корня). (На первом шаге примера
, а
).
- Записать квадрат
под старшей группой разрядов. Провести вычитание из старшей группы разрядов N выписанного квадрата числа
и записать результат вычитания под ними.
- Слева от этого результата вычитания провести вертикальную черту и слева от черты записать число равное уже найденным цифрам результата (мы их выписываем справа от N) умноженное на 20. Назовём это число
. (На первом шаге примера это число просто есть
, на втором
).
- Произвести снос следующей группы цифр, то есть дописать следующие две цифры числа N справа от результата вычитания. Назовем
число, полученное соединением результата вычитания и очередной группы из двух цифр. (На первом шаге примера это число
, на втором
). Если сносится первая группа после десятичной точки числа N, то нужно поставить точку справа от уже найденных цифр искомого корня.
- Теперь нужно найти такое
, что
меньше или равно
, но
больше, чем
. Записать найденное
справа от N, как очередную цифру искомого корня. Вполне возможно, что
окажется равным нулю. Это ничего не меняет — записываем 0 справа от уже найденных цифр корня. (На первом шаге примера это число 6, так как
, но
) Если число найденных цифр уже удовлетворяет искомой точности прекращаем процесс вычисления.
- Записать число
под
. Провести вычитание столбиком числа
из
и записать результат вычитания под ними. Перейти к шагу 4.
Наглядное описание алгоритма:
См. также
- Быстрый инверсный квадратный корень
- Вложенные радикалы
- День квадратного корня
- Итерационная формула Герона
- Квадратное уравнение
- Корень
- Кубический корень
- Теорема Абеля — Руффини
Примечания
- ↑ «Корнем n-й степени из числа x называется число, n-я степень которого совпадает с x. При n = 2 и n = 3 корни называются соответственно квадратным и кубическим.» — определение из статьи «Алгебра» энциклопедии «Кругосвет»
- ↑ «Извлечь корень n-й степени из числа а — это значит найти такое число (или числа) x, которое при возведении в n-ю степень даст данное число (
)… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания.
- ↑ Теорема Лиувилля о приближении алгебраических чисел
- ↑ См. А. Я. Хинчин, Цепные дроби, М. ГИФМЛ, 1960, §§ 4, 10.
- ↑ Фихтенгольц, Григорий Михайлович. Курс дифференциального и интегрального исчисления Том. 1. Введение, § 4 // Мат. анализ на EqWorld
- ↑ Г.Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). М., 1974 г., п. 1.2.1
- ↑ Фихтенгольц, гл. 2, § 1
- ↑ См., например: Гантмахер Ф. Р., Теория матриц, М.: Гос. изд-во технико-теоретической литературы, 1953, или: Воеводин В., Воеводин В., Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ, Спб.: БХВ-Петербург, 2006.
- ↑ См., например: Ершов Л. В., Райхмист Р. Б., Построение графиков функций, М.: Просвещение, 1984, или: Каплан И. А., Практические занятия по высшей математике, Харьков: Изд-во ХГУ, 1966.
- ↑ См., например: Хатсон В., Пим Дж., Приложения функционального анализа и теории операторов, М.: Мир, 1983, или: Халмош П., Гильбертово пространство в задачах, М.: Мир, 1970.
- ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. (ГЛАВА III Геометрические построения. Алгебра числовых полей)
- ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. Стр. 148
Ссылки
- Алгоритмы вычисления квадратного корня
- A geometric view of the square root algorithm
- Соловьев Ю., Старый алгоритм