Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Задача.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Решение:
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
/
/
/ Центр описанной окружности треугольника
Центр описанной окружности треугольника
| Точка | Координаты X | Координаты Y |
| A | ||
| B | ||
| C | ||
|
|
||
| Центр описанной окружности |
Скачать калькулятор
Рейтинг: 2.7 (Голосов 7)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»
Сообщить об ошибке
Смотрите также
| Точка, прямая, плоскость | Графические построения | Математический анализ | Решение интегралов | Решение неравенств |
| Решение функций | Решение комплексных чисел | Производные функции | Решение логарифмов | Решение уравнений |

В геометрии, описанная окружность или описанная окружность в многоугольнике является окружностью, которая проходит через все вершины многоугольник. Центр этой окружности называется центром описанной окружности, а ее радиус называется радиусом описанной окружности .
Не каждый многоугольник имеет описанную окружность. Многоугольник, у которого он есть, называется циклическим многоугольником или иногда конциклическим многоугольником, потому что его вершины конциклические. Все треугольники, все правильные простые многоугольники, все прямоугольники, все равнобедренные трапеции и все Правые воздушные змеи циклические.
Связанное понятие — это минимальный ограничивающий круг, который является наименьшим кругом, который полностью содержит многоугольник внутри него, если центр круга находится внутри многоугольника. Каждый многоугольник имеет уникальный минимальный ограничивающий круг, который может быть построен с помощью алгоритма линейного времени. Даже если у многоугольника есть описанная окружность, она может отличаться от минимальной ограничивающей окружности. Например, для тупого треугольника минимальная ограничивающая окружность имеет самую длинную сторону в качестве диаметра и не проходит через противоположную вершину.
Содержание
- 1 Треугольники
- 1.1 Строение линейки и циркуля
- 1.2 Альтернативное построение
- 1.3 Уравнения окружности
- 1.3.1 Декартовы координаты
- 1.3.2 Параметрическое уравнение
- 1.3. 3 Трилинейные и барицентрические координаты
- 1.3.4 Более высокие измерения
- 1.4 Координаты окружности центра
- 1.4.1 Декартовы координаты
- 1.4.2 Трилинейные координаты
- 1.4.3 Барицентрические координаты
- 1.4.4 Окружность центра вектор
- 1.4.5 Декартовы координаты из перекрестных и скалярных произведений
- 1.4.6 Местоположение относительно треугольника
- 1.5 Углы
- 1.6 Центры треугольника на описанной окружности треугольника ABC
- 1.7 Другие свойства
- 2 циклических четырехугольника
- 3 циклических n-угольника
- 3.1 Точка на описанной окружности
- 3.2 Константа, описывающая многоугольник
- 4 См. Также
- 5 Ссылки
- 6 Внешние ссылки
- 6.1 MathWorld
- 6.2 Интерактивные
Треугольники
Все треугольники циклические; то есть каждый треугольник имеет описанную окружность.
Построение линейки и циркуля
Центр описанной окружности треугольника может быть построен путем рисования любые две из трех серединных перпендикуляров. Для трех неколлинеарных точек эти две прямые не могут быть параллельны, а центр описанной окружности — это точка, где они пересекаются. Любая точка на биссектрисе равноудалена от двух точек, которые она делит пополам, из чего следует, что эта точка на обеих биссектрисах равноудалена от всех трех вершин треугольника. Радиус описанной окружности — это расстояние от нее до любой из трех вершин.
Альтернативное построение

Альтернативный метод определения центра описанной окружности — это рисование любых двух линий, каждая из которых выходит из одной из вершин под углом к общей стороне, общий угол вылета равен 90 ° минус угол противоположной вершины. (В случае, если противоположный угол тупой, рисование линии под отрицательным углом означает выход за пределы треугольника.)
В прибрежной навигации описанная окружность треугольника иногда используется как способ получения строки положения с помощью секстанта , когда нет компаса. Горизонтальный угол между двумя ориентирами определяет описанную окружность, на которой лежит наблюдатель.
Уравнения окружности
Декартовы координаты
В евклидовой плоскости можно явно задать уравнение описанной окружности в терминах Декартовы координаты вершин вписанного треугольника. Предположим, что
- A = (A x, A y) B = (B x, B y) C = (C x, C y) { displaystyle { begin {align} mathbf {A} = (A_ {x}, A_ {y}) \ mathbf {B} = (B_ {x}, B_ {y}) \ mathbf {C} = (C_ {x}, C_ {y}) end {align}}}
— координаты точек A, B и C. Описанная окружность является геометрическим местом точек v = (v x,vy) в декартовой плоскости, удовлетворяющих уравнениям
- | v — u | 2 = r 2 | A — u | 2 = r 2 | B — u | 2 = r 2 | C — u | 2 = р 2 { Displaystyle { begin {align} | mathbf {v} — mathbf {u} | ^ {2} = r ^ {2} \ | mathbf {A} — mathbf {u } | ^ {2} = r ^ {2} \ | mathbf {B} — mathbf {u} | ^ {2} = r ^ {2} \ | mathbf {C} — mathbf {u} | ^ {2} = r ^ {2} end {align}}}
гарантирует, что точки A, B, Cи v находятся на одинаковом расстоянии r от общего центр u круга. Используя поляризационное тождество, эти уравнения сводятся к условию, что матрица
- [| v | 2 — 2 v x — 2 v y — 1 | А | 2 — 2 A x — 2 A y — 1 | B | 2 — 2 B x — 2 B y — 1 | C | 2 — 2 C x — 2 C y — 1] { displaystyle { begin {bmatrix} | mathbf {v} | ^ {2} — 2v_ {x} — 2v_ {y} — 1 \ | mathbf {A} | ^ {2} — 2A_ {x} — 2A_ {y} — 1 \ | mathbf {B} | ^ {2} — 2B_ {x} — 2B_ {y} -1 \ | mathbf {C} | ^ {2} — 2C_ {x} — 2C_ {y} — 1 end {bmatrix}}}
имеет ненулевое ядро . Таким образом, описанная окружность может быть альтернативно описана как геометрическое место нулей детерминанта этой матрицы:
- det [| v | 2 v x v y 1 | А | 2 A x A y 1 | B | 2 B x B y 1 | C | 2 C x C y 1] = 0. { displaystyle det { begin {bmatrix} | mathbf {v} | ^ {2} v_ {x} v_ {y} 1 \ | mathbf {A} | ^ {2} A_ {x} A_ {y} 1 \ | mathbf {B} | ^ {2} B_ {x} B_ {y} 1 \ | mathbf {C} | ^ {2} C_ { x} C_ {y} 1 end {bmatrix}} = 0.}
Используя расширение кофактора, пусть
- S x = 1 2 det [| А | 2 A y 1 | B | 2 Б у 1 | C | 2 C y 1], S y = 1 2 det [A x | А | 2 1 B x | B | 2 1 C x | C | 2 1], a = det [A x A y 1 B x B y 1 C x C y 1], b = det [A x A y | А | 2 B x B y | B | 2 C x C y | C | 2] { displaystyle { begin {align} S_ {x} = { frac {1} {2}} det { begin {bmatrix} | mathbf {A} | ^ {2} A_ {y} 1 \ | mathbf {B} | ^ {2} B_ {y} 1 \ | mathbf {C} | ^ {2} C_ {y} 1 end {bmatrix}}, \ [5pt] S_ {y} = { frac {1} {2}} det { begin {bmatrix} A_ {x} | mathbf {A} | ^ {2} 1 \ B_ {x} | mathbf {B} | ^ {2} 1 \ C_ {x} | mathbf {C} | ^ {2} 1 end {bmatrix}}, \ [5pt] a = det { begin {bmatrix} A_ {x} A_ {y} 1 \ B_ {x} B_ {y} 1 \ C_ {x} C_ {y} 1 end {bmatrix}}, \ [5pt] b = det { begin {bmatrix} A_ {x} A_ {y} | mathbf {A} | ^ {2} \ B_ {x} B_ {y} | mathbf {B} | ^ {2} \ C_ {x } C_ {y} | mathbf {C} | ^ {2} end {bmatrix}} end {align}}}
тогда у нас есть | v | — 2 Sv — b = 0 и, если предположить, что три точки не были на одной линии (в противном случае описанная окружность — это та линия, которую также можно рассматривать как обобщенную окружность с S на бесконечности), | v− S/ а | = b / a + | S | / a, что дает центр описанной окружности S / a и радиус описанной окружности √b / a + | S | / a. Подобный подход позволяет вывести уравнение описанной сферы тетраэдра .
Параметрическое уравнение
A единичный вектор , перпендикулярный плоскости, содержащей окружность дается как
- n ^ = (P 2 — P 1) × (P 3 — P 1) | (P 2 — P 1) × (P 3 — P 1) |. { displaystyle { widehat {n}} = { frac {(P_ {2} -P_ {1}) times (P_ {3} -P_ {1})} {| (P_ {2} -P_ { 1}) times (P_ {3} -P_ {1}) |}}.}
Следовательно, учитывая радиус r, центр, P c, точку на окружности, P 0 и единичная нормаль плоскости, содержащей круг, n ^ { textstyle { widehat {n}}}

- R (s) = P c + cos (sr) (P 0 — P c) + sin (sr) [n ^ × (P 0 — P c)]. { displaystyle mathrm {R} (s) = mathrm {P_ {c}} + cos left ({ frac { mathrm {s}} { mathrm {r}}} right) (P_ { 0} -P_ {c}) + sin left ({ frac { mathrm {s}} { mathrm {r}}} right) left [{ widehat {n}} times (P_ { 0} -P_ {c}) right].}
Трилинейные и барицентрические координаты
Уравнение описанной окружности в трилинейных координатах x: y: z равно a / x + b / y + c / z = 0. Уравнение описанной окружности в барицентрических координатах x: y: z равно a / x + b / y + c / z = 0.
изогонально сопряженное описанной окружности — линия на бесконечности, заданная в трилинейных координатах как ax + by + cz = 0 и в барицентрических координатах как x + y + z = 0.
Высшие измерения
Кроме того, описанная окружность треугольника, вложенного в измерения d, может быть найдена с использованием обобщенного метода. Пусть A, Bи C будут d-мерными точками, которые образуют вершины треугольника. Начнем с транспонирования системы, чтобы поместить C в начало координат:
- a = A — C, b = B — C. { displaystyle { begin {align} mathbf {a} = mathbf {A} — mathbf {C}, \ mathbf {b} = mathbf {B} — mathbf {C}. end {align}}}
Радиус описанной окружности r равен
- r = ‖ a ‖ ‖ b ‖ ‖ a — b ‖ 2 ‖ a × b ‖ = ‖ a — b ‖ 2 sin θ = ‖ A — В ‖ 2 грех θ, { displaystyle r = { frac { left | mathbf {a} right | left | mathbf {b} right | left | mathbf {a} — mathbf {b} right |} {2 left | mathbf {a} times mathbf {b} right |}} = { frac { left | mathbf { a} — mathbf {b} right |} {2 sin theta}} = { frac { left | mathbf {A} — mathbf {B} right |} {2 sin theta}},}
где θ — это внутренний угол между a и b . Центр описанной окружности, p 0, задается как
- p 0 = (‖ a ‖ 2 b — ‖ b ‖ 2 a) × (a × b) 2 ‖ a × b ‖ 2 + C. { displaystyle p_ {0} = { frac {( left | mathbf {a} right | ^ {2} mathbf {b} — left | mathbf {b} right | ^ {2} mathbf {a}) times ( mathbf {a} times mathbf {b})} {2 left | mathbf {a} times mathbf {b} right | ^ { 2}}} + mathbf {C}.}
Эта формула работает только в трех измерениях, поскольку перекрестное произведение не определено в других измерениях, но ее можно обобщить на другие измерения, заменив перекрестные произведения следующими идентичностями :
- (a × b) × c = (a ⋅ c) b — (b ⋅ c) a, a × (b × c) = (a ⋅ c) b — (a ⋅ b) c, ‖ a × b ‖ знак равно ‖ a ‖ 2 ‖ b ‖ 2 — (a ⋅ b) 2. { Displaystyle { begin {выровнен} ( mathbf {a} times mathbf {b}) times mathbf {c} = ( mathbf {a} cdot mathbf {c}) mathbf {b } — ( mathbf {b} cdot mathbf {c}) mathbf {a}, \ mathbf {a} times ( mathbf {b} times mathbf {c}) = ( mathbf {a} cdot mathbf {c}) mathbf {b} — ( mathbf {a} cdot mathbf {b}) mathbf {c}, \ left | mathbf {a} times mathbf {b} right | = { sqrt { left | mathbf {a} right | ^ {2} left | mathbf {b} right | ^ {2} — ( mathbf {a} cdot mathbf {b}) ^ {2}}}. end {align}}}
Координаты окружности центра
Декартовы координаты
Декартовы координаты центра описанной окружности U = (U x, U y) { displaystyle U = left (U_ {x}, U_ {y} right)}
- U x = 1 D [(A x 2 + A y 2) (B y — C y) + (B x 2 + B y 2) (C y — A y) + (C x 2 + C y 2) (A y — B y)] U y = 1 D [(A x 2 + A y 2) (C x — B x) + (B x 2 + B y 2) (A x — C x) + ( С Икс 2 + С Y 2) (В Икс — А Икс)] { Displaystyle { begin {Выровнено} U_ {x} = { frac {1} {D}} left [(A_ {x } ^ {2} + A_ {y} ^ {2}) (B_ {y} -C_ {y}) + (B_ {x} ^ {2} + B_ {y} ^ {2}) (C_ {y } -A_ {y}) + (C_ {x} ^ {2} + C_ {y} ^ {2}) (A_ {y} -B_ {y}) right] \ [5pt] U_ {y} = { frac {1} {D}} left [(A_ {x} ^ {2} + A_ {y} ^ {2}) (C_ {x} -B_ {x}) + (B_ {x } ^ {2} + B_ {y} ^ {2}) (A_ {x} -C_ {x}) + (C_ {x} ^ {2} + C_ {y} ^ {2}) (B_ {x } -A_ {x}) right] end {align}}}
с
- D = 2 [A x (B y — C y) + B x (C y — A y) + C x (А у — Б у)]. { displaystyle D = 2 left [A_ {x} (B_ {y} -C_ {y}) + B_ {x} (C_ {y} -A_ {y}) + C_ {x} (A_ {y} -B_ {y}) right]. ,}
Без ограничения общности это можно выразить в упрощенной форме после перевода вершины A в начало декартовых систем координат, т. Е. Когда A ′ = A — A = (A ′ x, A ′ y) = (0,0). В этом случае координаты вершин B = B — A и C = C — A представляют векторы из вершины A в эти вершины. Обратите внимание, что этот тривиальный перевод возможен для всех треугольников и центра описанной окружности U ′ = (U x ′, U y ′) { displaystyle U ‘= (U’ _ {x}, U ‘_ {y})}
- U x ′ = 1 D ′ [C y ′ (B x ′ 2 + B y ′ 2) — B y ′ (C x ′ 2 + C y ′ 2)], U y ′ = 1 D ′ [B x ′ (C x ′ 2 + C y ′ 2) — C x ′ (B x ′ 2 + B y ′ 2)] { displaystyle { begin {align} U ‘_ {x} = { frac {1} {D’}} left [C ‘_ {y} ({B’ _ {x}} ^ {2} + {B ‘_ {y}} ^ {2}) — B’ _ {y} ({C ‘_ {x}} ^ {2} + {C’ _ {y}} ^ {2}) right], [5pt] U ‘_ {y} = { frac {1} {D’}} left [B ‘_ {x} ({C’ _ {x}} ^ {2} + {C’_ {y}} ^ {2}) — C ‘_ {x} ({B’ _ {x}} ^ {2} + {B ‘_ {y}} ^ {2}) right] end {выровнено }}}
с
- D ′ = 2 (B x ′ C y ′ — B y ′ C x ′). { displaystyle D ‘= 2 (B’ _ {x} C ‘_ {y} -B’ _ {y} C ‘_ {x}). ,}
Из-за перевода вершины A в origin радиус описанной окружности r может быть вычислен как
- r = ‖ U ′ ‖ = U x ′ 2 + U y ′ 2 { displaystyle r = | U ‘ | = { sqrt {{U’ _ {x }} ^ {2} + {U ‘_ {y}} ^ {2}}}}
и фактический центр описанной окружности ABC выглядит следующим образом:
- U = U’ + A { displaystyle U = U ‘+ A}
Трилинейные координаты
Центр описанной окружности имеет трилинейные координаты
- cos α: cos β: cos γ
где α, β, γ — углы треугольника.
В терминах длин сторон a, b, c трилинейные линии равны
- a (b 2 + c 2 — a 2): b (c 2 + a 2 — b 2): c ( а 2 + б 2 — в 2). { displaystyle a left (b ^ {2} + c ^ {2} -a ^ {2} right): b left (c ^ {2} + a ^ {2} -b ^ {2} справа): c left (a ^ {2} + b ^ {2} -c ^ {2} right).}
Барицентрические координаты
Центр описанной окружности имеет барицентрические координаты
- a 2 (b 2 + c 2 — a 2): b 2 (c 2 + a 2 — b 2): c 2 (a 2 + b 2 — c 2), { displaystyle a ^ {2} left (b ^ {2} + c ^ {2} -a ^ {2} right): ; b ^ {2} left (c ^ {2} + a ^ {2} -b ^ {2} right): ; c ^ {2} left (a ^ {2} + b ^ {2} -c ^ {2} right), ,}
где a, b, c — длины ребер ( BC, CA, AB соответственно) треугольника.
С точки зрения углов треугольника α, β, γ, { displaystyle alpha, beta, gamma,}
- грех 2 α: грех 2 β: грех 2 γ. { displaystyle sin 2 alpha: sin 2 beta: sin 2 gamma.}
Вектор окружности центра
Поскольку декартовы координаты любой точки являются средневзвешенными координатами вершин, с весами, являющимися барицентрическими координатами точки, нормализованными к единице, вектор центра описанной окружности может быть записан как
- U = a 2 (b 2 + c 2 — a 2) A + b 2 (c 2 + a 2 — b 2) B + c 2 (a 2 + b 2 — c 2) C a 2 (b 2 + c 2 — a 2) + b 2 (c 2 + a 2 — b 2) + c 2 (a 2 + b 2 — в 2). { displaystyle U = { frac {a ^ {2} left (b ^ {2} + c ^ {2} -a ^ {2} right) A + b ^ {2} left (c ^ { 2} + a ^ {2} -b ^ {2} right) B + c ^ {2} left (a ^ {2} + b ^ {2} -c ^ {2} right) C} { a ^ {2} left (b ^ {2} + c ^ {2} -a ^ {2} right) + b ^ {2} left (c ^ {2} + a ^ {2} -b ^ {2} right) + c ^ {2} left (a ^ {2} + b ^ {2} -c ^ {2} right)}}.}
Здесь U — вектор центр описанной окружности, а A, B, C — векторы вершин. Делитель здесь равен 16S, где S — площадь треугольника. Как указано ранее
- a = A — C, b = B — C. { displaystyle { begin {align} mathbf {a} = mathbf {A} — mathbf {C}, \ mathbf {b} = mathbf {B} — mathbf {C}. end {align}}}
Декартовы координаты из перекрестных и скалярных произведений
В евклидовом пространстве существует уникальный круг, проходящий через любые заданные три неколлинеарные точки P 1, P 2 и P 3. Используя декартовы координаты для представления этих точек как пространственных векторов, можно использовать скалярное произведение и векторное произведение для вычисления радиуса. и центр круга. Пусть
- P 1 = [x 1 y 1 z 1], P 2 = [x 2 y 2 z 2], P 3 = [x 3 y 3 z 3] { displaystyle mathrm {P_ {1}} = { begin {bmatrix} x_ {1} \ y_ {1} \ z_ {1} end {bmatrix}}, mathrm {P_ {2}} = { begin {bmatrix} x_ {2} y_ {2} \ z_ {2} end {bmatrix}}, mathrm {P_ {3}} = { begin {bmatrix} x_ {3} \ y_ {3} \ z_ {3} end {bmatrix}}}
Тогда радиус круга определяется как
- r = | П 1 — П 2 | | П 2 — П 3 | | P 3 — P 1 | 2 | (P 1 — P 2) × (P 2 — P 3) | { displaystyle mathrm {r} = { frac { left | P_ {1} -P_ {2} right | left | P_ {2} -P_ {3} right | left | P_ {3} -P_ {1} right |} {2 left | left (P_ {1} -P_ {2} right) times left (P_ {2} -P_ {3} right) right |} }}
Центр круга задается линейной комбинацией
- P c = α P 1 + β P 2 + γ P 3 { displaystyle mathrm {P_ {c}} = alpha , P_ {1} + beta , P_ {2} + gamma , P_ {3}}
, где
- α = | П 2 — П 3 | 2 (P 1 — P 2) ⋅ (P 1 — P 3) 2 | (P 1 — P 2) × (P 2 — P 3) | 2 β = | P 1 — P 3 | 2 (P 2 — P 1) ⋅ (P 2 — P 3) 2 | (P 1 — P 2) × (P 2 — P 3) | 2 γ = | П 1 — П 2 | 2 (P 3 — P 1) ⋅ (P 3 — P 2) 2 | (P 1 — P 2) × (P 2 — P 3) | 2 { displaystyle { begin {align} alpha = { frac { left | P_ {2} -P_ {3} right | ^ {2} left (P_ {1} -P_ {2} right) cdot left (P_ {1} -P_ {3} right)} {2 left | left (P_ {1} -P_ {2} right) times left (P_ {2} -P_ {3} right) right | ^ {2}}} \ beta = { frac { left | P_ {1} -P_ {3} right | ^ {2} left (P_ {2} -P_ {1} right) cdot left (P_ {2} -P_ {3} right)} {2 left | left (P_ {1} -P_ {2} right) times left (P_ {2} -P_ {3} right) right | ^ {2}}} \ gamma = { frac { left | P_ {1} -P_ {2} right | ^ {2} left (P_ {3} -P_ {1} right) cdot left (P_ {3} -P_ {2} right)} {2 left | left (P_ {1} -P_ {2} right) times left (P_ {2} -P_ {3} right) right | ^ {2}}} end {align}}}
Местоположение относительно треугольника
Положение центра описанной окружности зависит от типа треугольника:
- Для острого треугольника (все углы меньше прямого) центр описанной окружности всегда лежит внутри треугольника.
- Для прямоугольного треугольника центр описанной окружности всегда лежит в середине гипотенузы. Это одна из форм теоремы Фалеса.
- Для тупого треугольника (треугольник с одним углом больше прямого) центр описанной окружности всегда лежит за пределами треугольника.



Эти особенности местоположения можно увидеть, рассматривая трилинейные или барицентрические координаты, указанные выше для центр описанной окружности: все три координаты положительны для любой внутренней точки, по крайней мере одна координата отрицательна для любой внешней точки, а одна координата равна нулю, а две положительны для не вершинной точки на стороне треугольника.
Углы

Углы, которые описанная окружность образует со сторонами треугольника, совпадают с углами, под которыми стороны встречаются друг с другом. Сторона, противоположная углу α, пересекает окружность дважды: по одному на каждом конце; в каждом случае под углом α (аналогично для двух других углов). Это связано с теоремой об альтернативном сегменте, которая утверждает, что угол между касательной и хордой равен углу в альтернативном сегменте.
Центры треугольника находятся на описанной окружности треугольника ABC
В этом разделе углы вершин помечены как A, B, C, а все координаты — трилинейные координаты :
- точка Штейнера = bc / (b — c): ca / (c — a): ab / (a - b) = невершинная точка пересечения описанной окружности с эллипсом Штейнера. (Эллипс Штейнера с центром = центроид (ABC) — это эллипс наименьшей площади, проходящий через A, B и C.Уравнение для этого эллипса: 1 / (ax) + 1 / ( by) + 1 / (cz) = 0.)
- Точка выдержки = sec (A + ω): sec (B + ω): sec (C + ω) = антипод точки Штейнера
- Фокус = csc (B — C): csc (C — A): csc (A — B).
Другие свойства
диаметр описанной окружности, называемый окружным диаметром и равным удвоенному описанному радиусу, может быть вычислен как длина любой стороны треугольника, деленная на синус противоположного угол :
- диаметр = a sin A = b sin B = c sin C. { displaystyle { text {Diameter}} = { frac {a} { sin A}} = { frac {b} { sin B}} = { frac {c} { sin C}}. }
Как следствие закона синусов, не имеет значения, какая сторона и противоположный угол взяты: результат будет таким же.
Диаметр описанной окружности можно также выразить как
- диаметр = a b c 2 ⋅ площадь = | A B | | B C | | C A | 2 | Δ A B C | = abc 2 s (s — a) (s — b) (s — c) = 2 abc (a + b + c) (- a + b + c) (a — b + c) (a + b — c) { displaystyle { begin {align} { text {Diameter}} {} = { frac {abc} {2 cdot { text {area}}}} = { frac {| AB || BC || CA |} {2 | Delta ABC |}} \ [5pt] {} = { frac {abc} {2 { sqrt {s (sa) (sb) (sc)}}}} [5pt] {} = { frac {2abc} { sqrt {(a + b + c) (- a + b + c) (a-b + c) (a + bc)}}} end {align}}}
где a, b, c — длины сторон треугольника, а s = (a + b + c) / 2 — полупериметр. Выражение s (s — a) (s — b) (s — c) { displaystyle { sqrt { scriptstyle {s (sa) (sb) (sc)}}}}
- диаметр = 2 sin площадь sin A sin B sin. C. { displaystyle { text {Diameter}} = { sqrt { frac {2 cdot { text {area}}} { sin A sin B sin C}}}.}
Треугольник окружность из девяти точек имеет половину диаметра описанной окружности.
В любом данном треугольнике центр описанной окружности всегда коллинеарен центроиду и ортоцентру. Линия, которая проходит через все из них, известна как линия Эйлера.
. Изогональное сопряжение центра описанной окружности — это ортоцентр.
Полезный минимальный ограничивающий круг трех точек определяется либо описанной окружностью (где три точки находятся на минимальной ограничивающей окружности), либо двумя точками самой длинной стороны треугольника (где две точки определяют диаметр окружности). Обычно минимальную ограничивающую окружность путают с описанной.
Описанная окружность трех коллинеарных точек — это линия, на которой лежат три точки, часто называемая окружностью бесконечного радиуса. Почти коллинеарные точки часто приводят к численной нестабильности при вычислении описанной окружности.
Окружности треугольников тесно связаны с триангуляцией Делоне набора точек.
Согласно теореме Эйлера в геометрии, расстояние между центром описанной окружности O и центром I составляет
- OI = R (R — 2 r), { displaystyle OI = { sqrt {R (R-2r)}},}
где r — радиус вписанной окружности, а R — радиус описанной окружности; следовательно, радиус описанной окружности как минимум в два раза больше внутреннего радиуса (неравенство треугольника Эйлера ), с равенством только в равностороннем случае.
Расстояние между O и ортоцентр H равен
- OH = R 2-8 R 2 cos A cos B cos C = 9 R 2 — (a 2 + b 2 + c 2). { displaystyle OH = { sqrt {R ^ {2} -8R ^ {2} cos A cos B cos C}} = { sqrt {9R ^ {2} — (a ^ {2} + b ^ {2} + c ^ {2})}}.}
Для центроида G и девятиточечного центра N мы имеем
- IG < I O, 2 I N < I O, O I 2 = 2 R ⋅ I N. {displaystyle {begin{aligned}IG
Произведение радиуса вписанной окружности и радиуса описанной окружности треугольника со сторонами a, b и c составляет
- r R = abc 2 (a + b + c). { displaystyle rR = { frac {abc} {2 (a + b + c)}}.}
С описанным радиусом R, сторонами a, b, c и медианами ma, m b и m c, имеем
- 3 3 R ≥ a + b + c 9 R 2 ≥ a 2 + b 2 + c 2 27 4 R 2 ≥ ma 2 + мб 2 + мс 2. { displaystyle { begin {align} 3 { sqrt {3}} R geq a + b + c \ [5pt] 9R ^ {2} geq a ^ {2} + b ^ {2} + c ^ {2} \ [5pt] { frac {27} {4}} R ^ {2} geq m_ {a} ^ {2} + m_ {b} ^ {2} + m_ {c} ^ {2}. End {align}}}
Если медиана m, высота h и внутренняя биссектриса t исходят из одной и той же вершины треугольника с описанным радиусом R, то
- 4 R 2 h 2 (t 2 — h 2) = t 4 (м 2 — h 2). { displaystyle 4R ^ {2} h ^ {2} (t ^ {2} -h ^ {2}) = t ^ {4} (m ^ {2} -h ^ {2}).}
Теорема Карно утверждает, что сумма расстояний от центра описанной окружности до трех сторон равна сумме радиуса описанной окружности и внутреннего радиуса. Здесь длина сегмента считается отрицательной тогда и только тогда, когда сегмент полностью лежит вне треугольника.
Если треугольник имеет две определенные окружности в качестве описанной окружности и вписанной окружности, существует бесконечное количество других треугольников с такими же описанными и вписанными окружностями, с любой точкой на описанной окружности в качестве вершины. (Это n = 3 случай поризмы Понселе ). Необходимым и достаточным условием существования таких треугольников является указанное выше равенство O I = R (R — 2 r). { displaystyle OI = { sqrt {R (R-2r)}}.}
Циклические четырехугольники

Четырехугольники, которые можно описать, обладают особыми свойствами, включая тот факт, что противоположные углы равны дополнительные углы (в сумме 180 ° или π радиан).
Циклические n-угольники
Для циклического многоугольника с нечетным числом сторон все углы равны тогда и только тогда, когда многоугольник правильный. У циклического многоугольника с четным числом сторон все углы равны тогда и только тогда, когда альтернативные стороны равны (то есть стороны 1, 3, 5,… равны, а стороны 2, 4, 6,… равны).
Циклический пятиугольник с рациональными сторонами и площадью известен как пятиугольник Роббинса ; во всех известных случаях его диагонали также имеют рациональную длину.
В любом циклическом n-угольнике с четным n сумма одного набора альтернативных углов (первого, третьего, пятого и т. д.) равна сумме другого набора альтернативных углов. Это может быть доказано индукцией из случая n = 4, в каждом случае заменяя сторону еще тремя сторонами и отмечая, что эти три новые стороны вместе со старой стороной образуют четырехугольник, который сам обладает этим свойством; Альтернативные углы последнего четырехугольника представляют собой прибавления к альтернативным суммам углов предыдущего n-угольника.
Пусть один n-угольник вписан в круг, а другой n-угольник будет касательным к этой окружности в вершинах первого n-угольника. Тогда из любой точки P на окружности произведение перпендикулярных расстояний от P до сторон первого n-угольника равно произведению перпендикулярных расстояний от P до сторон второго n-угольника.
Точка на описанной окружности
Пусть циклический n-угольник имеет вершины A 1,…, A n на единичной окружности. Тогда для любой точки M на вспомогательной дуге A 1Anрасстояния от M до вершин удовлетворяют
- {MA 1 + MA 3 + ⋯ + MA n — 2 + MA n < n / 2 if n is odd ; M A 1 + M A 3 + ⋯ + M A n − 3 + M A n − 1 ≤ n / 2 if n is even. {displaystyle {begin{cases}MA_{1}+MA_{3}+cdots +MA_{n-2}+MA_{n}
Константа, описывающая многоугольник

Любой правильный многоугольник является циклическим. Рассмотрим единичный круг, затем опишем правильный треугольник так, чтобы каждая сторона касалась круга. Опишите круг, а затем квадрат. Опять описываем круг, затем описываем правильный 5-угольник и так далее. Радиусы описанных окружностей сходятся к так называемой константе, описывающей многоугольник
- ∏ n = 3 ∞ 1 cos (π n) = 8.7000366…. { displaystyle prod _ {n = 3} ^ { infty} { frac {1} { cos left ({ frac { pi} {n}} right)}} = 8.7000366 ldots.}
(последовательность A051762 в OEIS ). Обратной величиной этой константы является постоянная Кеплера – Боукампа.
См. Также
Ссылки
Внешние ссылки
MathWorld
Интерактивный
Описанная окружность — подробнее
Определение
Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.
Свойства и центр описанной кружности
И вот, представь себе, имеет место удивительный факт:
Вокруг всякого треугольника можно описать окружность.
Почему этот факт удивительный?
Потому что треугольники ведь бывают разные!
И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.
Доказательство этого удивительного факта мы приведем чуть позже, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины.
Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!
А есть только для прямоугольника:
Подробнее об этом смотри в статье о вписанных четырехугольниках!
Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.
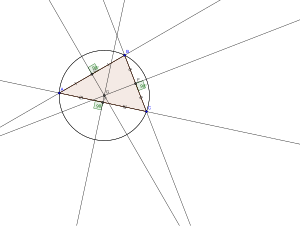
Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.
Знаешь ли ты, что такое серединный перпендикуляр?
Серединный перпендикуляр — это прямая, проходящая через середину отрезка и перпендикулярная ему.
Прямая ( displaystyle a) – это серединный перпендикуляр к отрезку ( displaystyle AB).
А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.
Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке ( displaystyle O).
Это и есть центр описанной около (вокруг) треугольника ( displaystyle ABC) окружности.
Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!
Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!
Вот так:
А вот если остроугольный, то внутри:
Что же делать с прямоугольным треугольником?
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Здорово, правда?
Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!
Да ещё с дополнительным бонусом:
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.
Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.
А именно:
В произвольном треугольнике:
( Large displaystyle frac{a}{sin angle A}=2R)
Ну и, конечно,
( displaystyle begin{array}{l}frac{b}{sin angle B}=2R\frac{c}{sin angle C}=2Rend{array})
Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.
То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол.
Хорошая формула? По-моему, просто отличная!
Доказательство теоремы
Теорема. Вокруг всякого треугольника можно описать окружность, при том единственным образом.
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Смотри, вот так:
Давай наберёмся мужества и докажем эту теорему.
Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.
Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).
Геометрическое место точек, обладающих свойством «( displaystyle X)» — такое множество точек, что все они обладают свойством «( displaystyle X)» и никакие другие точки этим свойством не обладают.
Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы.
А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют.
В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка.
Тут множество – это серединный перпендикуляр, а свойство «( displaystyle X)» — это «быть равноудаленной (точкой) от концов отрезка».
Проверим? Итак, нужно удостовериться в двух вещах:
- Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
- Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему
Приступим:
Проверим 1. Пусть точка ( displaystyle M) лежит на серединном перпендикуляре к отрезку ( displaystyle AB).
Соединим ( displaystyle M) с ( displaystyle A) и с ( displaystyle B).Тогда линия ( displaystyle MK) является медианой и высотой в ( displaystyle Delta AMB).
Значит, ( displaystyle Delta AMB) – равнобедренный, ( displaystyle MA=MB) – убедились, что любая точка ( displaystyle M), лежащая на серединном перпендикуляре, одинаково удалена от точек ( displaystyle A) и ( displaystyle B).
Теперь 2. Почти точно так же, но в другую сторону. Пусть точка ( displaystyle M) равноудалена от точек ( displaystyle A) и ( displaystyle B), то есть ( displaystyle MA=MB).
Возьмём ( displaystyle K) – середину ( displaystyle AB) и соединим ( displaystyle M) и ( displaystyle K). Получилась медиана ( displaystyle MK). Но ( displaystyle Delta AMB) – равнобедренный по условию ( displaystyle (MA=MB)Rightarrow MK) не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка ( displaystyle M) — точно лежит на серединном перпендикуляре.
Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.
Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».
Рассмотрим треугольник ( displaystyle ABC). Проведём два серединных перпендикуляра ( displaystyle {{a}_{1}}) и ( displaystyle {{a}_{2}}), скажем, к отрезкам ( displaystyle AB) и ( displaystyle BC). Они пересекутся в какой-то точке, которую мы назовем ( displaystyle O).
А теперь, внимание!
Точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{1}}Rightarrow OA=OB);
точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{2}}Rightarrow OB=OC).
И значит, ( displaystyle OA=OB=OC) и ( displaystyle OA=OC).
Отсюда следует сразу несколько вещей:
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 6. Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.
Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
ЕГЭ 6. Вписанная окружность
В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие свойства.
В какие фигуры можно, а в какие нельзя вписать окружность. Научимся решать задачи на вписанную окружность.
Уравнение окружности, описанной около треугольника
Задача
Составить уравнение окружности, описанной около треугольника, стороны которого заданы уравнениями (9x-2y-41=0), (7x+4y+7=0), (x-3y+1=0).
Решение
Найдем координаты вершин треугольника, решив совместно три системы уравнений:
$$
cases
{
9x-2y-41=0,
cr
7x+4y+7=0;
}
cases
{
9x-2y-41=0,
cr
x-3y+1=0;
}
cases
{
7x+4y+7=0,
cr
x-3y+1=0;
}
$$
В результате получим (A(3;-7),B(5;2),C(-1;0).)
Пусть искомое уравнение окружности имеет вид ((x-a)^2+(y-b)^2=r^2). Для нахождения (a), (b) и (r) напишем три равенства, подставив в искомое уравнение вместо текущих координат координаты точек (A), (B) и (C):
$$(3-a)^2+(-7-b)^2=r^2; (5-a)^2+(2-b)^2=r^2; (-1-a)^2+b^2=r^2.$$
Исключая (r^2), приходим к системе уравнений
$$cases
{
(3-a)^2+(-7-b)^2=(5-a)^2+(2-b)^2,
cr
(3-a)^2+(-7-b)^2=(-1-a)^2+b^2,
}
$$
или
$$cases
{
4a+18b=-29,
cr
8a-14b=57.
}
$$
Отсюда (a=3.1), (b=2.3). Значение (r^2) находим из уравнения ((-1-a)^2+b^2=r^2), т.е. (r^2=22.1). Итак, искомое уравнение записывается в виде ((x-3.1)^2+(y+2.3)^2=22.1).
2011-07-23 • Просмотров [ 19042 ]

![Rendered by QuickLaTeX.com [ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)




![{displaystyle {begin{aligned}S_{x}={frac {1}{2}}det {begin{bmatrix}|mathbf {A} |^{2}A_{y}1\|mathbf {B} |^{2}B_{y}1\|mathbf {C} |^{2}C_{y}1end{bmatrix}},\[5pt]S_{y}={frac {1}{2}}det {begin{bmatrix}A_{x}|mathbf {A} |^{2}1\B_{x}|mathbf {B} |^{2}1\C_{x}|mathbf {C} |^{2}1end{bmatrix}},\[5pt]a=det {begin{bmatrix}A_{x}A_{y}1\B_{x}B_{y}1\C_{x}C_{y}1end{bmatrix}},\[5pt]b=det {begin{bmatrix}A_{x}A_{y}|mathbf {A} |^{2}\B_{x}B_{y}|mathbf {B} |^{2}\C_{x}C_{y}|mathbf {C} |^{2}end{bmatrix}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1649c42b7532a101a98ee8d0eb5f18f72a4922a1)

![{ displaystyle mathrm {R} (s) = mathrm {P_ {c}} + cos left ({ frac { mathrm {s}}) { mathrm {r}}} right) (P_ {0} -P_ {c}) + sin left ({ frac { mathrm {s}} { mathrm {r}}} right) left [{ widehat {n}} times (P_ {0} -P_ {c}) right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a70aa6cf6f613352caa88916c82a86f03bbc8b4)




![{displaystyle {begin{aligned}U_{x}={frac {1}{D}}left[(A_{x}^{2}+A_{y}^{2})(B_{y}-C_ {y})+(B_{x}^{2}+B_{y}^{2})(C_{y}-A_{y})+(C_{x}^{2}+C_{y}^{2})(A_{y}-B_{y})right]\[5pt]U_{y}={frac {1}{D}}left[(A_{x}^{2}+A_{y}^{2})(C_{x}-B_{x})+(B_{x}^{2}+B_{y}^{2})(A_{x}-C_{x})+(C_{x}^{2}+C_{y}^{2})(B_{x}-A_{x})right]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79248a1cfbeff74ea283e3c6c07a289fe188fb4d)
![D=2left[A_{x}(B_{y}-C_{y})+B_{x}(C_{y}-A_{y})+C_{x}(A_{y}-B_{y})right].,](https://wikimedia.org/api/rest_v1/media/math/render/svg/34c6178eff86289b6ec6f7dd49c95d675180f944)
![{displaystyle {begin{aligned}U'_{x}={frac {1}{D'}}left[C'_{y}({B'_{x}}^{2}+{B'_{y}}^{2})-B'_{y}({C'_{x}}^{2}+{C'_{y}}^{2})right],\[5pt]U'_{y}={frac {1}{D'}}left[B'_{x}({C'_{x}}^{2}+{C'_{y}}^{2})-C'_{x}({B'_{x}}^{2}+{B'_{y}}^{2})right]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae86c30103fce308b05684855b6c7241218358ad)













![{displaystyle {begin{aligned}{text{diameter}}{}={frac {abc}{2cdot {text{area}}}}={frac {|AB||BC||CA|}{2|Delta ABC|}}\[5pt]{}={frac {abc}{2{sqrt {s(s-a)(s-b)(s-c)}}}}\[5pt]{}={frac {2abc}{sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47584c5d8064a85b773192bd5c30ff505b51ac6a)





![{displaystyle {begin{aligned}3{sqrt {3}}Rgeq a+b+c\[5pt]9R^{2}geq a^{2}+b^{2}+c^{2}\[5pt]{frac {27}{4}}R^{2}geq m_{a}^{2}+m_{b}^{2}+m_{c}^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/790d28d5425086fee0f7465ed10d65aab26b5586)



