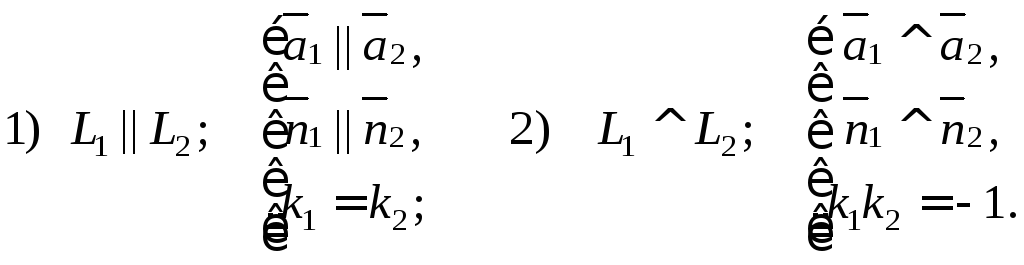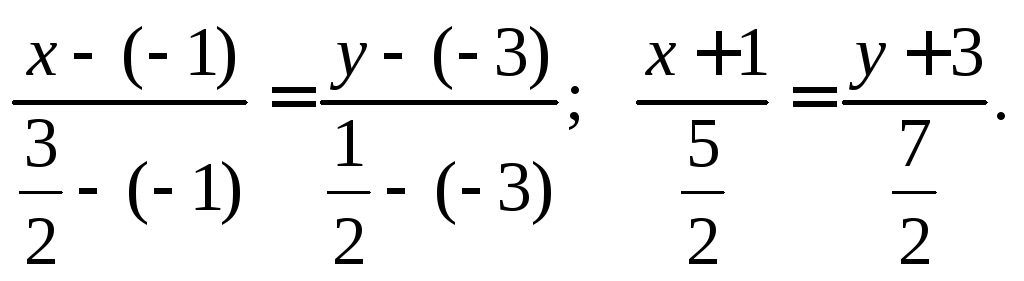Как найти уравнение медианы по координатам вершин - Avtoru.top

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

Найти координаты середины отрезка по координатам его концов.
Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Пример.

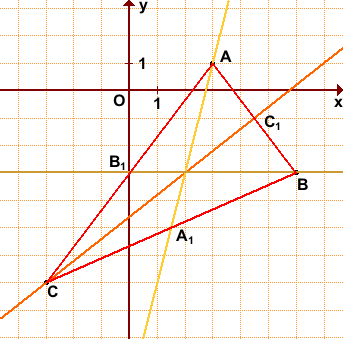
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Решение:

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

1) По формулам координат середины отрезка

$[x_{A_1 } = frac{{x_B + x_C }}{2} = frac{{6 + ( - 3)}}{2} = 1,5;]$

$[y_{A_1 } = frac{{y_B + y_C }}{2} = frac{{ - 3 + ( - 7)}}{2} = - 5.]$

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

$[left{ begin{array}{l} 1 = k cdot 3 + b; \ - 5 = k cdot 1,5 + b. \ end{array} right.]$

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

$[x_{B_1 } = frac{{x_A + x_C }}{2} = frac{{3 + ( - 3)}}{2} = 0;]$

$[y_{B_1 } = frac{{y_A + y_C }}{2} = frac{{1 + ( - 7)}}{2} = - 3.]$

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

$[x_{C_1 } = frac{{x_A + x_B }}{2} = frac{{3 + 6}}{2} = 4,5;]$

$[y_{C_1 } = frac{{y_A + y_B }}{2} = frac{{1 + ( - 3)}}{2} = - 1.]$

C(-3;-7), C(4,5;-1), y=kx+b:

$[left{ begin{array}{l} - 7 = k cdot ( - 3) + b; \ - 1 = k cdot 4,5 + b; \ end{array} right. Rightarrow k = 0,8;b = - 4,6.]$

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

Источник

Уравнение медианы треугольника

Как составить уравнение медианы треугольника по координатам его вершин?

Найти координаты середины отрезка по координатам его концов.
Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

3) Координаты точки C₁ — середины отрезка BC:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

Длина медианы треугольника

Медиана треугольника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.

Каждый треугольник имеет ровно три медианы, по одной из каждой вершины, и все они пересекаются друг с другом в центре треугольника. В случае равнобедренного и равностороннего треугольников, медиана делит пополам любой угол в вершине у которого две смежные стороны равны.

Калькулятор длины медианы треугольника

Онлайн калькулятор расчета длины медианы треугольника при условии, что известны координаты его вершин. Нахождение длины трех медиан треугольника

Формула расчета длины медианы

a,b,c — Длина сторон треугольника.

Пример расчета медиан:

Даны точки A( 1 , 5 ), B( 8 , 9 ) и C( 5 , 6 ). Найдите медианы треугольника.

Получаем:

A( 1 , 5 ) B( 8 , 9 ) C( 5 , 6 )

Решение:

Шаг 1:

Найдем длину сторон a,b,c используя формулу

Найдем длину стороны A между точками B( 8 , 9 ) and C( 5 , 6 )

a = √((5 — 2 + (6 — 9) 2 )= 4.242

Найдем длину стороны B между точками C( 5 , 6 ) и A( 1 , 5 )

b = √((1 — 5) 2 + (5 — 6) 2) = 4.123

Найдем длину стороны C между точками A( 1 , 5 ) и B( 8 , 9 )

c = √((8 — 1) 2 + (9 — 5) 2) = 8.062

Шаг 2:

Полученные значения a,b,c применяем в формулы

m_a = (1/2) √2c 2 + 2b 2 — a 2

m_b = (1/2) √(2c 2 + 2a 2 — b 2 )

m_c = (1/2) √(2a 2 + 2b 2 — c 2 )

m_a = (1/2)√(2(8.062) 2 + 2(4.123) 2 — 4.242 2 )= 6.042
m_b = (1/2)√(2(8.062) 2 + 2(4.242) 2 — 4.123 2 )= 6.103
m_c = (1/2)√2(4.242) 2 + 2(4.123) 2 — 8.062 2 = 1.118

Медиана треугольника

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

источники:

http://wpcalc.com/median-triangle/

http://www.resolventa.ru/spr/planimetry/mediana.htm

Источник

Лучший ответ

0 Голосов

Posted Декабрь 5, 2013 by Вячеслав Моргун

1. Вычислить длину медианы АМ.
Для нахождения длины медианы найдем координату точки M, зная координаты точки A найдем расстояние между этими точками, которое рассчитывается по формуле $$d = sqrt{(x_2-x_1)^2+(y_2-y_1)^2} quad (1)$$Найдем координаты точки M, которая находится по середине между точками B(1;-1) и C(3;5), координаты рассчитываются по формуле $$M(frac{x_B+x_C}{2};frac{y_B+y_C}{2})$$ подставляем значения координат и получаем $$M(frac{1+3}{2};frac{-1+5}{2}) => M(2;2)$$ Найдем длину медианы, подставим координаты точек в формулу (1) $$d_{AM} = sqrt{(8-2)^2+(0-2)^2} = 2sqrt{10}$$

2. Уравнение медианы AM.
Известны две точки A и M через которые проходит медиана. Для составления уравнения медианы, воспользуемся формула уравнения прямой, проходящей через две заданные точки $$frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}$$ Подставляем координаты точек и получаем уравнение медианы$$frac{x-8}{2-8}=frac{y-0}{2-0} => y = -frac{1}{3}x+frac{8}{3}$$

3. Наносим полученные точки и уравнение прямой на декартовую систему координат.

Другие ответы

Источник

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

9.1. Прямая на плоскости

Рассмотрим
различные случаи задания прямой L
на плоскости.

1. Если
задан ненулевой направляющий
вектор

и радиус-вектор
некоторой фиксированной точкито в этом случае радиус-векторпроизвольной точкизадается формулой

(9.1)

где

Уравнение (9.1)
называется
векторно-параметрическим уравнением
прямой L.

2. Если
– координаты точкикоторая лежит на прямойL,
(l, m)
– координаты направляющего вектора
то прямая задаетсяпараметрическими
уравнениями:

3. Если
– направляющий вектор, такой, чтои– точка, через которую проходит прямая,
то имеемканоническое
уравнение:

(9.2)

4. Если прямая L
не параллельна оси Ox,
то для всех направляющих векторов
отношение
По заданному угловому коэффициентуk
прямой L
и точке
уравнение прямойL
может быть задано в следующем виде:

– это уравнение
прямой с угловым коэффициентом
k,
проходящей
через точку
М₀.

В случае, если
– точка пересечения прямойL
с осью Oy,
это уравнение может быть записано в
следующем виде:

5. Координаты
направляющего вектора
прямойL
могут быть найдены, если известны две
точки
иэтой прямой:

Уравнение
прямой, проходящей через две заданные
точки:

(9.3)

6. Если известны
точки пересечения прямой L
с координатными осями, т. е. точки M₀(a,
0) и M₁(0,
b),
то справедливо уравнение
«в отрезках»:

7. Положение прямой
на плоскости однозначно определено и
в случае, когда задан ненулевой нормальный
вектор
этой прямой и точкаУсловие перпендикулярности векторовпозволяет перейти к векторному уравнению

и затем к его
координатной форме:

или

(9.4)

где

Уравнение (9.4)
называется общим
уравнением прямой
L.

8. Если в качестве
нормального вектора берется единичный
вектор
направленный из начала координат в
сторону прямой, т. е.

то справедливо
нормальное
уравнение
прямой L
на плоскости:

где
– расстояние от начала координат до
прямой.

Величина
δ(M₀,
L)
= x₀cos α
+ y₀cos β
– p,
где

называется отклонением точки М₀
от прямой L.
При этом δ
< 0, если точки M₀
и O(0,
0) лежат по одну сторону от прямой L,
δ
> 0 – если по разные. Расстояние d(M₀,
L)
от точки до прямой равно абсолютному
значению отклонения.

От общего уравнения
прямой к нормальному можно перейти с
помощью умножения на нормирующий
множитель:

где

Расстояние от
точки M₀(x₀,
y₀)
до прямой L:
Ax
+ By
+ C
= 0 может быть
найдено по формуле

(9.5)

Угол между прямыми
легко найти с помощью косинуса угла
между их направляющими или нормальными
векторами, а также по формуле

где k₁
и k₂
– угловые коэффициенты прямых.

При этом возможны
частные случаи:

Здесь L₁
и L₂
– прямые на плоскости, для которых
– угловые коэффициенты соответственно
прямыхи

В полярной системе
координат уравнение прямой имеет вид

ρcos(φ
– φ₀)
= p,

где p
– длина перпендикуляра, проведенного
из полюса к прямой, φ₀
– угол между полярной осью и перпендикуляром.

Пример 1.
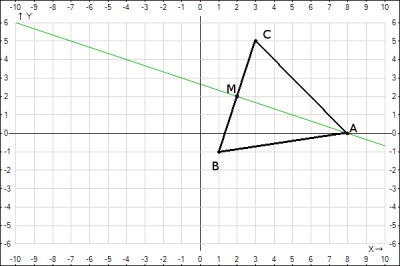
Даны вершины треугольника ABC:
A(1, 2),
B(–1, –3),
C(2, –1).
Найти:

1) уравнение прямой
BC;

2) уравнение высоты
AH
и ее длину;

3) уравнение медианы
BM;

4) угол между прямыми
BM
и AH;

5) уравнения
биссектрис внутреннего и внешнего углов
при вершине А.

Решение.
1) Для составления уравнения прямой BC
воспользуемся заданными координатами
точек B,
C
и уравнением прямой (9.3), проходящей
через две заданные точки. Так как B(–1,
–3), C(2,
–1), имеем:

Последнее уравнение
приведем к общему уравнению, использовав
основное свойство пропорции:

2(x
+ 1) = 3(y
+ 3) или 2x
– 3y
– 7 = 0.

Таким образом,
окончательно получаем:

ВС:
2x
– 3y
– 7 = 0.

2) Для построения
уравнения высоты АН
воспользуемся условием перпендикулярности
прямых AH
и ВС:
нормальным вектором прямой ВС
является
,
т. е.Этот вектор можно рассматривать как
направляющий вектор прямойАН.
Следовательно, каноническое уравнение
прямой AH
согласно формуле (9.2) имеет вид:

(9.6)

где А(1,
2)АН.

В общем виде получим
АН:
3х
+ 2у
– 7 = 0.

Чтобы найти длину
высотыАВС,
опущенной из вершины А,
воспользуемся формулой расстояния
(9.5):

3) Для составления
уравнения медианы ВМ
найдем координаты точки М,
являющейся серединой отрезка AC:

Получим M(3/2,
1/2). Запишем уравнение прямой BM
по двум известным точкам B(–1,
–3) и
используя формулу (9.3):

Приведя его к
общему уравнению, получим:

ВМ:
7x
– 5y
– 8 = 0.

4) Угол φ
между прямыми BM
и AH
найдем, используя угол между их нормальными
векторами:

Получаем

5) Пусть точка M(x,
y)
лежит на биссектрисе угла BАС.
Тогда по свойству биссектрисы d(M,
AB)
= d(M,
AC).
Запишем уравнения прямых АВ
и
АС. Имеем:

Следовательно,

Аналогично

т. е.

Используем формулу
расстояния (9.5):

Следовательно,

По основному
свойству пропорции и свойству модуля
имеем:

Итак, получили две
биссектрисы (внутреннего и внешнего
углов при вершине А):

Пример 2.
Даны две точки A(–3,
и B(2,
2). На оси Ox
найти такую точку M,
сумма расстояний от которой до двух
заданных точек была бы наименьшей.

Решение.
Воспользуемся утверждением, смысл
которого состоит в следующем: наименьший
путь между двумя точками достигается
в случае движения по прямой. Тогда задача
будет заключаться в поиске точки
пересечения прямой AB
(рис. 9.1) с осью Ox,
где B
– точка, симметричная точке В
относительно оси Ox
(или в нахождении точки пересечения
прямой AB
с осью Ox,
где A
– точка, симметричная точке А
относительно оси Ox).