Как найти угол взаимно перпендикулярны

Теорема

Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 180⁰.

Дано: АОВ, А₁О₁В₁, ОАО₁А₁, ОВО₁В₁.

Доказать: АОВ = А₁О₁В₁ или АОВ + А₁О₁В₁ = 180⁰.

Доказательство:

1 случай

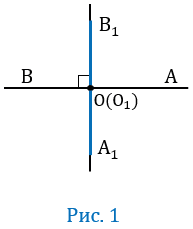
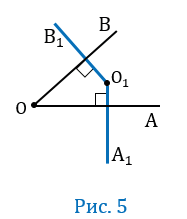
Пусть угол АОВ — развернутый (Рис. 1).

Угол АОВ — развернутый, значит лучи ОА  и ОВ будут лежать на одной прямой, при этом по условию ОАО₁А₁, ОВО₁В₁, значит, лучи О₁А₁  и О₁В₁  также будут лежать на одной прямой, следовательно, А₁О₁В₁  — будет развернутым, тогда АОВ = А₁О₁В₁.

2 случай

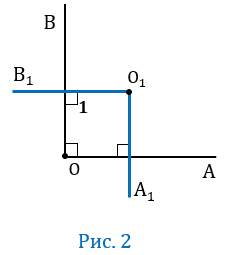
Пусть угол АОВ — прямой, т.е. равен 90⁰ (Рис.2). 

АОВ = 90⁰, то ОАОВ, при этом по условию ОАО₁А₁, следовательно, ОВО₁А₁. Итак, О₁В₁ — секущая относительно прямых ОВ и О₁А₁, ОВО₁А₁, тогда по теореме об односторонних углах их сумма равна 180⁰, т.е. 1 + А₁О₁В₁ = 180⁰, откуда А₁О₁В₁ = 180⁰ —1, при этом по условию ОВО₁В₁, значит 1 — прямой, т.е. 1 = 90⁰, следовательно, А₁О₁В₁ = 180⁰ — 90⁰ = 90⁰. Из равенств АОВ = 90⁰ и А₁О₁В₁ = 90⁰ следует, что АОВ = А₁О₁В₁   и АОВ + А₁О₁В₁ = 90⁰ + 90⁰ = 180⁰.

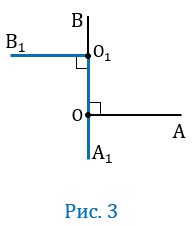
3 случай

Пусть ОО₁А₁ (Рис.3).

По условию ОО₁А₁, тогда лучи ОВ и О₁А₁ будут лежать на одной прямой А₁В. По условию ОАО₁А₁, ОВО₁В₁, значит, ОА и О₁В₁ будут перпендикулярны одной прямой А₁В, следовательно, ОАО₁В₁. Итак, ОАО₁В₁, А₁В — секущая относительно прямых ОА и О₁В₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90⁰, тогда АОВ + А₁О₁В₁ = 90⁰ + 90⁰ = 180⁰.

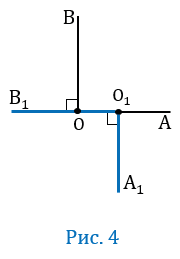
4 случай

Пусть ОО₁В₁ (Рис.4).

По условию ОО₁В₁, тогда лучи ОА и О₁В₁ будут лежать на одной прямой В₁А. По условию ОАО₁А₁, ОВО₁В₁, значит ОВ и О₁А₁ будут перпендикулярны одной прямой В₁А, следовательно, ОВО₁А₁. Итак, ОВО₁А₁, В₁А — секущая относительно прямых ОВ и О₁А₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90⁰, тогда АОВ + А₁О₁В₁ = 90⁰ + 90⁰ = 180⁰.

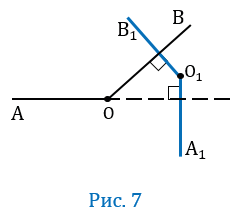
5 случай

Пусть угол АОВ — острый, т.е. меньше 90⁰, при этом ОО₁А₁, ОО₁В₁ (Рис.5).

Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными (т.е. ОАОС), а точки В и С лежали по разные стороны от прямой ОА. Далее проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными (т.е. ОВОD), а точки С и D лежали по одну сторону от прямой ОА (Рис.6).

Получим, что АОВ = 90⁰ — АОD, а СОD = 90⁰ — АОD, значит АОВ = СОD. Стороны угла СОD соответственно параллельны сторонам угла А₁О₁В₁, т.е. ОСО₁А₁ (т.к. две прямые перпендикулярные к третьей прямой параллельны друг другу, по построению ОАОС и по условию ОАО₁А₁), также ОDО₁В₁ (т.к. по построению ОВОD и по условию ОВО₁В₁), поэтому по теореме об углах с соответственно параллельными сторонами либо СОD = А₁О₁В₁, либо СОD + А₁О₁В₁ = 180⁰. Следовательно, учитывая то, что АОВ = СОD получим, либо АОВ = А₁О₁В₁, либо АОВ + А₁О₁В₁ = 180⁰.

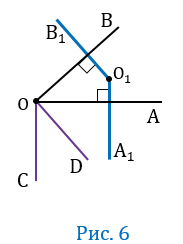
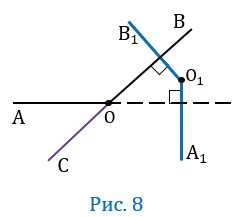
6 случай

Пусть угол АОВ — тупой, т.е. меньше 180⁰, но больше 90⁰, при этом ОО₁А₁, ОО₁В₁ (Рис.7).

Проведем луч ОС так, чтобы угол АОС был смежным с углом АОВ (Рис.8).

Угол АВС острый, и его стороны соответственно перпендикулярны сторонам угла А₁О₁В₁. Следовательно, либо АОС + А₁О₁В₁ = 180⁰, либо АОС = А₁О₁В₁ (смотри случай 5). Тогда, учитывая, что углы АОС и АОВ смежные, их сумма будет равна 180⁰, значит АОС = 180⁰ — АОВ, следовательно, в первом случае 180⁰ — АОВ + А₁О₁В₁ = 180⁰, откуда АОВ = А₁О₁В₁, а во втором случае 180⁰ — АОВ = А₁О₁В₁, откуда АОВ + А₁О₁В₁ = 180⁰. Что и требовалось доказать.

Skip to content

Перпендикулярные прямые

29 июня 2022

Перпендикулярные прямые — это просто две прямые, которые пересекаются под углом 90°:

Перпендикулярные прямые встречаются в огромном количестве задач. Прямоугольные треугольники, координаты и даже клеточки в вашей тетради — это всё перпендикулярные прямые. Поэтому разберёмся с ними.

Урок состоит из пяти частей:

1. Краткая вводная.
2. Определение перпендикулярных прямых.
3. Свойства перпендикулярных прямых.
4. Простые задачи.
5. Злые задачи.:)

Начнём с краткой вводной: что уже нужно знать про прямые и углы в данному моменту.

1. Кратная вводная

Для работы с перпендикулярными прямыми нам потребуются два вида углов: смежные и вертикальные.

1.1.Смежные углы

Определение. Два угла называются смежными, если одна сторона у них общая, а две другие являются продолжением друг друга.

Вот пример смежных углов с общей стороной $MN$:

Основное свойство таких углов: их сумма всегда равна 180°:

[angle 1+angle 2={180}^circ ]

Таким образом, зная один смежный угол, мы тут же найдём другой.

1.2. Вертикальные углы

Определение. Углы, которые образуются при пересечении двух прямых и лежат напротив друг друга, называются вертикальными.

На самом деле на пересечении двух прямых возникает сразу две пары таких углов:

Вертикальные углы всегда равны — и это их главное свойство. На рисунке мы видим, что $angle 1=angle 3$ и $angle 2=angle 4$.

1.3. Какие бывают углы

И вообще, нам пока известны четыре типа углов: острый, прямой, тупой и развёрнутый.

Интересное свойство прямого угла: если при пересечении двух прямых возник прямой угол, то все остальные углы (вертикальные, смежные с ним) тоже будут прямыми. И вот тут мы переходим к основной теме урока.

2. Определение перпендикулярных прямых

Определение. Если при пересечении двух прямых возникло четыре прямых угла, такие прямые называются перпендикулярными.

Мы уже знаем, что достаточно найти на таком пересечении всего один угол в 90 градусов — остальные три угла станут прямыми автоматически:

Перпендикулярные прямые обозначают значком «$bot $»: $ABbot CD$, $abot b$ и т.д.

Часто в задачах рассматриваются не все прямые, а лишь отрезки, лежащие на этих прямых

3. Свойства перпендикулярных прямых

Сначала разберём два «стандартных» свойства, которые вы найдёте в любом учебнике геометрии 7-го класса. А затем — одно «нестандартное», но именно оно чаще всего и встречается в настоящих задачах.

3.1. Теорема о двух прямых, перпендикулярных третьей

Теорема 1. Две прямые, перпендикулярные к третьей, не пересекаются.

Прямая $ABbot EF$ и прямая $MNbot EF$. Следовательно, прямые $AB$ и $MN$ не пересекаются. Проще говоря, они параллельны (см. урок «Параллельные прямые»).

3.2. Теорема о прямой, перпендикулярной данной

Теорема 2. Через каждую точку прямой можно провести прямую, перпендикулярную данной, и притом только одну.

Доказательство этой теоремы состоит из двух частей: сначала докажем, что такую прямую провести можно, а затем — что она единственная.

Прямая, перпендикулярная данной, строится очень просто. Рассмотрим прямую $a$, на которой отмечена точка $M$:

Отложим от луча $MK$ угол, равный 90°. В любую сторону: в верхнюю полуплоскость или нижнюю — не имеет значения. Получим луч $MN$:

Наконец, продолжим луч $MN$ в противоположную другую сторону (т.е. построим дополнительный луч). Получим искомую прямую $MNbot a$:

Единственность такого построения следует либо из аксиомы о том, что нужный угол можно отложить в нужном направлении одним и только одним способом, либо из предыдущей теоремы о двух прямых, перпендикулярных данной. В самом деле, пусть есть ещё одна прямая $ML$, которая, как и $MN$, перпендикулярна прямой $a$:

Поскольку $MNbot a$ и $MLbot a$, по предыдущей теореме эти прямые не пересекаются. Что противоречит нашему построению, в котором у прямых $MN$ и $ML$ есть общая точка $M$. Следовательно, прямые $MN$ и $ML$ совпадают, что и требовалось доказать.

3.3. Важное свойство прямого угла

Две теоремы, которые мы рассмотрели выше, редко встречаются в реальных примерах. Зато сейчас мы рассмотрим свойство, которое действительно помогает решать многие задачи. Звучит оно очень просто:

Теорема 3. Если прямой угол разделить на две части, то сумма этих новых углов равна 90°. Другими словами, если один угол равен $alpha $, то другой равен ${90}^circ -alpha $:

Это утверждение может показаться очевидным. И оно действительно является таковым. Однако деление прямого угла на части встречается в задачах настолько часто, что я не мог не упомянуть об этом.

Кроме того, начинающие ученики часто не замечают такие углы на чертежах. Поэтому сейчас мы будем отрабатывать эту теорему на реальных задачах.

4. Простые задачи

Начнём с простых задач.

Задача 1. На рисунке $ABbot MN$, $angle NOT={37}^circ $, $angle BOT+angle NOS={125}^circ $. Найдите углы $MOS$ и $SOT$.

Решение. Пусть $angle NOS=x$. Тогда из равенства

[angle BOT+angle NOS={125}^circ ]

получаем, что $angle BOT={125}^circ -x$. С другой стороны, углы $BOT$ и $NOT$ в сумме дают 90°. Потому

[begin{align}{125}^circ -x+{37}^circ &={90}^circ \ x&={72}^circ end{align}]

Теперь мы можем найти угол $SOT$:

[begin{align}angle SOT &=angle NOS+angle NOT= \ &={72}^circ +{37}^circ = \ &={109}^circ end{align}]

Кроме того, углы $MOS$ и $NOS$ — смежные, поэтому их сумма равна 180°. Отсюда получаем:

[begin{align}angle MOS&={180}^circ -angle NOS= \ &={180}^circ -{72}^circ = \ &={108}^circ end{align}]

Оба требуемых угла найдены. Задача решена.

Задача 2. Дан угол $AMC$, равный 140°. Внутри этого угла проведены лучи $MN$ и $MK$, причём $MNbot MC$ и $MKbot MA$. Найдите угол $KMN$.

Решение. Заметим, что угол $AMC$ составлен из углов $AMN$ и $CMN$, причём $angle CMN={90}^circ $ по условию. Найдём угол $AMN$:

[begin{align}angle AMN &=angle AMC-angle NMC= \ &={140}^circ -{90}^circ = \ &={50}^circ end{align}]

Точно так же найдём угол $CMK$, который вместе с углом прямым $AMK$ образует исходный угол $AMC$:

[begin{align}angle CMK &=angle AMC-angle AMN= \ &={140}^circ -{90}^circ = \ &={50}^circ end{align}]

Осталось найти искомый угол $KMN$:

[begin{align}angle KMN &=angle AMC-angle AMN-angle CMK= \ &={140}^circ -{50}^circ -{50}^circ = \ &={40}^circ end{align}]

Готово! Мы нашли нужный угол. Он равен 40 градусов.

Задача 3. Прямые $a$, $b$ и $c$ пересекаются в одной точке. Известно, что $abot b$ и $angle 1={36}^circ $. Найдите углы 2, 3 и 4.

Решение. Углы 1 и 3 — вертикальные, поэтому они равны:

[angle 3=angle 1={36}^circ ]

Кроме того, углы 1 и 2 вместе образуют прямой угол, поэтому их сумма равна 90 градусов:

[begin{align}angle 1+angle 2 &={90}^circ \ angle 2 &={90}^circ -angle 1= \ &={90}^circ -{36}^circ = \ &={54}^circ end{align}]

Наконец, углы 2 и 4 — тоже вертикальные, поэтому они тоже равны:

[angle 4=angle 2={54}^circ ]

Итого мы нашли все требуемые углы. Они равны 54, 36 и 54 градуса.

Задача 4. На рисунке угол $AMC$ — развёрнутый, луч $MBbot AC$, угол $KMN={90}^circ $. Докажите, что $angle BMN=angle CMK$.

Решение. Пусть $angle BMK=x$. Тогда, поскольку $ACbot MB$, углы $BMK$ и $CMK$ в сумме дают 90°. Отсюда получаем, что

[angle CMK={90}^circ -x]

С другой стороны, по условию задачи угол $NMK$ — прямой. Этот угол состоит из углов $BMN$ и $BMK$, поэтому

[angle BMN={90}^circ -x]

Видим, что углы $CMK$ и $BMN$ равны одной и той же величине: ${90}^circ -x$. Следовательно, эти углы равны, что и требовалось доказать.

5. Злые задачи

Деление задач на простые и сложные весьма условно. Часто «сложными» называют многошаговые задачи и доказательства.

Задача 5. Дан угол $AMB$, равный 64°. Из вершины этого угла проведены лучи $MC$ и $MD$, причём $MCbot MA$ и $MDbot MB$. Кроме того, полученный тупой угол $AMD$ содержит в себе лучи $MB$ и $MC$, которые деля этот угол на три части. Найдите углы $CMD$ и $AMD$.

Решение. Эта задача похожа на задачу 2. Взгляните на чертёж:

Поскольку угол $AMC$ — прямой, можем найти угол $BMC$:

[begin{align}angle BMC &={90}^circ -angle AMB= \ &={90}^circ -{64}^circ \ &={26}^circend{align}]

С другой стороны, угол $BMD$ — тоже прямой, поэтому можем найти угол $CMD$:

[begin{align}angle CMD &={90}^circ -angle BMC= \ &={90}^circ -{26}^circ = \ &={64}^circend{align}]

Вновь, как и в задаче 2, получили, что углы $AMB$ и $DMC$ равны. Но это не относится к делу. Найдём угол $AMD$, представив его как сумму углов $AMB$ и $BMD$:

[begin{align}angle AMD &=angle AMB+angle BMD= \ &={64}^circ +{90}^circ = \ &={154}^circ end{align}]

Задача 6. Дан прямой угол $AMB$. Луч $MC$ делит этот угол на два острых угла: $AMC$ и $BMC$. Угол между биссектрисами углов $AMC$ и $AMB$ равен 18°. Найдите углы $AMC$ и $BMC$.

Решение. Вот это уже довольно интересная задача. Взгляните на чертёж:

Красным цветом обозначена биссектриса прямого угла $AMB$. Она разбивает этого угол на два маленьких угла по 45°.

Синим цветом обозначена биссектриса искомого угла $AMC$. Обозначим половинки этого угла за $x$ (имеется в виду, что каждая из половин угла $AMC$ содержит по $x$ градусов).

Но тогда угол между биссектрисами — это часть угла между стороной $MA$ прямого угла $AMB$ и биссектрисой этого же угла. Откуда получаем уравнение

[begin{align}{45}^circ &=x+{18}^circ \ x &={45}^circ -{18}^circ ={27}^circ end{align}]

Но тогда угол $AMC$ будет вдвое больше:

[angle AMC=2x={54}^circ ]

А угол $BMC$, который дополняет $angle AMC$ до прямого, можно найти по формуле

[begin{align}angle BMC &={90}^circ -angle AMC= \ &={90}^circ -{54}^circ ={36}^circend{align}]

Итого искомые углы равны 54 и 36 градусов.

Задача 7. Два равных тупых угла имеют общую сторону. Две другие стороны этих углов взаимно перпендикулярны. Найдите величину тупого угла.

Решение. Пусть два равных тупых угла содержат по $x$ градусов. Вместе с прямым углом (т.е. углом в 90 градусов) они образуют полный поворот, т.е. 360 градусов. Получаем уравнение:

[begin{align}2x+{90}^circ&={360}^circ\ 2x &={270}^circ \ x &={135}^circend{align}]

Задача 8. Из вершины развёрнутого угла проведены два луча, которые делят этот угол на три равные части. Докажите, что биссектриса среднего угла перпендикулярна сторонам развёрнутого угла.

Доказательство. Обозначим развёрнутый угол как $AOD$, а дополнительные лучи — $OB$ и $OC$. Биссектриса угла $BOC$ — это луч $MO$ (отмечен красным цветом).

Поскольку углы $AOB$, $BOC$ и $COD$ равны и в сумме образуют развёрнутый угол, их градусные меры также равны и составляют треть от 180°:

[angle AOB=angle BOC=angle COD={60}^circ ]

Кроме того, поскольку $OM$ — биссектриса, то углы $BOM$ и $COM$ равны между собой:

[angle BOM=angle COM={30}^circ ]

Однако угол $AOM$ составлен из углов $AOB$ и $BOM$, поэтому

[begin{align}angle AOM &=angle AOB+angle BOM= \ &={60}^circ +{30}^circ ={90}^circ end{align}]

Получили, что $OMbot AD$, что и требовалось доказать.

Смотрите также:

1. Что такое вертикальные углы
2. Что такое смежные углы
3. Комбинаторика в задаче B6: легкий тест
4. Задача B15 — исследование функции с помощью производной
5. Координаты вершин правильного тетраэдра
6. Задача B4: обмен валют в трех различных банках

Теорему о свойстве углов с соответственно параллельными сторонами следует рассмотреть для случаев, когда данные углы или оба острые, или оба тупые, или один из них острый, а другой тупой.

Теорема находит широкое применение при изучении свойств различных фигур и, в частности, четырехугольника.

Встречающееся иногда при формулировке теорем указание на то, что стороны углов с соответственно параллельными сторонами могут иметь или одинаковое или противоположное направление, считаем ненужным.

Если пользоваться термином «направление», то следовало бы разъяснить, что должно понимать под этим словом. Достаточно обратить внимание учащихся на то, что углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые, если же один из углов тупой, а другой острый, то они в сумме составляют 2d.

Теорема об углах с соответственно перпендикулярными сторонами может быть дана непосредственно после теоремы о свойстве углов с соответственно параллельными сторонами. Учащимся приводятся примеры использования свойств углов с соответственно параллельными и перпендикулярными сторонами в приборах и деталях машин.

Сумма углов треугольника

При выводе теоремы о сумме углов треугольника можно использовать наглядные пособия. Вырезают треугольник АВС, пронумеровываются его углы, затем обрывают их и прикладывают друг к другу. Получается 1+2+3=2d. Проводят из вершины С треугольника АВС высоту СD и перегибают треугольник так, чтобы высота делилась пополам, т.е. вершина С упала в точку D — основание высоты. Линия перегиба MN есть средняя линия треугольника АВС. Затем перегибают равнобедренные треугольники АМD и DNB по их высотам, при этом вершины А и В совпадут с точкой D и 1+2+3=2d.

Следует помнить, что использованием наглядных пособий в систематическом курсе геометрии отнюдь не ставится задача подменить логическое доказательство какого-либо предложения опытной проверкой его.

Наглядные пособия должны лишь содействовать пониманию учащимися того или иного геометрического факта, свойств той или иной геометрической фигуры и взаимно расположения отдельных ее элементов.

При определении величины угла треугольника следует напомнить учащимся о рассмотренной ранее теореме о внешнем угле треугольника и указать, что теорема о сумме углов треугольника позволяет и построением и вычислением установить числовую зависимость между углами внешними и внутренними, не смежными с ними.

Как следствие из теоремы о сумме углов треугольника доказывается, что в прямоугольном треугольнике катет, лежащий против угла в 30 градусов, равен половине гипотенузы.

По ходу изложения материала учащимся следует задать вопросы и простые задачи, содействующие лучшему усвоению нового материала. Например,

1. Какие прямые называются параллельными?

2. При каком положении секущей равны все углы, образуемые двумя параллельными прямыми и этой секущей?

3. Прямая, проведенная в треугольнике параллельно основанию, отсекает от него малый треугольник. Доказать, что отсекаемый треугольник и данный равноугольны.

4. Вычислить все углы, образуемые двумя параллельными и секущей, если известно, что один из углов равен 72 градуса.

5. Внутренние односторонние углы соответственно равны 54⁰ и 123⁰. На сколько градусов надо повернуть одну из прямых вокруг точки ее пересечения с секущей, чтобы прямые были параллельны?

6. Доказать, что биссектрисы: а) двух равных, но не противоположных углов, образуемых двумя параллельными прямыми и секущей, параллельны, б) двух неравных углов при тех же прямых и секущей — перпендикулярны.

7. Даны две параллельные прямые АВ и CD и секущая EF, пересекающая данные прямые в точках K и L. Проведенные биссектрисы KM и KN углов AKL и BKL отсекают на прямой CD отрезок MN. Найти длину MN, если известно, что отрезок KL секущей, заключенный между параллельными, равен а. Ответ: 2а

8. Каков вид треугольника, в котором: а) сумма двух любых углов больше d, б) сумма двух углов равна d, в) сумма двух углов меньше d?

Ответ: а) остроугольный, б) прямоугольный, в) тупоугольный.

9. Во сколько раз сумма внешних углов треугольника больше суммы внутренних его углов? Ответ: в 2 раза.

10. Могут ли все внешние угля треугольника быть: а) острыми, б) тупыми, в) прямыми? Ответ: а) нет, б) да, в) нет.

11. В каком треугольнике каждый внешний угол вдвое больше каждого из внутренних углов? Ответ: равносторонний.