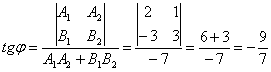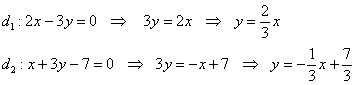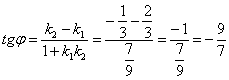Угол между векторами
Определение
Угол между векторами — это угол между отрезками, которые изображают эти две направляющие и которые отложены от одной точки пространства. Другими словами — это кратчайший путь, на который можно повернуть один из векторов вокруг его начала до положения общей направленности со вторым.
На изображении это α, который также можно обозначить следующим образом:
(left(widehat{overrightarrow a;overrightarrow b}right))
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как и любой другой угол, векторный может быть представлен в нескольких вариациях.
Острый:
Тупой:
Прямой:
С величиной (0^circ) (то есть, векторы сонаправлены):
С величиной (180^circ) (векторы направлены в противоположные стороны):
Нахождение угла между векторами
Как правило, угол между ( overrightarrow a) и (overrightarrow b) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.
Определение
Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.
Формула скалярного произведения:
(left(overrightarrow a;overrightarrow bright)=left|overrightarrow aright|timesleft|overrightarrow bright|timescosleft(widehat{overrightarrow a;overrightarrow b}right))
- Если α — острый, то СП (скалярное произведение) будет положительным числом (cos острого угла — положительное число).
- Если векторы имеют общую направленность, то есть угол между ними равен (0^circ), а косинус — 1, то СП будет тоже положительным.
- Если α — тупой, то скалярное произведение будет отрицательным (cos тупого угла — отрицательное число).
- Если α равен (180^circ), то есть векторы противоположно направлены, то СП тоже отрицательно, потому что cos данного угла равен 1.
- Если α — прямой, то СП равно 0, так как косинус (90^circ) равен 0.
В случае, если overrightarrow a и overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})
Расчет угла, если вектор задан координатами
В случае, когда направляющие расположены на двухмерной плоскости с заданными координатами в виде (overrightarrow a=left(a_x;a_yright)) и (overrightarrow b=left(b_x;b_yright)), то угол между ними можно найти следующим образом:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}})
Если же координаты находятся в трехмерном пространстве и заданы в виде:
(overrightarrow a=left(a_x;a_y;a_zright))
( overrightarrow b=left(b_x;b_y;b_zright))
то формула принимает такой вид:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})
Расчет угла, если заданы три точки в прямоугольной системе координат
В этом случае проще будет разобраться с объяснениями сразу на примере.
Допустим, нам известны три точки и их координаты: A(3,-2), B(2,1), C (6,-1). Нужно найти косинус угла между (overrightarrow{AC}) и (overrightarrow{BC}).
Решение
Для начала найдем их координаты по известным координатам заданных точек:
(overrightarrow{AC}=(6-3, -1-(-2))=(3,1))
(overrightarrow{BC}=(6-2, -1-1)=(4,-2))
После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:
(cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac{(overrightarrow{AC};;overrightarrow{BC})}{left|overrightarrow{AC}right|cdotleft|overrightarrow{BC}right|}=frac{3cdot4+1cdot(-2)}{sqrt{3^2+1^2}cdotsqrt{4^2+{(-2)}^2}}=frac{10}{sqrt{10}cdot2sqrt5}=frac{10}{10sqrt2}=frac1{sqrt2})
Ответ: (cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac1{sqrt2}.)
Примеры решения задач
Для наглядности, взглянем на примеры решения задач по данной теме.
Задача 1
Известно, что (overrightarrow a) и (overrightarrow b). Их длины равны 3 и 6 соответственно, а скалярное произведение равно -9. Нужно найти cos угла между векторами и его величину.
Решение
Применим формулу:
( cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})
Подставим известные значения:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{-9}{3cdot6}=-frac12)
Далее найдем угол между данными векторами:
(arccosleft(-frac12right)=frac{3pi}4)
Ответ: (left(widehat{overrightarrow a;overrightarrow b}right)=-frac12,;left(widehat{overrightarrow a;overrightarrow b}right)=frac{3pi}4.)
Задача 2
В пространстве даны координаты (overrightarrow a=(8; -11; 7)) и (overrightarrow b=(-2; -7; 8)). Вычислить угол α между ними.
Решение
Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})
Подставляем значения и получаем:
(cosleft(alpharight)=frac{8cdot(-2)+(-11)cdot(-7)+7cdot8}{sqrt{8^2+{(-11)}^2+7^2}cdotsqrt{{(-2)}^2+{(-7)}^2+8^2}}=frac{117}{sqrt{234}cdotsqrt{117}}=frac{sqrt{117}}{sqrt{234}}=frac1{sqrt2}=frac2{sqrt2})
Теперь находим угол α:
(alpha=arccosleft(frac2{sqrt2}right)=45^circ)
Ответ: (45^circ).
Задача 3
Известны (overrightarrow a=(3; 4)) и (overrightarrow b=(2; 5)). Найти угол между ними.
Решение
Для расчета используем формулу:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}})
Подставим известные значения и получим:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}}=frac{3cdot2+4cdot5}{sqrt{3^2+4^2}cdotsqrt{2^2+5^2}}=frac{26}{sqrt{25}cdotsqrt{29}}=frac{26}{5sqrt{29}})
Ответ: (cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{26}{5sqrt{29}})
Координаты вектора в декартовой системе координат (ДСК)
Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.
Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.
С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.
Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач
Прямоугольная система координат на плоскости обычно обозначается O x y , где O x и O y – оси коорднат. Ось O x называют осью абсцисс, а ось O y – осью ординат (в пространстве появляется ещё одна ось O z , которая перпендикулярна и O x и O y ).
Итак, нам дана прямоугольная декартова система координат O x y на плоскости если мы отложим от начала координат векторы i → и j → , направление которых соответственно совпадет с положительными направлениями осей O x и O y , и их длина будет равна условной единице, мы получим координатные векторы. То есть в данном случае i → и j → являются координатными векторами.
Координатные векторы
Векторы i → и j → называются координатными векторами для заданной системы координат.
Откладываем от начала координат произвольный вектор a → . Опираясь на геометрическое определение операций над векторами, вектор a → может быть представлен в виде a → = a x · i → + a y · j → , где коэффициенты a x и a y — единственные в своем роде, их единственность достаточно просто доказать методом от противного.
Разложение вектора
Разложением вектора a → по координатным векторам i → и j → на плоскости называется представление вида a → = a x · i → + a y · j → .
Коэффициенты a x и a y называются координатами вектора в данной системе координат на плоскости.
Координаты вектора в данной системе координат принято записывать в круглых скобках, через запятую, при этом заданные координаты следует отделять от обозначения вектора знаком равенства. К примеру, запись a → = ( 2 ; — 3 ) означает, что вектор a → имеет координаты ( 2 ; — 3 ) в данной системе координат и может быть представлен в виде разложения по координатным векторам i → и j → как a → = 2 · i → — 3 · j → .
Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.
Опираясь на определения координат вектора и их разложения становится очевидным, что единичные векторы i → и j → имеют координаты ( 1 ; 0 ) и ( 0 ; 1 ) соответственно, и они могут быть представлены в виде следующих разложений i → = 1 · i → + 0 · j → ; j → = 0 · i → + 1 · j → .
Также имеет место быть нулевой вектор 0 → с координатами ( 0 ; 0 ) и разложением 0 → = 0 · i → + 0 · j → .
Равные и противоположные векторы
Векторы a → и b → равны тогда, когда их соответствующие координаты равны.
Противоположным вектором называется вектор противоположный данному.
Отсюда следует, что координаты такого вектора будут противоположны координатам данного вектора, то есть, — a → = ( — a x ; — a y ) .
Все вышеизложенное можно аналогично определить и для прямоугольной системы координат, заданной в трехмерном пространстве. В такой системе координат имеет место быть тройка координатных векторов i → , j → , k → , а произвольный вектор a → раскладывается не по двум, а уже по трем координатам, причем единственным образом и имеет вид a → = a x · i → + a y · j → + a z · k → , а коэффициенты этого разложения ( a x ; a y ; a z ) называются координатами вектора в данной (трехмерной) системе координат.
Следовательно, координатные векторы в трехмерном пространстве принимают также значение 1 и имеют координаты i → = ( 1 ; 0 ; 0 ) , j → = ( 0 ; 1 ; 0 ) , k → = ( 0 ; 0 ; 1 ) , координаты нулевого вектора также равны нулю 0 → = ( 0 ; 0 ; 0 ) , и в таком случае два вектора будут считаться равными, если все три соответствующие координаты векторов между собой равны a → = b → ⇔ a x = b x , a y = b y , a z = b z , и координаты противоположного вектора a → противоположны соответствующим координатам вектора a → , то есть, — a → = ( — a x ; — a y ; — a z ) .
Координаты радиус-вектора точки
Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.
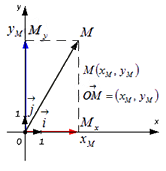
Пусть нам дана некоторая прямоугольная декартова система координат O x y и на ней задана произвольная точка M с координатами M ( x M ; y M ) .
Вектор O M → называется радиус-вектором точки M .
Определим, какие координаты в данной системе координат имеет радиус-вектор точки
Вектор O M → имеет вид суммы O M → = O M x → + O M y → = x M · i → + y M · j → , где точки M x и M y это проекции точки М на координатные прямые Ox и Oy соответственно (данные рассуждения следуют из определения проекция точки на прямую), а i → и j → — координатные векторы, следовательно, вектор O M → имеет координаты ( x M ; y M ) в данной системе координат.
Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.
Аналогично в трехмерном пространстве радиус-вектор точки M ( x M ; y M ; z M ) разлагается по координатным векторам как O M → = O M x → + O M y → + O M z → = x M · i → + y M · j → + z M · k → , следовательно, O M → = ( x M ; y M ; z M ) .
Системы координат
Декартова система координат.
Фиксируем в пространстве точку (O) и рассмотрим произвольную точку (M). Радиус-вектором точки (M) по отношению к точке (O) называется вектор (overrightarrow). Если в пространстве кроме точки (O) выбран некоторый базис, то точке (M) сопоставляется упорядоченная тройка чисел — компоненты ее радиус-вектора.
Декартовой системой координат в пространстве называется совокупность точки и базиса.
Точка носит название начала координат. Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат; первая — осью абсцисс, вторая — осью ординат, третья — осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.
Пусть дана декартова система координат (O), (boldsymbol>), (boldsymbol>), (boldsymbol>). Компоненты (x), (y), (z) радиус-вектора (overrightarrow) точки (M) называются координатами точки (M) в данной системе координат:
$$
overrightarrow = xboldsymbol> + yboldsymbol> + zboldsymbol>.nonumber
$$
Первая координата называется абсциссой, вторая — ординатой, а третья — аппликатой.
Аналогично определяются координаты на плоскости и на прямой линии. Разумеется, точка на плоскости имеет только две координаты, а на прямой линии — одну.
Координаты точки пишут в скобках после буквы, обозначающей точку. Например, запись (A(2, 1/2)) означает, что точка (A) имеет координаты 2 и 1/2 в ранее выбранной декартовой системе координат на плоскости (рис. 2.1).
Рис. 2.1
Координаты точки, как и компоненты вектора, — величины безразмерные. В частности, они не зависят от выбранной единицы измерения длин. В самом деле, раскладывая векторы в теореме о линейной зависимости систем векторов, мы сводили дело к разложению вектора по коллинеарному с ним ненулевому вектору. А в этом случае компонента равна отношению длин, взятому с определенным знаком.
Легко видеть, что при заданной системе координат координаты точки определены однозначно. С другой стороны, если задана система координат, то для каждой упорядоченной тройки чисел найдется единственная точка, имеющая эти числа в качестве координат. Система координат на плоскости определяет такое же соответствие между точками плоскости и парами чисел. Задание системы координат на прямой линии сопоставляет каждой точке вещественное число и каждому числу — точку.
Рис. 2.2
Рассмотрим две точки (A) и (B), координаты которых относительно некоторой декартовой системы координат (O), (boldsymbol>), (boldsymbol>), (boldsymbol>) соответственно (x_<1>), (y_<1>), (z_<1>) и (x_<2>), (y_<2>), (z_<2>). Поставим себе задачу найти компоненты вектора (overrightarrow). Очевидно, что (overrightarrow = overrightarrow-overrightarrow) (рис. 2.2). Компоненты радиус-векторов (overrightarrow) и (overrightarrow) равны ((x_<1>), (y_<1>), (z_<1>)) и ((x_<2>), (y_<2>), (z_<2>)) по определению координат. Из ранее доказанного предположения следует, что (overrightarrow) имеет компоненты ((x_<2>-x_<1>), (y_<2>-y_<1>), (z_<2>-z_<1>)). Этим доказано следующее утверждение.
Чтобы найти координаты вектора, нужно из координат его конца вычесть координаты его начала.
Деление отрезка в заданном отношении.
Найдем координаты точки (M) на отрезке (AB), которая делит этот отрезок в отношении (lambda/mu), то есть удовлетворяет условию
$$
frac<|AM|> <|MB|>= frac<lambda><mu>, lambda > 0, mu > 0nonumber
$$
(рис. 2.3). Это условие можно переписать в виде
$$
muoverrightarrow = lambdaoverrightarrow.label
$$
Рис. 2.3
Обозначив через ((x_<1>), (y_<1>), (z_<1>)) и ((x_<2>), (y_<2>), (z_<2>)) соответственно координаты точек (A) и (B), а через ((x), (y), (z)) координаты точки (M), разложим обе части равенства по базису, причем компоненты векторов (overrightarrow) и (overrightarrow) найдем по предложению 1. Тогда
$$
mu(x-x_<1>) = lambda(x_<2>-x), mu(y-y_<1>) = lambda(y_<2>-y), mu(z-z_<1>) = lambda(z_<2>-z).nonumber
$$
Из этих равенств можно найти (x), (y) и (z), поскольку (lambda + mu neq 0):
$$
x = frac <mu x_<1>+ lambda x_<2>><lambda + mu>, y = frac <mu y_<1>+ lambda y_<2>><lambda + mu>, z = frac <mu z_<1>+ lambda z_<2>><lambda + mu>label
$$
Если в формулах eqref мы будем считать одно из чисел (lambda) или (mu) отрицательным, то из равенства eqref увидим, что (M) находится на той же прямой вне отрезка (AB), деля его в отношении |(lambda/mu)|. Поэтому из формул eqref можно найти координаты точки, делящей отрезок в заданном отношении как внутренним, так и внешним образом.
На плоскости и на прямой линии задача о делении отрезка решается точно так же, только из трех равенств в eqref остается соответственно два и одно равенство.
Декартова прямоугольная система координат.
Общие декартовы системы координат используются реже, чем специальный класс таких систем — декартовы прямоугольные системы координат.
Базис называется ортонормированным, если его векторы попарно ортогональны и по длине равны единице. Декартова система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.
Нетрудно проверить, что координаты точки относительно декартовой прямоугольной системы координат в пространстве по абсолютной величине равны расстояниям от этой точки до соответствующих координатных плоскостей. Они имеют знак плюс или минус в зависимости от того, лежит точка по ту же или по другую сторону от плоскости, что и конец базисного вектора, перпендикулярного этой плоскости.
Аналогично находят координаты точки относительно декартовой прямоугольной системы координат на плоскости.
Полярная система координат.
Декартовы системы координат не единственный способ определять при помощи чисел положение точки на плоскости. Для этого используются многие другие типы координатных систем. Здесь мы опишем некоторые из них.
На плоскости часто употребляется полярная система координат. Она определена, если задана точка (O), называемая полюсом, и исходящий из полюса луч (l), который называется полярной осью. Положение точки (M) фиксируется двумя числами: радиусом (r = overrightarrow) и углом (varphi) между полярной осью и вектором (overrightarrow). Этот угол называется полярным углом (рис. 2.4).
Рис. 2.4
Мы будем измерять полярный угол в радианах и отсчитывать от полярной оси против часовой стрелки. У полюса (r = 0), а (varphi) не определено. У остальных точек (r > 0), а (varphi) определяется с точностью до слагаемого, кратного 2(pi). Это означает, что пары чисел ((r, varphi)), ((r, varphi + 2pi)) и вообще ((r), (varphi + 2kpi)), где (k) — любое целое число, представляют собой полярные координаты одной и той же точки.
Иногда ограничивают изменение полярного угла какими-нибудь условиями, например, (0 leq varphi 0), то паре ((r, varphi)) ставим в соответствие точку, радиус-вектор которой имеет длину (r) и составляет с полярной осью угол (varphi). При этом парам чисел ((r, varphi)) и ((r_<1>, varphi_<1>)) сопоставляется одна и та же точка, если (r = r_<1>), а (varphi = varphi_ <1>= 2pi k), где (k) — целое число.
Выберем на плоскости декартову прямоугольную систему координат, поместив ее начало в полюс (O) и приняв за базис векторы (boldsymbol>) и (boldsymbol>) длины (l), направленные соответственно вдоль полярной оси и под углом (pi/2) к ней (угол отсчитывается против часовой стрелки). Как легко видеть из рис. 2.4, декартовы координаты точки выражаются через ее полярные координаты формулами
$$
x = r cos varphi, y = r sin varphi.label
$$
Цилиндрические и сферические координаты.
В пространстве обобщением полярных систем координат являются цилиндрические и сферические системы координат. И для тех, и для других фигура, относительно которой определяется положение точки, состоит из точки (O), луча (l), исходящего из (O), и вектора (boldsymbol), равного по длине 1 и перпендикулярного к (l). Через точку (O) проведем плоскость (Theta), перпендикулярную вектору (boldsymbol). Луч (l) лежит в этой плоскости.
Пусть дана точка (M). Опустим из нее перпендикуляр (MM’) на плоскость (Theta).
Цилиндрические координаты точки (M) — это три числа (r), (varphi), (h). Числа (r) и (varphi) — полярные координаты точки (M’) по отношению к полюсу (O) и полярной оси (l), a (h) — компонента вектора (overrightarrow) по вектору (boldsymbol). Она определена, так как эти векторы коллинеарны (рис. 2.5).
Рис. 2.5
Сферические координаты точки — три числа ((r), (varphi), (theta)). Они определяются так: (r = |overrightarrow|). Как и для цилиндрических координат, (varphi) — угол вектора (overrightarrow>) с лучом (l), а (theta) — угол вектора (overrightarrow) с плоскостью (Theta) (рис. 2.6).
Рис. 2.6
Системы координат
Положение любой точки P в пространстве (в частности, на плоскости) может быть определено при помощи той или иной системы координат. Числа, определяющие положение точки, называются координатами этой точки.
Наиболее употребительные координатные системы — декартовы прямоугольные.
Кроме прямоугольных систем координат существуют косоугольные системы. Т.к. я не встречал примеров применения косоугольных систем, то я их не рассматриваю. Прямоугольные и косоугольные координатные системы объединяются под названием декартовых систем координат.
Иногда на плоскости применяют полярные системы координат, а в пространстве — цилиндрические или сферические системы координат.
Обобщением всех перечисленных систем координат являются криволинейные системы координат.
Рис. 1: Классификация систем координат
Радиус-вектор
Радиус-вектор (обычно обозначается или просто ) — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки, называемой началом координат.
Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.
Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.
На плоскости углом радиус-вектора называется угол, на который радиус-вектор переместится относительно оси абсцисс в направлении против часовой стрелки.
- · Декартовы координаты:
- · Полярные координаты:
- · Декартовы координаты:
- · Цилиндрические координаты:
- · Сферические координаты:
http://univerlib.com/analytic_geometry/vector_algebra/coordinate_systems/
http://vuzlit.ru/832032/sistemy_koordinat
2.5.7. Как найти угол между прямыми?
Новая картинка за очередным поворотом:
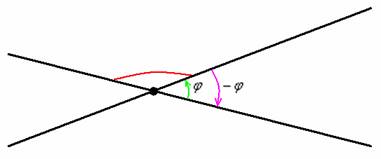
МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым. На рисунке угол, обозначенный красной дугой, не считается углом
между пересекающимися прямыми. А считается таковым его «зелёный» сосед или
отрицательно ориентированный «малиновый» угол . Если прямые
перпендикулярны, то за угол между ними можно принять любой из 4 углов.
…что-то не понятно? Срочно изучаем Приложение Тригонометрия!
Однако ещё раз: чем отличаются углы ? Ориентацией (направлением «прокрутки» угла).
Напоминаю, что отрицательно ориентированный угол «прокручивается» по часовой стрелке и записывается со знаком «минус».
Следует отметить, что ориентацию угла часто не принимают во внимание, и рассматривают «просто угол», который .
Как найти угол между двумя прямыми? Существуют три основные формулы.
Способ первый. Рассмотрим две прямые, заданные общими уравнениями в декартовой системе
координат:
Если , то прямые перпендикулярны (
либо
).
Если , то прямые не перпендикулярны и ориентированный угол
между ними можно вычислить с помощью
формулы:
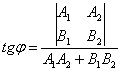
Знаменатель этой формулы – в точности, скалярное произведение направляющих векторов: ,
которое равно нулю тогда и только тогда, когда векторы ортогональны. …надеюсь, не забыли.
Задача 83
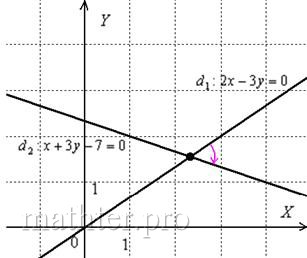
Найти угол между прямыми , заданными в декартовой системе координат.
Исходя из вышесказанного, решение удобно оформить в два шага:
1) Вычислим произведение:
, значит, прямые не перпендикулярны.
2) Угол между прямыми найдём с помощью формулы:
И с помощью обратной функции (см. Приложение Тригонометрия) легко найти сам угол, при этом используем нечётность арктангенса:
Ответ:
В ответе указываем точное значение, а также приближённое значение (желательно и в градусах, и в радианах), вычисленное с помощью
калькулятора.
Ну, минус, так минус, ничего страшного, вот геометрическая иллюстрация:
Неудивительно, что угол получился отрицательной ориентации, ведь в условии задачи «первым номером» идёт прямая и «открутка» угла началась именно с неё. Если очень хочется получить положительное значение, то нужно
поменять прямые местами, то есть коэффициенты взять из второго уравнения
, а коэффициенты
– из первого уравнения
. Короче
говоря, начать нужно
с прямой .
Скрывать не буду, сам подбираю прямые в том порядке, чтобы угол получился положительным. Так красивее, но не более того.
Способ второй, он удобен, когда прямые заданы уравнениями с
угловым коэффициентом: (в декартовых координатах).
Если , то прямые перпендикулярны (
либо
).
Если , то ориентированный угол
между ними можно найти с помощью формулы:
, и на самом деле это частный случай предыдущей формулы.
К слову, из равенства следует полезная взаимосвязь угловых
коэффициентов перпендикулярных прямых: , которая используется в некоторых
задачах.
Решим Задачу 83 вторым способом, для этого перепишем прямые в нужном виде:
Таким образом, угловые коэффициенты: , и алгоритм похож:
1) Проверим, будут ли прямые перпендикулярны:
, значит, прямые не перпендикулярны.
2) Используем формулу:
Ответ:
И третий способ состоит нахождении угла между направляющими векторами прямых с помощью скалярного произведения: , но здесь не принимается во внимание ориентация угла (по любому получится
). Кроме того, он может оказаться тупым, и тогда придётся делать оговорку, что угол между
прямыми – это меньший угол, и из радиан (не из
!) вычитать получившийся арккосинус.
Какой способ выбрать? Ориентируйтесь на вашу задачу, методичку или ситуацию.
Задача 84
Найти угол между прямыми .
Самостоятельно, всеми тремя способами! Решение и ответ в конце книги.
И по просьбам учащихся ещё один пункт:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Угол между векторами на плоскости и в пространстве
Пусть на плоскости или в трехмерном пространстве заданы два ненулевых вектора 



Определение.
Углом между векторами 

Угол между векторами 


Угол между векторами может принимать значения от до 








Определение.
Векторы 



Если хотя бы один из векторов 


Нахождение угла между векторами, примеры и решения
Косинус угла между векторами 



Разберем эти случаи.
По определению скалярное произведение векторов есть 





Пример.
Вычислите косинус угла между векторами 



Решение.
В условии задачи даны все величины необходимые для применения формулы 



Теперь находим угол между векторами: 
Ответ:

Существуют задачи, где векторы заданы координатами в прямоугольной системе координат на плоскости или в пространстве. В этих случаях для нахождения косинуса угла между векторами можно использовать все ту же формулу 
Длина вектора есть корень квадратный из суммы квадратов его координат, скалярное произведение векторов равно сумме произведений соответствующих координат. Следовательно, формула для вычисления косинуса угла между векторами 



Пример.
Найдите угол между векторами 
Решение.
Можно сразу воспользоваться формулой 
А можно для нахождения косинуса угла между векторами использовать формулу 
Ответ:

К предыдущему случаю сводится задача, когда даны координаты трех точек (например А, В и С) в прямоугольной системе координат и требуется найти какой-нибудь угол (например, 
Действительно, угол 


Пример.
На плоскости в декартовой системе координат заданы координаты трех точек 


Решение.
Определим координаты векторов 

Теперь воспользуемся формулой для нахождения косинуса угла между векторами на плоскости в координатах:
Ответ:

Угол между векторами 











Вычисление ортогональной проекции(сво-во проекции):
Проекция вектора 


Док-во: Если φ= 




Если φ> 






Если φ= 


Следствие: Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нуле, если этот угол – прямой.
Следствие: Проекции равных векторов на одну и ту же ось равны между собой.
Вычисление ортогональной проекции суммы векторов (сво-во проекции):
Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.
Док-во: Пусть, например, 















РИС. 11
Вычисление произведения вектора на число:
При умножеии вектора 


Док-во: При λ > 0 имеем прl (λ* 


При λl (λ* 





Свойство справедливо и при
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
Нахождение угла между векторами
Как правило, угол между ( overrightarrow a) и (overrightarrow b) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.
Определение
Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.
Формула скалярного произведения:
(left(overrightarrow a;overrightarrow bright)=left|overrightarrow aright|timesleft|overrightarrow bright|timescosleft(widehat{overrightarrow a;overrightarrow b}right))
- Если α — острый, то СП (скалярное произведение) будет положительным числом (cos острого угла — положительное число).
- Если векторы имеют общую направленность, то есть угол между ними равен (0^circ), а косинус — 1, то СП будет тоже положительным.
- Если α — тупой, то скалярное произведение будет отрицательным (cos тупого угла — отрицательное число).
- Если α равен (180^circ), то есть векторы противоположно направлены, то СП тоже отрицательно, потому что cos данного угла равен 1.
- Если α — прямой, то СП равно 0, так как косинус (90^circ) равен 0.
В случае, если overrightarrow a и overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})
Видео
Примеры решений
| Пример 1 |
| Найти угол между векторами $ overline{a} = (2;4) $ и $ overline{b} = (3;1) $ |
| Решение |
|
Сначала находим косинус угла между векторами по формуле: $$ cos phi = frac{(overline{a},overline{b})}{|overline{a}| cdot |overline{b}|} = frac{2cdot 3 + 4 cdot 1}{sqrt{2^2 + 4^2} cdot sqrt{3^2 + 1^2} } = frac{10}{sqrt{20} cdot sqrt{10}} = $$ $$ = frac{10}{sqrt{200}} = frac{1}{sqrt{2}} = frac{sqrt{2}}{2} $$ Теперь искомый угол $ phi $ находим по другой формуле: $$ phi = arccos (cos phi) = arccos (cos frac{sqrt{2}}{2}) = 45^0 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Угол между двумя векторами равен $ phi = 45^0 $ |
| Пример 2 |
| Найти угол $ phi $ между двумя векторами $ overline{a} = (8;-11;7) $ и $ overline{b} = (-2;-7;8) $ |
| Решение |
|
Подставляем координаты в формулу и вычисляем: $$ cos phi = frac{8cdot (-2) + (-11)cdot (-7) + 7cdot 8}{sqrt{8^2+(-11)^2+7^2} cdot sqrt{(-2)^2+(-7)^2+8^2} } = $$ $$ = frac{-16+77+56}{sqrt{234} cdot sqrt{117}} = frac{117}{sqrt{234} cdot sqrt{117}} = $$ $$ = frac{sqrt{117}}{sqrt{234}} = frac{1}{sqrt{2}} = frac{sqrt{2}}{2} $$ Далее находим сам угол $ phi $ с помощью арккосинуса: $$ phi = arccos frac{sqrt{2}}{2} = 45^0 $$ |
| Ответ |
| Угол $ phi = 45^0 $ |
Теги
Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Пример 1. Найти угол между векторами a = {3; 4} и b = {4; 3}.
Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
|a| = √32 + 42 = √9 + 16 = √25 = 5
|b| = √42 + 32 = √16 + 9 = √25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| |a| · |b| | 5 · 5 | 25 |
Пример 2. Найти угол между векторами a = {7; 1} и b = {5; 5}.
Решение: Найдем скалярное произведение векторов:
a·b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
|a| = √72 + 12 = √49 + 1 = √50 = 5√2
|b| = √52 + 52 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| |a| · |b| | 5√2 · 5√2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Пример 3. Найти угол между векторами a = {3; 4; 0} и b = {4; 4; 2}.
Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
|a| = √32 + 42 + 02 = √9 + 16 = √25 = 5
|b| = √42 + 42 + 22 = √16 + 16 + 4 = √36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| |a| · |b| | 5 · 6 | 15 |
Пример 4. Найти угол между векторами a = {1; 0; 3} и b = {5; 5; 0}.
Решение: Найдем скалярное произведение векторов:
a·b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
|a| = √12 + 02 + 32 = √1 + 9 = √10
|b| = √52 + 52 + 02 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
cos α =
a · b|a| · |b|
=
5√10 · 5√2
=
12√5
=
√510
= 0.1√5