Как найти угол сдвига фаз на конденсаторе - Avtoru.top

Включение конденсатора в цепь переменного
тока не вызывает разрыва цепи, так как
ток в цепи все время поддерживается за
счет заряда и разряда конденсатора.
Пусть напряжение (рис. 2.8 а)

Тогда

(2.17)

Формула
(2.17) показывает, чтоток
опережает приложенное напряжение на
угол

(рис. 2.8 б, в). Нулевым значениям тока
соответствуют максимальные значения
напряжения. Физически это объясняется
тем, что при достижении электрическим
зарядом и соответственно напряжением
максимального значения ток становится
равным нулю.

Под фазовым сдвигом тока относительно
напряжения здесь, как и раньше,
подразумевается разность начальных
фаз напряжения и тока, т.е.

Таким образом, в отличие от цепи с
катушкой, где
,
угол сдвига фаз в цепи с конденсатором
отрицателен.

Из (2.17) видно,
что амплитуды тока и напряжения связаны
законом Ома

где–емкостное сопротивление, имеющее
размерностьОм.

Мгновенная
мощность, поступающая в конденсатор

колеблется
синусоидально с угловой частотой 2,
имея амплитуду, равную(рис. 2.8 г). Поступая от источника, энергия
временно запасается в электрическом
поле конденсатора, затем возвращается
источнику при исчезновении электрического
поля. Таким образом, здесь, как и в цепи
с катушкой, происходит колебание энергии
между источником и конденсатором, причем
активная мощность= 0. Амплитуду колебания мощности в
цепи с конденсатором называютреактивной
(емкостной) мощностью

2.3. Анализ цепей синусоидального тока с помощью векторных диаграмм

Совокупность векторов, изображающих
синусоидальные ЭДС, напряжения и токи
одной частоты и построенных на плоскости
с соблюдением их ориентации друг
относительно друга, называют векторной
диаграммой. Векторные диаграммы
широко применяются при анализе режимов
работы цепей синусоидального тока,
что делает расчет цепи наглядным.

2.3.1. Цепь, содержащая резистор и индуктивную катушку

Реальная катушка в цепи переменного
тока представляет сочетание активной
и индуктивной составляющих сопротивления.
Схема замещения индуктивной катушки
представлена на рис 2.9 а. Пусть по катушке
протекает ток
.


а)	б)	в)

Рис. 2.9

В соответствии со вторым законом Кирхгофа
для мгновенных значений

,
(2.18)

где
–
напряжение на активном сопротивлении;– напряжение на индуктивном
сопротивлении.

Для действующих значений уравнение
(2.18) можно записать

.
(2.19)

Построим векторную
диаграмму в соответствии с (2.19) в такой
последовательности. Изобразим вектор
тока
(основной вектор) на координатной
плоскости–(рис. 2.9 б). Затем строим вектор напряжения
на активной составляющей сопротивления.
Он совпадает по фазе с током. Вектор
напряженияопережает вектор тока на 90°. Сумма двух
векторов дает вектор напряжения
источника, который опережает вектор
тока на угол.
Из векторной диаграммы следует

отсюда

,. (2.20)

где z – полное
сопротивление цепиR,L.

Треугольник ОАВ(рис. 2.9 б) назовемтреугольником напряжений. Составляющая
напряжения, находящаяся в фазе с током,
называетсяактивнойсоставляющей
напряжения

.
(2.21)

Составляющая
напряжения, перпендикулярная вектору
тока, называется реактивнойсоставляющей напряжения

.
(2.22)

Если стороны
треугольника напряжений (рис. 2.9 б)
разделить на действующее значение тока,
то получим треугольник
сопротивлений
(рис. 2.9 в). Из треугольника сопротивлений
получают соотношения для угла сдвига
фаз, а также связь между параметрами
цепи

;(2.23)

Цепь имеет индуктивный
характер, если 0<<.
Крайние значения= 0 и=соответствуют чисто активной и чисто
индуктивному характеру нагрузки.

Соседние файлы в папке Лекции

Источник

Достаточно сложным и чаще всего не изучаемым аспектом темы переменный ток является метод построения векторных диаграмм. Анализируя вынужденные электромагнитные колебания, мы уже обсудили сдвиг тока и напряжения на реактивных сопротивлениях (катушка индуктивности и конденсатор) по сравнению с активным сопротивлением (резистор). Тогда одним из задаваемых вопросов задачи является вопрос о направлении суммарного тока или напряжения в данный конкретный момент времени. Для ответа на этот вопрос и используется метод построения векторных диаграмм.

Векторная диаграмма — это изображение гармонически изменяющихся величин (текущего тока и напряжения) в виде векторов на плоскости.

Рис. 1. Векторная диаграмма

Построение векторных диаграмм происходит в прямоугольной декартовой системе координат. Построение начинается с проведения вектора, численно равного амплитудному значению тока в цепи. Данный вектор сонаправим в осью ОХ (рис. 1.1).

Т.к. напряжение на активном сопротивлении находится в одной фазе с током, то вектор амплитуды напряжения сонаправлен с вектором тока (рис. 1.2. красный).

На катушке напряжение опережает ток, поэтому отложим вектор амплитуды напряжения на катушке ( $displaystyle {{90}^{circ }}$ ) вверх под углом $displaystyle {{90}^{circ }}$ относительно вектора тока (рис. 1.2. синий).

На конденсаторе напряжение отстаёт от тока, поэтому отложим вектор амплитуды напряжения на конденсаторе ( $displaystyle {{90}^{circ }}$ ) вниз под углом $displaystyle {{90}^{circ }}$ относительно вектора тока (рис. 1.2. зелёный).

Угол $displaystyle {{90}^{circ }}$ , используемый в логике построений, используется в случае идеальности контура и катушки.

Для построения общего вектора напряжения достаточно векторно сложить напряжения:

$displaystyle {{vec{U}}_{o}}={{vec{U}}_{L}}+{{vec{U}}_{C}}+{{vec{U}}_{R}}$ (1)

Проще всего сначала найти вектор-сумму $displaystyle {{U}_{C}}-{{U}_{L}}$ (т.к. они расположены вдоль одной прямой). В нашем случае, эти вектора разнонаправлены, найдём $displaystyle {{U}_{C}}-{{U}_{L}}$ (рис. 1.3. жёлтый).

И последнее, осталось сложить получившийся вектор с вектором $displaystyle {{U}_{R}}$ для получения значения полного напряжения в цепи (рис. 1.4. оранжевый). Для получения модуля вектора воспользуемся теоремой Пифагора, т.к. вектора находятся под прямым углом. Тогда:

$displaystyle {{U}_{o}}=sqrt{U_{R}^{2}+{{({{U}_{C}}-{{U}_{L}})}^{2}}}$ (2)

где

Угол displaystyle varphi — угол между вектором силы тока и полного напряжения называется сдвигом фаз между колебаниями силы тока и напряжения. Данный параметр можно найти и исходя из параметров системы:

$displaystyle cos varphi =frac{R}{Z}$ (3)

где

Вывод: задачи на данную тематику касаются поиска сдвига фаз между колебаниями силы тока и напряжения через график (рис. 1.4) или через соотношение (3), а также поиска полного напряжения в цепи также через график (рис. 1.4) или через соотношение (2).

Источник

Содержание книги

Предыдующая страница

§18. Переменный электрический ток

18.4 Емкость в цепи переменного тока. Емкостное сопротивление.

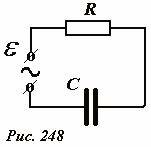
Рассмотрим электрическую цепь, содержащую резистор с активным сопротивлением R и конденсатор емкости C, подключенную к источнику переменной ЭДС (Рис. 248).

Конденсатор, подключенный к источнику постоянной ЭДС полностью препятствует прохождения тока – за некоторый промежуток времени конденсатор заряжается, напряжение между его обкладками становится равным ЭДС источника, после чего ток в цепи прекращается. Если же конденсатор включен в цепь переменного тока, то ток в цепи не прекращается – фактически конденсатор периодически перезаряжается, заряды на его обкладках периодически изменяются как по величине, так и по знаку. Конечно, никакие заряды не протекают между обкладками, электрического тока в строгом определении между ними нет. Но, часто не вдаваясь в детали и не слишком корректно, говорят о токе через конденсатор, подразумевая под этим ток в цепи, к которой подключен конденсатор. Такой же терминологией будем пользоваться и мы.

По-прежнему, для мгновенных значений справедлив закон Ома для полной цепи: ЭДС источника равна сумме напряжений на всех участках цепи. Применение этого закона к рассматриваемой цепи приводит к уравнению

(~varepsilon = U_R + U_C = IR + frac{q}{C}) , (1)

здесь (U_R = IR) — напряжение на резисторе, (U_C = frac{q}{C}) — напряжение на конденсаторе, q — электрический заряд на его обкладках. Уравнение (1) содержит три изменяющихся во времени величины (известную ЭДС, и пока неизвестные силу тока и заряд конденсатора), учитывая, что сила тока равна производной по времени от заряда конденсатора (I = q′), это уравнение может быть точно решено. Так как ЭДС источника изменяется по гармоническому закону, то и напряжение на конденсаторе и сила тока в цепи также будут изменяться по гармоническим законам с той же частотой – это утверждение непосредственно следует и уравнения (1).

Сначала установим связь между силой тока в цепи напряжением на конденсаторе. Зависимость напряжения от времени представим в виде

(~U_C(t) = U_0 cos omega t) . (2)

Подчеркнем, что в данном случае напряжение на конденсаторе отличается от ЭДС источника, как будет видно из дальнейшего изложения, между этими функциями существует также и разность фаз. Поэтому при записи выражения (2), мы выбираем произвольную начальную фазу нулевой, при таком определении фазы ЭДС, напряжения на резисторе и силы тока отсчитываются относительно фазы колебаний напряжения на резисторе.

Используя связь между напряжением и зарядом конденсатора, запишем выражение для зависимости последнего от времени

(~q = U_0 C cos omega t) , (3)

которое позволяет найти временную зависимость силы тока

(~I_C = q’ = -U_0 C omega sin omega t = U_0 C omega cos left( omega t + frac{pi}{2} right)) , (4)

на последнем шаге использована тригонометрическая формула приведения, для того, чтобы в явном виде выделить сдвиг фаз между током и напряжением.

Итак, мы получили, что амплитудное значение силы тока через конденсатор связано с напряжением на нем соотношением

(~I_{C0} = U_{C0} C omega) , (5)

а также между колебаниями силы тока и напряжения существует разность фаз, равна (~Delta varphi = frac{pi}{2}). Эти результаты суммированы на рис. 249, где также представлена векторная диаграмма колебаний силы тока и напряжения.

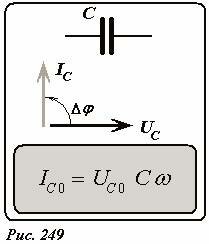
Для того, чтобы сохранить форму закона Ома для участка цепи, вводят понятие емкостного сопротивления, которое определяется по формуле

(~Z_C = frac{1}{C omega}) . (6)

В этом случае соотношение (5) становится традиционным для закона Ома

(~I_{C0} = frac{U_{C0}}{Z_C}) . (7)

При изучении закона Ома для цепей постоянного тока, мы указывали, что электрическое поле заставляет упорядоченно двигаться заряженные частицы внутри проводника, то есть создает электрический ток. Иными словами, «напряжение является причиной возникновения тока». В данном случае ситуация обратная – благодаря электрическому току на обкладках возникают электрические заряды, создающие электрическое поле, поэтому можно сказать, что в данном случае «сила тока является причиной возникновения напряжения». Хотя, к данным рассуждениям следует относиться несколько скептически, так движение зарядов (электрический ток) и электрическое поле «подстраиваются» друг к другу, пока между ними не устанавливается определенное соотношение, соответствующее установившемуся режиму. Так при постоянном токе условием стационарности является условие постоянства тока. В цепи переменного тока в установившемся режиме согласуются не только амплитудные значения токов и напряжений, но разность фаз между ними. Иными словами, обсуждаемый здесь причинно-следственный вопрос подобен вопросу о том, «что появилось раньше, курица или яйцо?»

Так как между током и напряжением существует сдвиг фаз равный (~Delta varphi = frac{pi}{2}), то средняя мощность тока через конденсатор равна нулю. Действительно,

= <U_C(t) cdot I_C(t)> = U_{C0} cdot I_{C0} <cos omega t cdot cos left( omega t + frac{pi}{2} right)> = 0) .</center>

Иными словами, потерь энергии при протекании тока через конденсатор в среднем не происходит. Конечно, конденсатор влияет на протекание тока в цепи. В ходе зарядки конденсатора энергия электрического тока превращается в энергию электростатического поля между обкладками конденсатора, а при разрядке конденсатор отдает в цепь накопленную энергию, при этом, средняя энергия, потребляемая конденсатором, остается равной нулю. Поэтому емкостное сопротивление называют реактивным.

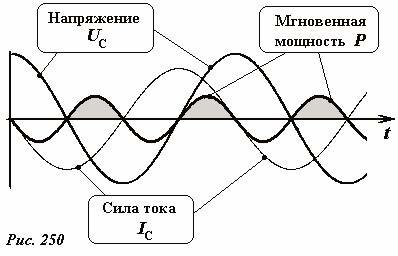
Графики зависимости силы тока, напряжения и мгновенной мощности тока в рассматриваемой цепи показаны на рис. 250.

Заливкой выделены промежутки времени, в течении которых конденсатор накапливает энергия – в этих промежутках сила тока и напряжение имеют один знак.

Уменьшение емкостного сопротивления при возрастании частоты очевидна – чем выше частота тока, тем меньший заряд на конденсаторе успевает накопиться на обкладках конденсатора за половину периода (пока ток идет в одном направлении), тем меньше напряжение на нем, тем меньше он препятствует прохождению тока в цепи. Аналогичные рассуждения справедливы и для объяснения зависимости этого сопротивления от емкости конденсатора.

Вернемся к рассмотрению цепи, показанной на рис. 248, которая описывается уравнением (1). Пренебрегая внутренним сопротивлением источника, запишем явное выражение для напряжения, создаваемого источником

<center>(~U_0 cos omega t = IR + frac{q}{C}) . (8)</center>

Здесь U₀ — амплитудное значение напряжения, равное амплитудному значению ЭДС источника. Кроме того, теперь мы считаем начальную фазу ЭДС источника равной нулю (ранее за нуль мы принимали фазу колебаний напряжения на резисторе).

Используя это уравнение и связь между силой тока и зарядом конденсатора, найдем явное выражение для зависимости силы тока в цепи от времени. Представим эту зависимость в виде

<center>(~I = I_0 cos (omega t + varphi)) , (9)</center>

где I₀ и φ — подлежащие определению амплитудное значение силы тока и разности фаз между колебаниями тока и напряжения источника. Легко заметить, что в этом случае заряд конденсатора изменяется по закону

<center>(~q(t) = q_0 sin (omega t + varphi) = frac{I_0}{omega} sin (omega t + varphi)) . (10)</center>

Для проверки этого соотношения достаточно вычислить производную от приведенной функции и убедится, что она совпадает с функцией (9).

Подставим эти выражения в уравнение (8)

<center>(~U_0 cos omega t = I_0 R cos (omega t + varphi) + frac{I_0}{C omega} sin (omega t + varphi))</center>

и преобразуем тригонометрическую сумму

<center>(~begin{matrix} R cos (omega t + varphi) + frac{1}{C omega} sin (omega t + varphi) = \ = sqrt{R^2 + left( frac{1}{C omega} right)^2} left( frac{R}{sqrt{R^2 + left( frac{1}{C omega} right)^2}} cos (omega t + varphi) + frac{frac{1}{C omega}}{sqrt{R^2 + left( frac{1}{C omega} right)^2}} sin (omega t + varphi) right) = \ = sqrt{R^2 + left( frac{1}{C omega} right)^2} cos (omega t + varphi + varphi_1) end{matrix}) ,</center>

где через φ₁ обозначена величина, удовлетворяющая условию

<center>(~operatorname{tg} varphi_1 = — frac{frac{1}{C omega}}{R}) .</center>

Теперь видно, что для того, чтобы функция (9) являлась решение уравнения (8), необходимо, чтобы ее параметры принимали значения:

амплитуда

<center>(~I_0 = frac{U_0}{sqrt{R^2 + left( frac{1}{C omega} right)^2}}) ; (11)</center>

искомая разность фаз связана с появившимся параметром φ₁ соотношением (varphi + varphi_1 = 0), то есть

<center>(~operatorname{tg} varphi = frac{frac{1}{C omega}}{R}) . (12)</center>

Таким образом, найдена явная зависимость силы тока от времени.

В принципе таким методом, можно рассчитать любую цепь переменного тока. Но такой подход требует громоздких тригонометрических и алгебраических преобразований. К тем же результатам можно прийти гораздо проще, используя формализм векторных диаграмм. Покажем, как метод векторных диаграмм применяется к рассматриваемой цепи. Самое важное при использовании этого метода – построение векторной диаграммы, изображающей колебания токов и напряжений на различных участках цепи.

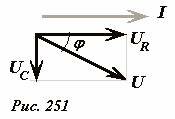
Так как конденсатор и резистор соединены последовательно, то силы токов через них одинаковы в любой момент времени. Изобразим силу тока в идее произвольно направленного вектора (например, горизонтально^[1], как на рис. 251). Далее изобразим векторы колебаний напряжения на резисторе U_R, который параллелен вектору колебаний тока (так как сдвиг фаз между этими колебаниями равен нулю) и напряжения на конденсаторе U_C, который перпендикулярен вектору колебаний тока (так как сдвиг фаз меду ними равен (~frac{pi}{2}) — см. Рис. 249). Сумма этих напряжений равна напряжению источника, поэтому вектор суммы векторов, изображающих колебания U_R и U_C, изображает колебания напряжения источника U(t). Из построенной диаграммы следует, что амплитудные значения рассматриваемых напряжений связаны соотношением (следующим из теоремы Пифагора)

Выражая амплитуды напряжений через амплитуду силы тока с помощью известных соотношений (~U_{R0} = I_{R0} R) и (~U_{C0} = frac{I_{C0}}{C omega}), получаем элементарное уравнение для определения амплитуды силы тока

<center>(~U^2_0 = (I_0 R)^2 + left( frac{I_0}{C omega} right)^2) , (13)</center>

из которого находим амплитуду силы тока в цепи

<center>(~I_0 = frac{U_0}{sqrt{R^2 + left( frac{1}{C omega} right)^2}}) ; (14)</center>

что, естественно, совпадает с выражением (11), полученным ранее громоздким алгебраическим методом. Векторная диаграмма также позволяет легко определить сдвиг фаз между колебаниями силы тока и напряжения источника

<center>(~operatorname{tg} varphi = frac{U_C}{U_R} = frac{frac{1}{C omega}}{R}) , (15)</center>

что также совпадает с полученным ранее.

Как видно, метод векторных диаграмм позволяет полностью рассчитать характеристики цепей переменного тока, гораздо проще, чем рассмотренным выше методом аналитического решения соответствующего уравнения.

Следует подчеркнуть, что физическая сущность обоих методов одна и та же, она выражается уравнением (10), различие только в математическом языке, на котором решается это уравнение.

Рассчитаем, среднюю мощность, развиваемую источником. Мгновенное значение этой мощности равно произведению ЭДС на силу тока (P = varepsilon I). Подставляя явные значения для этих величин и проводя усреднение, получим

<center>(~<P> = <varepsilon I> = <U_0 cos omega t cdot I_0 cos (omega t + varphi)> = U_0 I_0 <cos omega t cdot cos (omega t + varphi)> = frac{U_0 I_0}{2} cos varphi) . (16)</center>

Обратите внимание, что полученное выражение для средней мощности является общим для переменного тока: средняя мощность переменного тока равна половине произведения амплитуд силы тока, напряжения и косинуса разности фаз между ними. Если использовать не амплитудные, а действующие значения силы тока и напряжения, то формула (16) приобретает вид

<center>(~<P> = U_D I_D cos varphi) , (17)</center>

средняя мощность переменного электрического тока равна произведению действующих значений силы тока, напряжения и косинуса разности фаз между ними. Часто косинус сдвига фаз между силой тока и напряжением называют коэффициентом мощности.

В тех случаях, когда по электрической линии требуется передать максимальную мощность, необходимо стремиться, чтобы сдвиг фаз между током и напряжением был минимальным (оптимально – нулевым), так как в этом случае передаваемая мощность будет максимальна.

Применим полученную формулу для расчета мощности тока в рассматриваемой цепи, для чего выразим косинус сдвига фаз из выражения (12) и подставим в формулу (17), в результате чего получим

<center>(~<P> = frac{U_0 I_0}{2} frac{R}{sqrt{R^2 + left( frac{1}{C omega} right)^2}} = frac{1}{2} I^2_0 R = I^2_D R) , (18)</center>

При выводе этого соотношения использована формула (14) для амплитуды силы тока в цепи. Полученный результат очевиден – средняя мощность, развиваемая источником, равна средней мощности теплоты, выделяющейся на резисторе. Этот вывод еще раз подтверждает, что на конденсаторе не происходит потерь энергии электрического тока. Расчет мощности тока также можно проводить с помощью построенной векторной диаграммы, из которой следует, что произведение амплитуды напряжения источника на косинус сдвига фаз равно амплитуде напряжения на резисторе (U_0 cos varphi = U_{R0}), откуда сразу следует формула (18).

Так как амплитудные и действующие значения сил токов и напряжений пропорциональны друг другу, то длины векторов векторных диаграмм можно считать пропорциональными действующим (а не амплитудным) значениям. При таком определении среднее произведение двух гармонических функций равно скалярному произведению векторов, изображающих эти функции.

Примечания

↑ Мы постоянно подчеркиваем, что начальная фаза отдельного колебания, ни в каких процессах не существенна, она может быть изменена простым переносом начала отсчета времени. Физический смысл имеют разности фаз между различными величинами, изменяющимися по гармоническим законам. Здесь мы как бы, очередной раз изменяем «точку отчета» фазы – при горизонтальном расположении вектора колебаний тока мы неявно принимаем начальную фазу колебаний силы тока равной нулю.

<p style=»text-align:right»> Следующая страница

Источник

Сдвиг фаз между током и напряжением в цепи переменного тока

Содержание

1 Определения и основные формулы
2 ПТ и активная нагрузка
3 Конденсатор в цепи ПТ
4 Индуктивность в цепи ПТ
5 Видео по теме

При транспортировке электрической энергии от мест её генерации (тепловые, атомные и гидроэлектростанции) до конечных потребителей необходимо неоднократно варьировать величину напряжения (понижать или повышать). С наибольшей эффективностью эти преобразования удаётся сделать, когда в линиях электропередачи используется переменное напряжение. При этом электрический ток, возникающий в результате действия переменного электрического поля, будет также переменным, изменяясь во времени периодически с такой же частотой. Если в сети присутствуют реактивные элементы (ёмкости, индуктивности), то возникает сдвиг фаз между переменным током и напряжением.

Определения и основные формулы

Переменным принято называть ток, изменяющийся с течением времени как по величине, так и по амплитуде. В английской технической литературе используется термин alternating current (AC). Он переводится как «чередующийся ток» или ток, изменяющий свою полярность.

Периодический переменный ток (ПТ) — это ток, который через идентичные интервалы времени принимает исходную величину, совершая таким образом циклический процесс, аналогичный гармоническому колебанию маятника. Гармонические колебания описываются с помощью синусоидальной функции:

Величина, которая определяется как произведение ω на t и имеет размерность угла (в радианах угол 90 градусов соответствует π/2 радиан), называется фазой синусоидальной переменной. В данном случае тока. Формула справедлива для случая, когда измерение тока стартует с точки отсчёта t = 0. В общем случае рабочая формула выглядит так:

Используя специальный измерительный прибор — осциллограф, можно наблюдать синусоиду напряжения на экране и определять её параметры.

ПТ и активная нагрузка

Если к источнику переменного тока подключено обычное сопротивление (резистор), то согласно закону Ома ток на резисторе, равен:

В приведенной выше формуле величина I₀ = U₀/ R — амплитуда ПТ. Видно, что ток в цепи с активным сопротивлением изменяется с течением времени абсолютно синхронно с напряжением.

Таким образом, на активной нагрузке угол сдвига фаз между током и напряжением равен нулю.

Конденсатор в цепи ПТ

Конструкция конденсатора препятствует протеканию постоянного тока, полностью его блокируя. Поочерёдно заряжаясь и разряжаясь конденсаторные пластины поддерживают ток в цепи, поскольку по определению ток I — это изменение заряда Q за единицу времени:

Ниже представлена картинка, объясняющая подключение конденсатора С к источнику переменного напряжения U.

Напряжение на конденсаторе в любой момент времени равно напряжению:

Тогда заряд Q(t) на обкладках конденсатора определим, используя выражение:

Пользуясь формулой для тока, получим первую производную от заряда по времени, которая равна ёмкостному току I_c(t):

Из графиков, представленных на картинке ниже, видно, что максимальная амплитуда тока наступает на четверть периода раньше, чем напряжения. Из этого следует, что фаза напряжения на π/2 радиан меньше фазы электротока. То есть, в цепи синусоидального тока существует отставание напряжения по фазе (фазовый сдвиг) на π/2.

Данное явление может быть объяснено по-другому. Из курса тригонометрии известно, что:

С помощью формул, приведенных выше, можно получить такое выражение:

Данное соотношение в явном виде показывает, что фазовый сдвиг равен π/2.

Индуктивность в цепи ПТ

Катушка индуктивности в цепях СПТ является реактивным элементом, поскольку ее активное сопротивление практически равно нулю. При подключении катушки также возникает фазовый сдвиг, но его причина несколько иная, чем в цепи с емкостью.

При практически нулевом омическом сопротивлении не может возникнуть короткое замыкание (резкий рост тока), поскольку переменный характер напряжения включает иной механизм сопротивления. Согласно закону, открытому британским учёным Майклом Фарадеем, в катушке появляется переменное магнитное поле, которое создает магнитный поток F, инициирующий появление электродвижущей силы (ЭДС самоиндукции) на концах катушки индуктивности:

В соответствии с законом Фарадея:

Откуда следует, что:

Используя данную формулу, находим определение для тока на индуктивности:

Как известно,

Следовательно, в идеальном индуктивном элементе угол сдвига фаз между напряжением и током равен π/2, причём ток отстаёт по фазе от напряжения.

Из графика видно, что максимум силы тока достигается на четверть периода позже, чем максимум напряжения, что соответствует отставанию по фазе на π/2.

От угла сдвига фаз зависит, какова будет реактивная мощность и, следовательно, коэффициент мощности, который выражается через cosφ и является очень важной характеристикой для оценки эффективности работы электрооборудования. Его значение может находиться в диапазоне от нуля до единицы. Если cosφ = 0, это означает, что в электроцепи присутствуют лишь реактивные токи. На практике такая ситуация невозможна, но чтобы потери мощности, связанные с реактивными токами, были меньше, используют компенсационные устройства.

Принцип действия таких устройств основывается на свойстве конденсаторов и катушек сдвигать фазу в противоположных направлениях. Компенсаторы зачастую используют в производственных цехах, где работает большое количество электрооборудования. Это приводит к ощутимым потерям электроэнергии и ухудшению качества электротока. Устройство компенсации решает подобные проблемы. Им успешно силу тока изменяют, если что-то сдвигают. Обычно такое устройство состоит из блоков конденсаторов довольно большой емкости, которые помещаются в отдельных шкафах.

Видео по теме

Источник

2.3. Анализ цепей синусоидального тока с помощью векторных диаграмм

2.3.1. Цепь, содержащая резистор и индуктивную катушку

§18. Переменный электрический ток

18.4 Емкость в цепи переменного тока. Емкостное сопротивление.

Примечания

Сдвиг фаз между током и напряжением в цепи переменного тока

Определения и основные формулы

ПТ и активная нагрузка

Конденсатор в цепи ПТ

Индуктивность в цепи ПТ

Видео по теме

Не пропустите также: