Угол при вершине равнобедренного треугольника
Как найти угол при вершине равнобедренного треугольника?
Каким может быть угол при вершине равнобедренного треугольника?
Найти угол при вершине равнобедренного треугольника, если угол при его основании равен α.
Дано: ∆ ABC,
∠A=∠C (как углы при основании равнобедренного треугольника).
Значит, α+∠B+α=180º, откуда ∠B=180º-2α.
1) Угол при вершине равнобедренного треугольника равен 180º минус удвоенный угол при его основании.
2) Чем больше угол при основании равнобедренного треугольника, тем меньше угол при его вершине.
3) Если угол при основании α=45º, угол при вершине равнобедренного треугольника — прямой, так как
Если угол при основании больше 45º, угол при вершине — острый, так как
при α>45º произведение 2α>90º, откуда 180º-2α 90º.
Внешний угол треугольника
Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:
Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:
Из этого следует, что
Сократив обе части полученного равенства на одно и тоже число (∠4), получим:
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°
Рассмотрим треугольник ABC:
Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:
(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
∠1 + ∠2 + ∠3 = 540° — (∠4 + ∠5 + ∠6) = 540° — 180° = 360°.
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
http://izamorfix.ru/matematika/planimetriya/vneshnie_ugly_treug.html
http://ru.onlinemschool.com/math/formula/triangle/
Geometry has been a part of human development from ancient times to the modern world. A glimpse of geometry can be seen in crafts of our ancient architecture. Over time the knowledge of shape and structure has developed way further. In recent times, geometry is a major part of developing infrastructure and it has also made its mark in technological development.
Geometry is a branch of mathematics that deals with the study of shapes, structures, and their properties.
The term geometry originates from the Greek words ‘geo’ which means earth and ‘materia’ which means measurement respectively. A distinct approach for geometrical study and its emphasis can be observed. Geometry is being applicable for constructional development. Along with that, it is also being used in computing designs, blueprints, programming, etc. The given article is a study of part of the geometry that is vertex angle and its properties.
Angle
An angle can be defined as a space between two intersecting lines meeting at a common point. The word is derived from the Latin word ‘angulus’ which means ‘ a corner’. They are measured in a degree that ranges from 0degree to 360degree. An angle consists of a common meeting point and two intersecting arms. Angle is a space formed at the meeting point of two intersecting arms. Carpus of Antioch was the first to suppose angle.
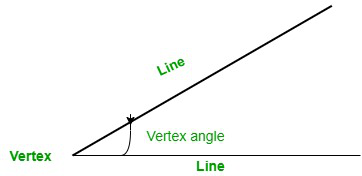
Vertex angle
The point at which arms meet and the angle is measured is the angle’s vertex. And the angle measured at the vertex point is called vertex angle. It can be simply defined as a shape or corner formed by two intersecting lines. The figure given shows the vertex point, angle, and intersecting lines.
How to find the Vertex angle?
Solution:
It is known that the vertex angle is formed at the vertex. Vertex angles are different for each polygon shape. The angle formula for a regular polygon is given by,
The sum of the interior angles in a regular polygon,
Sum = 180 (n – 2)
For the degree of each interior angle in a regular polygon,
Angle (∠) = 180 (n – 2)/n
Where n = number of sides
List of vertex angles for different shapes
Name of shape Vertex angle Equilateral triangle 60°
Square 90°
Pentagon 108°
Hexagon 120°
Heptagon 128.6°
Octagon 135°
Nonagon 140°
Decagon 144°
Sample Questions
Question 1: What is the vertex of a circle?
Answer:
A circle consists of constant curvature. Hence, every point in a circle is a vertex.
Question 2: What is the vertex angle of an isosceles triangle?
Answer:
An isosceles triangle has one vertex angle and two congruent base angles. The sum angle is 180
.
Question 3: Why is vertex angle important?
Answer:
Vertex angle is important as it helps to define the low point and high point of a shape. For example, it defines the low point of a parabola or high point of an isosceles triangle.
Question 4: What is a common vertex?
Answer:
A common vertex is a point shared by two angles.
Question 5: What is the difference between a corner and a vertex?
Answer:
A corner and vertex are the same as both are defined as the meeting point of two intersecting lines.
Question 6: How many vertexes does a cone have?
Answer:
A cone is a shape with one vertex.
Question 7: List out the number of vertex of different shapes.
Answer:
Shapes number of vertices Cube 8 vertices Square 4 vertices Cone 1 vertex Cylinder 0 vertex sphere 0 vertex
Last Updated :
29 Nov, 2021
Like Article
Save Article

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Внешний угол треугольника
Определение и формула внешнего угла треугольника
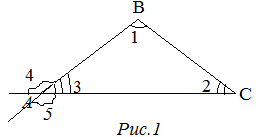
На рисунке 1 внешний угол треугольника при вершине
отмечен номером 4.
Для внешнего угла треугольника справедливо утверждение: Внешний угол треугольника равен сумме внутренних углов, не смежных с ним:
Свойства внешнего угла
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Как найти угол при вершине равнобедренного треугольника?
Каким может быть угол при вершине равнобедренного треугольника?
Задача
Найти угол при вершине равнобедренного треугольника, если угол при его основании равен α.
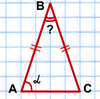
AB=BC,
∠A=α,
Найти: ∠B.
Решение:
Так как сумма углов треугольника равна 180º,
∠A+∠B+∠C=180º.
∠A=∠C (как углы при основании равнобедренного треугольника).
Значит, α+∠B+α=180º, откуда ∠B=180º-2α.
Ответ: 180º-2α.
Выводы:
1) Угол при вершине равнобедренного треугольника равен 180º минус удвоенный угол при его основании.
2) Чем больше угол при основании равнобедренного треугольника, тем меньше угол при его вершине.
3) Если угол при основании α=45º, угол при вершине равнобедренного треугольника — прямой, так как
180º-2∙45º=90º.
Если угол при основании больше 45º, угол при вершине — острый, так как
при α>45º произведение 2α>90º, откуда 180º-2α<90º.
Если угол при основании меньше 45º, угол при вершине равнобедренного треугольника — тупой:
при α<45º произведение 2α<90º, откуда 180º-2α>90º.
Высота равнобедренного треугольника, которая лежит под прямым углом к основанию, создает внутри еще два одинаковых прямоугольных треугольника, являясь катетом в каждом из них. Второй катет такого треугольника представляет собой половину основания, так как эта высота является одновременно медианой и биссектрисой, а гипотенузой будет боковая сторона равнобедренного треугольника. Соответственно, зная высоту и угол α при основании, через прямоугольный треугольник можно узнать стороны равнобедренного треугольника. (рис.88.2)
a=h/sinα
b=2h/tanα
Поскольку сумма всех углов в треугольнике равна 180 градусам, следовательно, угол при вершине будет равен разности 180 градусов и двух углов при основании.
β=180°-2α
Периметр равнобедренного треугольника через высоту и угол α равен сумме двух отношений высоты к синусу угла и двух отношений высоты к тангенсу. Площадь, в свою очередь, преобразовывается в квадрат высоты, деленный на тангенс.
P=2a+b=2h/sinα +2h/tanα
S=hb/2=h^2/tanα
Чтобы найти высоту, опущенную на боковую сторону равнобедренного треугольника (любую, так как они одинаковы), можно воспользоваться готовой формулой через стороны треугольника, заменив их на тригонометрические отношения и упростив выражение. Аналогично вычисляются медианы и биссектрисы через высоту.
m_a=√(a^2+2b^2 )/2=√((h/sinα )^2+2(2h/tanα )^2 )/2=(h√(1/cosα +8))/(2 tanα )
h_a=(b√((4a^2-b^2)))/2a=(b√((4(h/sinα )^2-(2h/tanα )^2)))/(2 h/sinα )=b sin^2α
l_a=(b√(a(2a+b) ))/(a+b)=(2h/tanα √(h/sinα (2 h/sinα +2h/tanα )))/(h/sinα +2h/tanα )=(2h√(2+2/cosα ))/(tanα+2 sinα )
Чтобы вычислить среднюю линию, необходимо разделить на два ту сторону треугольника, которая ей параллельна. Поскольку ни одна из сторон не известна, то средняя линия, параллельная основанию, равна высоте, деленной на тангенс угла α, а средняя линия, параллельная боковой стороне равна высоте, деленной на два синуса угла α. (рис.88.5)
M_b=b/2=h/tanα
M_a=a/2=h/(2 sinα )
Чтобы вычислить радиус вписанной в равнобедренный треугольник окружности, нужно подставить вместо сторон a и b в формулу отношения высоты и тангенса или синуса соответственно, а затем упростить выражение (рис.88.6)
r=b/2 √((a-2b)/(a+2b))=h/tanα √((h/sinα -2 2h/tanα )/(h/sinα +2 2h/tanα ))=h/tanα √((1-4 cosα)/(1+4 cosα ))
Радиус окружности, описанной вокруг равнобедренного треугольника также зависит от обеих сторон – основания и боковой стороны, поэтому его формула видоизменяется аналогично радиусу вписанной окружности. (рис.88.7)
R=a^2/√(4a^2-b^2 )=(h/sinα )^2/√(4(h/sinα )^2-(2h/tanα )^2 )=h/(2 sin^2α )