Как найти угол наименьшего отклонения

From Wikipedia, the free encyclopedia

In a prism, the angle of deviation (δ) decreases with increase in the angle of incidence (i) up to a particular angle. This angle of incidence where the angle of deviation in a prism is minimum is called the minimum deviation position of the prism and that very deviation angle is known as the minimum angle of deviation (denoted by δ_min, D_λ, or D_m).

Light is deflected as it enters a material with refractive index > 1.

A ray of light is deflected twice in a prism. The sum of these deflections is the deviation angle.

When the entrance and exit angles are equal, the deviation angle of a ray passing through a prism will be minimal.

The angle of minimum deviation is related with the refractive index as:

${displaystyle n_{21}={dfrac {sin left({dfrac {A+D_{m}}{2}}right)}{sin left({dfrac {A}{2}}right)}}}$

This is useful to calculate the refractive index of a material. Rainbow and halo occur at minimum deviation. Also, a thin prism is always set at minimum deviation.

Formula[edit]

This section needs expansion with: the derivation of the expression for minimum deviation using Calculus. You can help by adding to it. (June 2020)

In minimum deviation, the refracted ray in the prism is parallel to its base. In other words, the light ray is symmetrical about the axis of symmetry of the prism.^[1]^[2]^[3]
Also, the angles of refractions are equal i.e. r₁ = r₂. And, the angle of incidence and angle of emergence equal each other (i = e). This is clearly visible in the graph below.

The formula for minimum deviation can be derived by exploiting the geometry in the prism. The approach involves replacing the variables in the Snell’s law in terms of the Deviation and Prism Angles by making the use of the above properties.

From the angle sum of ,

${displaystyle A+angle OPQ+angle OQP=180^{circ }}$
${displaystyle implies A=180^{circ }-(90-r)-(90-r)}$
${displaystyle implies r={frac {A}{2}}}$

Using the exterior angle theorem in ,

${displaystyle D_{m}=angle RPQ+angle RQP}$
${displaystyle implies D_{m}=i-r+i-r}$
${displaystyle implies 2r+D_{m}=2i}$
${displaystyle implies A+D_{m}=2i}$
${displaystyle implies i={frac {A+D_{m}}{2}}}$

This can also be derived by putting i = e in the prism formula: i + e = A + δ

From Snell’s law,

${displaystyle n_{21}={dfrac {sin i}{sin r}}}$

${displaystyle therefore n_{21}={dfrac {sin left({dfrac {A+D_{m}}{2}}right)}{sin left({dfrac {A}{2}}right)}}}$

^[4]^[3]^[1]^[2]^[5]^{[excessive citations]}

${displaystyle therefore D_{m}=2sin ^{-1}left(nsin left({frac {A}{2}}right)right)-A}$

(where n is the refractive index, A is the Angle of Prism and D_m is the Minimum Angle of Deviation.)

This is a convenient way used to measure the refractive index of a material(liquid or gas) by directing a light ray through a prism of negligible thickness at minimum deviation filled with the material or in a glass prism dipped in it.^[5]^[3]^[1]^[6]

Worked out examples:

The refractive index of glass is 1.5. The minimum angle of deviation for an equilateral prism along with the corresponding angle of incidence is desired.
Answer: 37°, 49° Solution: Here, A = 60°, n = 1.5 Plugging them in the above formula, ${textstyle {frac {sin left({frac {60+delta }{2}}right)}{sin left({frac {60}{2}}right)}}=1.5}$ ${textstyle implies {frac {sin left(30+{frac {delta }{2}}right)}{sin(30)}}=1.5}$ ${textstyle implies sin left(30+{frac {delta }{2}}right)=1.5times 0.5}$ ${textstyle implies 30+{frac {delta }{2}}=sin ^{-1}(0.75)}$ ${textstyle implies {frac {delta }{2}}=48.6-30}$ ${textstyle therefore delta approx 37^{circ }}$ Also, ${textstyle i={frac {(A+delta )}{2}}={frac {60+2times 18.6}{2}}approx 49^{circ }}$ This is also apparent in the graph below.

The refractive index of glass is 1.5. The minimum angle of deviation for an equilateral prism along with the corresponding angle of incidence is desired.

Answer: 37°, 49°

Solution:

Here, A = 60°, n = 1.5

Plugging them in the above formula,

${textstyle {frac {sin left({frac {60+delta }{2}}right)}{sin left({frac {60}{2}}right)}}=1.5}$

${textstyle implies {frac {sin left(30+{frac {delta }{2}}right)}{sin(30)}}=1.5}$

${textstyle implies sin left(30+{frac {delta }{2}}right)=1.5times 0.5}$

${textstyle implies 30+{frac {delta }{2}}=sin ^{-1}(0.75)}$

${textstyle implies {frac {delta }{2}}=48.6-30}$

${textstyle therefore delta approx 37^{circ }}$

Also,

${textstyle i={frac {(A+delta )}{2}}={frac {60+2times 18.6}{2}}approx 49^{circ }}$

This is also apparent in the graph below.

If the minimum angle of deviation of a prism of refractive index 1.4 equals its refracting angle, the angle of the prism is desired.
Answer: 60° Solution: Here, ${textstyle implies delta ={frac {A}{2}}}$ Using the above formula, ${textstyle {frac {sin left({frac {A+{frac {A}{2}}}{2}}right)}{sin left({frac {A}{2}}right)}}=1.4}$ ${textstyle implies {frac {sin left({frac {3A}{4}}right)}{sin left({frac {A}{2}}right)}}={frac {frac {1}{2}}{frac {1}{sqrt {2}}}}}$ ${textstyle implies {frac {sin left({frac {3A}{4}}right)}{sin left({frac {A}{2}}right)}}={frac {sin 45^{circ }}{sin 30^{circ }}}}$ ${textstyle therefore A=60^{circ }}$

If the minimum angle of deviation of a prism of refractive index 1.4 equals its refracting angle, the angle of the prism is desired.

Answer: 60°

Solution:

Here,

${textstyle implies delta ={frac {A}{2}}}$

Using the above formula,

${textstyle {frac {sin left({frac {A+{frac {A}{2}}}{2}}right)}{sin left({frac {A}{2}}right)}}=1.4}$

${textstyle implies {frac {sin left({frac {3A}{4}}right)}{sin left({frac {A}{2}}right)}}={frac {frac {1}{2}}{frac {1}{sqrt {2}}}}}$

${textstyle implies {frac {sin left({frac {3A}{4}}right)}{sin left({frac {A}{2}}right)}}={frac {sin 45^{circ }}{sin 30^{circ }}}}$

${textstyle therefore A=60^{circ }}$

Also, the variation of the angle of deviation with an arbitrary angle of incidence can be encapsulated into a single equation by expressing e in terms of i in the prism formula using Snell’s law:

${displaystyle delta =i-A+sin ^{-1}left(ncdot sin left(A-sin ^{-1}left({frac {sin i}{n}}right)right)right)}$

Finding the minima of this equation will also give the same relation for minimum deviation as above.

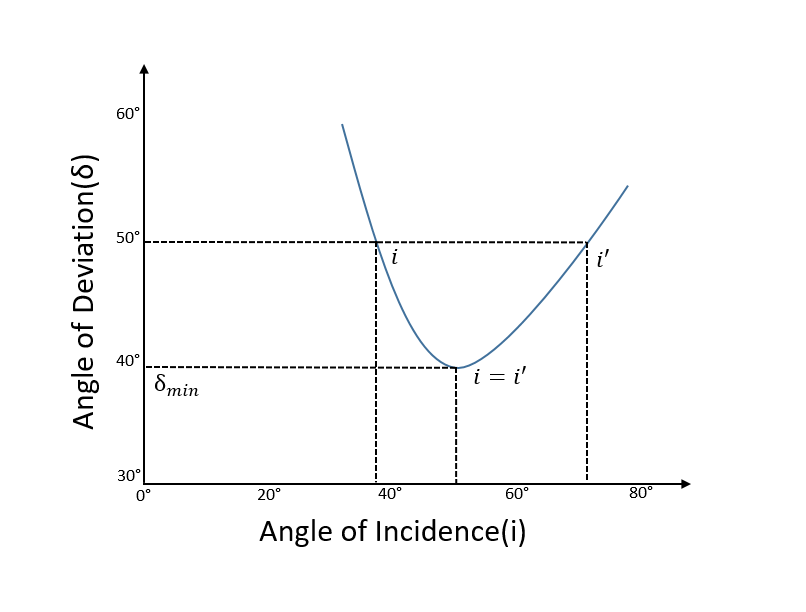
In this graph of the angle of deviation vs the angle of incidence, δ corresponds to two values of i and e(i’). For minimum deviation, however, i equals e.

For thin prism[edit]

In a thin or small angle prism, as the angles become very small, the sine of the angle nearly equals the angle itself and this yields many useful results.

Because D_m and A are very small,

${displaystyle {begin{aligned}n&approx {dfrac {frac {A+D_{m}}{2}}{frac {A}{2}}}\n&={frac {A+D_{m}}{A}}\D_{m}&=An-Aend{aligned}}}$

${displaystyle therefore D_{m}=A(n-1)}$

^[1]^[4]

Interestingly, using a similar approach with the Snell’s law and the prism formula for an in general thin-prism ends up in the very same result for the deviation angle.

Because i, e and r are small,

${displaystyle napprox {frac {i}{r_{1}}},napprox {frac {e}{r_{2}}}}$

From the prism formula,
${displaystyle {begin{aligned}delta &=nr_{1}+nr_{2}-A\&=n(r_{1}+r_{2})-A\&=nA-A\&=A(n-1)end{aligned}}}$

Thus, it can be said that a thin prism is always in minimum deviation.

Experimental determination[edit]

This section needs expansion with: virtual simulation, video, detailed explanation, etc. You can help by adding to it. (May 2020)

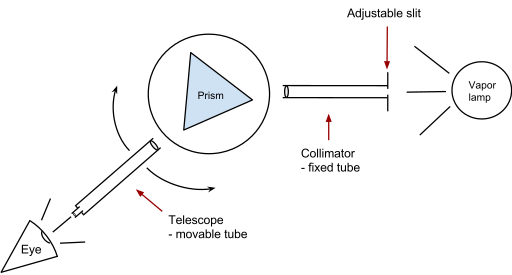
Minimum deviation can be found manually or with spectrometer. Either the prism is kept fixed and the incidence angle is adjusted or the prism is rotated keeping the light source fixed.^[7]^[8]^[9]^[10]^[11]

Minimum angle of dispersion[edit]

The angle of dispersion in a prism

This section needs expansion. You can help by adding to it. (May 2020)

The minimum angle of dispersion^[12] for white light is the difference in minimum deviation angle between red and violet rays of a light ray through a prism.^[2]

For a thin prism, the deviation of violet light, ${displaystyle delta _{v}}$ is ${displaystyle (n_{v}-1)A}$ and that of red light, ${displaystyle delta _{r}}$ is ${displaystyle (n_{r}-1)A}$ . The difference in the deviation between red and violet light, ${displaystyle (delta _{v}-delta _{r})=(n_{v}-n_{r})A}$ is called the Angular Dispersion produced by the prism.

Applications[edit]

Drawing radii to the points of interference reveals that the angles of refraction are equal, thereby proving minimum deviation.

One of the factors that causes a rainbow is the bunching of light rays at the minimum deviation angle that is close to the rainbow angle (42°).^[3]^[13]

It is also responsible for phenomena like halos and sundogs, produced by the deviation of sunlight in mini prisms of hexagonal ice crystals in the air bending light with a minimum deviation of 22°.^[3]^[14]

References[edit]

^ ^a ^b ^c ^d «Chapter Nine, RAY OPTICS AND OPTICAL INSTRUMENTS». Physics Part II Textbook for Class IX (PDF). NCERT. p. 331.
^ ^a ^b ^c «Optics-Prism». A-Level Physics Tutor.
^ ^a ^b ^c ^d ^e Mark A. Peterson. «Minimum Deviation by a Prism». mtholyoke. Mount Holyoke College. Archived from the original on 2019-05-23.
^ ^a ^b «Refraction through Prisms». SchoolPhysics.
^ ^a ^b «Prism». HyperPhysics.
^ «Determination of the refractive index of the material of the prism». BrainKart.
^ «Angle of Minimum Deviation». Scribd.
^ «Theory of the Prism Spectrometer». www.ukessays.com.
^ «Experimental set up for the measurements of angle of minimum deviation using prism spectrometer». ResearchGate.
^ «Measurement of the dispersion of glass with a prism spectrometer». studylib.net.
^ «Determination of Minimum Deviation For Given Prism». BYJU’S.
^ «ISRO», SpringerReference, Berlin/Heidelberg: Springer-Verlag, 2011, doi:10.1007/springerreference_222294, retrieved 2021-10-22
^ «Rainbow». www.schoolphysics.co.uk.
^ «Halo 22°». HyperPhysics.

External links[edit]

Minimum Deviation Part 1 and Part 2 at Khan Academy
Refraction through a Prism in NCERT Tectbook
Minimum Deviation by Prism by Mark A Peterson, Mount Holyoke College

Источник

На рынке кроме монохроматоров и спектрографов широко представлены приборы, доукомплектованные всем необходимым для решения какого-то конкретного круга задач. Их называют спектрометрами, квантометрами, спектрофотометрами, спектрофлуориметрами и т.д. Но все это – просто варианты использования СП и Вы легко разберетесь в их устройстве, если будете знать, как устроено их ядро.

В этом пособии рассматриваются параметры основных элементов СП – призмы и дифракционной решетки, описаны некоторые необходимые оптические дополнительные элементы и устройства и затем – оптические схемы некоторых реальных СП.

Во II физической лаборатории Вы будете работать с несколькими разными СП. Их устройство Вы здесь также найдете.

Cпектральной призмой называется многогранник, сделанный из прозрачного вещества, обладающего значительной дисперсией показателя преломления dn/dλ.

Для изготовления хороших приборов должен использоваться материал с очень высокой прозрачностью, дисперсией, оптической однородностью и изотропностью. Удовлетворить всем этим требованиям трудно, поэтому для различных областей спектра используются разные материалы. Например, для ультрафиолетовой области спектра пригоден кристаллический или плавленый кварц, для видимой области спектра основным материалом является стекло, в ИК-области – ионные кристаллы и т.д.

Обычно в приборах используются сложные, составные призмы, позволяющие получать и высокое разрешение, и удобную форму фокальной поверхности. Здесь мы рассмотрим только основные свойства простейших трехгранных призм. Более подробно с этим вопросом можно ознакомиться по книгам [1, 2, 3, 4, 5, 6]

Рассмотрим призму, форма которой приведена на рис. 2.1.1. Дву-

гранный угол с ребром АВ называется преломляющим. Плоскости АВСD и АВС’D’ называются преломляющими гранями призмы. Плоскость, перпендикулярная ребру призмы и проходящая через его середину, называется плоскостью главного сечения.

Пусть на грань призмы с преломляющим углом А и коэффициентом преломления n в плоскости главного сечения падает пучок лучей,

122

составляющих угол α1 с нормалью N1 к первой грани призмы (рис. 2.1.2). Угол преломления этого луча обозначим β1, угол падения его на вторую грань – β2 и угол выхода из нее – α2. Угол ϕ, составленный падающим и выходящим лучами, называется углом отклонения.

	A	N1	A


		α1	ϕ	N2
		α2

C’	C	β1 β2


D’	D	Рис. 2.1.2 Обозначения к соотношениям
Рис. 2.1.1	Простейшая
	призма		(2.1.1)–(2.1.4)

Закон преломления и простые геометрические соображения дают четыре уравнения, связывающие семь величин:

ϕ = α1 + α2 – А,	(2.1.1)
А = β1 + β2,	(2.1.2)
sinα1	= n sinβ1,	(2.1.3)
sinα2	= n sinβ2.	(2.1.4)

Обычно величины А, n и α1 заданы, а этого достаточно, чтобы определить четыре остальные.

2.1.1. Угол наименьшего отклонения

Ни в какой реальной оптической схеме не возможно создать идеально параллельный пучок лучей. Следовательно, всегда будут присутствовать аберрации, обусловленные тем фактом, что угол отклонения ϕ зависит от угла падения α1, причем нелинейно. Для того, чтобы минимизировать эти аберрации, следует использовать такую установку призмы, при которой зависимость ϕ(α) минимальна, т.е. – в экстремуме. Система уравнений (2.1.1) – (2.1.4) позволяет найти условия экстремума ϕ(α). Для этого приравняем нулю производную dϕ/dα1 и из (2.1.1) получим:

	dα2	= −1 .	(2.1.5)
	dα

1
Дифференцирование остальных уравнений даст:
		dβ1+dβ2 = 0,	(2.1.6)
		123

cosα1 dα1	= n cosβ1 dβ1 ,	(2.1.7)
cosα2 dα2	= n cosβ2 dβ2 .	(2.1.8)
Отсюда:
	dα2	= −	cos α1 cosβ2	= −1 .	(2.1.9)
	dα1
		cos α2 cosβ1
Из (2.1.9), заменив углы β на α по (2.1.3) и (2.1.4), получим иско-
мое условие:

cos2 α	=	cos2 α	2	.	(2.1.10)
1
n2 −sin2 α
	n2 −sin2 α	2
1

Это равенство удовлетворяется при α1 = α2 = α, что соответствует минимуму угла отклонения ϕ. Из α1 = α2 следует и β1 = β2. Падающий и выходящий лучи оказываются симметричными по отношению к граням призмы.

В условиях минимального отклонения угол падения α, преломляющий угол призмы А, угол отклонения ϕ и показатель преломления n связаны соотношением:

sinα = n sin(A 2)= sin((A + ϕ) 2),

(2.1.11)

которое легко получить из (2.1.1) – (2.1.4).

Во всех практических схемах используется установка призмы в минимуме отклонения, тем более, что такая установка, как мы увидим позже, замечательна во многих отношениях. В том числе и разрешающая способность призмы максимальна именно в минимуме отклонения.

2.1.2. Угловая дисперсия

Для вычисления угловой дисперсии Dϕ = dϕ/dλ продифференцируем по λ основные уравнения (2.1.1) – (2.1.4). Учтем, что dα1/dλ = 0, и получим:

dϕ	=	dα2		,					(2.1.12)
dλ		dλ

cosα2	dα2		= ncosβ2	dβ2	+ sinβ2	dn	(из (2.1.4)),	(2.1.13)
dλ		dλ	dλ

								124

sinβ1

= −ncosβ1

dβ1

(из 2.1.11),

(2.1.14)

dλ

dβ1

= −

dβ2

(2.1.15)

dλ

Отсюда:

dϕ

sin A

(2.1.16)

dλ

dλ cosβ cosα

или, в минимуме отклонения, т.е. при α1 = α2 = α и β1 = β2 = А/2:

dϕ

sin(A / 2)

= 2

(2.1.17)

dλ

{1 − n2 sin2 (A / 2)}

При продвижении в длинноволновую сторону уменьшается и

, и n. А с уменьшением n растет знаменатель в (2.1.17), так что дис-

dλ

персия призмы

dϕ

убывает быстрее, чем дисперсия ее материала,

dλ

2.1.3. Угловое увеличение

Пусть на поверхность призмы падает узкий пучок лучей из точки I, рис. 2.1.3а. Малый угол между крайними лучами пучка в плоскости главного сечения обозначим θ. В результате преломления продолжения этих лучей пересекутся в точке I′ под углом ψ, который отличен от θ. Величина Г = ψ/θ называется угловым увеличением призмы. Угол θ равен изменению угла падения Δα1 для крайних лучей пучка, а угол ψ – изменению угла выхода лучей —Δα2 из призмы. Полагая углы ψ и θ малыми, заменим конечные разности дифференциалами. Таким образом,

Г= –dα2/dα1.

Вобщем случае, см. (2.1.5) – (2.1.9), получим:

Γ =	cosα1 cosβ2	.	(2.1.18)

	cosα	2	cosβ
		1

При установке в минимуме отклонения угловое увеличение равно единице. Если α1 < α, то Г > 1, при α1 > α – Г < 1. Если Г ≠ 1, то в меридиональной плоскости размер пучка, либо падающего, либо прошедшего, при прохождении через призму должен уменьшиться. На рис.

125

Источник

Условие, при котором угол отклонения минимален в призме

В призме угол отклонения (δ { displaystyle delta} delta ) уменьшается с увеличением угла падения (i { displaystyle i}) до определенного угла. Этот угол падения, при котором угол отклонения призмы минимален, называется положением минимального отклонения призмы, а сам угол отклонения известен как минимальный угол отклонения (обозначен на δ min { displaystyle delta _ {min}} ${ displaystyle delta _ {min}}$ , D λ { displaystyle D _ { lambda}} ${ displaystyle D _ { lambda}}$ или D m { displaystyle D_ {m}} ${ displaystyle D_ {m}}$ ).

Свет отклоняется при попадании в материал с показателем преломления>1. Луч света дважды отклоняется в призме. Сумма этих отклонений и составляет угол отклонения. Когда углы входа и выхода равны, угол отклонения луча, проходящего через призму, будет минимальным.

В режиме минимального отклонения преломленный луч в призме равен параллельно его основанию. Другими словами, световой луч симметричен относительно оси симметрии призмы. Кроме того, углы преломления равны, то есть r 1 = r 2 { displaystyle r_ {1} = r_ {2}} ${ displaystyle r_ {1} = r_ {2}}$ . И угол падения и угол выхода равны друг другу (i = e { displaystyle i = e}). Это хорошо видно на графике в следующем разделе.

Содержание

1 Формула и график
- 1.1 Для тонкой призмы
2 Экспериментальное определение
3 Минимальный угол рассеивания
4 Применения
5 См. Также
6 Ссылки / дополнительная информация Чтение
7 Внешние ссылки

Формула и график

Формула для минимального отклонения может быть получена путем использования геометрии призмы. Подход включает замену переменных в Законе Снеллиуса с точки зрения отклонения и углов призмы с использованием вышеуказанных свойств.

Из суммы углов из △ OPQ { textstyle треугольник OPQ},

A + ∠ OPQ + ∠ OQP = 180 ∘ { displaystyle A + angle OPQ + angle OQP = 180 ^ { circ}} ${ displaystyle A + angle OPQ + angle OQP = 180 ^ { circ}}$

⟹ A = 180 ∘ — (90 — r) — (90 — r) { displaystyle подразумевает A = 180 ^ { circ} — (90-r) — (90- r)} ${ displaystyle подразумевает A = 180 ^ { circ} - (90-r) - (90-r)}$

⟹ r = A 2 { displaystyle подразумевает r = { frac {A} {2}}} ${ displaystyle подразумевает r = { frac {A} {2}}}$

Использование теоремы о внешнем угле в △ PQR { textstyle треугольник PQR},

D m = ∠ RPQ + ∠ RQP { displaystyle D_ {m} = angle RPQ + angle RQP} ${ displaystyle D_ {m} = angle RPQ + angle RQP}$

⟹ D m = i — r + i — r { displaystyle означает, что D_ {m} = i-r + ir} ${ displaystyle подразумевает D_ {m} = i-r + ir}$

⟹ 2 r + D m = 2 i { displaystyle подразумевает 2r + D_ {m} = 2i} ${ displaystyle подразумевает 2r + D_ {m} = 2i}$

⟹ A + D m = 2 i { displaystyle подразумевает A + D_ {m} = 2i} ${ displaystyle подразумевает A + D_ {m} = 2i}$

⟹ i = A + D m 2 { displaystyle implies i = { frac {A + D_ {m}} {2}}} ${ displaystyle подразумевает i = { frac {A + D_ {m}} {2}}}$

Это также можно получить, поместив i = e { textstyle i = e}в: i + e = A + δ { textstyle i + e = A + delta}

Из закона Снеллиуса,

n 21 = грех ⁡ i sin ⁡ r { displaystyle n_ {21} = { dfrac { sin i} { sin r}}} ${ displaystyle n_ {21} = { dfrac { sin i} { sin r}}}$

∴ n 21 = sin ⁡ (A + D m 2) грех ⁡ (A 2) { displaystyle , следовательно, n_ {21} = { dfrac { sin left ({ dfrac {A + D_ {m}} {2}} right)} { sin left ({ dfrac {A} {2}} right)}}}

${ displaystyle , следовательно, n_ {21} = { dfrac { sin left ({ dfrac {A + D_ {m}} {2}} right)} { sin left ({ dfrac {A} {2}} right)}}}$

∴ D m = 2 sin — 1 ⁡ (n sin ⁡ (A 2)) — A { displaystyle , следовательно, D_ {m} = 2 sin ^ {- 1} left (n sin left ({ frac {A} {2}} right) right) -A}

${ displaystyle , следовательно, D_ {m} = 2 sin ^ {- 1} left (n sin left ({ frac {A} {2}} right) right) -A}$

(где n { textstyle n}— показатель преломления, A { textstyle A}— угол призмы и D m { textstyle D_ {m}} ${ textstyle D_ {m}}$ — минимальный угол отклонения.)

Это удобный способ, используемый для измерения показателя преломления материала (жидкости или газа) путем направления светового луча через призму пренебрежимо малого толщина при минимальном отклонении заполненного материала или погруженной в него стеклянной призмы.

Проработанные примеры:

Показатель преломления стекла 1,5. Желателен минимальный угол отклонения для равносторонней призмы вместе с соответствующим углом падения.
Ответ: 37 ∘, 49 ∘ { displaystyle 37 ^ { circ}, 49 ^ { circ}} ${ displaystyle 37 ^ { circ }, 49 ^ { circ}}$ Сол.: Здесь A = 60 ∘ { textstyle A = 60 ^ { circ}} ${ textstyle A = 60 ^ { circ}}$ , n = 1.5 { textstyle n = 1.5} Подключив их к формула выше, грех ⁡ (60 + δ 2) грех ⁡ (60 2) = 1,5 { textstyle { frac { sin left ({ frac {60+ delta} {2}} right) } { sin left ({ frac {60} {2}} right)}} = 1,5} ${ textstyle { frac { sin left ({ frac {60+ delta} {2}} right)} { sin left ({ frac {60} {2}} right)}} = 1,5}$ ⟹ sin ⁡ (30 + δ 2) sin ⁡ (30) = 1,5 { textstyle подразумевает { frac { sin left (30 + { frac { delta} {2}} right)} { sin (30)}} = 1,5} ${ textstyle подразумевает { frac { sin left (30 + { frac { delta} {2}} right)} { sin (30)}} = 1,5}$ ⟹ sin ⁡ (30 + δ 2) = 1,5 × 0,5 { textstyle подразумевает грех влево (30 + { frac { delta} {2}} вправо) = 1,5 раз 0,5} ${ textstyle подразумевает sin left (30 + { frac { delta} {2}} right) = 1,5 times 0,5}$ ⟹ 30 + δ 2 = грех — 1 ⁡ (0,75) { textstyle подразумевает 30 + { frac { delta} {2}} = sin ^ {- 1} (0,75)} ${ textstyle подразумевает 30 + { frac { delta} {2}} = sin ^ {- 1} (0,75)}$ ⟹ δ 2 = 48,6 — 30 { textstyle подразумевает { frac { дельта} {2}} = 48,6-30} ${ textstyle подразумевает { frac { delta} {2}} = 48.6-30}$ ⟹ δ = 2 × 18,6 { textstyle подразумевает delta = 2 times 18,6} ∴ δ ≈ 37 ∘ { textstyle поэтому delta приблизительно 37 ^ { circ}} ${ textstyle поэтому delta примерно 37 ^ { circ}}$ Кроме того, i = (A + δ) 2 = 60 + 2 × 18,6 2 ≈ 49 ∘ { textstyle i = { frac {(A + delta)} {2}} = { frac {60 + 2 times 18.6} {2}} приблизительно 49 ^ { circ}} ${ textstyle i = { frac {(A + delta)} {2}} = { frac {60 + 2 times 18,6} {2}} приблизительно 49 ^ { circ}}$ Это также видно на графике ниже.

Показатель преломления стекла 1,5. Желателен минимальный угол отклонения для равносторонней призмы вместе с соответствующим углом падения.

Ответ: 37 ∘, 49 ∘ { displaystyle 37 ^ { circ}, 49 ^ { circ}} ${ displaystyle 37 ^ { circ }, 49 ^ { circ}}$

Сол.:

Здесь A = 60 ∘ { textstyle A = 60 ^ { circ}} ${ textstyle A = 60 ^ { circ}}$ , n = 1.5 { textstyle n = 1.5}

Подключив их к формула выше,

грех ⁡ (60 + δ 2) грех ⁡ (60 2) = 1,5 { textstyle { frac { sin left ({ frac {60+ delta} {2}} right) } { sin left ({ frac {60} {2}} right)}} = 1,5} ${ textstyle { frac { sin left ({ frac {60+ delta} {2}} right)} { sin left ({ frac {60} {2}} right)}} = 1,5}$

⟹ sin ⁡ (30 + δ 2) sin ⁡ (30) = 1,5 { textstyle подразумевает { frac { sin left (30 + { frac { delta} {2}} right)} { sin (30)}} = 1,5} ${ textstyle подразумевает { frac { sin left (30 + { frac { delta} {2}} right)} { sin (30)}} = 1,5}$

⟹ sin ⁡ (30 + δ 2) = 1,5 × 0,5 { textstyle подразумевает грех влево (30 + { frac { delta} {2}} вправо) = 1,5 раз 0,5} ${ textstyle подразумевает sin left (30 + { frac { delta} {2}} right) = 1,5 times 0,5}$

⟹ 30 + δ 2 = грех — 1 ⁡ (0,75) { textstyle подразумевает 30 + { frac { delta} {2}} = sin ^ {- 1} (0,75)} ${ textstyle подразумевает 30 + { frac { delta} {2}} = sin ^ {- 1} (0,75)}$

⟹ δ 2 = 48,6 — 30 { textstyle подразумевает { frac { дельта} {2}} = 48,6-30} ${ textstyle подразумевает { frac { delta} {2}} = 48.6-30}$

⟹ δ = 2 × 18,6 { textstyle подразумевает delta = 2 times 18,6}

∴ δ ≈ 37 ∘ { textstyle поэтому delta приблизительно 37 ^ { circ}} ${ textstyle поэтому delta примерно 37 ^ { circ}}$

Кроме того,

i = (A + δ) 2 = 60 + 2 × 18,6 2 ≈ 49 ∘ { textstyle i = { frac {(A + delta)} {2}} = { frac {60 + 2 times 18.6} {2}} приблизительно 49 ^ { circ}} ${ textstyle i = { frac {(A + delta)} {2}} = { frac {60 + 2 times 18,6} {2}} приблизительно 49 ^ { circ}}$

Это также видно на графике ниже.

Если минимальный угол отклонения призмы с показателем преломления 1,4 равен ее углу преломления, желателен угол призмы.
Ответ: 60 ∘ { displaystyle 60 ^ { circ}} ${ displaystyle 60 ^ { circ}}$ Сол.: Здесь δ = r { textstyle delta = r} ⟹ δ = A 2 { textstyle подразумевает delta = { frac {A} {2} }} ${ textstyle подразумевает delta = { frac {A} {2}}}$ Используя приведенную выше формулу, sin ⁡ (A + A 2 2) sin ⁡ (A 2) = 1.4 { textstyle { frac { sin left ({ frac {A + { frac {A} {2}}} {2}} right)} { sin left ({ frac {A} {2}} right)}} = 1.4} ${ textstyle { frac { sin left ({ frac {A + { frac {A} {2}}} {2}} right)} { sin left ({ frac {A} {2}} справа)}} = 1,4}$ ⟹ sin ⁡ (3 A 4) грех ⁡ (A 2) = 1 2 1 2 { textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac { A} {2}} right)}} = { frac { frac {1} {2}} { frac {1} { sqrt {2}}}}} ${ textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac {A} {2}} right)}} = { frac { frac {1} {2}} { frac {1} { sqrt {2} }}}}$ ⟹ sin ⁡ (3 A 4) грех ⁡ (A 2) = грех ⁡ 45 ∘ грех ⁡ 30 ∘ { textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac {A} {2}} right)}} = { frac { sin 45 ^ { circ}} { sin 30 ^ { circ}}}} ${ textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac {A} {2}} right)}} = { frac { sin 45 ^ { circ}} { sin 30 ^ { circ}}}}$ ∴ A = 60 ∘ { textstyle , следовательно, A = 60 ^ { circ}} ${ textstyle следовательно, A = 60 ^ { circ}}$

Если минимальный угол отклонения призмы с показателем преломления 1,4 равен ее углу преломления, желателен угол призмы.

Ответ: 60 ∘ { displaystyle 60 ^ { circ}} ${ displaystyle 60 ^ { circ}}$

Сол.:

Здесь δ = r { textstyle delta = r}

⟹ δ = A 2 { textstyle подразумевает delta = { frac {A} {2} }} ${ textstyle подразумевает delta = { frac {A} {2}}}$

Используя приведенную выше формулу,

sin ⁡ (A + A 2 2) sin ⁡ (A 2) = 1.4 { textstyle { frac { sin left ({ frac {A + { frac {A} {2}}} {2}} right)} { sin left ({ frac {A} {2}} right)}} = 1.4} ${ textstyle { frac { sin left ({ frac {A + { frac {A} {2}}} {2}} right)} { sin left ({ frac {A} {2}} справа)}} = 1,4}$

⟹ sin ⁡ (3 A 4) грех ⁡ (A 2) = 1 2 1 2 { textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac { A} {2}} right)}} = { frac { frac {1} {2}} { frac {1} { sqrt {2}}}}} ${ textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac {A} {2}} right)}} = { frac { frac {1} {2}} { frac {1} { sqrt {2} }}}}$

⟹ sin ⁡ (3 A 4) грех ⁡ (A 2) = грех ⁡ 45 ∘ грех ⁡ 30 ∘ { textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac {A} {2}} right)}} = { frac { sin 45 ^ { circ}} { sin 30 ^ { circ}}}} ${ textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac {A} {2}} right)}} = { frac { sin 45 ^ { circ}} { sin 30 ^ { circ}}}}$

∴ A = 60 ∘ { textstyle , следовательно, A = 60 ^ { circ}} ${ textstyle следовательно, A = 60 ^ { circ}}$

Кроме того, изменение угла отклонения с вилкой Маршрутный угол падения можно заключить в одно уравнение, выразив e { textstyle e}через i { textstyle i}в формуле призмы используя закон Снеллиуса:

δ = i — A + sin — 1 ⁡ (n ⋅ sin ⁡ (A — sin — 1 ⁡ (sin ⁡ in))) { displaystyle delta = i-A + sin ^ {- 1} left (n cdot sin left (A- sin ^ {- 1} left ({ frac { sin i} {n}} right) right) right)}

${ displaystyle delta = i-A + sin ^ {- 1} left (n cdot sin left (A - sin ^ {- 1} left ({ frac { sin i} {n}} right) right) right)}$

Нахождение минимумов этого уравнения также даст такое же соотношение для минимального отклонения, как указано выше.

Для тонкой призмы

В тонкой или малоугловой призме, когда углы становятся очень маленькими, синус угла почти равен самому углу, и это дает много полезных результатов.

∵ D m { textstyle , потому что D_ {m}} ${ textstyle , потому что D_ {m}}$ и A { textstyle A}очень маленькие,

⟹ n ≈ (A + D м 2) (A 2) { displaystyle подразумевает п приблизительно { гидроразрыва { left ({ frac {A + D_ {m}} {2}} right)} { left ({ frac {A} {2}} right)}}} ${ Displaystyle impli es n приблизительно { frac { left ({ frac {A + D_ {m}} {2}} right)} { left ({ frac {A} {2}} right)}}}$

⟹ n = A + D m A { displaystyle подразумевает n = { frac {A + D_ {m}} {A}}} ${ displaystyle подразумевает n = { frac {A + D_ { m}} {A}}}$

⟹ A N — A = D m { displaystyle подразумевает An-A = D_ {m}} ${ displaystyle подразумевает An-A = D_ {m}}$

∴ D m = A (n — 1) { displaystyle , следовательно, D_ {m} = A (n-1)}

${ displaystyle , следовательно, D_ {m} = A (n-1)}$

Интересно, что использование аналогичного подхода с законом Снеллиуса и для тонкой призмы в целом приводит к тому же результату для угла отклонения.

∵ i, e { textstyle , потому что i, e}и r { textstyle r}маленькие,

n ≈ ir 1 { displaystyle n приблизительно { frac {i} {r_ {1}}}} ${ displaystyle п приблизительно { гидроразрыва {i} {r_ {1}}}}$ и

n ≈ er 2 { displaystyle n приблизительно { frac {e} {r_ {2} }}} ${ displaystyle n приблизительно { frac {e} {r_ {2}}}}$

Из,

δ = i + e — A { displaystyle delta = i + eA}

= nr 1 + nr 2 — A { displaystyle = nr_ {1} + nr_ {2} -A} ${ displaystyle = nr_ {1} + nr_ {2} -A}$

= n (r 1 + r 2) — A { displaystyle = n (r_ {1} + r_ {2}) — A} ${ displaystyle = n (r_ {1} + r_ {2}) - A}$

= n A — A { displaystyle = nA-A}

= A (n — 1) { displaystyle = A (n-1)}

Таким образом, можно сказать, что тонкая призма всегда находится в минимальном отклонении .

Экспериментальное определение

Минимальное отклонение можно найти вручную или с помощью спектрометра . Либо призма остается фиксированной и угол падения регулируется, либо призма поворачивается, сохраняя источник света фиксированным.

Минимальный угол рассеивания

Минимальный угол рассеивания для белого света — это разница в минимальном отклонении угол между красными и фиолетовыми лучами светового луча через призму.

Применение

Рисование радиусов в точках интерференции показывает, что углы преломления равны, что доказывает минимальное отклонение.

Один из факторов, которые вызывает радугу — это группирование световых лучей при минимальном угле отклонения, который близок к углу радуги (42 °).

Он также отвечает за такие явления, как гало и песы, полученные отклонением солнечного света в мини-призмах гексагональных кристаллов льда в воздухе, изгибающем свет с минимальным отклонением 22 °.

См. Также

физический портал

Ссылки / Дополнительная литература

^ «Глава 9, ЛУЧЕВАЯ ОПТИКА И ОПТИЧЕСКИЕ ПРИБОРЫ ». Учебник по физике для IX класса (PDF). NCERT. п. 331.
^ «Оптика-призма». Репетитор физики A-Level.
^ Марк А. Петерсон. «Минимальное отклонение призмы». mtholyoke. Колледж Маунт-Холиок. Архивировано из оригинала 23.05.2019.
^ «Refraction through Prisms». SchoolPhysics.
^ «Призма». HyperPhysics.
^«Определение показателя преломления материала призмы». BrainKart.
^«Угол минимального отклонения». Scribd.
^»Теория призменного спектрометра». www.ukessays.com.
^«Экспериментальная установка для измерения угла минимального отклонения призменным спектрометром». ResearchGate.
^«Измерение дисперсии стекла призменным спектрометром». studylib.net.
^«Определение минимального отклонения для данной призмы». BYJU’S.
^»Радуга». www.schoolphysics.co.uk.
^»Halo 22 °». HyperPhysics.

Внешние ссылки

Минимальное отклонение Часть 1 и Часть 2 в Академии Хана

Преломление через призму в NCERT Tectbook

Минимальное отклонение по призме Марк А. Петерсон, Колледж Маунт-Холиок

Источник

В призме угол отклонения ( δ ) уменьшается с увеличением угла падения ( i ) до определенного угла. Этот угол падения, при котором угол отклонения призмы минимален, называется положением минимального отклонения призмы, а сам угол отклонения известен как минимальный угол отклонения (обозначается δ _min , D _λ или D _m ).

Свет отклоняется при попадании в материал с показателем преломления> 1.

Луч света дважды отклоняется призмой. Сумма этих прогибов и есть угол отклонения.

Когда углы входа и выхода равны, угол отклонения луча, проходящего через призму, будет минимальным.

Угол минимального отклонения связан с показателем преломления как:

${ displaystyle n_ {21} = { dfrac { sin left ({ dfrac {A + D_ {m}} {2}} right)} { sin left ({ dfrac {A} {2 }}верно)}}}$

Это полезно для расчета показателя преломления материала. Радуга и нимб возникают при минимальном отклонении. Также тонкая призма всегда настраивается на минимальное отклонение.

Формула

При минимальном отклонении преломленный луч в призме параллелен ее основанию. Другими словами, световой луч симметричен относительно оси симметрии призмы. Кроме того, углы преломления равны, т.е. r ₁ = r ₂ . И угол падения и угол выхода равны друг другу ( i = e ). Это хорошо видно на графике ниже.

Формулу минимального отклонения можно получить, используя геометрию призмы. Подход включает замену переменных в законе Снеллиуса с точки зрения отклонения и углов призмы с использованием вышеуказанных свойств.

Из суммы углов в ,

${ Displaystyle А + угол OPQ + угол OQP = 180 ^ { circ}}$
${ displaystyle подразумевает A = 180 ^ { circ} - (90-r) - (90-r)}$
${ displaystyle подразумевает r = { frac {A} {2}}}$

Используя теорему о внешнем угле в ,

${ Displaystyle D_ {м} = угол RPQ + угол RQP}$
${ displaystyle подразумевает D_ {m} = i-r + ir}$
${ displaystyle подразумевает 2r + D_ {m} = 2i}$
${ displaystyle подразумевает A + D_ {m} = 2i}$
${ displaystyle подразумевает, что я = { frac {A + D_ {m}} {2}}}$

Это также можно получить, положив i = e в формулу призмы : i + e = A + δ

Из закона Снеллиуса ,

${ displaystyle n_ {21} = { dfrac { sin i} { sin r}}}$

${ displaystyle , следовательно, n_ {21} = { dfrac { sin left ({ dfrac {A + D_ {m}} {2}} right)} { sin left ({ dfrac {A}) {2}} right)}}}$

${ displaystyle , следовательно, D_ {m} = 2 sin ^ {- 1} left (n sin left ({ frac {A} {2}} right) right) -A}$

(где n — показатель преломления, A — угол призмы, а D _m — минимальный угол отклонения.)

Это удобный способ измерения показателя преломления материала (жидкости или газа) путем направления светового луча через призму незначительной толщины с минимальным отклонением, заполненную материалом, или стеклянную призму, погруженную в нее.

Проработанные примеры:

Показатель преломления стекла 1,5. Требуется минимальный угол отклонения для равносторонней призмы вместе с соответствующим углом падения.
Ответ: 37 °, 49 ° Решение: Здесь A = 60 ° , n = 1,5. Вставляя их в формулу выше, ${ textstyle { frac { sin left ({ frac {60+ delta} {2}} right)} { sin left ({ frac {60} {2}} right)}} = 1,5}$ ${ textstyle подразумевает { frac { sin left (30 + { frac { delta} {2}} right)} { sin (30)}} = 1,5}$ ${ textstyle подразумевает sin left (30 + { frac { delta} {2}} right) = 1,5 times 0,5}$ ${ textstyle подразумевает 30 + { frac { delta} {2}} = sin ^ {- 1} (0,75)}$ ${ textstyle подразумевает { frac { delta} {2}} = 48,6-30}$ ${ textstyle поэтому delta приблизительно 37 ^ { circ}}$ Также, ${ textstyle i = { frac {(A + delta)} {2}} = { frac {60 + 2 times 18,6} {2}} приблизительно 49 ^ { circ}}$ Это также видно на графике ниже.

Показатель преломления стекла 1,5. Требуется минимальный угол отклонения для равносторонней призмы вместе с соответствующим углом падения.

Ответ: 37 °, 49 °

Решение:

Здесь A = 60 ° , n = 1,5.

Вставляя их в формулу выше,

${ textstyle { frac { sin left ({ frac {60+ delta} {2}} right)} { sin left ({ frac {60} {2}} right)}} = 1,5}$

${ textstyle подразумевает { frac { sin left (30 + { frac { delta} {2}} right)} { sin (30)}} = 1,5}$

${ textstyle подразумевает sin left (30 + { frac { delta} {2}} right) = 1,5 times 0,5}$

${ textstyle подразумевает 30 + { frac { delta} {2}} = sin ^ {- 1} (0,75)}$

${ textstyle подразумевает { frac { delta} {2}} = 48,6-30}$

${ textstyle поэтому delta приблизительно 37 ^ { circ}}$

Также,

${ textstyle i = { frac {(A + delta)} {2}} = { frac {60 + 2 times 18,6} {2}} приблизительно 49 ^ { circ}}$

Это также видно на графике ниже.

Если минимальный угол отклонения призмы с показателем преломления 1,4 равен ее углу преломления, угол призмы желателен.
Ответ: 60 ° Решение: Здесь, ${ textstyle подразумевает delta = { frac {A} {2}}}$ Используя приведенную выше формулу, ${ textstyle { frac { sin left ({ frac {A + { frac {A} {2}}} {2}} right)} { sin left ({ frac {A} {2 }} right)}} = 1,4}$ ${ textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac {A} {2}} right)}} = { frac { frac {1} {2}} { frac {1} { sqrt {2}}}}}$ ${ textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac {A} {2}} right)}} = { frac { sin 45 ^ { circ}} { sin 30 ^ { circ}}}}$ ${ textstyle , следовательно, A = 60 ^ { circ}}$

Если минимальный угол отклонения призмы с показателем преломления 1,4 равен ее углу преломления, угол призмы желателен.

Ответ: 60 °

Решение:

Здесь,

${ textstyle подразумевает delta = { frac {A} {2}}}$

Используя приведенную выше формулу,

${ textstyle { frac { sin left ({ frac {A + { frac {A} {2}}} {2}} right)} { sin left ({ frac {A} {2 }} right)}} = 1,4}$

${ textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac {A} {2}} right)}} = { frac { frac {1} {2}} { frac {1} { sqrt {2}}}}}$

${ textstyle подразумевает { frac { sin left ({ frac {3A} {4}} right)} { sin left ({ frac {A} {2}} right)}} = { frac { sin 45 ^ { circ}} { sin 30 ^ { circ}}}}$

${ textstyle , следовательно, A = 60 ^ { circ}}$

Кроме того, изменение угла отклонения с произвольным углом падения можно выразить в одном уравнении, выразив e через i в формуле призмы с использованием закона Снеллиуса:

${ Displaystyle дельта = я-А + грех ^ {- 1} влево (п CDOT грех влево (А- грех ^ {- 1} влево ({ гидроразрыва { грех я} {п}) } right) right) right)}$

На этом графике зависимости угла отклонения от угла падения δ соответствует двум значениям i и e (i ‘). Однако для минимального отклонения i равно e.

Для тонкой призмы

Поскольку D _m и A очень малы,

${ displaystyle { begin {align} n & приблизительно { dfrac { frac {A + D_ {m}} {2}} { frac {A} {2}}} \ n & = { frac {A + D_ {m}} {A}} \ D_ {m} & = An-A end {align}}}$

${ displaystyle , следовательно, D_ {m} = A (n-1)}$

Интересно, что использование аналогичного подхода с законом Снеллиуса и формулой призмы для тонкой призмы в целом приводит к тому же результату для угла отклонения.

Поскольку i , e и r малы,

${ displaystyle n приблизительно { гидроразрыва {i} {r_ {1}}}, п приблизительно { frac {e} {r_ {2}}}}$

По формуле призмы
${ displaystyle { begin {align} delta & = nr_ {1} + nr_ {2} -A \ & = n (r_ {1} + r_ {2}) - A \ & = nA-A & = A (n-1) end {выровнено}}}$

Таким образом, можно сказать, что тонкая призма всегда находится в минимальном отклонении .

Экспериментальная решимость

Минимальное отклонение можно определить вручную или с помощью спектрометра. Либо призма остается неподвижной и угол падения регулируется, либо призма поворачивается, сохраняя фиксированный источник света.

Минимальный угол рассеивания

Угол рассеивания в призме

Минимальный угол рассеивания белого света — это разница в минимальном угле отклонения красных и фиолетовых лучей светового луча через призму.

Для тонкой призмы, отклонение фиолетового света, это и красного света, является . Разница в отклонении между красным и фиолетовым светом называется угловой дисперсией, создаваемой призмой.
${ displaystyle delta _ {v}}$ ${ displaystyle (n_ {v} -1) A}$ ${ displaystyle delta _ {r}}$ ${ displaystyle (n_ {r} -1) A}$ ${ displaystyle ( delta _ {v} - delta _ {r}) = (n_ {v} -n_ {r}) A}$

Приложения

Проведение радиусов к точкам интерференции показывает, что углы преломления равны, что доказывает минимальное отклонение.

Одним из факторов, вызывающих появление радуги, является группировка световых лучей при минимальном угле отклонения, близком к углу радуги (42 °).

Он также отвечает за такие явления, как ореолы и солнечные лучи , возникающие из-за отклонения солнечного света в мини-призмах гексагональных кристаллов льда в воздухе, изгибающем свет с минимальным отклонением 22 °.

Смотрите также

Призма
Преломление
Геометрическая оптика

Внешние ссылки

Минимальное отклонение, часть 1 и часть 2 в Khan Academy
Преломление через призму в NCERT Tectbook
Минимальное отклонение с помощью призмы. Автор Марк А. Петерсон, Колледж Маунт-Холиок.

Источник

Formula[edit]

For thin prism[edit]

Experimental determination[edit]

Minimum angle of dispersion[edit]

Applications[edit]

See also[edit]

References[edit]

External links[edit]

2.1.1. Угол наименьшего отклонения

2.1.2. Угловая дисперсия

2.1.3. Угловое увеличение

Содержание

Формула и график

Для тонкой призмы

Экспериментальное определение

Минимальный угол рассеивания

Применение

См. Также

Ссылки / Дополнительная литература

Внешние ссылки

Формула

Для тонкой призмы

Экспериментальная решимость

Минимальный угол рассеивания

Приложения

Смотрите также

Рекомендации

Внешние ссылки

Не пропустите также: