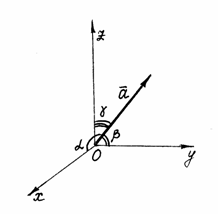
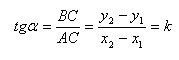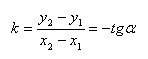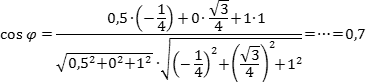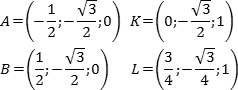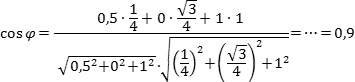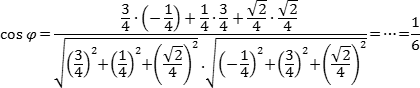Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Пример 1. Найти угол между векторами a = {3; 4} и b = {4; 3}.
Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
|a| = √32 + 42 = √9 + 16 = √25 = 5
|b| = √42 + 32 = √16 + 9 = √25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| |a| · |b| | 5 · 5 | 25 |
Пример 2. Найти угол между векторами a = {7; 1} и b = {5; 5}.
Решение: Найдем скалярное произведение векторов:
a·b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
|a| = √72 + 12 = √49 + 1 = √50 = 5√2
|b| = √52 + 52 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| |a| · |b| | 5√2 · 5√2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Пример 3. Найти угол между векторами a = {3; 4; 0} и b = {4; 4; 2}.
Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
|a| = √32 + 42 + 02 = √9 + 16 = √25 = 5
|b| = √42 + 42 + 22 = √16 + 16 + 4 = √36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| |a| · |b| | 5 · 6 | 15 |
Пример 4. Найти угол между векторами a = {1; 0; 3} и b = {5; 5; 0}.
Решение: Найдем скалярное произведение векторов:
a·b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
|a| = √12 + 02 + 32 = √1 + 9 = √10
|b| = √52 + 52 + 02 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
cos α =
a · b|a| · |b|
=
5√10 · 5√2
=
12√5
=
√510
= 0.1√5
Угол между векторами
Определение
Угол между векторами — это угол между отрезками, которые изображают эти две направляющие и которые отложены от одной точки пространства. Другими словами — это кратчайший путь, на который можно повернуть один из векторов вокруг его начала до положения общей направленности со вторым.
На изображении это α, который также можно обозначить следующим образом:
(left(widehat{overrightarrow a;overrightarrow b}right))
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как и любой другой угол, векторный может быть представлен в нескольких вариациях.
Острый:
Тупой:
Прямой:
С величиной (0^circ) (то есть, векторы сонаправлены):
С величиной (180^circ) (векторы направлены в противоположные стороны):
Нахождение угла между векторами
Как правило, угол между ( overrightarrow a) и (overrightarrow b) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.
Определение
Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.
Формула скалярного произведения:
(left(overrightarrow a;overrightarrow bright)=left|overrightarrow aright|timesleft|overrightarrow bright|timescosleft(widehat{overrightarrow a;overrightarrow b}right))
- Если α — острый, то СП (скалярное произведение) будет положительным числом (cos острого угла — положительное число).
- Если векторы имеют общую направленность, то есть угол между ними равен (0^circ), а косинус — 1, то СП будет тоже положительным.
- Если α — тупой, то скалярное произведение будет отрицательным (cos тупого угла — отрицательное число).
- Если α равен (180^circ), то есть векторы противоположно направлены, то СП тоже отрицательно, потому что cos данного угла равен 1.
- Если α — прямой, то СП равно 0, так как косинус (90^circ) равен 0.
В случае, если overrightarrow a и overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})
Расчет угла, если вектор задан координатами
В случае, когда направляющие расположены на двухмерной плоскости с заданными координатами в виде (overrightarrow a=left(a_x;a_yright)) и (overrightarrow b=left(b_x;b_yright)), то угол между ними можно найти следующим образом:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}})
Если же координаты находятся в трехмерном пространстве и заданы в виде:
(overrightarrow a=left(a_x;a_y;a_zright))
( overrightarrow b=left(b_x;b_y;b_zright))
то формула принимает такой вид:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})
Расчет угла, если заданы три точки в прямоугольной системе координат
В этом случае проще будет разобраться с объяснениями сразу на примере.
Допустим, нам известны три точки и их координаты: A(3,-2), B(2,1), C (6,-1). Нужно найти косинус угла между (overrightarrow{AC}) и (overrightarrow{BC}).
Решение
Для начала найдем их координаты по известным координатам заданных точек:
(overrightarrow{AC}=(6-3, -1-(-2))=(3,1))
(overrightarrow{BC}=(6-2, -1-1)=(4,-2))
После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:
(cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac{(overrightarrow{AC};;overrightarrow{BC})}{left|overrightarrow{AC}right|cdotleft|overrightarrow{BC}right|}=frac{3cdot4+1cdot(-2)}{sqrt{3^2+1^2}cdotsqrt{4^2+{(-2)}^2}}=frac{10}{sqrt{10}cdot2sqrt5}=frac{10}{10sqrt2}=frac1{sqrt2})
Ответ: (cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac1{sqrt2}.)
Примеры решения задач
Для наглядности, взглянем на примеры решения задач по данной теме.
Задача 1
Известно, что (overrightarrow a) и (overrightarrow b). Их длины равны 3 и 6 соответственно, а скалярное произведение равно -9. Нужно найти cos угла между векторами и его величину.
Решение
Применим формулу:
( cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})
Подставим известные значения:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{-9}{3cdot6}=-frac12)
Далее найдем угол между данными векторами:
(arccosleft(-frac12right)=frac{3pi}4)
Ответ: (left(widehat{overrightarrow a;overrightarrow b}right)=-frac12,;left(widehat{overrightarrow a;overrightarrow b}right)=frac{3pi}4.)
Задача 2
В пространстве даны координаты (overrightarrow a=(8; -11; 7)) и (overrightarrow b=(-2; -7; 8)). Вычислить угол α между ними.
Решение
Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})
Подставляем значения и получаем:
(cosleft(alpharight)=frac{8cdot(-2)+(-11)cdot(-7)+7cdot8}{sqrt{8^2+{(-11)}^2+7^2}cdotsqrt{{(-2)}^2+{(-7)}^2+8^2}}=frac{117}{sqrt{234}cdotsqrt{117}}=frac{sqrt{117}}{sqrt{234}}=frac1{sqrt2}=frac2{sqrt2})
Теперь находим угол α:
(alpha=arccosleft(frac2{sqrt2}right)=45^circ)
Ответ: (45^circ).
Задача 3
Известны (overrightarrow a=(3; 4)) и (overrightarrow b=(2; 5)). Найти угол между ними.
Решение
Для расчета используем формулу:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}})
Подставим известные значения и получим:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}}=frac{3cdot2+4cdot5}{sqrt{3^2+4^2}cdotsqrt{2^2+5^2}}=frac{26}{sqrt{25}cdotsqrt{29}}=frac{26}{5sqrt{29}})
Ответ: (cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{26}{5sqrt{29}})
Два вектора
a→
и
b→
всегда образуют угол.
Угол между векторами может принимать значения от
0°
до
180°
включительно.
Если векторы не параллельны, то их можно расположить на пересекающихся прямых.
Векторы могут образовать:
1. острый угол;
2. тупой угол;
3. прямой угол (векторы перпендикулярны).
Если векторы расположены на параллельных прямых, то они могут образовать:
4. угол величиной
0°
(векторы сонаправлены);
5. угол величиной
180°
(векторы противоположно направлены).
Если один из векторов или оба вектора нулевые, то угол между ними будет равен
0°
.
Угол между векторами записывают так:
Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
a→⋅b→=a→⋅b→⋅cosa→b→ˆ
.
Результат скалярного произведения векторов является числом (в отличие от результата рассмотренных ранее действий с векторами — сложения, вычитания и умножения на число. В таких случаях результатом был вектор). При умножении вектора на вектор получается число, так как длины векторов — это числа, косинус угла — число — соответственно, их произведение также будет являться числом.
1. Если угол между векторами острый, то скалярное произведение будет положительным числом (так как косинус острого угла — положительное число).
Если векторы сонаправлены, то угол между ними будет равен
0°
, а косинус равен (1), скалярное произведение также будет положительным.
2. Если угол между векторами тупой, то скалярное произведение будет отрицательным (так как косинус тупого угла — отрицательное число).
Если векторы направлены противоположно, то угол между ними будет равен
180°
. Скалярное произведение также отрицательно, так как косинус этого угла равен (-1).
Справедливы и обратные утверждения:
1. Если скалярное произведение векторов — положительное число, то угол между данными векторами острый.
2. Если скалярное произведение векторов — отрицательное число, то угол между данными векторами тупой.
Особенный третий случай!
Обрати внимание!
3. Если угол между векторами прямой, то скалярное произведение векторов равно нулю, так как косинус прямого угла равен (0).
Обратное суждение: если скалярное произведение векторов равно нулю, то эти векторы перпендикулярны.
Вектор, умноженный на самого себя, будет числом, которое называется скалярным квадратом вектора. Скалярный квадрат вектора равен квадрату длины данного вектора и обозначается как
a→2
.
Свойства скалярного произведения
Для любых векторов и любого числа справедливы следующие свойства:
1.
a→2≥0
, к тому же
a→2>0
, если
a→≠0→
.
2. Переместительный, или коммутативный, закон скалярного произведения:
a→⋅b→=b→⋅a→
.
3. Распределительный, или дистрибутивный, закон скалярного произведения:
a→+b→⋅c→=a→⋅c→+b→⋅c→
.
4. Сочетательный, или ассоциативный, закон скалярного произведения:
k⋅a→⋅b→=k⋅a→⋅b→
.
Использование скалярного произведения
Удобно использовать скалярное произведение векторов для определения углов между прямыми и между прямой и плоскостью.
Угол между прямыми
Ознакомимся с ещё одним определением.
Вектор называют направляющим вектором прямой, если он находится на прямой или параллелен этой прямой.
Чтобы определить косинус угла между прямыми, надо определить косинус угла между направляющими векторами этих прямых, то есть найти векторы, параллельные прямым, и определить косинус угла между векторами.
Для этого необходимо рассмотреть определение скалярного произведения, если векторы даны в координатной системе.
Если
a→x1;y1;z1
,
b→x2;y2;z2
, то
a→⋅b→=x1⋅x2+y1⋅y2+z1⋅z2
.
Прежде была рассмотрена формула определения длины вектора в координатной форме.
Теперь, объединив эти формулы, получим формулу для определения косинуса угла между векторами в координатной форме. Так как из формулы скалярного произведения следует, что
cosα=a→⋅b→a→⋅b→
, то
.
Угол между прямой и плоскостью
Введём понятие о нормальном векторе плоскости.
Нормальный вектор плоскости — это любой ненулевой вектор, лежащий на прямой, перпендикулярной к данной плоскости.
Используя следующий рисунок, легко доказать, что косинус угла
β
между нормальным вектором
n→
данной плоскости и неким вектором
b→
равен синусу угла
α
между прямой и плоскостью, так как
α
и
β
вместе образуют угол в
90°
.
При нахождении косинуса угла между
n→
и
b→
можно использовать это число как синус угла между прямой, на которой лежит вектор
b→
, и плоскостью.
Как найти угол между двумя векторами
Совет
от Наталья
Алтынбаева, автор
КакПросто,
добавлено 19 Август 2011
Угол
между двумя векторами, выходящими из
одной точки, это кратчайший угол, на
который необходимо повернуть один из
векторов вокруг своего начала до
положения второго вектора. Определить
градусную меру этого угла можно, если
известны координаты векторов.
Начало
формы
Конец
формы
Инструкция
1Пусть
на плоскости заданы два ненулевых
вектора, отложенные от одной точки:
вектор A с координатами (x1, y1) и вектор
B с координатами (x2, y2). Угол между ними
обозначен как θ. Чтобы найти градусную
меру угла θ необходимо воспользоваться
определением скалярного произведения.
2Скалярным
произведением двух ненулевых векторов
называется число, равное произведению
длин этих векторов на косинус угла
между ними, то есть (A,B)=|A|*|B|*cos(θ). Теперь
нужно выразить из данной записи косинус
угла: cos(θ)=(A,B)/(|A|*|B|).
3Скалярное
произведение можно найти также по
формуле (A,B)=x1*x2+y1*y2, так как скалярное
произведение двух ненулевых векторов
равно сумме произведений соответствующих
координат этих векторов. Если скалярное
произведение ненулевых векторов равно
нулю, то векторы являются перпендикулярными
(угол между ними равен 90 градусов) и
дальнейшие вычисления можно не
производить. Если скалярное произведение
двух векторов положительно, то угол
между этими векторами острый, а если
отрицательно, то угол тупой.
4Теперь
посчитайте длины векторов A и B по
формулам: |A|=√(x1²+y1²), |B|=√(x2²+y2²). Длина
вектора вычисляется как квадратный
корень из суммы квадратов его координат.
5Найденные
значения скалярного произведения и
длин векторов подставьте в полученную
в шаге 2 формулу для нахождения косинуса
угла, то есть
cos(θ)=(x1*x2+y1*y2)/(√(x1²+y1²)+√(x2²+y2²)). Теперь,
зная значение косинуса, чтобы найти
градусную меру угла между векторами
нужно воспользоваться таблицей Брадиса
или взять из этого выражения арккосинус:
θ=arccos(cos(θ)).
6Если
векторы A и B заданы в трехмерном
пространстве и имеют координаты (x1, y1,
z1) и (x2, y2, z2) соответственно, то при
нахождении косинуса угла добавляется
еще одна координата. В этом случае
косинус угла равен:
cos(θ)=(x1*x2+y1*y2+z1*z2)/(√(x1²+y1²+z1²)+√(x2²+y2²+z2²))
|
9)Направляющие |
|
Направление
Рис.
Из
Легко
1) 2) координаты |
10)
Определение
векторного произведения
Три
некомпланарных вектора a, b и с,
взятые в указанном порядке, образуют
правую тройку, если с конца третьего
вектора с кратчайший поворот от первого
вектора а ко
второму вектору b виден
совершающимся против часовой стрелки,
и левую, если по часовой (см. рис. 16).

Векторным
произведением вектора а на
вектор b называется
вектор с,
который:
1.
Перпендикулярен векторам a и b,
т. е. са и сb;
2. Имеет
длину, численно равную площади
параллелограмма, построенного на
векторах а и b как
на сторонах (см. рис. 17), т. е.
3.Векторы a, b и с образуют
п
равую
тройку.
Векторное
произведение обозначается а х b или
[а,b].
Из определения векторного произведения
непосредственно вытекают следующие
соотношения между ортами i , j и k (см.
рис. 18):
i х j = k, j х k = i, k х i = j.
Докажем,
например, что iхj=k.
1) ki, kj;
2) |k|=1,
но | i x j|
= |i|
• |J|
• sin(90°)=1;
3) векторы i , j и k образуют
правую тройку (см. рис. 16).
Свойства
векторного произведения
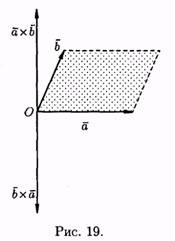
1.
При перестановке сомножителей векторное
произведение меняет знак, т.е. а хb =(b хa )
(см. рис. 19).
Векторы ахb и b ха коллинеарны,
имеют одинаковые модули (площадь
параллелограмма остается неизменной),
но противоположно направлены
(тройки а , b , а хb и a , b , bxa противоположной
ориентации). Стало быть axb =
-(bxa ).
2.
Векторное произведение обладает
сочетательным свойством относительно
скалярного множителя, т. е. (а хb )
= (а )
х b = а х
(b ).
Пусть >0.
Вектор (ахb )
перпендикулярен векторам а и b .
Вектор ( а)хb также
перпендикулярен векторам а и b (векторы а, а лежат
в одной плоскости). Значит, векторы (ахb )
и ( а)хb коллинеарны.
Очевидно, что и направления их совпадают.
Имеют одинаковую длину:
Поэтому (a хb )= ахb .
Аналогично доказывается при <0.
3.
Два ненулевых вектора а и b коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулевому вектору,
т. е. а||b <=>ахb =0.
В
частности, i *i =j *j =k *k =0.
4.
Векторное произведение обладает
распределительным свойством:
(a+b) хс= ахс+b хс.
Примем
без доказательства.
11)
Смешанное
произведение векторов и его свойства
Смешанным
произведением векторов
называется
число
,
равное скалярному произведению
вектора
на
векторное произведение векторов
и
.
Смешанное произведение обозначается
.
Геометрические
свойства смешанного произведения
1.
Модуль смешанного произведения
некомпланарных векторов
равен
объему
параллелепипеда,
построенного на этих векторах.
Произведение
положительно,
если тройка векторов
—
правая, и отрицательно, если тройка
—
левая, и наоборот.
2.
Смешанное произведение
равно
нулю тогда и только тогда, когда
векторы
компланарны:
векторы
компланарны.
Докажем
первое свойство. Найдем по определению
смешанное произведение:
,
где
—
угол между векторами
и
.
Модуль векторного произведения (по
геометрическому свойству 1) равен
площади
параллелограмма,
построенного на векторах
и
: .
Поэтому
.
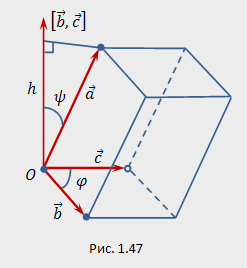
Алгебраическое значение
длины
проекции вектора
на
ось, задаваемую вектором
,
равно по модулю высоте
параллелепипеда,
построенного на векторах
(рис.
1.47). Поэтому модуль смешанного произведения
равен объему
этого
параллелепипеда:
Знак
смешанного произведения определяется
знаком косинуса угла
.
Если тройка
правая,
то
и
смешанное произведение
положительно.
Если же тройка
левая,
то
и
смешанное произведение
отрицательно.
Докажем
второе свойство. Равенство
возможно
в трех случаях:
или
(т.е.
),или
(т.е.
вектор
принадлежит
плоскости векторов
и
).
В каждом случае векторы
компланарны
(см.
разд. 1.1)
Алгебраические
свойства смешанного произведения
1.
При перестановке двух множителей
смешанное произведение изменяет знак
на противоположный:
При
циклической (круговой) перестановке
множителей смешанное произведение не
изменяется:
2.
Смешанное произведение линейно по
любому множителю.
Первое
свойство следует из геометрического
свойства 1 и свойств ориентации троек
векторов (см.
разд. 1.9),
поскольку от перестановки двух множителей
модуль смешанного произведения не
изменяется, а меняется только ориентация
тройки. При циклической перестановке
векторов ориентация тройки не изменяется.
Второе
свойство следует из линейности скалярного
произведения и свойства 1
Пример
1.21. Объем параллелепипеда, построенного
на векторах
,
равен
.
Найти объем параллелепипеда, построенного
на векторах .
Решение. Используя
алгебраические и геометрические
свойства, найдем смешанное произведение
а
затем его модуль
.
По первому геометрическому свойству
смешанного произведения искомый объем
равен
.
Теорема
1.9 (формула вычисления смешанного
произведения). Если векторы
в
правом ортонормированном базисе
имеют
координаты
;
;
соответственно,
то смешанное произведение этих векторов
находится по формуле
В
самом деле, учитывая (1.10) и (1.15), по
определению находим:
что и требовалось
доказать.
12)
Общее уравнение прямой на
плоскости.
Рассмотрим уравнение
прямой с угловым коэффициентом
.
Перенесем все слагаемые в левую часть
и перепишем его в следующем виде:
,
— (3.6)общее
уравнение прямой,
где
и
не
равны нулю одновременно, т.е.
.
Рассмотрим
частные случаи уравнения (3.6).
1)Пусть
.
Тогда уравнение
можно
записать в виде:
.
Обозначим
.
Если
,
,
то получим
(уравнение
прямой с угловым коэффициентом);
Если
,
,
то
(уравнение
прямой, проходящей через начало
координат);
Если
,
,
то
(уравнение
прямой, параллельной оси Оу);
Если
,
,
то
(уравнение
оси Ох).
3)
Пусть
,
.
Тогда уравнение
примет
вид
.
Обозначим
.
Если
,
то получим
(уравнение
прямой, параллельной оси Оу);
Если
,
то
(уравнение
оси Оу).
Т.о.,
при любых значениях коэффициентов
,
(не
равных одновременно нулю) и
уравнение
есть
уравнение некоторой прямой линии на
плоскости Оху.
—
общее уравнение прямой.
13)
Уравнение прямой с угловым коэффициентом.
Пусть
дана прямая L на координатной плоскости Оху.
Определение.
Углом наклона прямой к оси абсцисс
называется уголповорота
оси абсцисс вокруг любой ее точки против
часовой стрелки до положения параллельности
(или совпадения) с данной прямой.
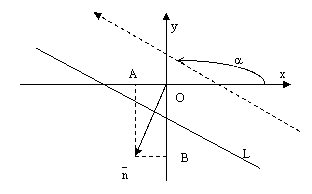
рис.1.
Из определения следует,
что угол наклона
прямой
L к оси Ох может изменяться от нуля
до
:
.
Если прямая
,
то
.
Пусть
(1)
– общее
уравнение прямой L, где
–
нормальный вектор прямой L и
.
Тогда
и
(см.
рис.1). Выразим у изуравнения (1)
.
,
.
Уравнение
прямой L принимает вид:
.
Определение.
Уравнение прямой вида
(2)
называется
уравнением прямой с угловым коэффициентом,
а коэффициент k называется угловым
коэффициентом данной прямой.
Теорема.
В уравнении прямой с угловым коэффициентом
угловой
коэффициент k равен тангенсу угла
наклона прямой к оси абсцисс:
.
(3)
Доказательство.
1) Если прямая
,
то
и
.
С другой стороны, ее нормальный
вектор
и
.
Тогда
и,
следовательно,
,
ч.т.д.
2)
Пусть
,
тогда
,
и
.
Пусть F – точка пересечения прямой L
с осью абсцисс.
Тогда
,
.
Опишем
окружность единичного радиуса с центром
в точке F , а в точке оси Ох с
координатой
проведем
касательную m к этой окружности. См.
рис.2.
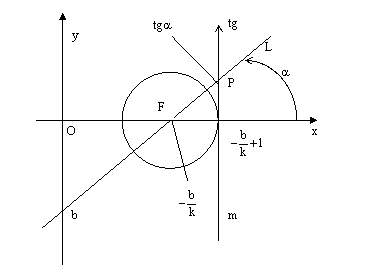
рис.2.
Выберем
положительное направление на прямой
m, так, чтобы
.
Тогда ось m является осью тангенсов
для данной единичной (тригонометрической)
окружности.
Пусть
Р – точка пересечения прямой L
с осью тангенсов
m. Тогда, с одной стороны,
,
где
– угол наклона
прямой L к оси Ох, а, с другой стороны,
точка
и
,
откуда и следует равенство
,
ч.т.д.
Теорема
доказана.
Заметим,
что приведенное доказательство
принадлежит автору этих лекций.
Достоинством этого доказательства
является то, что оно не зависит ни от
величины угла наклона
,
ни от величины коэффициента
.
В
заключение отметим, что коэффициент b
в уравнении (2) равен величине отрезка,
отсекаемого прямой от оси ординат (см.
рис.2).
Угловой
коэффициент в уравнении прямой.
Геометрический смысл коэффициента.
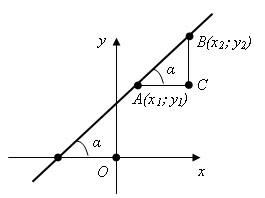
Преобразуем
уравнение прямой ax + by + c=0 к виду
Введем
обозначения
Тогда
получим y = kx + l.
Возьмем
две точки на прямой A (x1; y1) и B (x2; y2), такие
что x1 < x2.
Их
координаты удовлетворяют уравнению
прямой:
Вычитая
эти равенства почленно, получим
Проведя
прямую через точку A параллельно оси x
и прямую через точку B параллельную оси
y, мы получим треугольник ABC. Замечаем,
что
Если
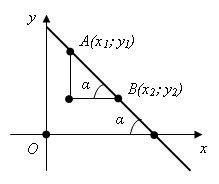
прямая расположена следующим образом
:
То
Таким
образом, коэффициент k в уравнении
прямой с точностью до знака равен
тангенсу острого угла, который образует
прямая с осью x.
Коэффициент
k в уравнении прямой называется угловым
коэффициентом прямой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Угол между двумя прямыми
30 мая 2011
Буду кратким. Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x1; y1; z1) и b = (x2; y2; z2), то сможете найти угол. Точнее, косинус угла по формуле:
Посмотрим, как эта формула работает на конкретных примерах:
Задача. В кубе ABCDA1B1C1D1 отмечены точки E и F — середины ребер A1B1 и B1C1 соответственно. Найдите угол между прямыми AE и BF.

Поскольку ребро куба не указано, положим AB = 1. Введем стандартную систему координат: начало в точке A, оси x, y, z направим вдоль AB, AD и AA1 соответственно. Единичный отрезок равен AB = 1. Теперь найдем координаты направляющих векторов для наших прямых.
Найдем координаты вектора AE. Для этого нам потребуются точки A = (0; 0; 0) и E = (0,5; 0; 1). Поскольку точка E — середина отрезка A1B1, ее координаты равны среднему арифметическому координат концов. Заметим, что начало вектора AE совпадает с началом координат, поэтому AE = (0,5; 0; 1).
Теперь разберемся с вектором BF. Аналогично, разбираем точки B = (1; 0; 0) и F = (1; 0,5; 1), т.к. F — середина отрезка B1C1. Имеем:
BF = (1 − 1; 0,5 − 0; 1 − 0) = (0; 0,5; 1).
Итак, направляющие векторы готовы. Косинус угла между прямыми — это косинус угла между направляющими векторами, поэтому имеем:
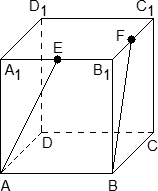
Задача. В правильной трехгранной призме ABCA1B1C1, все ребра которой равны 1, отмечены точки D и E — середины ребер A1B1 и B1C1 соответственно. Найдите угол между прямыми AD и BE.

Введем стандартную систему координат: начало координат в точке A, ось x направим вдоль AB, z — вдоль AA1. Ось y направим так, чтобы плоскость OXY совпадала с плоскостью ABC. Единичный отрезок равен AB = 1. Найдем координаты направляющих векторов для искомых прямых.
Для начала найдем координаты вектора AD. Рассмотрим точки: A = (0; 0; 0) и D = (0,5; 0; 1), т.к. D — середина отрезка A1B1. Поскольку начало вектора AD совпадает с началом координат, получаем AD = (0,5; 0; 1).
Теперь найдем координаты вектора BE. Точка B = (1; 0; 0) считается легко. С точкой E — серединой отрезка C1B1 — чуть сложнее. Имеем:
Осталось найти косинус угла:
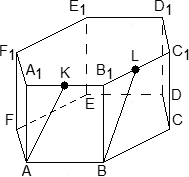
Задача. В правильной шестигранной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, отмечены точки K и L — середины ребер A1B1 и B1C1 соответственно. Найдите угол между прямыми AK и BL.

Введем стандартную для призмы систему координат: начало координат поместим в центр нижнего основания, ось x направим вдоль FC, ось y — через середины отрезков AB и DE, а ось z — вертикально вверх. Единичный отрезок снова равен AB = 1. Выпишем координаты интересующих нас точек:
Точки K и L — середины отрезков A1B1 и B1C1 соответственно, поэтому их координаты находятся через среднее арифметическое. Зная точки, найдем координаты направляющих векторов AK и BL:
Теперь найдем косинус угла:
Задача. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки E и F — середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF.

Введем стандартную систему координат: начало в точке A, оси x и y направим вдоль AB и AD соответственно, а ось z направим вертикально вверх. Единичный отрезок равен AB = 1.
Точки E и F — середины отрезков SB и SC соответственно, поэтому их координаты находятся как среднее арифметическое концов. Выпишем координаты интересующих нас точек:
A = (0; 0; 0); B = (1; 0; 0)
Зная точки, найдем координаты направляющих векторов AE и BF:
Координаты вектора AE совпадают с координатами точки E, поскольку точка A — начало координат. Осталось найти косинус угла:
Смотрите также:
- Задача 14: Угол между плоскостями сечения
- Видеоурок по задачам C2: расстояние от точки до плоскости
- Тест к уроку «Что такое логарифм» (средний)
- Решение задач B12: №440—447
- Текстовые задачи про рельсы
- Задача B4: Семья из трех человек едет из Москвы в Нижний Новгород