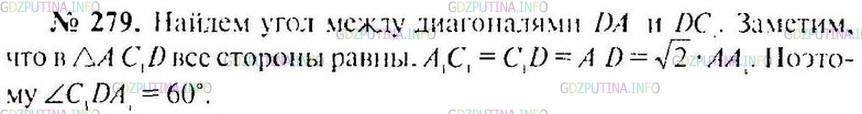Лучший ответ
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
If you were to take a square and draw two diagonals lines, they would cross in the center, and form four right triangles. The two diagonals cross at 90 degrees. You might intuitively guess that two diagonals of a cube, each running from one corner of the cube to its opposite corner and crossing in the center, would also cross at right angles. You would be mistaken. Determining the angle at which two diagonals in a cube cross one another is slightly more complicated than it might appear at first glance, but it does make great practice for understanding the principles of geometry and trigonometry.
Define the length of an edge as one unit. By definition, every edge on the cube has an identical length of one unit.
Use the Pythagorean theorem to determine the length of a diagonal running from one corner, to the opposite corner on the same face. Call this a “short diagonal’ for the sake of clarity. Each side of the right triangle formed is one unit, so the diagonal must be equal to √2.
Use the Pythagorean theorem to determine the length of a diagonal running from one corner to the opposite corner of the opposite face. Call this a “long diagonal.” You have a right triangle with one side equal to 1 unit and one side equal to a “short diagonal,” √2 units. The square of the hypotenuse is equal to the sum of the squares of the sides, so the hypotenuse must be √3. Each diagonal running from one corner of the cube to the opposite corner is √3 units long.
Draw a rectangle to represent two long diagonals crossing in the center of the cube. You want to find the angle of their intersection. This rectangle will be 1 unit tall and √2 units wide. The long diagonals bisect one another in the center of this rectangle and form two different types of triangle. One of these triangles has one side equal to one unit and the other two sides equal to √3/2 (one half the length of a long diagonal). The other also has two sides equal to √3/2 but its other side is equal to √2. You only need to analyze one of the triangles, so take the first one and solve for the unknown angle.
Use the trigonometric formula c^2 = a^2 + b^2 – 2ab cos C to solve for the unknown angle of this triangle. C=1, and both a and b are equal to √3/2. Plugging these values into the equation, you will determine that the cosine of your unknown angle is 1/3. Taking the inverse cosine of 1/3 gives an angle of 70.5 degrees.
Если бы вы взяли квадрат и нарисовали две диагональные линии, они пересеклись бы в центре и образовали четыре прямоугольных треугольника. Две диагонали пересекаются под углом 90 градусов. Вы можете интуитивно догадаться, что две диагонали куба, каждая из которых проходит от одного угла куба к противоположному углу и пересекается в центре, также пересекаются под прямым углом. Вы бы ошиблись. Определить угол, под которым две диагонали в кубе пересекают друг друга, немного сложнее, чем это может показаться на первый взгляд, но это действительно хорошая практика для понимания принципов геометрии и тригонометрии.
Определите длину ребра как одну единицу. По определению каждое ребро куба имеет одинаковую длину в одну единицу.
Используйте теорему Пифагора, чтобы определить длину диагонали, бегущей от одного угла до противоположного угла на той же грани. Назовите это «короткой диагональю» для ясности. Каждая сторона сформированного прямоугольного треугольника составляет одну единицу, поэтому диагональ должна быть равна √2.
Используйте теорему Пифагора, чтобы определить длину диагонали, бегущей от одного угла до противоположного угла противоположной грани. Назовите это «длинной диагональю». У вас есть прямоугольный треугольник с одной стороной, равной 1 единице, и одной стороной, равной «короткой диагонали», √2 единиц. Квадрат гипотенузы равен сумме квадратов сторон, поэтому гипотенуза должна быть √3. Каждая диагональ, идущая от одного угла куба к противоположному углу, имеет длину √3 единиц.
Нарисуйте прямоугольник, чтобы представить две длинные диагонали, пересекающиеся в центре куба. Вы хотите найти угол их пересечения. Этот прямоугольник будет иметь высоту 1 единицу и ширину √2 единицы. Длинные диагонали делят пополам друг друга в центре этого прямоугольника и образуют два разных типа треугольника. Один из этих треугольников имеет одну сторону, равную одной единице, а две другие стороны равны √3 / 2 (одна половина длины длинной диагонали). Другая также имеет две стороны, равные √3 / 2, но другая ее сторона равна √2. Вам нужно только проанализировать один из треугольников, поэтому возьмите первый и найдите неизвестный угол.
Используйте тригонометрическую формулу c ^ 2 = a ^ 2 + b ^ 2 — 2ab cos C, чтобы найти неизвестный угол этого треугольника. C = 1, а a и b равны √3 / 2. Подставляя эти значения в уравнение, вы определите, что косинус вашего неизвестного угла равен 1/3. Взятие обратного косинуса 1/3 дает угол 70, 5 градусов.
ГДЗ (готовое домашние задание из решебника) на Номер №279 по учебнику Геометрия. 10-11 классы: учебник для общеобразовательных учреждений : базовый и профильный уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. — 22-е изд. — Просвещение, 2013-2019г
Условие
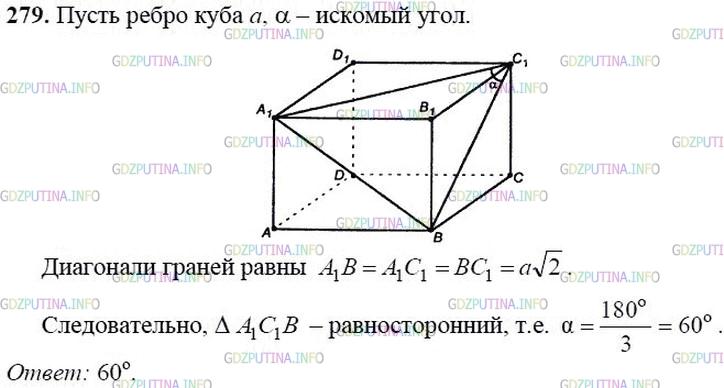
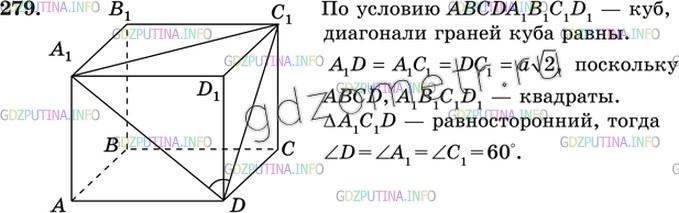
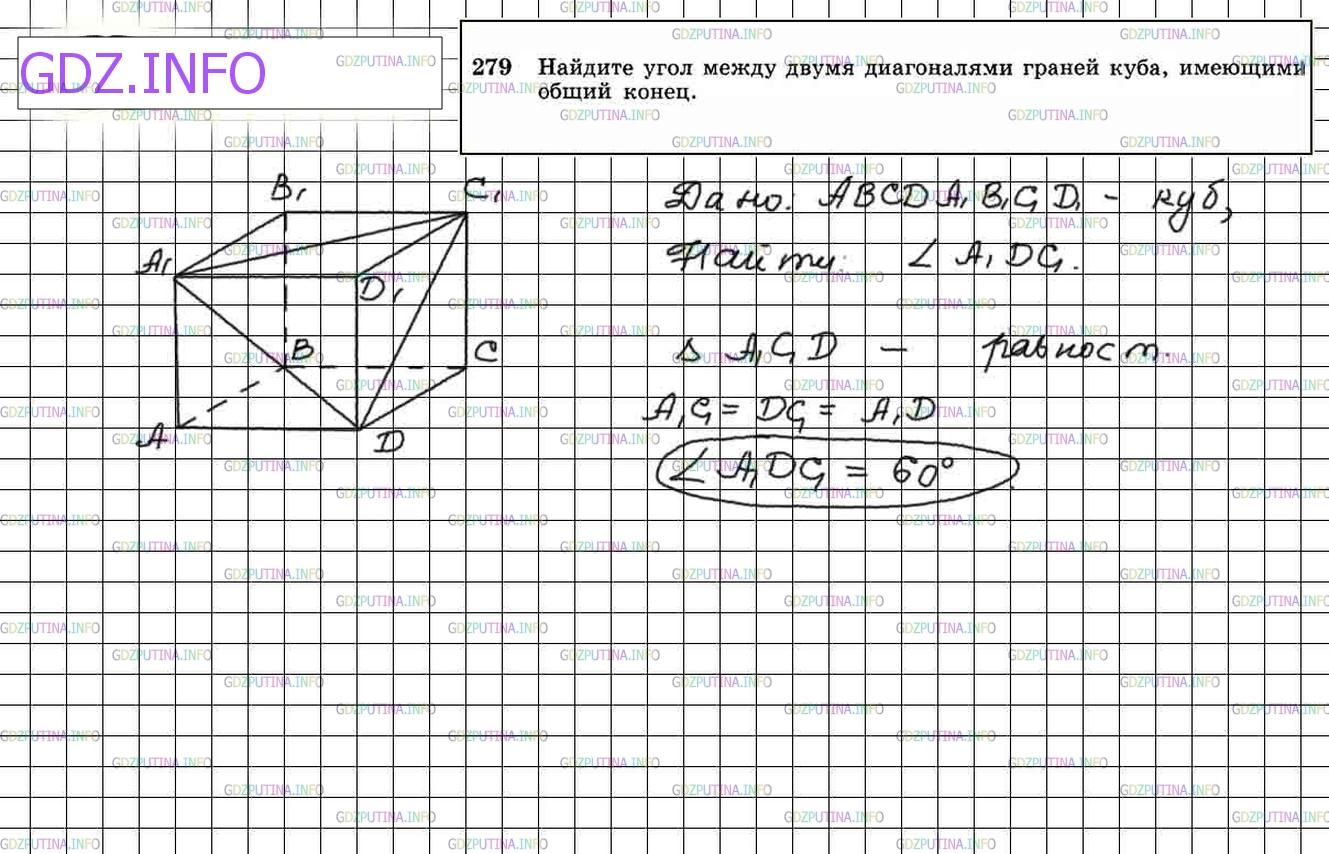
Найдите угол между двумя диагоналями граней куба, имеющими общий конец.
Решение 1
Решение 2
Решение 3
Решение 4
Решение 5
Другие задачи из этого учебника
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
Авторы: , Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г..
Издательство:
Просвещение 2015
Тип: Учебник
Подробный решебник (ГДЗ) по Геометрии за 10‐11 (десятый‐одиннадцатый) класс — готовый ответ 10 класс — 279. Авторы учебника: Атанасян, Бутузов, Кадомцев, Киселева, Позняк. Издательство: Просвещение 2015.
Условие /
10 класс / 279
279. Найдите угол между двумя диагоналями граней куба, имеющими общий конец.
Решебник №1 / 10 класс / 279
Видеорешение / 10 класс / 279
Решебник №2 / 10 класс / 279
Решебник №3 / 10 класс / 279
Решебник №4 / 10 класс / 279
Оцените решебник:
4.4/5
1476