Как найти угол через косинус формула

Найти угол, зная косинус угла: примеры решения

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Имея на руках значение косинуса угла, выяснить угол, которому он принадлежит, совсем не сложно.

Существует специальная тригонометрическая функция, которой можно воспользоваться для этого и называется она арккосинусом (записывается как $arccos$).

Замечание 1

Для того чтобы воспользоваться ей и узнать значение угла, можно применить специальную расширенную таблицу со значениями углов и соответствующих им тригонометрических функций. Эта таблица называется таблицей Брадиса.

Также наиболее часто встречающиеся значения углов и соответствующих им синусов-косинусов собраны в небольшую таблицу внизу:

Рисунок 1. Зная косинус или синус, найти угол. Автор24 — интернет-биржа студенческих работ

Но есть и другой, более современный вариант нахождения угла по значению косинуса: достаточно включить режим Scientific (Научный) и найти кнопку переключения функций на калькуляторе.

В Windows 10 она обозначается стрелкой как показано на рисунке. При её нажатии кнопка $sin$ поменяется на $sin^{-1}$, а $cos$ на $cos^{-1}$. Теперь для того чтобы узнать значение угла по косинусу — просто набираете значение функции и жмёте кнопку $cos^{-1}$. Не забудьте выбрать нужную единицу измерения — градусы или радианы.

Рисунок 2. Как узнать угол, зная косинус угла. Автор24 — интернет-биржа студенческих работ

Пример 1

Найдите, чему равен $arccos 0,456$.

Решение:

Воспользуемся калькулятором в Научном режиме, на рисунке представлен калькулятор Mac OC, кнопка переключения между $sin$ и $sin^{-1}$ обведена красным:

Рисунок 3. Как по косинусу угла найти угол. Автор24 — интернет-биржа студенческих работ

После нажатия кнопки мы получили значение $α = 27,129°$.

Пример 2

Определите, чему равен угол, если известен его косинус, и он равен $0,95$.

Решение:

Воспользуемся вновь калькулятором и получим, что $α = 18,19°$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 07.05.2023

Источник

Загрузить PDF

Теорема косинусов широко применяется в тригонометрии. Ее используют при работе с неправильными треугольниками, чтобы находить неизвестные величины, например стороны и углы. Теорема схожа с теорема Пифагора, и ее довольно легко запомнить. Теорема косинусов гласит, что в любом треугольнике $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ .

1
Запишите известные величины. Чтобы найти неизвестную сторону треугольника, нужно знать две другие стороны и угол между ними.^[1]
- Например, дан треугольник XYZ. Сторона YX равна 5 см, сторона YZ равна 9 см, а угол Y равен 89°. Чему равна сторона XZ?
2

Запишите формулу теоремы косинусов. Формула: $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ , где — неизвестная сторона, — косинус угла, противоположного неизвестной стороне, и — две известные стороны.^[2]
3
4
Найдите косинус известного угла. Сделайте это с помощью калькулятора. Введите значение угла, а затем нажмите кнопку . Если у вас нет научного калькулятора, найдите онлайн-таблицу значений косинусов, например, здесь.^[4] Также в Яндексе можно ввести «косинус Х градусов» (вместо X подставьте значение угла), и поисковая система отобразит косинус угла.
- Например, косинус 89° ≈ 0,01745. Итак: $c^{{2}}=5^{{2}}+9^{{2}}-2(5)(9)(0,01745)$ .
5

Перемножьте числа. Умножьте на косинус известного угла.
6

Сложите квадраты известных сторон. Помните, чтобы возвести число в квадрат, его нужно умножить на само себя. Сначала возведите в квадрат соответствующие числа, а затем сложите полученные значения.
7

Вычтите два числа. Вы найдете $c^{{2}}$ .
8

Извлеките квадратный корень из полученного значения. Для этого воспользуйтесь калькулятором. Так вы найдете неизвестную сторону.^[5]

Реклама

1
Запишите известные величины. Чтобы найти неизвестный угол треугольника, нужно знать все три стороны треугольника.^[6]
- Например, дан треугольник RST. Сторона СР = 8 см, ST = 10 см, РТ = 12 см. Найдите значение угла S.
2

Запишите формулу теоремы косинусов. Формула: $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ , где — косинус неизвестного угла, — известная сторона, противолежащая неизвестному углу, и — две другие известные стороны. ^[7]
3
4
Перемножьте числа. Умножьте на косинус неизвестного угла.
- Например, $12^{{2}}=8^{{2}}+10^{{2}}-160cos {C}$ .
5
Возведите в квадрат. То есть умножьте число само себя.
- Например, $144=8^{{2}}+10^{{2}}-160cos {C}$
6

Сложите квадраты и . Но сначала возведите соответствующие числа в квадрат.
7

Изолируйте косинус неизвестного угла. Для этого вычтите сумму $a^{{2}}$ и $b^{{2}}$ из обеих частей уравнения. Затем разделите каждую часть уравнения на коэффициент (множитель) при косинусе неизвестного угла.
8
Вычислите арккосинус. Так вы найдете значение неизвестного угла.^[9] На калькуляторе функция арккосинуса обозначается $COS^{{-1}}$ .
- Например, арккосинус 0,0125 равен 82,8192. Итак, угол S равен 82,8192°.
Реклама

1

Найдите неизвестную сторону треугольника. Известные стороны равны 20 см и 17 см, а угол между ними равен 68°.
2

Найдите угол H в треугольнике GHI. Две стороны, прилегающие к углу Н, равны 22 и 16 см. Сторона, противоположная углу H, равна 13 см.
3

Найдите длину тропы. Речная, Холмистая и Болотная тропы образуют треугольник. Длина Речной тропы — 3 км, длина Холмистой тропы — 5 км; эти тропы пересекаются друг с другом под углом 135°. Болотная тропа соединяет два конца других троп. Найдите длину Болотной тропы.

Реклама

Советы

Проще пользоваться теоремой синусов. Поэтому сначала выясните, можно ли применить ее к данной задаче.

Об этой статье

Эту страницу просматривали 5444 раза.

Была ли эта статья полезной?

Источник

Страница содержит полную информацию о теореме косинусов, а также калькулятор, с помощью которого можно найти стороны и угол треугольника и формулу теоремы косинусов.

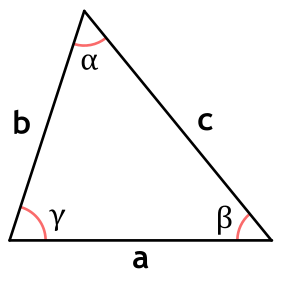
Теорема косинусов обобщает теорему Пифагора на произвольные плоские треугольники и устанавливает соотношение между сторонами треугольника и его углами.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов

{a^2 = b^2 + c^2-2bc cos (alpha)}
{b^2 = a^2 + c^2-2ac cos (beta)}
{c^2 = a^2 + b^2-2ab cos (gamma)}

a, b, c — стороны треугольника,

α, β, γ — углы треугольника.

Источник

Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.

Формула косинуса:

a² = b² + c² – 2b.c.cosα
b² = a² + c² – 2a.c.cosβ
c² = a² + b² – 2a.b.cosγ

Например:

Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.

Решение по формуле a² = b² + c² – 2b.c.cosα:

b = 12 см

c = 8 см

cos α = cos 120º = — 1/2 (это значение можно найти в таблицах)

a² = 12² + 8² – 2×12×8×(- 1/2)

a² = 144 + 64 – (–96)

a² = 304

a = √304

a ≈ 17,436

Длина третьей стороны — примерно 17,436 см.

Следствия

Следствие косинуса угла треугольника

При помощи теоремы косинусов можно найти косинус угла треугольника.

Формула:

Либо

Например:

сторона c = 6

сторона b = 7

сторона a = 8

Используйте теорему косинусов, чтобы найти угол β.

Решение:

Будем использовать эту версию формулы:

cos β = (6² + 8² − 7²) / 2×6×8

= (36 + 64 − 49) / 96

= 51 / 96

= 0,53125

= cos¯¹(0,53125)

≈ 57,9°

Следствие верхней части формулы cos α

Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):

b²+c²−a²<0, значит угол α — тупой;
b²+c²−a²=0, значит угол α — прямой;
b²+c²−a²>0, значит угол α — острый.

Доказательство теоремы косинусов

Нужно доказать, что c² = a² + b² − 2a.b.cos C

1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a <=> CD = a.cos C.

2. Вычитаем это из стороны b, так мы получим DA:

DA = b − a.cosC

3. Мы знаем из определения синуса, что в том же треугольнике BCD:

sin C = BD/a <=> BD = a.sinC.

4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²

5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²

6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C

6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC

7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC

8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C

Q.E.D.

Теорема косинусов для равнобедренного треугольника

В равнобедренном треугольнике:

две его стороны равны;
углы при основании равны.

Рассмотрим пример:

Используем формулу теоремы косинусов

a² = b² + c² – 2b.c.cosα

Подставляем все известные:

x² = 8² + 8² – 2×8×8×cos140º

x² = 64 + 64 – 128 × (-0,766)

x² ≈ √226,048

x ≈ 15,035.

Теорема синусов

Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:

Узнайте также, что такое Теорема Пифагора и Теорема Менелая.

Источник

Определение арккосинуса(arccos)

Арккосинус(y = arccos(x)) – это обратная тригонометрическая функция к косинусу x = cos(y). Область определения -1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.

Функция арккосинус не является четной или нечетной

Видео

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a² = b² + c² — 2bc cos α

b² = c² + a² — 2ca cos β

c² = a² + b² — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Теорема косинусов

Для любого треугольника справедливо равенство:

a² = b² + c² — 2b × c × cosA,

где угол A — это угол, противолежащий стороне a.

Данное уравнение правдиво для любых плоских треугольников и при помощи него легко определить угол или одну из сторон. Если угол A — прямой, то выражение 2b×c×cosA обращается в ноль, так как cos90 = 0. Следовательно, напротив прямого угла лежит наибольшая сторона или гипотенуза, а теорема косинусов превращается в классическую теорему Пифагора:

a² = b² + c²,

где a — гипотенуза.