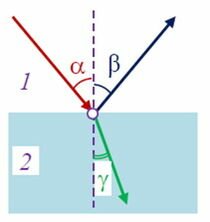
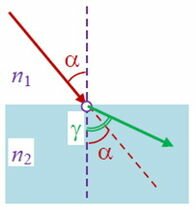
Рассмотрим точку О – это точка падения света на поверхность, к этой точке проведен перпендикуляр CD (ее также называют нормалью). Относительно этой нормали и определяются углы. Таким образом: угол падения – это (alpha), а (beta) – угол рефракции. Световой поток ОВ – преломленный луч, а угол β и будет углом преломления – угол между потоком света ОВ и нормалью CD.
Вещества, которые являются прозрачными для света, имеют свою характеристику – показатель преломления, имеющий прямую зависимость от скорости света для конкретного вещества. Для различных сред этот показатель (n) различен. Для воздуха (n = 1,0003), таким образом, можно принять (n = 1). Этот показатель (n) принимается таким же, как и показатель для вакуума и это значение применяется при расчетных задачах.
Закон преломления «воздух – среда»
Падающий и отклонённый световой поток, а также нормаль, проведенная к поверхности, находятся в единой плоскости.
Отношение синусов углов падения и преломления светового потока равны (n):
$$ frac{sin{alpha}}{sin{beta}}=n. ,,(1)$$
Учитывая, что (n) всегда больше единицы ((n ≥1)), то из формулы (1) получается: (sin{alpha}>=sin{beta}) или (beta<alpha).
Значение показателя (n) напрямую связано со скоростью света (v) в рассматриваемой среде, причем скорость света в веществе меньше скорости в вакууме ((v≤c)). Учитывая это можно записать:
$$ n=frac{c}{v}. ,,(2)$$
Объединяем (1) и (2):
$$ frac{sin{alpha}}{sin{beta}}=frac{c}{v}. ,,(3)$$
То есть отношение скорости в воздухе к скорости света в среде будет равно синусам углов падающего и преломленного лучей.
Обратимость световых лучей
Возьмем поток света, выходящий из более плотной среды и попадающий в воздух.
Принцип обратимости
Этот принцип гласит – луч, движется по пути прямого потока света, но в обратном направлении проходит тот же путь, как и в прямом. Этот принцип демонстрируется на рис.2.
Повторение
- Углом падения α называется угол между падающим лучом света и перпендикуляром к границе раздела двух сред, восстановленным в точке падения (рис. 1).
- Углом отражения β называется угол между отраженным лучом света и перпендикуляром к отражающей поверхности, восстановленным в точке падения (см. рис. 1).
- Углом преломления γ называется угол между преломленным лучом света и перпендикуляром к границе раздела двух сред, восстановленным в точке падения (см. рис. 1).
-
Под лучом понимают линию, вдоль которой переносится энергия электромагнитной волны.
- Условимся изображать оптические лучи графически с помощью геометрических лучей со стрелками. В геометрической оптике волновая природа света не учитывается (см. рис. 1).
- Лучи, выходящие из одной точки, называют расходящимися, а собирающиеся в одной точке — сходящимися.
- Примером расходящихся лучей может служить наблюдаемый свет далеких звезд, а примером сходящихся — совокупность лучей, попадающих в зрачок нашего глаза от различных предметов.
При изучении свойств световых лучей были экспериментально установлены четыре основных закона геометрической оптики:
- закон прямолинейного распространения света;
- закон независимости световых лучей;
- закон отражения световых лучей;
- закон преломления световых лучей.
Преломление света
Измерения показали, что скорость света в веществе υ всегда меньше скорости света в вакууме c.
- Отношение скорости света в вакууме c к ее скорости в данной среде υ называется абсолютным показателем преломления:
(n=frac{c}{upsilon }.)
Словосочетание «абсолютный показатель преломления среды» часто заменяют «показатель преломления среды».
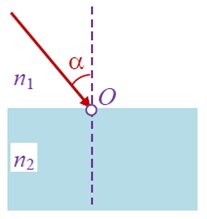
Рассмотрим луч, падающий на плоскую границу раздела двух прозрачных сред с показателями преломления n1 и n2 под некоторым углом α (рис. 2).
- Изменение направления распространения луча света при прохождении через границу раздела двух сред называется преломлением света.
Законы преломления:
- отношение синуса угла падения α к синусу угла преломления γ есть величина постоянная для двух данных сред
(frac{sin alpha }{sin gamma }=frac{n_2}{n_1}.)
- лучи, падающий и преломленный, лежат в одной плоскости с перпендикуляром, проведенным в точке падения луча к плоскости границы раздела двух сред.
Для преломления выполняется принцип обратимости световых лучей:
- луч света, распространяющийся по пути преломленного луча, преломившись в точке O на границе раздела сред, распространяется дальше по пути падающего луча.
Из закона преломления следует, что если вторая среда оптически более плотная через первая среда,
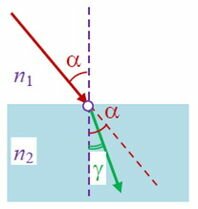
- т.е. n2 > n1, то α > γ (left( frac{n_2}{n_1} > 1, ;;; frac{sin alpha }{sin gamma } > 1 right)) (рис. 3, а);
- если n2 < n1, то α < γ (рис. 3, б).
-
а
-
б
Рис. 3
Первые упоминания о преломлении света в воде и стекле встречаются в труде Клавдия Птолемея «Оптика», вышедшего в свет во II веке нашей эры. Закон преломления света был экспериментально установлен в 1620 г. голландским ученым Виллебродом Снеллиусом. Заметим, что независимо от Снеллиуса закон преломления был также открыт Рене Декартом.
Закон преломления света позволяет рассчитывать ход лучей в различных оптических системах.
На границе раздела двух прозрачных сред обычно одновременно с преломлением наблюдается отражение волн. Согласно закону сохранения энергии сумма энергий отраженной Wo и преломленной Wnp волн равна энергии падающей волны Wn:
Wn = Wnp + Wo.
Полное отражение
Как уже говорилось выше, при переходе света из оптически более плотной среды в оптически менее плотную среду (n1 > n2), угол преломления γ становится больше угла падения α (см. рис. 3, б).
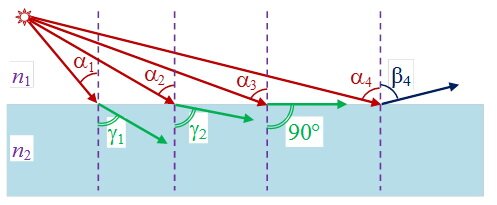
По мере увеличения угла падения α (рис. 4), при некотором его значении α3, угол преломления станет γ = 90°, т. е. свет не будет попадать во вторую среду. При углах больших α3 свет будет только отражаться. Энергия преломленной волны Wnp при этом станет равной нулю, а энергия отраженной волны будет равна энергии падающей: Wn = Wo. Следовательно, начиная с этого угла падения α3 (в дальнейшем будет обозначать его α0), вся световая энергия отражается от границы раздела этих сред.
Это явление получило название полное отражение (см. рис. 4).
- Угол α0, при котором начинается полное отражение, называется предельным углом полного отражения.
Значение угла α0 определяется из закона преломления при условии, что угол преломления γ = 90°:
(sin alpha_{0} = frac{n_{2}}{n_{1}} ;;; left( n_{2} < n_{1} right).)
Литература
Жилко, В.В. Физика: учеб. Пособие для 11 класса общеобразоват. шк. с рус. яз. обучения / В.В.Жилко, Л.Г.Маркович. — Минск: Нар. Асвета, 2009. — С. 91-96.
Из прошлых уроков вы уже знаете, что в однородной среде свет распространяется прямолинейно. Но в жизни много ситуаций, когда свет проходит через разные вещества до того, как достигнет наших глаз.
Например, через оконные стекла мы отлично видим все, что происходит на улице. А через стекла в межкомнатных дверях мы можем видеть только размытые силуэты того, что находится за дверью. Тот же самый пример можно привести и с прозрачной и мутной водой.
Значит, получаемое нашими глазами изображение как-то связано с тем, через какие среды проходит свет. Двигаясь прямолинейно в одной среде, он переходит в другую и снова двигается прямолинейно. Что же происходит при этом переходе из одной среды в другую?
Так, вам предстоит узнать новое понятие — преломление света. В ходе данного урока вы узнаете закономерности этого явления, рассмотрите различные опыты и научитесь применять полученные знания для решения задач.
Явление преломления света
Рассмотрим простой опыт. Для него нам понадобится прозрачный стакан с водой и обычный карандаш (рисунок 1).
Сначала опустим карандаш в воду вертикально (рисунок 1, а). Части карандаша в воздухе и в воде не изменились.
А теперь поменяем угол наклона карандаша (рисунок 2, б). Мы увидим интересную картинку. Нам кажется, что карандаш переломился на границе воды и воздуха.
Что произошло? Мы видим карандаш, потому что на него падает свет от какого-то источника. Его лучи отражаются от карандаша и попадают нам в глаза. Когда мы опустили карандаш в воду под каким-то углом, световые лучи дошли до наших глаз не только через воздух, но еще и через воду в стакане. При этом они поменяли направление своего распространения при переходе из одной среды в другую. В таком случае говорят, что свет преломился.
Преломление света — это явление изменения направления распространения света при переходе из одной среды в другую.
Но, если свет преломляется при переходе из одной среды в другую, почему на рисунке 1 (а) мы все равно видим карандаш без изменений? Чтобы разобраться с этим вопросом, нам необходимо более подробно изучить природу преломления света.
Скорость света и оптическая плотность среды
Свет распространяется в пространстве с определенной скоростью. Эта скорость настолько велика, что нам кажется, будто свет появляется мгновенно. Например, когда в темной комнате мы щелкаем переключателем, и включается свет.
Ученые не только рассчитали значение этой скорости, но и доказали, что скорость света различается в разных средах (таблица 1).
| Вещество | $c$, $frac{км}{с}$ |
| Воздух | 300 000 |
| Вода | 225 000 |
| Стекло | 198 000 |
| Сероуглерод | 184 000 |
| Алмаз | 124 000 |
Значения скорости света в вакууме и воздухе практически не отличаются, поэтому используют одно значение — $300 000 frac{км}{с}$. Эта величина обозначается буквой $c$.
В других же средах наблюдается значительная разница в значениях скорости. Например, в воде скорость света меньше, чем в воздухе. При этом говорят, что вода является оптически более плотной средой, чем воздух.
Оптическая плотность — это величина, которая характеризует различные среды в зависимости от значения скорости распространения света в них.
Если пучок света падает на поверхность, разделяющую две прозрачные среды с разной оптической плотностью, то часть света отразится от этой поверхности, а другая часть проникнет во вторую среду. При этом луч света изменит свое направление — происходит преломление света.
Схема преломления светового луча. Угол преломления
Рассмотрим преломление света более подробно (рисунок 2).
Перечислим элементы, обозначенные на рисунке 2:
- MN — граница раздела воздуха и воды
- Луч AO — падающий луч
- Луч OB — преломленный луч
- CD — перпендикуляр, опущенный к поверхности раздела двух сред и проведенный через точку падения O
- Угол AOC — угол падения ($alpha$)
- Угол DOB — угол преломления ($gamma$)
Угол преломления — это угол между перпендикуляром, опущенным к границе раздела двух сред в точке падения светового луча, и преломленным лучом.
Направления луча при переходе в воду изменилось. Луч света стал ближе к перпендикуляру CD. Т.е., $gamma < alpha$. Рассмотрим опыт, который нам наглядно демонстрирует этот факт.
Возьмем стеклянный сосуд и наполним его водой. Воду подкрасим флуоресцентной жидкостью. Она будет светится в тех местах, где на нее будет попадать яркий свет — это удобно для наших наблюдений. На дно сосуда поместим плоское зеркало (рисунок 3).
Теперь на поверхность воды с помощью маленького фонарика направим пучок света. Сделаем это таким образом, чтобы пучок света падал под каким-то углом.
Мы увидим, как луч поменяет свое направление на границе воздуха и воды. При этом угол преломления заметно меньше угла падения ($gamma_1 < alpha_1$).
Далее луч отразится от плоского зеркала и снова достигнет границы раздела двух сред. Теперь мы видим, что луч падения заметно меньше луча преломления ($gamma_2 > alpha_2$).
Вода — более плотная оптическая среда, чем воздух. Из всего этого мы можем сделать следующие выводы:
- Если свет идет из оптически менее плотной среды в более плотную, то угол преломления всегда меньше угла падения: $gamma < alpha$
- Если свет идет из оптически более плотной среды в менее плотную, то угол преломления всегда больше угла падения: $gamma > alpha$
Если в ходе опытов мы будем менять угол падения, то заметим, что угол преломления тоже будет изменяться. При этом вышеописанные нами закономерности будут исполняться.
Показатель преломления
Давайте выясним, как именно углы падения и преломления связаны друг с другом. Рассматривать будем луч света падающий из воздуха в воду.
При увеличении угла падения, будет увеличиваться угол преломления (рисунок 4). Но отношение между этими углами ($frac{alpha}{gamma}$) не будет постоянным.
Постоянным будет оставаться другое отношение этих углов — отношение их синусов:
$frac{sin 30 degree}{sin 23 degree} = frac{sin 45 degree}{sin 33 degree} = frac{sin 60 degree}{sin 42 degree} approx 1.33$.
Полученное число (1.3) называют относительным показателем преломления. Обозначают эту величину буквой $n_{21}$.
Так, для любой пары веществ с разными оптическими плотностями можно записать:
$frac{sin alpha}{sin gamma} = n_{21}$.
Чем больше относительный показатель преломления, тем сильнее преломляется световой луч при переходе из одной среды в другую.
В чем физический смысл этой величины? Ранее мы говорили, что оптическая плотность характеризует вещество по скорости распространения света в нем. Показатель преломления делает то же самое.
Относительный показатель преломления — это величина, показывающая, во сколько раз скорость света в первой по ходу луча среде отличается от скорости распространения света во второй среде:
$n_{21} = frac{upsilon_1}{upsilon_2}$.
Если луч света падает из вакуума или воздуха в какое-то вещество, то используется еще одна величина — абсолютный показатель преломления.
Абсолютный показатель преломления — это величина, показывающая во сколько раз скорость света в вакуумевоздухе больше, чем в данной среде:
$n = frac{c}{upsilon}$,
где $c = 3 cdot 10^8 frac{м}{с}$.
В таблице 2 представлены значения абсолютных показателей преломления некоторых веществ. Иногда их называют относительными показателями преломления относительно воздуха, потому что для воздуха $n = 1$.
| Вещество | $n$ |
| Воздух | 1.00 |
| Лед | 1.31 |
| Вода | 1.33 |
| Спирт | 1.36 |
| Стекло (обычное) | 1.50 |
| Стекло (оптическое) | 1.47 — 2.04 |
| Рубин | 1.76 |
| Алмаз | 2.42 |
Выразим относительный показатель преломления $n_{21}$ через абсолютные показатели преломления $n_1$ и $n_2$:
$n_{21} = frac{upsilon_1}{upsilon_2} = frac{frac{c}{n_1}}{frac{c}{n_2}} = frac{n_2}{n_1}$.
Относительный показатель преломления $n_{21}$ имеет нижний индекс $21$, который читается как: «два один». Этот индекс связан с полученной нами формулой: $n_{21} = frac{n_2}{n_1}$. То есть, относительный показатель преломления $n_{21}$ равен отношению абсолютных показателей $n_2$ к $n_1$. При этом нижние индексы обозначают последовательность сред, через которые проходит световой луч.
Здесь мы вернемся к вопросу о том, почему на рисунке 1 (а) мы не видим преломления.
Если падающий луч падает перпендикулярно на границу раздела двух сред, то он не испытывает преломления.
Доказывается это опытным путем. При любых других углах падения, отличных от $0 degree$, преломление света происходит по вышеописанным закономерностям.
Закон преломления света
Итак, преломление света происходит по определенному закону.
Закон преломления света:
падающий и преломленный лучи и перпендикуляр, проведенный к границе раздела двух сред в точке падения луча, лежат в одной плоскости. При этом отношение синуса угла падения к синусу угла преломления — постоянная величина для двух сред:
$frac{sin alpha}{sin gamma} = frac{n_2}{n_1} = n_{21}$.
Мнимое изображение, образованное преломлением света. Призмы
Преломление света, как и отражение света плоским зеркалом, создает “кажущееся” изменение положение источника света. Мы наблюдали такое изменение в самом первом опыте этого урока на рисунке 1, б.
Но, дело в том, что мнимое положение источника света в случае преломления будет различным для лучей, падающих на границу раздела двух сред под разными углами. Поэтому мнимое положение источника света при преломлении обычно подробно не рассматривают.
Тем не менее, мы часто замечаем эти изменения. Например, в прозрачной воде в закрытых водоемах или в море кажется, что предметы, лежащие на дне и находящиеся в толще воды, находятся на другом расстоянии от нас, чем они есть на самом деле.
Рассмотрим наглядный опыт с монеткой (рисунок 5).
Возьмем неглубокую широкую чашку и положим на ее дно монетку. Выберем такое положение для наблюдения, чтобы она была не видна (рисунок 5, а).
Оставаясь в этой же точке наблюдения, нальем в чашку воду. Теперь монета стала видна (рисунок 5, б). То есть, мы видим не саму монету, а ее мнимое изображение, образованное преломлением света.
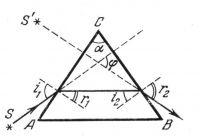
В различных оптических приборах используют эти особенности преломления. Часто свет проходит сквозь тело, имеющее форму призмы (рисунок 6, а).
Световой луч, падающий на боковую грань призмы дважды преломляется (рисунок 6, б): при входе в призму и при выходе из нее. Такой луч на выходе из призмы будет отклоняться к основанию треугольника.
В оптических приборах используют не просто призмы, но и их различные сочетания. Например, на рисунке 7 изображены 3 коробки, в которых находятся треугольные призмы.
Вы можете оценить, как при разных положениях призм изменяется ход лучей на выходе из коробки. При этом падающие лучи во всех трех случаях (а, б, в) были параллельны и имели одинаковое направление.
Примеры задач
Задача №1
Луч света переходит из скипидара в воздух. Определите абсолютный показатель преломления скипидара, если при угле падения, равном $30 degree$, угол преломления равен $45 degree$ (рисунок 8). Чему равна скорость распространения света в скипидаре?
Дано:
$alpha = 30 degree$
$gamma = 45 degree$
$n_2 = 1$
$c = 3 cdot 10^8 frac{м}{с}$
$n_1 — ?$
$upsilon_1 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Так как световой луч проходит из скипидара (первая среда) в воздух (вторая среда), мы обозначили абсолютный показатель скипидара как $n_1$, а воздуха как $n_2$.
По закону преломления света:
$frac{sin alpha}{sin gamma} = n_{21} = frac{n_2}{n_1}$.
Для воздуха $n_2 = 1$, поэтому:
$frac{sin alpha}{sin gamma} = frac{1}{n_1}$.
Выразим $n_1$:
$n_1 = frac{sin gamma}{sin alpha}$.
Рассчитаем $n_1$:
$n_1 = frac{sin 45 degree}{sin 30 degree} = frac{frac{sqrt{2}}{2}}{frac{1}{2}} = sqrt{2} approx 1.41$.
По определению абсолютного показателя преломления для скипидара мы можем записать:
$n_1 = frac{c}{upsilon_1}$.
Выразим $upsilon_1$ и рассчитаем:
$upsilon_1 = frac{c}{n_1} = frac{3 cdot 10^8 frac{м}{с}}{1.41} approx 2 cdot 10^8 frac{м}{с}$.
Ответ: $n_1 approx 1.41$, $upsilon_1 approx 2 cdot 10^8 frac{м}{с}$.
Задача №2
Световой луч падает из воздуха в стекло. Абсолютный показатель преломления стекла равен $1.73$. Чему равен угол преломления, если отраженный луч образует с перпендикуляром, опущенным в точку падения луча на границе раздела двух сред, угол, равный $60 degree$?
При решении задачи мы будем использовать рисунок 9.
$AO$ — падающий луч, а угол $alpha$ — угол падения. Луч $AO$ падает на границу раздела двух сред (воздуха и стекла). Образуются отраженный луч $OB$ и преломленный луч $OC$. Им соответствуют угол отражения $beta$ и угол преломления $gamma$.
Теперь запишем условие задачи и решим ее.
Дано:
$n_1 = 1$
$n_2 = 1.73$
$beta = 60 degree$
$gamma — ?$
Посмотреть решение и ответ
Скрыть
Решение:
По закону отражения света:
$alpha = beta = 60 degree$.
По закону преломления света:
$frac{sin alpha}{sin gamma} = frac{n_2}{n_1}$.
Для воздуха $n_1 = 1$, поэтому:
$frac{sin alpha}{sin gamma} = n_2$.
Выразим синус угла преломления и рассчитаем его:
$sin gamma = frac{sin alpha}{n_2} = frac{sin 60 degree}{1.73} = frac{frac{sqrt{3}}{2}}{1.73} = frac{sqrt{3}}{3.46} approx frac{1.73}{3.46} = 0.5 = frac{1}{2}$.
Если $sin gamma = frac{1}{2}$, то $gamma = 30 degree$.
Ответ: $gamma = 30 degree$.
Задача №3
На дне пруда глубиной $3 space м$ находится источник света. Показатель преломления воды равен $1.33$, а воздуха — $1$. На какой глубине наблюдатель увидит источник света, если он смотрит вертикально вниз с лодки.
Условие задачи дает понять, что в глаз наблюдателя попадает луч, который падает перпендикулярно границе раздела двух сред. В таком случае, преломление наблюдаться не будет. Тем не менее, как и в настоящей жизни, мы все равно увидим преломленное изображение источника света. Он будет казаться ближе. В ходе решения этой задачи вы узнаете, почему так происходит.
Для начала рассмотрим рисунок 10.
Источник света $S$ находится на глубине $H$. Мы опишем его двумя лучами: $SA$ и $SO$. Луч $SA$ перпендикулярен к границе раздела двух сред. Поэтому он не преломляется. Луч $SO$ достигает границы раздела под некоторым углом. Он образует с перпендикуляром $CD$ угол падения $alpha$. Далее этот луч преломляется под углом преломления $gamma$ и попадает в глаза наблюдателя (точка $B$).
Продолжим преломленный луч до луча $SA$. Этот луч мы будем использовать как перпендикуляр к поверхности воды, чтобы оценивать глубину. Мы получили точку $S_1$ — мнимое изображение источника света. Соответственно длина отрезка $AS$ — это реальная глубина пруда $H$, а длина отрезка $AS_1$ — мнимая глубина $h$.
Обратите внимание, что мы взяли второй луч $SO$ не просто так — он падает под крайне малым углом $alpha$. После преломления мы получаем такой малый угол $gamma$, что он попадает в глаз наблюдателя. Т.е., на рисунке 8 схематическая область увеличена для нашего удобства во много раз. Мы рассматриваем настолько малые углы, что преломленный луч $SB$ достигает глаза, и мы видим мнимое изображение, образованное преломлением света.
Теперь мы можем записать условие задачи и решить ее.
Дано:
$H = 3 space м$
$n_1 = 1.33$
$n_2 = 1$
$h — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Рассмотрим две прямые $AS$ и $CD$. Они параллельны, а прямая $SO$ — секущая. Тогда накрест лежащие углы равны друг другу:
$angle ASO = alpha$.
Запишем тангенс этого угла в прямоугольном треугольнике $ASO$:
$tg alpha = frac{AO}{AS} = frac{AO}{H}$.
Тогда, $AO = H cdot tg alpha$.
Теперь попробуем выразить $AO$ из другого треугольника — $AS_1O$.
Если рассмотрим $S_1O$ как прямую, пересекающую две параллельные прямые, то $angle AS_1O = gamma$.
Запишем тангенс этого угла:
$tg gamma = frac{AO}{AS_1} = frac{AO}{h}$.
Тогда, $AO = h cdot tg gamma$.
Получается, что $H cdot tg alpha = h cdot tg gamma$.
Выразим отсюда мнимую глубину $h$:
$h = H cdot frac{tg alpha}{tg gamma}$.
Так как углы $alpha$ и $gamma$ крайне малы, мы можем смело использовать следующие приближения:
$tg alpha approx sin alpha$,
$tg gamma approx sin gamma$.
Тогда, $h = H cdot frac{sin alpha}{sin gamma} = H cdot frac{n_2}{n_1}$.
Так как $n_2 = 1$, мы можем записать, что $h = frac{H}{n_1}$.
$h = frac{3 space м}{1.33} approx 2.3 space м$.
Ответ: $h = 2.3 space м$.
Более 8-ми тысяч учебных материалов на нашем сайте в свободном доступе
Закон преломления света и полное внутреннее отражение
- Подробности
- Категория: Оптика
Закон преломления света
Наблюдение преломления света.
На границе двух сред свет меняет направление своего распространения. Часть световой энергии возвращается в первую среду, т. е. происходит отражение света. Если вторая среда прозрачна, то свет частично может пройти через границу сред, также меняя при этом, как правило, направление распространения. Это явление называется преломлением света.
Вследствие преломления наблюдается кажущееся изменение формы предметов, их расположения и размеров. В этом нас могут убедить простые наблюдения. Положим на дно пустого непрозрачного стакана монету или другой небольшой предмет. Подвинем стакан так, чтобы центр монеты, край стакана и глаз находились на одной прямой. Не меняя положения головы, будем наливать в стакан воду. По мере повышения уровня воды дно стакана с монетой как бы приподнимается. Монета, которая ранее была видна лишь частично, теперь будет видна полностью. Установим наклонно карандаш в сосуде с водой.
Если посмотреть на сосуд сбоку, то можно заметить, что часть карандаша, находящаяся в воде, кажется сдвинутой в сторону (рис. 96).
Эти явления объясняются изменением направления лучей на границе двух сред — преломлением света.
Закон преломления света определяет взаимное расположение падающего луча АВ (рис. 97), преломленного DB и перпендикуляра СЕ к поверхности раздела сред, восставленного в точке падения. Угол а называется углом падения, а угол β— углом преломления.
Падающий, отраженный и преломленный лучи нетрудно наблюдать, сделав узкий световой пучок видимым. Ход такого пучка в воздухе можно проследить, если пустить в воздух немного дыма или же поставить экран под небольшим углом к лучу. Преломленный пучок также виден в подкрашенной флюоресцеином воде аквариума (рис. 98).
Вывод закона преломления света. Закон преломления света был установлен опытным путем в XVII веке. Мы его выведем с помощью принципа Гюйгенса.
Преломление света при переходе из одной среды в другую вызвано различием в скоростях распространения света в той и другой среде. Обозначим скорость волны в первой среде через v1, а во второй — через v2.
Пусть на плоскую границу раздела двух сред (например, из воздуха в воду) падает плоская световая волна (рис. 99). Волновая поверхность АС перпендикулярна лучам А1А и В1В. Поверхности MN сначала достигнет луч А1А. Луч В1В достигнет поверхности спустя время
Поэтому в момент, когда вторичная волна в точке В только начнет возбуждаться, волна от точки А уже имеет вид полусферы радиусом
Волновую поверхность преломленной волны можно получить, проведя поверхность, касательную ко всем вторичным волнам во второй среде, центры которых лежат на границе раздела сред. В данном случае это плоскость BD. Она является огибающей вторичных волн.
Угол падения α луча равен углу САВ в треугольнике АВС (стороны одного из этих углов перпендикулярны сторонам другого). Следовательно,
Угол преломления β равен углу ABD треугольника ABD. Поэтому
Разделив почленно (5.2) на (5.3), получим
где n — постоянная величина, не зависящая от угла падения.
Из построения (рис. 99) видно, что падающий луч, луч преломленный и перпендикуляр, восставленный в точке падения, лежат в одной плоскости. Данное утверждение совместно с уравнением (5.4), согласно которому отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред, представляет собой закон преломления света.
Убедиться в справедливости закона преломления можно экспериментально, измеряя углы падения и преломления и вычисляя отношение их синусов при различных углах падения. Это отношение остается неизменным.
Показатель преломления. Постоянная величина, входящая в закон преломления света, называется относительным показателем преломления или показателем преломления второй среды относительно первой.
Из принципа Гюйгенса не только следует закон преломления, но с помощью этого принципа раскрывается физический смысл показателя преломления. Он равен отношению скоростей света в средах, на границе между которыми происходит преломление:
Если угол преломления β меньше угла падения а, то согласно (5.4) скорость света во второй среде меньше, чем в первой.
Показатель преломления среды относительно вакуума называют абсолютным показателем преломления этой среды. Он равен отношению синуса угла падения к синусу угла преломления при переходе светового луча из вакуума в данную среду.
Пользуясь формулой (5.5), можно выразить относительный показатель преломления через абсолютные показатели преломления n1 и n2 первой и второй сред.
Действительно, так как n1=c/v1 и n2=c/v2 , где с — скорость света в вакууме, то
Среду с меньшим абсолютным показателем преломления принято называть оптически менее плотной средой.
Абсолютный показатель преломления определяется скоростью распространения света в данной среде, которая зависит от физического состояния среды, т. е. от температуры вещества, его плотности, наличия в нем упругих напряжений. Показатель преломления зависит также и от характеристик самого света. Для красного света он меньше, чем для зеленого, а для зеленого — меньше, чем для фиолетового.
Поэтому в таблицах значений показателей преломления для разных веществ обычно указывается, для какого света приведено данное значение n и в каком состоянии находится среда. Если таких указаний нет, то это означает, что зависимостью от указанных факторов можно пренебречь.
В большинстве случаев приходится рассматривать переход света через границу воздух — твердое тело или воздух — жидкость, а не через границу вакуум — среда. Однако абсолютный показатель преломления n2 твердого или жидкого вещества отличается от показателя преломления того же вещества относительно воздуха незначительно. Так, абсолютный показатель преломления воздуха при нормальных условиях для желтого света равен приблизительно n1≈1,000292. Следовательно,
Значения показателей преломления для некоторых веществ относительно воздуха приведены в таблице 2 (данные относятся к желтому свету).
Ход лучей в треугольной призме.
Закон преломления света позволяет рассчитать ход лучей в различных оптических устройствах, например в треугольной призме, изготовленной из стекла или других прозрачных материалов.
На рисунке 100 изображено сечение стеклянной призмы плоскостью, перпендикулярной ее боковым ребрам. Луч в призме отклоняется к основанию, преломляясь на гранях ОА и ОВ. Угол φ между этими гранями называют преломляющим углом призмы. Угол 0 отклонения луча зависит от преломляющего угла призмы ф, показателя преломления n материала призмы и угла падения а. Он может быть вычислен с помощью закона преломления (5.4).
ПОЛНОЕ ОТРАЖЕНИЕ
При прохождении света из оптически менее плотной среды в более плотную, например из воздуха в стекло или воду, v1 и v2 согласно закону преломления (5.4) показатель преломления 1. Поэтому а>β (рис. 101, а):
преломленный луч приближается к перпендикуляру к границе раздела сред. Если направить луч света в обратном направлении — из оптически более плотной среды в оптически менее плотную вдоль бывшего преломленного луча (рис. 101, б), то закон преломления запишется так:
Преломленный луч по выходе из оптически более плотной среды пойдет по линии бывшего падающего луча, поэтому а<β, т. е. преломленный луч отклоняется от перпендикуляра. По мере увеличения угла а угол преломления β растет, оставаясь все время больше угла а. Наконец, при некотором угле падения значение угла преломления приблизится к 90° и преломленный луч пойдет почти по границе раздела сред (рис. 102). Наибольшему возможному углу преломления β = 90° соответствует угол падения ао.
Попробуем сообразить, что произойдет при а>ао. При падении света на границу двух сред световой луч, как об этом уже упоминалось, частично преломляется, а частично отражается от нее. При а>a0 преломление света невозможно. Значит, луч должен полностью отразиться. Это явление и называется полным отражением света.
Для наблюдения полного отражения можно использовать стеклянный полуцилиндр с матовой задней поверхностью. Полуцилиндр закрепляют на диске так, чтобы середина плоской поверхности полуцилиндра совпадала с центром диска (рис. 103). Узкий пучок света от осветителя направляют снизу на боковую поверхность полуцилиндра перпендикулярно его поверхности. На этой поверхности луч не преломляется. На плоской поверхности луч частично преломляется и частично отражается. Отражение происходит в соответствии с законом отражения, а преломление — в соответствии с законом преломления (5.4).
Если увеличивать угол падения, то можно заметить, что яркость (и следовательно, энергия) отраженного пучка растет, в то время как яркость (энергия) преломленного пучка падает. Особенно быстро убывает энергия преломленного пучка, когда угол преломления приближается к 90°. Наконец, когда угол падения становится таким, что преломленный пучок идет вдоль границы раздела (см. рис. 102), доля отраженной энергии составляет почти 100%. Повернем осветитель, сделав угол падения а большим ао. Мы увидим, что преломленный пучок исчез и весь свет отражается от границы раздела, т. е. происходит полное отражение света.
На рисунке 104 изображен пучок лучей от источника, помещенного в воде недалеко от ее поверхности. Большая интенсивность света показана большей толщиной линии, изображающей соответствующий луч.
Угол падения ао, соответствующий углу преломления 90°, называют предельным углом полного отражения
При sin β= 1 формула (5.8) при нимает вид
Из этого равенства и может быть найдено значение предельного угла полного отражения ао. Для воды (n = 1,33) он оказывается равным 48°35′, для стекла (n =1,5) он принимает значение 41°51′, а для алмаза (n— 2,42) этот угол составляет 24°40′. Во всех случаях второй средой является воздух.
Явление полного отражения легко наблюдать на простом опыте. Нальем в стакан воду и поднимем его несколько выше уровня глаз. Поверхность воды при рассматривании ее снизу сквозь стенку кажется блестящей, словно посеребренной вследствие полного отражения света.
Полное отражение используют в так называемой волоконной оптике для передачи света и изображения по пучкам прозрачных гибких волокон — световодов. Световод представляет собой стеклянное волокно цилиндрической формы, покрытое оболочкой из прозрачного материала с меньшим, чем у волокна, показателем преломления. За счет многократного полного отражения свет может быть направлен по любому (прямому или изогнутому) пути (рис. 105). Волокна набираются в жгуты. При этом по каждому из волокон передается какой-нибудь элемент изображения (рис. 106). Жгуты из волокон используются, например, в медицине для исследования внутренних органов.
По мере улучшения технологии изготовления длинных пучков волокон— световодов все шире начинает применяться связь (в том числе и телевизионная) с помощью световых лучей.
Трехсантиметровые волны: закон отражения (металл)
Полное внутреннее отражение
Искривление луча в неоднородной среде
Модель световода
Куб и призма на пути трехсантиметровой волны
Трехсантиметровые волны: закон отражения (диэлектрик)
Трехсантиметровые волны: интерференция при отражении (просветление)
Трехсантиметровые волны: диэлектрическая линза
Трехсантиметровые волны: диэлектрическая призма
Решётка — зеркало для трёхсантиметровых волн
Дециметровые волны: «хорошее» и «плохое» зеркала
Для того, чтобы знания преломлялись в твоем сознании без больших искажений, нужно, чтобы знания попадали в среду, с оптической плотностью равной оптической плотности знаний.
Интерактивное изложение материала Преломление сета. Законы преломления света

Преломление света – это явление изменения направления движения светового луча при переходе из одной среды в другую. Различные среды, пропускающие свет, имеют различную оптическую плотность. Скорость света в них различна. Чем больше оптическая плотность среды, тем меньше в ней скорость света, и тем сильнее она будет преломлять свет, попадающий извне.
Как происходит преломление света?
Предположим, что из воздуха на поверхность воды падает пучок света. Если провести перпендикуляр к поверхности воды и измерить угол падения, то выяснится, что угол луча после попадания в воду изменился, он стал меньше. То же самое произойдет в случае попадания луча из воздуха в стекло.
Угол, который образует падающий луч к проведенному к границе двух сред перпендикуляру после попадания во вторую среду, называется углом преломления. Опытным путем установлено, что если свет падает из среды оптически менее плотной в более плотную, то угол падения будет
больше угла преломления. Если же наоборот – оптическая плотность первой среды больше оптической плотности вещества второй среды, то угол падения будет меньше угла преломления. При изменении угла падения угол преломления будет также меняться. Однако отношение этих углов не остается постоянным. А вот отношение синусов этих углов – это постоянная величина.
где α – угол падения, B – угол преломления, n – постоянная величина для двух конкретных сред, не зависящая от угла падения.
Закон преломления света
Падающий и преломленный луч лежат в одной плоскости, причем отношение синуса угла падения к синусу угла преломления – величина постоянная для двух сред.
Вследствие преломления света объекты на дне водоема кажутся ближе, чем они есть на самом деле, звезды на небосводе кажутся выше, чем они есть на самом деле.
Законы отражения и преломления света обусловливают многие явления в нашей жизни.
Если мы возьмем кусок стекла с параллельными гранями, например, оконное стекло, то получим незначительное смещение изображения, видимого сквозь окно. То есть, войдя в стекло, лучи света преломляться, а попадая снова в воздух, вновь преломляться до прежних значений угла падения, только при этом немного сместятся, причем величина
смещения будет зависеть от толщины стекла.
Возьмем стекло, плоскости которого будут расположены друг к другу наклонно, например, призму, то эффект будет совсем иным. Лучи, проходящие сквозь призму,
всегда преломляются к ее основанию. Это несложно проверить. Для этого нарисуем треугольник, источник света и начертим входящий в любую из его боковых сторон луч. Пользуясь законом преломления света, проследим дальнейший путь луча. Проделав эту процедуру