-
Емельян
30 ноября, 20:06
0
Объём конуса: V=Sh/3 ⇒h=3V/S=3V / (πR²) = 3π / (π·3²) = 1/3.
В прямоугольном тр-ке, образованным высотой конуса, образующей и радиусом основания, образующая — гипотенуза треугольника.
tgα=R/h=3 / (1/3) = 9.
∠α=arctg9≈83.7° — это ответ.
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Найдите угол Альфа между образующей конуса и его высотой если радиус основания равен 3 а его объем равен П …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Новые вопросы по геометрии
Главная » Геометрия » Найдите угол Альфа между образующей конуса и его высотой если радиус основания равен 3 а его объем равен П
Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.
Треугольник (POA) вращается вокруг стороны (PO).
(PO) — ось конуса и высота конуса.
(P) — вершина конуса.
(PA) — образующая конуса.
Круг с центром (O) — основание конуса.
(AO) — радиус основания конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось (PO) конуса.
Осевое сечение конуса — это равнобедренный треугольник.
(APB) — осевое сечение конуса.
— углы между образующими и основанием конуса.
Для конуса построим развёртку боковой поверхности. Это круговой сектор.
Сектор имеет длину дуги, равную длине окружности в основании конуса
2πR
, угол развёртки боковой поверхности
α
.
В конусе нельзя обозначить угол развёртки.
На развёртке конуса нельзя обозначить высоту и радиус конуса.
Образующая конуса (l) является радиусом сектора.
Таким образом, боковая поверхность конуса является частью полного круга с радиусом (l):
Длина дуги также является частью длины полной окружности с радиусом (l), но в то же время длина дуги — это длина окружности основания конуса с радиусом (R).
Сравним выражения длины дуги и выразим
α
через (R):
2πl⋅α360°=2πR;α=2πR⋅360°2πl=R⋅360°l.
Получаем ещё одну формулу боковой поверхности конуса; не используется угол развёртки боковой поверхности:
.
Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом.
Также усечённый конус можно рассматривать как тело вращения, которое образовалось в результате вращения прямоугольной трапеции вокруг боковой стороны (которая перпендикулярна к основанию трапеции) или в результате вращения равнобедренной трапеции вокруг высоты, проведённой через серединные точки оснований трапеции.
— ось конуса и высота конуса.
Круги с центрами (O) и
O1
— основания усечённого конуса.
(AO) и
A1O1
— радиусы оснований конуса.
Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось
OO1
конуса.
Осевое сечение конуса — это равнобедренная трапеция.
— осевое сечение конуса.
Боковая поверхность определяется как разность боковой поверхности данного конуса и отсечённого конуса:
Sбок.=πR⋅PA−πr⋅PA1=πR⋅PA1+AA1−πr⋅PA1==πR⋅PA1+πR⋅AA1−πr⋅PA1==πR⋅l+πR−πr⋅PA1.
Так как
ΔPAO∼ΔPA1O1
, то стороны их пропорциональны:
PAPA1=Rr;l+PA1PA1=Rr;r⋅l+PA1=R⋅PA1;rl=R⋅PA1−r⋅PA1;PA1⋅R−r=rl;PA1=rlR−r.
Таким образом получаем формулу боковой поверхности усечённого конуса, которая содержит радиусы оснований и образующую усечённого конуса:
Sбок.=πRl+π⋅PA1⋅R−r=πRl+π⋅rlR−r⋅R−r;Sбок.=πRl+πrl=πl⋅R+r.
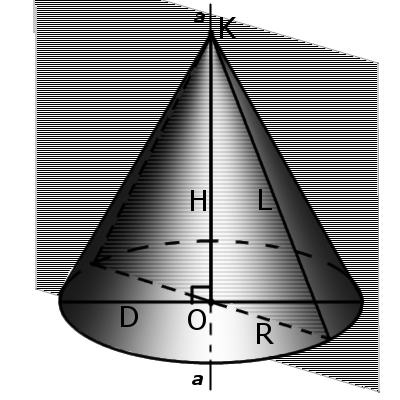
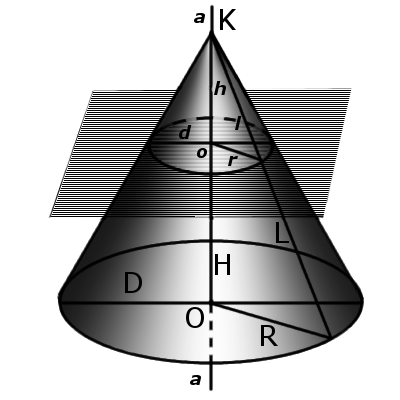
Элементы конуса
Определение. Вершина конуса — это точка (K), из которой исходят лучи.
Определение. Основание конуса — это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.
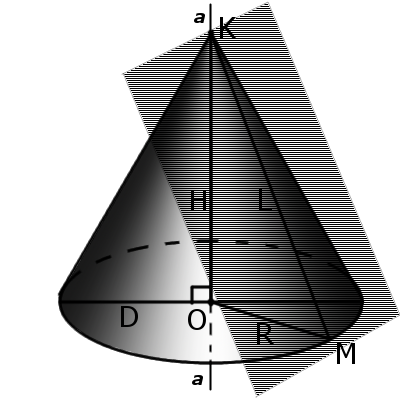
Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.
Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):
L2 = R2 + H2
Определение. Направляющая конуса — это кривая, которая описывает контур основания конуса.
Определение. Боковая поверхность конуса — это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.
Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.
Определение. Высота конуса (H) — это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.
Определение. Ось конуса (a) — это прямая, проходящая через вершину конуса и центр основания конуса.
Определение. Конусность (С) конуса — это отношение диаметра основания конуса к его высоте. В случае усеченного конуса — это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:
где C — конусность, D — диаметр основания, d — диаметр меньшего основания и h — расстояние между основаниями.
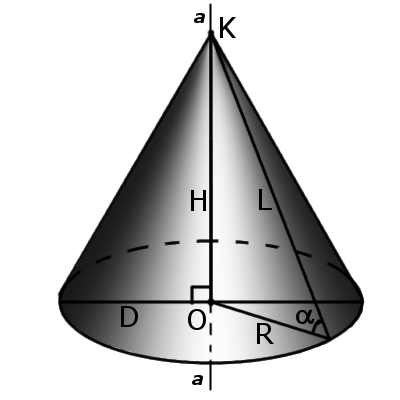
Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:
где R — радиус основы, а H — высота конуса.
Определение. Осевое сечение конуса — это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника — это диаметр основания конуса.
Определение. Касательная плоскость к конусу — это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.
Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).
Определение. Прямой конус — это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.
Формула. Объём кругового конуса:
где R — радиус основы, а H — высота конуса.
Формула. Площадь боковой поверхности (Sb) прямого конуса через радиус R и длину образующей L:
Sb = πRL
Формула. Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:
Sp = πRL + πR2
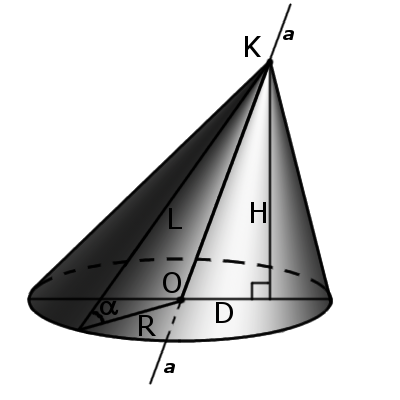
Определение. Косой (наклонный) конус — это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.
Формула. Объём любого конуса:
где S — площадь основы, а H — высота конуса.
Определение. Усеченный конус — это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.
Формула. Объём усеченного конуса:
где S1 и S2 — площади меньшей и большей основы соответственно, а H и h — расстояние от вершины конуса до центра нижней и верхней основы соответственно.
Уравнение конуса
1. Уравнение прямого кругового конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | — | z2 | = 0 |
| a2 | a2 | c2 |
2. Уравнение прямого эллиптического конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | = | z2 |
| a2 | b2 | c2 |
Основные свойства кругового конуса
1. Все образующие прямого кругового конуса равны между собой.
2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.
3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.
4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)
5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).
6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).
7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).
8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.
Выкройка для конуса
Вместо слова «выкройка» иногда употребляют «развертка», однако этот термин неоднозначен: например, разверткой называют инструмент для увеличения диаметра отверстия, и в электронной технике существует понятие развертки. Поэтому, хоть я и обязан употребить слова «развертка конуса», чтобы поисковики и по ним находили эту статью, но пользоваться буду словом «выкройка».
Построение выкройки для конуса — дело нехитрое. Рассмотрим два случая: для полного конуса и для усеченного. На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).
1. Полный конус
Обозначения:
Параметры выкройки рассчитываются по формулам:
;
;
где 
.
2. Усеченный конус
Обозначения:
Формулы для вычисления параметров выкройки:
;
;
;
где 
.
Заметим, что эти формулы подойдут и для полного конуса, если мы подставим в них 
.
3. Угол при вершине конуса
Иногда при построении конуса принципиальным является значение угла при его вершине (или при мнимой вершине, если конус усеченный). Самый простой пример — когда нужно, чтобы один конус плотно входил в другой. Обозначим этот угол буквой 
(см. картинку).
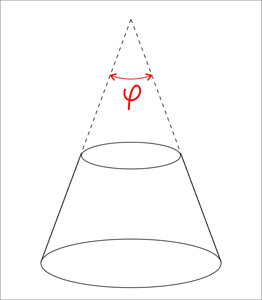
В этом случае мы можем его использовать вместо одного из трех входных значений: 
, 
или 
. Почему «вместо«, а не «вместе«? Потому что для построения конуса достаточно трех параметров, а значение четвертого вычисляется через значения трех остальных. Почему именно трех, а не двух и не четырех — вопрос, выходящий за рамки этой статьи. Таинственный голос мне подсказывает, что это как-то связано с трехмерностью объекта «конус». (Сравните с двумя исходными параметрами двухмерного объекта «сегмент круга», по которым мы вычисляли все остальные его параметры в статье Геометрия круга.)
Ниже приведены формулы, по которым определяется четвертый параметр конуса, когда заданы три.
4. Методы построения выкройки
- Вычислить значения на калькуляторе и построить выкройку на бумаге (или сразу на металле) при помощи циркуля, линейки и транспортира.
- Занести формулы и исходные данные в электронную таблицу (например, Microsoft Excel). Полученный результат использовать для построения выкройки при помощи графического редактора (например, CorelDRAW).
- использовать мою программу Cones, которая нарисует на экране и выведет на печать выкройку для конуса с заданными параметрами. Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.
5. Не параллельные основания
Что касается усеченных конусов, то программа Cones пока строит выкройки для конусов, имеющих только параллельные основания.
Для тех, кто ищет способ построения выкройки усеченного конуса с не параллельными основаниями, привожу ссылку, предоставленную одним из посетителей сайта:
Усеченный конус с не параллельными основаниями.
| Элементы конуса | Расчетные формулы | Элементы конуса | Расчетные формулы |
| K | K = (D-d)/ lK = 2tga | D | D = K× l + dD = 2× l×tga + d |
| a | tga = (D-d)/ 2ltga = K / 2 | d | d = D — 2× l×tgad = D — K× l |
Угол a вычисляют по тригонометрической функции тангенса.
Нормальные конические поверхности должны быть изготовлены по стандартным размерам, некоторые из которых указаны в табл.4.
Кроме этих поверхностей, различают также конусы Морзе и метрические конусы. Наружные конусы Морзе выполняют на хвостовой части сверл (см. рис.6
), зенкеров, разверток, центров, а внутренние конусы — в отверстиях шпинделей, оправок, переходных втулок, в которые эти инструменты устанавливают. Существуют семь номеров конусов Морзе (от до
6
) со своими размерами и углами наклона
a
. Наименьшим является конус Морзе (
1:19,212
), наибольшим — конус Морзе
6
(
1:19,18
). Их размеры приведены в стандарте СТ СЭВ 147-75. Недостатком конусов Морзе следует считать разные углы наклона
a
у различных номеров.
Таблица 4
Стандартные размеры конусов деталей
| Конусность K | Угол конуса 2a | Угол наклона a | Обозначение конусности |
| 1:100 1:50 1:20 1:10 1:3 1:1,866 1:1,207 1:0,866 | 0 0 34¢23² 1 0 8¢45² 2 0 51¢51² 5 0 43¢29² 18 0 55¢30² 30 0 45 0 60 0 | 0 0 17¢12² 0 0 34¢23² 1 0 25¢56² 2 0 51¢45² 9 0 27¢45² 15 0 22 0 30¢ 30 0 | 1:100 1:50 1:20 1:10 1:3 30 0 45 0 60 0 |
Метрические конусы 4, 6, 80, 100, 120, 160, 200
(см. тот же стандарт) имеют одинаковую конусность
1:20
(и угол
a
), а номер конуса обозначает размер диаметра большого основания.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения:
Да какие ж вы математики, если запаролиться нормально не можете.
8406 — | 7319 — или читать все.
188.64.173.93 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock! и обновите страницу (F5)
очень нужно
Источник: studopedia.ru
Угол раствора и радиус конуса
Угол раствора и радиус конуса способствуют вычислению всех возможных параметров конуса за счет двух треугольников, которые они образуют. Первый треугольник – равнобедренный, с двумя образующими и диаметром конуса, из которого можно рассчитать угол наклона конуса, между образующей и основанием. Второй треугольник – прямоугольный с высотой и радиусом в качестве катетов и образующей конуса, как гипотенузой. (рис. 40.2, 40.1) β=(180°-α)/2 h=r tanβ l=r/cosβ
Зная радиус конуса, можно сразу найти его диаметр, а также периметр основания и площадь, не прибегая к дополнительным заменам. d=2r P=2πr S_(осн.)=πr^2
Чтобы найти площадь боковой поверхности, кроме радиуса понадобится образующая конуса, которая равна отношению радиуса к косинусу угла наклона, а чтобы найти площадь полной поверхности, к полученному выражению нужно прибавить площадь основания конуса. S_(б.п.)=πrl=(πr^2)/cosβ S_(п.п.)=S_(б.п.)+S_(осн.)=πr(r+l)=πr^2 (1+1/cosβ )
Объем конуса равен одной трети произведения площади основания на высоту, а так как высота представляет собой произведение радиуса на тангенс угла наклона, то объем получится уменьшенным в три раза произведением числа π на куб радиуса и тангенс угла. V=(hS_(осн.))/3=(πr^3 tanβ)/3
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения. Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Углы и конусы. Методы и средства измерений и контроля углов и конусов.
В соответствии с ГОСТ 2875 — 88 призматические угловые меры изготавливают пяти типов: I, II, III, IV, V с рабочими углами α, β, γ, δ.
Плитки типа I имеют следующие номинальные размеры угла а: от 1 до 29′ с градацией через 2′ и от 1 по 9° с градацией через Г. Плитки типа II имеют следующие номинальные размеры угла α: от 10 до 75°50′ с градацией значений угла 15″, Т, 10′, 1°, 15°10′. Соответствующим ГОСТом установлены номинальные размеры рабочих углов α, β, γ, δ для плиток типа III, призм типа IV и призм типа V.
По точности изготовления различают угловые меры трех классов: 0, 1,2. Допускаемые отклонения рабочих углов, а также допускаемые отклонения от плоскостности и расположения измерительных поверхностей регламентируются в зависимости от типа мер и класса точности. Так, допускаемые отклонения рабочих углов находятся в пределах от +3 до +5″ для мер 0-го класса и в пределах ±30″ — для мер 2-го класса. Допускаемые отклонения от плоскостности установлены в пределах от 0,10 до 0,30 мкм.
Угловые меры комплектуются в наборы и могут поставляться в виде отдельных мер всех классов.
Рабочие поверхности угловых мер обладают свойством притираемости, т. е. из них могут создаваться блоки. С этой целью, а также для получения внутренних углов предусмотрены специальные принадлежности и лекальные линейки, которые комплектуются в набор принадлежностей. При составлении блоков угловых мер необходимо соблюдать те же правила, что и при составлении блоков из плоскопараллельных концевых мер длины (см. подразд. 2.2.1).
Угольники поверочные — это угловая мера с рабочим углом 90°. При контроле с помощью угольников оценивают величину просвета между угольником и контролируемой деталью. Просвет определяют на глаз или сравнением с просветом, созданным при помощи концевых мер длины и лекальной линейкой, а также набором щупов.
Рис. 2.51. Угловые меры
В соответствии с ГОСТ 3749 — 77 угольники различаются: по конструктивным признакам — шесть типов (рис. 2.52), по точности— три класса (0, 1, 2). Лекальные угольники (типы УЛ, УЛП, УЛШ, УЛЦ) изготавливают закаленными классов 0 и 1 и применяют для лекальных и инструментальны работ (рис. 2.52, а, б). Слесарные угольники типов УП и УШ (рис. 2.52, в, г) применяют для нормальных работ в машиностроении и приборостроении.
Рис. 2.52. Угольники поверочные:
а и б — лекальные угольники; в и г — слесарные угольники
Допускаемые отклонения угольников установлены в зависимости от их класса и высоты Н. Так, для угольника 1-го класса с высотой 160 мм отклонение от перпендикулярности измерительных поверхностей к опорам не должно превышать 7 мкм, отклонение от плосткостности и прямолинейности измерительных поверхностей должно находиться в пределах 3 мкм. Для угольника с высотой 400 мм эти значения составляют соответственно 12 и 5 мкм, а для аналогичных угольников 2-го класса 30 и 10 мкм.
Рис. 2.53. Угломеры с нониусом:
а и б — угломеры типа УН; в — порядок отсчета по нониусу; гид- угломеры типа УМ; 1 — полудиск; 2 — ось; 3 — винт зажима угольника; 4 — добавочный угольник; 5 — подвижная линейка; 6 — неподвижная линейка; 7 и 8 — устройства для микрометрической подачи; 9 — стопорный винт; 10 — нониус
Рис. 2.54. Синусные линейки:
а — тип I; б — тип II; в — тип III: 7 — стол; 2 — роликовые опоры; 3 — боковые планки; 4 — резьбовые отверстия; 5 — передняя планка
Угломерные приборы.
Эти приборы основаны на прямом измерении углов с помощью угломерной шкалы. Наиболее известными средствами измерений из этого ряда являются утломеры с нониусом, оптические делительные головки (см. подразд. 2.2.4), оптические утломеры, уровни, гониометры и др.
Угломеры с нониусом (ГОСТ 5378 — 88) предназначены для измерения угловых размеров и разметки деталей. Угломеры выпускаются двух типов. Угломеры типа УН (рис. 2.53, а, б) предназначены для измерения наружных углов от 0 до 180°, внутренних углов от 40 до 180° и имеют величину отсчета по нониусу 2 и 5′. Угломер состоит из следующих основных деталей: полудиска (сектора) 1, неподвижной линейки 6, подвижной линейки 5, зажимного винта угольника 3, нониуса 10, стопорного винта 9, устройств для микрометрической подачи 7 и 8, добавочного угольника 4, винта зажима добавочного угольника 3. Для измерения углов от нуля до 90° на неподвижную линейку 6 устанавливают добавочный угольник 4. Измерение углов от 90 до 180° производится без добавочного угольника 4. Порядок отсчета на угловом нониусе угломера аналогичен отсчету на линейном нониусе штангенциркуля (рис. 2.53, в).
Угломеры типа УМ предназначены для измерения наружных углов от 0 до 180° и имеют величину отсчета по нониусу 2 и 5′ (рис. 2.53, г) и 15′ (рис. 2.53, д). Предел допускаемой погрешности угломера равен величине отсчета по нониусу.
Рис. 2.55. Измерение углов конусов на синусной линейке:
1 — измеряемый конус; 2 — индикатор; 3— стол; 4 — блок концевых мер длины; 5 — поверочная плита
Для косвенных измерений углов при контрольно-измерительных работах, а также в процессе механической обработки применяют синусные линейки. Линейки выпускают трех типов:
— тип I (рис. 2.54, а) без опорной плиты с одним наклоном;
— тип II (рис. 2.54, б) с опорной плитой с одним наклоном;
— тип III (рис. 2.54, в) с двумя опорными плитами с двойным наклоном.
Синусная линейка типа I представляет собой стол 1, установленный на двух роликовых опорах 2. Боковые планки 3 и передняя планка 5 служат упорами для деталей, которые прикрепляются к поверхности стола прижимами с помощью резьбовых отверстий 4.
Синусные линейки выпускаются классов точности 1 и 2. Расстояние L между осями роликов может составлять 100, 200, 300 и 500 мм.
Измерение углов конусов на синусной линейке представлено на рис. 2.55. Стол 3, на котором закреплен измеряемый конус 1, устанавливают на требуемый номинальный угол а к плоскости поверочной плиты 5 с помощью блока концевых мер длины 4. Размер блока концевых мер определяют по формуле
h = Lsinα,
где h — размер установочного блока концевых мер, мм; L — расстояние между осями роликов линейки, мм; α — угол поворота линейки.
Индикатором 2, установленным на штативе, определяют разность положений δh поверхности конуса на длине 1. Отклонение угла, «, при вершине конуса рассчитывают по формуле
δα = 2*105δh/l.
Действительный угол проверяемого конуса ак определяют по формуле
αк = α ± δα ± Δл,
где Δл — погрешность измерения синусной линейкой, которая зависит от угла α, погрешности блока концевых мер длины и погрешности расстояния между осями роликов L.
Так, погрешности измерения углов синусными линейками с расстоянием между осями роликов 200 мм для измеряемых углов до 15 ° составляют 3″, при измерении углов до 45° — 10″, при измерении углов до 600 — 17″, при измерении углов до 80° — 52″.
Пределы допускаемой погрешности линеек при установке их на углы до 45 ° не должны превышать для 1-го класса ±10″, а для 2-го класса — ±15″.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах. Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20. Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
Объём усечённого конуса
Это часть прямого конуса, которая находится в пространстве между основой и плоскостью, параллельной этому основанию. В общем виде выглядит следующим образом:
Объём данного тела можно вычислить по формуле:
Важно! S и S1 это площади соответствующих основ, которые равняются ПR2 и ПR12 При нахождении этих значений поможет онлайн калькулятор.
Построение уклона и конусности
Уклоном называют величину, характеризующую наклон одной прямой линии к другой прямой. Уклон выражают дробью или в процентах. Уклон / отрезка В С относительно отрезка ВЛ определяют отношением катетов прямоугольного треугольника ЛВС (рисунок 50, а), т. е.
- Для построения прямой ВС (рисунок 50. а) с заданной величиной уклона к горизонтальной прямой, например 1:4, необходимо от точки А влево отложить отрезок АВ, равный четырем единицам длины, а вверх отрезок АС, равный одной единице длины. Точки С и В соединяют прямой, которая даст направление искомого уклона.
- Уклоны применяются при вычерчивании деталей, например, стальных балок и рельсов, изготовляемых на прокатных станах, и некоторых деталей, изготовленных литьем.
При вычерчивании контура детали с уклоном сначала строится линия уклона, а затем контур. Если уклон задается в процентах, например, 20 % (рисунок 50, б)> то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100 %, а другого — 20 %.
Очевидно, что уклон 20 % есть иначе уклон 1:5. Г1о ГОСТ 2.307—68 перед размерным числом, определяющим уклон, наносят условный знак, острый угол которого должен быть направлен в сторону уклона (рисунок 50, а и б). Подробнее обозначение уклона приведено в разделе 1.7 «Нанесение размеров и предельных отклонений».
Свойства кругового конуса
Выделяют несколько особенностей, которыми обладает фигура данного типа:
- Образующие кругового конуса равны друг другу.
- Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.
- Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.
Интересный факт!
Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.
Примеры решения в задачах
| Методические указания и учебники | решения и формулы |
| задачи и методички | теория |
Конусностью называется отношение диаметра основания конуса к его высоте (рисунок 51, а). Обозначается конусность буквой С. Если конус усеченный (рисунок 51, б) решение задач по высшей математике с диаметрами оснований D и d и длиной L, то конусность определяется по формуле: Например (рисунок 51, б), если известны размеры D= 30 мм, d- 20 мм и L = 70 мм, то Если известны конусность С, диаметр одного из оснований конуса d и длина конуса можно определить второй диаметр конуса.
- Например, С- 1:7, d- 20 мм и 1 = 70 мм; D находят по формуле (рисунок 51, б). По ГОСТ 2.307—68 перед размерным числом, характеризующим конусность, необходимо наносить условный знак конусности, который имеет вид равнобедренного треугольника с вершиной, направленной в сторону вершины конуса (рисунок 51, б).
Подробнее обозначение конусности приведено в разделе 1.7 «Нанесение размеров и предельных отклонений». Вопросы для самопроверни 1. Что называется уклоном? 2. Что называется конусностью? 3. Как обозначается на чертеже конусность и уклон? 4. Как определяется конусность и уклон?