Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы.
Углы 0°,30°,45°,60°,90°,180°270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Sin, Cos, tg, ctg.
Раздел: Таблицы численных значений + Таблицы Брадиса:
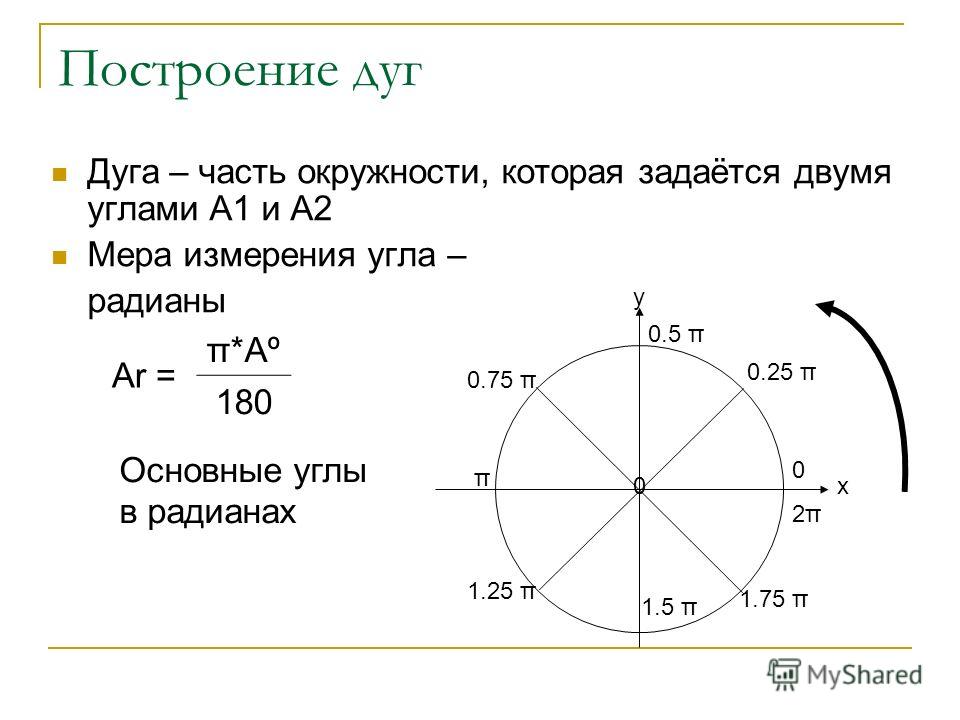
Единичная окружность
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
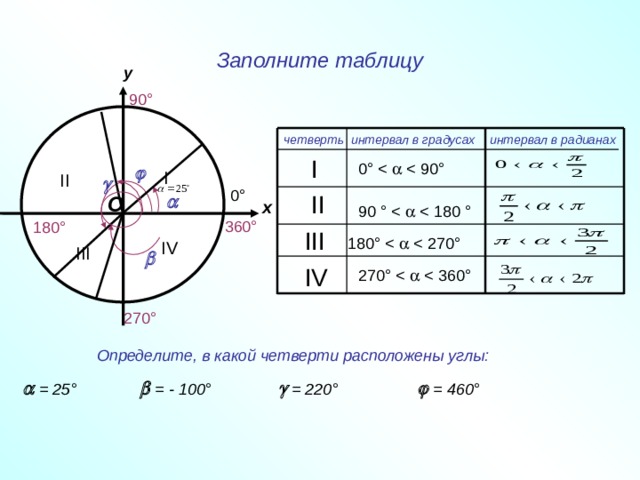
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Таблица СИНУСОВ для углов от 0° до 360° градусов
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 0 | 1/2 | √ 2/2 | √3 /2 | 1 | 0 | -1 | 0 |
Малая таблица значений тригонометрических функций (в радианах и градусах)
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° | 0 |
Полная таблица синусов для углов от 91° до 180°
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
Таблица синусов для углов 181° — 270°
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Таблица синусов для углов от 271° до 360°
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Чему равен синус 45? …
— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
http://skysmart.ru/articles/mathematic/edinichnaya-okruzhnost
http://kvn201.com.ua/table-of-sines.htm
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) |
|
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) |
|
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) |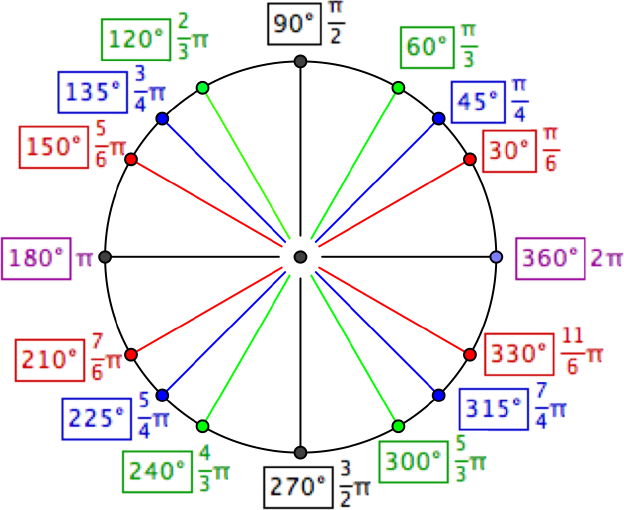
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) |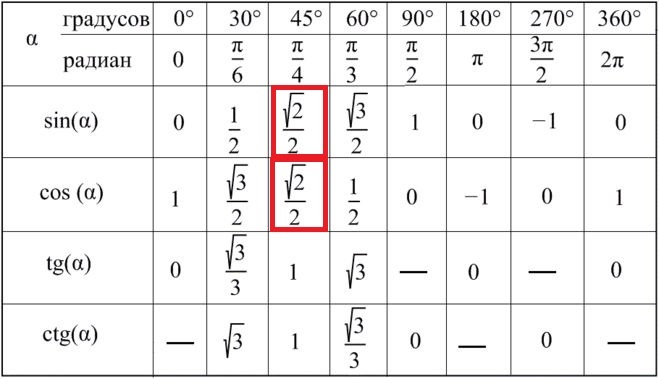
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) |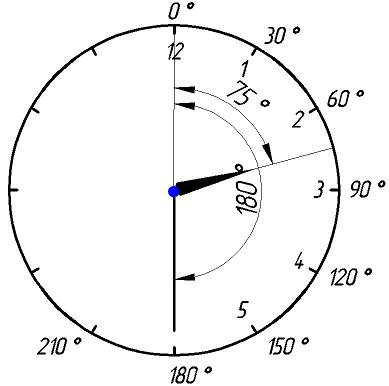
|
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) |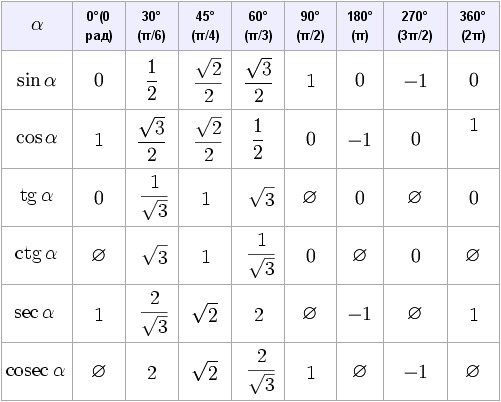
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) |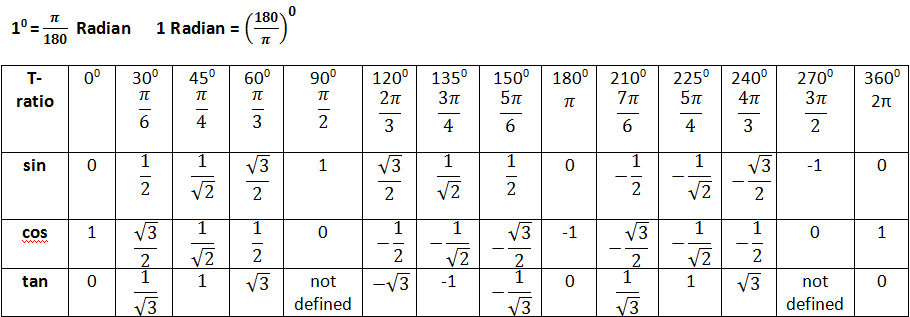
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Как перевести радианы в градусы? – Обзоры Вики
Чтобы преобразовать из радианов в градусы, умножьте радианы на 180°u03c0 радиан .
Точно так же чему равно π 4 радиана в градусах? Таблица углов
| Степени | Радиан | Байтовые двоичные радианы ( bbrad ) |
|---|---|---|
| 36° | Пи / 5 | 26 |
| 45° | Пи / 4 | 32 |
57. 296° |
1 | 41 |
| 60° | Пи / 3 | 43 |
• 17 октября 2020 г.
Как конвертировать градусы? Чтобы преобразовать значение угла в градусах в эквивалентные ему радианы, нам нужно умножьте данное значение на u03c0/180. Например, значение 180 градусов равно u03c0 в радианах.
Что такое 2 радиана в пересчете на число Пи? Пример. Преобразовать 2 угловых радиана в градусы: u03b1(степени) = u03b1(радиан) × 180° / u03c0 = 2 × 180° / 3.14159 = 114.592°
Во-вторых, что такое пи в градусах? Пи радианы равны 180 градусов.
Как найти угол в радианах?
Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12° 28′ — это 12 + 28/60, что равно 12.467°. Следующий умножить на π и разделить на 180 чтобы получить угол в радианах.
тогда пи 3.14 или 180? пи не равно 180.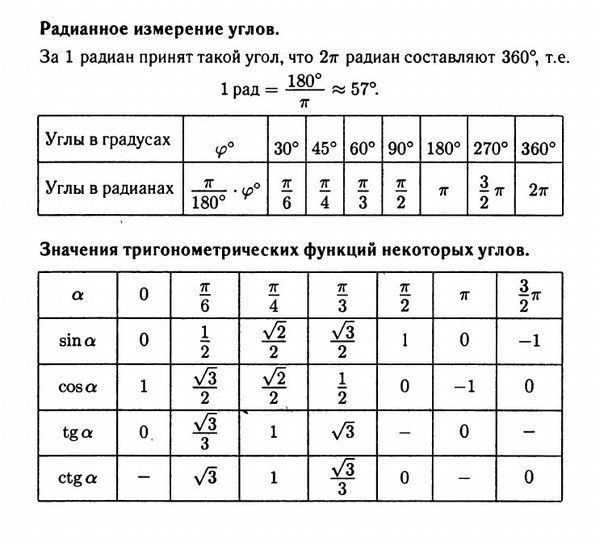
Это примерно 3.14, но цифры после запятой продолжаются вечно. Однако пи радианы равны 180 градусам, что может быть источником вашей путаницы.
Каково значение π? В десятичной форме значение числа пи равно приблизительно 3.14. Но пи — иррациональное число, что означает, что его десятичная форма не заканчивается (например, 1/4 = 0.25) и не становится повторяющейся (например, 1/6 = 0.166666…). (Всего с 18 десятичными знаками число пи равно 3.141592653589793238.)
π равно 180?
Хорошо, если весь круг равен 2π⋅r, половина будет только π⋅r, но половина круга соответствует 180° Ок, прекрасно…. Длина вашей дуги для половины окружности, как мы видели, равна π⋅r, деленному на r … вы получаете π радиан!!!!!!
Что такое градус и радиан? Градусы и радианы — это способы измерения углов. Радиан равен величине угла, который должен быть открыт для захвата дуга окружности, длина которой равна радиусу окружности. 360° (360 градусов) равно 2π радианам. GeometryGlossary of Geometry Fundamentals.
Что такое 1 радиан в Пи?
Итак, один радиан равен 180π градусов, что составляет примерно 57.3∘. Поскольку многие углы в градусах можно выразить простыми дробями от 180, мы используем π как базовую единицу в радианах и часто выражаем углы как доли от π.
Что такое формула радиана? Используемая формула: Радианы = (Градусы × π) / 180 °. Радианы = (60 ° × π) / 180 ° = π / 3. Следовательно, 60 градусов, преобразованные в радианы, равны π / 3.
Почему мы принимаем число Пи за 180 градусов?
Первоначальный ответ: Почему 180 градусов равны пи радианам? Поскольку длина окружности равна 2pi. радианы, что равняется 360 градусам. Тогда 1/2 из 2 пи радиан равняется 1/2 360 градусов, следовательно, пи радиан равняется 180 градусам.
Что равно по значению sin180?
Мы знаем, что точное значение sin 0 градусов равно 0. Следовательно, значение sin 180 градусов = 0.
Что означает 1 радиан? Проще говоря, радиан — это единица измерения углов, основанная на радиусе окружности.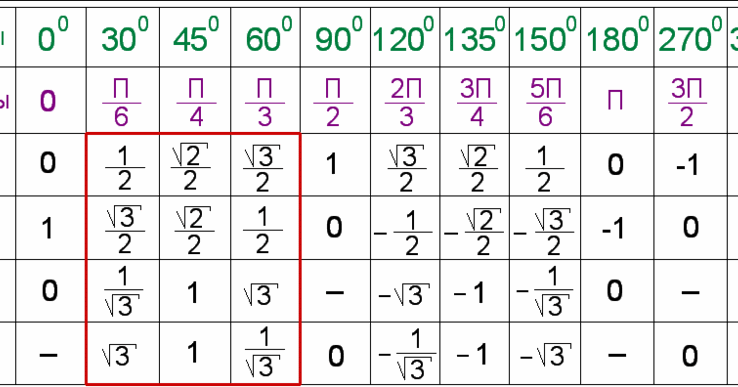
… Именно из этого соотношения мы говорим, что 2*π*r = 360 градусов или что 1 радиан = 180/π градусов и 1 градус = π / 180 радиан.
Почему число 3.14 называется числом пи? Только в 18 веке — примерно через два тысячелетия после того, как Архимед впервые вычислил значение числа 3.14 — имя «пи» впервые было использовано для обозначения числа. … «Он использовал его потому что греческая буква Пи соответствует букве «П»… А число «пи» находится по периметру круга ».
Почему число пи 22 делится на 7?
Дробное значение числа Пи равно 22/7. Так как пи является иррациональным числом, т.е. цифры после запятой никогда не заканчиваются и не заканчиваются, т.е. 3.1415926 … и так далее. Вот почему 22/7 используется для расчетов.
В чем разница между 22 7 и пи? 22/7 — это рациональное приближение к числу пи, как и 3.14 является. То есть и 22/7, и 3.14 — рациональные числа (дробная и конечная десятичная дробь, соответственно), которые достаточно близки к точному значению пи для элементарной работы.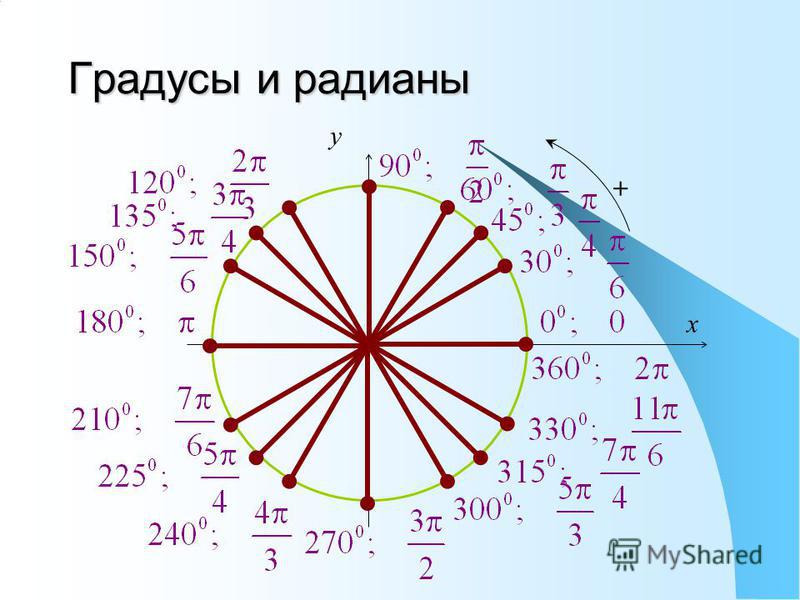
22/7 — рациональное число, а именно 3.1428571428571428571428571428571…
Что такое значение sin90?
Точное значение sin 90 градусов равно 1.
Почему пи радианы равны 180?
Первоначальный ответ: Почему 180 градусов равны пи радианам? Поскольку длина окружности равна 2pi. радианы, что равняется 360 градусам. Тогда 1/2 из 2 пи радиан равняется 1/2 360 градусов, следовательно, пи радиан равняется 180 градусам.
Что такое радиан? Ну, радиан, проще говоря, единица измерения углов, основанная на радиусе круга. … Исходя из этого соотношения, мы говорим, что 2 * π * r = 360 градусов или что 1 радиан = 180 / π градусов и 1 градус = π / 180 радиан.
Какой угол в радианах равен 270?
Объяснение: если 1 градус равен π180 радиан, то 270 градусов будут равны 270, умноженным на π180 радиан.
В каких радианах измеряется число 360? Пояснение: 360° представляет собой полный оборот, очерчивающий дугу 2π радиан. Радиан — это угол, образуемый дугой, длина которой равна радиусу, а полная длина окружности равна 2πr, где r — радиус. Таким образом, полная дуга окружности стягивается на 2πrr=2π радианах.
Что такое половина 3pi в радианах?
Градусы и радианы
| A | B |
|---|---|
| 270 градусов | 3pi / 2 радиана |
| 300 градусов | 5pi / 3 радиана |
| 315 градусов | 7pi / 4 радиана |
| 330 градусов | 11pi / 6 радиана |
Что такое радиан в 11 классе физики?
Радиан единица СИ плоского угла. Радиан — это угол, образуемый в центре окружности дугой, длина которой равна радиусу окружности. Один радиан равен 57.296 градусам.
Мэтуэй | Популярные задачи
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | |||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 |
|
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
92
Угол 270 градусов — конструкция, в радианах, примеры
LearnPracticeDownload
Углы определяются как размер раскрытия в точке пересечения двух линий или лучей.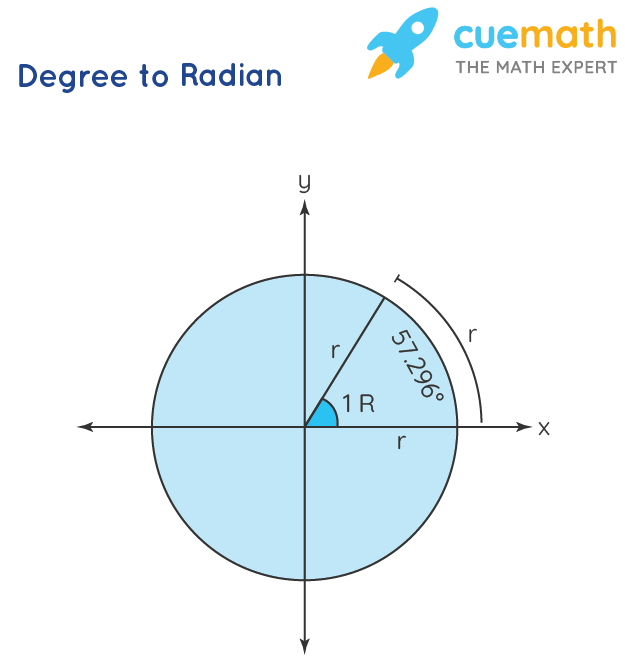
Угол 270 градусов — это угол, который больше прямого угла и поэтому известен как рефлекторный угол. В этой статье мы узнаем о рисовании под углом 270 градусов и преобразовании.
| 1. | Что такое угол 270 градусов? |
| 2. | Угол 270 градусов Наименование |
| 3. | Угол 270 градусов в пи |
| 4. | Как построить угол 270 градусов? |
| 5. | Часто задаваемые вопросы об угле 270 градусов |
Что такое угол 270 градусов?
Угол в 270 градусов, также обозначаемый как 270°, представляет собой угол, который больше прямого угла. Любой угол, превышающий 180º, известен как угол рефлекса. Следовательно, 270º — это угол рефлекса. Мы также можем определить угол 270 градусов как 3 прямых угла, потому что 270 градусов кратно 9.0º, т. е. можно выразить как 270º = 3 × 90º.
Угол 270° можно легко измерить с помощью транспортира, вычитая внутренний угол из 360°. Мы видим, что между стрелками часов в положении 9 часов образуется угол в 270 градусов.
Угол 270 градусов Название
Угол в 270 градусов также известен как угол рефлекса, поскольку он больше 180 градусов, но меньше угла в 360 градусов. Давайте посмотрим на представление угла 270 ° на единичной окружности при вращении против часовой стрелки.
Мы стартуем из точки А, двигаясь против часовой стрелки на три 90°, чтобы приземлиться в точке D, что дает нам 270°. Это потому, что 90° × 3 = 270°.
Этапы рисования угла 270 градусов с помощью транспортира
Давайте нарисуем угол 270 градусов с помощью транспортира, следуя шагам, описанным ниже.
- Шаг 1: Транспортир точно помещается в центр, совмещенный с линией 0º, и проводится линия, также известная как опорная линия.
- Шаг 2: Отсчет угла выполняется от 0º до 180º против часовой стрелки и до другого угла 90° от точки, где он заканчивался на 180°, чтобы получить угол 270°.
- Шаг 3: Отмечаем эту точку и соединяем ее с центром. Следовательно, отражение этого угла, взятого против часовой стрелки, дает нам 270°.
Чтобы измерить угол рефлекса XYZ, выполните шаги, указанные ниже.
- Шаг 1: Поместите центр транспортира точно в центр, совпадающий с линией 0°. Это опорная линия YZ.
- Шаг 2: Теперь найдите точку, где 180° завершается, начиная с опорной линии YZ, и отметьте ее.
- Шаг 3: Теперь измерьте дополнительную часть угла от 180° до второй линии XY. Здесь лишняя часть равна 90°.
- Шаг 4: После измерения угла за пределами 180° прибавьте его к 180°, чтобы получить требуемый угол отражения. Отсюда получаем значение 180° + 90° = 270°. Следовательно, угол рефлекса XYZ = 270°.
- Шаг 5: Для проверки мы измеряем внутренний угол XYZ и вычитаем его из 360°, чтобы проверить, получаем ли мы тот же результат. Здесь внутренний угол XYZ = 90°. Таким образом, рефлекс XYZ = 360° — 90° = 270°.
Здесь внутренний угол XYZ = 90°. Таким образом, рефлекс XYZ = 360° — 90° = 270°. Угол 270 градусов в пи
Преобразуем угол в 270 градусов в радианы в единицах пи или π. Согласно правилу преобразования градусов в радианы, мы используем эту формулу = Градусная мера × (π/180°). Следовательно, 270° = 270° × (π/180°) радиан = 3π/2 радиан. Кроме того, 1° = (π)/180 радиан = 0,017453 радиан. Следовательно, 270° = 270° × 0,017453 = 4,71239.радианы.
Таким образом, угол 270 градусов равен 3π/2 радиана или 4,71239 радиана.
Как построить угол 270 градусов?
Мы знаем, что 270 градусов = 360 градусов — 90 градусов. Поэтому мы сначала построим угол 90 градусов с помощью циркуля и линейки и найдем отражение этого угла, которое будет углом 270 градусов. Мы рассмотрим шаги для построения угла 270 градусов, как описано ниже.
- Шаг 1: Начертите с помощью линейки луч АВ.
- Шаг 2: Поместите точку компаса в точку A и нарисуйте дугу, пересекающую линию AB, и отметьте точку пересечения как C.
- Шаг 3: Поместите точку циркуля в точку C и нарисуйте дугу радиуса AC, пересекающую дугу, начерченную на шаге 2, и отметьте точку пересечения как D.
- Шаг 4: Держите компас в точке D, нарисуйте дугу радиуса AC, используя циркуль, чтобы разрезать дугу, начерченную на шаге 2, и отметьте точку пересечения как E.
- Шаг 5: Удерживая компас в точке D, начертите еще одну дугу того же радиуса AC между точками D и E.
- Шаг 6: Теперь, удерживая компас в точке E, нарисуйте еще одну дугу, используя тот же радиус AC, чтобы разрезать дугу, начерченную на шаге 5, и отметьте точку пересечения как F.
- Шаг 7: Соедините F и A. Угол FAB равен 90 градусов.
- Шаг 8: Угол рефлекса FAB будет равен полному углу FAB, т. е. угол рефлекса FAB = 360° — 90° = 270°. Таким образом, угол рефлекса FAB составляет искомый угол 270 градусов.
Похожие статьи об угле 270 градусов
Проверьте эти статьи, связанные с концепцией угла 270 градусов в геометрии.
- Транспортир
- Прямой угол
- Угол рефлекса
- Градусов в Радиан
- Угол 360 градусов
- Угол 30 градусов
- Угол 90 градусов
Примеры угла 270 градусов
-
Пример 1. Каково значение 2, умноженных на 270 градусов, в радианах?
Решение: Мы знаем, что угол 270 градусов = 4,71239 радиан.
Следовательно, 2 × угол 270 градусов = 2 × 4,71239 радиан = 9,42478 радиан.
Таким образом, значение 2, умноженное на 270 градусов, выраженное в радианах, равно 9,42478 радианам.
-
Пример 2: Найти значение ∠АОБ, если рефлекс ∠АОБ = 270° на данной диаграмме.
Решение: Данный рефлекс ∠AOB = угол 270 градусов.
Таким образом, ∠АОБ = 360° — рефлекс ∠АОБ
= 360° — 270°
= 90°
Следовательно, значение ∠АОБ равно 90°.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила.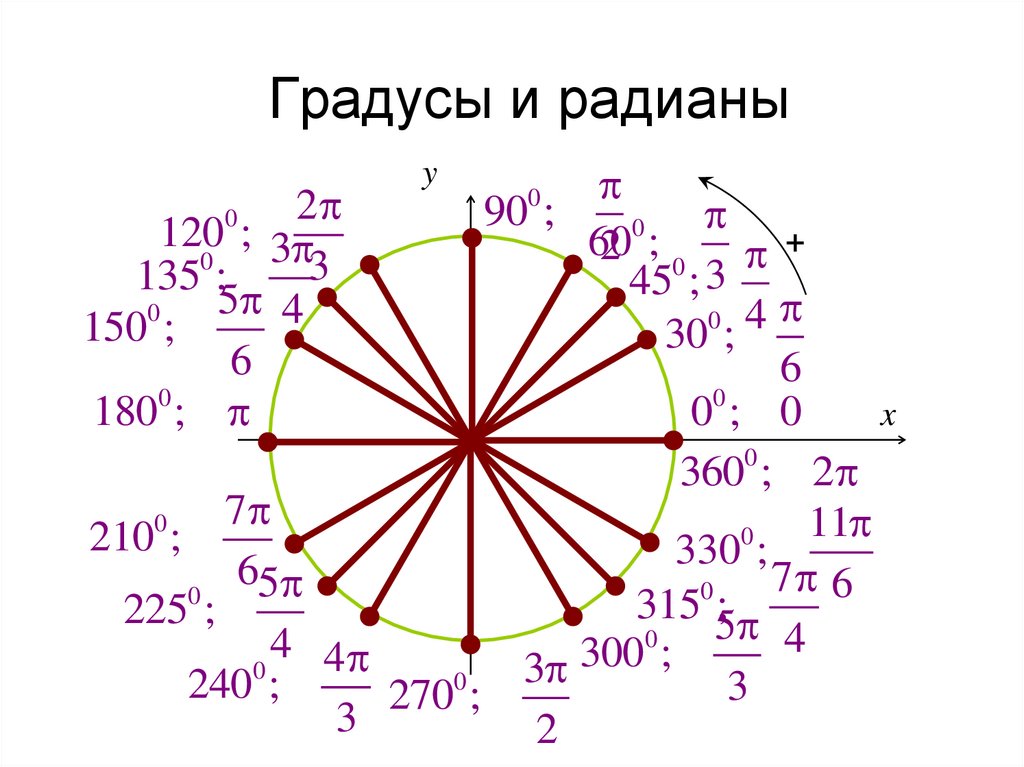
Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Записаться на бесплатный пробный урок
Практические вопросы по углу 270 градусов
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об угле 270 градусов
Что такое угол 270 градусов?
Угол в 270 градусов, также обозначаемый как 270º, является рефлекторным углом, поскольку он больше 180º. Он состоит из 3-х прямых углов. Его можно представить на единичной окружности, а также можно показать с помощью транспортира.
Как нарисовать угол 270 градусов с помощью транспортира?
Угол в 270 градусов можно нарисовать с помощью транспортира, следуя описанным шагам. Транспортир помещают точно в центр, совмещая с линией 0º, и проводят линию, также известную как опорная линия, после чего отсчитывают угол от 0º до 180º в направлении против часовой стрелки и поднимаются до другого угла 90° от точки. где он заканчивался на 180º, чтобы получился угол 270º.
Если угол составляет 270 градусов, то какой он — острый, прямой или тупой, или вообще какой-то другой? Простой алгоритм ниже уже определил вид данного угла.
270 градусов это
выпуклый угол.
Если угол лежит в пределах от 180° до 360° (не включительно), то такой угол считается выпуклым. Угол 270° как раз выпуклый, так как лежит в этих границах.
Еще примеры углов:
Угол 292° —
выпуклый.
Угол 30° —
острый.
Угол 217° —
выпуклый.
Угол 76° —
острый.
Угол 87° —
острый.
Угол 333° —
выпуклый.
Угол 226° —
выпуклый.
Угол 65° —
острый.
Нужны еще другие примеры уголов для тренировки? Просто перезагрузите данную страницу, и появятся новые углы выше.
Опубликовано 26.01.2018 по предмету
Математика
от Гость
ПОЖАЛУЙСТА ПОМОГИТЕ НАРИСОВАТЬ УГОЛ 270 ГРАДУСОВ ,
У МЕНЯ КОНТРОЛЬНАЯ,ПРОШУ,ПРОШУ.
КТО СДЕЛАЕТ ПРАВИЛЬНО,КОНФЕТКУ И БАЛЛЫ(50 или 40-25)
я в 5 КЛАССЕ!!!!
Я ФУТБОЛИСТКА,
(ЗАБЫЛА КАК РЕШАТЬ 270 градусов и больше)НО Я учила!!
ЧЕСТНО
НАРИСУЙТЕ,И СКИНЬТЕ ФОТКУ!!!
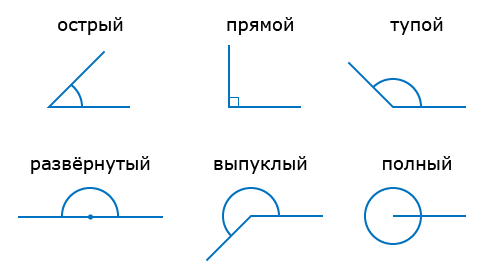
Виды углов
- Прилежащие углы
Каждый угол, в зависимости от его величины, имеет своё название:
- Острый угол — это угол, который меньше прямого угла (<90°).
- Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол обозначается буквой d и равен 90°.
Если два смежных угла равны между собой, то каждый из них называется прямым углом. Прямой угол обычно обозначается не дугой, а уголком:
∠AOC и ∠COB — прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O — основанием перпендикуляра.
Сумма двух прямых углов равна развёрнутому углу, значит, прямой угол равен половине развёрнутого угла.
- Тупой угол — это угол, который больше прямого угла, но меньше развёрнутого:
90° < тупой угол < 180°.
- Развёрнутый угол — это угол, образованный двумя дополнительными лучами.
Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180° или 2d.
Все развёрнутые углы равны между собой.
- Выпуклый угол — это угол, который больше развёрнутого угла, но меньше полного:
180° < выпуклый угол < 360°.
- Полный угол — это угол, обе стороны которого совпадают с одним лучом.
Полный угол равен сумме четырёх прямых углов, то есть 4d (360°).
Прилежащие углы
Прилежащие углы — это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.
∠AOB и ∠BOC — прилежащие углы, O — общая вершина, OB — общая сторона.
Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.
Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:
∠AOB = ∠AOC + ∠COB.
Каждый из прилежащих углов, ∠AOC и ∠COB, называется разностью углов AOB и другого прилежащего, то есть:
∠AOC = ∠AOB — ∠COB,
∠COB = ∠AOB — ∠AOC.