Трапеция — геометрическая фигура представляет собой выпуклый четырехугольник с параллельными
противоположными сторонами. Они называются основаниями. Две другие стороны — боковые.
Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон
образует у основания угол в 90 градусов-прямоугольной.
Прямая линия, проведенная от одного основания
к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.
Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции
они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.
- Угол трапеции при основании через высоту и прилегающую
боковую сторону - Угол трапеции через нижнее основание, боковую сторону и
диагональ - Угол равнобедренной трапеции через нижнее основание,
среднию линию и боковую сторону - Угол равнобедренной трапеции через среднию линию, верхнее
основание и боковую сторону - Острый угол при нижнем основании прямоугольной трапеции
через высоту и два основания - Острый угол при нижнем основании прямоугольной трапеции
через два основания и боковую сторону
Угол трапеции при основании через высоту и прилегающую боковую сторону
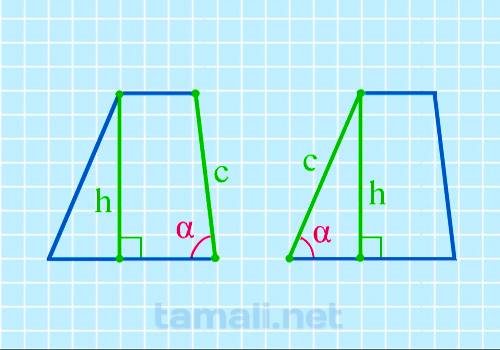
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с
помощью формулы
sin α = h/с
где: h — высота трапеции, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна
9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α =
55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует
величине 55 градусов.
Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции
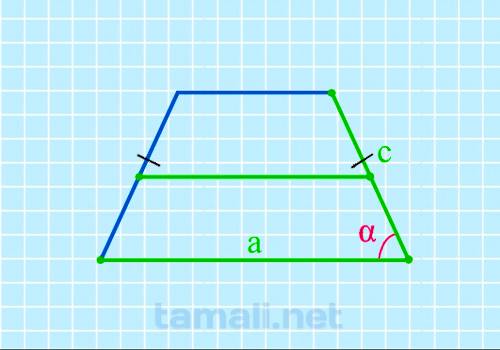
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по
формуле:
cos α = (2a-2m) / 2c
где а — нижнее основание, m — средняя линия, с — боковая сторона.
Цифр после
запятой:
Результат в:
Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8
см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65
градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α =
65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее
особенность.
Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали
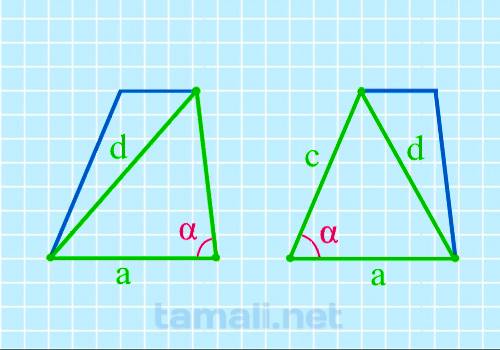
Если известны эти величины, воспользуемся формулой:
cos α= (a²+c²-d²) / 2ac
где а-нижнее основание, d-диагональ, с-боковая сторона.
Цифр после
запятой:
Результат в:
Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см,
боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по
таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534,
отсюда α = 85º.
Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции
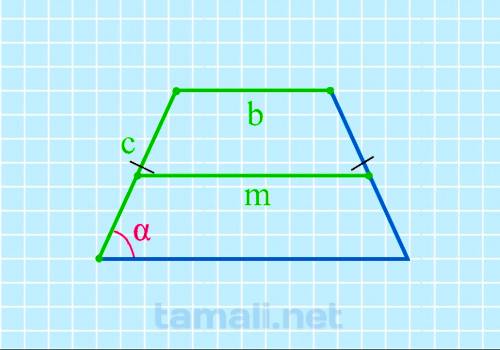
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону
выполняется по предложенной формуле:
cos α = (2m-2b) / 2c
где m — средняя линия, b — верхнее основание, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции
верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5.
Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5,
отсюда α = 60º
Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции
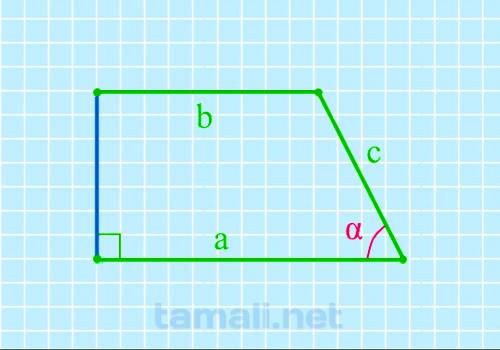
Находится по формуле
cos α = (a — b) / c
где a,b — основания, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный
пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой
стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833.
Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º
Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции
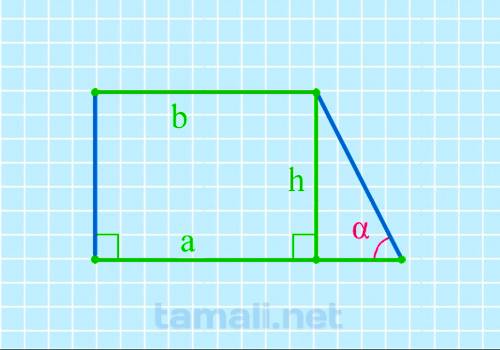
При известных указанных величинах воспользуемся следующей формулой:
tg(α) = h / (a-b)
где h — высота, a,b — верхнее и нижнее основания.
Цифр после
запятой:
Результат в:
Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15.
По таблице функций показатель соответствует 86 градусам.
Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла,
общая сумма которых составляет 360 градусов.
Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми
одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие —
острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением
высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению
высоты к боковой стороне.
Задача.
Диагональ равнобедренной трапеции делит её на два равнобедренных треугольника. Найти углы трапеции.

треугольники ABC и ADC — равнобедренные.
Найти: углы трапеции.
Решение:

1) Если AB=BC, то треугольник ABC — равнобедренный с основанием AC.
Если AC=AD, то треугольник ADC — равнобедренный с основанием CD.
Так как углы при основании равнобедренного треугольника равны, то ∠BAC=∠BCA, ∠ADC=∠ACD.

3) Пусть ∠BAC=xº, тогда ∠BCA=xº, ∠DAC=xº.
∠BAD=∠BAC+∠DAC=2xº.
4) ∠ADC=∠BAD=2xº (как углы при основании равнобедренной трапеции).
Следовательно, ∠ACD=2xº, ∠BCD=∠BCA+∠ACD=3xº.
5) ∠BAD+∠BCD=180º (по свойству равнобедренной трапеции). Имеем уравнение:
2x+3x=180
5x=180
x=36
Значит, ∠BAD=2∙36=72º, ∠BCD=3∙36=108º.
II.
Если AB=AC, то треугольник ABC — равнобедренный с основанием BC. Тогда у него углы при основании равны: ∠B=∠BCA. Но угол B — тупой, а два тупых угла в треугольнике быть не может. Следовательно, AB не может быть равным AC (отсюда и CD не может быть равным AC, так как AB=CD по условию).
Ответ: 72º, 108º.
Трапеция. Формулы, признаки и свойства трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
Виды трапеций:
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m — b
b = 2m — a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a — h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a — c·cos α — d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Определение.
Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 — 2ad·cos β
d2 = √a2 + c2 — 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab — | a(d 2 — c2) |
| a — b |
| d2 = | √ | c2 + ab — | a(c2 — d 2) |
| a — b |
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a — h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a — h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab — d22
d2 = √c2 + d 2 + 2ab — d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 — | ( | (a — b)2 + c2 — d 2 | ) | 2 |
| 2 | 2(a — b) |
5. Формула Герона для трапеции
| S = | a + b | √(p — a)(p — b)(p — a — c)(p — a — d) |
| |a — b| |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p — a)(p — c)(p — d1) |
где
a — большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Как вычислить угол трапеции
Главной особенностью четырехугольной трапеции является параллельность двух ее сторон, называемых основаниями, и не параллельность боковых сторон фигуры. В случае, когда эти боковые стороны равны по длине, трапеция называется равнобедренной.

Инструкция
В решении большинства задач по определению углов четырехугольной трапеции учитываются те или иные свойства фигуры. При этом результаты задач могут быть различны из-за вариативных исходных данных. Если перед началом решения даны условия, что известны только два угла, относящиеся к основанию трапеции, решение задачи сводится к следующим действиям:Определите буквенные значения для трапеции – MNOP, а известные углы назовите соответственно ∠NMP и ∠OMP. Значения для этих углов будут равняться: ∠NMP = a и ∠OMP = b. Вам необходимо вычислить углы при верхнем основании ∠MNO и ∠NOP.
Воспользуйтесь свойством трапеции, когда сумма обоих углов при боковой стороне равняется 180°. В этом случае искомые углы: ∠MNO = (180° – a), а ∠NOP = (180° – b).
При других исходных данных – равенства определенных сторон трапеции и известном значении одного из углов – набор действий по решению задачи может принять следующий вид. Используйте те же обозначения для трапеции MNOP, только в данном случае задайте, что ее стороны MN и OP, а также верхнее основание NO равны по длине между собой. Проведенная же диагональ MO составляет с основанием MP угол ∠OMP = с.
Учитывая, что в треугольнике MNO две его стороны равняются друг другу, он является равнобедренным и углы ∠NMO = ∠NOM = d, а угол ∠MNO = e. Поскольку сумма всех углов в треугольнике равняется 180°, следовательно (2d + e) = 180°. В результате e = (180° – 2d).
Используя свойство трапеции о сумме углов, прилегающих к одной стороне, равной 180°, определите другую формулу (e + d + c) = 180°. Тогда при e = (180° – 2d) формула приобретает вид (180° – 2d + d + c) = 180° или c = d.
В результате вы найдете углы ∠NMO = d = c и ∠MNO = e = 180° – 2c. Поскольку заданная трапеция является равнобедренной, то согласно ее свойству равнобокости диагонали ее равны и соответственно равны углы при обоих основаниях. Значит ∠OPM = ∠NOP = 180° – 2c.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание материала
- Свойства диагоналей трапеции
- Свойства отрезка, соединяющего середины диагоналей трапеции
- Свойства треугольников, образованных диагоналями трапеции
- Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
- Свойства трапеции, достроенной до треугольника
- Свойства отрезка, соединяющего основания трапеции
- Свойства отрезка, параллельного основаниям трапеции
- Видео
- Высота трапеции
- Формулы определения длины высоты трапеции:
- Свойства равнобедренной трапеции:
- Свойства трапеции
- Элементы трапеции: основания, боковые стороны, средняя линия и высота:
- Сторона трапеции
- Формулы определения длин сторон трапеции:
- Примеры решения задач
Свойства диагоналей трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции

Свойства треугольников, образованных диагоналями трапеции

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Свойства трапеции, достроенной до треугольника

- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции

Свойства отрезка, параллельного основаниям трапеции

- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Видео
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
h = Sm
Свойства равнобедренной трапеции:
1. Прямая, которая проходит через середины оснований, перпендикулярна основаниям, тем самым, является осью симметрии равнобедренной трапеции.
2. Высота, опущенная из вершины на большее основание равнобедренной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
3. Углы при любом основании равнобедренной трапеции равны.
4. Сумма противоположных углов равнобедренной трапеции равна 180°.
5. Длины диагоналей равнобедренной трапеции равны.
6. Вокруг равнобедренной трапеции можно описать окружность.
7. При перпендикулярности диагоналей в равнобедренной трапеции ее высота равна полусумме оснований.
Свойства трапеции
Итак, что ты должен знать о свойствах трапеции…
Сумма углов при каждой боковой стороне трапеции равна 180°. (у нас на рисунке ( displaystyle angle 1+angle 2=180{}^circ ) и ( displaystyle angle 3+angle 4=180{}^circ ))
Почему так?
Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая.
Вот и получается, что ( displaystyle angle 1) и ( displaystyle angle 2) – внутренние односторонние углы при параллельных ( displaystyle AD) и ( displaystyle BC) и секущей ( displaystyle AB).
Поэтому ( displaystyle angle 1+angle 2=180{}^circ ).
И точно так же ( displaystyle angle 3) и ( displaystyle angle 4) – внутренние односторонние углы при тех же параллельных ( displaystyle AD) и ( displaystyle BC), но секущая теперь – ( displaystyle CD).
Видишь: главное, что играет роль – это параллельность оснований. Давай разберем еще некоторые свойства трапеции.
Как у всякого четырехугольника, у трапеции есть диагонали. Их две – посмотри на рисунки:
Снова порассуждаем об углах:
Опять ( displaystyle AD) и ( displaystyle BC) – параллельные, а диагональ ( displaystyle AC) – секущая. Поэтому ( displaystyle angle 1=angle 2).
А теперь рассмотрим сразу 2 диагонали и 4 угла:
Что из этого может следовать?
Очень важный факт:
Треугольники ( displaystyle BOC) и ( displaystyle AOD) – подобны по двум углам.Их коэффициент подобия равен отношению оснований: ( displaystyle K=frac{a}{b}).
Элементы трапеции: основания, боковые стороны, средняя линия и высота:
Параллельные стороны трапеции называются основаниями трапеции, а две другие – непараллельные – боковыми сторонами.
Рис. 4. Трапеция
AD и BC – основания трапеции, AB и CD – боковые стороны трапеции.
AD – большее основание трапеции, BC – меньшее основание трапеции.
Отрезок, соединяющий середины боковых сторон трапеции, называется средняя линия.
Рис. 5. Трапеция и срединная линия
Расстояние между основаниями трапеции называется высотой трапеции.
Рис. 6. Трапеция
Высота трапеции (h) определяется формулой:
где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m — b
b = 2m — a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a — h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a — c·cos α — d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
с = h d = h sin α sin β
Примеры решения задач
ПРИМЕР 1
Задание В трапеции основания см и см. Диагонали трапеции пересекаются в точке . Площадь равна 10 см. Найти площадь . Решение Рассмотрим треугольники и . Они образованы пересечением диагоналей и лежат на основаниях трапеции. Из свойств трапеции следует, что они подобные Коэффициент подобия треугольников . Из этого следует, что
Ответ см2
ПРИМЕР 2
Задание Точка пересечения диагоналей трапеции делит одну из них на отрезки 6 см и 12 см, а разность оснований трапеций равна 36 см. Найдите среднюю линию трапеции. Решение Пусть . Отрезок соединяет середины диагоналей и лежит на средней линии :
Так как – середина диагонали, то
Треугольники и – подобные, а значит , откуда см. Следовательно,
Найдем среднюю линию трапеции
Ответ см







