Как найти углы параллелограмма если есть высота

У параллелограмма 4 угла, это частный случай четырехугольника, у которого противоположные стороны
попарно параллельны. Из этого свойства вытекает равенство противоположных сторон, равенство
противоположных углов и равенство суммы смежных углов двум прямым. Свойства параллелограмма широко
используются в быту и технике.

Острый угол параллелограмма через боковую сторону и высоту

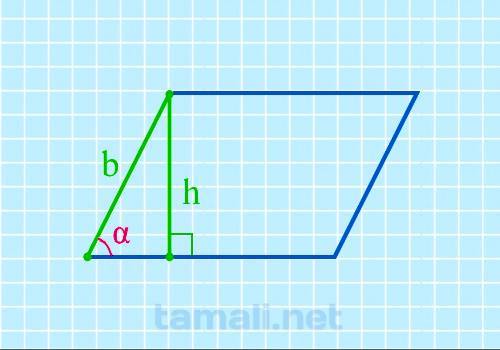
Если известна боковая сторона и высота, то можно найти острый угол параллелограмма по формуле:

sin α = h / b

где α – острый угол, h – высота, b – боковая сторона.

Пример. Пусть h = 4 см, b = 8 см. sin α = h / b = 8 / 4 = 2. α = 90°.

Острый угол параллелограмма через площадь и две стороны

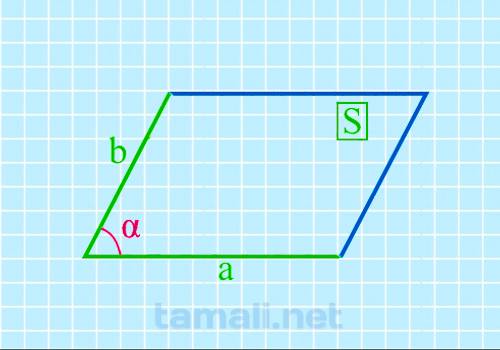
Если известна площадь и две стороны, то можно найти острый угол параллелограмма по формуле:

sin α= S / ab

где α – острый угол, S — площадь параллелограмма, a и b – его стороны.

Пример.  Пусть S=50 м², a=10 м, b=5 м. sin α= S / ab = 50 / (10 * 5) = 1. α = 90°.
Угол прямой, смежные стороны не равны, имеем дело с прямоугольником.

Острый угол параллелограмма через высоту, сторону и периметр

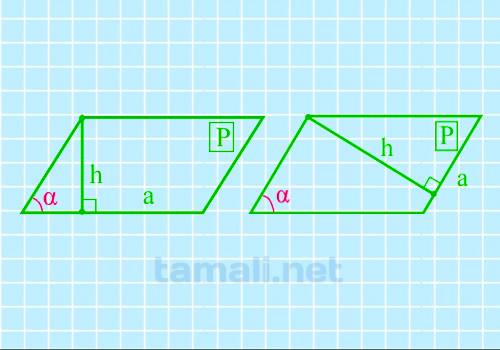
Если известна высота, сторона и периметр, то можно найти острый угол параллелограмма по формуле:

sin α = (2h + a) / P

где α – острый угол, h — высота, a — сторона, P — периметр.

Высота опускается на известную и подставляемую в формулу сторону a. Параллелограмм с заданным
периметром приходится строить, если, например, периметр определен длиной веревки, которую требуется
растянуть на местности в форме параллелограмма.

Пример. Пусть h=10 м, a=15 м, P=70 м. sin α=(2h + a) / P= (2 * 10 + 15) / 70 = 0,5. α = 30°.

Острый угол параллелограмма через две стороны и короткую диагональ

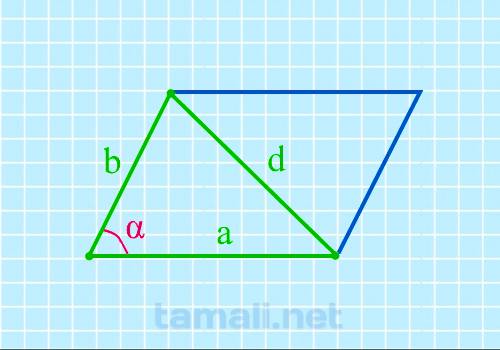
Если известны две стороны и короткая диагональ, то можно найти острый угол параллелограмма по
формуле:

cos α = (a² + b² — d²) / 2ab

где α – острый угол, a и b – стороны параллелограмма, d – его короткая диагональ.

Пример расчета: в данном частном случае 2 прилежащие стороны и короткая диагональ
равны, а именно: a = b = d = 26 мм. cos α=(a² + b² — d²) / 2ab = (26² + 26² — 26²) / (2 * 26 * 26) = 0,5. α=60°.

Из равенства прилежащих сторон следует, что это ромб, а результат расчета показывает, что острый угол
в ромбе равен 60°. Знаете, что это за ромб с подобными размерами? Это нагрудный академический знак
для лиц, окончивших советские высшие учебные заведения, установленный с 1961 года.

Тупой угол параллелограмма через две стороны и длинную диагональ

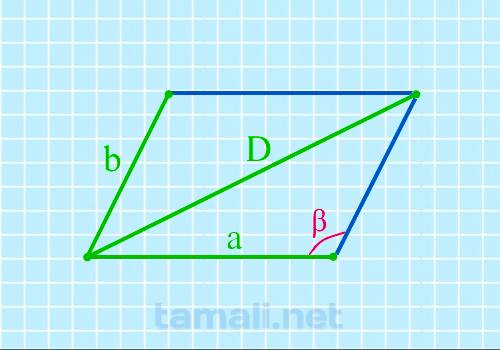
Если известны две стороны и длинная диагональ, то можно найти тупой угол параллелограмма по
формуле:

cos β = (a² + b² — D²) / 2ab

где α – тупой угол, a и b – стороны параллелограмма, D – его длинная диагональ.

Пример расчета: вновь ромб со сторонами a = b = 26 мм и длинной диагональю D=43 мм.
cos β = (a² + b² — D²) / 2ab = (26² + 26² — 43²) / (2 * 26 * 26) = -0,368. α = 112°.
Это опять-таки нагрудный академический знак из предыдущего примера, небольшое отличие полученного
результата от 120° (при остром угле 60° по предыдущему примеру) объясняется округлением исходных
данных до целого числа миллиметров.

Свойства параллелограмма

У любого выпуклого четырехугольника сумма всех внутренних углов равна 360°, исходя из общей формулы
суммы внутренних углов выпуклого многоугольника в градусах s = 180 (n — 2), где n – количество
сторон. Следовательно, если хотя-бы 1 угол параллелограмма равен прямому (90°), остальные 3 угла
также являются прямыми, и параллелограмм вырождается в свой частный вид – прямоугольник.

Если 2 смежные стороны параллелограмма равны, то равны все его 4 стороны, и параллелограмм
вырождается в ромб. И, наконец, если у параллелограмма равны 2 смежные стороны, а угол между ними
прямой, параллелограмм является одновременно и прямоугольником, и ромбом, и вырождается в квадрат.
Зачастую возникает необходимость определения неизвестных характеристик параллелограмма через
известные. Выше ряд примеров подобного рода.

Самый наглядный пример параллелограмма – пантограф электропоезда. При подключении опущенного
пантографа к контактной сети железной дороги изменяется конфигурация пантографа при сохранении длин
сторон, в результате изменяется вертикальная диагональ и происходит касание с подачей электрического
тока.
Форму параллелограмма имеет автомобильный реечный домкрат, велосипедная рама (с
диагональю для увеличения жесткости). Ведь параллелограмм — фигура нежесткая, в отличие от
треугольника. Из нежесткости параллелограмма следует, что знания одних длин сторон недостаточно для
вычисления площади фигуры. Так, пантограф электропоезда можно «сложить» до нулевой площади.
Стеклоочиститель лобового стекла автобуса также представляет собой параллелограмм, и именно
нежесткость фигуры позволяет стеклоочистителю «ометать» при движении стекло.

Высота в параллелограмме формирует прямоугольный треугольник, в котором относится к противоположной стороне, как синус угла α. Исходя из этого, противоположная сторона параллелограмма равна отношению высоты к синусу. (рис.106.1)
h_b=a sin⁡α
h_a=b sin⁡α
a=h_b/sin⁡α
b=h_a/sin⁡α

Второй угол параллелограмма β равен разности 180 градусов и угла α, так как полусумма углов параллелограмма равна по значению развернутому углу, что значит, что они дополняют друг друга до 180 градусов.
β=180°-α

Диагонали параллелограмма делят его на два треугольника каждая. В таком треугольнике, сторонами являются стороны параллелограмма и диагональ, при этом один из углов параллелограмма находится напротив диагонали, что дает возможность использовать теорему косинусов, чтобы вычислить диагональ. (рис.106.2)
d_1=√(a^2+b^2+2ab cos⁡α )
d_2=√(a^2+b^2-2ab cos⁡α )

Найти углы между диагоналями можно по той же теореме косинусов, но в другом треугольнике, сторонами которого являются половины диагоналей, так как точкой пересечения диагонали делятся пополам, а угол между диагоналями находится прямо напротив стороны параллелограмма. (рис.106.3)
cos⁡γ=(〖d_1/4〗^2+〖d_2/4〗^2-a^2)/((d_1 d_2)/4)=(〖d_1〗^2+〖d_2〗^2-4a^2)/(2d_1 d_2 )
cos⁡δ=(〖d_1〗^2+〖d_2〗^2-4b^2)/(2d_1 d_2 )

Биссектриса параллелограмма берет свое начало в вершине угла α или β, и откладывает на длинной стороне параллелограмма длину меньшей стороны таким образом, чтобы получить равнобедренный треугольник. В этом треугольнике биссектриса находится напротив угла, дополнительного до 180 градусов тому, который она разделила. Из теоремы косинусов для равнобедренного треугольника можно найти биссектрису. (рис.106.4)
l_α=√(2a^2-2a^2 cos⁡β )=a√(2-2 cos⁡β )
l_β= b√(2-2 cos⁡α )

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Дано: ABCD — параллелограмм, BH — высота, угол ABH = 30 градусов.

Найти: углы ABC, BCD, CDA, BAD.

Решение:
1. Т.к. угол ABH = 30 градусов => угол BAD = 60 градусов.
В паралеллограмме противоположные углы равны => угол BAD = углу BCD = 60 градусов.
2. Найдем угол ABC.
угол ABC = углу CDA = 180 градусов – 60 градусов = 120 градусов.

Ответ: угол BAD = углу BCD = 60 градусов, угол ABC = углу CDA = 120 градусов.

Чему равен угол между высотами параллелограмма? Это зависит от того, из вершины какого угла — острого или тупого — проведены эти высоты.

Утверждение I

Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма.

Дано: ABCD — параллелограмм,

∠ABC — тупой,

BM, BN — высоты параллелограмма.

Доказать:

∠MBN=∠C.

Доказательство:

1-й способ

1) Рассмотрим треугольник NBC — прямоугольный (∠BNC=90º, поскольку BN — высота параллелограмма).

Так как сумма острых углов прямоугольного треугольника равна 90º, то ∠NBC+∠C=90º. Следовательно, ∠NBC=90º-∠C.

2) Так как BM — высота параллелограмма, то ∠MBC=90º.

∠MBC=∠MBN+∠NBC.

Отсюда, ∠MBN=90º-∠NBC.

Так как ∠NBC=90º-∠C,

∠MBN=90º-(90º-∠C)=90º-90º+∠C=∠C.

Что и требовалось доказать.

2-й способ

1)∠C+∠D=180° (как сумма внутренних односторонних углов при AD∥BC и секущей CD).

Значит, ∠C=180°-∠D.

2) Сумма углов четырёхугольника равна 360°.

В четырёхугольнике MBND ∠BMD+∠BND=90°+90°=180°.

Следовательно, ∠MBN+∠D=360°-180°=180°.

Отсюда ∠MBN=180°-∠D=∠C.

Что и требовалось доказать.

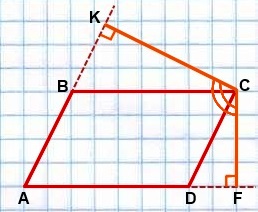
Утверждение II

Угол между высотами параллелограмма, проведенными из вершины острого угла, равен тупому углу параллелограмма.

Дано: ABCD — параллелограмм,

  ∠BCD — острый,

CK и CF — высоты параллелограмма.

Доказать:

∠KCF=∠ABC

Доказательство:

1-й способ

1) ∠ABC+∠KBC=180º (как смежные).

Следовательно, ∠KBC=180º-∠ABC.

2) Так как CF — высота параллелограмма ABCD, то она перпендикулярна к прямым, содержащим стороны AD и BC. Поэтому ∠BCF=90º.

3) Рассмотрим треугольник KBC — прямоугольный (∠KBC=90º, так как CK- высота параллелограмма ABCD).

Так как сумма острых углов прямоугольного треугольника равна 90º, то

∠KCB=90º-∠KBC=90º-(180º-∠ABC)=90º-180º+∠ABC=∠ABC-90º.

4) ∠KCF=∠KCB+∠BCF=∠ABC-90º+90º=∠ABC.

Что и требовалось доказать.

2-й способ

1) ∠ADC для треугольника DCF — внешний. Следовательно, он равен сумме двух внутренних углов, не смежных с ним:

∠ADC=∠DFC+∠DCF=90º+∠DCF.

2) ∠KCF=∠KCD+∠DCF.

∠KCD=90º (так как KC — высота параллелограмма). Отсюда,

∠KCF=90º+∠DCF=∠ADC.

Что и требовалось доказать.

3-й способ

1)∠A+∠ABC=180° (как сумма внутренних односторонних углов при AD∥BC и секущей AB).

Значит, ∠ABC=180°-∠A.

2) В четырёхугольнике AKCF ∠A+∠AKC+∠KCF+∠AFC=360°.

∠AKC=∠AFC=90°.

Поэтому ∠A+∠KCF=180°,

∠KCF=180°-∠A=∠ABC.

Что и требовалось доказать.