Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:
Приняв вектор k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.
Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.
Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Что такое угловая скорость
Угловая скорость (обозначается как (omega)) — векторная величина, характеризующая скорость и направление изменения угла поворота со временем.
Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.
Единица измерения
В Международной системе единиц (СИ) принятой единицей измерения угловой скорости является радиан в секунду (рад/с)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формула угловой скорости
Вектор угловой скорости определяется отношением угла поворота ((varphi)) к интервалу времени ((mathcal t)), за которое произошел поворот:
(omega=frac{trianglevarphi}{trianglemathcal t})
Зависимость угловой скорости от времени
Зависимость (varphi ) от (mathcal t) наглядно показана на графике:
Угол, на который повернулось тело, характеризуется площадью под кривой.
Угловая скорость вращения, формула
Через частоту
(omega=2pimathcal n)
(mathcal n) — частота вращения ((1/с))
(pi) — число Пи ((approx 3,14))
(mathcal n=frac1T)
(T )— период вращения (время, за которое тело совершает один оборот)
Через радиус
(omega=frac vR)
(v) — линейная скорость(м/с)
(R) — радиус окружности (м)
Как определить направление угловой скорости
Направление скорости в физике можно определять двумя способами:
- Правило буравчика. Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.
- Правило правой руки. Представим, что взяли тело в правую руку. Следует направлять и вращать его туда, куда указывают четыре пальца. Отведенный в сторону большой палец покажет направление угловой скорости при этом вращении.
Связь линейной и угловой скорости
Линейная скорость ((v)) тела, расположенного на расстоянии (R) от оси вращения, прямо пропорциональна угловой скорости.
(v=Romega)
(R) — радиус окружности (м)
Чему равна мгновенная угловая скорость
Мгновенную угловую скорость нужно находить как предел, к которому стремится средняя угловая скорость при (trianglemathcal trightarrow0) :
(omega=lim_{trianglerightarrow0}frac{trianglevarphi}{trianglemathcal t})
Измеряется в рад/с
Содержание:
- Определение и формула угловой скорости
- Равномерное вращение
- Формула, связывающая линейную и угловую скорости
- Единицы измерения угловой скорости
- Примеры решения задач
Определение и формула угловой скорости
Определение
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность
с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота
$(varphi)$ . Часто используют вектор элементарного поворота
$bar{dvarphi}$ , который равен по величине элементарному углу поворота тела
$(d varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.
Определение
Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой
$omega$ . Математически определение угловой скорости записывают так:
$$bar{omega}=frac{d bar{varphi}}{d t}=dot{bar{varphi}}(1)$$
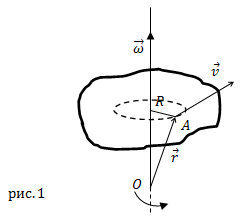
Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее
с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости),
так и за счет поворота оси вращения в пространстве ($bar{omega}$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
$$omega=frac{varphi}{t}(2)$$
где $(varphi)$ – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот
($Delta varphi=2 pi$). Угловая скорость связана с периодом обращения как:
$$omega=frac{2 pi}{T}(3)$$
С числом оборотов в единицу времени ($nu) угловая скорость связана формулой:
$$omega=2 pi nu(4)$$
Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения,
но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно
с данной мгновенной величиной скорости.
Формула, связывающая линейную и угловую скорости
Линейная скорость $bar{v}$ точки А (рис.1), которая расположена
на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:
$$bar{v}=[bar{omega} bar{R}](5)$$
где $bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки
$A (bar{r})$ (рис.1). Вектор
$bar{r}$ проводят от точки, находящейся на оси вращения к рассматриваемой точке.
Единицы измерения угловой скорости
Основной единицей измерения угловой скорости в системе СИ является: [$omega$]=рад/с
В СГС: [$omega$]=рад/с
Примеры решения задач
Пример
Задание. Движение тела с неподвижной осью задано уравнением
$varphi=2 t-4 t^{3}$,
$(varphi)$ в рад, t в сек.
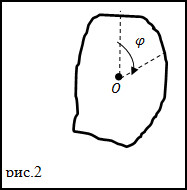
Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении (
относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.
Решение. Для нахождения модуля угловой скорости применим формулу:
$$omega=frac{d varphi}{d t}(1.1)$$
Используем заданную в условии задачи функцию
$varphi(t)$, возьмем производную от нее по времени, получим функцию
$omega(t)$:
$$omega(t)=2-8 t^{2}(1.2)$$
Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):
$$omega(t)=2-8(0,5)^{2}=0left(frac{r a d}{c}right)$$
Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Скорости вращения тела заданы системой уравнений:
$$left{begin{array}{c}bar{omega}_{1}=t^{2 bar{i}} \ bar{omega}_{2}=2 t^{2} bar{j}end{array}right.$$
где $bar{i}$ и
$bar{j}$ – единичные ортогональные векторы. На какой угол $(varphi)$ поворачивается тело за время равное 3 с?
Решение. Определим, какова функция, которая связывает модуль скорости вращения тела и время (t)
($omega(t)$). Так как вектора
$bar{i}$ и
$bar{j}$ перпендикулярны друг другу, значит:
$$omega=sqrt{omega_{1}^{2}+omega_{2}^{2}}=sqrt{left(t^{2}right)^{2}+left(2 t^{2}right)^{2}}=t^{2} sqrt{5}(2.2)$$
Модуль угловой скорости связан с углом поворота как:
$$omega=frac{d varphi}{d t}(2.3)$$
Следовательно, угол поворота найдем как:
$$varphi=int_{t_{1}}^{t_{2}} omega d t=int_{0}^{3} t^{2} sqrt{5} d t=left.sqrt{5} frac{t^{3}}{3}right|_{0} ^{3} approx 20(mathrm{rad})$$
Ответ. $varphi = 20$ рад.
Читать дальше: Формула удельного веса.
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
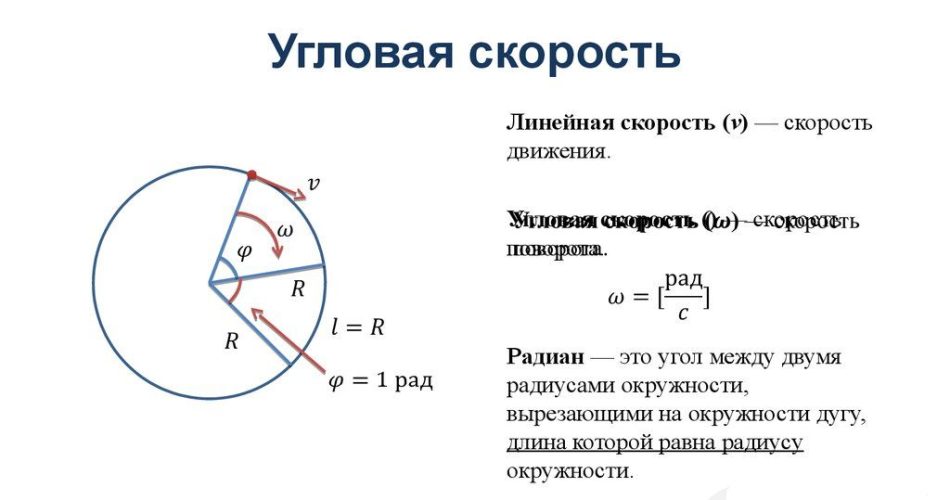
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Движение по окружности
Для описания движения по окружности наряду с линейной скоростью вводят понятие угловой скорости. Если точка при движении по окружности за время (Delta t) описывает дугу, угловая мера которой (Delta varphi), то угловая скорость (omega = frac<<Delta varphi >><<Delta t>>).
Рисунок 1
Угловая скорость (omega) связана с линейной скоростью (upsilon) соотношением (upsilon = omega r), где (r) — радиус окружности, по которой движется точка (рис. 1). Понятие угловой скорости особенно удобно для описания вращения твердого тела вокруг оси. Хотя линейные скорости у точек, находящихся на разном расстоянии от оси, будут неодинаковыми, их угловые скорости будут равны, и можно говорить об угловой скорости вращения тела в целом.
Задача
Диск, радиуса (r) катится без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянная и равна (upsilon_п). С какой угловой скоростью при этом вращается диск?
Каждая точка диска участвует в двух движениях — в поступательном движении со скоростью (upsilon_п) вместе с центром диска и во вращательном движении вокруг центра с некоторой угловой скоростью (omega).
Рисунок 2
Для нахождения (omega) воспользуемся отсутствием проскальзывания, то есть тем, что в каждый момент времени скорость точки диска, соприкасающейся с плоскостью, равна нулю. Это означает, что для точки А (рис. 2) скорость поступательного движения (upsilon_п) равна по величине и противоположна по направлению линейной скорости вращательного движения (<upsilon _<вр>> = omega r). Отсюда сразу получаем (omega = frac<<<upsilon _п>>>).
Задача
Найти скорости точек В, С и D того же диска (рис. 3).
Рисунок 3
Рассмотрим вначале точку В. Линейная скорость ее вращательного движения направлена вертикально вверх и равна (<upsilon _<вр>> = omega r = frac<<<upsilon _п>>>r = <upsilon _п>), то есть по величине равна скорости поступательного движения, которая, однако, направлена горизонтально. Складывая векторно эти две скорости, находим, что результирующая скорость (upsilon_B) по величине равна (<upsilon _п>sqrt 2 ) и образует угол 45° с горизонтом. У точки С скорости вращательного и поступательного движения направлены в одну сторону. Результирующая скорость (upsilon_C) равна (2upsilon_п), и направлена горизонтально. Аналогично находится и скорость точки D (см. рис. 3).
Даже в том случае, когда скорость точки, движущейся по окружности, не меняется по величине, точка имеет некоторое ускорение, так как меняется направление вектора скорости. Это ускорение называется центростремительным. Оно направлено к центру окружности и равно
((R) — радиус окружности, (omega) и (upsilon) — угловая и линейная скорости точки).
Если же скорость точки, движущейся по окружности, меняется не только по направлению, но и по величине, то наряду с центростремительным ускорением существует и так называемое тангенциальное ускорение. Оно направлено по касательной к окружности и равно отношению (frac<<Delta upsilon >><<Delta t>>) ((<Delta upsilon >) — изменение величины скорости за время (Delta t)).
Задача
Найти ускорения точек А, В, С и D диска радиуса (r), катящегося без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянна и равна (upsilon_п) (рис. 3).
В системе координат, связанной с центром диска, диск вращается с угловой скоростью (omega), а плоскость движется поступательно со скоростью (upsilon_п). Проскальзывание между диском и плоскостью отсутствует, следовательно, (omega = frac<<<upsilon _п>>>). Скорость поступательного движения (upsilon_п) не меняется, поэтому угловая скорость вращения диска постоянная и точки диска имеют только центростремительное ускорение ( = <omega ^2>r = frac<<<upsilon_п^2>>>), направленное к центру диска. Так как система координат движется без ускорения (с постоянной скоростью (upsilon_п)), то в неподвижной системе координат ускорения точек диска будут теми же.
Перейдем теперь к задачам на динамику вращательного движения. Вначале рассмотрим простейший случай, когда движение по окружности происходит с постоянной скоростью. Так как ускорение тела при этом направлено к центру, то и векторная сумма всех сил, приложенных к телу, должна быть тоже направлена к центру, и по II закону Ньютона (m = sum F).
Следует помнить, что в правую часть этого уравнения входят только реальные силы, действующие на данное тело со стороны других тел. Никакой центростремительной силы при движении по окружности не возникает. Этим термином пользуются просто для обозначения равнодействующей сил, приложенных к телу, движущемуся по окружности. Что касается центробежной силы, то она возникает только при описании движения по окружности в неинерциальной (вращающейся) системе координат. Мы пользоваться здесь понятием центростремительной и центробежной силы вообще не будем.
Задача
Определить наименьший радиус закругления дороги, которое автомобиль может пройти при скорости (upsilon=70) км/ч и коэффициенте трения шин о дорогу (k=0,3).
На автомобиль действуют сила тяжести (P=mg), сила реакции дороги (N) и сила трения (F_<тр>) между шинами автомобиля и дорогой. Силы (P) и (N) направлены вертикально и равны по величине: (P=N). Сила трения, препятствующая проскальзыванию («заносу») автомобиля, направлена к центру поворота и сообщает центростремительное ускорение: (> = frac<>>). Максимальное значение силы трения (> = kN = kmg), поэтому минимальное значение радиуса окружности, по которой еще возможно движение со скоростью (upsilon), определяется из уравнения (frac<>> = kmg). Отсюда (R = frac<<<upsilon ^2>>><> approx 130;м).
Сила реакции дороги (N) при движении автомобиля по окружности не проходит через центр тяжести автомобиля. Это связано с тем, что ее момент относительно центра тяжести должен компенсировать момент силы трения, стремящийся опрокинуть автомобиль. Величина силы трения тем больше, чем больше скорость автомобиля (left( <> = frac<>>> right)). При некотором значении скорости момент силы трения превысит момент силы реакции и автомобиль опрокинется.
Задача
При какой скорости автомобиль, движущийся по дуге окружности радиуса (R=130) м, может опрокинуться? Центр тяжести автомобиля находится на высоте (h=1) м над дорогой, ширина следа автомобиля (l=1,5) м (рис. 4).
Рисунок 4
В момент опрокидывания автомобиля как сила реакции дороги (N), так и сила трения (F_<тр>) приложены к «внешнему» колесу. При движении автомобиля по окружности со скоростью (upsilon) на него действует сила трения (left( <> = frac<>>> right)). Эта сила создает момент относительно центра тяжести автомобиля (> = frac<>>h). Максимальный момент силы реакции дороги (N=mg) относительно центра тяжести равен (mgfrac<2>) (в момент опрокидывания сила реакции проходит через внешнее колесо). Приравнивая эти моменты, найдем уравнение для максимальной скорости, при которой автомобиль еще не опрокинется:
[upsilon = sqrt <frac<><<2h>>> approx 30;м/с approx 110;км/ч.]
Чтобы автомобиль мог двигаться с такой скоростью, необходим коэффициент трения (k geq frac<<<upsilon ^2>>><>) (см. предыдущую задачу).
Аналогичная ситуация возникает при повороте мотоцикла или велосипеда. Сила трения, создающая центростремительное ускорение, имеет момент относительно центра тяжести, стремящийся опрокинуть мотоцикл. Поэтому для компенсации этого момента моментом силы реакции дороги мотоциклист наклоняется в сторону поворота (рис. 5).
Задача
Мотоциклист едет по горизонтальной дороге со скоростью (upsilon=70) км/ч, делая поворот радиусом (R=100) м. На какой угол (alpha) к горизонту он должен при этом наклониться, чтобы не упасть?
Рисунок 5
Сила трения между мотоциклом и дорогой (<> = frac<>>>), так как она сообщает мотоциклисту центростремительное ускорение. Сила реакции дороги (N=mg). Условие равенства моментов силы трения и силы реакции относительно центра тяжести дает уравнение: (> cdot lsin alpha = Nlcos alpha), где (l) — расстояние OA от центра тяжести до следа мотоцикла (см. рис. 5).
Подставляя сюда значения (F_<тр>) и (N), находим что (<text>alpha = frac<><<<upsilon ^2>>>) или (alpha = <text>frac<><<<upsilon ^2>>> approx 70^circ). Отметим, что равнодействующая сил (N) и (F_<тр>) при этом угле наклона мотоцикла проходит через центр тяжести, что и обеспечивает равенство нулю суммарного момента сил (N) и (F_<тр>).
Для того, чтобы увеличить скорость движения по закруглению дороги, участок дороги на повороте делают наклонным. При этом в создании центростремительного ускорения, кроме силы трения, участвует и сила реакции дороги.
Задача
С какой максимальной скоростью (upsilon) может двигаться автомобиль по наклонному треку с углом наклона (alpha) при радиусе закругления (R) и коэффициенте трения шин о дорогу (k)?
Рисунок 6
На автомобиль действуют сила тяжести (mg), сила реакции (N), направленная перпендикулярно плоскости трека, и сила трения (F_<тр>), направленная вдоль трека (рис. 6). Так как нас не интересуют в данном случае моменты сил, действующих на автомобиль, мы нарисовали все силы приложенными к центру тяжести автомобиля. Векторная сумма всех сил должна быть направлена к центру окружности, по которой движется автомобиль, и сообщать ему центростремительное ускорение. Поэтому сумма проекций сил на направление к центру (горизонтальное направление) равна (frac<>>), то есть (frac<>> = Nsin alpha + >cos alpha).
Сумма проекций всех сил на вертикальное направление равна нулю:
[Ncos alpha – mg – >sin alpha = 0.]
Подставляя в эти уравнения максимальное возможное значение силы трения (F_<тр>=kN) и исключая силу (N), находим максимальную скорость (upsilon = sqrt >alpha >><<1 – k<text>alpha >>>), с которой еще возможно движение по такому треку. Это выражение всегда больше значения (sqrt ), соответствующего горизонтальной дороге.
Разобравшись с динамикой поворота, перейдем к задачам на вращательное движение в вертикальной плоскости.
Задача
Автомобиль массы (m=1,5) т движется со скоростью (upsilon=70) км/ч по дороге, показанной на рисунке 7. Участки дороги АВ и ВС можно считать дугами окружностей радиуса (R=200) м, касающимися друг друга в точке В. Определить силу давления автомобиля на дорогу в точках А и С. Как меняется сила давления при прохождении автомобилем точки В?
Рисунок 7
В точке A на автомобиль действуют сила тяжести (P=mg) и сила реакции дороги (N_A). Векторная сумма этих сил должна быть направлена к центру окружности, то есть вертикально вниз, и создавать центростремительное ускорение: (frac<>> = P – ), откуда ( = mg – frac<>> approx 12 cdot <10^3>;Н). Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе реакции. В точке С векторная сумма сил направлена вертикально вверх: (frac<>> = – P) и ( = mg + frac<>> = 18 cdot <10^3>;Н).
Таким образом, в точке А сила давления меньше силы тяжести, а в точке С — больше.
В точке В автомобиль переходит с выпуклого участка дороги на вогнутый (или наоборот). При движении по выпуклому участку проекция силы тяжести на направление к центру должна превышать силу реакции дороги (N_), причем (Pcos alpha – > = frac<>>). При движении по вогнутому участку дороги, наоборот, сила реакции дороги (N_) превосходит проекцию силы тяжести:
Из этих уравнений получаем, что при прохождении точки В сила давления автомобиля на дорогу меняется скачком на величину (frac<<2m<upsilon ^2>>> approx 6 cdot <10^3>) Н. Разумеется, такие ударные нагрузки действуют разрушающе как на автомобиль, так и на дорогу. Поэтому дороги и мосты всегда стараются делать так, чтобы их кривизна менялась плавно.
При движении автомобиля по окружности с постоянной скоростью сумма проекций всех сил на направление, касательное к окружности, должна быть равна нулю. В нашем случае касательная составляющая силы тяжести уравновешивается силой трения между колесами автомобиля и дорогой.
Величина силы трения регулируется вращательным моментом, прикладываемым к колесам со стороны мотора. Этот момент стремится вызвать проскальзывание колес относительно дороги. Поэтому возникает сила трения, препятствующая проскальзыванию и пропорциональная приложенному моменту. Максимальное значение силы трения равно (kN), где (k) — коэффициент трения между шинами автомобиля и дорогой, (N) — сила давления на дорогу. При движении автомобиля вниз сила трения играет роль тормозящей силы, а при движении вверх, наоборот, роль силы тяги.
Задача
Автомобиль массой (m=0,5) т, движущийся со скоростью (upsilon=200) км/ч, совершает «мертвую петлю» радиуса (R=100) м (рис. 8). Определить силу давления автомобиля на дорогу в верхней точке петли A; в точке B, радиус-вектор которой составляет угол (alpha=30^circ) с вертикалью; в точке С, в которой скорость автомобиля направлена вертикально. Возможно ли движение автомобиля по петле с такой постоянной скоростью при коэффициенте трения тин о дорогу (k=0,5)?
В верхней точке петли сила тяжести и сила реакции дороги (N_A) направлены вертикально вниз. Сумма этих сил создает центростремительное ускорение: (frac<>> = + mg).
Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе (N_A).
В точке В центростремительное ускорение создается суммой силы реакции и проекции силы тяжести на направление к центру: (frac<>> = + mgcos alpha). Отсюда
Легко видеть, что ( > ); с увеличением угла (alpha) сила реакции дороги увеличивается.
В точке С сила реакции ( = frac<>> approx 15 cdot <10^3>) Н; центростремительное ускорение в этой точке создается только силой реакции, а сила тяжести направлена по касательной. При движении по нижней части петли сила реакции будет превышать (frac<>>) и максимальное значение (frac<>> – mg approx 20 cdot <10^3>) Н сила реакции имеет в точке D. Значение ( = frac<>> – mg), таким образом, является минимальным значением силы реакции.
Скорость автомобиля будет постоянной, если касательная составляющая силы тяжести не превышает максимальной силы трения (kN) во всех точках петли. Это условие заведомо выполняется, если минимальное значение (kN = k = kmleft( <frac<<<upsilon ^2>>> – g> right)) превосходит максимальное значение касательной составляющей силы веса. В нашем случае это максимальное значение равно (mg) (оно достигается в точке С), и условие (kmleft( <frac<<<upsilon ^2>>> – g> right) > mg) выполняется при (k=0,5), (upsilon=200) км/ч, (R=100) м.
Таким образом, в нашем случае движение автомобиля по «мертвой петле» с постоянной скоростью возможно.
Рассмотрим теперь движение автомобиля по «мертвой петле» с выключенным мотором. Как уже отмечалось, обычно момент силы трения противодействует моменту, приложенному к колесам со стороны мотора. При движении автомобиля с выключенным мотором этого момента нет, и силой трения между колесами автомобиля и дорогой можно пренебречь.
Скорость автомобиля уже не будет постоянной — касательная составляющая силы тяжести замедляет или ускоряет движение автомобиля по «мертвой петле». Центростремительное ускорение тоже будет меняться. Создается оно, как обычно, равнодействующей силы реакции дороги и проекции силы тяжести на направление к центру петли.
Задача
Какую наименьшую скорость должен иметь автомобиль в нижней точке петли D (см. рис. 8 ) для того, чтобы совершить ее с выключенным мотором? Чему будет равна при этом сила давления автомобиля на дорогу в точке В? Радиус петли (R=100) м, масса автомобиля (m=0,5) т.
Рисунок 8
Посмотрим, какую минимальную скорость может иметь автомобиль в верхней точке петли А, чтобы продолжать двигаться по окружности?
Центростремительное ускорение в этой точке дороги создается суммой силы тяжести и силы реакции дороги (frac<> = mg + ). Чем меньшую скорость имеет автомобиль, тем меньшая возникает сила реакции (N_A). При значении ( <upsilon _A>= sqrt ) эта сила обращается в нуль. При меньшей скорости сила тяжести превысит значение, необходимое для создания центростремительного ускорения, и автомобиль оторвется от дороги. При скорости ( <upsilon _A>= sqrt ) сила реакции дороги обращается в нуль только в верхней точке петли. В самом деле, скорость автомобиля на других участках петли будет большей, и как легко видеть из решения предыдущей задачи, сила реакции дороги тоже будет большей, чем в точке А. Поэтому, если автомобиль в верхней точке петли имеет скорость ( <upsilon _A>= sqrt ), то он нигде не оторвется от петли.
Теперь определим, какую скорость должен иметь автомобиль в нижней точке петли D, чтобы в верхней точке петли А его скорость ( <upsilon _A>= sqrt ). Для нахождения скорости (upsilon_D) можно воспользоваться законом сохранения энергии, как если бы автомобиль двигался только под действием силы тяжести. Дело в том, что сила реакции дороги в каждый момент направлена перпендикулярно перемещению автомобиля, а следовательно, ее работа равна нулю (напомним, что работа (Delta A = FDelta Scos alpha), где (alpha) — угол между силой (F) и направлением перемещения (Delta S)). Силой трения между колесами автомобиля и дорогой при движении с выключенным мотором можно пренебречь. Поэтому сумма потенциальной и кинетической энергии автомобиля при движении с выключенным мотором не меняется.
Приравняем значения энергии автомобиля в точках А и D. При этом будем отсчитывать высоту от уровня точки D, то есть потенциальную энергию автомобиля в этой точке будем считать равной нулю. Тогда получаем
Подставляя сюда значение ( <upsilon _A>= sqrt ) для искомой скорости (upsilon _D), находим:
Если автомобиль въедет в петлю с такой скоростью, то он сможет совершить ее с выключенным мотором.
Определим теперь, с какой силой при этом автомобиль будет давить на дорогу в точке В. Скорость автомобиля в точке В опять легко находится из закона сохранения энергии:
Подставляя сюда значение ( <upsilon_D>= sqrt <5gR>), находим, что скорость ( <upsilon _B>= sqrt right)>).
Воспользовавшись решением предыдущей задачи, по заданной скорости находим силу давления в точке В:
Аналогично можно найти силу давления в любой другой точке «мертвой петли».
Упражнения
- Найти угловую скорость искусственного спутника Земли, вращающегося по круговой орбите с периодом обращения (T=88) мин. Найти линейную скорость движения этого спутника, если известно, что его орбита расположена на расстоянии (R=200) км от поверхности Земли.
- Диск радиуса (R) помещен между двумя параллельными рейками. Рейки движутся со скоростями (upsilon_1) и (upsilon_2). Определить угловую скорость вращения диска и скорость его центра. Проскальзывание отсутствует.
- Диск катится по горизонтальной поверхности без проскальзывания. Показать, что концы векторов скоростей точек вертикального диаметра находятся на одной прямой.
- Самолет движется по окружности с постоянной горизонтальной скоростью (upsilon=700) км/ч. Определить радиус (R) этой окружности, если корпус самолета наклонен на угол (alpha=5^circ).
- Груз массы (m=100) г, подвешенный на нити длины (l=1) м, равномерно вращается по кругу в горизонтальной плоскости. Найти период обращения груза, если при его вращении нить отклонена по вертикали на угол (alpha=30^circ). Определить также натяжение нити.
- Автомобиль движется со скоростью (upsilon=80) км/ч по внутренней поверхности вертикального цилиндра радиуса (R=10) м по горизонтальному кругу. При каком минимальном коэффициенте трения между шинами автомобиля и поверхностью цилиндра это возможно?
- Груз массой (m) подвешен на нерастяжимой нити, максимально возможное натяжение которой равно (1,5mg). На какой максимальный угол (alpha) можно отклонить нить от вертикали, чтобы при дальнейшем движении груза нить не оборвалась? Чему будет равно при этом натяжение нити в тот момент, когда нить составит угол (frac<alpha><2>) с вертикалью?
Источник: Журнал “Квант”, №5 1972 г. Автор: Л. Асламазов.
http://easyfizika.ru/articles/dvizhenie-po-okruzhnosti/
Определение угловой скорости
Угловая скорость — важное физическое понятие, применяемое к объектам, движущимся по круговой траектории. В этой статье будет рассмотрено понятие угловой скорости и ее связь с линейной скоростью.
Что такое угловая скорость?
В этом разделе вы поймете угловую скорость и ее роль во вращательном движении.
Чтобы понять угловую скорость, нужно понять, что такое вращение. Чтобы помочь вам с вашим пониманием, давайте рассмотрим ветряную мельницу. Ветряная мельница представляет собой твердое тело, вращающееся вокруг неподвижной оси. Ветряная мельница совершает вращательное движение, когда лопасти ветряной мельницы вращаются вокруг оси, проходящей через ротор. Скорость, связанная с твердыми телами, когда они вращаются вокруг фиксированной оси, называется угловой скоростью.
Определение угловой скорости
В физике мы определяем угловую скорость следующим образом:
Угловая скорость — это векторная мера скорости вращения, которая относится к тому, насколько быстро объект вращается относительно другой точки.
Проще говоря, угловая скорость — это скорость, с которой объект вращается вокруг оси. Угловая скорость обозначается греческой буквой омега (ω, иногда Ω). Измеряется в углах в единицу времени; следовательно, единицей угловой скорости в СИ является радиан в секунду. Размерная формула угловой скорости [M 0 L 0 T -1 ].
Для объекта, вращающегося вокруг оси, каждая точка объекта имеет одинаковую угловую скорость. Но точки, расположенные дальше от оси вращения, движутся с другой тангенциальной скоростью, чем точки, расположенные ближе к оси вращения. Угловая скорость также известна как скорость вращения и вектор угловой частоты.
Формула угловой скорости
Поскольку угловая скорость объекта представляет собой угловое смещение объекта во времени, угловая скорость выражается следующим образом:
begin{array}{l}omega =frac{Theta }{t}end{array}
Где ω — угловая скорость, θ — угловое смещение, t — изменение во времени t.
По соглашению, положительная угловая скорость указывает на вращение против часовой стрелки, а отрицательная — по часовой стрелке.
Средняя угловая скорость
Средняя угловая скорость вращающегося твердого тела есть отношение углового смещения к интервалу времени.
begin{array}{l}omega _{avg}=frac{Delta Theta }{Delta t}=frac{Theta_{2}-Theta_{1} }{t_{1}-t_{2}}end{array}
Мгновенная угловая скорость
Мгновенная угловая скорость определяется как предел средней угловой скорости при приближении интервала времени к нулю.
begin{array}{l}omega_{ins}=lim_{Delta trightarrow 0}frac{Delta Theta }{Delta t}=frac{dTheta }{dt}end{array}
Нахождение направления угловой скорости
Направление угловой скорости трудно отследить, потому что точка на вращающемся объекте постоянно меняет направление. Ось вращающегося объекта — единственная точка, в которой объект имеет фиксированное направление. С помощью оси вращения направление угловой скорости определяется по правилу правой руки.
Правило правой руки
Направление угловой скорости находится по правилу правой руки. Для лучшего понимания рассмотрим вращающийся диск, как показано на рисунке ниже. Представьте себе полюс, проходящий через центр диска на оси вращения. Используя правило правой руки, ваша правая рука будет держаться за шест так, чтобы ваши четыре пальца следовали за направлением вращения. Кроме того, ваш большой палец направлен прямо по оси, перпендикулярно другим пальцам.
Направление угловой скорости — это направление, в котором указывает большой палец, когда вы сгибаете пальцы в направлении вращения диска. Направление угловой скорости всегда перпендикулярно плоскости вращения.
Связь между угловой скоростью и линейной скоростью
Угловая скорость аналогична линейной скорости. Чтобы найти взаимосвязь между угловой скоростью и линейной скоростью, давайте рассмотрим пример ямки на компакт-диске (данные компакт-диска хранятся в виде серии крошечных углублений, известных как «ямки»).
Яма перемещается на длину дуги Δs за время Δt, поэтому ее линейная скорость определяется следующим уравнением:
begin{array}{l}v = frac{Delta s}{Delta t} ,,—–(1)end{array}
Угол поворота Δθ — это отношение длины дуги к радиусу кривизны, поэтому
begin{array}{l}Delta Theta =frac{Delta s }{r}end{array}
Преобразовывая приведенное выше уравнение, мы получаем
begin{array}{l}Delta s=Delta Theta r,,—–(2)end{array}
Подставляя (2) в (1), получаем
begin{array}{l}v=rcdot frac{Delta Theta }{Delta t}end{array}
Упрощая далее, получаем
begin{array}{l}v = rcdot omegaend{array}
Следовательно,
begin{array}{l}v = rcdot omegaend{array}
обозначает связь между угловой скоростью и линейной скоростью.
Примеры угловой скорости из реальной жизни
Угловая скорость Земли
Планета Земля совершает три движения: вращается вокруг своей оси, вращается вокруг Солнца и проходит через Млечный Путь вместе с остальной частью Солнечной системы. Теперь мы знаем, что Земле требуется 23 часа 56 минут и 4,09 секунды, чтобы повернуться вокруг своей оси вращения. Этот процесс известен как звездные сутки, а скорость, с которой он движется, известна как угловая скорость Земли.
Полный радиан равен 360 градусам; отсюда мы знаем, что Земля совершает два радиана при полном вращении вокруг оси. Следовательно, угловая скорость вращения Земли может быть рассчитана как:
begin{array}{l}omega =frac{Delta Theta }{Delta t}end{array}
begin{array}{l}omega =frac{2pi }{1,{day}(86400,{seconds})}end{array}
Подсчитав, получаем,
begin{array}{l}omega =7.2921159times 10^{-5},{radians/second}end{array}
Угловая скорость вращения Земли равна,
begin{array}{l}omega =7.2921159times 10^{-5},{radians/second}end{array}