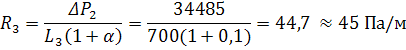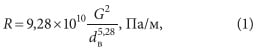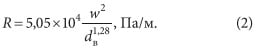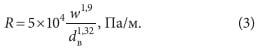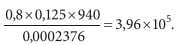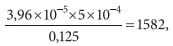Как найти удельные потери давления

Третья статья в цикле статей по теоретическим основам гидравлики посвящена определению потерь напора.

Как рассказывалось ранее, при своем движении жидкость испытывает сопротивление, что выражается затратами ее энергии, т.е. затратами ее напора, что называют потерями напора.

Два вида потерь напора

Потери напора принципиально делятся на два типа:

1. Местные (на рисунке обведены красным)
2. Потери по длине (на рисунке подчеркнуты зеленым)

Местные потери конкретно на данном рисунке: поворот, задвижка (условное обозначение по ГОСТ – «бантик»), еще один поворот и внезапное (т.е. не плавное) расширение.

Потери по длине здесь – это потери на прямолинейных участках l₁, l₂, l₃, l₄.

Местные потери

Местные потери напора (говорят также “потери напора на местные сопротивления“) – это потери напора, которые происходят в основном из-за вихреобразования в конкретных местах трубопровода (потому и «местные»). Любое препятствие на пути движения потока жидкости является местным сопротивление. Чем сильнее деформируется поток, тем больше будет потеря напора. Например, на рисунке ниже показано внезапное сужение трубопровода. Хорошо видны 4 вихревые зоны до и после сужения.

Местную потерю напора можно определить, зная коэффициент сопротивления для данного сопротивления (обозначается буквой дзэта ζ, не имеет размерности) и среднюю скорость потока в сопротивлении V.

h_м = ζ · V² / 2g

(g – ускорение свободного падения, g = 9,81 м/с² , для быстрых подсчетов можно округлить до 10 м/с²)

Пример. Определить потерю напора в вентиле, установленном на трубе внутренним диаметром d = 51 мм, при расходе Q = 2 л/с.

Сначала по уравнению неразрывности (ссылка на статью 2) определим среднюю скорость движения жидкости.

V = Q / ω = 4 · Q / 3,14 · d² = 4 · 0,002 / 3,14 · 0,051² = 0,98 м/с

Теперь необходим коэффициент сопротивления вентиля. Такие данные берут из гидравлических справочников или у производителей конкретной арматуры. По справочным данным находим, что коэффициент местного сопротивления вентиля равен 6.

Тогда потеря напора на вентиле: h_вент = ζ · V²/ 2 · g = 6 · 0,98² / 2 · 10 = 0,29 м.

При расчете трубопроводных систем (внутренний водопровод здания, наружная водопроводная сеть и т.п.) обычно высчитывают не все сопротивления (так как их может быть очень много), а только самые существенные, создающие наибольшие сопротивления: например, счетчик воды. Потеря напора на остальных местных сопротивлениях учитывается коэффициентом, на который умножается значение потерь напора по длине (1,05 – 1,15 для наружных сетей, 1,1 – 1,3 для внутренних сетей здания).

Потери по длине

Потери напора по длине – потери напора на участках трубопровода. Возникают из-за работы сил трения. (сила трения возникает между слоями движущейся жидкости). Величина потерь напора, также, как и местных потерь, напрямую зависит от скорости движения жидкости. При достаточно высокой скорости усиливается влияние шероховатости стенок трубы.

Потерю напора по длине можно увидеть по разнице в уровнях воды между двумя пьезометрами

Точное определение потерь напора по длине является довольно сложной задачей, для этого необходимо устанавливать режим движения жидкости (бывает ламинарный и турбулентный), подбирать расчетную формулу для коэффициента гидравлического трения в зависимости от числа Рейнольдса Re, характеризующего степень турбулизации потока. Это изучается студентами в рамках курса механики жидкости.

При этом для быстрого расчета потерь напора были составлены специальные таблицы для инженеров, позволяющие, зная материал трубы и ее диаметр, а также расход воды, быстро определить так называемые удельные потери напора (сколько напора теряется на 1 м трубы). Эта величина называется 1000i, значение 1000i = 254 означает, что поток, проходя 1 м такой трубы теряет 254 мм (миллиметра) напора, т.е. 0,254 метра. Это значение также называется «гидравлический уклон», и это нельзя путать с геодезическим, т.е. просто с физическим уклоном (наклоном) самой трубы. Для расчета стальных труб используют таблицы Шевелева.

Скачать таблицы таблицы Шевелева  в формате PDF можно на нашем сайте.

Таблицы Шевелева для определения потерь напора

Например, из данного фрагмента видно, что если вода с расходом 1,50 л/с пойдет по трубе диаметром 50 мм, то скорость в этой трубе будет 0,47 м/с, а 1000i составит 9,69 мм на метр (на каждом метре трубы теряется 9,69 миллиметров напора).

Чтобы определить, сколько метров напора будет потеряно на всем участке – нужно перемножить 1000i с длиной участка. Чтобы ответ получился в метрах, 1000i делят на 1000.

Итак, потери напора по длине: h_l = 1000i·l / 1000 = i·l

Если наш участок трубы имеет длину, скажем, 25 метров, то потеря напора на нем:

h_l = 9,69*25/1000 = 0,24 м.

Учтем и местные сопротивления, тогда полная потеря напора на данном участке:

­h_l = 0,24*1,3 = 0,31 м.

Таблицы были переведены в электронный вид в виде программы, созданной Любчуком Ю.Е.
Загрузить программу “Таблицы Шевелева” можно с нашего сайта.

С помощью этой программы, можно легко посчитать потери напора в трубах из различных материалов. В следующей статье подробно опишем, как пользоваться данной программой на задаче из жизни.

Потери
давления, Па
на участках тепловой сети складываются
из потерь давления на трение по длине
трубопровода (линейные потери) и в
местных сопротивлениях:

Потери
давления на трение
определяются по формуле:

где

длина участка трубопровода, м;

удельные потери давления, Па/м, определяются
по формуле:

где

коэффициент трения;

внутренний диаметр участка трубопровода,
м;

плотность теплоносителя, кг/м³;

скорость движения теплоносителя, м/с.

Потери
давления в местных сопротивлениях
определяют по формуле:

где

сумма
коэффициентов местных сопротивлений.

Потери
давления в местных сопротивлениях могут
быть также вычислены по формуле:

где

эквивалентная длина местных сопротивлений,
которую определяют по формуле:

При
известном располагаемом давлении
для всей сети, а также для ответвлений
предварительно определяют ориентировочные
средние
удельные потери давления ,
Па/м:

где
суммарная
протяженность расчетной ветви
(ответвления), на потери давления, в
которой используется величина .

коэффициент, учитывающий долю потерь
давления в местных сопротивлениях.
Различные значения коэффициента
приведены в [11, табл. 6.2].

При
неизвестном располагаемом перепаде
давления
удельные потери давления на участках
главной магистрали могут быть приняты
в пределах 30-80 Па/м, для ответвлений –
по располагаемому перепаду давления,
но не более 300 Па/м.

Невязка
между потерями давления в ответвлениях
и располагаемым давлением не должна
превышать 10%. Если
такая увязка невозможна, то излишний
напор на ответвлениях должен быть
погашен соплами элеваторов, дроссельными
диафрагмами и авторегуляторами
потребителей.

Конечные
результаты гидравлического расчета
следует перевести в м.вод.ст., если по
его данным предполагается построение
пьезометрического графика.

ПРИМЕР
5. Определить
потери давления на участках 1, 2, 3 расчетной
схемы магистральной тепловой сети
(рисунок 5) . Суммарный
расчетный расход сетевой воды для всех
участков взять из примера 4. Для компенсации
температурных деформаций предусмотреть
сальниковые компенсаторы.

Рисунок 5. Расчетная
схема магистральной тепловой сети

Решение:

1. Вначале
   производим расчет главной магистрали.
   Для участков 1, 2 исходя из расчетных
   расходов сетевой воды и нормируемым
   потерям давления R=30-80
   Па/м по номограмме (приложение 10)
   определяем диаметры труб, действительные
   значения удельных потерь R_д
   и скорость движения теплоносителя ω и
   результаты занесем в таблицу 5.

Таблица
5 – Гидравлический
расчет тепловой сети

1. По
   известным диаметрам на участках главной
   магистрали определим сумму коэффициентов
   местных сопротивлений
   , их эквивалентные длины ,
   приведенные длины, а также потери
   давления:

На
участке №1 имеется головная задвижка
(,
тройник на проход при разделении потока
(.
(Значения коэффициентов местных
сопротивлений
определяются по приложению 11).

Количество
сальниковых компенсаторов
на участке №1 определим в зависимости
от длины участка L
и максимального
допустимого расстояния между неподвижными
опорами. По приложению 12 для D_у
= 300 мм это
расстояние составляет 100 м. Следовательно
на участке № 1 длиной 800 м необходимо
предусмотреть 8 сальниковых компенсаторов.

Сумма
коэффициентов местных сопротивлений
на данном участке составляет:

По
приложению 13 эквивалентная длина
при k_э
= 0,0005 м составляет 14 м.

Эквивалентная
длина участка №1 составит:

Определяем
приведенную длину участка №1:

Определим
потери давления на участке № 1:

или
в линейных единицах измерения при
𝜌=1000
кг/м³:

Аналогичный
расчет выполним для участка №2 главной
магистрали:

на
данном участке имеется внезапное сужение
трубопровода (,
задвижка( ,
10 сальниковых компенсаторов

Сумма
коэффициентов местных сопротивлений
на данном участке составляет:

Эквивалентная
длина участка №2 составит:

Приведенная
длина участка №2:

Потери
давления на участке 2:

или
в линейных единицах измерения:

1. Затем
   приступаем к расчету ответвления. По
   принципу увязки

потери
давления ΔP
от точки
деления потоков до концевых точек

(кварталов) для
различных ветвей системы должны быть
равны между

собой.
Поэтому при гидравлическом расчете
ответвления необходимо стремиться к
выполнению следующего условия: .

В соответствии с
этим условиями найдем ориентировочные
удельные потери давления для ответвления

Коэффициент
,
учитывающий долю потерь давления на
местные сопротивления, определим по
формуле:

тогда

Ориентируясь
на
Па/м, определим по номограмме (приложение
10) диаметр трубопроводов, действительные
удельные потери давления на трение
,
скорость движения теплоносителя и
потери давления на участке 3. (таблица
5).

На
участке №3 имеется внезапное сужение
трубопровода (,
тройник на ответвление при разделении
потока ,
2 задвижки ,
8 сальниковых компенсаторов (

Сумма
коэффициентов местных сопротивлений
на данном участке составляет:

Эквивалентная
длина участка №3 составит:

Приведенная
длина участка №3:

Потери
давления на участке № 3 составят:

или
в линейных единицах измерения:

Определим невязку
потерь давления на ответвлении 3

В практике проектирования систем теплоснабжения удельные потери давления на трение R [Па/м], определяются по величине скорости воды w [м/с] и (или) расходу воды G [кг/ч (т/ч)], и по наружному диаметру трубопровода с указанием толщины стенки d_н × δ, мм. Для стальных электросварных труб по ГОСТ 10704 «Трубы стальные электросварные прямошовные. Сортамент» можно воспользоваться табл. 9.11 [1] с соответствующим пересчетом к единицам системы СИ.

В ней значения R приведены с достаточно подробным шагом по G, в среднем 5–10 т/ч, а на малых расходах даже ниже. Тем не менее, может потребоваться вычисление удельных потерь для промежуточных скоростей и расходов. Для этого необходима интерполяция таблицы. Но если расчет проводится с применением ЭВМ, например, с использованием электронных таблиц MS Excel, что очень удобно, так как гидравлический расчет трубопроводов всегда записывается в табличной форме, целесообразно иметь простую и в то же время достаточно точную формулу для R.

По физическим соображениям, однако, такая формула должна составляться относительно внутреннего диаметра d_в, который можно определить по величине d_н и δ с использованием данных ГОСТ 10704. В руководстве [1] и других источниках приводятся известные из гидравлики общие выражения для R через коэффициент гидравлического трения, но они достаточно сложны для массовых инженерных расчетов.

Если построить по данным табл. 9.11 из [1] номограмму для R (рис. 1), можно увидеть, что при изображении в логарифмических координатах она представляет собой набор прямых линий. Это означает, что величина R должна находиться в степенной зависимости от параметров w (или G) и d_в. Подобная номограмма содержится и в работе [1]. В результате обработки с помощью метода наименьших квадратов таблица хорошо аппроксимируется формулой:

дающей для наиболее употребительного в практике проектирования диапазона скоростей 0,8–2,5 м/с и наружных диаметров в пределах 108–325 мм погрешность не более 0,15 %. При крайних значениях данных параметров отклонение не превысит 0,5 %, что также заведомо находится в области обычной погрешности инженерных расчетов. Соотношение (1) справедливо при величине среднего значения плотности воды 940 кг/м³, характерной для температур в теплосетях [1]. При других плотностях необходим пропорциональный пересчет. С учетом связи между скоростью и расходом воды и сечением трубопровода получаем:

Здесь уже результат непосредственно от плотности зависеть не будет, поскольку она входит в уравнение неразрывности потока, которое было использовано при переходе от (1) к (2), и в процессе преобразований сокращается. Нетрудно заметить, что выражение (2) весьма напоминает как по форме, так и по числовым коэффициентам, в том числе уровню показателей степени при w и d_в, полученную ранее автором зависимость [2, 3] для потерь давления в стальных водогазопроводных трубах, используемых в системах водяного отопления (3):

В то же время отсюда можно сделать вывод об определенном различии режима течения воды в системах отопления и теплоснабжения — в первом случае он является переходным между режимом гидравлической гладкости и зоной квадратичного сопротивления, а во втором имеет место чисто квадратичная зона.

Это связано с более высокой эквивалентной шероховатостью труб теплосетей k_э, равной 0,5 мм, то есть 5 × 10–4 м [1], по сравнению с трубопроводами систем отопления (0,2 мм [4]) и с увеличенными скоростями воды, характерными для теплосетей, а также с ее меньшей вязкостью из-за повышенной температуры. В самом деле, для наименьших использованных значений d_в = 125 мм = 0,125 м и скорости w = 0,8 м/с величина критерия Рейнольдса Re будет равна

Здесь 0,0002376 Па⋅с — динамическая вязкость воды при плотности 940 кг/м³ [5]. Если теперь вычислить соотношение Re k_э/d_в, получим

что значительно больше предельного значения, характеризующего окончательный переход к квадратичному режиму сопротивления [5]. При более высоких скоростях уровень Re k_э/d_в будет еще выше, а значит, и режим течения заведомо остается в квадратичной зоне. Диаметр трубопроводов на полученные выводы при этом не влияет, поскольку сокращается при расчете комплекса Re k_э/d_в.

Для сравнения отметим, что для внутреннего водопровода средний показатель степени при w равен 1,76 [6], что практически соответствует гидравлически гладким трубам, поскольку в этом случае известная формула Блазиуса дает значение этого показателя, равное 1,75. Если теперь провести технико-экономическую оценку аналогично выполненной в [7] для систем отопления, окажется, что в силу квадратичного режима сопротивления оптимальная скорость воды в трубопроводах теплосетей wопт уже не будет зависеть от G, а величина оптимального диаметра d_в.опт будет строго пропорциональна √G.

Формула для d_в.опт при w_опт около 0,9 м/с в этом случае получается в следующем виде, где G следует подставлять в [кг/ч]:

d_в.опт = 0,6√G, мм. (4)

Это меньше, чем для отопления, а wопт, напротив, значительно выше (примерно в 1,5 раза), главным образом, из-за гораздо более высокого КПД сетевых консольных насосов по сравнению с циркуляционными, как правило, выполненными с «мокрым ротором». Вследствие этого для теплосетей становится выгоднее уменьшать капитальные затраты на трубопроводы, поскольку расход электроэнергии на привод насосов при этом будет расти медленнее, чем в отопительных системах.

Таким образом, формулы, приведенные в настоящей работе, очень просты, наглядны и доступны для инженерных расчетов, особенно при использовании электронных таблиц MS Excel, а также в учебном процессе. Их применение позволяет отказаться от интерполяции таблиц при сохранении точности, требуемой для инженерных расчетов, и непосредственно вычислять удельное сопротивление трубопроводов в широком диапазоне скоростей и расходов воды и диаметрах вплоть до d_н = 325 мм. Этого вполне достаточно для проектирования водяных тепловых сетей в большинстве современных случаев.

МНЕНИЕ

Валентин Воропаев, главный специалист по теплоснабжению ООО «Миран-Проект»: «В практике проектирования инженерных систем зданий мы, проектировщики, сталкиваемся с гидравлическими расчетами различных систем, будь то система отопления, система горячего водоснабжения, холодоснабжения и так далее, а также с гидравлическими расчетами наружных сетей — как теплоснабжения, так и водопровода. И для этих расчетов приходится пользоваться различными таблицами в разных справочниках. Поэтому я могу только приветствовать появление методики, позволяющей автоматизировать разные гидравлические расчеты. А если еще в этой методике будут учтены различные режимы, среды и материалы трубопроводов, то получится очень неплохой и удобный справочник, облегчающий жизнь проектировщикам».

Библиографическое описание:

Попов, А. В. Сравнительный анализ некоторых зависимостей гидравлического расчета водяных тепловых сетей / А. В. Попов. — Текст : непосредственный // Молодой ученый. — 2018. — № 24 (210). — С. 79-82. — URL: https://moluch.ru/archive/210/51528/ (дата обращения: 27.05.2023).

Гидравлический расчет является одним из важных видов расчета при проектировании, эксплуатации, наладке и обследовании водяных тепловых сетей. При его выполнении решается ряд задач, а именно:

1. Вычисление диаметров трубопровода.
2. Вычисление потерь напора (давления) как на отдельных участках тепловой сети, так и в сумме по всей длине магистрали или сложного ответвления.
3. Вычисление напора (давления) в разных точках тепловой сети.
4. Увязка ответвлений с магистралью для обеспечения правильного распределения расхода теплоносителя и требуемых напоров в сети и у потребителей.
5. Определение пропускной способности сети при известных диаметрах и заданном падении напора.

И, как следствие, от его правильного выполнения зависят: денежные затраты при строительстве и эксплуатации теплосетей, выбор оптимального оборудования, рекомендации по наладке и оптимизации работы существующих тепловых сетей.

На сегодняшний день большинство методик гидравлического расчета трубопроводов основывается на уравнении Дарси-Вейсбаха [1]. Согласно ему, потери давления в трубопроводе равны, Па:

(1)

где λ — безразмерная величина, называемая коэффициентом гидравлического трения; L — расчетная длина трубопровода, м; ρ — плотность теплоносителя, кг/м³; w — средняя скорость течения теплоносителя, м/с; d — расчетный диаметр трубопровода, м.

В инженерной практике формула (1) часто используется в следующем виде, Па:

(2)

где R — удельные потери давления на трение, которые определяются по формуле, Па/м:

(3)

В формуле (3) наибольшую трудность представляет задача по определению значения коэффициента гидравлического трения λ, так как данная величина в общем случае зависит от режима течения жидкости и свойств материала трубопровода. Теплосети работают в области турбулентного режима, для которого предложено множество формул по расчету коэффициента гидравлического трения. Наиболее простой для применения в практических расчетах является универсальная формула Альтшуля:

(4)

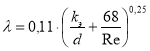
где k_э — коэффициент эквивалентной шероховатости, м; Re — безразмерная величина, называемая критерием Рейнольдса, которая характеризует режим течения жидкости и определяется по формуле:

(5)

где ν — кинематическая вязкость, м²/с.

Поэтому, с учетом формулы (4), зависимость (3) можно записать в следующем виде, Па/м:

(6)

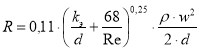
В литературе [2] формула удельных потерь давления, с учетом предположения о том, что большинство тепловых сетей работают в области квадратичного режима и принимая плотность теплоносителя постоянной, принимает следующий вид, Па/м:

(7)

где G — массовый расход теплоносителя, кг/с.

В то же время в работе [3] на основе обобщения и упрощения известных данных и зависимостей приведена следующая формула, Па/м:

(8)

где A, a, b — эмпирические коэффициенты, зависящие от материала трубопровода и его назначения; d — расчетный диаметр трубопровода, мм.

Формулы (6) — (8) для определения удельных потерь давления на трение используются при гидравлическом расчете тепловых сетей, но все они могут давать различные между собой результаты. Поэтому необходимо провести сравнение результатов гидравлического расчета по этим зависимостям.

Для этого была выбрана тепловая сеть, расположенная на территории г. Владимира, спроектированная из стальных труб (k_э =0.0005 м) на температурный график 150/70 ° С. Исходные данные для расчета по участкам теплосети приведены в таблице 1.

Таблица 1

Исходные данные для расчета

В водяных тепловых сетях обычно вместо потерь давления оперируют величиной потерь напора, которая вычисляются по формуле м:

(9)

где g — ускорение свободного падения, равное 9,81 м/с².

Для удобства расчета каждому из расчетов были присвоены следующие номера:

I — расчет удельных потерь давления и потерь напора с использованием формулы (6);

II — расчет удельных потерь давления и потерь напора с использованием формулы (7);

III- расчет удельных потерь давления и потерь напора с использованием формулы (8).

В таблице 2 приведены результаты расчета удельных потерь давления и потерь напора по каждому участку. В формуле (7) значение коэффициента A^B_R = 13,62 · 10 ^-6 м^3,25/кг при k_э равным 0.0005 м. В формуле (8) для водяных тепловых сетей А=6,01; а = 1,9; b= 1,3.

Таблица 2

Результаты расчета удельных потерь давления ипотерь напора по участкам

Как видно из таблицы 2, результаты расчетов отличаются друг от друга. Для дальнейшего анализа необходимо вычислить относительную погрешность расчета потерь напора, которая определяется по формуле, %:

(10)

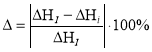
где i — номер расчета, ΔН — потери напора, м.

За точные результаты примем значения, полученные в расчете I, так как зависимость для определения коэффициента гидравлического трения, входящая в нее, используется в большинстве практических расчетов и дает результаты, которые хорошо соотносятся с опытными данными различных исследователей.

В таблице 3 представлены расчеты погрешности относительно расчета I как по каждому участку, так и по суммарным потерям напора на всей магистрали в целом.

Таблица 3

Расчет относительной погрешности удельных потерь давления ипотерь напора

Как видно из таблицы 3, относительная ошибка по суммарным потерям на магистрали не превышает 4 % для расчета по формуле (8) и не превышает 7 % по формуле (9), что для инженерной практики можно считать весьма удовлетворительным. Однако стоит заметить, что в результате расчета по формуле (9), относительная ошибка на отдельных участках выше 15 %, что накладывает ограничения на применение данной формулы. Например, при увязке ответвлений, относительная ошибка между ответвлением и рассматриваемой частью магистрали не должна превышать 15 %.

В заключение хотелось бы отметить, что существует множество расчетных зависимостей по определению потерь давления (напора) в трубопроводах, но все они так или иначе применимы для определенных случаев с учетом ряда допущений. Применяя даже упрощенные варианты известных зависимостей, приходится выполнять расчеты по каждому из участков тепловой сети, что делает расчет весьма трудоемким, особенно при конфигурации сети с большим количеством участков и ответвлений. Все это создает предпосылки для дальнейшего совершенствования подходов гидравлического расчета.

Литература:

1. Гидравлика и гидропривод: Учебное пособие /Н. С. Гудилин, Е. М. Кривенко, В. С. Маховиков и др. — М.: Изд-во МГГУ, 2001. — 520 с.
2. Соколов Е. Я. Теплофикация и тепловые сети: учебник для вузов. — 7-е изд., стереотип. — М.: Изд-во МЭИ, 2001. — 472 с.
3. Самарин О. Д. Построение универсальной зависимости для потерь давления в трубопроводах// Журнал С. О. К., № 1/2016.