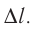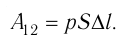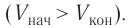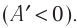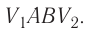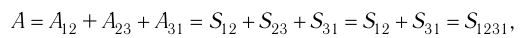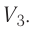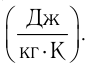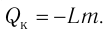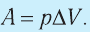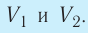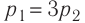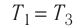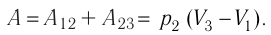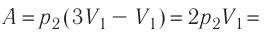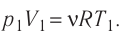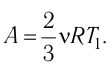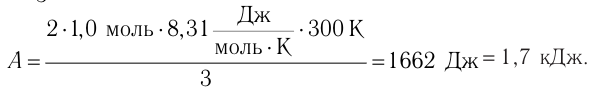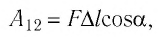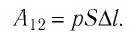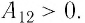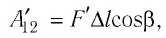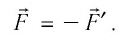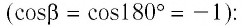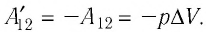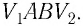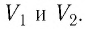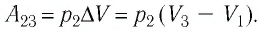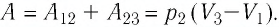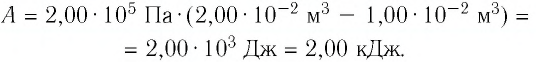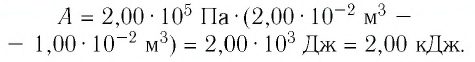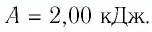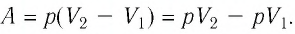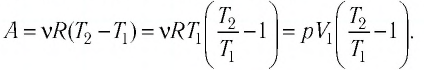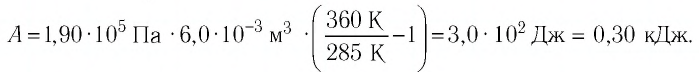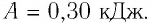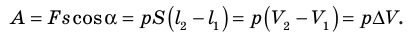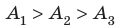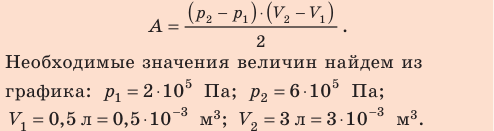2. Основные законы термодинамики
В технической термодинамике используются три основные функции состояния: удельная внутренняя энергия $u$, удельная энтальпия $h$ и удельная энтропия $s$. Эти функции зависят только от состояния рабочего тела, их изменение в ходе термодинамического процесса не зависит от хода процесса.
Удельная внутренняя энергия – функция состояния закрытой термодинамической системы, определяемая тем, что ее приращение в любом процессе, происходящем в этой системе, равно сумме теплоты, сообщенной системе, и работы, совершенной над ней.
Если рабочее тело – идеальный газ, то внутренняя энергия зависит только от температуры.
$$mathrm{d}u=c_v mathrm{d}T.$$
Тогда для процесса идеального газа изменение внутренней энергии равно:
$$∆u=intop_{T_1}^{T_2} c_v mathrm{d}T.$$
Условно принимают, что при нормальных условиях ($t=0$ °C) внутренняя энергия равна $0$, тогда в данном состоянии, характеризуемом температурой $t$, внутренняя энергия равна:
$$u =intop_{273.15 K}^T c_v mathrm{d}T.$$
Удельная работа изменения объема совершается при любом изменении объема неподвижного газа. Эта работа обозначается $l$ (Дж/кг, кДж/кг). При элементарном изменении объема $1$ кг газа соответствующая элементарная работа равна:
$$mathrm{d}l=pmathrm{d}v.$$
Для термодинамического процесса, в котором объем $1$ кг рабочего тела изменяется от $v_1$ до $v_2$, работа изменения объема равна:
$$l=intop_{v_1}^{v_2} pmathrm{d}v.$$
Для нахождения удельной работы изменения объема по выражению выше надо знать функциональную связь между $p$ и $v$ в ходе процесса. Для анализа работы рабочего тела удобно пользоваться диаграммой $p-v$.
Первый закон термодинамики представляет собой закон сохранения энергии, примененный к процессам, протекающим в термодинамических системах. Этот закон можно сформулировать так: энергия изолированной термодинамической системы остается неизменной независимо от того, какие процессы в ней протекают. Для незамкнутого термодинамического процесса, протекающего в простейшей изолированной системе, состоящей из источника теплоты, рабочего тела и объекта работы, уравнение баланса энергии примет вид:
$$mathrm{d}q=mathrm{d}u+mathrm{d}l.$$
или
$$mathrm{d}q=mathrm{d}u+pmathrm{d}v.$$
Последнее выражение можно видоизменить, введя в него энтальпию и техническую работу:
$$mathrm{d}q=mathrm{d}u+mathrm{d}(pv)-vdmathrm{d}=mathrm{d}(u+pv)-vdmathrm{d}=mathrm{d}h+mathrm{d}l’.$$
Удельная энтальпия – функция состояния термодинамической системы, равная сумме внутренней энергии и произведения удельного объема на давление:
$$h = u + p·v.$$
Энтальпия идеального газа зависит только от температуры. Изменение энтальпии в процессе идеального газа подсчитывается по формуле:
$$∆h=intop_{T_1}^{T_2} c_p mathrm{d}T.$$
Поскольку энтальпия при нормальных условиях принимается равной нулю, то энтальпия рабочего тела в данном состоянии равна:
$$h =intop_{273.15 K}^T c_p mathrm{d}T.$$
Удельная техническая работа совершается потоком движущегося газа за счет изменения кинетической энергии газа. Эта работа обозначается и $l’$ (Дж/кг, кДж/кг). Элементарная техническая работа равна:
$$mathrm{d}l’=-vmathrm{d}p.$$
Для термодинамического процесса удельная техническая работа $1$ кг рабочего тела равна:
$$l’=-intop_{p_1}^{p_2} v mathrm{d}p.$$
Второй закон термодинамики определяет напавление, в котором протекают процессы, устанавливает условия преобразования тепловой энергии в механическую, а также определяет максимальное значение работы, которое может быть произведена тепловым двигателем.
Второй закон термодинамики математически может быть выражен следующим образом:
$$mathrm{d}s≥frac{mathrm{d}q}{T}.$$
Знак неравенства соответствует необратимым процессам, а знак равенства – обратимым. Следовательно, аналитическое выражение второго закона термодинамики для бесконечно малого обратимого процесса имеет вид:
$$mathrm{d}q=Tmathrm{d}s.$$
Тогда согласно первому закону термодинамики:
$$Tmathrm{d}s=mathrm{d}u+pmathrm{d}v.$$
Удельная энтропия – функция состояния термодинамической системы, определяемая тем, что ее дифференциал $mathrm{d}s$ при элементарном равновесном (обратимом) процессе равен отношению бесконечно малого количества теплоты $mathrm{d}q$, сообщенной системе, к термодинамической температуре $T$ системы:
$$mathrm{d}s=frac{mathrm{d}q}{T}.$$
Изменения удельной энтропии между двумя произвольными состояниями газа определяют по следующим формулам:
$$mathrm{d}s=frac{mathrm{d}u}{T}+frac{mathrm{d}l}{T}=frac{mathrm{d}u}{T}+frac{pmathrm{d}v}{T}=frac{mathrm{d}u}{T}+frac{Rmathrm{d}v}{v}.$$
$$∆s=intop_{T_1}^{T_2} frac{c_v}{T} mathrm{d}T + intop_{v_1}^{v_2} frac{R}{v} mathrm{d}v.$$
или
$$mathrm{d}s=frac{mathrm{d}h}{T}+frac{mathrm{d}l’}{T}=frac{mathrm{d}h}{T}+frac{-vmathrm{d}p}{T}=frac{mathrm{d}h}{T}-frac{Rmathrm{d}p}{p}.$$
$$∆s=intop_{T_1}^{T_2} frac{c_p}{T} mathrm{d}T-intop_{p_1}^{p_2} frac{R}{p} mathrm{d}p.$$
Поскольку в технической термодинамике приходится иметь дело не с абсолютными значениями энтропии, а с ее изменением, отсчет значений энтропии можно вести от любого состояния. Для газов принято считать значение энтропии равным нулю при нормальных условиях, тогда значение энтропии отсчитанного от нормального состояния можно определить по формулам:
$$s=intop_{273.15 K}^T frac{c_v}{T}·mathrm{d}T+intop_{v_н}^v frac{R}{v} mathrm{d}v.$$
или
$$s=intop_{273.15 K}^T frac{c_p}{T}·mathrm{d}T-intop_{p_н}^p frac{R}{p} mathrm{d}p.$$
Максимальная полезная работа, которую может произвести система – это часть максимальной работы за вычетом работы, затрачиваемой на сжатие окружающей среды:
$$l_{max}=l-l_0.$$
Предположим далее, что температура $T_0$ и давление $p_0$ окружающей среды неизменны или, во всяком случае, не зависят от того, сообщается ли теплота среде или забирается у нее. Поскольку в общем случае $p≠p_0$ и $T≠T_0$, то рассматриваемая изолированная система неравновесна и, следовательно, способна произвести работу.
Учитывая первый закон термодинамики, можно написать выражение для максимальной полезной работы изолированной системы:
$$l_{max}=(u-u_0 )+p_0·(v-v_0 )-T_0·(s-s_0 ).$$
Как видно из этого соотношения, максимальная полезная работа системы однозначно определяется начальными параметрами источника работы и параметрами окружающей среды.
Эксергия. Максимальную полезную работу (работоспособность) в современной термодинамике принято называть эксергией. В данном случае величина $l_{max}$ – это эксергия источника работы.
Кроме понятия «работа изменения объема», в термодинамических расчетах широко используют понятие «работа изменения давления».
Работой изменения давления называется работа перемещения жидкостей, газов и паров из области высокого давления () в область низкого давления (
). Ее значение определяют либо по формулам:
, (6.7)
, (6.8)
либо графически, пользуясь -диаграммой.
Здесь W – работа изменения давления; V – средний объем; w – удельная работа изменения давления; v – средний удельный объем.
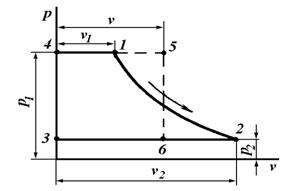
Графически удельная работа изменения давления определяется площадью 1234 на -диаграмме (рис. 6.3), ограниченной осью ординат и двумя абсциссами , проведенными из крайних точек линии процесса.
В результате замены этой площади (пл.) равновеликой ей площадью прямоугольника 3456 высотой, равной разности , и основанием, равным среднему удельному объему газа (v) в процессе, устанавливаем, что
пл. 1234 = пл. 3456 = .
Работа изменения давления положительная, если >
, и отрицательная, если
<
.
Найдем связь между удельными работами изменения объема (l) и изменения давления (w).
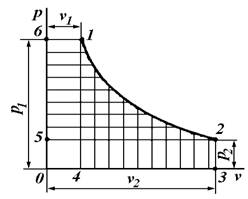
Пусть на -диаграмме линия 1 – 2 изображает процесс произвольного состояния рабочего тела (рис. 6.4). В этом случае пл. 1234 (заштрихованная вертикальными линиями) графически изображает удельную работу изменения объема (l) ,а пл. 1256 (заштрихованная горизонтальными линиями) – удельную работу изменения давления (w).
Рис. 6.3. PV-диаграмма
Рис. 6.4. PV-диаграмма
Из рисунка 6.4 видно что
пл. 1234 + пл. 6140 – пл. 5032 = пл. 6125
или
,
откуда
. (6.9)
После подстановки удельной работы изменения объема, определенной по формуле (6.9), в уравнение первого начала термодинамики (6.2) имеем:
.
Сгруппируем слагаемые последнего выражения следующим образом:
. (6.10)
Введем обозначение:
.
Величина h называется удельной энтальпией, и поскольку ее определяют три параметра состояния, то и сама она является параметром состояния.
Подставив значения h в формулу (6.9) ,получим еще один вид уравнения первого начала термодинамики:
. (6.11)
Значения удельной энтальпии определяют по справочникам.
Физический смысл величины h можно выяснить путем исследования уравнения (6.11), записанного в дифференциальной форме:
.
При p = const имеем:
,
т.е. dh есть элементарное количество теплоты, подведенное к термодинамическому телу в процессе при постоянном давлении.
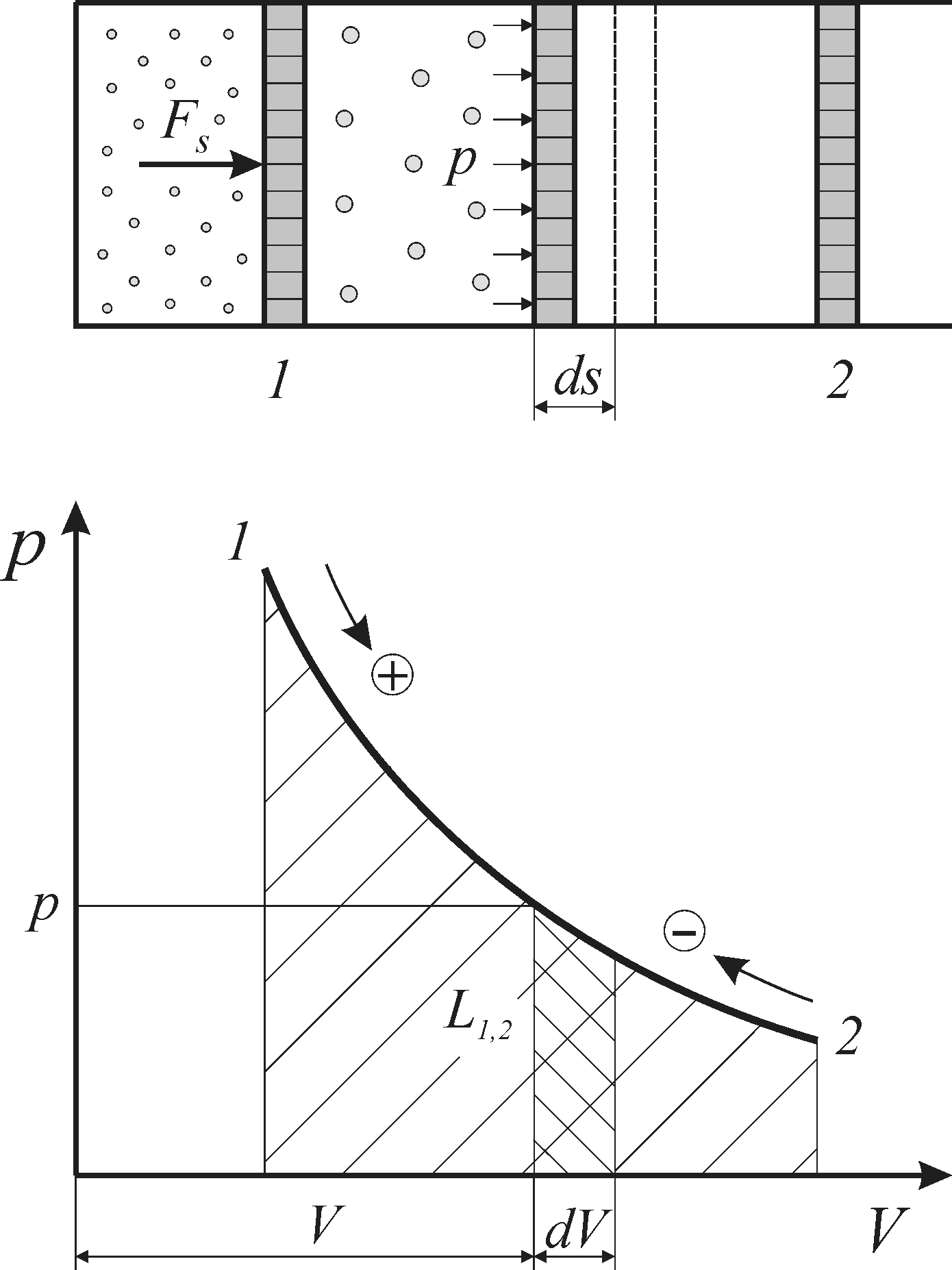
Рис. 1.1.Термодинамическая
работа обратимого изменения объема
Удельная
элементарная термодинамическая работа
обратимого изменения объема
(Дж/кг)
определяется:
.
(1.1)
Поскольку
термодинамическая работа зависит от
пути (вида) процесса, для вычисления
интегральных значений полной (),
или
удельной ()
работы должны быть заданы уравнения
процессов изменения состояния тела в
форме,
либо его графическое изображение в
диаграммах состоянияр–V(v).
Как
следует из соотношений (1.1), работа
определяется площадью под кривой
процесса независимо от вида рабочего
тела и его свойств (рис. 1.1). В силу этого
координаты р–V
и р–v
называются
универсальными
координатами работы.
В
частном случае для изобарного процесса
(p
= idem)
интегральные значения полной и
удельной термодинамической работы
определяются по следующим соотношениям:
L1,2
=
=
;l1,2
=
=
.
Работа
расширения считается положительной
(,
),
а работа сжатия – отрицательной ().
Эффективная
работа реального процесса
равна разности обратимой работы изменения
объемаи работы необратимых потерь
:
.
Необратимые
потери термодинамической работы ()
превращается в теплоту внутреннего
теплообмена (),
как и у потенциальной.
Потенциальная
(техническая) работа
Потенциальная
работа — работа по перемещению сплошных
масс (газа, пара или жидкости) из области
одного давления (p1)
в область другого давления (p2),
т.е. потенциальная работа — это работа
обратимого изменения давления.
Элементарная
потенциальная работа простого тела
определяется из соотношения
.
(1.5)
Удельная
потенциальная работа в элементарном
процессе
определяется по формуле
.
(1.6)
Для
определения интегральных значений
полной ()
или удельной ()
работы надо знать уравнение процесса
изменения состояния рабочего телаили его графическое изображение в
диаграммах состоянияр–V
или р–v.
Как
следует из соотношений, работа определяется
в кооординатах р–V
площадью независимо от вида рабочего
тела и его свойств.
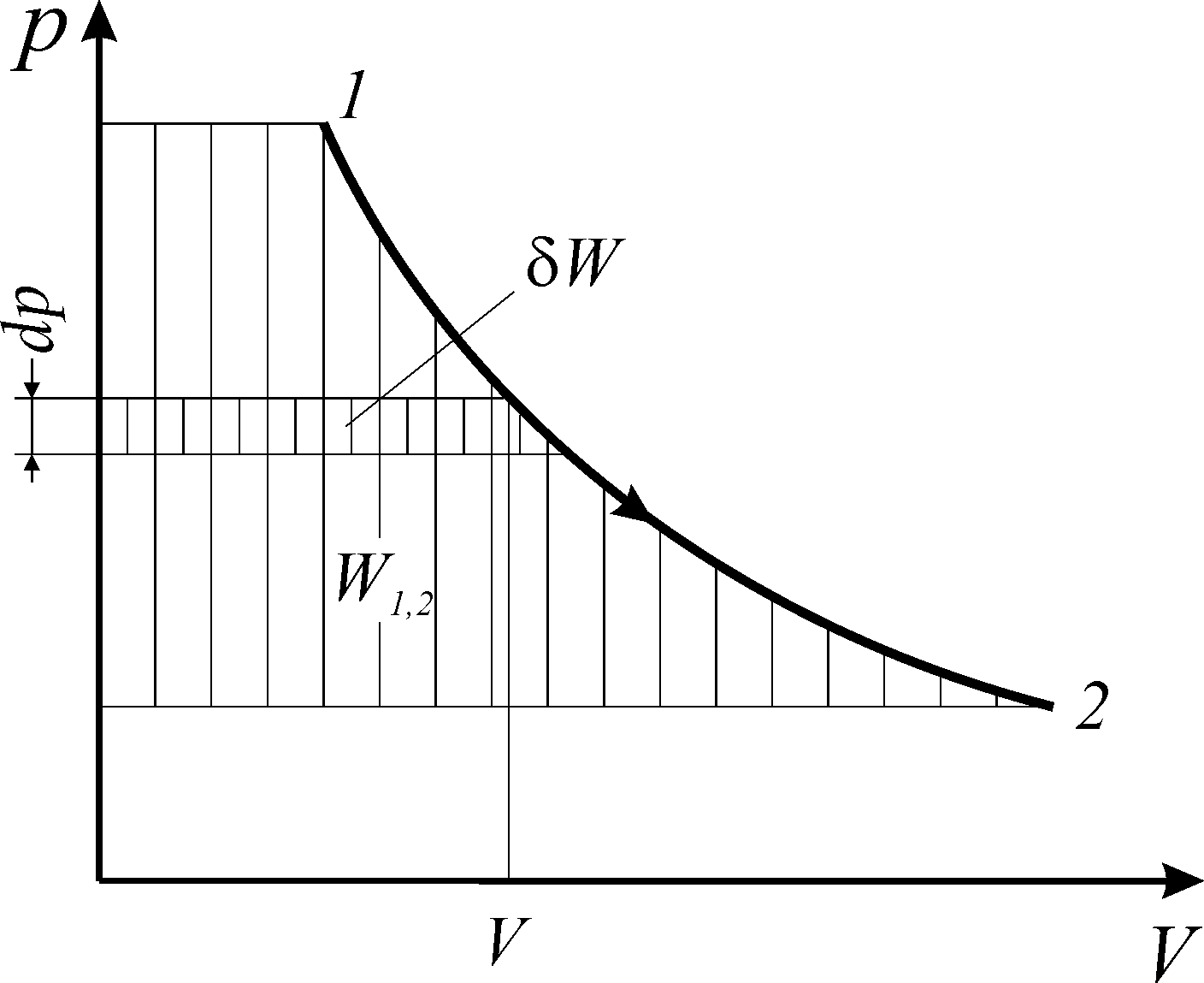
Рис. 1.2. Потенциальная
работа обратимого изменения давления
В
частном случае для изохорного процесса
(v
= idem)
интегральные значения полной и
удельной потенциальной работы
определяются по следующим соотношениям:
;
.
(1.7)
Потенциальная
работа (+) при снижении давления ()
и (-) –
().
Потенциальная
работа в обратимом процессе ()
есть сумма эффективной работыи необратимых потерь работы
:
=
+
.
Эффективная
т/д работа ()
простого тела в замкнутом пространстве
и эффективная потенциальная работа ()
потока передаются внешней системе (или
)
и используются для изменения энергии
внешнего положения тела (dEcz):
=
+ dEcz;
=
+
dEcz
.
В
условиях механических процессов
(dEcz=GcЕdcЕ+Ggdz)
уравнение
распределения термодинамической
и потенциальной работ формулируется :
;
,
где
cE
– скорость
движения тела, dz
– изменение
высоты центра тяжести тела в поле
тяготения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
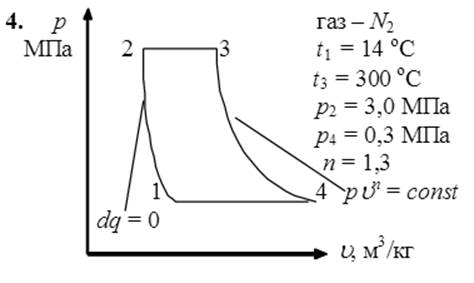
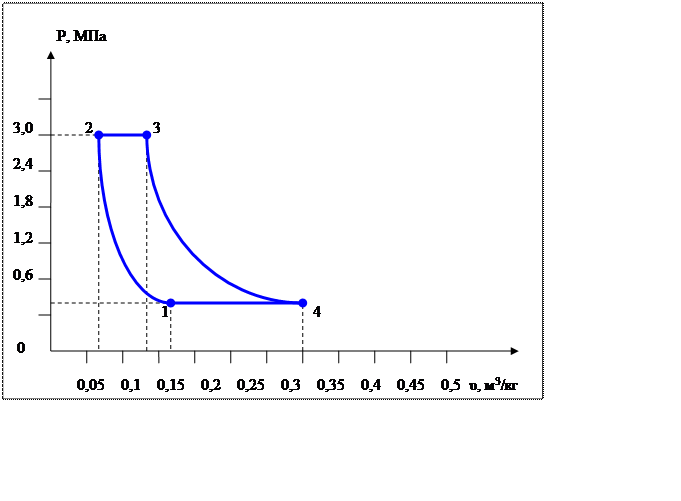
Рассмотрим обратимый цикл, который совершает воздух. Процессы цикла:
1-2 – адиабатное сжатие;
2-3 – изобарный нагрев;
3-4 – политропное расширение;
4-1 – изобарное сжатие;
РАСЧЕТ ГАЗОВОГО ЦИКЛА
|
Точки процессов |
Р, МПа |
υ, м3/кг |
Т, К |
u, кДж/кг |
i, кДж/кг |
|
1 |
0,3 |
0,284 |
287 |
207,788 |
293,027 |
|
2 |
3,0 |
0,055 |
561 |
406,164 |
572,781 |
|
3 |
3,0 |
0,056 |
573 |
414,852 |
585,033 |
|
4 |
0,3 |
0,329 |
337 |
243,988 |
344,077 |
В рυ координатах дан цикл, состоящий из нескольких термодинамических процессов, где отмечены исходные параметры отдельных точек (pi , υi, Ti ) и процессов (n, ∆s, q). На их основе необходимо вычислить неизвестные параметры состояния по характеристическому уравнению состояния для 1 кг заданного газа:
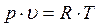
где p – абсолютное давление, Па; υ – удельный объем, м3/кг; R – газовая постоянная, Дж/(кг∙К); T – абсолютная температура, К.
Газовая постоянная определяется по формуле:
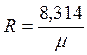
где μ – молекулярная масса газа, кг/моль.
Для политропических процессов показатель политропы n можно вычислить по формуле (например, для процесса 1-2):
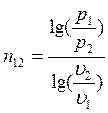
Удельные значения внутренней энергии и энтальпии определяются по выражениям:
, (1.4)
где 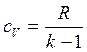
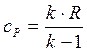
В точке 1: по условию t1 = 14°С = 287К; по условию процесс 4-1 – изобарный, поэтому р4 = р1 = 0,3МПа. Газовая постоянная для воздуха равна (согласно (1.2)): 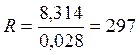
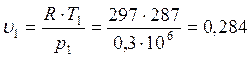
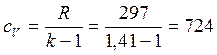
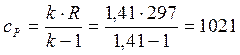
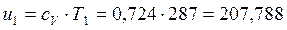
В точке 2: по условию р2 = 3,0МПа; процесс 1-2 – адиабатный, поэтому из уравнения Пуассона получаем:
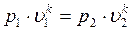
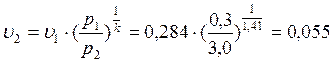
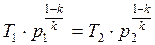
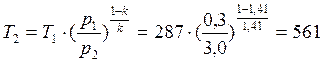
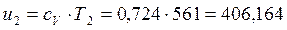
В точке 3: по условию р3 = р2 = 3,0МПа, Т3 = 573К; процесс 2-3 изобарный, поэтому из уравнения процесса: 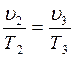
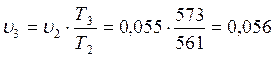
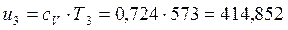
В точке 4: процесс 4-1 – изобарный, поэтому: МПа; процесс 3-4 политропный, поэтому:
→
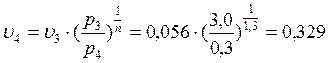
→
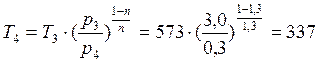
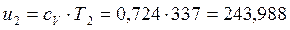
Изменения удельной внутренней энергии и удельной энтальпии для каждого процесса, входящего в цикл, определяются по формулам (например, для процесса 1-2):
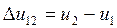
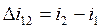
где значения u и i берутся из таблицы 1.1.
Для всех процессов изменение удельной энтропии ∆s , удельную работу изменения объема газа l , удельное количество теплоты q , показатель политропы n , теплоемкость политропного процесса c определяют по известным формулам, данным в литературных источниках.
Доля тепла расходуемого в рассматриваемом процессе на изменение внутренней энергии газа и работу изменения объема определяется по формулам:
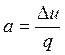
|
Процессы |
n |
C, кДж/(кг∙К) |
∆u, кДж/кг |
∆i, кДж/кг |
∆s, кДж/(кг∙К) |
q, кДж/кг |
l, кДж/кг |
a |
b |
|
1-2 |
1,41 |
0 |
198,376 |
279,754 |
0 |
0 |
-198,376 |
∞ |
— ∞ |
|
2-3 |
0 |
1,021 |
8,688 |
12,252 |
0,022 |
11,688 |
3 |
0,743 |
0,257 |
|
3-4 |
1,3 |
-0,265 |
-170,864 |
-240,956 |
0,142 |
54,909 |
225,773 |
— 3,112 |
-4,112 |
|
4-1 |
0 |
1,021 |
-36,2 |
-51,05 |
-0,164 |
-49,7 |
-13,5 |
0,728 |
0,272 |
Теплоемкость политропного процесса: 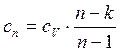
Согласно (1.5):
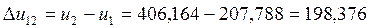
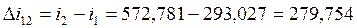
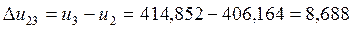
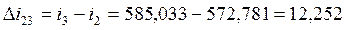
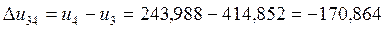
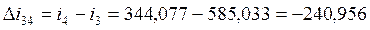
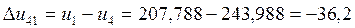
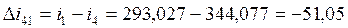
Согласно (1.3):
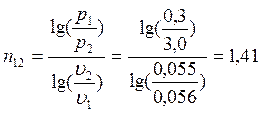
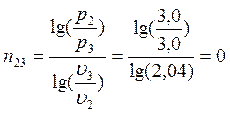
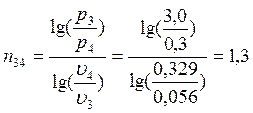
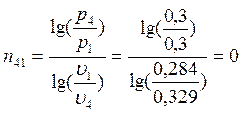
Изменение энтропии процессов:
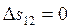
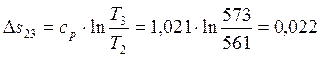
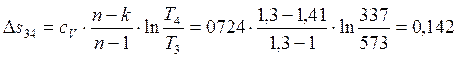
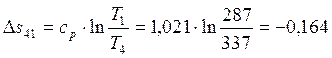
Работа в процессах:
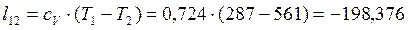
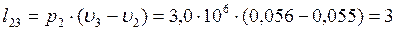
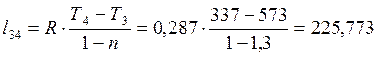
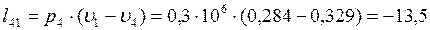
Согласно первому закону термодинамики теплота процессов равна: 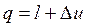
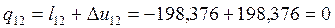
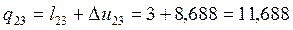
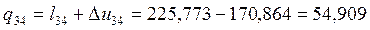
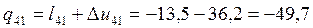
Согласно (1.6):
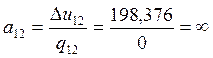
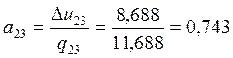
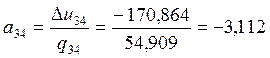
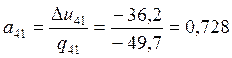
Проверяем правильность вычислений:
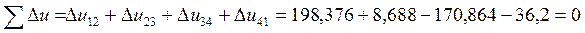
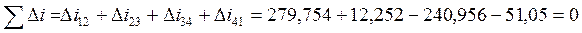
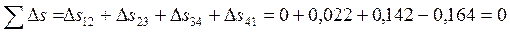
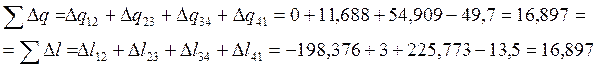
КПД цикла равен: 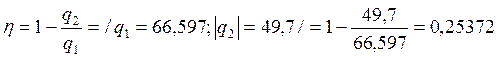
Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку.
Содержание:
Работа в термодинамике:
В 9 классе вы узнали, что работа силы (механическая работа) связана с превращением одного вида энергии в другой, например, механической энергии во внутреннюю. Работу силы рассматривают как меру изменения энергии физической системы. А как определить работу в термодинамике? Как может быть выражена эта работа через макроскопические параметры — давление и об1
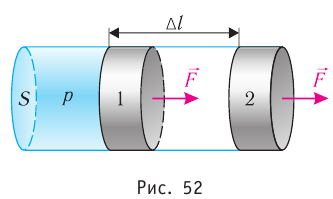
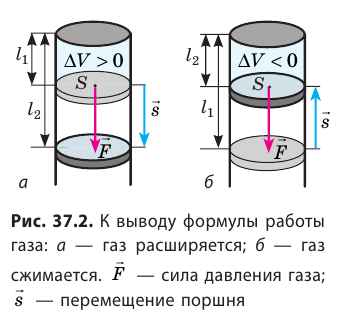
Рассмотрим газ, находящийся в цилиндрическом сосуде с площадью основания S, закрытом подвижным поршнем (рис. 52).
Взаимодействие газа с поршнем, а также со стенками сосуда можно характеризовать давлением р, которое газ оказывает на них. Допустим, что в результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние
Модуль силы давления газа, действующей на поршень, F = pS. Эта сила совершает работу по перемещению поршня
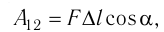
где а — угол между направлениями силы и перемещения. В рассматриваемом примере а = 0, тогда
Произведение 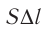
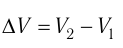
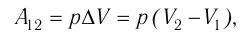
где 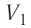
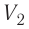
Так как давление р газа всегда величина положительная, из формулы (10.2) следует, что, если газ расширяется 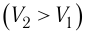
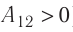
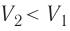
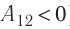
Процесс медленного изобарного сжатия газа из состояния 2 с начальным объёмом 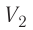
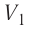
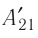
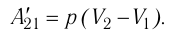
Из сравнения равенств (10.2) и (10.3) вытекает соотношение между работой 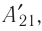
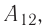
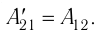
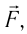
направление, противоположное силе давления 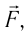
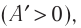
Если газ расширяется 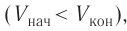
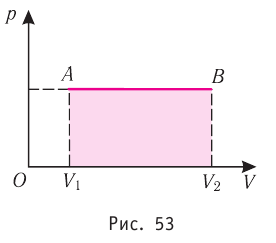
Геометрическое толкование работы
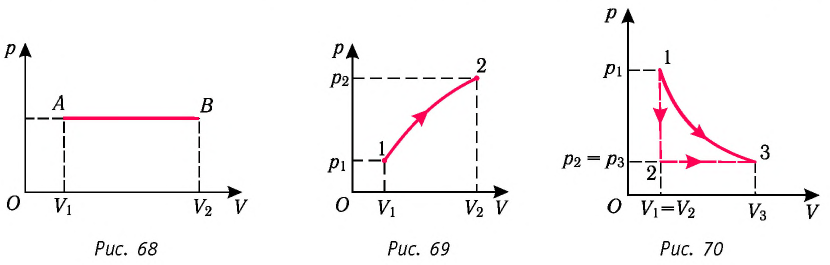
Построим график зависимости давления газа от его объёма при р = const. Как видно из рисунка 53, при изобарном расширении газа работа, совершённая силой давления газа, численно равна площади прямоугольника
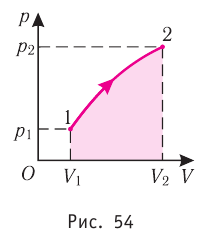
Если процесс перехода газа из начального состояния в конечное не является изобарным, то работа, совершённая силой давления газа при изменении его объёма от 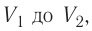
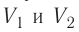
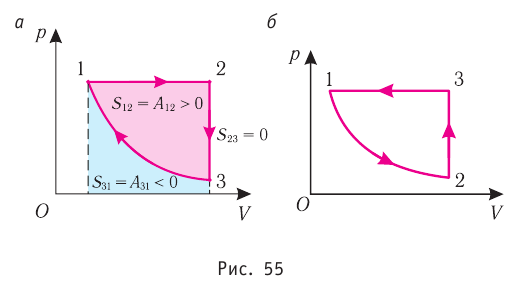
Процесс, при котором термодинамическая система, прошедшая некоторую последовательность состояний, снова возвращается в исходное состояние, называют циклическим процессом или циклом (рис. 55). Работа, совершаемая системой при циклическом процессе, или работа цикла, равна площади фигуры, ограниченной линиями, которые изображают цикл:
где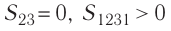
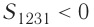
Если «кривая расширения» (изобара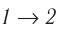
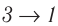
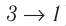
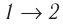
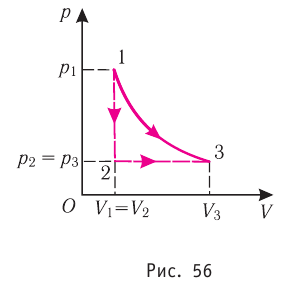
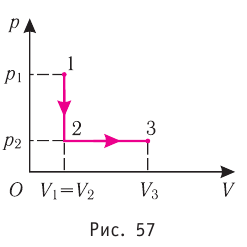
Из рисунка 56 видно, что численное значение работы цикла определяется не только начальным и конечным состояниями системы, но и видом процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения, либо сначала изохорно понизив его давление до значения 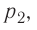
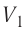
Как видно из рисунка 56, в первом случае работа, совершённая силами давления газа, больше, чем во втором. Следовательно, работа, совершаемая при переходе термодинамической системы из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.
Количество теплоты и удельная теплоёмкость
Итак, существуют два способа передачи энергии от одного тела к другому. Первый характеризуется передачей энергии в процессе механического взаимодействия тел — механическая энергия одного тела переходит в энергию хаотического движения частиц вещества другого тела или, наоборот, убыль энергии хаотического движения частиц вещества одного тела сказывается на увеличении механической энергии другого тела. Такую форму передачи энергии в термодинамике (как и в механике) называют работой. Так, например, в рассмотренной нами ранее термодинамической системе (газ в цилиндрическом сосуде под поршнем) расширение газа приводит к перемещению поршня. При этом убыль внутренней энергии газа равна работе, совершённой силой давления газа, под действием которой поршень переместился.
Второй способ передачи энергии осуществляется при непосредственном обмене энергией между хаотически движущимися частицами взаимодействующих тел. За счёт переданной при этом энергии увеличивается внутренняя энергия одного тела и уменьшается внутренняя энергия другого. Если, например, привести в соприкосновение два тела с разными температурами, то частицы более нагретого тела будут передавать часть своей энергии частицам более холодного тела. В результате внутренняя энергия первого тела уменьшается, а второго тела увеличивается. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей. Как вы уже знаете, существуют три вида теплопередачи: теплопроводность, конвекция и излучение.
Количественной мерой энергии, переданной телу в процессе теплопередачи, является количество теплоты Q. В СИ единицей количества теплоты является джоуль (Дж). Иногда для измерения количества теплоты используют внесистемную единицу — калорию (1 кал = 4,19Дж).
Если процесс теплопередачи не сопровождается изменением агрегатного состояния вещества, то
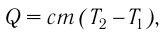
где m — масса тела, 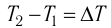
теплоемкость измеряют в джоулях, деленных на килограмм, кельвин
Физическая величина, равная произведению массы тела на удельную теплоёмкость вещества, носит название теплоёмкости тела. Обозначают теплоёмкость тела С и измеряют в джоулях на кельвин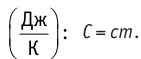
Удельная теплота плавления
Физическую величину, численно равную количеству теплоты, необходимому для превращения кристаллического вещества массой 1 кг, взятого при температуре плавления, в жидкость той же температуры, называют удельной теплотой плавления 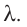
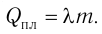
Удельная теплота парообразования
Физическую величину, численно равную количеству теплоты, которое необходимо передать жидкости массой 1 кг, находящейся при температуре кипения, для превращения её при постоянной температуре в пар, называют удельной теплотой парообразования L. Количество теплоты, необходимое для превращения жидкости массой m, предварительно нагретой до температуры кипения, в пар, определяют по формуле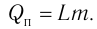
Удельная теплота сгорания топлива
Физическую величину, численно равную количеству теплоты, выделяющемуся при полном сгорании топлива массой 1 кг, называют удельной теплотой сгорания топлива q. Количество теплоты, выделившееся при полном сгорании некоторой массы m топлива, определяют по формуле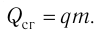
Отметим, что в результате теплопередачи могут изменяться как обе составляющие внутренней энергии тела, так и одна из них. При нагревании (охлаждении) изменяются кинетическая энергия хаотического движения частиц, которые составляют тело, и потенциальная энергия их взаимодействия. При плавлении (кристаллизации), кипении (конденсации) изменяется только потенциальная энергия взаимодействия частиц вещества.
При совершении работы также может изменяться как кинетическая, так и потенциальная энергия частиц вещества. Следовательно, как при теплопередаче, так и при совершении работы происходит изменение кинетической и потенциальной энергий частиц вещества, что приводит к изменению внутренней энергии тела.
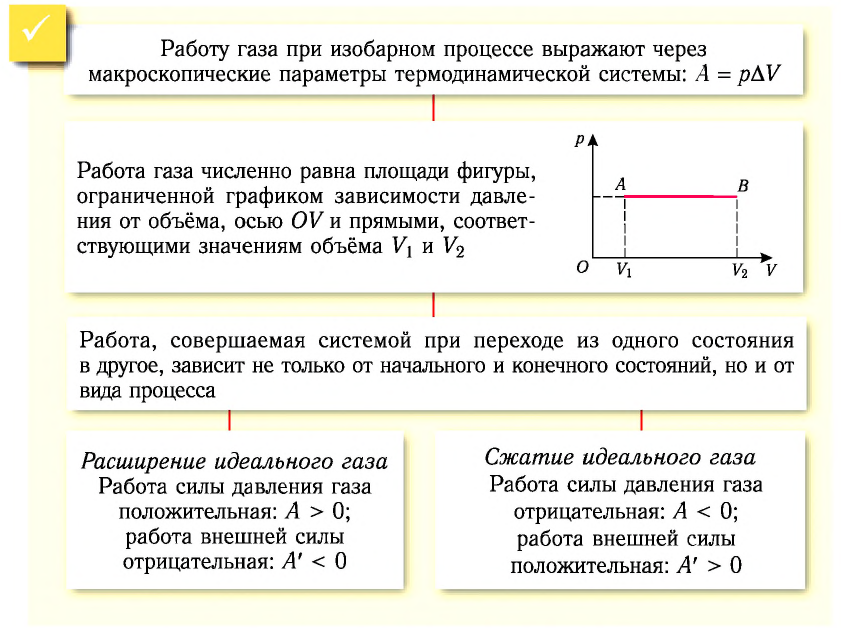
1. Работу газа при изобарном процессе выражают через макроскопические параметры термодинамической системы:
2. Работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёмов
3. Работа, совершаемая при переходе системы из одного состояния в другое, зависит не только от начального и конечного состояний, но и от вида процесса.
4. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей.
Пример №1
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от 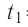
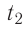
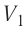
Дано:
Пример №2
Состояние идеального газа, взятого в количестве v=l,0 моль при температуре 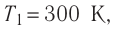
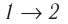
Дано:
v = 1,0 моль
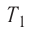
А — ?
Решение. Работа Л газа в ходе всего процесса равна сумме работ на участках 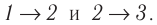
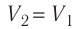
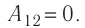
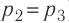
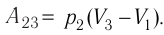
Так как по условию 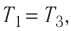
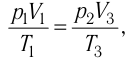
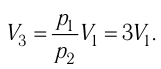
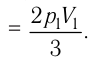
Тогда
Ответ: А = 1,7 кДж.
Работа в термодинамике
В 9-м классе вы узнали, что передача энергии путём совершения работы происходит в процессе силового взаимодействия тел. То есть работа, совершённая над рассматриваемым телом, есть не что иное, как работа сил, приложенных к этому телу со стороны всех остальных (внешних) тел, с которыми оно взаимодействует. Работа, совершённая над телом, может непосредственно изменить любой вид энергии этого тела, например внутреннюю энергию, поэтому работу силы рассматривают как меру изменения энергии физической системы.
Одним из способов изменения внутренней энергии термодинамической системы является совершение работы. Этот способ характеризуется передачей энергии в процессе механического взаимодействия тел. При этом механическая энергия одного тела переходит во внутреннюю энергию другого тела или, наоборот, убыль внутренней энергии одного тела сказывается на увеличении механической энергии другого тела.
Таким образом, при совершении работы происходит превращение энергии из одной формы в другую.
Поскольку для описания термодинамических систем используют макропараметры (давление, объём, температура), то работу в термодинамике необходимо выражать, применяя эти параметры.
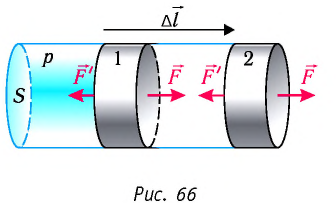
Рассмотрим газ в цилиндре, закрытом поршнем, площадь которого S (рис. 66). Давление газа в цилиндре 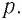
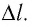
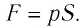
где 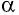
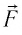
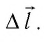
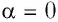
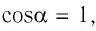
Произведение 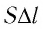
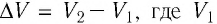
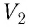
Таким образом, работа силы давления газа при его изобарном расширении:
Так как давление р газа — величина положительная, то из формулы (12.1) следует, что
При изобарном расширении газа из состояния 1 в состояние 2 работа силы 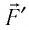
где 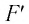
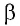
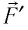
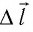
Перемещение 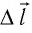
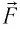
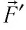
Следовательно, работы 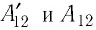
Таким образом, можно сделать следующие выводы.
Геометрическое толкование работы:
Работу газа можно определить графически. Изобразим график зависимости давления газа от его объёма при 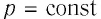
Если процесс перехода газа из начального состояния в конечное не является изобарным (рис. 69), то работа силы давления газа при изменении объёма от 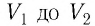
Работу газа определяют не только начальное и конечное состояния системы, но и вид процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения (рис. 70), либо сначала изохорно понизив его давление до значения 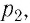
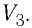
Следовательно, работа, совершаемая термодинамическом системой при переходе из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.
Пример №3
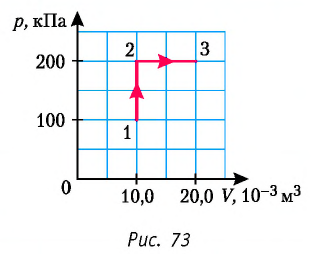
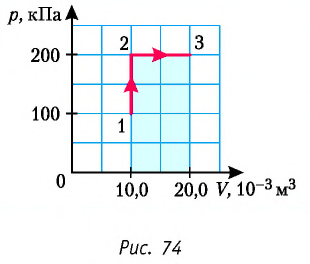
Определите работу, совершаемую силой давления идеального газа определённой 200 массы при переходе из состояния 1 в состояние 3 (рис. 73).
Решение. 1 способ. Работа А газа в ходе всего процесса равна сумме работ на участках 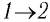
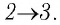
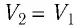
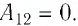
Тогда при переходе из состояния 1 в состояние 3 работа
2 способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёма 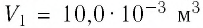
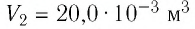
Ответ:
Пример №4
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от 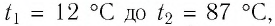
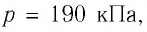
Решение. Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому
Согласно уравнению Клапейрона—Менделеева,
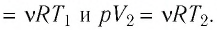
Ответ:
Как определить работу в термодинамике
В конце XVIII в. английский физик Бенджамин Томпсон (граф Румфорд) исследовал тепло, выделяющееся при сверлении бронзовых пушек. Румфорд успевал вскипятить поставленные на пушки котлы с водой за счет тепла, которое выделялось, пока лошади приводили в движение очень тупое сверло. В данном случае энергия механического движения сверла превращалась в энергию хаотического движения молекул бронзы и воды. А можно ли сделать наоборот?
Почему при изменении объема газа изменяется его внутренняя энергия
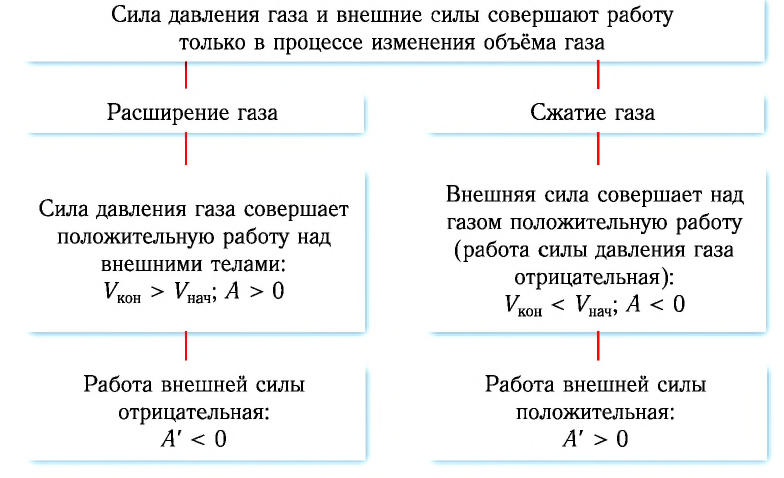
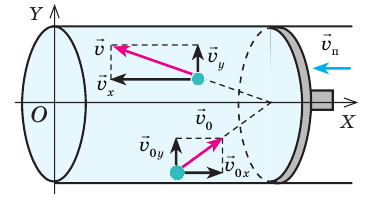
Внутренняя энергия газа может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ сжимают (газ совершает отрицательную работу) (рис. 37.1) и он при этом не отдает энергию окружающей среде, то скорость движения молекул газа, а соответственно, и внутренняя энергия, и температура газа увеличиваются. И наоборот: если газ расширяется (то есть совершает положительную работу), то скорость движения молекул, температура и внутренняя энергия газа уменьшаются.
Рис. 37.1. При сжатии газа скорость его молекул после столкновения с поршнем увеличивается (v > 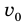
Как вычислить работу газа
Вычислим работу, которую совершает сила давления газа при изменении его объема от 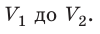
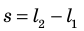
Таким образом, работа газа при его изобарном расширении равна:
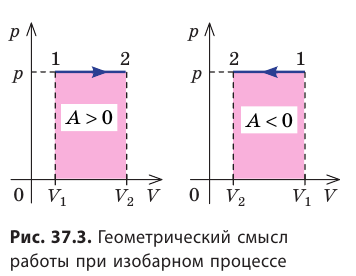
Работе газа при изобарном расширении (или сжатии) можно дать простое геометрическое толкование: работа газа численно равна площади прямоугольника под графиком зависимости p(V) (рис. 37.3).
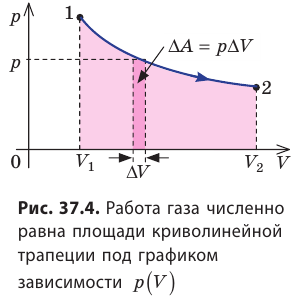
Пусть некоторый газ переходит из состояния 1 в состояние 2 (рис. 37.4). Если изменение объема газа (∆V) достаточно мало, то давление газа можно считать неизменным. Тогда работа газа численно равна площади выделенной на рисунке полосы. Полная работа при изменении объема от 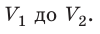
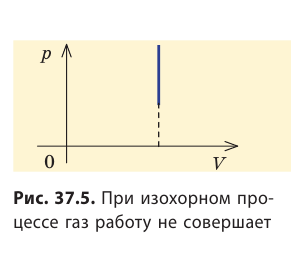
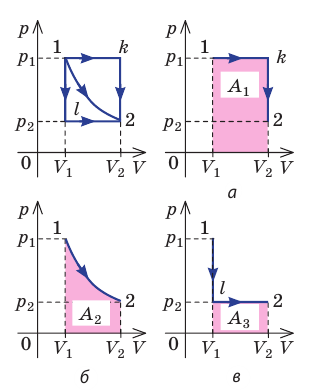
Очевидно, что при изохорном процессе (V = const) площадь фигуры под графиком зависимости p (V) равна нулю (рис. 37.5), — газ работу не совершает (A = 0) . Работа газа зависит от того, каким образом происходил переход газа из начального состояния в конечное (рис. 37.6).
Рис. 37.6. три пути перехода газа из состояния 1 в состояние 2: а — газ изобарно расширяется (участок 1k), затем изохорно охла ждается (участок k2); б — газ изотермически расширяется; в — газ изохорно охлаждается (участок 1l), затем изобарно расширяется (участок l2). сравнив площади фигур под графиками, видим, что:
Пример №5
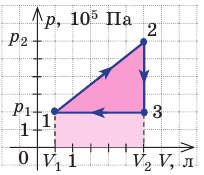
На рисунке графически изображен циклический процесс, совершаемый идеальным газом. Определите работу газа за цикл.
Решение:
Полная работа за цикл равна сумме работ, совершенных газом в ходе каждого процесса цикла. Работа газа в ходе процесса 1–2 численно равна площади трапеции, основания которой равны 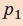
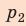
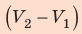
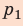
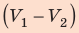
Выводы:
- При отсутствии теплообмена с окружающей средой, если над газом совершают работу, внутренняя энергия газа увеличивается; если газ сам совершает работу, его внутренняя энергия уменьшается.
- Если объем газа увеличивается, то газ совершает положительную работу. Если объем газа уменьшается, то работа газа отрицательна.
- Работа газа численно равна площади фигуры под графиком зависимости p (V). При изобарном процессе работу газа можно определить по формуле A=p∆V, при изохорном процессе работа газа равна нулю: A = 0.
- Первый закон термодинамики
- Второй закон термодинамики
- Тепловые двигатели и их КПД
- Тепловое состояние тел
- Термодинамика — основные понятия, формулы и определения
- Необратимость тепловых процессов
- Адиабатический процесс
- Молекулярно-кинетическая теория