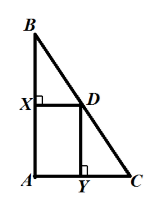Как найти удаленную точку в треугольнике

Четыре замечательные точки треугольника

Замечательные точки треугольника — это точки, расположение которых однозначно определяется треугольником и не зависит от того, в каком порядке рассматривать его стороны и углы.

Всего замечательных точек четыре. Две из них открыл Евклид, вписывая в треугольник окружности, третья, точка пересечения медиан, обнаружена Архимедом. Четвертая, в которой пересекаются высоты треугольника, не упоминалась в трудах Евклида, но описывалась в трудах его современников. Возможно, Евклид и Архимед просто упорядочили и записали доказательства теорем, известных задолго до них.

Особенность замечательных точек в том, что они в любом треугольнике являются пересечением трех линий, при этом их свойства не меняются:

• биссектрисы пересекаются в центре вписанного круга;
• перпендикуляры от середин сторон пересекаются в центре описанного круга;
• высоты пересекаются в ортоцентре, точки, симметричные ортоцентру относительно сторон треугольника, находятся на описанном круге;
• медианы пересекаются в барицентре (он же центроид, или геометрический центр).

В XVIII веке математик Леонард Эйлер, исследуя геометрию треугольников, доказал, что три из этих точек — ортоцентр, барицентр и центр описанного круга — всегда расположены на одной линии. Она называется прямой Эйлера. Точки стали называть «замечательными» или «особенными».

Четыре замечательные точки треугольника

Точка пересечения медиан треугольника

В ней находится центр тяжести однородной треугольной пластины, также она является средним арифметическим положений всех точек треугольника.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Медианы треугольника пересекаются в его геометрическом центре и делятся в этой точке в отношении 2:1, считая от вершин.

Доказательство

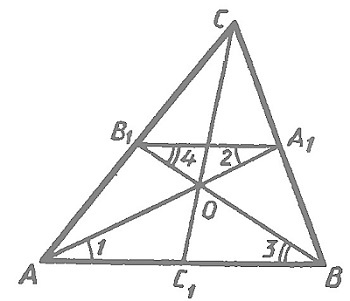
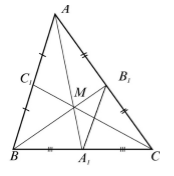
Обозначим точку пересечения медиан О и проведем среднюю линию треугольника (А^1В^1) .

Отрезок (А_1В_1) параллелен (АВ) , поэтому углы 1, 2, 3 и 4 равны друг другу. Таким образом, треугольники (АОВ) и (А_1ОВ_1) подобны по двум углам, и их стороны пропорциональны. (АВ = 2А_1В_1) , значит, (АО = 2А_1О) и (ВО = 2В_1О) , а точка О разделяет медианы на отрезки с отношением 2:1, считая от вершин. Аналогично она делит медиану (СС_1) .

Точка пересечения биссектрис треугольника

Точка пересечения трех биссектрис расположена на равном расстоянии от всех сторон треугольника и находится в центре вписанного в треугольник круга.

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

Биссектрисы треугольника пересекаются в одной точке.

Доказательство

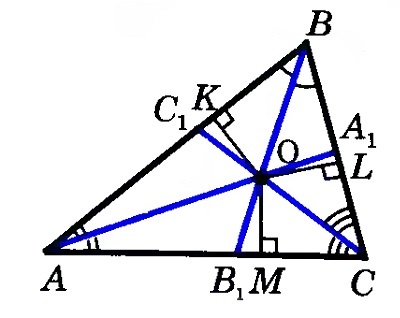
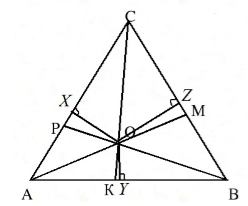
Проведем из точки пересечения биссектрис (АА_1) и (ВВ_1) отрезки (ОК) , (ОL) и (ОМ) , перпендикулярные трем сторонам треугольника.

Согласно теореме о равной удаленности точек биссектрисы от сторон угла, ОК = ОМ и ОК = ОL. Соответственно, ОМ = ОL, точка О находится на равном расстоянии от сторон угла АСВ и расположена на биссектрисе. Таким образом, все три биссектрисы пересекутся в одной точке.

Точка пересечения серединных перпендикуляров треугольника

Линии, проходящие через середины сторон треугольника перпендикулярно к ним, пересекаются в центре круга, описанного вокруг треугольника. В остроугольном треугольнике точка пересечения перпендикуляров расположена внутри него, в тупоугольном — снаружи. Если треугольник прямоугольный, точка находится на гипотенузе.

Каждая точка серединного перпендикуляра равноудалена от концов отрезка, к которому он перпендикулярен.

Серединные перпендикуляры от сторон треугольника пересекаются в одной точке.

Доказательство

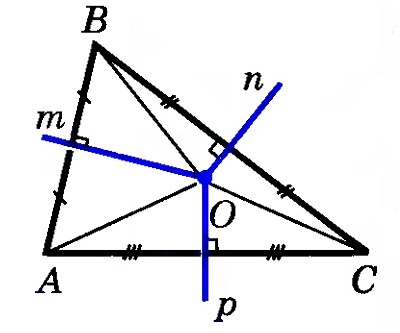
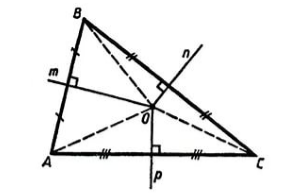
Изобразим внутри треугольника АВС перпендикуляры m и n, отметим точку их пересечения О.

Согласно теореме о равной удаленности серединных перпендикуляров от концов отрезка, ОВ = ОА и ОВ = ОС. Соответственно, ОА = ОС, и точка О находится на одинаковом расстоянии от точек А и С. Таким образом, серединный перпендикуляр р к отрезку АС тоже будет проходить через точку О, и все три перпендикуляра пересекутся в одной точке.

Точка пересечения высот треугольника

Высоты или их продолжения могут пересекаться как внутри треугольника, если он остроугольный, так и вне его, если он тупоугольный. Если треугольник прямоугольный, тогда ортоцентр совпадает с вершиной прямого угла.

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство

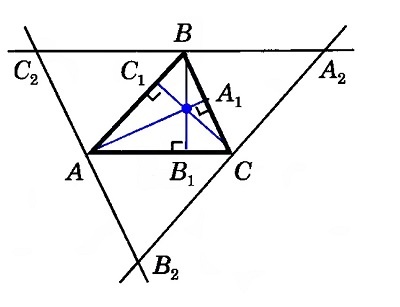
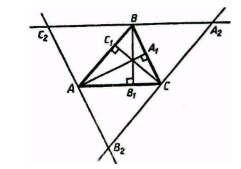
Изобразим произвольный треугольник (АВС) и прямые (AA_1) , (BB_1) и (СС_1) , содержащие его высоты. Проведем через каждую вершину прямые, параллельные противоположным сторонам треугольника, получив треугольник ( A_2B_2C_2) . Точки А, В и С окажутся серединами его сторон. ( АВ = A_2C = В_2C) , так как эти отрезки являются противоположными сторонами параллелограммов (АВА_2С) и (АВСВ_2) . Соответственно, (С_2А = АВ_2) и (С_2В = ВА_2) .

Из построения следует, что отрезок (СС_1) перпендикулярен (А_2В_2) , (АА_1 perp В_2С_2) и (ВВ_1 perp А_2С_2) . Следовательно, прямые (АА_1) , (ВВ_1) и (СС_1) — серединные перпендикуляры сторон треугольника (А_2В_2С_2) , которые пересекутся в одной точке.

Примеры решения задач

Задача 1

Серединные перпендикуляры к сторонам АВ и АС треугольника АВС пересекаются в точке D, лежащей на стороне треугольника ВС. Докажите, что точка D — середина стороны ВС.

Решение

Изобразим треугольник АВС.

Все серединные перпендикуляры должны пересекаться в одной точке, если два из них уже пересеклись, третий тоже должен проходить через точку D. Таким образом, точка D является основанием третьего серединного перпендикуляра и расположена посередине стороны ВС.

Задача 2

Биссектрисы (AA_1) и (BB_1) треугольника АВС пересекаются в точке D. Найдите углы АСD и ВСD, если известно, что угол АDB составляет (136^circ) .

Решение

Поскольку биссектрисы пересекаются в точке D, луч СD является биссектрисой. Тогда

(angle АСD;=;angle BCD;=;136^circ;-;90^circ;=;46^circ)

Насколько полезной была для вас статья?

Рейтинг: 4.25 (Голосов: 12 )

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Комплексное число — это выражение вида x=a+bcdot i , где a и b — вещественные числа, а i — так называемая «мнимая единица». Если возвести ее в квадрат, получится отрицательное число. Таким образом, она определяется равенством i=sqrt или i^2=-1. Извлечение корня Определение Корнем со степенью n, извлеченным из комплексного числа z называют то число w, у которого n-ая степень равна z и обозначается как sqrt[n]z. Не существует однозначного извлечения корня из комплексного числа, так как он имеет то количество значений, которое равно его степени. Тригонометрическая форма Если число z представлено в тригонометрической форме z=left|zright|cdotleft(cosleft(фright)+isinleft(фright)right), то значения корня n-ой степени находятся по формуле: sqrt[n]z=sqrt[n]cdot(cosleft(fracnright)+isinleft(fracnright)). Где |z| — модуль комплексного числа, ф — аргумент, k — параметр, значения у которого 0,1,2…n-1. Если посмотреть на извлечение корня n-ой степени с точки зрения геометрии, центр окружности с радиусом sqrt[n]z расположен в точке О (0; 0), а все полученные значения, расположенные на ней, образуют правильный n-угольник (как это представлено на чертеже выше). Алгебраическая форма Если из данного числа z нужно извлечь корень n-ой степени, а он представлен в алгебраической или показательной форме, необходимо выполнить извлечение по пунктам: Представить число в тригонометрической форме: вычислить модуль left|zright| и аргумент (ф). Полученные значения применить в тригонометрической форме: z=left|zright|cdotleft(cosleft(фright)+isinleft(фright)right). Извлечь корни по формуле, приведенной выше. Алгоритм вычисления квадратного и кубического корня Задача на кубический корень Задача: Извлечь кубический корень sqrt[3]z, где z=frac12+frac12cdot i в алгебраической форме. Решение: Вспомним, что тригонометрическая форма записи комплексного числа выглядит так: z=left|zright|cdotleft(cosleft(фright)+isinleft(фright)right). По условию мы знаем, что a=frac12 и b=frac12. Можем вычислить исходное значение комплексного числа: r=sqrt=sqrt=sqrt=frac1. Теперь посчитаем аргумент исходного комплексного числа: ф=arg(z)=arctanleft(fracright)=arctanleft(1right)=fracpi4. Далее подставим значения в тригонометрическую форму записи и получим: z=frac2cdotleft(cosleft(fracpi4right)+isinleft(fracpi4right)right). Мы знаем, что корнем n-ой степени некоторого числа z=left|zright|cdotleft(cosleft(фright)+isinleft(фright)right) является комплексное число, определяемое следующим равенством: sqrt[n]z=sqrt[n]cdot(cosleft(fracnright)+isinleft(fracnright)). Воспользуемся этой формулой: Для k=0: w_1=sqrt[3]z=sqrt[3]>cdotleft(cosleft(fracpiright)+icdotsinleft(fracpiright)right). Для k=1 будет справедливо уравнение: w_2=sqrt[3]z=sqrt[3]>cdotleft(cosleft(frac3right)+icdotsinleft(frac3right)right)=sqrt[3]>cdotleft(cosleft(frac4right)+icdotsinleft(frac4right)right). Для k=2: w_3=sqrt[3]z=sqrt[3]>cdotleft(cosleft(frac3right)+icdotsinleft(frac3right)right)=sqrt[3]>cdotleft(cosleft(fracright)+icdotsinleft(fracright)right). Задача на квадратный корень Задача: Извлечь корень sqrt z для заданных комплексных чисел в показательной форме: z=3cdot e^. Решение: Определим значение модуля и аргумента в тригонометрической форме записи: z=left|zright|cdotleft(cosleft(фright)+isinleft(фright)right): r=3, ф=fracpi3. Подставляем ф в равенство: z=3cdotleft(cosleft(fracpi3right)+isinleft(fracpi3right)right). Воспользуемся формулой sqrt[n]z=sqrt[n]cdot(cosleft(fracnright)+isinleft(fracnright)). Для k=0 справделиво уравнение: w_1=sqrt z=sqrt3cdotleft(cosleft(fracpi6right)+isinleft(fracpi6right)right); Для k=1: w_2=sqrt z=sqrt3cdotleft(cosleft(frac2right)+isinleft(frac2right)right)=sqrt3cdotleft(cosleft(frac6right)+isinleft(frac6right)right).

Ход урока

1. Проверить решение задачи № 24 по записям (с пробелами), сделанными на доске до начала урока.

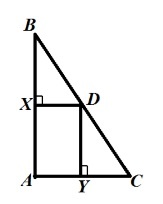
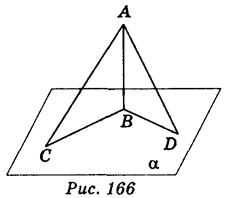
Решение задачи № 24 Пусть АВα (рис. 166).

1) ВС = 40 см, BD =. ; пусть AD = х см, тогда АС=. С ΔАВ D : АВ2 = х2 -122 = х2 — 144. Из ΔАВС АВ2. Тогда х2 — 144 = (х + 26)2 — 402; 52х=. ; х =15. Следовательно, AD=. AC = 41 см.

2) BD=. BC=7 см; пусть А D =. тогда AC = 2х см.

С ΔАВ D AB2=. Из Δ АВС АВ2 = 4х2 — 49.

Тогда х2 — 1 = . ; 3х2 = . ; х2 = 16. Отсюда х = . ; следовательно, AD =. AC = 2·4 = 8 (см).

Ответ. 1) 15 см и 41 см; 2) 4 см и 8 см.

2. Математический диктант.

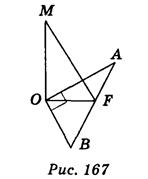
МО — перпендикуляр к плоскости ОАВ; AOB = 90° (рис. 167); МА и МВ — наклонные.

Вариант 1 — МО = 1 см, ОА = 3 см, MB = см;

вариант 2 — МЕ = 1 см, ОВ = 4 см, МА = см. Пользуясь рисунком, найдите:

1) длину неизвестной наклонной; (2 балла)

2) длину неизвестной проекции наклонной; (2 балла)

3) длину отрезка АВ; (2 балла)

4) расстояние от точки В до середины отрезка АВ; (2 балла)

5) расстояние от точки М до середины отрезка АВ; (2 балла)

6) расстояние от точки А до плоскости ЯЗЫКОВ. (2 балла)

Ответ. Вариант 1.1) см; 2) см; 3) см; 4) см; 5) см; 6) 3 см.

Вариант 2. 1) см; 2) 3 см; 3) 5 см; 4) 2,5 см; 5) см; 6) 3 см.

II. Восприятие и осознание нового материала

Свойство точки, равноудаленной от вершины многоугольника

Если через центр окружности, описанной вокруг многоугольника, проведено прямую, перпендикулярную к плоскости многоугольника, то каждая точка этой прямой равноудалена от вершин многоугольника.

Доведение

Пусть ABCD — четырехугольник, вокруг которого описана окружность с центром в точке О, и OS(ABC). Докажем, что SA = SB = SC = SD (рис. 168).

ΔASO = ΔBSO = ΔCSO = ΔDSO (за двумя катетами: SO — общая, АО = BO = CO = DO).

Из равенства треугольников следует, что SA = SB = SC = SD.

Если некоторая точка равноудалена от вершин многоугольника, то основание перпендикуляра, опущенного из данной точки на плоскость многоугольника, совпадает с центром окружности, описанной вокруг многоугольника.

Доведение

Пусть ABCD — данный четырехугольник, для точки S пространства SA = SB = SC = SD и SOАВС. Докажем, что точка О — центр окружности, описанной вокруг ABCD (рис. 168). ΔASO = ΔBSО = ΔCSO = ΔDSO (по гипотенузой и катетом: SO — совместный, AS = BS = CS = DS — по условию). Из равенства треугольников следует, что АО = BO = CO = DO, т.е. точка О — центр окружности, описанной вокруг четырехугольника ABCD.

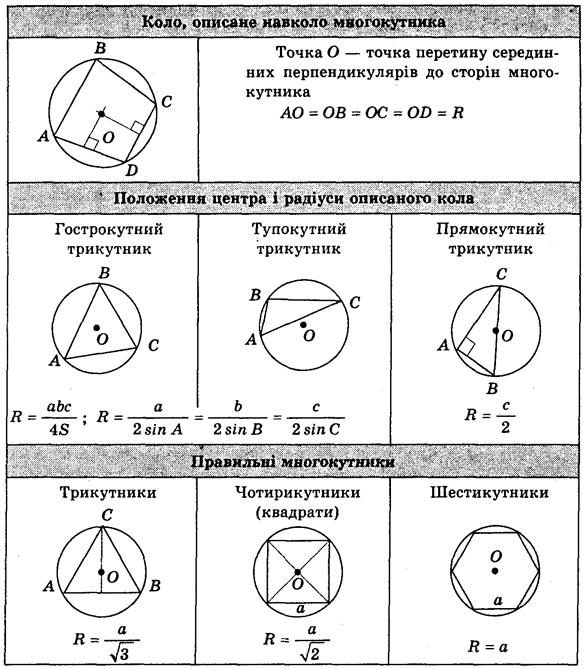
Далее следует напомнить формулы для нахождения радиуса круга, описанного вокруг некоторых многоугольников, с помощью данной настенной таблицы.

1. ABC = 90°; МА = MB = МС (рис. 169). Опустите из точки М перпендикуляр на плоскость АВС.

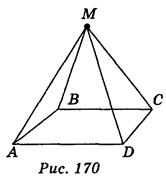
2. ABCD — квадрат, АВ = 4 см, МА = MB = MC = MD = 5 см (рис. 170). Найдите расстояние от точки М до плоскости АВС.

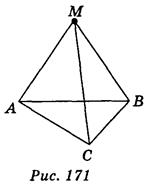
3. АВ = ВС = АС = 5 см; МА = MB = MC = 13 см (рис. 171). Найдите расстояние от точки М до плоскости АВС.

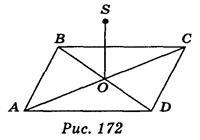
4. ABCD — квадрат, SO( ABC ), SO = 2см, АВ = 4 см (рис. 172). Найдите расстояние от точки S до вершин квадрата.

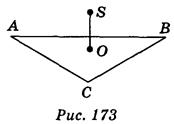
5. Δ АВС — правильный; точка О — центр треугольника; АВ = 3см; SO(АВС); SO = см (рис. 173). Найдите расстояние от точки 5 до вершин треугольника АВС.

6. Задача 21 из учебника (с. 35).

7. Задача 20* из учебника (с. 35).

III. Домашнее задание

Задачи № 6, 17-19 (с. 34-35).

IV. Подведение итога урока

Вопрос к классу

1) Какое свойство имеют точки, которые лежат на перпендикуляре, проведенном к плоскости многоугольника через центр окружности, описанной вокруг многоугольника?

2) Где находятся точки, равноудаленные от вершин некоторого многоугольника?

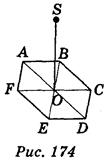
3) Через центр О правильного шестиугольника ABCDEF проведем перпендикуляр SO к плоскости АВС (рис. 174). Укажите, какие из приведенных утверждений правильные, а какие — неправильные:

а) расстояния от точки S до вершин шестиугольника ABCDEF разные;

б) угол OAS равен углу OCS;

в) если ОА = 1 cm, SO = 1 см, то SA = cm;

г) если SO = OB, то OSB = 60°.

4) Расстояния от точки S до всех вершин прямоугольника ABCD равны, точка О — точка пересечения диагоналей АС и BD прямоугольника ABCD. Укажите, какие из приведенных утверждений правильные, а какие — неправильные:

Четыре замечательные точки треугольника

В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.

Точка пересечения медиан треугольника

О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).

Рисунок 1. Медианы треугольника

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Точка пересечения биссектрис треугольника

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

Рассмотрим треугольник $ABC$, где $AM, BP, CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM и BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Готовые работы на аналогичную тему

Для доказательства нам потребуется следующая теорема.

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ, OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

Точка пересечения серединных перпендикуляров треугольника

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

Пусть дан треугольник $ABC$, $n, m, p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n и m$ (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: $OB=OC, OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.

Точка пересечения высот треугольника

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство.

Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).

Рисунок 4. Высоты треугольника

Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что $_1bot A_2B_2, _1bot A_2C_2, _1bot C_2B_2$. Следовательно, $_1, _1, _1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты $_1, _1, _1$ пересекаются в одной точке.

Пример задачи на использование 4 замечательных точек треугольника

Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что

а) точка $D$ — середина стороны $BC$.

б) $angle A=angle B+angle C$

Решение.

а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.

б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$angle A=angle DXB$, как соответственные углы. Значит, $angle A=^0$. Тогда$angle B+angle C=^0-angle A=^0-^0=^0=angle A$