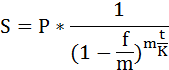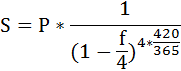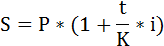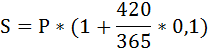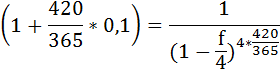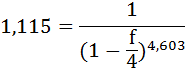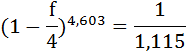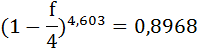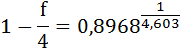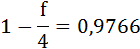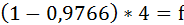Как найти учетную ставку формула

При антисипативном
способе начисления процентов сумма
по­лучаемого дохода рассчитывается
исходя из суммы, получаемой по прошествии
интервала начисления (т. е. из наращенной
сум­мы). Эта сумма и считается величиной
получаемого кредита (или ссуды). Так как
в данном случае проценты начисляются
в начале каждого интервала начисления,
заемщик, естественно, получает эту сумму
за вычетом процентных денег. Такая
операция называ­ется дисконтированием
по учетной ставке, а также коммерческим
или банковским учетом.

Дисконт — это
доход, полученный по учетной ставке, т.
е. раз­ница между размером кредита и
непосредственно выдаваемой суммой.

Пусть теперь d(%}
— простая
годовая учетная ставка;

d —
относительная величина учетной ставки;

Dς — сумма
процентных денег, выплачиваемая за год;

D — общая сумма
процентных денег;

S
— сумма, которая должна быть возвращена;

Р — сумма,
получаемая заемщиком.

Тогда, согласно
определениям, имеем следующие формулы:

(2.1)

D
ς =dS;

(2.2)

D
= n D ς,
= n d S;

(2.3)

P=S-D=S(1-nd)
= S[1-(
ð /K)d].

(2.4)

Преобразуя последнее
выражение, получаем формулу для
опре­деления наращенной суммы:

90

(2.5)

Из этой формулы
легко видеть, что в отличие от случая
простых ставок ссудного процента простые
учетные ставки не могут при­нимать
любые значения. Именно для того, чтобы
выражение (2.5) имело смысл, необходимо,
чтобы знаменатель дроби в правой части
был строго больше нуля, т. е. (1 —
nd) > 0, или
d < 1/n. Прав­да, со значениями d, близкими
к предельным, вряд ли можно встретиться
в жизни.

На практике учетные
ставки применяются главным образом при
учете (т. е. покупке) векселей и других
денежных обяза­тельств. Вопрос
получения дохода по векселям будет
подробно рассмотрен в разделе 2.8.

Из приведенных
формул можно вывести еще две формулы
для определения периода начисления и
учетной ставки при прочих заданных
условиях:

(2.6)

(2.7)

Пример
7

Кредит выдается
на полгода по простой учетной ставке
20%. Рассчитать сумму, получаемую заемщиком,
и величину дисконта, если требуется
возвратить 30 000 000 руб. Решение По формуле
(2.4) получаем

Р = 30 000 000 (1 — 0,5 •
0,2) = 27 000 000 (руб.). Далее

D
= S
— Р = 30 000 000 — 27 000 000 = 3 000 000 (руб.).

Пример 8

Кредит в размере
40 000 000 руб. выдается по простой учетной
ставке 25% годовых. Определить срок, на
который предоставляет­ся кредит, если
заемщик желает получить 35 000 000 руб.

Решение

Расчет проводится
по формуле (2.6):

п
= (40 000 000 — 35 000 000)/(40 000 000 • 0,25) = 0,5 года.

91

Пример 9

Рассчитать учетную
ставку, которая обеспечивает получение
9 000 000 руб., если сумма в 10 000 000 руб. выдается
в ссуду на полгода.

Решение

По формуле (2.7):

d=(10000000-9000000)/(10000000-0,5)
=0,2=20%.

2.3. Сложные ставки ссудных процентов

Если после очередного
интервала начисления доход (т. е.
на­численные за данный интервал
проценты) не выплачивается, а присоединяется
к денежной сумме, имеющейся на начало
этого интервала, для определения
наращенной суммы применяют фор­мулы
сложных процентов. Сложные ссудные
проценты в настоя­щее время являются
весьма распространенным видом применяе­мых
в различных финансовых операциях
процентных ставок.

Пусть

i_с
— относительная величина годовой
ставки сложных ссудных процентов;

kн.с — коэффициент
наращения в случае сложных процен­тов;

j —
номинальная ставка сложных ссудных
процентов (ее определение будет дано в
дальнейшем).

Если за интервал
начисления принимается год, то по
прошест­вии первого года наращенная
сумма в соответствии с формулой (1.7),
составит

S1=P(1+
i_c).

Еще через год это
выражение применяется уже к сумме S₁:

S₂ = S₁ ( l +
i_c) = P (l + i_c)²

и так далее.
Очевидно, что по прошествии п лет
наращенная сум­ма составит

S=P(1+i_c)ⁿ

(3.1)

Множитель наращения
k н.с
соответственно будет равен

k_н.с
= (1 + i_с)ⁿ
(3.2)

При начислении
простых процентов он составил бы по
форму­лам (1.5) и (1.7):

k_н
= (1 + n i).

92

Сравнивая два
последних выражения для коэффициентов
нара­щения, можно видеть, что чем
больше период начисления, тем больше
разница в величине наращенной суммы
при начислении простых и сложных
процентов.

Эту разницу можно
наглядно представить с помощью графи­ков,
изображенных на рис. 1. Здесь, как и на
всех последующих рисунках, по горизонтальной
оси откладываются годы, по верти­кальной
— тысячи рублей. Первоначальная сумма
составляет 1000 руб., процентная ставка
— 30% годовых. Верхняя линия соответ­ствует
наращению денежной массы в случае
применения сложной процентной ставки.
Она представляет собой пример
экспоненци­ального роста (чем больше
п, тем круче кривая уходит вверх), в то
время как нижняя линия (соответствующая
случаю простых про­центов) является
прямой с очень небольшим углом наклона.

Поэтому, когда
возникает возможность выбора межцу
низкой сложной процентной ставкой и
более высокой простой, следует отдавать
предпочтение первому варианту.
Естественно, если в на­шем распоряжении
более или менее значительный период
време­ни. Сумма, наращенная по сложной
процентной ставке, уже через небольшое
(в зависимости от разницы в величине
процентных ставок) количество интервалов
начисления превысит сумму, на­ращенную
по простой ставке (см. рис. 1). Подробно
этот вопрос рассматривается в разделе
2.5.

Рис. 1. Наращение
вложенной суммы по простои и сложной
процентным ставкам (i = i_с= 30%)

Если срок ссуды п
в годах не является целым числом,
множи­тель наращения определяют по
выражению:

93

k_н.с.=(1+i_c)^na(1+_nbi_c),

(3.3)

где n = n_а
+ n_b

n_а
— целое число лет;

n_b
— оставшаяся дробная часть года.

На практике в
данном случае часто предпочитают
пользоваться формулой (3.1) с соответствующим
нецелым показателем степени. Но нужно
иметь в виду, что с точки зрения сущности
начисления процентов этот способ
является приблизительным, и погрешность
при вычислениях будет тем больше, чем
больше значения входя­щих в формулу
величин. Наибольшее расхождение мы
получим при n_b= 1/2, как раз в том
случае, когда очень удобно применить
формулу (3.1), ведь на всех калькуляторах
есть операция извлече­ния квадратного
корня (т. е. возведения в степень 1/2).
Следует учитывать, что приблизительный
метод дает меньший, чем в дей­ствительности,
результат.

Таким образом, в
современной ситуации, когда номиналы
де­нежных сумм достаточно велики, от
этого метода лучше отказать­ся вовсе.
В конце раздела будет приведен пример,
позволяющий оценить разницу в результатах
при двух способах вычисления множителя
наращения по формулам (3.2) и (3.3).

Предположим теперь,
что уровень ставки сложных процентов
будет разным на различных интервалах
начисления.

Пусть n1, п2, …, пN—
продолжительность интервалов начисле­ния
в годах; i1, i2, …,
iN — годовые
ставки процентов, соответст­вующие
данным интервалам. Тогда наращенная
сумма в конце первого интервала начисления
в соответствии с формулой (1.7), составит

S₁
= Р(1+
n₁i₁).

В конце второго
интервала:

S₂=P(l+n₁i₁)(l+i₂)

и т.д.

При N интервалах
начисления наращенная сумма в конце
всего периода начисления составит

(3.4)

Если все интервалы
начисления одинаковы (как и бывает
обыч­но на практике) и ставка сложных
процентов одна и та же, фор­мула (3.4)
принимает вид:

94

S_N=
P(1 +тi)^N.

(3.5)

Начисление сложных
процентов может осуществляться не один,
а несколько раз в году. В этом случае
оговаривается номи­нальная ставка
процентов у — годовая ставка, по которой
опреде­ляется величина ставки
процентов, применяемая на каждом
ин­тервале начисления.

При т равных
интервалах начисления и номинальной
процент­ной ставке
j эта
величина считается равной
j/m.

Если срок ссуды
составляет п лет, то, аналогично формуле
(3.1), получаем выражение для определения
наращенной суммы:

S_mn=P(1+j/m)^mn,

(3.6)

где тп — общее
число интервалов начисления за весь
срок ссуды.

Если общее число
интервалов начисления не является целым
числом (mn
— целое число интервалов начисления,
I — часть ин­тервала начисления), то
выражение (3.6) принимает вид:

S=P(1+j/m)^mn(1+Ij/m).

(3.7)

Для целого числа
периодов начисления используется
формула сложных процентов (3.1), а для
оставшейся части — формула про­стых
процентов (1.7).

В России в
настоящее время наиболее распространенным
явля­ется начисление процентов по
полугодиям, поквартальное и еже­месячное
(иногда интервалом начисления может
являться и день). Такие проценты,
начисляемые с определенной периодичностью,
называются дискретными.

В мировой практике
часто применяется также непрерывное
на­числение сложных процентов (т. е.
продолжительность интервала начисления
стремится к нулю, а т — к бесконечности).

В этом случае для
вычисления наращенной суммы служит
сле­дующее выражение:

(3.8)

Для расчетов можно
использовать известную в математике
фор­мулу:

где е= 2,71828…

Из этой формулы
следует:

95

Тогда для наращенной
суммы получаем

S=
Ре^jn

(3.9)

Здесь

k_н.с=e^jn

(3.10)

Значения наращенной
суммы
S можно
вычислять с помощью финансового
калькулятора или находя значения е^jn
и других тре­буемых величин в специальных
таблицах.

Очевидно, что
непрерывный способ начисления процентов
да­ет максимальную величину наращенной
суммы при прочих рав­ных условиях (т.
е. при одинаковых
n,j, Р).

Аналогично случаю
простых процентов полученные формулы
можно преобразовывать, выражая одни
величины через другие, в зависимости
от того, что известно, а что требуется
найти.

Так, из формулы
(3.1) получаем

(3.11)

Напомним, что, как
и в случае простых процентов, определение
современной величины суммы S
называется
дисконтированием.

Коэффициент
дисконтирования а является величиной,
обрат­ной коэффициенту наращения, т.
е. k_н.с*
а = 1.

Формула (3.11), а
также соответствующие формулы для
случая простых ставок ссудного процента
и для учетных ставок дают лег­ко
понять, что текущий финансовый эквивалент
будущей денежной суммы тем ниже, чем
отдаленнее срок ее получения и чем выше
норма доходности.

Также из формулы
(3.1) имеем

(3.12)

Из формулы (3.6):

(3.13)

Применяя операцию
логарифмирования к обеим частям фор­мулы
(3.1), получаем

(3.14)

Подобным же образом
из формулы (3.6) получаем формулу:

96

(3.15)

Если нет специального
калькулятора, значения логарифмов также
находят по таблицам.

Существует несколько
правил, позволяющих быстро рассчитать
срок удвоения первоначальной суммы для
конкретной процент­ной ставки.

Правило
«72»:

Правило «69» (более
точное):

Здесь, однако,
следует иметь в виду, что при выводе
этих правил используются математические
формулы, дающие верный резуль­тат не
для любых значений входящих в них
величин. Например, выражение 1/х <= х (х
> 0) неверно при х < 1.

Данные правила
дают весьма точный результат при
небольших значениях i_с(%).
До i_c(%)
= 100(%) отклонения достаточно малы и ими
можно пренебречь. При процентной ставке,
равной, напри­мер, 120%, погрешность
(для правила «69») составляет 5,2% (для
правила «72» она будет больше) и растет
с ростом i_c.
При этом срок удвоения, полученный по
правилу «69», будет больше, чем в
действительности, а по правилу «72» —
меньше.

В качестве примера
найдем срок удвоения капитала при
годо­вых ставках: а) 20% и б) 110% по формуле
(3.14) и по правилам «б9» и «72».

а) n =
ln 2/ln 1,2 =
3,8 года, или

n
= 72/20 = 3,6 года, или

n = 69/20 + 0,35 = 3,8 года;

б) л =
ln 2/ln 2,1 =
0,93 года, или

n
= 72/110 = 0,65 года, или

n
= 69/110 + 0,35 = 0,98 года (разница с точным
зна­чением — 18 дней).

Следующие примеры
иллюстрируют использование получен­ных
формул.

Пример 10

Первоначальная
вложенная сумма равна 200 000 руб. Опреде­лить
наращенную сумму через пять лет при
использовании про­стой и сложной
ставок процентов в размере 28% годовых.
Решить

97

этот пример также
для случаев, когда проценты начисляются
по полугодиям, поквартально, непрерывно.

Решение

По формуле (1.7) для
простых процентных ставок имеем

S
= 200 000 (1 +5 *0,28)
= 480 000 (руб.). По формуле (3.1) для сложных
процентов:

S = 200 000 (1 + 0,28)⁵
= 687 194,7 (руб.). По формуле (3.6) для начисления
по полугодиям:

S=
200000(1 + 0,14)¹⁰
= 741 444,18
(руб.). Из той же формулы для поквартального
начисления:

S=200 000 (1 + 0,07)²⁰= 773 936,66 (руб.). По формуле (3.9) для непрерывного
начисления:

S = 200 000 е^1,4
= 811 000 (руб.).

Пример 11

Первоначальная
сумма долга равна 50 000 000 руб. Определить
наращенную сумму через 2,5 года, используя
два способа начис­ления сложных
процентов по ставке 25% годовых.

Решение

По формуле (3.3)
получаем S=50000000(1 +0,25)2(1 +0,125) =87890625 (руб.).

Для второго способа
используем формулу (3.1) с нецелым
по­казателем степени:

S = 50 000 000 (1 + 0,25)2’5 =
87 346 390 (руб.).

Отчетливо видно
расхождение: при использовании
приблизи­тельного метода упущенная
выгода могла бы составить около 550 000
руб.

Пример 12

Определить
современную (текущую, настоящую,
приведенную) величину суммы 100 000 000 руб.,
выплачиваемую через три года, при
использовании ставки сложных процентов
24% годовых.

Решение

Воспользуемся
формулой (3.11):

Р = 100 000 000/0 + 0,24)³
== 52 449 386 (руб.).

Учетная ставка подразумевает под собой два основных понятия:

• Это процентная ставка, по которой Центральный банк России предоставляет кредиты коммерческим банкам. На практике это показатель называют «ставкой рефинансирования». Этот показатель является основой для разрешения спорных вопросов по начислению штрафных мероприятий в отношении стороны, нарушившей условия договора. Так же ставка рефинансирования используется в законодательстве при расчете выплат между сторонами.
• Это цена, по которой приобретается вексель до наступлений сроков уплаты по нему.

24 марта 2017 года советом директоров Центрального банка России было принято решение об установлении учетной ставки на уровне 9,75%. А в соответствии с постановлением Центрального банка РФ от 31 декабря 2015 года о том, что ставка рефинансирования полностью соответствует учетной ставке и не устанавливается самостоятельно, ставка рефинансирования, на сегодняшний день так же составляет 9,75%.

Стоит отметить, что учетная ставка в виде ставки рефинансирования до 1 января 2016 года носила только справочный характер и применялась для расчетов штрафов и дополнительных выплат между физическими и юридическими лицами. Но уже в 2016 году стала приняться как мощный рычаг управления финансовыми потоками страны и регулятором экономической стабильности.

Стоит отметить, что с 01 января 2016 года происходит постоянное снижение ставки рефинансирования в России.

Виды учетной ставки

В экономической литературе выделяют три основных вида учетной ставки, которые рассчитываются по индивидуальным формулам, исходя из условий расчета.

Простая учетная ставка

Данный вид ставки предполагает одну и туже сумму взимаемого процента на протяжении действия всего договора. Это говорит о том, что база для начисления процента остается всегда неизменной, на протяжении всего периода расчетов.

Формула простой учетной ставки:

P=S-S*n*d=S(1-nd)

где:

• P – сумма выплаты;
• S – общая сумма обязательства (сумма выплаты плюс проценты);
• n – учетная ставка, выраженная в долях;
• d – число периодов до уплаты.

Сложная учетная ставка

Сложная учетная ставка отличается тем, что база для начисления процентов, каждый раз меняется. Причиной изменений является наращенные процента за прошедший период. Другими словами, накопленные проценты по вкладу становятся частью суммы, на которую начисляют проценты

Поэтому сумма, выдаваемая банком при учете векселя, рассчитывается по формуле:

P=S(1-〖d)〗^n

где:

• P – сумма выплаты;
• S – общая сумма обязательства (сумма выплаты плюс проценты);
• n – учетная ставка, выраженная в долях;
• d – число периодов до уплаты.

Номинальная учетная ставка

Пусть годовая ставка сложных процентов равна f, а число периодов начисления в году m. Тогда каждый раз проценты начисляют по ставке f/m. Ставка f называется поминальной.

Начисление процентов по номинальной ставке производится по формуле

P=S(1-〖f/m)〗^mn

где:

• P – сумма выплаты;
• S – общая сумма обязательства (сумма выплаты плюс проценты);
• n – учетная ставка, выраженная в долях;
• m – число периодов в году;
• f – номинальная ставка.

Принимая решение, о виде ставки используется метод сопоставления ставок разных государств. Таким образом, можно сделать вывод, что решение по учетной ставке в государстве принимается не только после анализа экономического положения в стране, но и на мировой арене.

При осуществлении вклада в иностранную валюту, учетная ставка – это первое на что стоит обратить внимание. Именно она, как индикатор, поможет определить стабильность национального денежного знака.

Темпы роста или снижения учетной ставки подскажут насколько государство настроено на борьбу с инфляцией (обесцениванием денег) в стране.

А сравнение учетной ставки нескольких стран поможет определиться между выбором иностранной валюты для вклада или кредита.

Регулирование учетной ставки

Формирование учетной ставки является сильным рычагом Центрального банка РФ по контролю деятельности каждого коммерческого банка страны. Изменение этого показателя контроль резервов банков России.

Существует два способа контроля коммерческих банков:

• Снижение учетной ставки. В случае, когда учетная ставка теряет свой процент, коммерческие банки начинают наращивать свои резервы, за счет уменьшения расходов на ссуды от ЦБ РФ, что приводит к увеличению сумм по операциям со своими клиентами.
• Повышение учетной ставки. Данная процедура имеет противоположный эффект. При росте процента учетной ставки приводит к сокращению резервов и соответственно, сокращение выдаваемых сумм по проводим операциям с клиентами коммерческих банков.

За счет сокращения банковских операций по заему денежных средств, снижается уровень инфляции, когда как снижение уровня учетной ставки усиливает уровень инфляции, что происходит из-за большего доступа к ссудам от государства. Однако понижение процента от ЦБ РФ приносит экономическую стабильность в стране, за счет увеличения доходов населения, через приобретение банковских кредитов.

Таким образом, изменения учетной ставки, как в ту, так и в другую сторону приносит различный экономический эффект, поэтому любые решения, касаемые учетной ставки, принимаются после тщательного анализа всех экономических показателей.

Так, например, в США в 1929-1933 гг. (первый экономический кризис в США) показатель учетной ставки уменьшился в восемь раз, а в 1957-1958 гг. (второй экономический кризис в США) – в четыре раза. В после кризисное время этот же показатель возрос в семь раз, а к 1981 году учетная ставка возросла уже в семнадцать раз, по сравнению этого процента в кризисное время.

При детальном анализе мировой практики экономического регулирования странами, за счет регулирования процента учетной ставки, выделяются два направления кредитно-денежной политики. И выбрав одно из этих направлений, правительство страны определяет свои действия по отношению к состоянию экономики государства.

1. Первое направление объединяет в себе следующие действия: Центральный банк содействует увеличению числа денежных знаков в оборотных банковских операциях, числа выдаваемых кредитов за счет снижения процента учетной ставки. Однако оборотной стороной этой «медали» – это увеличение цен товаров на рынке, рост инфляции национальной валюты и как следствие обесценивание денег. Такое направление кредитно-денежной политики получило название «дешевые деньги».
2. Второй направление сводится к ограничению числа денежных знаков в обращении, способствует сокращению числа выдаваемых кредитов. Как результат происходит снижение цен на товары и услуги, а так же контроль уровня инфляции. В такой ситуации происходит увеличение уровня национальной валюты и покупательной способности населения страны. Однако такая политика приводит к росту процента кредитов в коммерческих банках, поэтому они становиться малодоступными. Это направление получило название «дорогих денег».

Из-за несовершенства данного способа регулирования денежно-кредитной политики государств в развитых странах предпочитают не использовать его. В таких странах регулирование происходит за счет прямого контроля ставок по кредитам в коммерческих банках.

Похожие статьи

1. Целевой кредит
2. Тезаврация
3. Срочный вклад
4. Бланковый кредит
5. Таможенные платежи

Какой годовой учетной ставкой при ежеквартальной  капитализации можно заменить в контракте простую процентную ставку 10% (К=365), не изменяя финансовых последствий.

Срок операции – 420 дней.

Решение:

При наращении сложных процентов по учётной ставке несколько раз в году (m раз) наращенная сумма определяется по формуле:

f – номинальная учётная ставка,

m – число периодов начисления процентов в течение года;

n – число лет.

При наращении по простой процентной ставке наращенная сумма определяется по формуле:

Так как S и P не изменились, то приравняем множители наращения и решим уравнение относительно f:

Итак, простую процентную ставку в контракте можно заменить годовой учётной ставкой:

f = 0,094 или 9,4%.

Процентная ставка является одним из ключевых понятий современной финансовой жизни. В отличие от математики, где есть только одна разновидность процента, в экономике их несколько. Существует сложная и простая процентная ставка. Каждая из них имеет определённые особенности.

Виды ставок

Чаще всего ставка фигурирует в кредитном договоре и финансовом соглашении. При подписании такого документа заёмщик берёт перед кредитором обязательства по выплате конкретной суммы. Она определяется как отношение процентных денег, выплачиваемых за фиксированный отрезок времени, к величине ссуды. Называется ставкой, считается в процентах.

Способы начисления процентов бывают разными и зависят от условий контракта. Ставки могут применяться в одной и той же начальной сумме на протяжении всего периода кредитования или к сумме с начисленными в предыдущем периоде процентами.

Первый вариант расчётов называется простой процентной ставкой, второй — сложной. Простая ставка действует в отношении одной и той же первоначальной суммы долга на протяжении всего срока, т. е. исходная база (денежная сумма) всегда одна и та же (без учёта последовательного её погашения). Такой способ начисления используется в потребительском кредитовании.

Сложная применяется к наращенной сумме кредита, т. е. к сумме, возросшей на величину процентов, начисленных за предыдущий период. Поэтому исходная база постоянно растёт.

Помимо простой и сложной, существует ещё несколько разновидностей ставок. Дополнительно выделяют:

• Фиксированную. Устанавливается в виде конкретного числа в финансовых контрактах.
• Переменную. Дискретно изменяется во времени, не имеет конкретной числовой характеристики.
• Плавающую. Привязывается к определённой величине, изменяющейся во времени, состоит из базы и надбавки к ней (маржи). База представляет собой начальную величину, маржа — переменную, которая зависит от таких условий, как срок операции, финансовое положение заёмщика и пр.

Также в экономике есть понятие номинальных, обыкновенных, точных и реальных процентов. Все они имеют свои особенности.

Расчётные формулы

Для каждого вида процентов существует своя формула, помогающая её определить. Прежде чем приступать к расчётам, следует разобраться в основных терминах, которые применяются в формулах:

• Период начисления. Промежуток времени, к которому приурочена простая и сложная процентная ставка.
• Капитализация. Суммирование начисленных процентов с основной суммой задолженности.
• Наращение. Увеличение денежной суммы во времени, вызванное капитализацией.

Процедуру, обратную наращению, называют дисконтированием. Оно подразумевает уменьшение суммы на величину, равную дисконту (скидке).

Наращение и дисконтирование характеризуются соответствующими множителями. Первый рассчитывается как L = S (n) / S (0), второй как v = S (0) / S (n). S (0) соответствует первоначальной сумме кредита, S (n) равняется величине долга в конце срока n.

Чтобы узнать n (срок задолженности в долях от периода t), требуется разделить срок долга в днях (t) на фиксированный временной промежуток, к которому относится ставка (t*). Обычно t* равен 365 дней (иногда уменьшен до 360).

Зная необходимые параметры, можно высчитать процент (i), используя выражение i = (S (t*) — S (0)): S (0). В случае с прямыми процентами исходной базой для определения процентной ставки в течение всего срока долга на каждом периоде применения процента служит первоначальная сумма долга S (0).

На основе этих же данных можно определить значение учётной ставки по формуле d = (S (t*) — S (0)): S (t*). Учётной считается та ставка, которая используется Центробанком для предоставления заёмов коммерческим банком.

Если срок задолженности t состоит из k этапов, то чтобы при действующей схеме простых процентов узнать размер наращенного вклада по окончании срока, придётся применить выражение S (n) = S (0) * (1 + n1 * i1 + … + nk * ik).

Допустим, что в первом полугодии простой процент составляет 0,09 годовых, затем в следующем году он сокращается на 0,01, а в следующих двух полугодиях возрастает на 0,005 в каждом. Первональный взнос равен 800 у.е.

Получается, что S (0) = 800, n1 = 0,5, i1 = 0,09, n2 = 1, n3 = 0,5, n4 = 0,5. Высчитываем i2 = 0,09 — 0,01 = 0,08, i3 = 0,08 + 0,005 = 0,085, i4 = 0,085 + 0,005 = 0,09.

Подставляем полученные цифры в формулу и узнаём, что величина наращенного вклада в конце срока составит S (n) = 800 * (1 + 0,5 * 0,09 + 1 * 0,08 + 0,5 * 0,085 + 0,5 * 0,09) = 980,97.

Особенности сложного процента

Сложной ставкой в экономике принято называть величину, образующуюся при сложении прибыли с основной суммой и участвующую в последующем создании нового дохода. То есть по окончании каждого отчётного периода (месяца, квартала, года) начисленный процент суммируется с вкладом. Полученная сумма выступает базисом для последующего образования прибыли.

Формула обязательно учитывает капитализацию процентов. Если ставка является годовой, то для её расчёта следует применять выражение S = P * (1 + i/100)n. В нём фигурируют следующие величины:

• Общая сумма, включающая тело вклада и проценты по нему (S).
• Первоначальный размер вклада (P).
• Ставка в процентах за год (i).
• Количество операций по капитализации за весь срок использования денежных средств (n).

Сложные проценты с ежемесячным внесением платежа часто применяются для обеспечения прибыли по срочным банковским вкладам. В таком случае они могут начисляться не раз в год, а раз в месяц или в квартал. Периодичность оговаривается в договоре с банком.

Если вкладчик внесёт на счёт 50 тысяч рублей на 5 лет по ставке 10% в год, то его прибыль в виде срочной ставки будет равна S = 50000 * (1 + 10/100)5 = 80 525,5 рублей.

Бывают вклады, где доход начисляется ежемесячно. В них также закладывается сложная процентная ставка. Формула принимает вид S = P * (1 + i/(100*12))n. Показатель n здесь считается в месяцах.

Допустим, вклад, рассчитанный на 10 лет (120 месяцев), подразумевает ставку в 11% годовых и проценты по нему капитализируются ежемесячно. Тогда при взносе 10000 рублей доход по истечении установленного периода составит S = 10000 * (1 + 11: (100 * 12)120 = 298914,96 рублей.

Когда требуется определить прибыль за квартал, годовую ставку необходимо делить на 4, а вместо n указывать количество кварталов. В случае с полугодовыми периодами общий процент делится на 2, n равняется количеству полугодий.

При открытии долгосрочного вклада фактором, характеризующим его прибыльность, становится процентная ставка. Её можно узнать, выведя обратную формулу из выражения для определения сложного процента. % = (S / P)1/n — 1. Таким образом, чтобы 50000 рублей за 10 лет увеличились до 100000, нужно выбрать ставку, равную % = (100000: 50000)1/10 — 1 = 0,0718 = 7,18% годовых.

Банковские расчёты

Банки иногда используют другие формулы для определения прибыли по разным вкладам. Такая формула подразумевают более сложный и точный расчёт. В случае с простой ставкой она выглядит, как S = P * I * t /K. В ней:

• s — объём начисленных процентов;
• p — размер взноса;
• I — процентная ставка за год, разделённая на 100%;
• t — количество дней, за которые начисляется прибыль;
• k — число дней в году.

Пусть размер вклада равен 100 тысяч рублей, срок — 181 день, а годовая ставка — 7%. В день его закрытия вкладчик получит доход в размере 100 000 x 0,07 x 181 / 365 = 3 471,23 рублей.

Для сложной ставки применяется выражение S = P * (1 + I * j / K) n — P. Помимо указанных выше параметров, здесь дополнительно используется j — календарные дни в периоде, в течение которого осуществляется капитализация по вкладу, и n — периодичность начисления.

Если к аналогичным исходным данным добавить n = 2 и j = 90, получится, что доход в виде сложных процентов составит 100 000 x (1 + 0,07 x 90 / 365)2 — 100 000 = 3 481,85 рублей.

Из примеров становится понятно, что вклад со сложной ставкой значительно выгоднее, чем с простой.