Как найти тупой угол треугольника формула

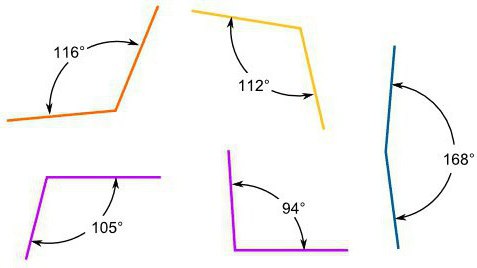
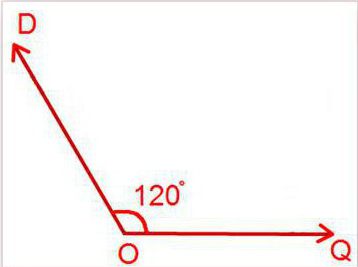
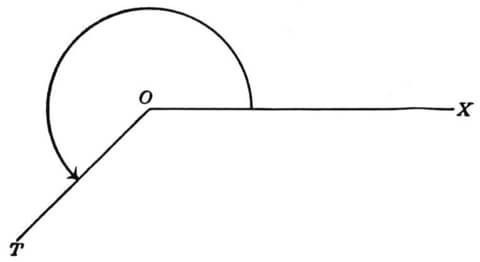
В данной публикации мы рассмотрим, что такое тупой угол, а также разберем примеры задач, в которых он участвует.

Определение тупого угла

Угол является тупым, если его градусная мера находится между 90 и 180 градусами.

∠α – тупой, если 90° < α < 180°.

То есть тупой угол больше прямого (90°), но меньше развернутого (180°).

Примеры задач

Задание 1
Дан треугольник, у которого известны два угла – 34° и 27°. Найдем третий и определим, является ли он тупым.

Решение:
Примем неизвестную величину за “α“. Как мы знаем, сумма углов треугольника равняется 180 градусам, значит:

α = 180° – 34° – 27° = 119°.

Следовательно, угол α – тупой.

Задание 2
Дан ромб, площадь (S) которого составляет 12,5 см², а длина (a) стороны – 5 см. Найдем его углы и определим, являются ли они тупыми.

Решение:
Синус угла ромба (α) можно найти следующим образом (выведено из формулы расчета площади фигуры):

Следовательно, α = 30° (arcsin 0,5), является острым.

Как мы знаем, сумма соседних углов ромба составляет 180 градусов, значит второй угол β равен 150° (180° – 30°), и он является тупым.

Тупой угол

Тупой угол — это угол, больший прямого, но меньший развёрнутого.

Градусная мера тупого угла — от 90º до 180º.

∠ABC, ∠DEF, ∠PTK — тупые углы.

Построить тупой угол заданной градусной меры можно с помощью транспортира.

Построить с помощью транспортира угол 140º.

1) Отмечаем точку — вершину угла.

2) От точки проводим луч — сторону угла.

3) Отметку в центре транспортира (у разных моделей отметка может располагаться в разных местах) совмещаем с вершиной угла таким образом, чтобы отметка 0º находилась на стороне угла.

4) Находим 140º на той шкале, где находится 0º, и ставим точку.

5) От вершины угла к отмеченной точке проводим луч — вторую сторону угла.

На рисунках показано построение угла 140º с началом отсчёта по разным шкалам — по нижней и по верхней.

Чтобы найти тупой угол на рисунке при помощи угольника, нужно приложить вершину угольника к вершине угла так, чтобы сторона угольника проходила вдоль одной из сторон угла. Если угол тупой, то его другая сторона выйдет за вторую сторону угольника.

Тупые углы: описание и особенности

Треугольник – это геометрическая фигура, имеющая три соединенные между собой линиями точки, которые лежат не на единой прямой в плоскости. Вершины треугольника – точки в основании углов, а линии, соединяющие их, называют сторонами треугольника. Чтобы определить площадь такой фигуры, часто используют внутреннее пространство треугольника.

Классификация

Кроме треугольников, имеющих неодинаковые стороны, существуют равнобедренные, то есть обладающие двумя одинаковыми сторонами. Их называют боковыми, а еще одну сторону – основанием фигуры. Существует еще один вид таких многоугольников – равносторонние. Все три их стороны имеют одинаковую длину.

Для треугольников присуща градусная система измерения. Эти фигуры могут иметь разные углы, поэтому их классифицируют так:

• Прямоугольные – имеющие угол 90 градусов. Две стороны, прилежащие к этому углу, называют катетами, а третью – гипотенузой;
• Остроугольные – это треугольники, обладающие всеми острыми углами, не превышающими 90 градусов;
• Тупоугольные – один угол больше 90 градусов.

Определение и параметры треугольника

Как уже было отмечено, треугольник – это один из видов многоугольников, имеющий три вершины и столько же прямых, их объединяющих. Обозначают линии, как правило, одинаково: углы – маленькими латинскими буквами, а противоположные стороны каждого – соответствующей большой буквой.

Если сложить все углы какого-либо треугольника, получится сумма в 180 градусов. Чтобы узнать внутренний угол, нужно из 180 градусов вычесть величину внешнего угла треугольника. Для того чтобы узнать, чему равняется угол, находящийся снаружи, стоит сложить два раздельных от него угла внутри.

В каждом треугольнике, имеет он острые или тупые углы, противоположно большому углу находится наибольшая сторона. Если же прямые между вершинами одинаковы, то, соответственно, и каждый угол равняется 60 градусам.

Тупоугольный треугольник

Тупой угол треугольника всегда больше 90-градусного угла, но меньше развернутого. Таким образом, тупой угол равен от 90 до 180 градусов.

Возникает вопрос: бывает ли более одного тупого угла в такой фигуре? Ответ находится на поверхности: нет, потому что сумма углов должна быть менее 180 0 . Если два угла будут иметь, например, по 95 градусов, то третьему просто не найдется места.

Два тупоугольных многоугольника равны:

• если равны обе их стороны и угол, находящийся между ними;
• если одна сторона и два угла, находящиеся рядом с ней, равны;
• если три стороны тупоугольных треугольников имеют равенство.

Замечательные линии тупоугольного треугольника

Во всех треугольниках, имеющих тупые углы, есть линии, называемые замечательными. Первая из них – высота. Она представляет собой перпендикуляр из одной из вершин на соответствующую ей сторону. Все высоты сталкиваются в точке, которая именуется как ортоцентр. В треугольнике с тупыми углами он будет находиться за пределами самой фигуры. Что касается острых углов, то центр там находится в самом треугольнике.

Еще одна линия – медиана. Это черта, проведенная от вершины к центру соответствующей стороны. Все медианы сходятся в треугольнике, а место их совмещения – это центр тяжести такого многоугольника.

Биссектриса – линия, делящая пополам как тупые углы, так и остальные. Пересечение трех таких линий всегда бывает только в самой фигуре и определяется как центр круга, вписанного в треугольник.

В свою очередь, центр круга, описанного вокруг фигуры, можно получить из трех срединных перпендикуляров. Это линии, которые были опущены из середин прямых, соединяющих вершины. Место пересечения трех срединных перпендикуляров в треугольнике, имеющем тупые углы, находится снаружи фигуры.

Остроугольный, прямоугольный и тупоугольный треугольники.

Виды треугольников

Остроугольный треугольник — это треугольник,
в котором все углы острые.

Прямоугольный треугольник — это треугольник,
в котором один из углов прямой.

Тупоугольный треугольник — это треугольник,
в котором один из углов тупой.

Как определить вид треугольника

Для того, чтобы понять какой треугольник — остроугольный, прямоугольный или тупоугольный
нужно знать какая градусная мера у углов в треугольнике.

Если один из углов в треугольнике прямой, значит треугольник прямоугольный. Все углы острые в треугольнике — значит треугольник остроугольный. Если в треугольнике один из углов тупой, значит треугольник тупоугольный.

В произвольном треугольнике все углы острые, или два угла острые, а третий прямой или тупой. Если в треугольнике вам известно, что один углов тупой или прямой, значит сумма двух других углов не больше 90 градусов.

В прямоугольном треугольнике стороны напротив острых углов называются катетами, а сторона напротив прямого угла называется гипотенузой.

Градусные меры острого, тупого, прямого углов в треугольниках

Чтобы понять как называется угол и как называется треугольник с этими углами — надо знать его градусную меру:

1. Острый угол в любом из треугольников не больше 90 градусов.
2. Прямой угол в любом из треугольников равен 90 градусам.
3. Тупой угол в любом из треугольников больше 90 градусов, но меньше 180 градусов.

Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.

Угол треугольника через три стороны

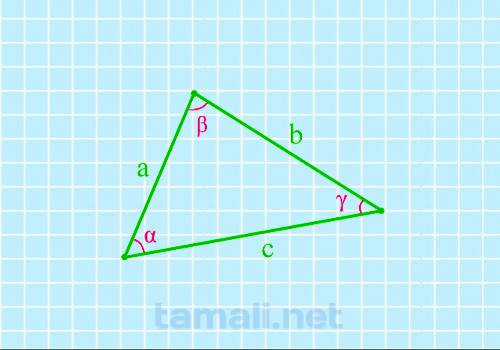
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить

cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb

где a, b, c — стороны треугольника.

Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.

Угол прямоугольного треугольника через две стороны

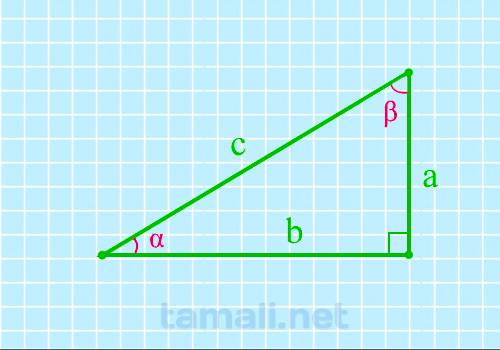
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.

sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a

где a, b — катеты, c — гипотенуза.

Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.

Острый угол прямоугольного треугольника через катет и площадь

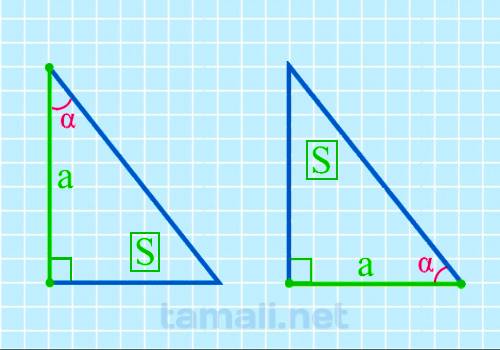
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:

tg(α) = a² / 2S

где a — катет, S — площадь прямоугольного треугольника.

Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.

Угол треугольника через высоту и катет

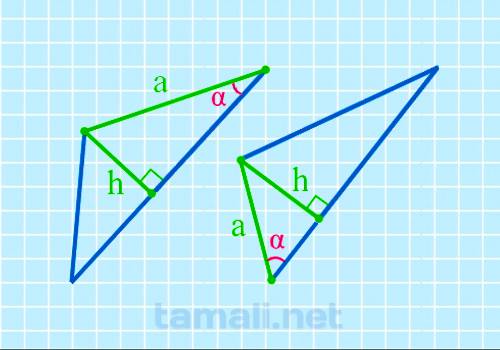
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.

sin α = h / a

где h — высота, a — катет.

Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°

Угол при основании равнобедренного треугольника через биссектрису и основание

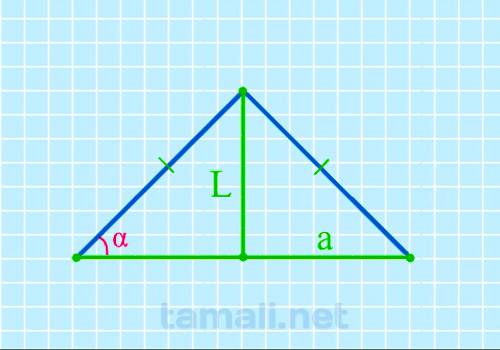
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:

tg α = L / (a/2)

где L — биссектриса, a — основание.

Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º

Угол при основании равнобедренного треугольника через биссектрису и боковую сторону

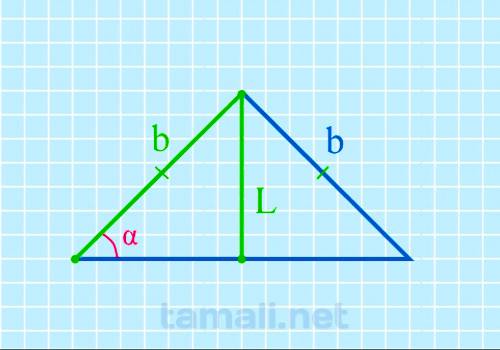
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:

sin α = L / b

где L — биссектриса, b — боковая сторона.

Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.

Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону

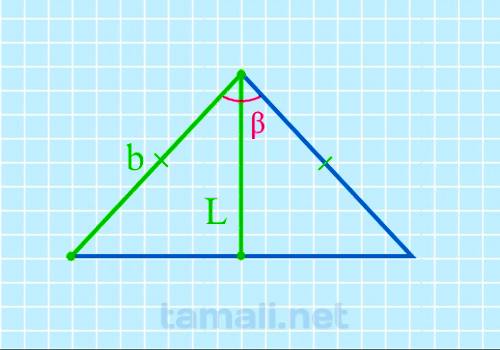
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).

2cos(β) = L / b

где L — биссектриса, b — боковая сторона.

Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону

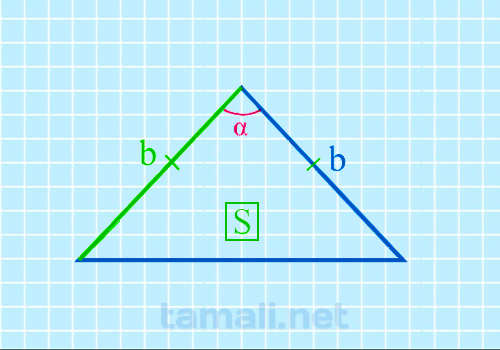
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:

sin(α) = 2S / b²

где b — боковая сторона равнобедренного треугольника, S — площадь.

Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º

Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.

Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.

Тупоугольный треугольник, элементы, свойства, признаки и формулы.

Тупоугольный треугольник – это треугольник, у которого один угол тупой.

Тупоугольный треугольник (понятие и определение)

Элементы тупоугольного треугольника

Свойства тупоугольного треугольника

Формулы тупоугольного треугольника

Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник

Тупоугольный треугольник (понятие и определение): 

Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.

Тупоугольный треугольник – это треугольник, у которого один угол тупой, а два других – острые. В свою очередь, тупой угол – это угол, градусная мера которого составляет 90° до 180°, а острый угол – это угол, градусная мера которого составляет менее 90 градусов

Рис. 1. Тупоугольный треугольник

∠ BАC– тупой угол треугольника,

∠ АВС, ∠ BСA – острые углы треугольника

По определению, тупоугольным треугольником не может быть правильный (равносторонний) треугольник, т.к. у него каждый угол составляет 60°.

Рис. 2. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника,

∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника 

По определению, тупоугольным треугольником не может быть прямоугольный треугольник , т.к. у него один угол составляет 90° и сумма двух других углов также составляет 90°.

Рис. 3. Прямоугольный треугольник

Тупоугольный треугольник также может быть одновременно равнобедренным треугольником. Но не всякий равнобедренный треугольник тупой.

Рис. 4. Равнобедренный треугольник

АВ = AС – боковые стороны, BС – основание,

∠ ВАС – вершинный угол, ∠ АBC и ∠ BСA – углы при основании

Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.

Элементы тупоугольного треугольника:

Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.

Рис. 5. Тупоугольный треугольник и внешний угол

∠ ВAD – острый угол

Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника

MA – медиана тупоугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника

MС – высота тупоугольного треугольника

Высота тупоугольного треугольника может лежать за пределами треугольника.

Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы  пересекаются в точке, которая является центром вписанной окружности.

Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника

MA – биссектриса тупого угла тупоугольного треугольника

Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Свойства тупоугольного треугольника:

Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 9. Тупоугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 10. Тупоугольный треугольник с равными боковыми сторонами

АВ = АС

3. Сумма углов тупоугольного треугольника равна 180°.

4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:

• • a < b + c;
  • a > b – c;
  • b < a + c,
  • b > a – c;
  • c < a + b;
  • c > a – b.

Квадрат

Овал

Остроугольный треугольник

Полукруг

Прямой угол

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Ромб

Трапеция

Тупой угол

Тупоугольный треугольник

Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
20 693

Информация по назначению калькулятора

Треугольник — это одна из основных геометрических фигур: многоугольник с тремя углами (или вершинами) и тремя сторонами (или ребрами), которые являются прямыми отрезками.

В евклидовой геометрии любые три неколлинеарные точки определяют треугольник и единственную плоскость, то есть двумерное декартово пространство.

Сумма длин любых двух сторон треугольника всегда превышает длину третьей стороны. Это и есть неравенство треугольника.

Треугольники могут быть классифицированы в соответствии с относительной длиной их сторон:

⇒ В равностороннем треугольнике все стороны имеют одинаковую длину. Равносторонний треугольник также является равноугольным многоугольником, т.е. все его внутренние углы равны, а именно 60° — это правильный многоугольник.

⇒ В равнобедренном треугольнике две стороны имеют одинаковую длину. Равнобедренный треугольник также имеет два совпадающих угла (а именно, углы, противоположные совпадающим сторонам). Равносторонний треугольник — это равнобедренный треугольник, но не все равнобедренные треугольники являются равносторонними треугольниками.

⇒ В скалярном треугольнике все стороны имеют разную длину. Внутренние углы в скалярном треугольнике все разные.

Треугольники также могут быть классифицированы в соответствии с их внутренними углами:

⇒ Прямоугольный треугольник имеет один внутренний угол 90° (прямой угол). Сторона, противоположная прямому углу, является гипотенузой; это самая длинная сторона в прямоугольном треугольнике. Две другие стороны — катеты треугольника.

⇒ Тупой треугольник имеет один внутренний угол, больший 90° (тупой угол).

⇒ Острый треугольник имеет внутренние углы, которые все меньше 90° (три острых угла). Равносторонний треугольник — это острый треугольник, но не все острые треугольники являются равносторонними треугольниками.

⇒ Наклонный треугольник имеет только углы, которые меньше или больше 90°. Следовательно, это любой треугольник, который не является прямоугольным треугольником.

Онлайн калькулятор поможет найти параметры треугольника, такие как:

• Длины сторон

— равны в равностороннем треугольнике

• Углы

— также равны в равностороннем треугольнике

• Высота

— это прямая линия, проходящая через вершину и перпендикулярная противоположной стороне (т. е. образующая прямой угол с ней)

• Периметр

— равен сумме всех 3х сторон (P=AB+BC+AC)

• Площадь

— равна половине произведения высоты и стороны к которой построена высота (S=1/2 * H * AC)

• Медианы
• Биссектрисы
• Радиус Вписанной и Описанной окружностей
• Диаметр Вписанной и Описанной окружностей
• Длина Вписанной и Описанной окружностей
• Площадь Вписанной и Описанной окружностей