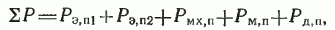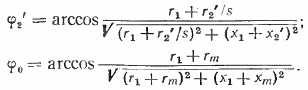Как найти ток обмотки статора

АСИНХРОННЫЕ ДВИГАТЕЛИ

Примеры расчета

Задача 1.

Асинхронный трехфазный двигатель с
короткозамкнутым ротором типа 4A100S4
имеет следующие паспортные данные:
напряжение U = 220/380В,
номинальная мощность P_н
= 3 кВт, частота вращения n_н
= 1434 об/мин, К.П.Д. =
82,0%, коэффициент мощности cos
= 0,83, кратность пускового тока α = 6,0
перегрузочная способность двигателя
λ= 2,4, кратность пускового
момента β = 2,0.

Определить, номинальный и пусковой токи
двигателя при соединении обмотки статора
в треугольник и звезду. Построить
механическую характеристику не менее
чем по 6 расчетным точкам. Возможен ли
пуск нагруженного двигателя, если
подводимое напряжение на 10% ниже
номинального и если пуск производится
путем переключения обмоток статора со
звезды на треугольник от сети с напряжением
220В?

Решение:

Для определения числа пар полюсов можно
воспользоваться маркировкой двигателя,
частотой вращения магнитного поля или
ротора.

Структура типоразмера двигателя
следующая:

Y A
X X
XXX X
X X
X X

1 2 3 4 5 6 7 8 9 10

1 – Порядковый номер серии;

2 – род двигателя – асинхронный;

3 – исполнение по степени защиты (Н –
1Р23, отсутствие данного знака — 1Р44);

4 — исполнение двигателя
по материалу станины и щита (А – станина
и щиты алюминиевые; X
– станина алюминиевая, щиты чугунные
или наоборот; отсутствие данного знака
означает, что станина и щиты чугунные
или стальные);

5 — высота оси вращения;

6 — условная длина
станины по МЭК (S,M,L);

7 – длина сердечника статора (А или В,
отсутствие данного знака означает одну
длину в установочном размере);

8 – климатические исполнения по ГОСТ
15150-69 (У – для умеренного климата);

9 – число полюсов: 2,4,6,8,10,12;

10 – категория размещения по ГОСТ
15150-69(3) (1 – на открытом воздухе; 2 – в
помещения, в которых отсутствует прямое
воздействие атмосферных осадков и
солнечной радиации; 3 – закрытые помещения
с естественной вентиляцией без
искусственно регулируемых климатических
условий).

Для заданного двигателя
число полюсов по маркировке – 4,
следовательно, две пары полюсов p=2

Частота вращения
магнитного поля n₁
= 60f₁/p
= 1500 об/мин. Эту же величину можно получить
отталкиваясь от номинальной частоты
вращения ротора n_н
= 1434 об/мин и используя стандартную шкалу
скоростей, при этом частота вращения
поля будет иметь ближайшее большее
значение — n₁
= 1500 об/мин.

Номинальное значение скольжения

или 4,4 %

1. Определение электрических характеристик
   двигателя.

Для определения фазных, линейных и
пусковых токов (фазными токами являются
токи в обмотках статора, линейными –
токи в подводящих проводах) нужно учесть,
что если двигатель рассчитан на работу
от сети переменного тока с напряжением
220/380В, то это значит, что каждая фаза
обмотки статора рассчитана на напряжение
220В. Обмотку необходимо включить по
схеме “треугольник”, если в сети
линейное напряжение U =
220В, и по схеме “звезда”, если в сети
линейное напряжение U =
380В (рис 3.6)

Мощность потребляемая двигателем из
сети:

Определим фазный, линейный и пусковой
токи при линейном напряжении U_Л
= 220В и соединении обмотки статора по
схеме “треугольник”, при этом U_Л=U_Ф

Фазный ток в обмотке статора:

Линейный ток – ток в проводах, питающих
двигатель:

Пусковой ток:

Найдем значения фазных, линейных и
пусковых токов, если обмотки статора
включены по схеме “звезда” и
подключены к сети с линейным напряжением
U = 380 В.

Значение фазного тока найдем из формулы
мощностей для линейных значений токов
и напряжений с учетом того, что при
данном соединении линейный ток равен
фазному:

Пусковой ток:

Из сопоставления токов можно увидеть,
что фазные токи получились одинаковыми,
а линейные и пусковые токи при схеме
включения по схеме «треугольник» больше
в √3 раз. Для уменьшения этих токов на
момент пуска обмотки статора включают
по схеме «звезда».

1. Определение механических параметров
   и построение механической характеристики

Механическая характеристика двигателя
является основной характеристикой и
представляет собой зависимость М
= f(n₂),
а в свою очередь n₂
= f(s).

Механическая характеристика строится
по четырем основным и нескольким
вспомогательным токам. Основные точки
следующие:

1. Режим холостого хода: М = 0, s
   = 0, n₂ = n₁=1500
   об/мин.

2. Номинальный режим: М= М_н,
   s = s_н,
   n₂ = n_н.

Номинальный вращающий момент двигателя:

n₂ = n_н.=1434
об/мин

1. Критическая точка: М = М_max,
   s = s_кр,
   n₂ = n_кр

Максимальный момент определяется по
заданной перегрузочной способности
двигателя:

Критическое скольжение – s_кр,
при котором асинхронная машина развивает
максимальный вращающий момент.

Используя основную формулу скольжения
(3.2) можно определить n_кр

1. Момент пуска: М = М_n,
   s = 1, n₂
   = 0.

Пусковой момент определяется по заданной
кратности пускового момента β:

Для расчета промежуточных точек
воспользуемся упрощенной формулой
(3.6), которая позволяет определить момент
при любых значениях скольжения:

Следует только учесть, что эта формула
наиболее точно описывает механическую
характеристику на участке устойчивой
работы (от холостого хода до достижения
максимального момента), на участке
неустойчивой работы и, особенно при
значениях скольжения, близких к пусковым,
появляется значительная погрешность.
Двигатели рассматриваемой серии
конструктивно выполнены с глубоким
пазом, то есть с улучшенными пусковыми
свойствами, а в данной формуле это не
учтено.

Выбираем
две промежуточные расчетные точки при
значениях скольжения в диапазоне
устойчивой работы двигателя: 0,02 (интервал
между точкой холостого хода и номинальным
режимом) и 0,1 (интервал между номинальным
режимом и критической точкой). Скорость
вращения ротора n₂
при этих скольженьях вычисляем исходя
из основной формулы скольжения:

Результаты расчета механической
характеристики сводим в таблицу:

Механическая характеристика имеет вид:

Критич.

Номин.

Пуск.

Хол.ход.

1. Определение возможности пуска
   двигателя при номинальной нагрузке и
   пониженном напряжении.

Вращающий момент на валу двигателя в
соответствии с выражением (3.8)

Где C
– постоянный коэффициент, зависящий
от конструктивных данных двигателя; U
– подводимое к статору напряжение.

При понижении
напряжения на 10% подводимое напряжение
станет U^´
= 0.9U_н,
вращающий момент:

M’
= C(U^´)²
= C(0.9U_н)²
= 0.81CU²_н
= 0.81M_н
= 0.81·20=16,2Нм

Соответственно пусковой момент:

M_п^´
=βM^´=2,0·16,2=32,4Нм,

Сравниваем этот
момент с номинальным – М_п^´>М_н,
т.е. пуск возможен

Для понижения пусковых токов часто пуск
асинхронных двигателей осуществляют
при пониженном напряжении. Двигатели,
работающие при соединении обмоток
статора по схеме “треугольник”, пускают
без нагрузки путем включения обмоток
статора на время пуска по схеме «звезда».
Определим пусковой момент двигателя
при данном виде пуска.

В момент пуска обмотки
находятся под напряжением U_ф
= U_л/3
= 220/3
= 127B,
что составляет 57,7% от U_н,
пусковой момент при этом:

M_n
= CU²
= C(0.577U_н)²
= 0.33CU²_н
= 0.33M_н
= 0.33·20=6,6 Нм.

Полученный момент меньше номинального,
именно поэтому пуск осуществляют в
режиме холостого хода. После разгона
двигателя обмотки переключают на схему
«треугольник» и нагружают двигатель
номинальным моментом.

Пусковой ток при этом уменьшится в √3
раз по сравнению с прямым пуском по
схеме «треугольник» и составит:

Соседние файлы в папке электротех

• #
• #
• #

Здравствуйте, уважаемые читатели и гости сайта «Заметки электрика».

Решил написать статью о расчете номинального тока для трехфазного электродвигателя.

Этот вопрос является актуальным и кажется на первый взгляд не таким и сложным, но почему-то в расчетах зачастую возникают ошибки.

В качестве примера для расчета я возьму трехфазный асинхронный двигатель АИР71А4 мощностью 0,55 (кВт).

Вот его внешний вид и бирка с техническими данными.

Если двигатель Вы планируете подключать в трехфазную сеть 380 (В), то значит его обмотки нужно соединить по схеме «звезда», т.е. на клеммнике необходимо соединить выводы V2, U2 и W2 между собой с помощью специальных перемычек.

При подключении этого двигателя в трехфазную сеть напряжением 220 (В) его обмотки необходимо соединить треугольником, т.е. установить три перемычки: U1-W2, V1-U2 и W1-V2.

Если же Вы решите подключить этот двигатель в однофазную сеть 220 (В), то его обмотки также должны быть соединены треугольником.

Для информации: почитайте подробную статью о схемах соединения обмоток в «звезду» и «треугольник».

Для правильного выбора автоматического выключателя (или предохранителей) и тепловых реле для защиты двигателя, а также для выбора контактора для его управления, в первую очередь нам нужно знать номинальный ток двигателя для конкретной схемы соединения обмоток.

Обычно, номинальные токи указаны прямо на бирке, поэтому можно смело ориентироваться на них. Но иногда циферки не видны или стерты, а известна только лишь мощность двигателя или другие его параметры.

Такое очень часто встречается, но еще чаще бирка вообще отсутствует или так затерта, что на ней абсолютно ничего не видно — приходится только догадываться, что там изображено.

Но это отдельный случай и что делать в таких ситуациях, я расскажу Вам в ближайшее время.

В данной же статье я хочу акцентировать Ваше внимание на формулу по расчету тока двигателя, потому что даже не все «специалисты» ее знают, хотя может и знают, но не хотят вспомнить основы электротехники.

Итак, приступим.

Внимание! Мощность на шильдике двигателя указывается не электрическая, а механическая, т.е. полезная механическая мощность на валу двигателя. Об этом отчетливо говорится в действующем ГОСТ Р 52776-2007, п.5.5.3:

Полезную механическую мощность обозначают, как Р2.

Чаще всего мощность двигателя указывают не в ваттах (Вт), а в киловаттах (кВт). Для тех кто забыл, читайте статью о том, как перевести ватты в киловатты и наоборот.

Еще реже, на бирке указывают мощность в лошадиных силах (л.с.), но такого я ни разу еще не встречал на своей практике. Для информации: 1 (л.с.) = 745,7 (Ватт).

Но нас интересует именно электрическая мощность, т.е. мощность, потребляемая двигателем из сети. Активная электрическая мощность обозначается, как Р1 и она всегда будет больше механической мощности Р2, т.к. в ней учтены все потери двигателя.

1. Механические потери (Рмех.)

К механическим потерям относятся трение в подшипниках и вентиляция. Их величина напрямую зависит от оборотов двигателя, т.е. чем выше скорость, тем больше механические потери.

У асинхронных трехфазных двигателей с фазным ротором еще учитываются потери между щетками и контактными кольцами. Более подробно об устройстве асинхронных двигателей Вы можете почитать здесь.

2. Магнитные потери (Рмагн.)

Магнитные потери возникают в «железе» магнитопровода. К ним относятся потери на гистерезис и вихревые токи при перемагничивании сердечника.

Величина магнитных потерь в статоре зависит от частоты перемагничивания его сердечника. Частота всегда постоянная и составляет 50 (Гц).

Магнитные потери в роторе зависят от частоты перемагничивания ротора. Эта частота составляет 2-4 (Гц) и напрямую зависит от величины скольжения двигателя. Но магнитные потери в роторе имеют малую величину, поэтому в расчетах чаще всего не учитываются.

3. Электрические потери в статорной обмотке (Рэ1)

Электрические потери в обмотке статора вызваны их нагревом от проходящих по ним токам. Чем больше ток, чем больше нагружен двигатель, тем больше электрические потери — все логично.

4. Электрические потери в роторе (Рэ2)

Электрические потери в роторе аналогичны потерям в статорной обмотке.

5. Прочие добавочные потери (Рдоб.)

К добавочным потерям можно отнести высшие гармоники магнитодвижущей силы, пульсацию магнитной индукции в зубцах и прочее. Эти потери очень трудно учесть, поэтому их принимают обычно, как 0,5% от потребляемой активной мощности Р1.

Все Вы знаете, что в двигателе электрическая энергия преобразуется в механическую. Если объяснить чуть подробнее, то при подведенной к двигателю электрической активной мощности Р1, некоторая ее часть затрачивается на электрические потери в обмотке статора и магнитные потери в магнитопроводе. Затем остаточная электромагнитная мощность передается на ротор, где она расходуется на электрические потери в роторе и преобразуется в механическую мощность. Часть механической мощности уменьшается за счет механических и добавочных потерь. В итоге, оставшаяся механическая мощность — это и есть полезная мощность Р2 на валу двигателя.

Все эти потери и заложены в единственный параметр — коэффициент полезного действия (КПД) двигателя, который обозначается символом «η» и определяется по формуле:

η = Р2/Р1

Кстати, КПД примерно равен 0,75-0,88 для двигателей мощностью до 10 (кВт) и 0,9-0,94 для двигателей свыше 10 (кВт).

Еще раз обратимся к данным, рассматриваемого в этой статье двигателя АИР71А4.

На его шильдике указаны следующие данные:

• тип двигателя АИР71А4
• заводской номер № ХХХХХ
• род тока — переменный
• количество фаз — трехфазный
• частота питающей сети 50 (Гц)
• схема соединения обмоток ∆/Y
• номинальное напряжение 220/380 (В)
• номинальный ток при треугольнике 2,7 (А) / при звезде 1,6 (А)
• номинальная полезная мощность на валу Р2 = 0,55 (кВт) = 550 (Вт)
• частота вращения 1360 (об/мин)
• КПД 75% (η = 0,75)
• коэффициент мощности cosφ = 0,71
• режим работы S1
• класс изоляции F
• класс защиты IP54
• название предприятия и страны изготовителя
• год выпуска 2007

Расчет номинального тока электродвигателя

В первую очередь необходимо найти электрическую активную потребляемую мощность Р1 из сети по формуле:

Р1 = Р2/η = 550/0,75 = 733,33 (Вт)

Величины мощностей подставляются в формулы в ваттах, а напряжение — в вольтах. КПД (η) и коэффициент мощности (cosφ) — являются безразмерными величинами.

Но этого не достаточно, потому что мы не учли коэффициент мощности (cosφ), а ведь двигатель — это активно-индуктивная нагрузка, поэтому для определения полной потребляемой мощности двигателя из сети воспользуемся формулой:

S = P1/cosφ = 733,33/0,71 = 1032,85 (ВА)

Найдем номинальный ток двигателя при соединении обмоток в звезду:

Iном = S/(1,73·U) = 1032,85/(1,73·380) = 1,57 (А)

Найдем номинальный ток двигателя при соединении обмоток в треугольник:

Iном = S/(1,73·U) = 1032,85/(1,73·220) = 2,71 (А)

Как видите, получившиеся значения равны токам, указанным на бирке двигателя.

Для упрощения, выше приведенные формулы можно объединить в одну общую. В итоге получится:

Iном = P2/(1,73·U·cosφ·η)

Поэтому, чтобы определить номинальный ток двигателя, необходимо в данную формулу подставлять механическую мощность Р2, взятую с бирки, с учетом КПД и коэффициента мощности (cosφ), которые указаны на той же бирке или в паспорте на электродвигатель.

Перепроверим формулу.

Ток двигателя при соединении обмоток в звезду:

Iном = P2/(1,73·U·cosφ·η) = 550/(1,73·380·0,71·0,75) = 1,57 (А)

Ток двигателя при соединении обмоток в треугольник:

Iном = P2/(1,73·U·cosφ·η) = 550/(1,73·220·0,71·0,75) = 2,71 (А)

Надеюсь, что все понятно.

Примеры

Решил привести еще несколько примеров с разными типами двигателей и мощностями. Рассчитаем их номинальные токи и сравним с токами, указанными на их бирках.

1. Асинхронный двигатель 2АИ80А2ПА мощностью 1,5 (кВт)

Как видите, этот двигатель можно подключить только в трехфазную сеть напряжением 380 (В), т.к. его обмотки собраны в звезду внутри двигателя, а в клеммник выведено всего три конца, поэтому:

Iном = P2/(1,73·U·cosφ·η) = 1500/(1,73·380·0,85·0,82) = 3,27 (А)

Полученный ток 3,27 (А) соответствует номинальному току 3,26 (А), указанному на бирке.

2. Асинхронный двигатель АОЛ2-32-4 мощностью 3 (кВт)

Данный двигатель можно подключать в трехфазную сеть напряжением, как на 380 (В) звездой, так и на 220 (В) треугольником, т.к. в клеммник у него выведено 6 концов:

Iном = P2/(1,73·U·cosφ·η) = 3000/(1,73·380·0,83·0,83) = 6,62 (А) — звезда

Iном = P2/(1,73·U·cosφ·η) = 3000/(1,73·220·0,83·0,83) = 11,44 (А) — треугольник

Полученные значения токов при разных схемах соединения обмоток соответствуют номинальным токам, указанных на бирке.

3. Асинхронный двигатель АИРС100А4 мощностью 4,25 (кВт)

Аналогично, предыдущему.

Iном = P2/(1,73·U·cosφ·η) = 4250/(1,73·380·0,78·0,82) = 10,1 (А) — звезда

Iном = P2/(1,73·U·cosφ·η) = 4250/(1,73·220·0,78·0,82) = 17,45 (А) — треугольник

Расчетные значения токов при разных схемах соединения обмоток соответствуют номинальным токам, указанных на шильдике двигателя.

4. Высоковольтный двигатель А4-450Х-6У3 мощностью 630 (кВт)

Этот двигатель можно подключить только в трехфазную сеть напряжением 6 (кВ). Схема соединения его обмоток — звезда.

Iном = P2/(1,73·U·cosφ·η) = 630000/(1,73·6000·0,86·0,947) = 74,52 (А)

Расчетный ток 74,52 (А) соответствует номинальному току 74,5 (А), указанному на бирке.

Дополнение

Представленные выше формулы это конечно хорошо и по ним расчет получается более точным, но есть в простонародье более упрощенная и приблизительная формула для расчета номинального тока двигателя, которая наибольшее распространение получила среди домашних умельцев и мастеров.

Все просто. Берете мощность двигателя в киловаттах, указанную на бирке и умножаете ее на 2 — вот Вам и готовый результат. Только данное тождество уместно для двигателей 380 (В), собранных в звезду. Можете проверить и поумножать мощности приведенных выше двигателей. Но лично я же настаиваю Вам использовать более точные методы расчета.

P.S. А вот теперь, как мы уже определились с токами, можно приступать к выбору автоматического выключателя, предохранителей, тепловой защиты двигателя и контакторов для его управления. Об этом я расскажу Вам в следующих своих публикациях. Чтобы не пропустить выход новых статей — подписывайтесь на рассылку сайта «Заметки электрика». До новых встреч.

Если статья была Вам полезна, то поделитесь ей со своими друзьями:

 Рабочие характеристики асинхронного двигателя — зависимости потребляемого тока I₁ и мощности Р₁, КПД, cos φ и скольжения s от полезной механической мощности P₂. Эти характеристики определяются при постоянном напряжении U₁ и частоте f₁ сети.

Рабочие характеристики асинхронного двигателя могут быть получены экспериментально (опытным путем) и рассчитаны с помощью схемы замещения.

Ниже приводится расчет рабочих характеристик асинхронного двигателя по схеме замещения.

По обмотке статора асинхронной машины протекает многофазная система токов, обычно трехфазная, которая создает в воздушном зазоре машины вращающееся магнитное поле (магнитный поток Ф).

 Вращающееся магнитное поле в свою очередь индуктирует (наводит) в проводниках обмотки ротора ЭДС, под действием которой в замкнутой накоротко обмотке ротора протекает ток I₂. Этот ток, взаимодействуя с магнитным потоком Ф, создает механическую силу, стремящуюся привести ротор во вращение в сторону вращения магнитного поля.

Определим, с какой частотой вращения магнитное поле машины пересекает проводники ротора. Эта частота равна, об/мин:

             (9)

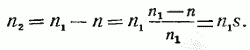
Определим частоту ЭДС f₂, которая наводится магнитным полем асинхронной машины в проводниках ротора, Гц:

f₂=р n₂/60.            (10)

Если учесть, что n₂=n₁s [см. формулу (9)], то можно записать

       (11)

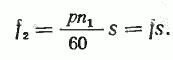
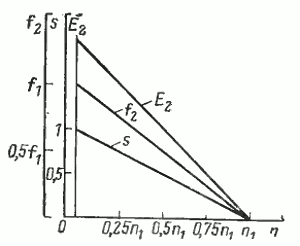
Из формулы (11) видно, что если ротор машины неподвижен (n=0, s=l), то частота ЭДС, наводимой в роторе, равна частоте сети. По мере увеличения частоты вращения ротора ЭДС понижается и при синхронной частоте будет равна нулю. На рис. 13 показаны изменения скольжения, частоты и ЭДС в роторе в зависимости от частоты вращения ротора.

Рис. 13. Зависимость скольжения s, частоты f₂ и ЭДС, наводимой в роторе, E2 от частоты вращения асинхронного двигателя n

Из закона электромагнитной индукции следует, что при гармоническом изменении магнитного поля наводимая в обмотке ЭДС равна:

E=4,44fwk_обФ_max,             (12)

где f — электрическая частота, Гц; w — число последовательно соединенных витков фазы; k_об — обмоточный коэффициент; Ф_max — максимальное значение рабочего потока, сцепленного с обмоткой, Вб.

Знание частоты f₂ в роторе дает возможность определить ЭДС ротора Е₂ при произвольной частоте вращения (скольжении), В, в виде

E₂=4,44f₂w2k_об2Ф_max,           (13)

где w₂ — число последовательно  соединенных витков обмотки ротора; k_об2 — обмоточный   коэффициент   ротора.

Подстановка f₂  из формулы (11) дает, В,

E_2s=4,44f s w₂k_об2Ф_max=sE₂,     (   14)

где Е₂ — ЭДС, наводимая в неподвижной обмотке ротора потоком Ф_max, В.

Осветим теперь важный для анализа работы асинхронных двигателей вопрос о зависимости вращающегося магнитного потока двигателя от режима работы машины. Для этого, чтобы представить себе эту зависимость, определим вначале, какую ЭДС Е₁ наводит этот поток в каждой фазе обмотки статора, В:

E₁=4,44fw₁k_об1Ф_max,     (15)

где w₁ — число витков одной фазы статора; k_об1 —обмоточный коэффициент обмотки статора.

Напряжение U₁, приложенное к статору, уравновешивается ЭДС E₁ и падением напряжения I₁z₁ на внутреннем сопротивлении z₁=r₁+jx₁ обмотки статора (х₁— индуктивное сопротивление обмотки, определяемое потоком рассеяния) . При изменении нагрузки двигателя от нуля (холостой ход) до номинальной падение напряжения составляет 5—10 % приложенного. Таким образом, с достаточной для качественного анализа точностью можно полагать, что напряжение U₁ полностью компенсируется ЭДС Е1 т. е. .

U₁≈E₁         (16)

Учитывая формулу (15), нетрудно заключить, что ЭДС и вращающийся магнитный поток двигателя зависят от приложенного к двигателю напряжения. При постоянном напряжении поток Фmах остается приблизительно постоянным независимо от изменения нагрузки двигателя.

Рассмотрим вначале явления, происходящие в машине с заторможенным ротором и замкнутой накоротко обмоткой ротора. Асинхронный двигатель в этом режиме подобен трансформатору с короткозамкнутой вторичной обмоткой. Отличие состоит в том, что вторичная магнитная цепь отделена от первичной воздушным зазором, первичная обмотка (статора) и вторичная обмотка (ротора) равномерно распределены по окружности, а магнитное поле вращающееся.

Как видно из формулы (14) и рис. 13, ЭДС, наводимая в обмотке ротора, когда он неподвижен, является максимальной. В силу этого и ток, проходящий по обмоткам статора и ротора, также будет наибольшим. Этот режим называется режимом короткого замыкания (КЗ). Ток статора в этом режиме называется током короткого замыкания и превышает его номинальный ток в 4—7 раз. Асинхронный двигатель в таких условиях нельзя длительно оставлять под полным напряжением из-за перегрева обмоток, который может привести к аварии.

Для определения тока короткого замыкания двигателя делают опыт КЗ. Этот опыт заключается в том, что к двигателю с заторможенным (неподвижным) ротором подводят пониженное напряжение, регулируя которое, устанавливают номинальный ток. Напряжение, подводимое к двигателю в опыте КЗ, оказывается малым (15— 20%) по сравнению с номинальным. На базе этого опыта можно в безопасных для двигателя условиях определить величину тока короткого замыкания /к при номинальном напряжении, А:

       (17)

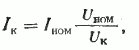
где U_ном — номинальное напряжение, В; U_к — напряжение в опыте КЗ при номинальном токе, В; I_ном — номинальный ток, А.

Замеряя в этом опыте по ваттметру мощность короткого замыкания Р_к, подводимую к одной фазе двигателя,  находят также  коэффициент  мощности в режиме  КЗ

      (18)

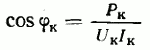
и эквивалентное активное сопротивление статора и ротора двигателя гк в режиме КЗ на одну фазу, Ом,

r_к=P_к/I_ном2              (19) 

Это эквивалентное активное сопротивление равно сумме активного сопротивления статора и приведенного активного сопротивления ротора. Понятие о приведенном активном и реактивном сопротивлении ротора будет дано ниже.

Определив угол φк по значению cosφк из формулы (18), легко найти и эквивалентное реактивное сопротивление двигателя в режиме короткого замыкания, Ом:

х_к=r_кctgφ_к (20)

Индуктивное сопротивление хк равно сумме индуктивного сопротивления статора и приведенного индуктивного сопротивления ротора.

Поскольку частота вращения ротора двигателя в этом режиме равна нулю, его механическая мощность также равна нулю. Потери в стали во время опыта короткого замыкания очень малы, так как мал вращающийся магнитный поток. Поэтому мощность Р_к, которая подводится к машине, почти вся идет на нагрев проводников обмоток статора и ротора. То же самое можно сказать о режиме КЗ при полном напряжении.

Теперь представим себе, что обмотка ротора разомкнута, а обмотка статора включена в сеть. Ток по роторной обмотке при этом не проходит и асинхронный двигатель подобен трансформатору, но уже в режиме холостого хода (XX). Так как ток в проводниках ротора отсутствует, то механическая сила не возникает и ротор остается неподвижным.

По обмотке статора при этом проходит ток холостого хода I₀, который создает магнитодвижущую силу (МДС), необходимую для создания магнитного потока Ф_max. Поскольку в магнитной цепи асинхронного двигателя имеется зазор, то для создания магнитного потока требуется относительно больший ток, чем в трансформаторе. В двигателях большой и средней мощности ток XX составляет 25—35, а в двигателях малой мощности — 35—60% номинального тока.

Наводимая в неподвижном роторе ЭДС может быть определена по формуле (14), если учесть, что скольжение в этом режиме равно 1. Отношение ЭДС в обмотке статора к ЭДС в обмотке ротора называется коэффициентом трансформации ЭДС и может быть определено по формуле

           (21)

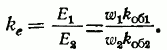
Мощность, потребляемая двигателем в режиме XX при неподвижном роторе, расходуется на потери в проводниках статора двигателя, потери на перемагничивание и вихревые токи в стали статора и в стали ротора.

Важно заметить, что режим XX при неподвижном роторе очень близок к режиму, который возникает, когда  асинхронный двигатель не выполняет полезной работы и вращается на холостом ходу. В этом случае частота вращения ротора двигателя почти равна синхронной, а  скольжение примерно равно нулю [см. формулы (4), (9) и рис. 13]. Электродвижущая сила в роторе будет близкой к нулю, и, следовательно, подобно режиму XX при неподвижном роторе практически равен  нулю ток в роторе. При холостом ходе вращающегося двигателя ток в обмотке статора, как и в случае холостого хода неподвижного двигателя, определяется в основном МДС, необходимой для создания магнитного потока Ф_max.

При вращении ротора в двигателе появляются потери, которых нет в случае неподвижного ротора; это механические потери на трение и вентиляционные. Однако когда частота вращения ротора примерно равна синхронной, исчезают потери в стали ротора двигателя, поскольку магнитное поле теперь очень медленно перемещается относительно ротора и его сталь почти не перемагничивается. Таким образом, потери и, следовательно, мощность в двух режимах холостого хода оказываются близкими.

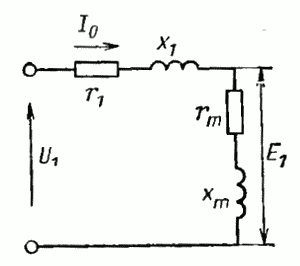
Асинхронная машина в режиме холостого хода может быть представлена схемой замещения, показанной на рис. 14. Для определения параметров и характеристик двигателя помимо опыта КЗ выполняют опыт XX, во время которого замеряют ток обмотки статора I₀ (А) и потребляемую мощность Р₀ (Вт). Это позволяет определить сопротивления в схеме замещения двигателя на холостом ходу, а также коэффициент мощности XX:

cosφ₀=P₀/(UI₀).            (22)

Рис. 14. Схема замещения первичной цепи (статора)   асинхронного  двигателя,  работающего  в режиме холостого хода

Перейдем теперь к рассмотрению общего случая режима нагрузки, когда ротор вращается с частотой, меньшей частоты XX. Определим, какой ток будет проходить по обмотке ротора во всем диапазоне рабочих режимов. Наводимая вращающимся магнитным потоком ЭДС в обмотке ротора зависит при постоянном напряжении только от скольжения и может быть найдена по (14). Ток ротора будет, очевидно, зависеть от ЭДС, наводимой в роторе, и сопротивления обмотки ротора, при этом полное сопротивление цепи в случае переменного тока определяется не только активным сопротивлением проводников обмотки, но и ее индуктивным сопротивлением. Индуктивное сопротивление обмотки ротора изменяется так же, как и ЭДС ротора E_2s, Ом:

x_2s=2πf₂L₂=s2πf₁L₂ =sx₂,      (23)

где L₂ — индуктивность обмотки ротора, Гн; х₂— индуктивное сопротивление рассеяния обмотки неподвижного ротора при s=l, Ом.

Теперь, используя закон Ома для цепей переменного тока, найдем ток ротора, А:

      (24)

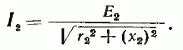
Учитывая (14) и (23), формулу (24) можно записать иначе:

           (25)

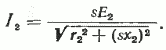
Таким образом, можно видеть, что при скольжении, равном нулю или близком к нему (это соответствует синхронной или близкой к синхронной частоте вращения ротора), ток ротора равен нулю или очень мал. Это совпадает с тем, что было сказано выше относительно режима XX при вращающемся роторе. По мере уменьшения частоты вращения двигателя, т. е. при увеличении скольжения, ток возрастает за счет увеличения ЭДС ротора, однако рост тока ограничивается увеличением индуктивного сопротивления ротора.

Если разделить числитель и знаменатель выражения (25) для тока ротора I₂ на s, то получим следующую формулу:

           (26)

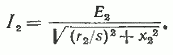
Из этого следует, что если мы примем, что ротор неподвижен, а его активное сопротивление меняется обратно пропорционально скольжению, то по его обмотке будет проходить точно такой же ток, как и при вращающемся роторе. Удобство такого преобразования состоит в том, что оно позволяет вместо вращающегося ротора (вращающаяся вторичная электрическая цепь) рассматривать неподвижный ротор (неподвижная вторичная цепь).

Однако изучение процессов, происходящих в асинхронной машине, и расчет ее характеристик можно сделать более удобными, если заменить реальную обмотку ротора эквивалентной с числом витков в фазе и числом фаз, равным им у первичной обмотки (обмотки статора), т. е. вместо обмотки ротора с числом фаз m₂, числом витков в фазе w₂ и обмоточным коэффициентом k_об2 будем полагать, что обмотка ротора имеет число фаз ти число витков в фазе w₁ и обмоточный коэффициент k_об1. Эта замена называется приведением обмотки ротора к обмотке статора. Нетрудно видеть, что магнитный поток Ф в этом случае будет наводить в эквивалентной (приведенной) обмотке ротора ЭДС, равную ЭДС обмотки статора E₂‘=E₁ (штрихом будем обозначать приведенные величины).

Замена обмотки ротора не должна привести к изменению потребляемой мощности, потерь, магнитодвижущей силы и фазы тока обмотки. Из этого условия определяются приведенные величины тока, активного и индуктивного сопротивлений обмотки ротора .

В соответствии с (13) имеем, В

           (27)

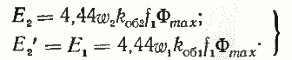
Из формул (27) вытекает отношение между ЭДС приведенной и реальной обмоток заторможенного ротора, которое называется коэффициентом трансформации ЭДС или напряжений. Он равен:

          (28)

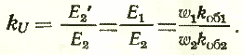
Из условия неизменности магнитодвижущих сил F₂‘ =F₂ следует, что

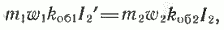
откуда вытекает отношение между токами, которое называется коэффициентом трансформации токов. Он равен:

          (29)

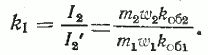
Из условия неизменности потерь в обмотке ротора при приведении следует, что

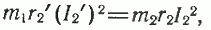
откуда

           (30)

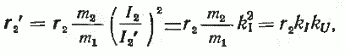
или r₂‘=k_rr₂,

где k_r=k_Ik_U — коэффициент приведения сопротивлений.

Из условия неизменности фазы тока обмотки ротора следует

           (31)

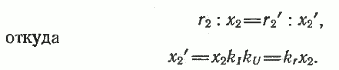
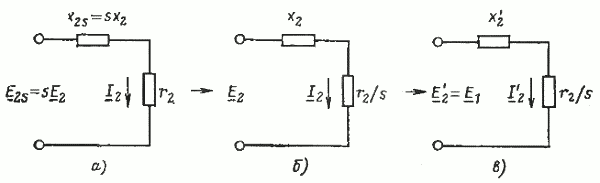
Процесс приведения цепи ротора показан на рис. 15. От схемы замещения обмотки вращающегося ротора (рис. 15,а) переходим к схеме замещения неподвижного ротора (рис. 15,б), а затем приводим обмотку ротора к обмотке статора (рис. 15, в).

Рис. 15. Схемы замещения: а — обмотки вращающегося ротора; б — неподвижного ротора; в — обмотки ротора, приведенной к обмотке статора

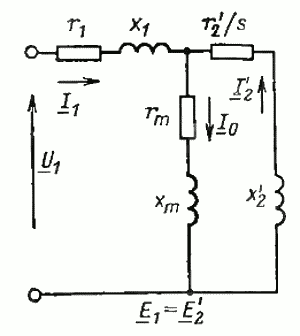
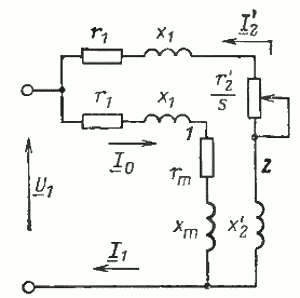
Поскольку теперь ЭДС Е₁ первичной обмотки равна ЭДС Е₂‘ вторичной обмотки, мы можем соединить электрически соответствующие точки схемы замещения обмотки статора и ротора. В результате получим схему замещения асинхронного двигателя, показанную на рис. 16. Здесь активное сопротивление r_m отражает наличие потерь в стали двигателя. Для двигателей средней и большой мощности удобнее пользоваться упрощенной схемой замещения, приведенной на рис. 17.

Рис. 16. Т-образная схема замещения  асинхронного двигателя

Рис. 17. Упрощенная Г-образная схема замещения  асинхронного двигателя

Используя последнюю схему, легко найти токи и ЭДС в обмотках, подводимую и полезную мощность, а также мощность потерь при любой частоте вращения двигателя. Для этого следует лишь найти скольжение, соответствующее заданной частоте n, по формуле (4)
и вычислить сопротивление r₂‘/s в схеме по рис. 17. После этого нетрудно найти ток намагничивания I₀ и приведенный ток I₂‘ в роторной цепи, А:

              (32)

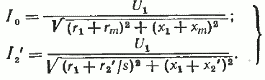
Это дает возможность вычислить электрические потери в обмотке статора трехфазного двигателя (m₁=3), Вт:

               (33)

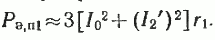
Электрические потери в обмотке ротора (Вт) можно найти, предварительно рассчитав по (30) приведенное сопротивление ротора r₂‘  (Ом):

              (34)

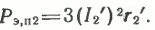
Суммарная активная мощность, передаваемая со статора на ротор, как видно из схемы (рис. 17), будет равна, Вт:

               (35)

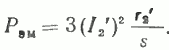
Эта мощность передается на ротор электромагнитным путем и поэтому называется электромагнитной мощностью.

Если из электромагнитной мощности вычесть мощность электрических потерь в обмотке ротора, то получим полную механическую мощность двигателя, Вт:

               (36)

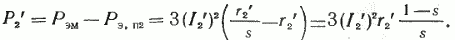
Полная механическая мощность расходуется на вращение приводного механизма (полезная механическая мощность) и на покрытие механических Р_мх.п и добавочных Р_д.п потерь самого двигателя. Поэтому полезная механическая мощность Р₂ будет равна, Вт:

               (37)

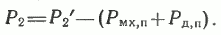
Коэффициент полезного действия двигателя по определению равен отношению отдаваемой (полезной механической) мощности к потребляемой (активной электрической) мощности. Разность между этими мощностями составляют потери в двигателе, равные, Вт:

где P_м.п=m₁I₀2r_m — магнитные потери или потери в стали. Таким образом, КПД двигателя равен:

              (38)

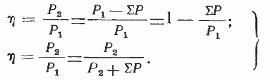
Использование первого или второго выражения для КПД определяется тем, какая из мощностей — P₁ или Р₂— известна. На практике наиболее часто применяется первое выражение (38).

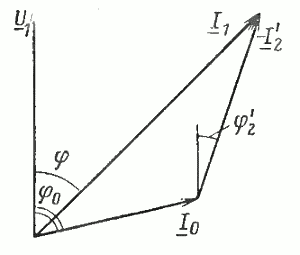
Используя схему замещения, можно определить также ток, потребляемый двигателем из сети, т. е. ток статора, который равен сумме двух токов. Первый из них — это ток XX, который протекает по цепи 1 (рис. 17) и не изменяется при изменении частоты вращения ротора, второй — ток ротора I₂‘, который определяется по (32). Складывая геометрически эти два тока, можно получить ток статорной обмотки. Такое геометрическое сложение показано на рис. 18. Углы φ₂‘, φ₀, необходимые для построения, можно найти с помощью схемы замещения (см. рис. 17):

Таким образом, знание параметров схемы замещения (r₁, x₁, r₂‘, х₂‘, rm, хm) и приложенного напряжения U₁ (напряжение сети) позволяет с помощью приведенных выше формул определить полезную мощность, токи, потери, КПД, коэффициент мощности двигателя при различных скольжениях (частоте вращения).

Рис. 18. Диаграмма токов асинхронного двигателя  

Зависимости потребляемого тока I₁ и мощности Р₁, КПД, cosφ и скольжения s от полезной механической мощности P₂ носят название рабочих характеристик двигателя. Эти характеристики определяются при постоянном напряжении U₁ и частоте f₁ сети. Пример рабочих характеристик приведен на рис. 19.

Рис. 19. Рабочие характеристики асинхронного двигателя 

Рассмотрим рабочие характеристики асинхронного двигателя. При холостом ходе (полезная мощность Р₂—0) скольжение s также равно нулю (частота вращения ротора n практически равна синхронной), сопротивление r₂/’s равно бесконечности (см. рис. 17) и ток I₂‘==0. По обмотке статора протекает ток холостого хода I₀. Коэффициент полезного действия η равен нулю, так как равна нулю полезная мощность Р₂, а коэффициент мощности равен коэффициенту мощности для тока холостого хода (cosφ₁=cosφ₀).

При увеличении нагрузки частота вращения ротора уменьшается и увеличивается скольжение s. За счет увеличения s уменьшается сопротивление цепи 2 (см. рис. 17) и увеличивается ток ротора, а следовательно, и ток статоpa. Поскольку увеличивается полезная мощность, растет, КПД двигателя, а также коэффициент мощности.

Обычно номинальная мощность на валу двигателя достигается уже при небольшом понижении частоты вращения ротора и вся область рабочих режимов находится в диапазоне скольжений от 0 до 2—5%.

Поэтому скоростная характеристика n=f(P₂) у асинхронного двигателя имеет небольшой наклон к оси абсцисс. Характеристики такого вида принято называть жесткими. Соответственно характеристика s=f(P₂) имеет слабый подъем при возрастании нагрузки. В асинхронном двигателе частота вращения ротора меньше частоты вращения поля, за счет чего обеспечивается наведение ЭДС, а также создание тока 1% в обмотке ротора и вращающего электромагнитного момента, под действием которого ротор приходит во вращение.

Характеристика cosφ=f(P₂) лежит в области значений, меньших 1, так как асинхронный двигатель всегда потребляет ток I₀, почти не зависящий от нагрузки в диапазоне мощностей от Р₀ до Р₂≈Р_ном. При XX обычно  φ₀<0,2, т. е. он содержит большую реактивную составляющую. При увеличении нагрузки cosφ быстро возрастает и достигает максимального значения при мощности Р₂≈Р_2ном. При увеличении нагрузки выше номинальной cosφ  несколько снижается.

Коэффициент полезного действия достигает своего максимального значения при Р₂≈ (0,6÷0,8)Р_2ном и снижается при дальнейшем росте нагрузки. Поскольку двигатель обычно работает при переменной нагрузке, изменяющейся в пределах (0,6—1)Р_2ном, то КПД в этом диапазоне изменения нагрузки должен быть достаточно высок.