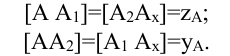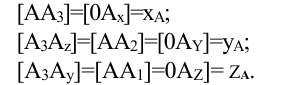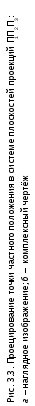Печатать книгу
Укажите способы построения аксонометрических проекций и их особенности. Как строят аксонометрические проекции плоских фигур?
- Вы узнаете: как построить прямоугольные изометрические проекции геометрических тел, как найти точки на их поверхностях.
- Вы научитесь: выполнять прямоугольные изометрические проекции геометрических тел, находить точки на их поверхностях.
| Сайт: | Профильное обучение |
| Курс: | Черчение. 10 класс |
| Книга: | § 19. Аксонометрические проекции геометрических тел. Нахождение точек, лежащих на поверхности геометрических тел |
| Напечатано:: | Гость |
| Дата: | Воскресенье, 28 Май 2023, 11:54 |
Оглавление
- Вступление
- Аксонометрические проекции многогранников
- Аксонометрические проекции поверхностей вращения
- Проверим знания
- Вопросы и задания повышенной сложности
- Практическая работа № 10. Аксонометрические проекции геометрических тел
- Практическая работа №10.1. Чертеж аксонометрической проекции.
- Практическая работа №10.2. Аксонометрическая проекция по чертежу.
Вступление
Геометрические тела правильной формы (многогранники и поверхности вращения) часто встречаются в конструкции деталей машин и механизмов. Правильные геометрические тела характеризуются наличием в них различных осей и плоскостей симметрии, что позволяет строить аксонометрические изображения этих тел по принципу симметрии.
Построение аксонометрических проекций геометрических тел начинают с построения горизонтальной проекции его нижнего основания, к которому достраиваются другие его элементы (грани, ребра, верхнее основание).
Аксонометрические проекции многогранников
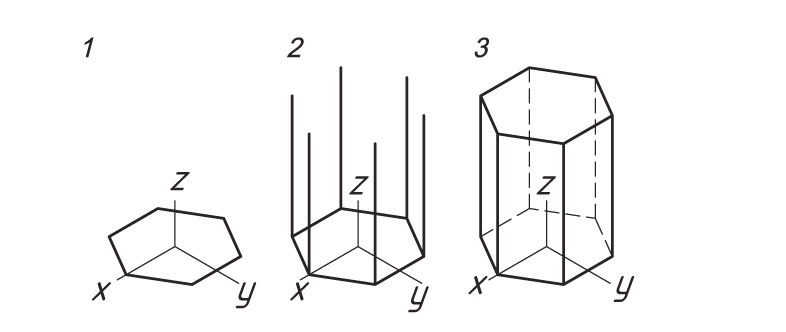
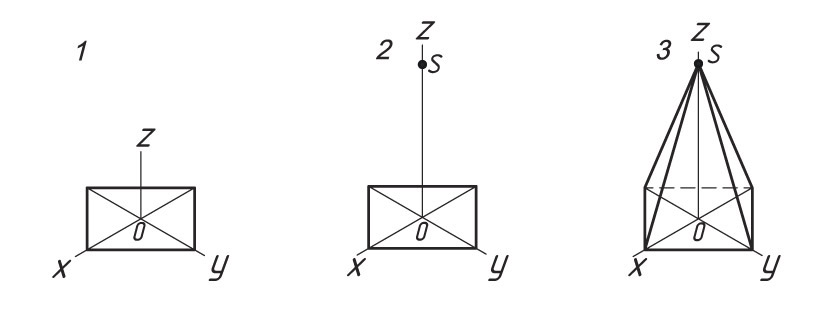
1. Проводят оси изометрической проекции. Затем строят нижнее основание призмы.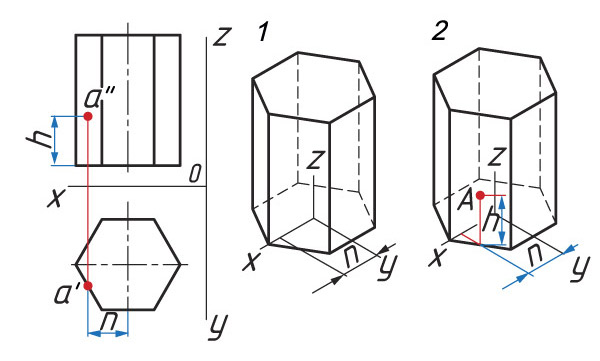
3. Через полученные точки проводят прямые, параллельные ребрам основания. Определяют видимость ребер.
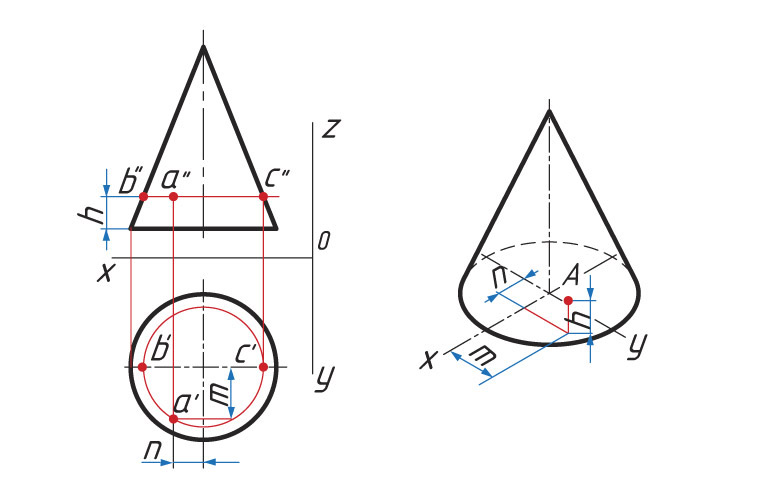
Определение расположения точки А:
1. От центра основания по оси х проводят прямую хА = n. Из точки n проводят прямую, параллельную оси у, до пересечения с основанием призмы.
2. Из полученной точки параллельно оси z проводят прямую
zА = h.
Определите последовательность построения проекции точки, расположенной на ребре призмы.
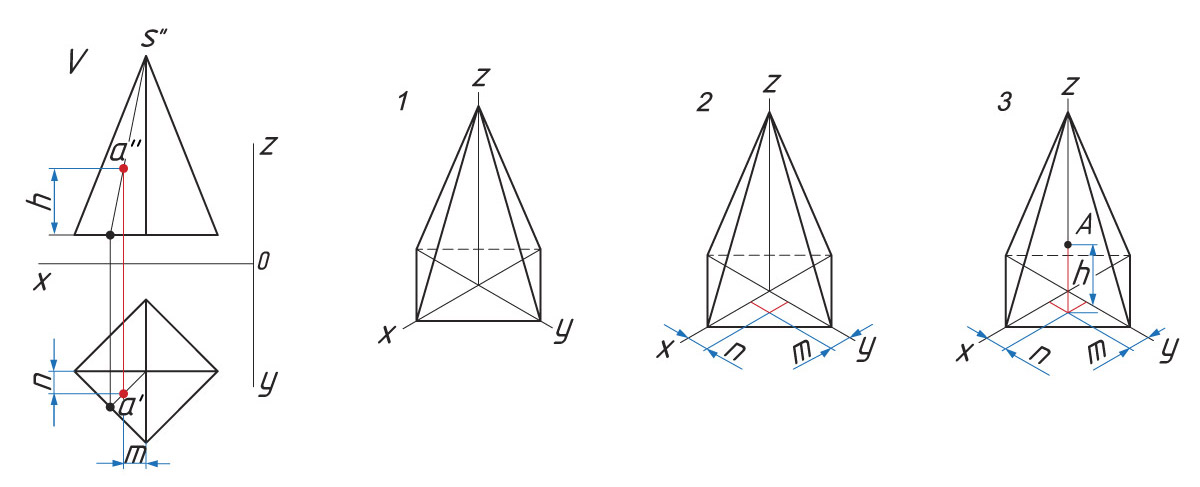
Прямоугольная изометрическая проекция пирамиды (например, четырехгранной). Основание пирамиды — ромб. Высота пирамиды (OS) совпадает с осью z, а основание расположено в плоскости осей x и y.
1. Проводят оси изометрической проекции. Размеры пирамиды определяются размерами ее основания и высотой. Затем строят нижнее основание пирамиды, параллельное горизонтальной плоскости.
2. Из центра основания О восстанавливают перпендикуляр, на котором откладывают высоту пирамиды.
3. Соединяют полученную точку S с вершинами основания. Определяют видимость ребер.
Определение расположения точки А
1. От центра основания О по оси х откладывают расстояние хА = m.
2. На оси у откладывают расстояние уА = n.
3. Параллельно оси z проводят отрезок zA = h.
Аксонометрические проекции поверхностей вращения
Окружности, лежащие в основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости проекций. Построение проекций цилиндра и конуса начинают с проведения осей симметрий и построения нижнего основания. Нижнее основание аксонометрических проекций цилиндра и конуса — эллипс.
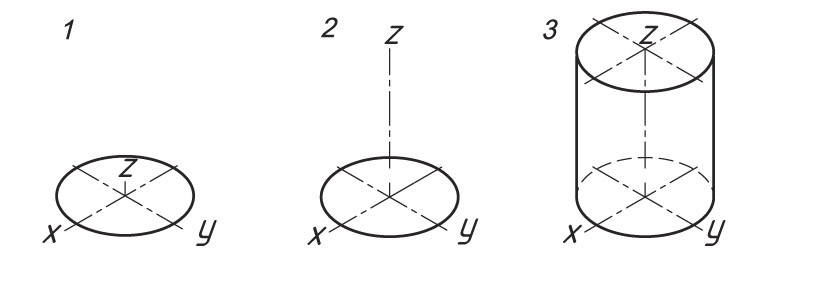
Прямоугольная изометрическая проекция цилиндра. Основание цилиндра — эллипс. Высота цилиндра совпадает с осью z, а основание расположено в плоскости осей x и y. Размеры определяются высотой и диаметром основания.
1. Проводят оси изометрической проекции. Затем строят нижнее основание цилиндра.
2. Из центра основания восстанавливают перпендикуляр и откладывают высоту цилиндра. Строят верхнее основание (эллипс).
3. Проводят боковые образующие цилиндрической поверхности, определяют видимость нижнего основания.
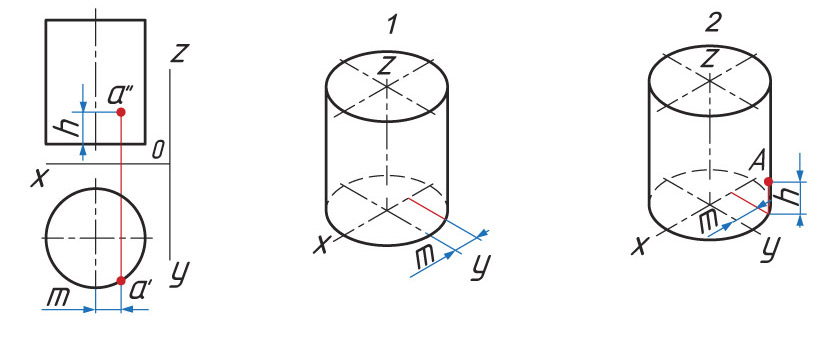
Определение расположения точки А
1. От центра основания по оси х проводят прямую хА= m. Из точки m проводят прямую, параллельную оси у до пересечения с основанием.
2. Из полученной точки параллельно оси z проводят прямую zА= h
Составьте алгоритм нахождения точки на поверхности цилиндра, учитывая тот факт, что точка расположена на нижнем основании цилиндра.
Прямоугольная изометрическая проекция конуса. Основание конуса — эллипс. Построение проекции конуса схоже с построением проекции цилиндра. Определение расположения точек на поверхности конуса подобно построениям точек на пирамиде.
Используя ранее изученный материал, укажите способ нахождения положения точек В и С, изображенный на рисунке.
Проверим знания
1. Что такое показатель (коэффициент) искажения? Какие виды аксонометрии вы знаете? Как располагаются оси прямоугольной изометрии?
2. В какой последовательности выполняют аксонометрическую проекцию геометрического тела?
3. Приведите примеры использования аксонометрических проекций в различных сферах профессиональной деятельности.
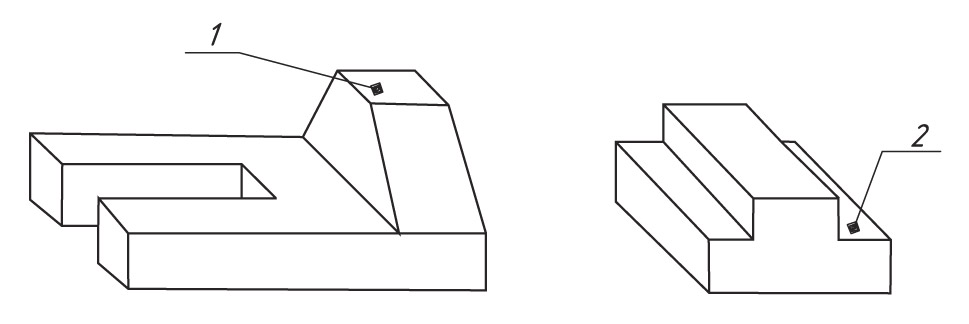
4. Мысленно удалите элемент 1, заменив его на элемент 2. Выполните изометрическую проекцию получившейся детали.
Вопросы и задания повышенной сложности
1. Назовите общие для фронтальной диметрической и изометрической проекций этапы построения цилиндра.
2. Постройте в изометрической проекции правильные треугольную и шестиугольную призмы. Основания призмы расположены горизонтально, длина сторон основания 30 мм, высота 60 мм.
Практическая работа № 10. Аксонометрические проекции геометрических тел
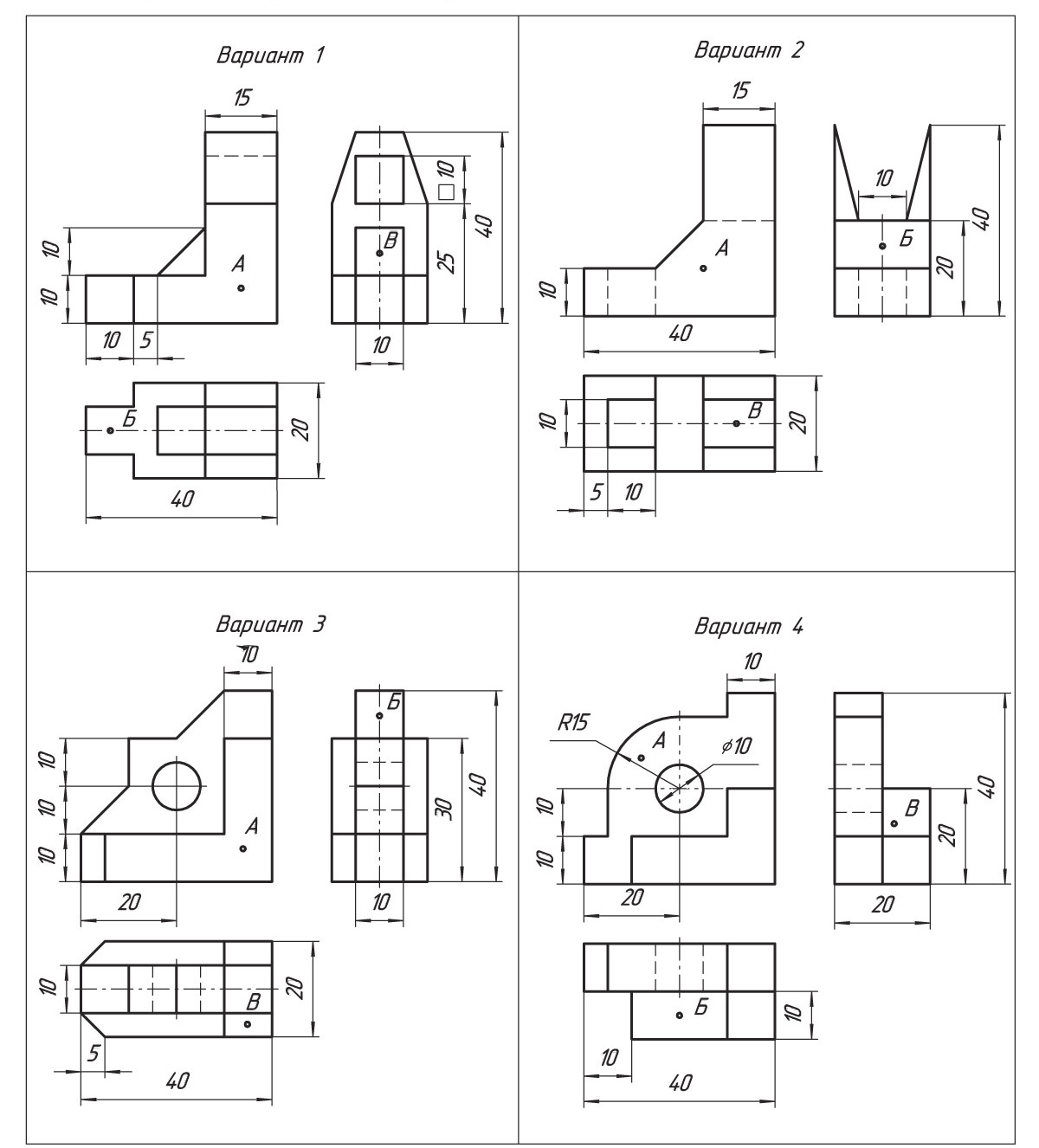
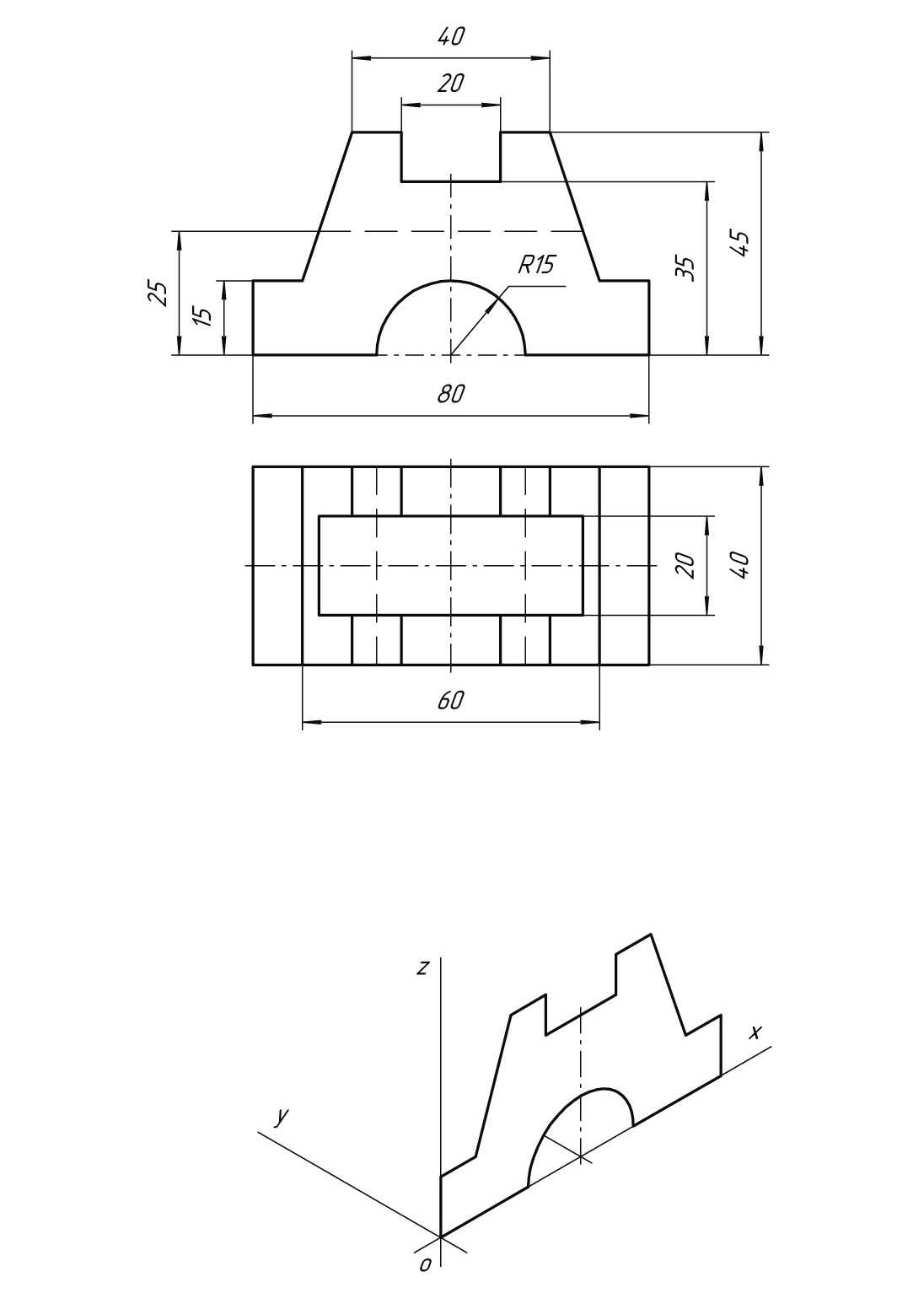
В рабочей тетради выполните по чертежу изометрическую проекцию детали в масштабе 2,5:1. На аксонометрической проекции определите расположение точек А, Б и В.
Практическая работа №10.1. Чертеж аксонометрической проекции.
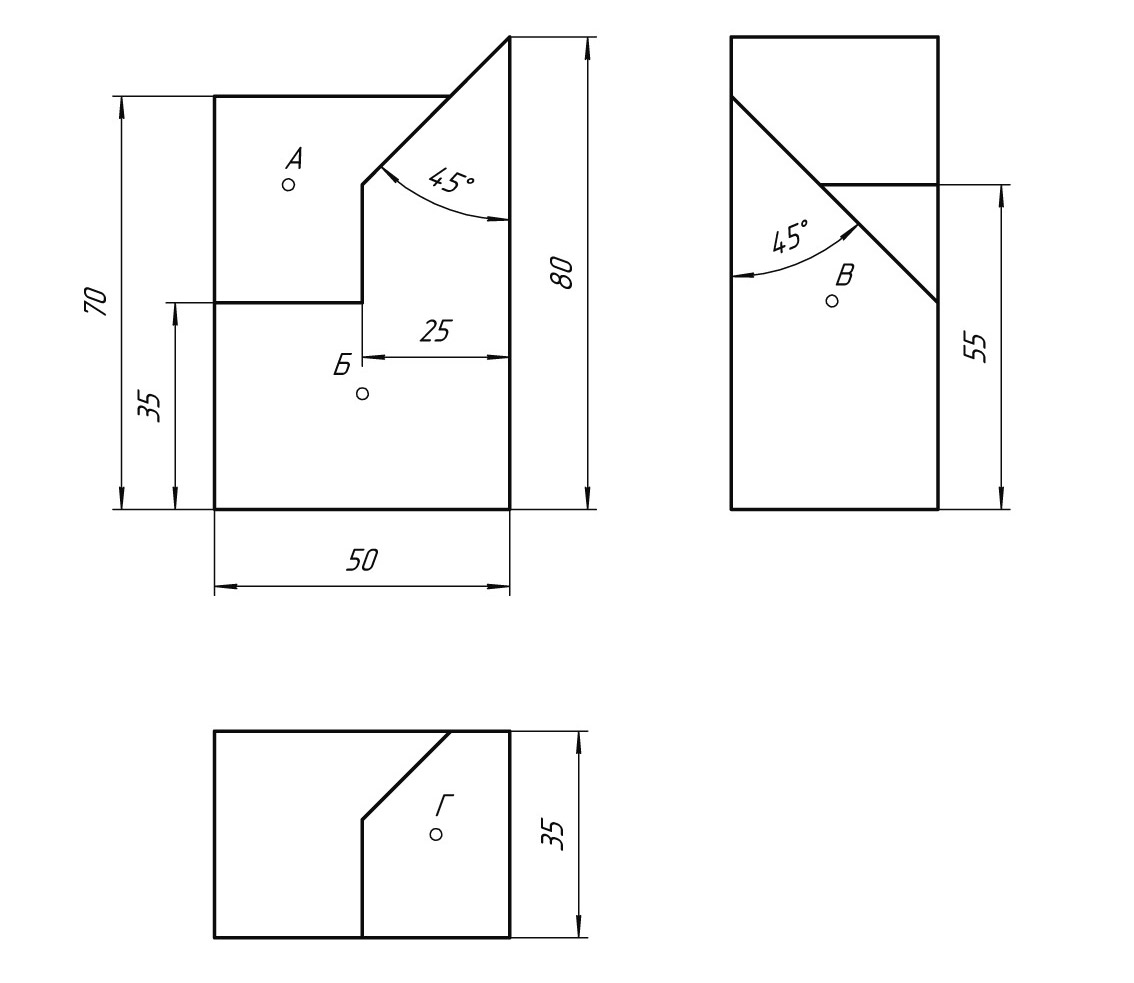
На формате А4 выполнить чертеж детали и аксонометрическую проекцию детали. На аксонометрической проекции покажите точки А, Б, В, Г.
Практическая работа №10.2. Аксонометрическая проекция по чертежу.
Руководствуясь двумя видами на формате А4, выполните чертеж детали в трех проекциях, закончите построение аксонометрической проекции.
Проецирование точки на две и три плоскости проекций:
Если из точки А, находящуюся в пространстве, относительно двух плоскостей проекций
Они характеризуются координатами, которые численно равны расстоянию от точки А до соответствующих плоскостей проекций. Координаты обозначаются теми же буквами, что и оси вдоль которых измеряется расстояние, с присвоением индекса самой буквы.
Так, для точки А:
Плоскость прямоугольника 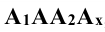
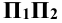
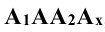
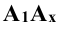
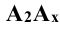
Изображение точки и её проекций на рис.3.1 является пространственным чертежом, что не всегда удобно для практики.
Рис. 2.4 Чтобы получить плоский чертёж, поворачивают плоскость 
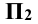
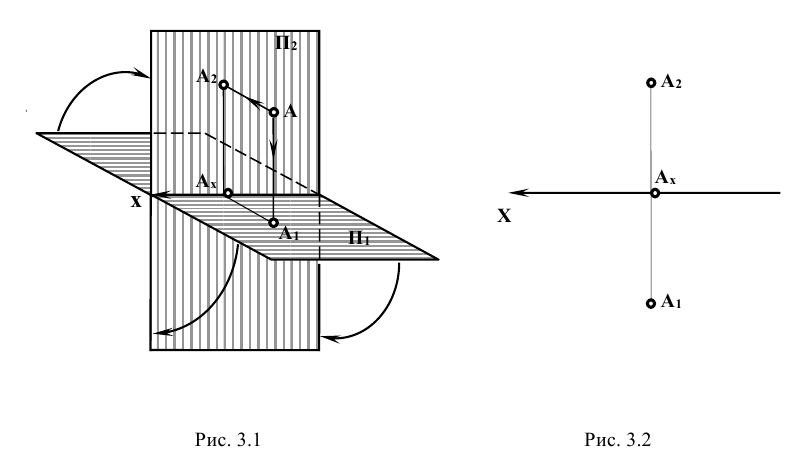
Проекции 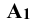
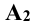
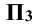
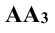
Для получения плоского чертежа в этом случае уже две плоскости 
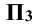
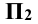
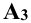
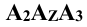
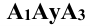
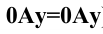
Перенос точки Ау в точку (Aу) — понятен из чертежа, а сам отрезок есть не что иное, как координата YA.
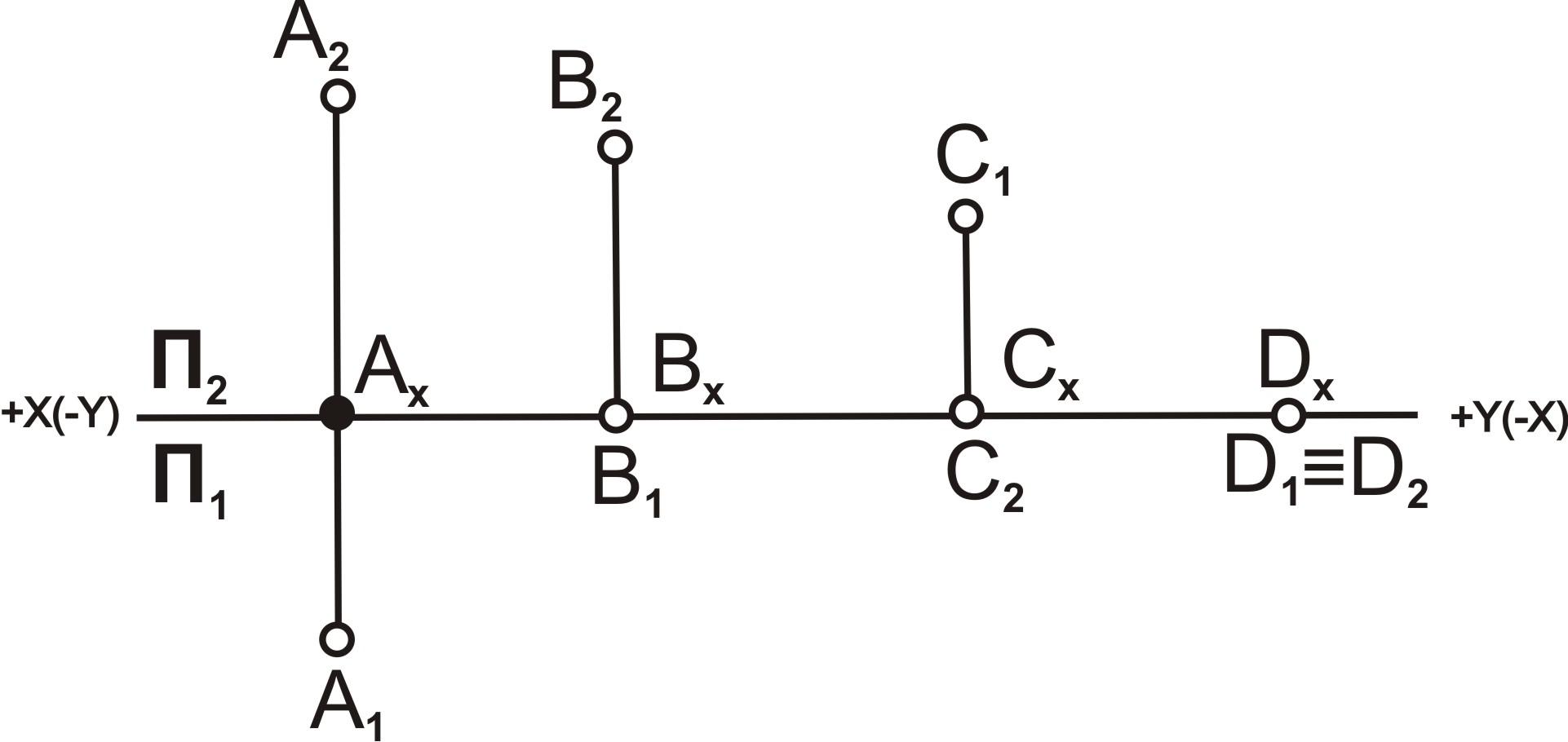
На плоском трёхмерном чертеже положительное направление оси х совпадает с отрицательным направлением оси у, а отрицательное направление оси y — с положительным направлением оси z.
Это не означает, что модули этих величин обязательно равны между собой, т.е. 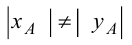
Таким образом, горизонтальная и фронтальная проекции точки А на плоском чертеже лежат на одной линии проекционной связи, перпендикулярной к оси x, а фронтальная и профильная проекции точки А на линии проекционной связи, перпендикулярной к оси z.
- Заказать чертежи
Определение по плоскому чертежу принадлежности точки тому или другому октанту пространства
Точка, например А, принадлежит:
Определение по плоскому чертежу принадлежности точки плоскостям проекций
Точка А принадлежит:
Любая точка лежит на оси проекций, если её смежные две проекции совпадают.
Так, точка А лежит на оси х, если 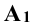
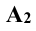
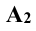
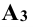
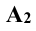
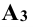
Правила знаков координат проекции точки
При построении проекции точки координата x всегда откладывается от начала координат (точка 0).
Положительное значение координаты у будут иметь точки, находящихся перед фронтальной плоскостью проекций 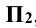
Положительное значение координаты z будут иметь точки, расположенные выше горизонтальной плоскости проекций 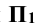
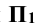
Таблица 3.1 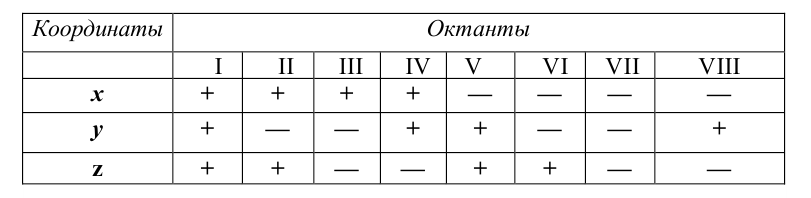
- Прямая в пространстве и ее изображение на чертеже
- Многогранники
- Поверхности вращения
- Пересечение прямой линии с поверхностью
- Собственные тени поверхностей вращения
- Построение падающих теней
- Проекции с числовыми отметкам
- Гранные поверхности



Здравствуйте! Сегодня мы научимся создавать ассоциативный чертеж по готовой 3d модели призмы и пирамиды. Их мы построили на уроке по 3d моделированию
Урок 2. Создаем 3d модели призмы, пирамиды, цилиндра и конуса. Или как создать четыре 3d модели за 10 минут.
Также на этом уроке вы узнаете, как находить проекции точек на чертежах призмы и пирамиды.
Создаем ассоциативный чертеж по 3d модели
Для того, чтобы создать ассоциативный чертеж выполним следующее: создаем чертеж→на компактной панели выбираем кнопку
панель стандартные виды
«Вид»→ ниже выбираем «Стандартные виды»→в открывшемся окне выбираем файл с 3d моделью (расширение .m3d)
выбираем 3d модель призмы
→ на панели свойств, вкладка «схема» подбираем количество видов и расстояние между ними→жмем на поле чертежа и все, три проекции призмы или пирамиды готовы.
схема видов чертежа
Остается только вставить изометрию и оформить чертеж по ГОСТу.
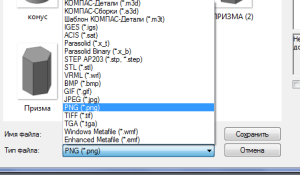
Чтобы вставить изометрию открываем файл с 3d моделью призмы (пирамиды) и пересохраняем ее как рисунок в формате .png.
сохраняем модель в формате рисунка
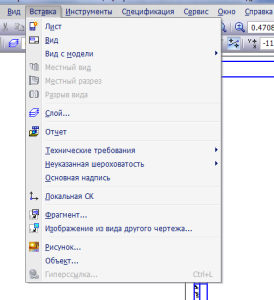
Возвращаемся к созданию ассоциативного чертежа. В строке главного меню жмем на вкладку «Вставка»→ «Рисунок»→ в открывшемся окне выбираем рисунок с призмой (пирамидой)→ вставляем рисунок в чертеж.
вставляем рисунок в чертеж
Как найти проекции точек на пирамиде и призме?
Как найти проекции точек на призме?
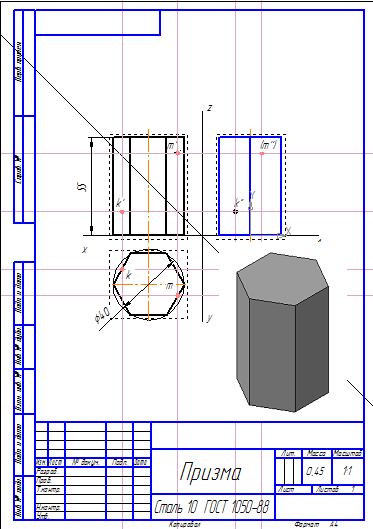
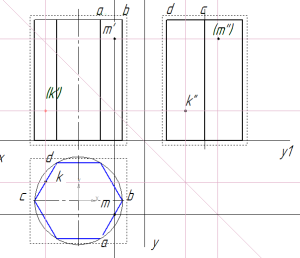
В задании на построение геометрических тел требуется найти недостающие проекции точек К и М (задачник Мироновой Р.С., стр. 65).
проекции точек на призме
Найдем проекции точек на призме.
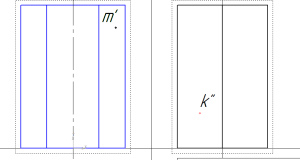
Задана фронтальная проекция точки М – m’ и профильная проекция точки К – k’’.
Найдем горизонтальную проекцию точки m. Для этого построим вспомогательную прямую через точку m’ до пересечения с горизонтальной проекцией призмы.
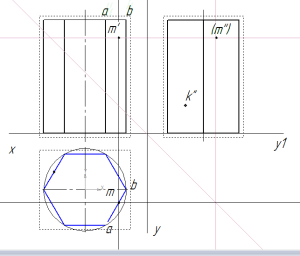
находим проекции точек на призме
Как видно из рисунка, точка m’ принадлежит грани ab. Поэтому горизонтальная проекция m будет находиться в месте пересечения вспомогательной прямой с гранью ab на горизонтальной проекции призмы.
Профильную проекцию находят с по линиям связи, построенным из m’ и m. Так как на профильной проекции призмы точку m’’ не видно, она взята в скобки.
Для того, чтобы найти недостающие проекции точки К поступаем аналогично.
строим горизонтальную и фронтальную проекции точек
По линиям связи находим горизонтальную проекцию k, принадлежащую грани cd. Фронтальную проекцию (k’) также строим по линиям связи.
Как найти проекции точек на пирамиде?
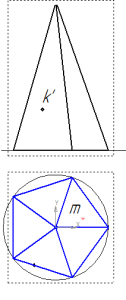
Точка М на пирамиде задана горизонтальной проекцией m, точка К – фронтальной проекцией k’.
точки на пирамиде
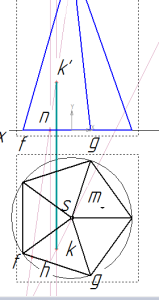
строим горизонтальную проекцию точки
Начнем с нахождения горизонтальной проекции k. Для этого через вершину пирамиды и k’ проводим вспомогательную прямую. Затем через полученную точку n проводим линию связи до пересечения с гранью fg. Через полученную точку h и вершину s проводим еще одну вспомогательную прямую.
И по линии связи опускаемся из точки k’ до пересечения с этой прямой hs. Горизонтальная проекция k найдена.
Профильную проекцию k’’ находим по линиям связи без дополнительных построений.
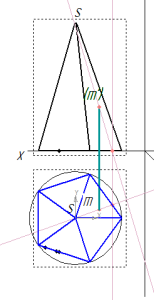
Фронтальную проекцию m’ находим аналогично построению горизонтальной проекции k. Описывать процесс не буду. Вот вам рисунок.
строим фронтальную проекцию точки М
Профильную проекцию m’’ найти особого труда не составит, все по тем же линиям связи.
Таким образом находят проекции точек на пирамиде и призме.
Чтобы лучше все уяснить посмотрите видеоурок.
Скачать чертежи бесплатно можно здесь
Теперь-то вы точно сможете быстро создать ассоциативный чертеж и найти по указанию преподавателя проекции точек на пирамиде или призме.

The following two tabs change content below.
- Bio
- Latest Posts
Рада приветствовать Вас в своем блоге! Я создала его с целью помочь всем желающим освоить программу Компас 3d. Мы пройдем весь путь от азов черчения до создания серьезных сборок. Присоединяйтесь!
Понравился материал? Подпишись на обновления!
Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.
Алгоритм построения комплексного чертежа точки по координатам
|
Словесная форма |
Графическая |
|
1. Отложить на |
|
|
2. Горизонтальная |
|
|
3. Фронтальная |
|
|
4. Профильная |
|
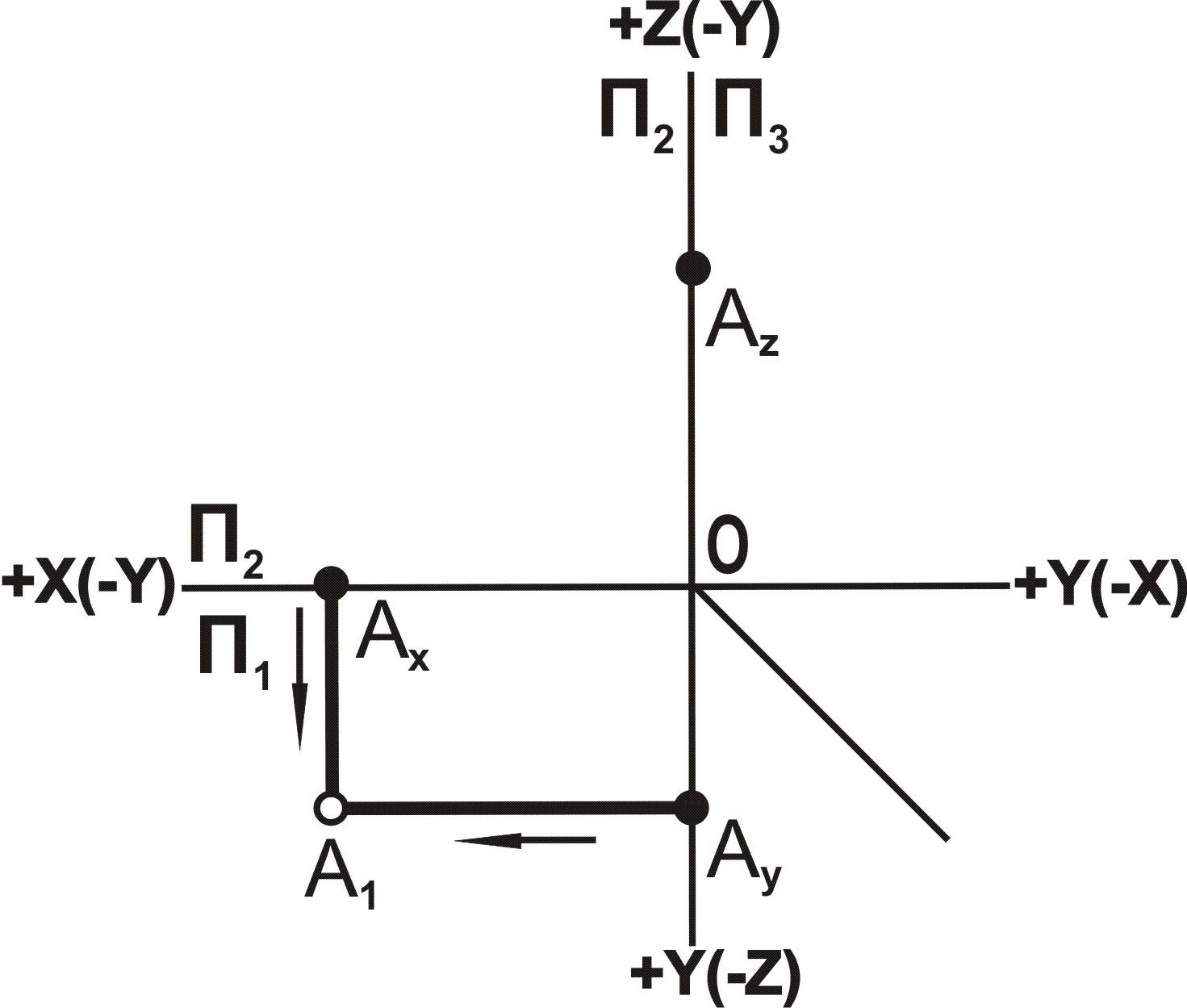
3.2. Положение точки относительно плоскостей проекций
Положение точки в пространстве
относительно плоскостей проекций
определяется её координатами. Координатой
Х определяется удалённость точки от
плоскости П3(проекция на П2или П1), координатой
У – удалённость
от плоскости П2(проекция на П3или П1), координатой
Z – удаленность
от плоскости П1(проекция на П3или П2). В зависимости от значения
этих координат точка может занимать в
пространстве как общее, так и частное
положение по отношению к плоскостям
проекций (рис. 3.1).
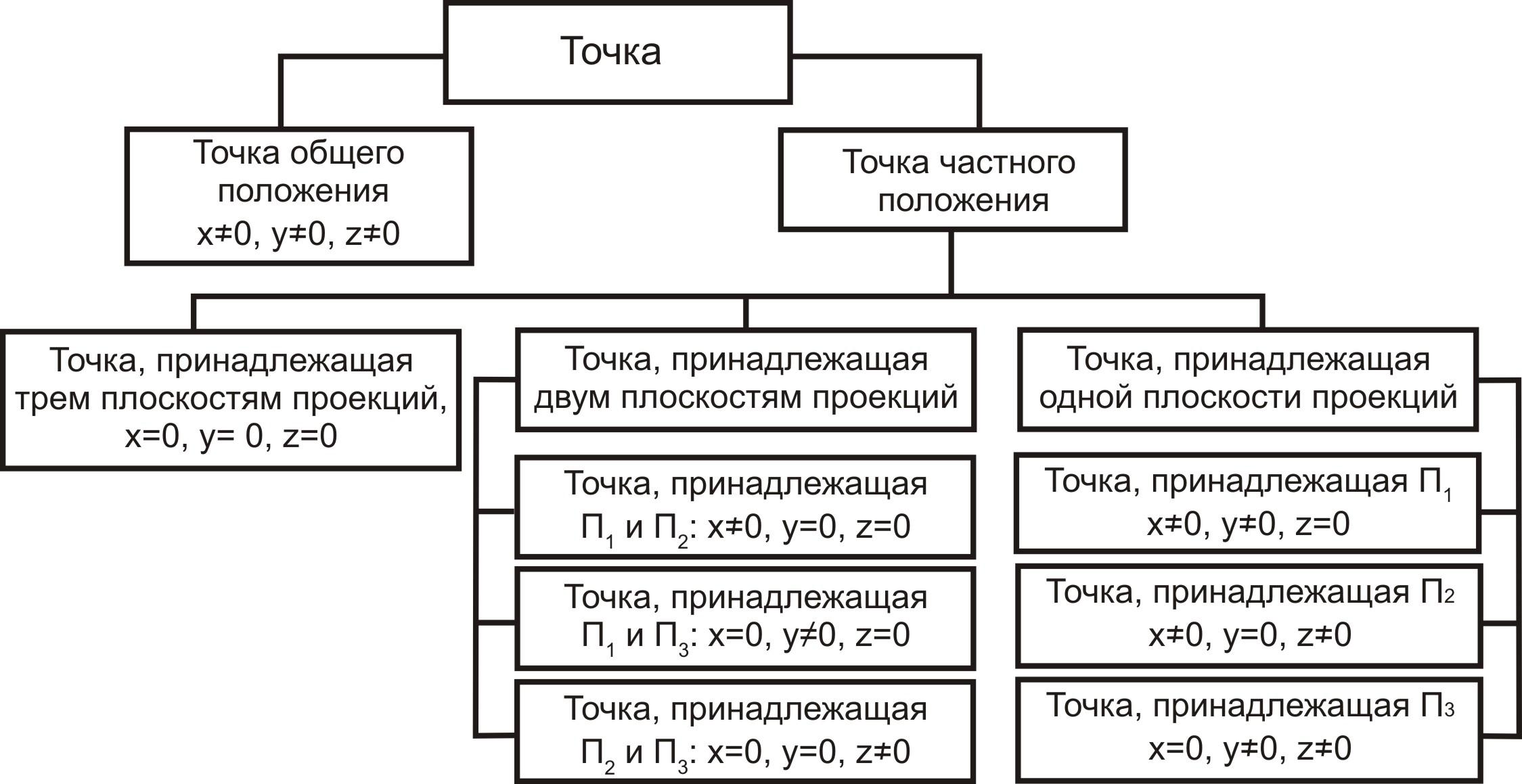
Рис.
3.1. Классификация точек
Точка
общего
положения.
Координаты
точки общего положения не равны нулю
(x≠0,y≠0,z≠0),
и в зависимости от знака координаты
точка может располагаться в одном из
восьми октантов (табл.
2.1).
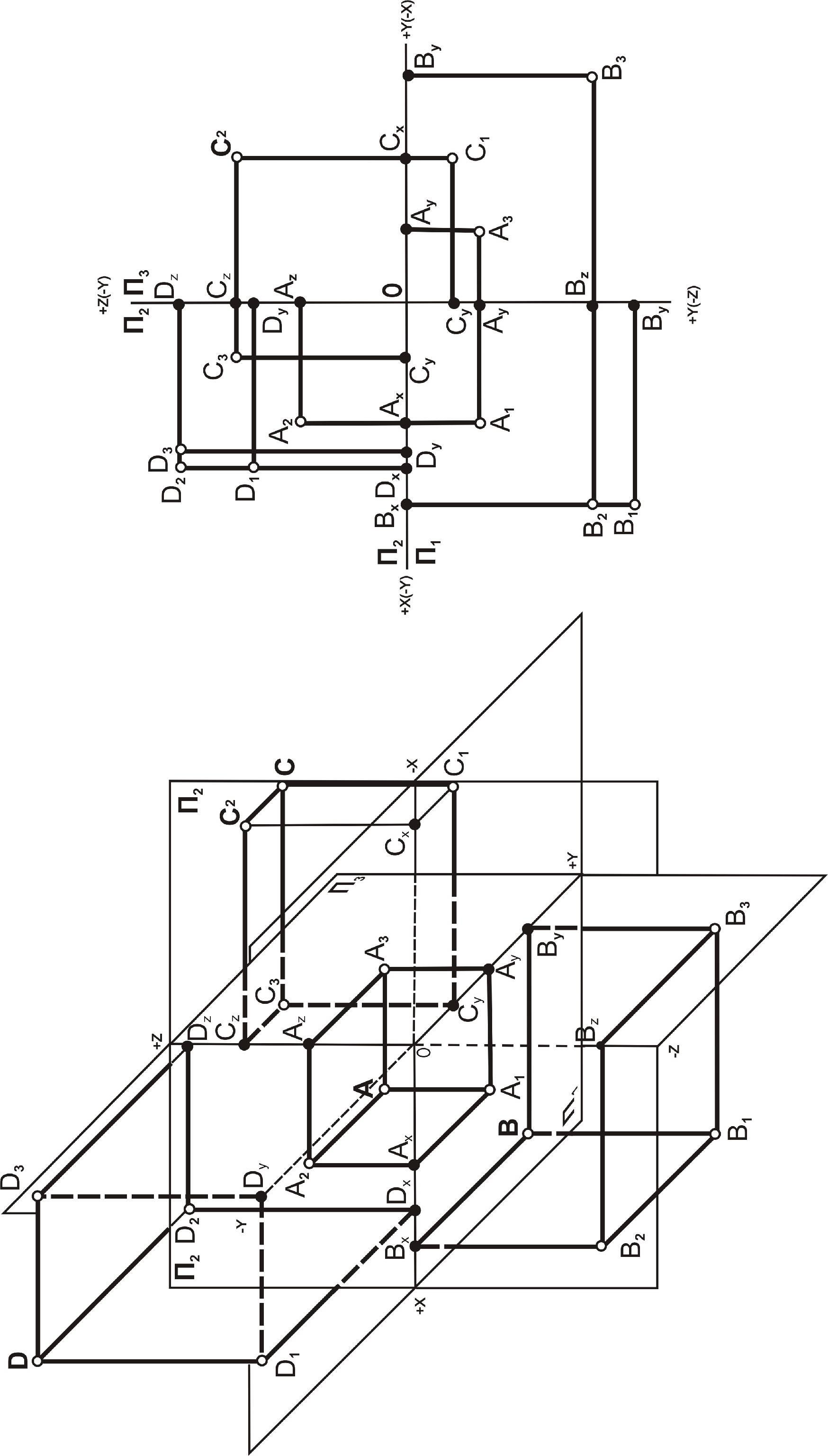
На рис. 3.2 даны чертежи точек общего
положения. Анализ их изображений
позволяет сделать вывод, что они
располагаются в следующих октантах
пространства: А(+X;+Y;
+Z(
Iоктанту;B(+X;+Y;-Z(
IVоктанту;C(-X;+Y;
+Z(
Vоктанту;D(+X;+Y;
+Z(
IIоктанту.
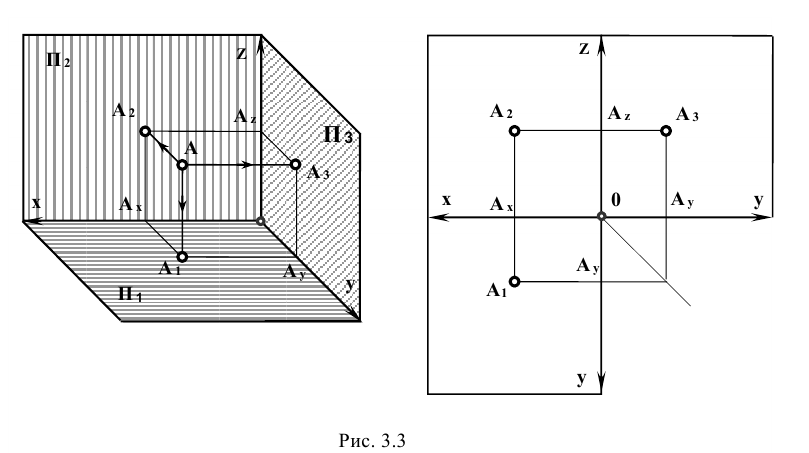
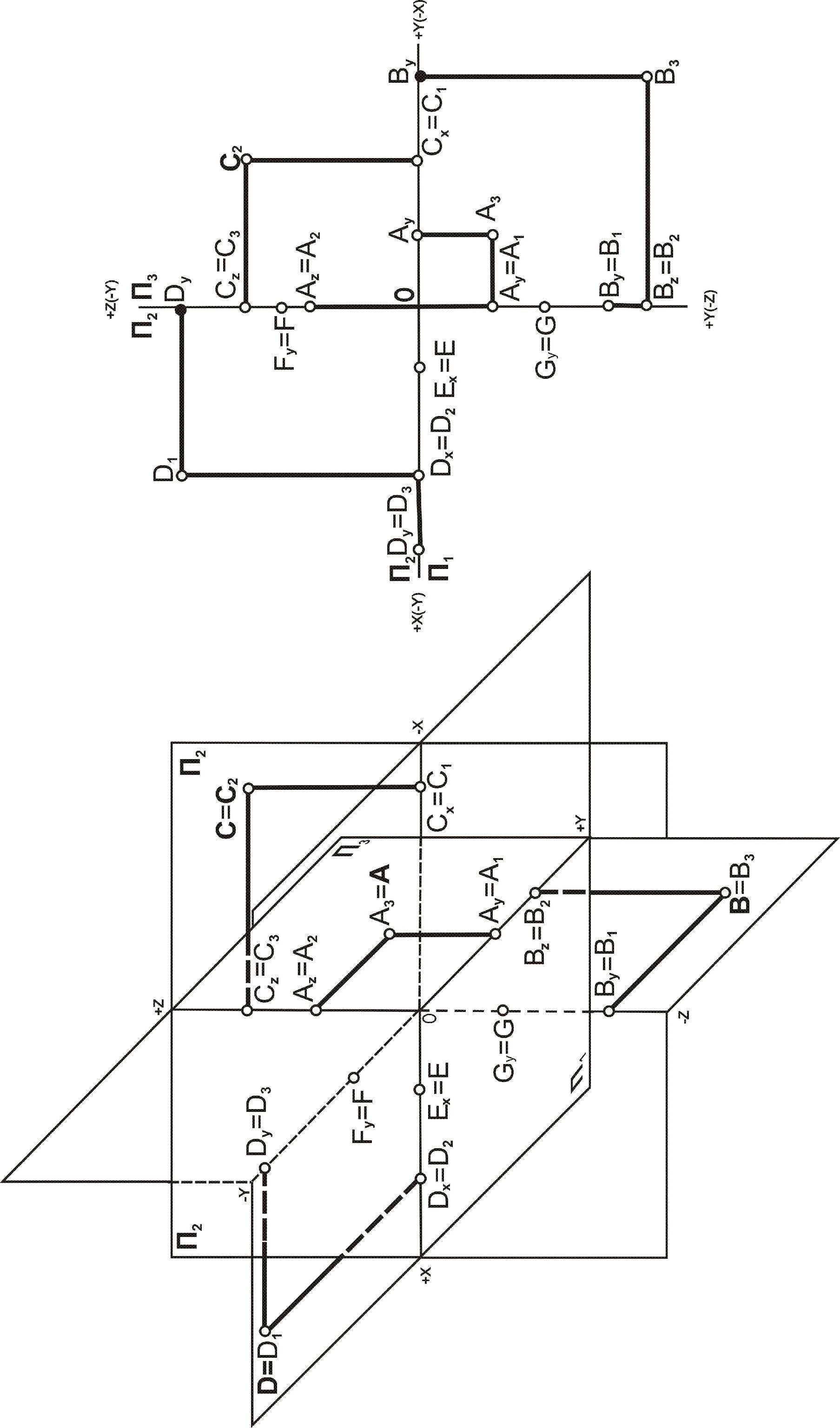
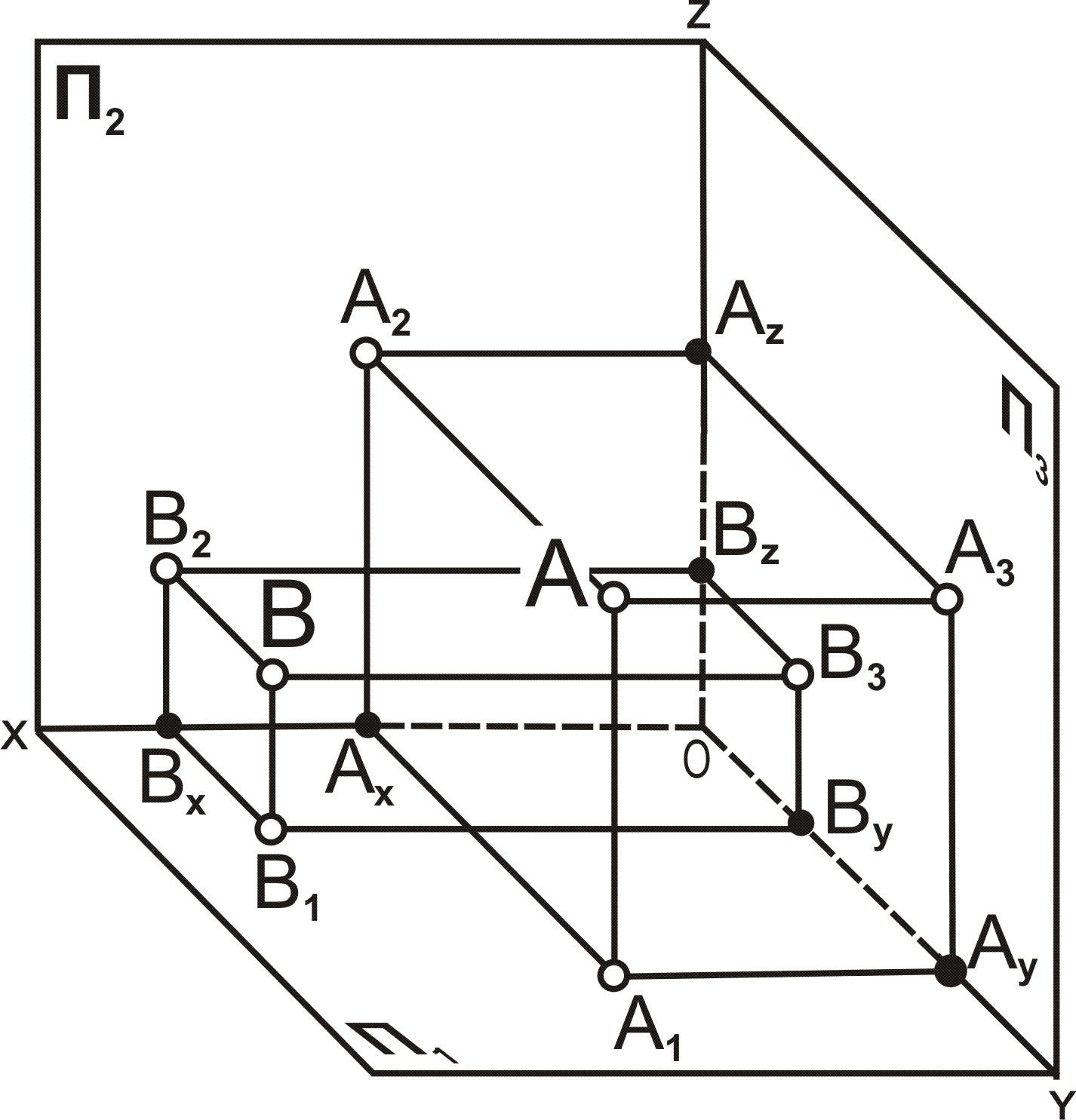
Точки частного положения. Одна из
координат у точки частного положения
равна нулю, поэтому проекция точки лежит
на соответствующем поле проекций, другие
две – на осях проекций. На рис. 3.3 такими
точками являются точки А, В,C,D,G.AП3,то
точка ХА=0; ВП3,то
точка ХВ=0; СП2,то
точкаYC=0;DП1,то
точкаZD=0.
Точка может принадлежать сразу двум
плоскостям проекций, если она лежит на
линии пересечения этих плоскостей –
оси проекций. У таких точек не равна
нулю только координата на этой оси. На
рис. 3.3 такой точкой
является точкаG(GOZ,то
точка ХG=0,YG=0).
3.3. Взаимное положение точек в пространстве
Рассмотрим три
варианта взаимного расположения точек
в зависимости от соотношения координат,
определяющих их положение в пространстве.
-
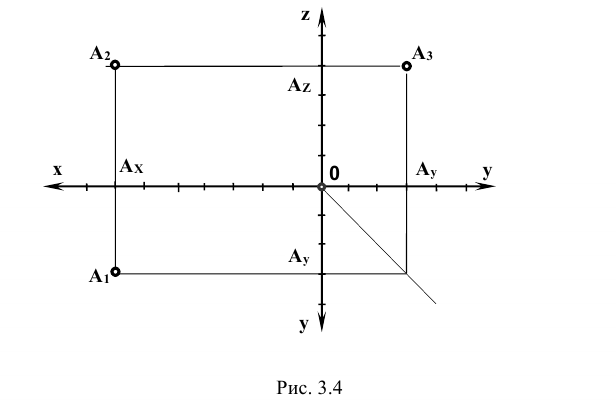
На
рис. 3.4 точки AиBимеют различные координаты.
|
а |
б |
|
Рис. |
Их
взаимное расположение можно оценить
по удаленности к плоскостям проекций:
YА>YВ, тогда точкаAрасположена дальше от плоскости П2и ближе к наблюдателю, чем точкаB;
ZА>ZВ, тогда точкаAрасположена дальше от плоскости П1и ближе к наблюдателю, чем точкаB;
XА<XВ, тогда точкаBрасположена дальше от плоскости П3и ближе к наблюдателю, чем (при взгляде
слева) точка А.
-
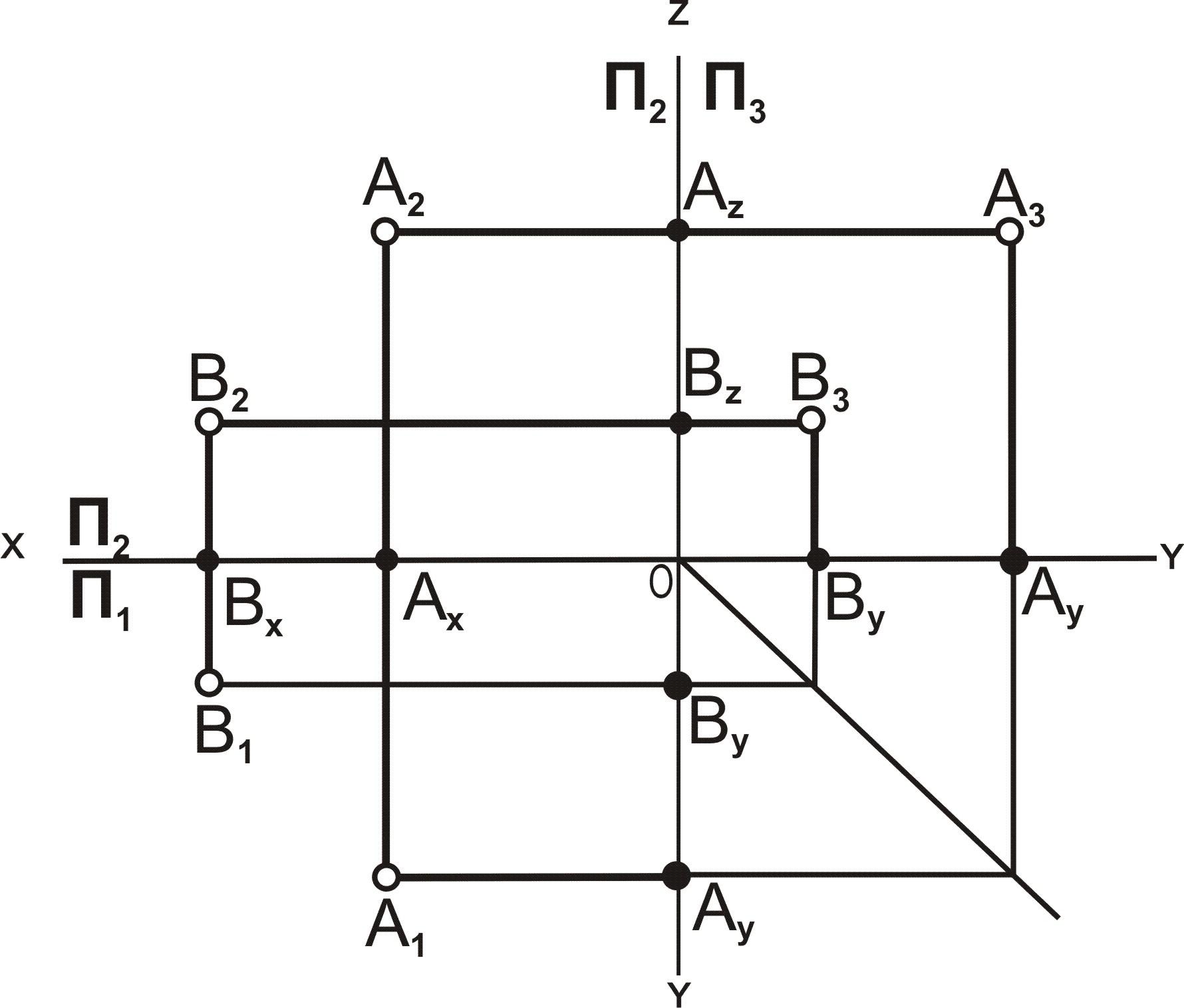
На рис. 3.5 представлены точки A, B, С, D, у
которых одна из координат совпадает,
а две другие отличаются.
|
а |
б |
|
Рис. |
Их
взаимное расположение можно оценить
по удалённости к плоскостям проекций
следующим образом:
YА=YВ=YD,
то точки А, В и D
равноудалены от плоскости П2,
и их горизонтальные и профильные
проекции расположены соответственно
на прямых [А1В1]llОХ
и [А3В3]llOZ.
Геометрическим местом таких точек
служит плоскость, параллельная П2;
ZА=ZВ=ZС,
то точки А, В и С равноудалены от плоскости
П1,
и их фронтальные и профильные проекции
расположены соответственно на прямых
[А2В2]llОХ
и [А3С3]llOY.
Геометрическим местом таких точек
служит плоскость, параллельная П1;
XА=XC=XD,
то точки А,
C
и D
равноудалены от плоскости П3
и их горизонтальные и фронтальные
проекции расположены соответственно
на прямых [А1C1]llOY
и [А2D2]llOZ
. Геометрическим местом таких точек
служит плоскость, параллельная П3.
3.
Если у точек равны две одноименные
координаты, то они называются
конкурирующими.
Конкурирующие точки расположены на
одной проецирующей прямой. На рис. 3.3
даны три пары таких точек, у которых:
XА=XD;
YА=YD;
ZD
>
ZА;
XA=XC;
ZA=ZC;
YC
>
YA;
YA=YB;
ZA=ZB;
XB
>
XA.
Различают
горизонтально конкурирующие точки А и
D, расположенные на горизонтально
проецирующей прямой АD, фронтально
конкурирующие точки A и C, расположенные
на фронтально проецирующей прямой AC,
профильно конкурирующие точки A и B,
расположенные на профильно проецирующей
прямой AB.
Выводы
по теме
1.
Точка
– линейный геометрический образ, одно
из основных понятий начертательной
геометрии. Положение точки в пространстве
можно определить её координатами. Каждая
из трёх проекций точки характеризуется
двумя координатами, их название
соответствует названиям осей, которые
образуют соответствующую плоскость
проекций: горизонтальная – A1(XA;
YA);
фронтальная – A2(XA; ZA);
профильная – A3(YA; ZA).
Трансляция координат между проекциями
осуществляется с помощью линий связи.
По двум проекциям можно построить
проекции точки либо с помощью координат,
либо графически.
3.
Точка по отношению к плоскостям проекций
может занимать в пространстве как общее,
так и частное положение.
4.
Точка общего положения – точка, не
принадлежащая ни одной
из плоскостей
проекций, т. е. лежащая в пространстве
между плоскостями проекций. Координаты
точки общего положения не равны нулю
(x≠0,y≠0,z≠0).
5.
Точка частного положения – это точка,
принадлежащая одной или двум плоскостям
проекций. Одна из координат у точки
частного положения равна нулю, поэтому
проекция точки лежит на соответствующем
поле плоскости проекций, другие две –
на осях проекций.
6.
Конкурирующие точки – точки, одноименные
координаты которых совпадают. Существуют
горизонтально конкурирующие точки,
фронтально конкурирующие точки, профильно
конкурирующие точки.
Ключевые
слова
-
Точка
-
Координаты
точки -
Точка
общего положения -
Точка
частного положения -
Конкурирующие
точки
Способы
деятельности, необходимые для решения
задач
– построение
точки по заданным координатам в системе
трех плоскостей проекций в пространстве;
– построение
точки по заданным координатам в системе
трех плоскостей проекций на комплексном
чертеже.
Вопросы
для самопроверки
1.
Как устанавливается связь расположения
координат на комплексном чертеже в
системе трех плоскостей проекций П1П2П3
с координатами проекций точек?
2.
Какими координатами определяется
удалённость точек до горизонтальной,
фронтальной, профильной плоскостей
проекций?
3.
Какие координаты и проекции точки будут
изменяться, если точка перемещается в
направлении, перпендикулярном
профильной плоскости проекций П3?
4.
Какие координаты и проекции точки будут
изменяться, если точка перемещается в
направлении, параллельном оси OZ?
5.
Какими координатами, определяется
горизонтальная (фронтальная, профильная)
проекция точки?
7.
В каком случае проекция точки совпадает
с самой точкой пространства и где
располагаются две другие проекции этой
точки?
8.
Может ли точка принадлежать одновременно
трём плоскостям проекций и в каком
случае?
9.
Как называют точки, одноимённые проекции
которых совпадают?
10.
Каким образом можно определить, какая
из двух точек ближе к наблюдателю, если
их фронтальные проекции совпадают?
Задания
для самостоятельного решения
|
|
|
Рис. 3.6. Условие |
1. Дать наглядное изображение точекA,B,C,Dотносительно плоскостей
проекций П1, П2. Точки заданы
своими проекциями (рис. 3.6).
2.
Построить проекции точек А и В по их
координатам на наглядном изображении
и комплексном чертеже: А(13,5; 20), В(6,5; –20).
Построить проекцию точки С, расположенной
симметрично точке А относительно
фронтальной плоскости проекций П2.
3. Построить проекции точек А, В, С по их
координатам на наглядном изображении
и комплексном чертеже: А(–20; 0; 0), В(–30;
-20; 10), С(–10, –15, 0). Построить точку D,
расположенную симметрично точке С
относительно осиOХ.
Пример решения типовой задачи
Задача
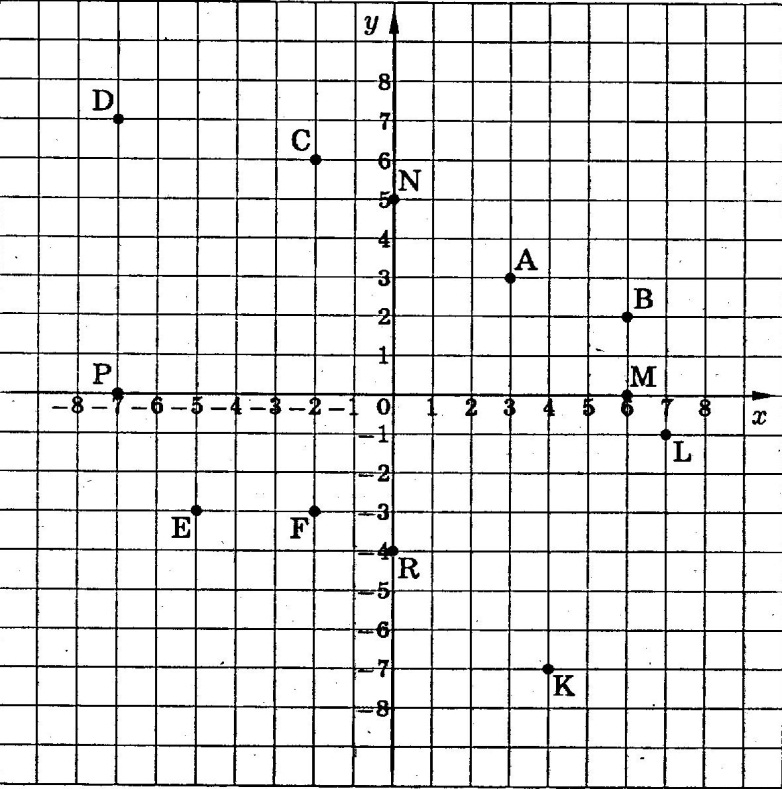
1. Даны координатыX,Y,ZточекA,B,C,D,E,F(табл. 3.3)
Таблица 3.3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Точка – это геометрический абстрактный объект, который имеет координаты. Точки также участвуют в создании чертежа.
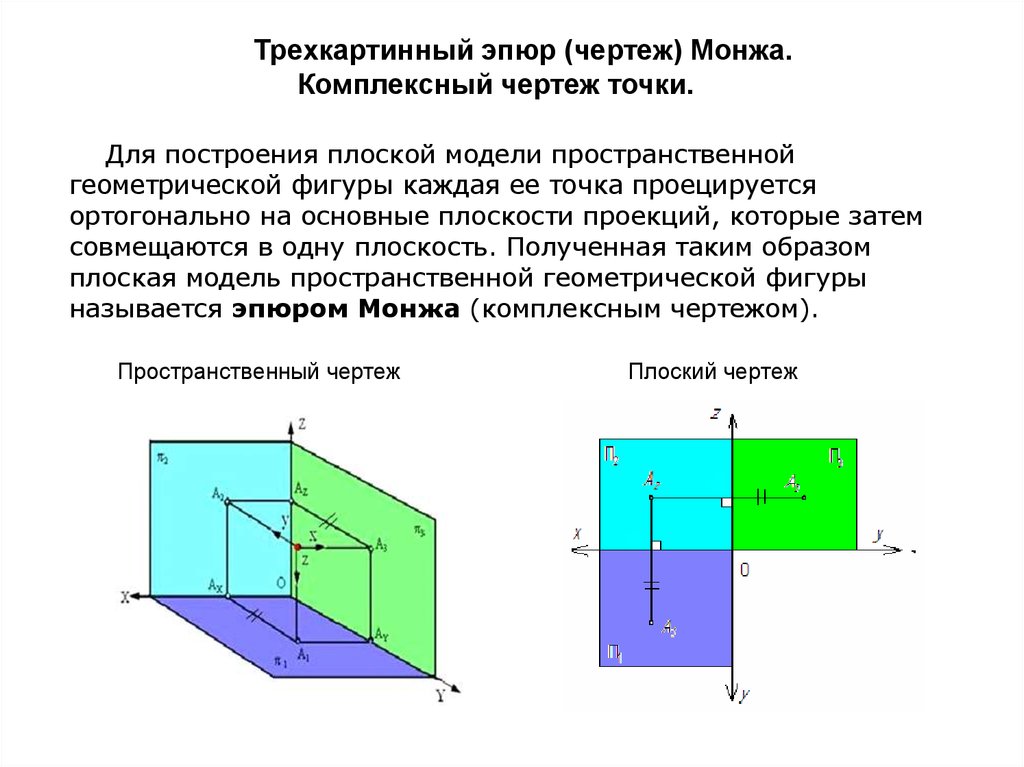
Комплексный чертеж и координаты точки
Комплексным называется чертеж, который был получен на фронтальной и горизонтальной плоскости проекции. Комплексный чертеж получается путем совмещения трех плоскостей проекций в одну.
Существует строгий порядок расположения проекций на чертеже, горизонтальная проекция должна располагаться под фронтальной, профильная проекция должна располагаться справа от фронтальной.
Рисунок 1. Координаты точки
Как найти точки на чертеже
Рассматривая предмет как сочетание граней, вершин и ребер мы можем находить проекции отдельных точек. Для начала нужно определить, какой плоскости или грани точка принадлежит. Затем находят горизонтальные проекции точки, для этого проводят вертикальную прямую линию связи из проекции точек. Видимость проекций определяется исходя из направления взгляда.
Как правильно расставлять точки
Чтобы правильно вычертить вид детали, необходимо уметь строить проекции. С помощью проекций можно определить местоположение точки. Вспомогательные линии позволяют определить место, где ее можно поставить и используются в качестве опорных. Вспомогательные линии двух проекций пересекаются под углом в 45 градусов. В местах пересечения линий связи с проекциями поверхности расставляют точки.
Видимые и невидимые точки
Видимые проекции изображают на чертеже без скобок, а невидимые в скобках, например, А’’ относится к видимой проекции, а (B’’) к невидимой.
Рисунок 2. Видимые и невидимые точки
Точки сопряжения
В месте, где сопрягаются две линии образуется точка перехода или точка сопряжения. Для нахождения точки сопряжения линий прямого угла используется циркуль, его ставят в вершину угла и проводят дугу R до пересечения со сторонами. Чтобы найти центр сопряжения из найденных точек снова проводят окружности радиусом R, в месте их пересечения находится точка центра сопряжения, установив в нее циркуль проводят радиус сопряжения.
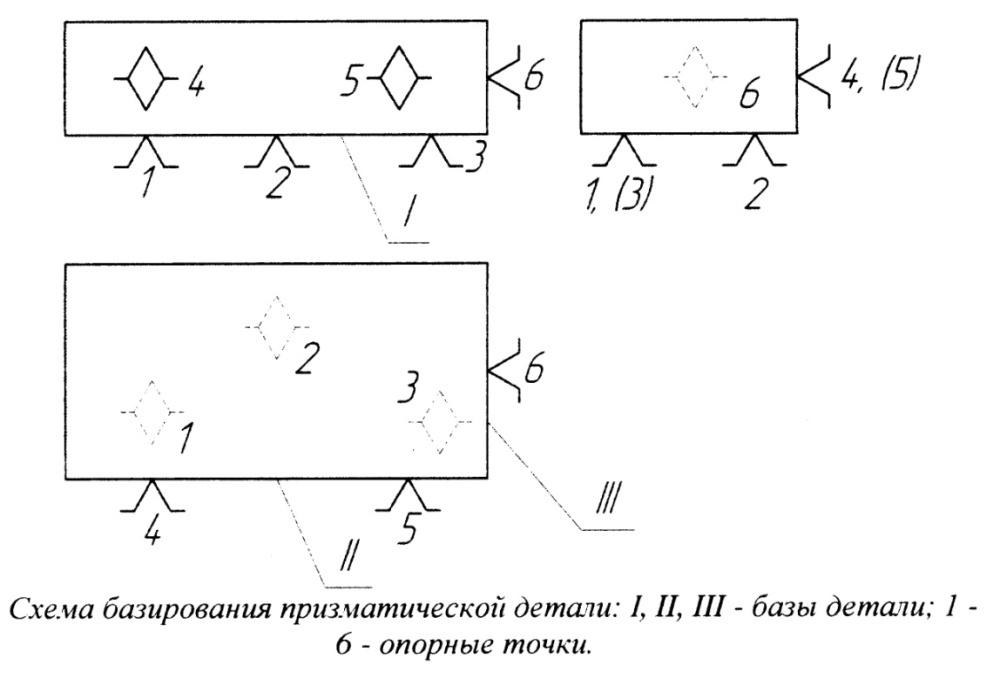
Опорные точки на чертеже
Опорные точки на схеме обозначают условными знакам согласно ГОСТ 21495-76, эти точки символизируют одну из связей заготовки иди изделия с выбранной системой координат. Нумерация опорных точек расставляется, начиная с базы, на которой расположено наибольшее число точек. Также опорные точки называют характерными, их число конечно, они выделяются своим особым положением относительно плоскости проекции и поверхности.
Рисунок 3. Опорные точки на чертеже
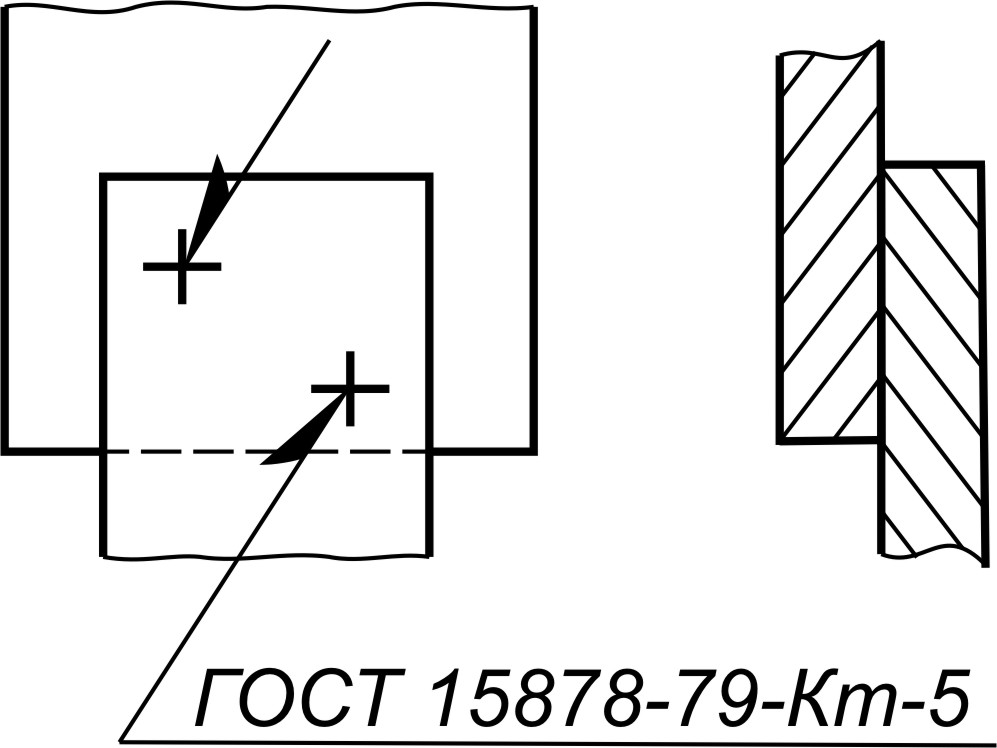
Сварные точки
Если детали соединяются сваркой, то ее также условно изображают на чертеже. В зависимости от расположения сварки можно увидеть шов или одиночную точку. Видимую одиночную точку обозначают знаком «+», невидимые одиночные точки на чертеже не обозначают. Видимый сварной шов обозначают основной сплошной линией, а невидимый штриховой линией.
Рисунок 4. Сварные точки на чертеже
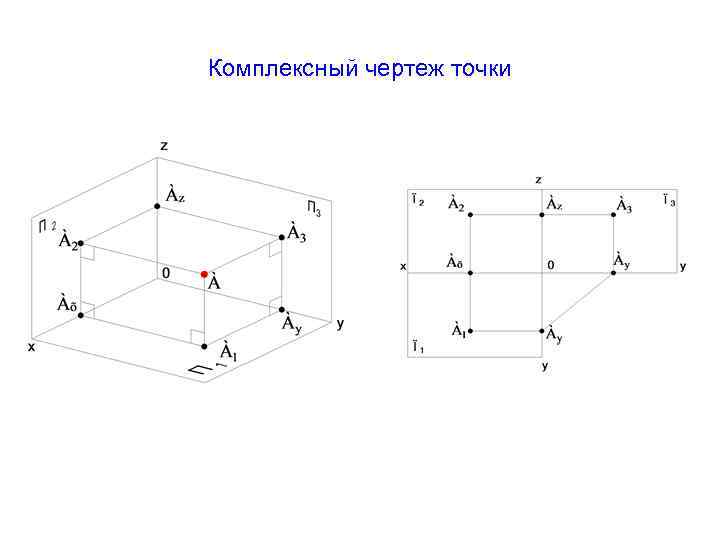
Трехкартинный чертеж точки
Трехкартинный чертеж или чертеж Монка представляет собой прямоугольник, сторонами которого являются линии связи, которые расположены перпендикулярно соответствующим осям проекции. При этом три вершины – проекции точки, а четвертая это точка перелома линии связи.
Рисунок 5. Трехкартинный чертеж точки
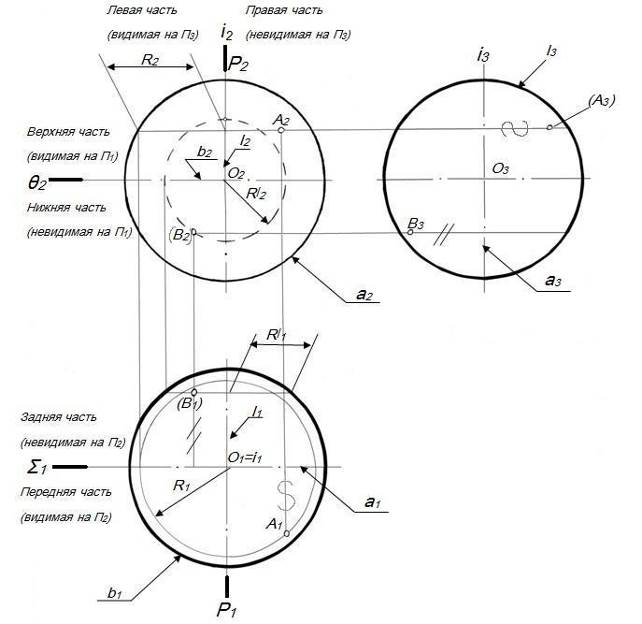
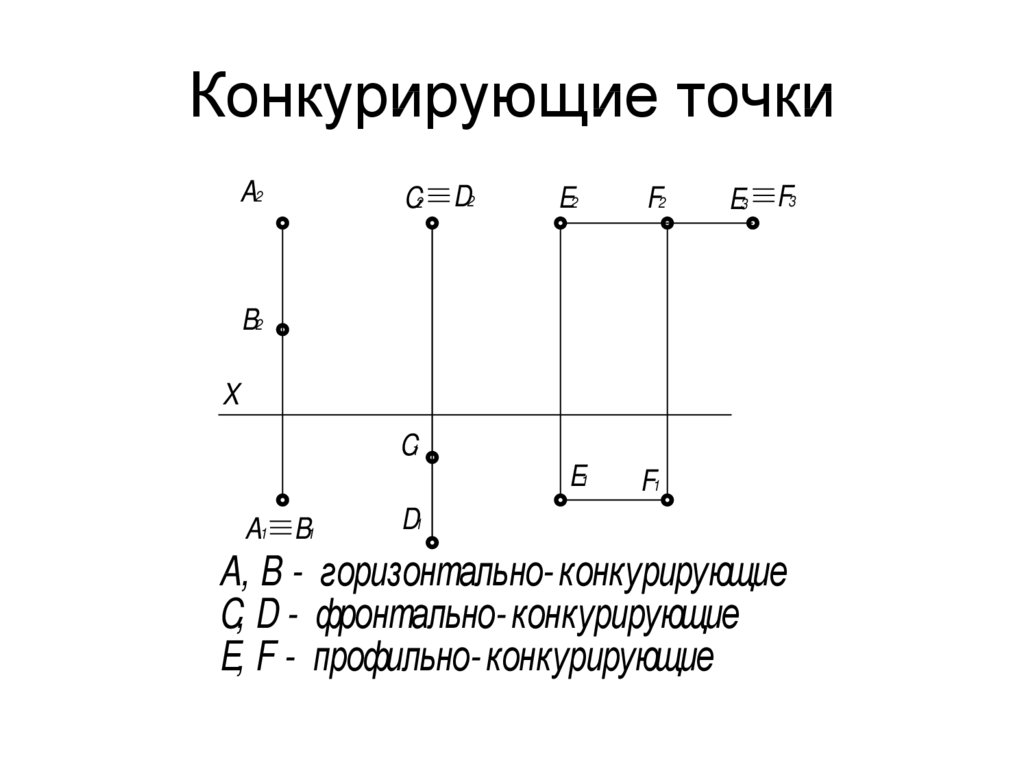
Конкурирующие точки на чертеже
Конкурирующие точки располагаются на одном проецирующем луче, таким образом для наблюдателя одна точка будет видимой, явной, а другая нет, что отразится и на чертеже.
Рисунок 6. Конкурирующие точки на чертеже
Что такое явная точка на чертеже
Одним из важных понятий чертежа является база. Под базой понимается поверхность (точка, ось или сочетание поверхностей), принадлежащие заготовке, которая предназначена для придания изделию требуемого положения. Поверхность, используемая для базирования, может быть установочной ( лишает изделие возможностей перемещения), опорной (лишает одной степени свободы) или направляющей (лишает изделие или заготовку двух степеней свободы). По характеру базы могут быть скрытые и явные. Скрытые находятся в воображаемой плоскости или точке, а явные — в реальной поверхности или точке пересечения рисок.
Как построить комплексный чертеж точки: инструкция
Чтобы построить комплексный чертеж точки используется метод ортогональных или прямоугольных проекций, часто применяемый в инженерной графике. Проекция находится на пересечении проецирующего луча и плоскости.
Построение комплексного чертежа точки А состоит следующих этапов:
- возьмем две плоскости, которые перпендикулярны друг другу и назовем их П1 и П2;
- в результате пересечения проецирующих лучей, перпендикулярных каждой из плоскостей получаем горизонтальную и вертикальную проекцию точки А;
- координаты точки описываются с помощью расстояния до плоскостей;
- для построения плоского чертежа плоскость П1 разворачивают так, чтобы она совпадал с плоскостью П2, а прямая соединяющая А1 и А2 называется линией связи;
- третья плоскость вводится для построения профильной проекции.
Рисунок 7. Построение комплексного чертежа точки
Как поставить точку на чертеже в Компасе
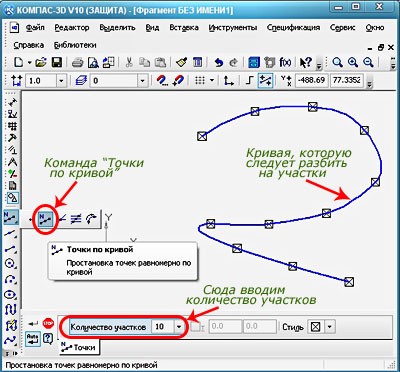
В меню программы Компас есть специальный инструмент «Точка», который позволяет сделать нужное действие за несколько шагов. Точку можно разместить, указав координаты, либо кликнув в месте рабочей области. Помимо основной функции команды, можно использовать расширенный список команд.
Рисунок 8. Как поставить точку в программе Компас
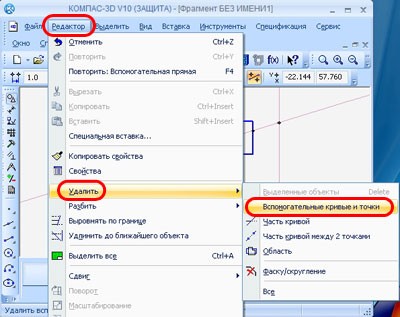
Как убрать точки на чертеже в Компасе
Убрать точки можно выделив их и нажав на клавишу «Delete», либо с помощью команды «Удалить вспомогательные кривые и точки».
Рисунок 9. Как убрать точку в программе Компас
Ответы на вопросы
Как правильно показать невидимую сварную точку?
Невидимые сварные точки не имеют обозначения, в отличие от швов.
Как на чертеже показать характерные точки отрезка?
Характерные точки зависят от объекта, у отрезка они находятся в начале и в конце прямой. Если какая-либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой. При этом длина проекции отрезка прямой общего положения меньше длины самого отрезка.
Чем отличается двухкартинный чертеж точки от трехкартинного?
Разница состоит в количестве проекций на поверхности. В двухкартинном чертеже используются горизонтальная и фронтальная плоскости, такой чертеж вполне позволяет описать форму и размеры фигуры. В трехкартинном чертеже используется еще и третья плоскость.