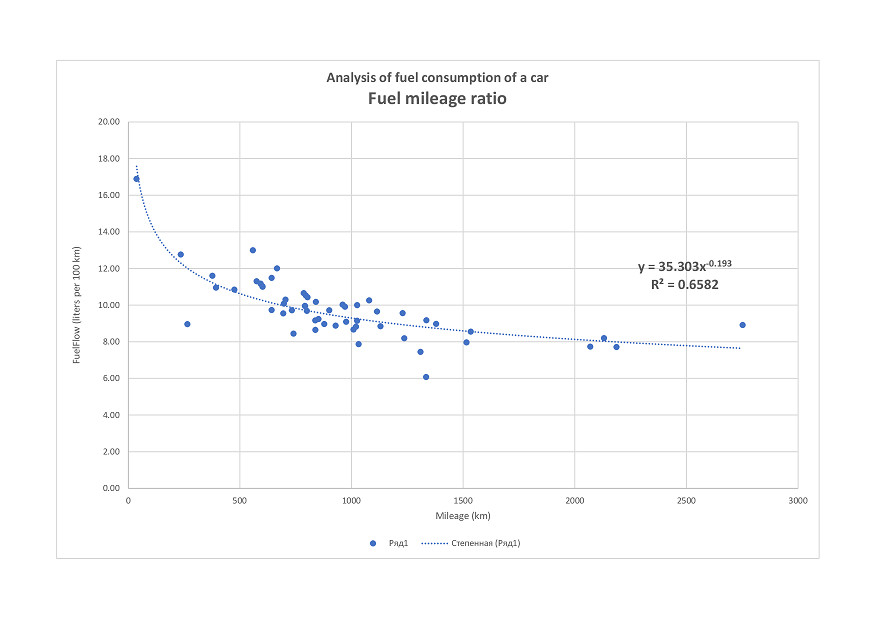
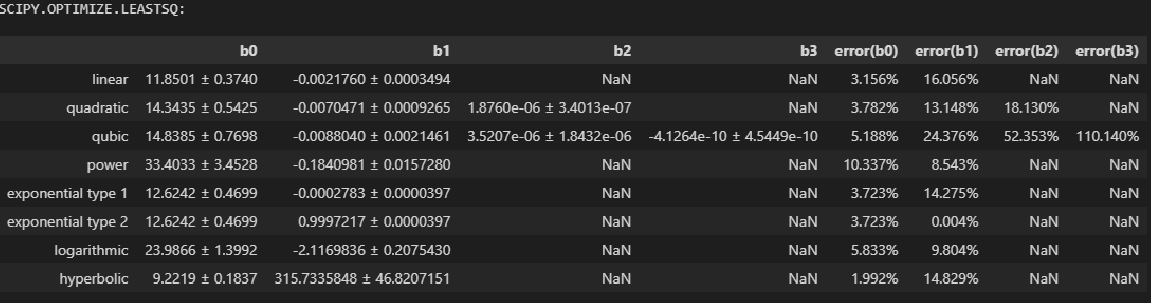
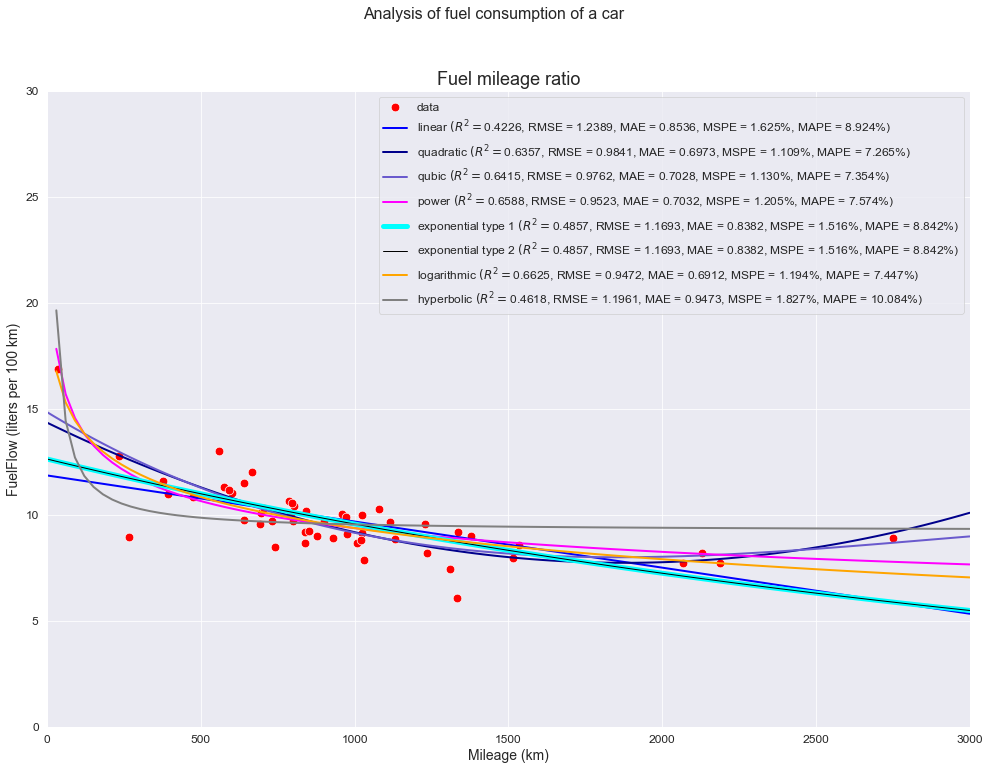
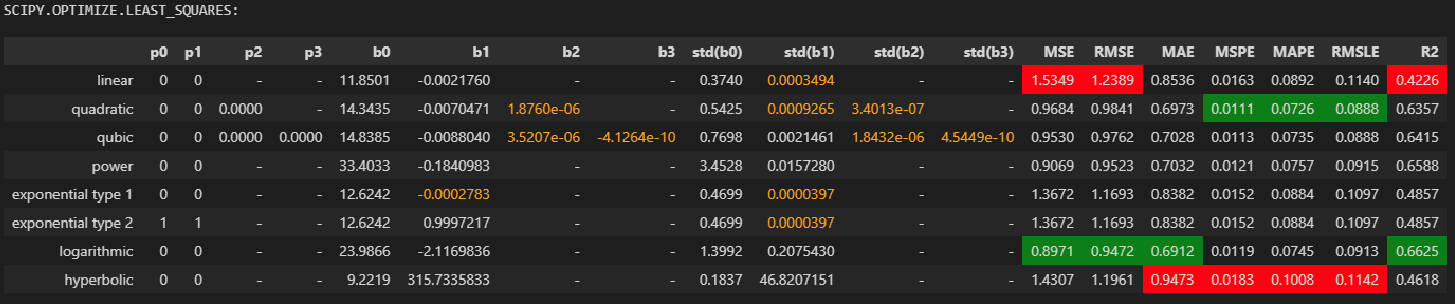
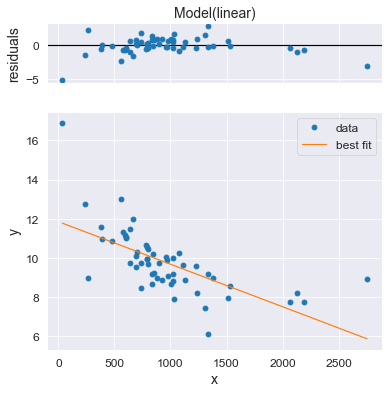
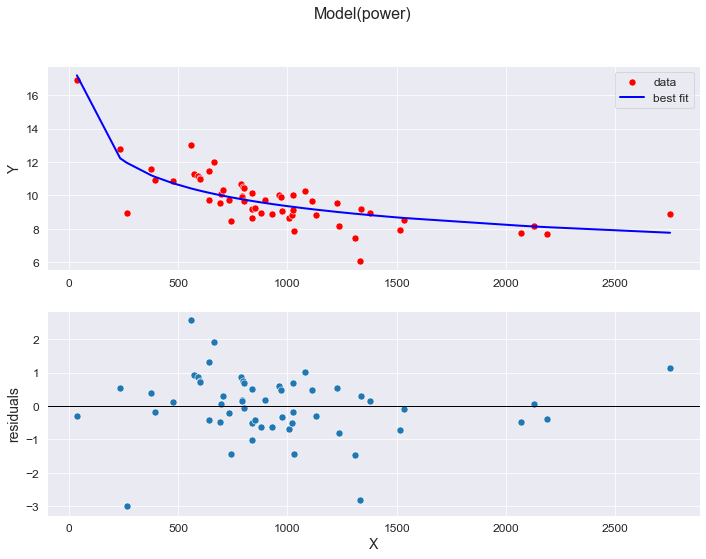
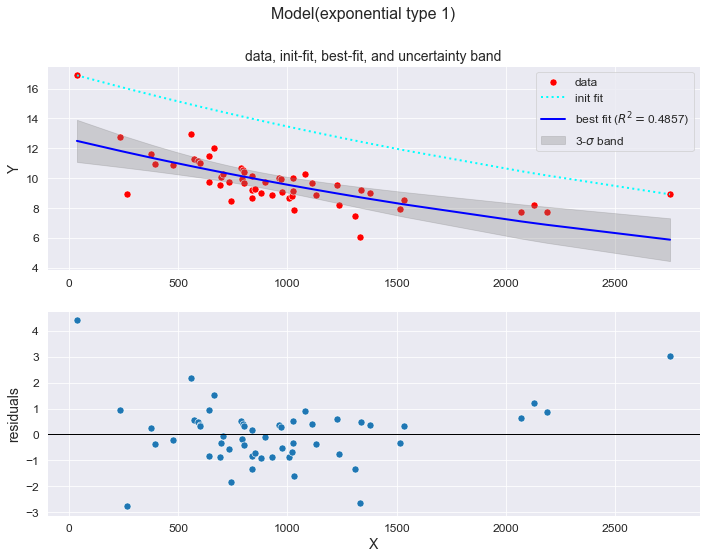
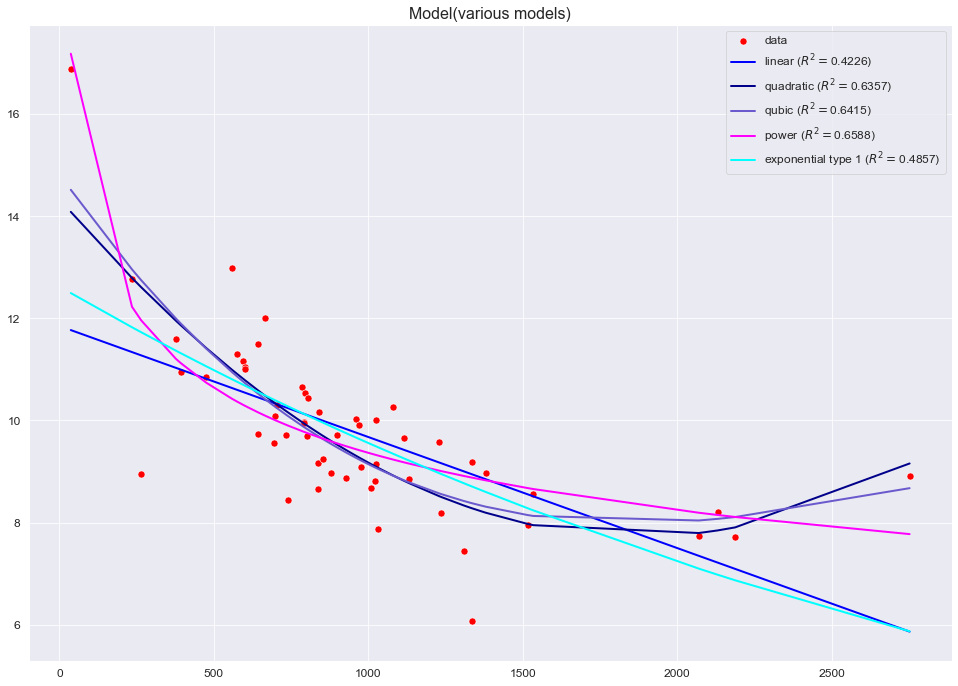
Как найти точку аппроксимации - Avtoru.top - решение различных проблем

При обработке экспериментальных данных часто возникает необходимость аппроксимировать их линейной функцией.

Аппроксимацией (приближением) функции f(x) называется нахождение такой функции (аппроксимирующей функции) g(x), которая была бы близка заданной. Критерии близости функций могут быть различные.

В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной.

В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.

Пусть задан дискретный набор точек, называемых узлами интерполяции, а также значения функции в этих точках. Требуется построить функцию g(x), проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi.

В качестве функции g(x) обычно выбирается полином, который называют интерполяционным полиномом.

В случае если полином един для всей области интерполяции, говорят, что интерполяция глобальная.

В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию).

Аппроксимация линейной функцией

Пример реализации

Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

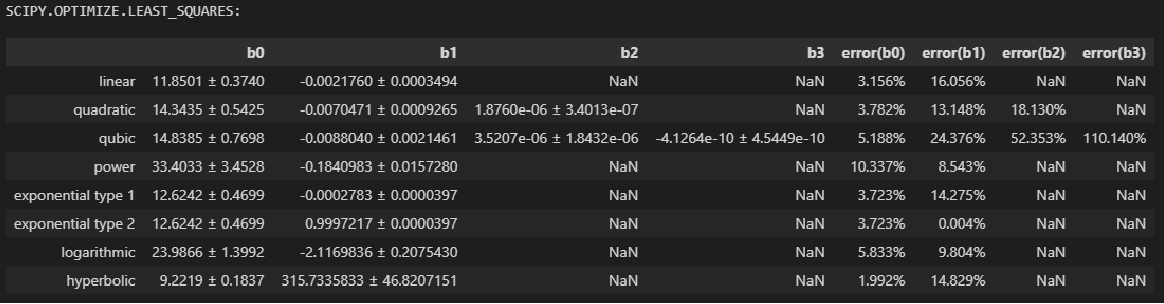
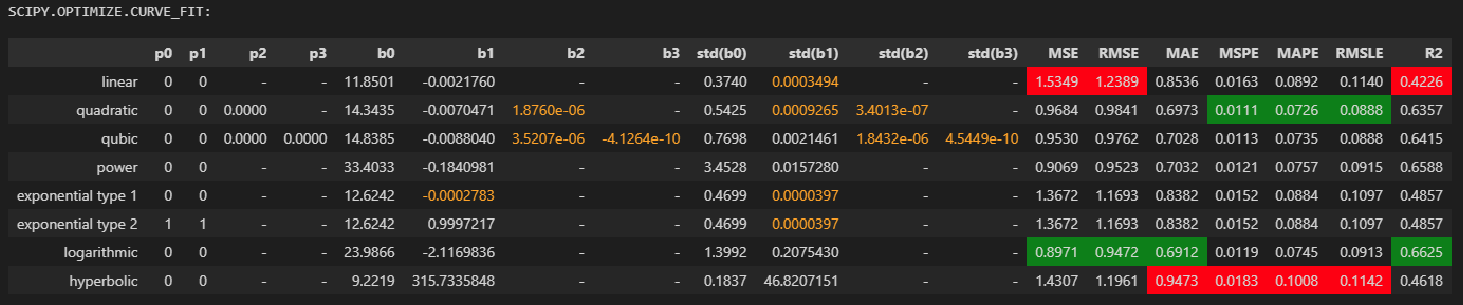
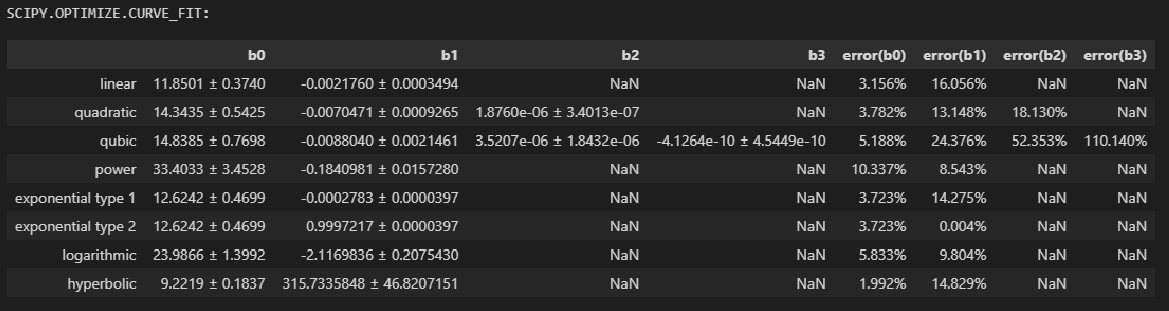
Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.

Реализация на Си

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// Задание начального набора значений
double ** getData(int n) {
  double **f;
  f = new double*[2];
  f[0] = new double[n];
  f[1] = new double[n];
  for (int i = 0; i<n; i++) {
    f[0][i] = (double)i;
    f[1][i] = 8 * (double)i — 3;
    // Добавление случайной составляющей
    f[1][i] = 8*(double)i — 3 + ((rand()%100)-50)*0.05;
  }
  return f;
}
// Вычисление коэффициентов аппроксимирующей прямой
void getApprox(double **x, double *a, double *b, int n) {
  double sumx = 0;
  double sumy = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += x[0][i];
    sumy += x[1][i];
    sumx2 += x[0][i] * x[0][i];
    sumxy += x[0][i] * x[1][i];
  }
  *a = (n*sumxy — (sumx*sumy)) / (n*sumx2 — sumx*sumx);
  *b = (sumy — *a*sumx) / n;
  return;
}
int main() {
  double **x, a, b;
  int n;
  system(«chcp 1251»);
  system(«cls»);
  printf(«Введите количество точек: «);
  scanf(«%d», &n);
  x = getData(n);
  for (int i = 0; i<n; i++)
    printf(«%5.1lf — %7.3lfn», x[0][i], x[1][i]);
  getApprox(x, &a, &b, n);
  printf(«a = %lfnb = %lf», a, b);
  getchar(); getchar();
  return 0;
}

Результат выполнения
Запуск без случайной составляющей

Запуск со случайной составляющей

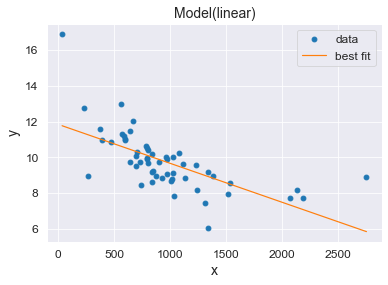
Построение графика функции

Для наглядности построим график функции, полученный аппроксимацией по методу наименьших квадратов. Подробнее о построении графика функции описано здесь.

Реализация на Си

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149

#include <windows.h>
const int NUM = 70; // количество точек
LONG WINAPI WndProc(HWND, UINT, WPARAM, LPARAM);
double **x; // массив данных
      // Определение коэффициентов линейной аппроксимации по МНК
void getApprox(double **m, double *a, double *b, int n) {
  double sumx = 0;
  double sumy = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += m[0][i];
    sumy += m[1][i];
    sumx2 += m[0][i] * m[0][i];
    sumxy += m[0][i] * m[1][i];
  }
  *a = (n*sumxy — (sumx*sumy)) / (n*sumx2 — sumx*sumx);
  *b = (sumy — *a*sumx) / n;
  return;
}
// Задание исходных данных для графика
// (двумерный массив, может содержать несколько рядов данных)
double ** getData(int n) {
  double **f;
  double a, b;
  f = new double*[3];
  f[0] = new double[n];
  f[1] = new double[n];
  f[2] = new double[n];
  for (int i = 0; i<n; i++) {
    double x = (double)i * 0.1;
    f[0][i] = x;
    f[1][i] = 8 * x — 3 + ((rand() % 100) — 50)*0.05;
  }
  getApprox(f, &a, &b, n); // аппроксимация
  for (int i = 0; i<n; i++) {
    double x = (double)i * 0.1;
    f[2][i] = a*x + b;
  }
  return f;
}
// Функция рисования графика
void DrawGraph(HDC hdc, RECT rectClient, double **x, int n, int numrow = 1) {
  double OffsetY, OffsetX;
  double MAX_X = 0;
  double MAX_Y = 0;
  double ScaleX, ScaleY;
  double min, max;
  int height, width;
  int X, Y;    // координаты в окне (в px)
  HPEN hpen;
  height = rectClient.bottom — rectClient.top;
  width = rectClient.right — rectClient.left;
  // Область допустимых значений X
  min = x[0][0];
  max = x[0][0];
  for (int i = 0; i<n; i++) {
    if (x[0][i] < min)
      min = x[0][i];
    if (x[0][i] > max)
      max = x[0][i];
  }
  double temp = max — min;
  MAX_X = max — min;
  OffsetX = min*width / MAX_X;  // смещение X
  ScaleX = (double)width / MAX_X; // масштабный коэффициент X
                  // Область допустимых значений Y
  min = x[1][0];
  max = x[1][0];
  for (int i = 0; i<n; i++) {
    for (int j = 1; j <= numrow; j++) {
      if (x[j][i] < min)
        min = x[j][i];
      if (x[j][i] > max)
        max = x[j][i];
    }
  }
  MAX_Y = max — min;
  OffsetY = max*height / (MAX_Y);  // смещение Y
  ScaleY = (double)height / MAX_Y; // масштабный коэффициент Y
                   // Отрисовка осей координат
  hpen = CreatePen(PS_SOLID, 0, 0); // черное перо 1px
  SelectObject(hdc, hpen);
  MoveToEx(hdc, 0, OffsetY, 0);  // перемещение в точку (0;OffsetY)
  LineTo(hdc, width, OffsetY);   // рисование горизонтальной оси
  MoveToEx(hdc, OffsetX, 0, 0);  // перемещение в точку (OffsetX;0)
  LineTo(hdc, OffsetX, height);  // рисование вертикальной оси
  DeleteObject(hpen);  // удаление черного пера
             // Отрисовка графика функции
  int color = 0xFF; // красное перо для первого ряда данных
  for (int j = 1; j <= numrow; j++) {
    hpen = CreatePen(PS_SOLID, 2, color); // формирование пера 2px
    SelectObject(hdc, hpen);
    X = (int)(OffsetX + x[0][0] * ScaleX);    // координаты начальной точки графика
    Y = (int)(OffsetY — x[j][0] * ScaleY);
    MoveToEx(hdc, X, Y, 0);  // перемещение в начальную точку
    for (int i = 0; i<n; i++) {
      X = OffsetX + x[0][i] * ScaleX;
      Y = OffsetY — x[j][i] * ScaleY;
      LineTo(hdc, X, Y);
    }
    color = color << 8; // изменение цвета пера для следующего ряда
    DeleteObject(hpen); // удаление текущего пера
  }
}
// Главная функция
int  WINAPI  WinMain(HINSTANCE  hInstance,
  HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow) {
  HWND hwnd;
  MSG msg;
  WNDCLASS w;
  x = getData(NUM); // задание исходных данных
  memset(&w, 0, sizeof(WNDCLASS));
  w.style = CS_HREDRAW | CS_VREDRAW;
  w.lpfnWndProc = WndProc;
  w.hInstance = hInstance;
  w.hbrBackground = CreateSolidBrush(0x00FFFFFF);
  w.lpszClassName = «My Class»;
  RegisterClass(&w);
  hwnd = CreateWindow(«My Class», «График функции»,
    WS_OVERLAPPEDWINDOW, 500, 300, 500, 380, NULL, NULL,
    hInstance, NULL);
  ShowWindow(hwnd, nCmdShow);
  UpdateWindow(hwnd);
  while (GetMessage(&msg, NULL, 0, 0)) {
    TranslateMessage(&msg);
    DispatchMessage(&msg);
  }
  return msg.wParam;
}
// Оконная функция
LONG WINAPI WndProc(HWND hwnd, UINT Message,
  WPARAM wparam, LPARAM lparam) {
  HDC hdc;
  PAINTSTRUCT ps;
  switch (Message) {
  case WM_PAINT:
    hdc = BeginPaint(hwnd, &ps);
    DrawGraph(hdc, ps.rcPaint, x, NUM, 2); // построение графика
    EndPaint(hwnd, &ps);
    break;
  case WM_DESTROY:
    PostQuitMessage(0);
    break;
  default:
    return DefWindowProc(hwnd, Message, wparam, lparam);
  }
  return 0;
}

Результат выполнения

Аппроксимация с фиксированной точкой пересечения с осью y

В случае если в задаче заранее известна точка пересечения искомой прямой с осью y, в решении задачи останется только одна частная производная для вычисления коэффициента a.

В этом случае текст программы для поиска коэффициента угла наклона аппроксимирующей прямой будет следующий (имя функции getApprox() заменено на getApproxA() во избежание путаницы).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// Задание начального набора значений
double ** getData(int n) {
  double **f;
  f = new double*[2];
  f[0] = new double[n];
  f[1] = new double[n];
  for (int i = 0; i<n; i++) {
    f[0][i] = (double)i;
    f[1][i] = 8 * (double)i — 3;
    // Добавление случайной составляющей
    //f[1][i] = 8 * (double)i — 3 + ((rand() % 100) — 50)*0.05;
  }
  return f;
}
// Вычисление коэффициентов аппроксимирующей прямой
void getApproxA(double **x, double *a, double b, int n) {
  double sumx = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += x[0][i];
    sumx2 += x[0][i] * x[0][i];
    sumxy += x[0][i] * x[1][i];
  }
  *a = (sumxy — b*sumx) / sumx2;
  return;
}
int main() {
  double **x, a, b;
  int n;
  system(«chcp 1251»);
  system(«cls»);
  printf(«Введите количество точек: «);
  scanf(«%d», &n);
  x = getData(n);
  for (int i = 0; i<n; i++)
    printf(«%5.1lf — %7.3lfn», x[0][i], x[1][i]);
  b = 0;
  getApproxA(x, &a, b, n);
  printf(«a = %lfnb = %lf», a, b);
  getchar(); getchar();
  return 0;
}

Результат выполнения программы поиска коэффициента угла наклона аппроксимирующей прямой при фиксированном значении b=0:

Назад: Алгоритмизация

Источник

Линейная аппроксимация

Аппроксимацией (приближением) функции f(x) называется нахождение такой функции ( аппроксимирующей функции ) g(x) , которая была бы близка заданной. Критерии близости функций могут быть различные.

В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной . Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Пусть задан дискретный набор точек, называемых узлами интерполяции , а также значения функции в этих точках. Требуется построить функцию g(x) , проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi .

В качестве функции g(x) обычно выбирается полином, который называют интерполяционным полиномом .

В случае если полином един для всей области интерполяции, говорят, что интерполяция глобальная .

В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Аппроксимация линейной функцией

Любая линейная функция может быть записана уравнением

Аппроксимация заключается в отыскании коэффициентов a и b уравнения таких, чтобы все экспериментальные точки лежали наиболее близко к аппроксимирующей прямой.

С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение:

Решение поставленной задачи сводится к нахождению экстремума указанной функции двух переменных. С этой целью находим частные производные функции функции по коэффициентам a и b и приравниваем их к нулю.

Решаем полученную систему уравнений

Определяем значения коэффициентов

Для вычисления коэффициентов необходимо найти следующие составляющие:
МНК
Тогда значения коэффициентов будут определены как

Пример реализации

Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

Реализация на Си

Результат выполнения
Запуск без случайной составляющей

Запуск со случайной составляющей

Построение графика функции

Реализация на Си

Результат выполнения

Аппроксимация с фиксированной точкой пересечения с осью y

Как по точкам определить функцию: Как по точкам найти функцию найти функцию по точкам Математика

Построение графиков функций — урок. Алгебра, 10 класс.

построить график функции y=x2+4×2−4.

Решение 1. Обозначим: f(x)=x2+4×2−4. Область определения этой функции: D(f)=(−∞;−2)∪(−2;2)∪(2;+∞), так как x≠2,x≠−2.

2. Проведём исследование функции на чётность/нечётность:

Функция чётная. Следовательно, можно построить ветви графика функции для x≥0 и отобразить их симметрично относительно оси ординат.

3. Определим асимптоты. Вертикальная асимптота: прямая (x=1), т. к. при (x=1) знаменатель дроби равен нулю, а числитель при этом не равен нулю. Для определения горизонтальной асимптоты вычисляем limx→∞f(x):

Следовательно, (y=1) — горизонтальная асимптота.

4. Определим стационарные и критические точки, точки экстремума и промежутки монотонности функции:

Производная существует на всей области определения функции, следовательно, критических точек у функции нет.

Стационарные точки определим из уравнения y′=0. Получаем: (-16x=0) — откуда получаем, что (x=0). При (x<0) имеем: y′>0; при (x>0) имеем: y′<0. Таким образом, в точке (x=0) функция имеет максимум, причём ymax=f(0)=02+402−4=−1.

При (x>0) имеем: y′<0. Учитывая точку разрыва (x=2), делаем вывод: функция убывает на промежутках 0;2) и (2;+∞).

5. Найдём несколько точек, принадлежащих графику функции f(x)=x2+4×2−4 при x≥0:

(0. 5)

6. Сначала нарисуем часть графика при x≥0, потом — часть, симметричную ей относительно оси (y). Полученный график имеет точку максимума ((0;-2)), горизонтальную асимптоту (y=1) и вертикальную асимптоту (x=2).

Как построить график функции

В этой статье разобран самый простой метод получения графика функции.

Суть метода: найти несколько точек принадлежащих графику, расставить их на координатной плоскости и соединить. Этот способ не лучший (лучший – построение графиков с помощью элементарных преобразований), но если вы все забыли или ничего не учили, то знайте, что у вас всегда есть план Б – возможность построить график по точкам.

Итак, алгоритм по шагам:

1. Представьте, как выглядит ваш график.

Строить гораздо легче, если вы понимаете, что примерно должны получить в итоге. Поэтому сначала посмотрите на функцию и представьте, как примерно должен выглядеть ее график. Все виды графиков элементарных функций вы можете найти здесь. Этот пункт желательный, но не обязательный.

Пример: Построить график функции (y=-)(frac)

Данная функция — гипербола с ветвями расположенными во второй и четвертой четверти. Её график выглядит как-то так:

2. Составьте таблицу точек, принадлежащих графику:

Теперь подставим разные значения «иксов» в функцию, и для каждого икса посчитаем значение «игрека».

(y) — не существует (делить на ноль нельзя)

Результат вычислений удобно представлять в виде таблицы, примерно такой:

Как вы могли догадаться, полученные пары «икс» и «игрек» — это точки, лежащие на нашем графике.

4. Постройте координатную плоскость и отметьте на ней точки из таблицы.

5. Если нужно, найдите еще несколько точек и нанесите их на координатную плоскость.

Пример: Чтобы построить график мне не хватает нескольких точек из отрицательной части, а также рядом с осью игрек, поэтому я добавлю столбцы с (x=-2), (x=-4), (x=)(frac) и (x=-)(frac)

6. Постройте график

Теперь аккуратно и плавно соединяем точки.

Онлайн уравнение прямой по двум точкам с подробным решением

Калькулятор уравнения прямой онлайн составлет общее уравнение прямой и уравнение прямой с угловым коэффициентом k по двум точкам.

Исходные данные:

A x + B y + C = 0 — общее уравнение прямой, где A и B одновременно не равны нулю:

составление общее уравнение прямой, где

расчет коэффициента А для общего уравнения прямой

расчет коэффициента B для общего уравнения прямой

расчет коэффициента C для общего уравнения прямой

y = k x + b — уравнение прямой с угловым коэффициентом k, равным тангенсу угла, образованного данной прямой и положительным направлением оси ОХ (ось абсцисс):

составление уравнения прямой с угловым коэффициентом, где

расчет углового коэффициента k

расчет коэффициента b

I. Порядок действий при составлении уравнения прямой, проходящей через 2 точки онлайн калькулятором:

Для составления уравнения прямой требуется ввести значеня координат 2 точек ([X₁, Y₁]; [X₂, Y₂]).

прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя ее точками. интерполяция — способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. линейная интерполяция — нахождение промежуточного значения функции по двум точкам (условно проведя прямую между ними). квадратичная интерполяция — нахождение промежуточного значения функции по трем точкам (интерполирующая функция многочлен второго порядка — парабола).

Аппроксимация в Matlab — CodeTown.ru

Приветствую! Сегодня продолжаем говорить об обработке экспериментальных данных. Сегодняшняя статья — продолжение предыдущей темы: Интерполяция в Matlab. Настоятельно советую с ней ознакомиться перед чтением данной статьи. По сути аппроксимация в Matlab очень похожа на интерполяцию, однако, для её реализации используются другие правила и функции.

Аппроксимация

Относительно интерполяции, аппроксимация получила более широкое распространение. Сущность этого метода состоит в том, что табличные данные аппроксимируют кривой, которая не обязательно должна пройти через все узловые точки, а должна как бы сгладить все случайные помехи табличной функции.

МНК (Метод Наименьших Квадратов)

Одним из самых популярных методов аппроксимации в Matlab и в других средах, это Метод Наименьших Квадратов ( МНК ). В этом методе при сглаживании опытных данных аппроксимирующую кривую стремятся провести так, чтобы её отклонения от табличных данных по всем узловым точкам были минимальными.

Суть МНК заключается в следующем: для табличных данных, полученных в результате эксперимента, отыскать аналитическую зависимость, сумма квадратов уклонений которой от табличных данных во всех узловых точках была бы минимальной.

Аппроксимация в Matlab по МНК осуществляется с помощью функции polyfit. Функция p = polyfit(x, y, n) находит коэффициенты полинома p(x) степени n, который аппроксимирует функцию y(x) в смысле метода наименьших квадратов. Выходом является строка p длины n+1, содержащая коэффициенты аппроксимирующего полинома.

Примеры задач

Разберём задачу, в которой разрешается использование встроенных матлабовских функций.

Осуществить аппроксимацию в Matlab табличных данных x = [0, 0.1 , 0.2, 0.3, 0.5] и y = [3, 4.5, 1.7, 0.7, -1] . Применяя метод наименьших квадратов, приблизить ее многочленами 1-ой и 2-ой степени. 2+coeff2(2)*x+coeff2(3)))

Вывод:
ans = 0.9253
ans = 0.8973

Однако, встречаются задачи, где требуется реализовать аппроксимацию в Matlab без использования специальных функций.

Найти у(0.25) путём построения аппроксимирующего полинома методом наименьших квадратов согласно данным:
x: 0, 0.1, 0.2, 0.3, 0.5
y: 3, 4.5, 1.7, 0.7, -1
p: 0.5, 0.8, 1.6, 0.8, 0.1
Построить этот полином без учёта весовых коэффициентов с использованием определителя Вандермонда и стандартных операторов.

Вывод:
a =
228.1447
-176.0984
22.7745
3.1590
qq = 228.1447 -176.0984 22.7745 3.1590
y2 = 1.4113

Как видите встроенные функции для аппроксимации в Matlab укорачивают алгоритм почти вдвое.

Существует также возможность реализации всего алгоритма через одну функцию, но для преподавателей студентов она скорее всего будет не приемлема. С помощью функции lsqcurvefit(fun,x0,xdata,ydata), где:
xdata,ydata– табличные значения аппроксимируемой функции;
x0 –стартовое значение параметров функции;
fun – функция аппроксимации, задаваемая пользователем

С аналитически-теоретической стороны, существуют такие виды аппроксимации:

Аппроксимация ортогональными классическими полиномами.
Аппроксимация каноническим полиномом

Но на практике их реализацию требуют редко.

Вот и вся основная информация по аппроксимации в Matlab, если остались вопросы, задавайте их в комментариях.

Скачать исходник первой задачи
Скачать исходник второй задачи

Поделиться ссылкой:

Получить функцию по точкам. Как по точкам найти функцию

Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:

Метрика программного обеспечения — это функция системы, документации или процесса, которые могут быть объективно измерены. Вот некоторые примеры: размер программного обеспечения, количество зарегистрированных дефектов, количество тестовых примеров на случай использования, количество людей, необходимых для разработки системного модуля, среди прочих. Метрики можно разделить на контроль или прогнозирование. Элементы управления обычно связаны с программными процессами, такими как: среднее усилие и время, необходимое для исправления дефекта.

Немного матчасти

Функции f i могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками P i ) называется сплайном .

Прогнозирующие показатели напрямую связаны с самой системой. Примерами являются: цикломатрическая сложность, строки кода, размер класса и другие. Прогнозирующие показатели могут влиять на принятие решений руководителями проектов. Менеджеры используют показатели процесса, чтобы решить, нужно ли вносить изменения в процесс. Предиктивные меры также используются для оценки усилий, необходимых для создания или внесения изменений в программное обеспечение. В этой статье, когда мы ссылаемся на показатели программного обеспечения, мы будем иметь дело с теми, которые классифицируются как прогноз.

В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.

Показатели программного обеспечения являются индикаторами, возникающими в результате измерительной деятельности процесса разработки программного обеспечения, которые помогают в управлении проектами. Существует несколько способов измерения системы. Еще некоторые, другие менее эффективны и эффективны. Некоторые вызывают больше, другие меньше влияют на команду. Некоторые из них могут применяться во всем программном процессе. В качестве примера можно привести строки кода, которые измеряют размер продукта.

Другим примером метрики является человекоподобное усилие или человеко-час. Ротация работоспособности также может считаться метрикой. Другими примерами являются точка использования и функциональная точка, которая является одной из наиболее часто используемых и широко распространенных показателей.

Ставим опыты

Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.

Анализ по функциональной точке имеет в качестве основной цели измерение функциональности системы на основе представления пользователя в соответствии со следующими характеристиками.

База основана на представлении пользователя.
Тем имеет смысл для конечных пользователей.
Используются оценки Утилиза.

Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a ;&nbspb ], это означает, что на [a ;&nbspb ] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз P i , то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.

Он в основном количественно определяет функции, содержащиеся в программном обеспечении, в значимых терминах для пользователей. Эта мера напрямую связана с функциональными требованиями. Хотя он очень популярен, его также критикуют многие авторы, которые считают, что это не объективная мера.

Чтобы рассказать о функциональной точке, необходимо выполнить несколько шагов, как показано на рисунке 1. Первый — это определить тип счета. На этом этапе вы определяете, что будет измеряться, тип подсчета, который будет использоваться для измерения дизайна программного обеспечения, как в процессе, так и в продукте. Возможны три типа подсчетов.

Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1 . Вот как он выглядит для наших данных:

Счетчик проекта развития, счетчик проектов улучшения, количество приложений. . В упрощенном виде первая измеряет функциональность, предоставляемую конечным пользователям, когда проект готов к моменту его установки. Этот счет также охватывает преобразование данных, необходимых для развертывания программного обеспечения.

Второе измеряет модификации существующего приложения, которое включает в себя функции, включенные, измененные и исключенные из системы проектом, в дополнение к функциям преобразования данных. Важно помнить, что всегда после подсчета обслуживания и его реализации количество функциональных точек приложения должно обновляться в соответствии с изменениями, внесенными в функциональные возможности. Это призвано постоянно обновлять подсчет точек функции приложения.

Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.

Третий и последний тип счета измеряет функциональность, предоставляемую пользователю установленным приложением и в процессе производства, так что текущая функциональность имеет меру. Шаги операций функции рисунка. Второй шаг для подсчета — это идентификация объема счета и границы приложения. На этом этапе область оцениваемой системы и ее граница ограничены.

Граница приложения определяет, что является внешним для приложения. — концептуальный интерфейс между приложением и внешними пользователями. Область определяет набор или подмножество программного обеспечения известного размера. Третий и четвертый шаги — это подсчет функций данных и функций транзакции. На этих шагах подсчитываются нескорректированные функциональные точки. На этих этапах рассматриваются.

Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа. Это полиномы степени n &nbsp–&nbsp1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
Но вот что получается:

Функции данных: внутренние логические файлы, файлы внешнего интерфейса, функции транзакции: внешние записи, внешние выходы и внешние запросы. Логическая обработка не должна иметь математической формулы или вычисления и не должна генерировать производные данные.

Пятым шагом для подсчета является расчет коэффициента корректировки. Эти факторы связаны с характеристиками приложения. Он отвечает за исправление искажений предыдущего шага и основывается на общих характеристиках системы, в которой определены 14 элементов, которые определяют значение уровня влияния каждого из этих элементов размера системы.

Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.

Легкость изменения. Шестой и последний шаг счетчика — это вычисление скорректированных точек функции. На этом шаге исправлены возможные искажения, возникающие при расчете нескорректированных функциональных точек, приближая измерения к реальной ситуации. Обычно и по контракту корректирующие коэффициенты равны 1, так что они не влияют на нескорректированные функциональные точки.

Он делится на циклы, называемые спринтами. Именно в этих спринтах выполняются мероприятия по проекту. Его практика осуществляется по этапам, известным как «Совещание по планированию», «Ежедневный анализ», «Обзор и ретроспектива». Существует также «Заготовка продукта» и «Спринт-отставание», где перечислены действия по проекту и будут разделены спринтами. Для этого расчет производится по следующей формуле.

В компьютерной графике очень широко применяются кривые Безье , представленные полиномами k -й степени.
Они не являются интерполирующими, так как из k &nbsp+&nbsp1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k &nbsp–&nbsp1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Вот пример кубической кривой Безье:

Как применить это в реальном случае? Пример 2 практической части этой статьи. Пример 1 — Регистрация клиентов. В этом примере рассмотрим экран «Мастер клиента», показанный на рисунке 2. Рисунок каркаса клиента. Давайте рассмотрим все этапы только для примера.

Регистрация клиентов. . Подсчет транзакций. Извлекая сложность и общие функциональные точки как функций данных, так и функций транзакций, необходимо вычислить нескорректированные функциональные точки, умножив количество функций, определенных для заданной сложности, на их вклад. Наконец, добавьте все найденные точки функции. Давайте рассмотрим пример нашего клиента, как показано на рисунке 3.

Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k -й степени (кстати, k &nbsp=&nbsp1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k &nbsp–&nbsp1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k &nbsp=&nbsp3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (P i ), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено .
Вот что получится на нашем тестовом наборе:

Расчет коэффициента корректировки выполняется для каждого приложения для каждого счета. Важно помнить, что показанные факторы связаны с характеристиками приложения и могут влиять на его размер. После вычислений нескорректированных функциональных точек и коэффициента корректировки вычисляется функция, скорректированная по формуле.

Коэффициент корректировки тока: значение корректировки, обнаруженное после проекта технического обслуживания. Таким образом, размер функциональности, который будет реализован, будет составлять 13 пунктов. Пример 2 — Отчет о регистрации клиентов. В этом примере только один спринт будет использоваться для реализации функциональных возможностей и доведения его до завершения тестирования. Запрос был подан в уже существующую систему и в производстве на клиенте.

Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.

Думаем и экспериментируем

В качестве прямых, на которых лежат точки C i &nbsp–&nbsp1 (2) , P i и C i (1) , целесообразно взять касательные к графику интерполируемой функции в точках P i . Это гарантирует отсутствие ложных экстремумов, так как кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).

Будет использоваться владелец продукта клиента, специалист, который будет поднимать, описывать и определять приоритеты требований и правил, которые должны быть разработаны. Прогноз «Идеальный день» был сделан для каждого вида деятельности с использованием шкалы, поэтому определение создания функциональности было всего лишь одним спринтом. При кодировании у нас будет 14, 5 дней. Остальные дни будут для документации, тестов и любых исправлений ошибок, обнаруженных командой тестирования.

Для расчета Идеального Дня было определено, что это будет считаться производительностью 90% в день 8 часов в день. Планирование показателей по Покеру было применено, и после нескольких обсуждений в итоге было достигнуто 125 баллов. Для каждой точки оценивалось почасовое значение в общей сложности 220 часов.

Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:

Эвристика 1

Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C 1 (1) и C n &nbsp–&nbsp1 (2) совпадают с точками P 1 и P n соответственно).
В этом случае получается вот такая кривая:

Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.

Отчет о регистрации клиентов. Для дидактических целей счет будет проходить через все этапы, как в примере 1. Проект улучшения. . Идентификация границы приложения. Извлекая сложность и общие функциональные точки как функций данных, так и функций транзакции, необходимо вычислить нескорректированные функциональные точки. Давайте посмотрим на наш пример отчета о записи клиентов на рисунке.

Рисунок Всего необычных точек функции. Коэффициент корректировки = 0, 65. Расчет скорректированных функциональных точек. После вычислений нескорректированных функциональных точек и коэффициента корректировки будет рассчитана функция, скорректированная в соответствии с формулой, представленной в примере 1.

К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки P i до точек C i &nbsp–&nbsp1 (2) и C i (1) , но при этом сохраняем их все лежащими на одной прямой:

Таким образом, размер функциональности, который будет реализован, будет составлять 3. 03 функциональных пункта. Мы можем заключить, что точка функции является метрикой, ориентированной на пользователя. Они описывают, что программное обеспечение должно делать с точки зрения задач и услуг.

Тем не менее, это очень распространенный, стандартизированный и один из наиболее широко используемых сегодня. И главное, не учитывает ни язык программирования, ни «чувство» профессионала на момент разработки, как и многие другие стратегии. Тем не менее, можно сделать совместное из двух методов, где сложность может быть оценена с учетом оценок, сделанных разработчиками, и размера, с учетом взгляда пользователя.

Эвристика для вычисления расстояний будет такой:

Эвристика 2

Расчёт l 1 и l 2 такой же, как в «эвристике 1».
При этом, однако, стоит ещё проверять, не совпали ли точки P i и P i &nbsp+&nbsp1 по ординате, и, если совпали, полагать l 1 &nbsp=&nbspl 2 &nbsp=&nbsp0. Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).

Результат получается такой:

В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы. Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:

Эвристика 3

Если абсцисса точки пересечения касательных в точках P i (x i ,&nbspy i ) и P i &nbsp+&nbsp1 (x i &nbsp+&nbsp1 ,&nbspy i &nbsp+&nbsp1) лежит в отрезке [x i ;&nbspx i &nbsp+&nbsp1 ], то l 1 либо l 2 полагаем равным нулю. В том случае, если касательная в точке P i направлена вверх, нулю полагаем максимальное из l 1 и l 2 , если вниз — минимальное.

На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код .

А как люди-то делают?

MS Excel

Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.

LibreOffice Calc

В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.

Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат:)

Highcharts , одна из самых популярных JS-библиотек для построения диаграмм

Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).

amCharts , ещё одна популярная JS-библиотека

Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.

Coreplot , самая популярная библиотека построения графиков для iOS и OS X

Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.

aChartEngine , вроде как самая популярная библиотека построения графиков для Android

Больше всего похоже на кривую Безье степени n &nbsp–&nbsp1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.

Вместо заключения

Метки: Добавить метки

Определите степень полинома, который будет использован для интерполирования. Он имеет вид: Кn*Х^n + К(n-1)*Х^(n-1) +.0.

Если вы не можете найти линейную функцию , а точнее распознать ее среди многих, то не переживайте. Трудного в этом ничего нет. Всего лишь пару простых правил, и вы будете всегда отличать функции друг от друга.

Линейная функция является самой просто из основных школьных функций. Если вы только начали изучать их, то, несомненно, у вас могут возникнуть некоторые трудности по распознаванию. Учителя зачастую считают, что дети легко и быстро усваивают материал. Но бывает , что пропустишь всего лишь одно занятие, а уже материал стал более сложны и непонятным, и самому его не разобрать . Поэтому первым делом вам нужно начать с определения, в котором говорится, что линейной функцией называется функция вида f(x)=ax+b. То есть вам необходимо запомнить общий вид, с помощью которого вы сможете находить подобные и определять, что данные функции линейные.

Если общий вид не помогает, и вы все равно никак не разыщите линейную функцию , то вам поможет график. По точкам постройте чертеж (можно даже схематический). Запомните одну важную вещь: у линейной функции график всегда прямая. Поэтому, сделав рисунок , вы сразу же увидите, линейная она у вас либо нет.

В случае, если график не удается построить, есть еще один способ распознавания , который является одним из наиболее простых. Запомните раз и навсегда, что линейная функция имеет степень не выше второй, то есть квадратичная функция никак не может быть линейной, также как и кубическая, и функция четвертой, пятой степеней и так далее. Даже если функция равна числу и в левой части не содержит х, то все равно она будет линейной.

Функция поиска уравнения по таблице точек

Поиск по уравнениям функций

Инструмент для нахождения уравнения функции по ее точкам, ее координатам x, y = f (x) в соответствии с некоторыми методами интерполяции и алгоритмами поиска уравнений

Функция поиска уравнений — dCode

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Ответы на вопросы (FAQ)

Как найти уравнение кривой?

Чтобы найти уравнение на графике:

Метод 1 (подгонка): проанализируйте кривую (посмотрев на нее), чтобы определить, какой тип функции это (линейная, экспоненциальная, логарифмическая, периодическая и т. Д.).) и укажите некоторые значения в таблице, и dCode найдет функцию, которая ближе всего подходит к этим точкам.

Метод 2 (интерполяция): из конечного числа точек существуют формулы, позволяющие создать многочлен, который проходит точно через эти точки (см. Интерполяция Лагранжа), указать значения определенных точек, и dCode вычислит проходящий полином по этим точкам. точки.

Как найти уравнение из набора точек?

Чтобы вывести уравнение функции из таблицы значений (или кривой), существует несколько математических методов.

Метод 1: обнаруживает замечательные решения , как и замечательные идентичности, иногда легко найти уравнение, анализируя значения (сравнивая два последовательных значения или идентифицируя определенные точные значения).

Пример: функция имеет для точек (пары $ (x, y) $) координаты: $ (1,2) (2,4), (3,6), (4,8) $, ординаты увеличиваются на 2, а абсциссы увеличиваются на 1, решение тривиально: $ f (x) = 2x $

Метод 2: использовать функцию интерполяции , более сложный, этот метод требует использования математических алгоритмов, которые могут найти многочлены, проходящие через любые точки.Наиболее известными интерполяциями являются лагранжева интерполяция, ньютоновская интерполяция и интерполяция Невилля.

NB: для данного набора точек существует бесконечное количество решений, потому что через определенные точки проходят бесконечные функции. dCode пытается предложить максимально упрощенные решения, основанные на аффинной функции или полиноме низкой степени (степени 2 или 3).

Как найти уравнение линии?

Исходный код

dCode сохраняет за собой право собственности на исходный код онлайн-инструмента Function Equation Finder.За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент «Function Equation Finder» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая «Функция» Функция Equation Finder (вычисление, преобразование, решение, расшифровка / шифрование, дешифрование / шифрование, декодирование / кодирование, перевод), написанная на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.), Без загрузки данных , скрипт, копипаст или доступ к API для «Function Equation Finder» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

уравнение, координата, кривая, точка, интерполяция, таблица

Источник: https: //www.dcode.2 + bx + c> ) задается тремя числами, разумно предположить, что мы могли бы подогнать параболу к трем точкам на плоскости. Это действительно так, и это полезная идея. На этом шаге мы увидим, как алгебраически подогнать параболу к трем точкам на декартовой плоскости. Это включает в себя вспоминание или обучение тому, как решить три уравнения с тремя неизвестными. Это полезный навык сам по себе.

Уникальный круг, проходящий через три неколлинеарных точки

Решение трех линейных уравнений с тремя неизвестными

Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) — Mathplanet

Линейное уравнение — это уравнение с двумя переменными, график которого представляет собой линию. График линейного уравнения — это набор точек на координатной плоскости, которые все являются решениями уравнения. Если все переменные представляют собой действительные числа, можно изобразить уравнение, нанеся на график достаточно точек для распознавания шаблона, а затем соединить точки, чтобы включить все точки.

Если вы хотите построить график линейного уравнения, у вас должно быть как минимум две точки, но обычно рекомендуется использовать более двух точек. При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.

Пример

Постройте функцию y = x + 2

Начните с выбора пары значений для x, например -2, -1, 0, 1 и 2 и вычислите соответствующие значения y.

X	Y = х + 2	Заказанная пара
-2	-2 + 2 = 0	(-2, 0)
-1	-1 + 2 = 1	(-1, 1)
0	0 + 2 = 2	(0, 2)
1	1 + 2 = 3	(1, 3)
2	2 + 2 = 4	(2, 4)

Теперь вы можете просто нанести пять упорядоченных пар на координатную плоскость

На данный момент это пример дискретной функции.Дискретная функция состоит из изолированных точек.

Проведя линию через все точки и продолжая линию в обоих направлениях, мы получаем противоположность дискретной функции, непрерывную функцию, которая имеет непрерывный график.

Если вы хотите использовать только две точки для определения вашей линии, вы можете использовать две точки, где график пересекает оси. Точка, в которой график пересекает ось x, называется отрезком x, а точка, в которой график пересекает ось y, называется отрезком y.Пересечение по оси x находится путем нахождения значения x, когда y = 0, (x, 0), а точка пересечения по оси y находится путем нахождения значения y, когда x = 0, (0, y).

Стандартная форма линейного уравнения —

$$ Ax + By = C, : : A, B neq 0 $$

Прежде чем вы сможете построить линейное уравнение в его стандартной форме, вы сначала должны решить уравнение относительно y.

Отсюда вы можете построить уравнение, как в примере выше.

График y = a представляет собой горизонтальную линию, где прямая проходит через точку (0, a)

В то время как график x = a представляет собой вертикальную линию, проходящую через точку (a, 0)

Постройте график линейного уравнения y = 3x — 2

Функции: графики и пересечения

Предполагать ж ( Икс ) а также грамм ( Икс ) это две функции, которые принимают на входе действительное число и выводят действительное число.

Тогда точки пересечения ж ( Икс ) а также грамм ( Икс ) эти числа Икс для которого ж ( Икс ) знак равно грамм ( Икс ) .

Иногда точные значения легко найти, решив уравнение ж ( Икс ) знак равно грамм ( Икс ) алгебраически.

Пример 1:

Какие точки пересечения функций ж ( Икс ) а также грамм ( Икс ) если ж ( Икс ) знак равно Икс + 6 а также грамм ( Икс ) знак равно — Икс ?

Точки пересечения ж ( Икс ) а также грамм ( Икс ) эти числа Икс для которого ж ( Икс ) знак равно грамм ( Икс ) .

Это, Икс + 6 знак равно — Икс .

Икс + 6 знак равно — Икс 2 Икс + 6 знак равно 0 2 Икс знак равно — 6 Икс знак равно — 3

Теперь вы можете использовать значение Икс найти соответствующий у -координата точки пересечения.

Подставьте значение Икс в любой из двух функций.

грамм ( — 3 ) знак равно — ( — 3 ) знак равно 3

Уравнения также можно решить графически, построив две функции на координатной плоскости и указав точку их пересечения.

В других случаях бывает сложно найти точные значения. Возможно, вам потребуется использовать технологию для их оценки.

Пример 2:

Найдите точку (точки) пересечения двух функций.

ж ( Икс ) знак равно | Икс — 5 | грамм ( Икс ) знак равно бревно Икс

Здесь не так-то просто решить алгебраически.Решения уравнения | Икс — 5 | знак равно бревно Икс не являются красивыми рациональными числами.

Изобразите функции на координатная плоскость .

Вы можете использовать графическую утилиту, чтобы определить, что координаты точек пересечения приблизительно равны ( 4,36 , 0,64 ) а также ( 5.76 , 0,76 ) .

1.1: Четыре способа представления функции

Определите, представляет ли отношение функцию.
Найдите значение функции.
Определите, является ли функция взаимно однозначной.
Используйте тест вертикальной линии для определения функций.
Изобразите функции, перечисленные в библиотеке функций.

Авиалайнер меняет высоту по мере увеличения расстояния от точки старта полета.Вес подрастающего ребенка со временем увеличивается. В каждом случае одно количество зависит от другого. Между двумя величинами существует взаимосвязь, которую мы можем описывать, анализировать и использовать для прогнозирования. В этом разделе мы разберем такие отношения.

Определение того, представляет ли отношение функцию

Отношение — это набор упорядоченных пар. Набор первых компонентов каждой упорядоченной пары называется областью, а набор вторых компонентов каждой упорядоченной пары называется диапазоном.Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.

Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная и часто обозначается строчной буквой (x ).Каждое значение в диапазоне также известно как выходное значение или зависимая переменная и часто обозначается строчной буквой (y ).

Функция (f ) — это отношение, которое присваивает одно значение в диапазоне каждому значению в домене. Другими словами, никакие (x ) — значения не повторяются. Для нашего примера, который связывает первые пять натуральных чисел с числами, удваивающими их значения, это отношение является функцией, потому что каждый элемент в домене, , связан ровно с одним элементом в диапазон, ( ).

Теперь давайте рассмотрим набор упорядоченных пар, который связывает термины «четный» и «нечетный» с первыми пятью натуральными числами. Он будет выглядеть как

Обратите внимание, что каждый элемент в домене не связан ровно с одним элементом в диапазоне ( ). Например, термин «нечетный» соответствует трем значениям из области ( ), а термин «четный» соответствует двум значениям из диапазона ( ).Это нарушает определение функции, поэтому это отношение не является функцией.

На рисунке ( PageIndex ) сравниваются отношения, которые являются функциями, а не функциями.

Рисунок ( PageIndex ): (a) Это отношение является функцией, потому что каждый вход связан с одним выходом. Обратите внимание, что входные (q ) и (r ) оба дают выход (n ). (б) Эта связь также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, потому что вход (q ) связан с двумя разными выходами.

Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим: «Выход — это функция входа».

Входные значения составляют область , а выходные значения составляют диапазон .

Как сделать: учитывая связь между двумя величинами, определите, является ли связь функцией

Определите входные значения.
Определите выходные значения.
Если каждое входное значение приводит только к одному выходному значению, классифицируйте отношение как функцию. Если какое-либо входное значение приводит к двум или более выходам, не классифицируйте отношение как функцию.

Пример ( PageIndex ): определение того, являются ли прайс-листы меню функциями

Меню кофейни, показанное на рисунке ( PageIndex ), состоит из предметов и их цен.

Цена зависит от товара?
Является ли товар функцией цены?

Решение

Начнем с рассмотрения ввода как пунктов меню. Выходные значения — это цены. См. Рисунок ( PageIndex ).

У каждого элемента в меню есть только одна цена, поэтому цена зависит от элемента.

Два пункта меню имеют одинаковую цену.Если мы рассматриваем цены как входные значения, а товары как выходные, то с одним и тем же входным значением может быть связано несколько выходных данных. См. Рисунок ( PageIndex ).

Следовательно, товар не зависит от цены.

Пример ( PageIndex ): определение того, являются ли правила оценки класса функциями

В конкретном математическом классе общая процентная оценка соответствует среднему баллу.Является ли средний балл функцией процентной оценки? Является ли процентная оценка функцией среднего балла? В таблице ( PageIndex ) показано возможное правило назначения оценок.

Процентное содержание	0–56	57–61	62–66	67–71	72–77	78–86	87–91	92–100
Средний балл	0.0	1,0	1,5	2,0	2,5	3,0	3,5	4,0

Таблица ( PageIndex ): баллы успеваемости за класс.

Решение

Для любой процентной оценки существует связанный средний балл, поэтому средний балл является функцией процентной оценки. Другими словами, если мы введем процентную оценку, на выходе получится конкретный средний балл.

В данной системе оценок существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу. Например, учащиеся, получившие средний балл 3,0, могут иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.

Таблица ( PageIndex ) перечисляет пять величайших бейсболистов всех времен в порядке рангов.

Является ли ранг функцией имени игрока?
Имя игрока зависит от ранга?

Ответ б

да.(Примечание: если бы два игрока были разделены, скажем, за 4-е место, то имя не зависело бы от ранга.)

Использование обозначения функций

Как только мы определим, что отношение является функцией, нам нужно отобразить и определить функциональные отношения, чтобы мы могли понять и использовать их, а иногда также, чтобы мы могли программировать их в компьютерах. Есть разные способы представления функций. Стандартные обозначения функций — это одно из представлений, облегчающих работу с функциями.

Чтобы представить «рост является функцией возраста», мы начинаем с определения описательных переменных (h ) для роста и (a ) для возраста. Буквы (f ), (g ) и (h ) часто используются для обозначения функций точно так же, как мы используем (x ), (y ) и (z ) для обозначения числа и (A ), (B ) и (C ) для представления множеств.

Помните, мы можем использовать любую букву для названия функции; обозначение (h (a) ) показывает нам, что (h ) зависит от (a ). Значение (a ) необходимо поместить в функцию (h ), чтобы получить результат. Скобки указывают, что возраст вводится в функцию; они не указывают на умножение.

Мы также можем дать алгебраическое выражение в качестве входных данных для функции.Например, (f (a + b) ) означает «сначала сложите (a ) и (b ), и результат будет входом для функции (f )». Для получения правильного результата операции необходимо выполнять именно в таком порядке.

Запись (y = f (x) ) определяет функцию с именем (f ). Это читается как « (y ) является функцией (x )». Буква (x ) представляет входное значение или независимую переменную. Буква (y ) или (f (x) ) представляет выходное значение или зависимую переменную.

Пример ( PageIndex ): использование обозначения функций для дней в месяце

Используйте обозначение функции для представления функции, вход которой является названием месяца, а выход — количеством дней в этом месяце.

Решение

Использование обозначения функций для дней в месяце

Количество дней в месяце является функцией названия месяца, поэтому, если мы назовем функцию (f ), мы напишем ( text = f ( text ) ) или (d = f (m) ). Название месяца — это вход в «правило», которое связывает определенное число (выход) с каждым входом.

Рисунок ( PageIndex ): функция (31 = f (январь) ), где 31 — результат, f — правило, а январь — вход.

Например, (f ( text ) = 31 ), потому что в марте 31 день. Обозначение (d = f (m) ) напоминает нам, что количество дней, (d ) (выход), зависит от названия месяца (m ) (вход).

Анализ

Обратите внимание, что входные данные функции не обязательно должны быть числами; входные данные функции могут быть именами людей, метками геометрических объектов или любым другим элементом, определяющим какой-либо вид вывода.Однако большинство функций, с которыми мы будем работать в этой книге, будут иметь числа как входы и выходы.

Пример ( PageIndex ): интерпретация обозначения функции

Функция (N = f (y) ) дает количество полицейских (N ) в городе в году (y ). Что означает (f (2005) = 300 )?

Решение

Когда мы читаем (f (2005) = 300 ), мы видим, что входной год — 2005. Выходное значение, количество полицейских ((N) ), равно 300.Помните, (N = f (y) ). Утверждение (f (2005) = 300 ) говорит нам, что в 2005 году в городе было 300 полицейских.

Используйте обозначение функций, чтобы выразить вес свиньи в фунтах как функцию ее возраста в днях (d ).

Ответ

Вопросы и ответы

Вместо обозначения, такого как (y = f (x) ), можем ли мы использовать тот же символ для вывода, что и для функции, например, (y = y (x) ), означающий « (y ) является функцией (x )? »

Да, это часто делается, особенно по прикладным предметам, использующим высшую математику, например физике и инженерии.Однако, исследуя математику, нам нравится проводить различие между такой функцией, как (f ) , которая является правилом или процедурой, и выходом y, который мы получаем, применяя (f ) к конкретному ввод (x ) . Вот почему мы обычно используем такие обозначения, как (y = f (x), P = W (d) ) и т. Д.

Представление функций с помощью таблиц

Общий метод представления функций — в виде таблицы. Строки или столбцы таблицы отображают соответствующие входные и выходные значения.В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях таблица предоставляет несколько избранных примеров из более полных отношений.

Таблица ( PageIndex ) перечисляет входное число каждого месяца ( ( text = 1 ), ( text = 2 ) и т. Д.) И вывод значение количества дней в этом месяце. Эта информация представляет все, что мы знаем о месяцах и днях для данного года (который не является високосным). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце (f ), где (D = f (m) ) идентифицирует месяцы целым числом, а не именем.

Номер месяца, (м ) (ввод)

Таблица ( PageIndex ) определяет функцию (Q = g (n) ) Помните, это обозначение говорит нам, что (g ) — это имя функции, которая принимает входные данные (n ) и дает результат (Q ).

(п )

Таблица ( PageIndex ) отображает возраст детей в годах и соответствующий им рост.В этой таблице показаны лишь некоторые из имеющихся данных о росте и возрасте детей. Мы сразу видим, что эта таблица не представляет функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма.

Возраст в годах, (a ) (ввод)

Как: по таблице входных и выходных значений определить, представляет ли таблица функцию

Определите входные и выходные значения.
Проверьте, сопряжено ли каждое входное значение только с одним выходным значением. Если это так, таблица представляет функцию.

Пример ( PageIndex ): определение таблиц, представляющих функции

Какая таблица, Таблица ( PageIndex ), Таблица ( PageIndex ) или Таблица ( PageIndex ), представляет функцию (если есть)?

Решение

Таблица ( PageIndex ) и Таблица ( PageIndex ) определяют функции.В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица ( PageIndex ) не определяет функцию, потому что входное значение 5 соответствует двум различным выходным значениям.

Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции.

Функция, представленная таблицей ( PageIndex ), может быть представлена записью

[f (2) = 1 text f (5) = 3 text f (8) = 6 nonumber ]

[g (−3) = 5 text g (0) = 1 text g (4) = 5 nonumber ]

представляют функцию в таблице ( PageIndex ).

Таблица ( PageIndex ) не может быть выражена аналогичным образом, потому что она не представляет функцию.

Представляет ли таблица ( PageIndex ) функцию?

Поиск входных и выходных значений функции

Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию.Оценка всегда дает один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.

Когда мы знаем выходное значение и хотим определить входные значения, которые будут производить это выходное значение, мы устанавливаем выход равным формуле функции и решаем вход. Решение может дать более одного решения, потому что разные входные значения могут давать одно и то же выходное значение.

Вычисление функций в алгебраических формах

Когда у нас есть функция в форме формулы, вычислить ее обычно несложно.2 + 2p − 3 = 0 & text \ (p + 3) (p − 1) = 0 & text End nonumber ]

Если ((p + 3) (p − 1) = 0 ), либо ((p + 3) = 0 ), либо ((p − 1) = 0 ) (или оба они равны (0 )). Мы установим каждый множитель равным (0 ) и решим относительно (p ) в каждом случае.

[(p + 3) = 0, ; p = −3 nonumber ]

[(p − 1) = 0, , p = 1 nonumber ]

Это дает нам два решения. Выход (h (p) = 3 ), когда вход либо (p = 1 ), либо (p = −3 ). Мы также можем проверить, построив график, как на рисунке ( PageIndex ).2 + 2п )

Учитывая функцию (g (m) = sqrt ), решите (g (m) = 2 ).

Ответ

Вычисление функций, выраженных в формулах

Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения . Если можно выразить выход функции с помощью формулы, включающей входную величину, то мы можем определить функцию в алгебраической форме.Например, уравнение (2n + 6p = 12 ) выражает функциональную связь между (n ) и (p ). Мы можем переписать его, чтобы решить, является ли (p ) функцией (n ).

Как: Для данной функции в форме уравнения напишите ее алгебраическую формулу.

Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства, а другую сторону как выражение, которое включает только входную переменную.
Используйте все обычные алгебраические методы для решения уравнений, такие как сложение или вычитание одной и той же величины с обеих сторон или от них, или умножение или деление обеих сторон уравнения на одинаковую величину.

Пример ( PageIndex ): поиск уравнения функции

Выразите отношение (2n + 6p = 12 ) как функцию (p = f (n) ), если это возможно.

Решение

Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где (p ) является функцией (n ), что означает запись его как (p = [ text п] ).

Следовательно, (p ) как функция от (n ) записывается как

[p = f (n) = 2− frac n nonumber ]

Анализ

Важно отметить, что не все отношения, выраженные уравнением, можно также выразить как функцию с формулой. 2 = 1 ) функцию с (x ) на входе и (y ) на выходе? Если это так, выразите отношение как функцию (y = f (x) ).y ), если мы хотим выразить y как функцию от x, не существует простой алгебраической формулы, включающей только (x ), которая равна (y ). Однако каждый (x ) определяет уникальное значение для (y ), и существуют математические процедуры, с помощью которых (y ) можно найти с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для (y ) как функции (x ), даже если формулу нельзя записать явно.

Оценка функции, заданной в табличной форме

Как мы видели выше, мы можем представлять функции в виде таблиц.И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев. И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов.

Функция, которая связывает тип питомца с продолжительностью его памяти, легче визуализировать с помощью таблицы (Table ( PageIndex )).

Память питомца

интервал в часах

Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений. Здесь вызовем функцию (P ). Область функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память питомца.Мы можем оценить функцию (P ) при входном значении «золотая рыбка». Мы бы написали (P (золотая рыбка) = 2160 ). Обратите внимание, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции P кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции.

Как сделать: для функции, представленной в виде таблицы, определить конкретные выходные и входные значения

1.Найдите данный вход в строке (или столбце) входных значений.
2. Определите соответствующее выходное значение в паре с этим входным значением.
3. Найдите заданные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.
4. Определите входные значения, соответствующие заданному выходному значению.

Пример ( PageIndex ): Вычисление и решение табличной функции

Использование таблицы ( PageIndex ),

а. Оцените (g (3) ).
г. Решите (g (n) = 6 ).

(п )

Решение

а.Вычисление (g (3) ) означает определение выходного значения функции (g ) для входного значения (n = 3 ). Выходное значение таблицы, соответствующее (n = 3 ), равно 7, поэтому (g (3) = 7 ).
г. Решение (g (n) = 6 ) означает определение входных значений n, которые производят выходное значение 6. Таблица ( PageIndex ) показывает два решения: 2 и 4.

(п )

Когда мы вводим 2 в функцию (g ), на выходе получается 6.Когда мы вводим 4 в функцию (g ), наш результат также равен 6.

Используя Table ( PageIndex ), вычислите (g (1) ).

Ответ

Поиск значений функций из графика

Оценка функции с помощью графика также требует нахождения соответствующего выходного значения для данного входного значения, только в этом случае мы находим выходное значение, глядя на график.Решение функционального уравнения с использованием графика требует нахождения всех экземпляров данного выходного значения на графике и наблюдения за соответствующими входными значениями.

Пример ( PageIndex ): чтение значений функций из графика

Учитывая график на рисунке ( PageIndex ),

Вычислить (f (2) ).
Решите (f (x) = 4 ).

Решение

Чтобы оценить (f (2) ), найдите точку на кривой, где (x = 2 ), затем прочтите координату y этой точки.Точка имеет координаты ((2,1) ), поэтому (f (2) = 1 ). См. Рисунок ( PageIndex ).

( PageIndex ): график положительной параболы с центром в ((1, 0) ) с отмеченной точкой ((2, 1) ), где (f (2) = 1 ) .

Чтобы решить (f (x) = 4 ), мы находим выходное значение 4 на вертикальной оси. Двигаясь горизонтально по прямой (y = 4 ), мы обнаруживаем две точки кривой с выходным значением 4: ((- 1,4) ) и ((3,4) ). Эти точки представляют два решения (f (x) = 4 ): −1 или 3. Это означает (f (−1) = 4 ) и (f (3) = 4 ), или когда вход — -1 или 3, выход — 4.См. Рисунок ( PageIndex ).

Рисунок ( PageIndex ): График обращенной вверх параболы с вершиной в ((0,1) ) и помеченными точками в ((- 1, 4) ) и ((3 , 4) ). Прямая в точке (y = 4 ) пересекает параболу в отмеченных точках.

Учитывая график на рисунке ( PageIndex ), решите (f (x) = 1 ).

Ответ

(x = 0 ) или (x = 2 )

Определение того, является ли функция однозначной

Некоторые функции имеют заданное выходное значение, соответствующее двум или более входным значениям.Например, на биржевой диаграмме, показанной на рисунке в начале этой главы, цена акции составляла 1000 долларов в пять разных дат, что означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.

Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции взаимно однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как указано в Таблице ( PageIndex ).

Letter Grade	Средний балл
A	4,0
В	3,0
С	2,0
D	1,0

Таблица ( PageIndex ): буквенные оценки и десятичные эквиваленты.

Эта система оценок представляет собой функцию «один-к-одному», потому что каждая вводимая буква дает один конкретный выходной средний балл, а каждый средний балл соответствует одной вводимой букве.

Чтобы визуализировать эту концепцию, давайте еще раз посмотрим на две простые функции, изображенные на рисунках ( PageIndex ) и ( PageIndex ). Функция в части (a) показывает взаимосвязь, которая не является взаимно однозначной, потому что входы (q ) и (r ) оба дают выход (n ). Функция в части (b) показывает взаимосвязь, которая является функцией «один-к-одному», потому что каждый вход связан с одним выходом.

Однозначная функция — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.2 ). Поскольку площади и радиусы являются положительными числами, существует ровно одно решение: ( sqrt > ). Таким образом, площадь круга однозначно зависит от радиуса круга.

Является ли остаток функцией номера банковского счета?
Является ли номер банковского счета функцией баланса?
Является ли баланс однозначной функцией номера банковского счета?

а.да, потому что на каждом банковском счете в любой момент времени имеется единый баланс;

г. нет, потому что несколько номеров банковских счетов могут иметь одинаковый баланс;

г. нет, потому что один и тот же выход может соответствовать более чем одному входу.

Если каждая процентная оценка, полученная на курсе, соответствует одной буквенной оценке, является ли буквенная оценка функцией процентной оценки?
Если да, то функция взаимно однозначная?

а.Да, буквенная оценка является функцией процентной оценки;
г. Нет, не один на один. Мы могли бы получить 100 различных процентных чисел, но только около пяти возможных буквенных оценок, поэтому не может быть только одного процентного числа, соответствующего каждой буквенной оценке.

Использование теста вертикальной линии

Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика. Графики отображают огромное количество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений.Обычно графики строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.

Наиболее распространенные графики называют входное значение (x ) и выходное значение (y ), и мы говорим, что (y ) является функцией (x ), или (y = f (x) ), когда функция названа (f ). График функции — это совокупность всех точек ((x, y) ) на плоскости, которая удовлетворяет уравнению (y = f (x) ). Если функция определена только для нескольких входных значений, то график функции представляет собой только несколько точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующим выходным значением.Например, черные точки на графике на рисунке ( PageIndex ) говорят нам, что (f (0) = 2 ) и (f (6) = 1 ). Однако множество всех точек ((x, y) ), удовлетворяющих (y = f (x) ), является кривой. Показанная кривая включает ((0,2) ) и ((6,1) ), потому что кривая проходит через эти точки

. Рисунок ( PageIndex ): График многочлена.

Тест вертикальной линии можно использовать для определения того, представляет ли график функцию. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, то график не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения.См. Рисунок ( PageIndex ) .

Рисунок ( PageIndex ): три графика, наглядно демонстрирующие, что является функцией, а что нет.

Практическое руководство. Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию

Проверьте график, чтобы увидеть, пересекает ли нарисованная вертикальная линия кривую более одного раза.
Если такая линия есть, определите, что график не представляет функцию.

Пример ( PageIndex ): Применение теста вертикальной линии

Какой из графиков на рисунке ( PageIndex ) представляет (ы) функцию (y = f (x) )?

Рисунок ( PageIndex ): график полинома (a), наклонной вниз прямой (b) и круга (c).

Решение

Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией. Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (a) и (b) рисунка ( PageIndex ). Из этого можно сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что не более чем значений x вертикальная линия пересекает график более чем в одной точке, как показано на рисунке ( PageIndex ).

Рисунок ( PageIndex ): График круга.

Представляет ли график на рисунке ( PageIndex ) функцию?

Рисунок ( PageIndex ): График функции абсолютного значения. Ответ

Использование теста горизонтальной линии

После того, как мы определили, что график определяет функцию, простой способ определить, является ли она взаимно однозначной функцией, — это использовать тест горизонтальной линии .Проведите через график горизонтальные линии. Если какая-либо горизонтальная линия пересекает график более одного раза, то график не представляет собой взаимно однозначную функцию.

Практическое руководство. Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график однозначную функцию

Проверьте график, чтобы увидеть, пересекает ли нарисованная горизонтальная линия кривую более одного раза.
Если такая линия есть, определите, что функция не взаимно однозначна.

Пример ( PageIndex ): Применение теста горизонтальной линии

Рассмотрим функции, показанные на рисунке ( PageIndex ) и рисунке ( PageIndex ). Являются ли какие-либо функции взаимно однозначными?

Решение

Функция на рисунке ( PageIndex ) не является взаимно однозначной. Горизонтальная линия, показанная на рисунке ( PageIndex ), пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках.)

Рисунок ( PageIndex ): График многочлена с горизонтальной линией, пересекающей 2 точки

Функция на рисунке ( PageIndex ) взаимно однозначна. Любая горизонтальная линия будет пересекать диагональную линию не более одного раза.

Является ли график, показанный на рисунке ( PageIndex ), взаимно однозначным?

Ответ

Нет, потому что он не проходит тест горизонтальной линии.

Ключевые понятия

Отношение — это набор упорядоченных пар.Функция — это особый тип отношения, в котором каждое значение домена или вход приводит ровно к одному значению диапазона или выходу.
Функциональная нотация — это сокращенный метод соотнесения ввода и вывода в форме (y = f (x) ).
В табличной форме функция может быть представлена строками или столбцами, которые относятся к входным и выходным значениям.
Чтобы оценить функцию, мы определяем выходное значение для соответствующего входного значения. Алгебраические формы функции можно оценить, заменив входную переменную заданным значением.
Чтобы найти конкретное значение функции, мы определяем входные значения, которые дают конкретное выходное значение.
Алгебраическая форма функции может быть записана из уравнения.
Входные и выходные значения функции можно определить по таблице.
Связь входных значений с выходными значениями на графике — еще один способ оценить функцию.
Функция взаимно однозначна, если каждое выходное значение соответствует только одному входному значению.
График представляет функцию, если любая вертикальная линия, проведенная на графике, пересекает график не более чем в одной точке.
График функции «один к одному» проходит проверку горизонтальной линии.

Глоссарий

зависимая переменная
выходная переменная

домен
набор всех возможных входных значений для отношения

функция
отношение, в котором каждое входное значение дает уникальное выходное значение

Проверка горизонтальной линии
Метод проверки взаимно однозначности функции путем определения того, пересекает ли какая-либо горизонтальная линия график более одного раза

независимая переменная
входная переменная

введите
каждый объект или значение в домене, который относится к другому объекту или значению посредством отношения, известного как функция

однозначная функция
функция, для которой каждое значение вывода связано с уникальным значением ввода

вывод
каждый объект или значение в диапазоне, который создается, когда входное значение вводится в функцию

диапазон
набор выходных значений, которые являются результатом входных значений в отношении

отношение
набор заказанных пар

Проверка вертикальной линии
Метод проверки того, представляет ли график функцию, путем определения того, пересекает ли вертикальная линия график не более одного раза

Авторы и авторство

Как рассчитать уклон в точке — Видео и стенограмма урока

Нахождение уклона в точке Шаги

Хорошо, теперь мы знаем взаимосвязь между производными и уклонами.Это соотношение уступает место этапам нахождения наклона функции в заданной точке ( x 1, y 1):

Найдите производную функции (есть много разных способов сделать это, в зависимости от на функции) и
Вставьте значение x , x 1 точки в производную (это наклон функции в точке)

Довольно просто, правда? Давайте применим это на практике! Снова рассмотрим наш пример с бассейном.Предположим, вода стекает 15 минут. Мы можем подключить 15 для x , чтобы увидеть, сколько воды осталось в бассейне:

A (15) = 4 (15) 2 — 320 (15) + 6400 = 2500

Через 15 минут слива , в бассейне осталось 2500 галлонов воды. Если мы хотим узнать скорость, с которой пул истощается в этот момент, мы просто выполняем функцию через предыдущие шаги.

Сначала находим производную функции. Для этой функции мы используем следующие факты, чтобы найти производную:

Производная суммы или разницы — это сумма или разность производных, соответственно
Производная константы равна 0, а
Производная от axn is тревогаn -1

Таким образом, производная A ( x ) = 4 x 2 — 320 x + 6400 равна A ‘( x ) = 8 x — 320

Следующий шаг состоит в том, чтобы вставить x = 15 в A ‘:

A ‘ (15) = 8 * 15 — 320 = -200

. вода, выходящая из бассейна, составляет 200 галлонов в минуту.Не позволяйте отрицательному ответу сбивать вас с толку. Это отрицательно, потому что вода уходит из бассейна, поэтому количество воды уменьшается. Если бы мы наполняли бассейн, то было бы положительно. В общем, когда значение функции уменьшается, ее наклон отрицательный, а когда значение функции увеличивается, ее наклон положительный.

Обратите внимание: если мы проведем касательную линию к графику функции, где x = 15, мы увидим, что это выглядит так, как будто наклон линии составляет примерно -200.

Мы видим, что мы вычислили наклон кривой в точке (15, 2500).

Дополнительная практика

Предположим, мы хотели узнать, как быстро истощается пул через 20 минут. Это тот же процесс. Мы уже нашли производную, поэтому просто подставляем x = 20 в производную A :

A ‘(20) = 8 * 20 — 320 = -160

Мы видим, что через 20 минут слива, вода выходит из бассейна со скоростью 160 галлонов в минуту.Опять же, мы можем заметить, что наклон касательной к кривой при x = 20 выглядит примерно как -160, поэтому мы знаем, что сделали это правильно.

Резюме урока

Хорошо, давайте на минутку рассмотрим то, что мы узнали. Производная функции дает формулу, которая позволяет нам вычислить наклон функции в любой заданной точке. Чтобы найти наклон функции в точке ( x 1, y 1), мы используем следующие шаги:

Найдите производную функции и
Вставьте x 1 в производную для x

Это дает вам наклон функции в точке ( x 1, y 1).

По сути, когда мы находим наклон функции в данной точке, мы находим скорость изменения этой функции в этой точке. Поскольку скорость изменений в мире вокруг нас постоянно меняется, это чрезвычайно полезное знание!

Линейные функции и их графики

Обзор линий графика

Напомним, что множество всех решений линейного уравнения может быть представлено на прямоугольной координатной плоскости с использованием прямой линии, проходящей по крайней мере через две точки; эта линия называется ее графиком.Например, чтобы построить график линейного уравнения 8x + 4y = 12, мы сначала решим для y .

8x + 4y = 12 Вычтем 8x с обеих сторон. 4y = −8x + 12 Разделим обе части на 4.y = −8x + 124 Упростим. Y = −8×4 + 124y = −2x + 3

В таком виде мы видим, что y зависит от x ; другими словами, x — это независимая переменная, которая определяет значения других переменных. Обычно мы думаем о x -значении упорядоченной пары ( x , y ) как о независимой переменной.и y — зависимая переменная — переменная, значение которой определяется значением независимой переменной. Обычно мы думаем о значении y упорядоченной пары ( x , y ) как о зависимой переменной. Выберите по крайней мере два значения x и найдите соответствующие значения y . Рекомендуется выбирать ноль, некоторые отрицательные числа, а также некоторые положительные числа. Здесь мы выберем пять значений x , определим соответствующие значения y , а затем сформируем репрезентативный набор упорядоченных парных решений.

Как найти функцию зная только точки?

Судя по всему, то, о чем Вы говорите — аппроксимация функции. В Википедии более подробна статья про интерполяцию.

По сути, Ваша задача сводится к 2м шагам:
1. По точкам и общим зависимостям выбирается форма функции (например, полиномиальная, экспоненциальная и.т.п).
2. Строится модель, в которой задаётся функция с неизвестными параметрами. Задача — найти такие параметры, чтобы минимизировать функцию невязки(часто это квадрат разности между реальными значениями в заданых точках и значениями модельной функции, см. МНК).

Источник

На практике часто неизвестна явная
связь между
и,
т. е. невозможно записать эту связь в
виде некоторой зависимости.Или
запись громоздка, содержит трудно
вычисляемые выражения.

Практически важен случай, когда вид
связь задается таблицей
.
Это означает, что дискретному множеству
значений аргументапоставлено в соответствие множество
значений функции.
Эти значения — либо результаты расчетов,
либо экспериментальные данные. На
практике нам могут понадобиться
значения величиныи
в других точках, отличных от узлов.
Мы приходим к необходимости
использования имеющихся табличных
данных для приближенного вычисленияпри любом значении (из некоторой области)
параметра,
поскольку точная связьне известна.

Задачао приближении (аппроксимации)
функций: данную функциютребуется приближенно заменить
(аппроксимировать) некоторой функциейтак, чтобы отклонениеотв заданной области было наименьшим.
Функцияпри этом называется аппроксимирующей.

Важен случай аппроксимации функции
многочленом

(1).

При этом коэффициенты
будут подбираться так, чтобы достичь
наименьшего отклонения многочлена
от данной функции.

Если приближение строится на заданном
дискретном множестве точек
,
то аппроксимация называется точечной.
К ней относятся интерполирование,
среднеквадратичное приближение и
другие. При построении приближения на
непрерывном множестве точек аппроксимация
называется непрерывной(или интегральной).

Точечная аппроксимация.

Одним из основных типов точечной
аппроксимации является интерполирование.
Оно состоит в следующем: для данной
функции
строим многочлен (1), принимающий в
заданных точках,
те же значения, что и функция,
т. е.

,(2).

При этом предполагается, что среди
значений
нет одинаковых, т. е.при.
Точкиназываются узлами интерполяции, а
многочлен—
интерполяционным многочленом.

Максимальная степень интерполяционного
многочлена
,
в этом случае говорят о глобальной
интерполяции, поскольку один многочлен

(3)

используется для интерполяции
на всем рассматриваемом интервале
аргумента.
Коэффициентымногочлена (3) находятся из системы
уравнений (2). При()
эта система имеет единственное решение.

Интерполяционные многочлены могут
строиться отдельно для разных частей
рассматриваемого интервала изменения
.
В этом случае имеем кусочную (или
локальную) интерполяцию.

При использовании интерполяции
многочленов вне рассматриваемого
отрезка
приближение называютэкстраполяцией.

При большом количестве узлов интерполяции
в случае глобальной интерполяции
получается высокая степень многочлена
(3). Кроме того, табличные данные, полученные
при измерениях, могут содержать ошибки.
Построение аппроксимирующего многочлена
с условием обязательного прохождения
ее графика через экспериментальные
точки означало бы тщательное повторение
допущенных при измерениях ошибок. Выход
из этого положения может быть найден
выбором такого многочлена, график
которого проходит близко от данных
точек.

Одним из таких видов приближения является
среднеквадратичное приближение функции
с помощью многочлена (1).При этом
;
случайсоответствует глобальной интерполяции.
На практике стараются подобрать
аппроксимирующий многочлен как можно
меньшей степени.

Мерой отклонения многочлена
от заданной функциина множестве точекпри среднеквадратичном приближении
является величина,
равная сумме квадратов разностей между
значениями многочлена и функции в данных
точках

(4).

Для построения аппроксимирующего
многочлена нужно подобрать коэффициенты
так, чтобы величинабыла наименьшей. В этом состоит метод
наименьших квадратов.

Равномерное приближение.

При построении приближения ставится
более жесткое условие: требуется, чтобы
во всех точках некоторого отрезка
отклонение многочленаот функциибыло по абсолютной величине меньшим
заданной величины:

В этом случае говорят, что многочлен
равномерно
аппроксимирует функциюс точностьюна отрезке.

Введем понятие абсолютного отклонения
многочленаот функциина отрезке. Оно равно максимальному значению
абсолютной величины разности между
ними
на данном отрезке:

(5).

По аналогии можно ввести понятие
среднеквадратичного отклонения
при
среднеквадратичном приближении функций.

Возможность построения многочлена,
равномерно приближающего данную функцию,
следует из теоремы Вейерштрасса об
аппроксимации.

Теорема.Если функциянепрерывна на отрезке, то для любогосуществует
многочленстепени,
абсолютное отклонение которого от
функциина
отрезкеменьше.

Существует также понятие наилучшего
приближения функции
многочленомфиксированной степени.
В этом случае коэффициенты многочленаследует выбрать так, чтобы на заданном
отрезкевеличина абсолютного отклонения (5) была
минимальной. Многочленназывается многочленом наилучшего
равномерного приближения. Существование
и единственность многочлена наилучшего
равномерного приближения вытекает из
следующей теоремы:

Теорема. Для любой функции,
непрерывной на замкнутом ограниченном
множестве,
и любого натуральногосуществует многочленстепени
не выше,
абсолютное отклонение которого от
функцииминимально, т. е.,
причем такой многочлен единственный.

(Множество
обычно представляет собой либо некоторый
отрезоклибо конечную совокупность точек.)

Источник

АКТУАЛЬНОСТЬ ТЕМЫ

В предыдущих обзорах (https://habr.com/ru/articles/690414/, https://habr.com/ru/articles/695556/) мы рассматривали линейную регрессию. Пришло время переходить к нелинейным моделями. Однако, прежде чем рассматривать полноценный нелинейный регрессионный анализ, остановимся на аппроксимации зависимостей.

Про аппроксимацию написано так много, что, кажется, и добавить уже нечего. Однако, кое-что добавить попытаемся.

При выполнении анализа данных может возникнуть потребность оперативно построить аналитическую зависимость. Подчеркиваю — речь не идет о полноценном регрессионном анализе со всеми его этапами, проверкой гипотез и т.д., а только лишь о подборе уравнения и оценке ошибки аппроксимации. Например, мы хотим оценить характер зависимости между какими-либо показателями в датасете и принять решение о целесообразности более глубокого исследования. Подобный инструмент предоставляет нам тот же Excel — все мы помним, как добавить линию тренда на точечном графике:

Такой же инструмент необходим и при работе в Python, причем желательно, сохранив главное достоинство — оперативность и удобство использования, избавиться от недостатков, присущих Excel:

ограниченный набор аналитических зависимостей и метрик качества аппроксимации;
невозможность построения нескольких зависимостей для одного набора данных;
невозможность установления ограничений на значения параметров зависимостей;
невозможность устранить влияние выбросов.

Использованием подобных инструментов мы и рассмотрим в данном обзоре.

Применение пользовательских функций

Как и в предыдущих обзорах, здесь будут использованы несколько пользовательских функций для решения разнообразных задач. Все эти функции созданы для облегчения работы и уменьшения размера программного кода. Данные функции загружается из пользовательского модуля my_module__stat.py, который доступен в моем репозитории на GitHub (https://github.com/AANazarov/MyModulePython).

Вот перечень данных функций:

graph_lineplot_sns — функция позволяет построить линейный график средствами seaborn и сохранить график в виде png-файла;
graph_scatterplot_sns — функция позволяет построить точечную диаграмму средствами seaborn и сохранить график в виде png-файла;
regression_error_metrics — функция возвращает ошибки аппроксимации регрессионной модели;

Пользовательскую функцию simple_approximation мы создаем в процессе данного обзора (она тоже включена в пользовательский модуль my_module__stat.py).

ИСХОДНЫЕ ДАННЫЕ

В качестве примера в данном обзоре продолжим рассматривать задачу нахождения зависимости среднемесячного расхода топлива автомобиля (л/100 км) (FuelFlow) от среднемесячного пробега (км) (Mileage) и среднемесячной температуры (Temperature) (этот же датасет я использовал в своих статьях: https://habr.com/ru/post/683442/, https://habr.com/ru/post/695556/).

# Общий заголовок проекта
Task_Project = "Analysis of fuel consumption of a car"

# Заголовок, фиксирующий момент времени
AsOfTheDate = ""

# Заголовок раздела проекта
Task_Theme = ""

# Общий заголовок проекта для графиков
Title_String = f"{Task_Project}n{AsOfTheDate}"

# Наименования переменных
Variable_Name_T_month = "Monthly data"
Variable_Name_Y = "FuelFlow (liters per 100 km)"
Variable_Name_X1 = "Mileage (km)"
Variable_Name_X2 = "Temperature (°С)"

Загрузим исходные данные из csv-файла. Это уже обработанный датасет, готовый для анализа (первичная обработка данных выполненная в отдельном файле Preparation of input data.py, который также доступен в моем репозитории на GitHub).

Столбцы таблицы:

Month — месяц (в формате Excel)
Mileage — месячный пробег (км)
Temperature — среднемесячная температура (°C)
FuelFlow — среднемесячный расход топлива (л/100 к

dataset_df = pd.read_csv(filepath_or_buffer='data/dataset_df.csv', sep=';')

Сохранение данных

Сохраняем данные в виде отдельных переменных (для дальнейшего анализа).
Среднемесячный расход топлива (л/100 км) / Fuel Flow (liters per 100 km):

Y = np.array(dataset_df['Y'])

Пробег автомобиля за месяц (км) / Mileage (km):

X1 = np.array(dataset_df['X1'])

Среднемесячная температура (°С) / Temperature (degrees celsius):

X2 = np.array(dataset_df['X2'])

Визуализация

Границы значений переменных (при построении графиков):

(X1_min_graph, X1_max_graph) = (0, 3000)
(X2_min_graph, X2_max_graph) = (-20, 25)
(Y_min_graph, Y_max_graph) = (0, 30)

Построение графика:

graph_scatterplot_sns(
    X1, Y,
    Xmin=X1_min_graph, Xmax=X1_max_graph,
    Ymin=Y_min_graph, Ymax=Y_max_graph,
    color='orange',
    title_figure=Title_String, title_figure_fontsize=14,
    title_axes='Dependence of FuelFlow (Y) on mileage (X1)', title_axes_fontsize=16,
    x_label=Variable_Name_X1,
    y_label=Variable_Name_Y,
    label_fontsize=14, tick_fontsize=12,
    label_legend='', label_legend_fontsize=12,
    s=80)

ОСНОВЫ ТЕОРИИ

Кратко остановимся на некоторых теоретических вопросах.

Инструменты Python для аппроксимации

Python предоставляет нам большой набор инструментов для аппроксимации (подробнее см. https://docs.scipy.org/doc/scipy/reference/optimize.html). Мы остановимся на некоторых из них:

функция scipy.optimize.leastsq (https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.leastsq.html#scipy.optimize.leastsq)
функция scipy.optimize.least_squares (https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.least_squares.html#scipy.optimize.least_squares)
функция scipy.optimize.curve_fit (https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html)
функция scipy.optimize.minimize (https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html#scipy.optimize.minimize)
библиотека lmfit (https://lmfit.github.io/lmfit-py/)

Основные виды моделей для аппроксимации

Не будем углубляться в классификацию моделей, об этом написаны сотни учебников, монографий, справочников и статей. Однако, в целях унификации в таблице ниже все-таки приведем основные виды моделей для аппроксимации — разумеется, это список не является исчерпывающим, но охватывает более или менее достаточный набор моделей для практического использования:

Наименование	Уравнение
линейная	‘
квадратическая
кубическая
полиномиальная
степенная	$Y=b_0cdot X^{b_1}$
экспоненциальная I типа	$Y=b_0cdot e^{b_1cdot X}$
экспоненциальная II типа
логарифмическая
обратная логарифмическая
гиперболическая I типа
гиперболическая II типа
гиперболическая III типа
логистическая кривая I типа	$Y=b_0 / (1+b_1cdot e^{-b_2cdot X})$
логистическая кривая II типа (Перла-Рида)	$Y=b_0 / (1+b_1cdot b_2^{-X})$
кривая Гомперца	$Y=b_0cdot {b_1}^{b_2^{X}}$
модифицированная экспонента I типа	$Y=b_0+b_1cdot e^{b_2cdot X}$
модифицированная экспонента II типа
обобщенная логистическая кривая I типа	$Y=b_0+b_1 / (1+b_2cdot e^{-b_3cdot X})$
обобщенная логистическая кривая II типа	$Y=b_0+b_1 / (1+b_2cdot b_3^{-X})$

Примечания:

Нелинейные модели в ряде источников принято делить на 2 группы:
- модели, нелинейные по факторам — путем замены переменных могут быть линеаризованы, т.е. приведены к линейному виду, и для оценки их параметров может применяться классический метод наименьших квадратов;
- модели, нелинейные по параметрам — не могут быть линеаризованы, и для оценки их параметров необходимо применять итерационные методы.

К моделям, нелинейным по параметрам, относятся, например, модифицированные кривые (модифицированная экспонента, обобщенная логистическая кривая), кривая Гомперца и пр. Оценка их параметров средствами Python требует особых приемов (предварительная оценка начальных значений). В данном разборе мы не будем особо останавливаться на этих моделях.

Оценка ошибок и доверительных интервалов для параметров моделей аппроксимации

Экспоненциальные модели могут быть выражены в 2-х формах:
- с помощью собственно экспоненциальной функции $Y=b_0cdot e^{b_1cdot X}$ ;
- в показательной форме
Не будем особо распространяться на опасности увлечения полиномиальными моделями для аппроксимации данных, отметим только, что использовать такие модели нужно очень осторожно, с особым обоснованием и содержательным анализом задачи, а полиномы выше 3-й степени вообще использовать не рекомендуется.

Метрики качества аппроксимации

Рассмотрим основные метрики качества:
1. Mean squared error (MSE) — среднеквадратическая ошибка и Root mean square error (RMSE) — квадратный корень из среднеквадратической ошибки MSE:
$begin{aligned} qquad MSE = frac{1}{n} cdot {displaystylesum_{i=1}^{n} (Y_{i} - widehat{Y}_{i})^2} = frac{1}{n} cdot {displaystylesum_{i=1}^{n} e_{i}^2} = frac{1}{n} cdot boldsymbol{e}^Tboldsymbol{e} end{aligned}$

Особенности: тенденция к занижение качества модели, чувствительность к выбросам.

2. Mean absolute error (MAE) — средняя абсолютная ошибка:

$begin{aligned} qquad MAE = frac{1}{n} cdot {displaystylesum_{i=1}^{n} |Y_{i} - widehat{Y}_{i}|} end{aligned}$

Особенность: гораздо менее чувствительна к выбросам, чем RMSE.

3. Mean squared prediction error (MSPE) — среднеквадратическая ошибка прогноза (среднеквадратическая ошибка в процентах):

$begin{aligned} qquad MSPE = frac{1}{n} cdot {displaystylesum_{i=1}^{n} bigg(frac{Y_{i} - widehat{Y}_{i}}{Y_{i}}bigg)^2} end{aligned}$

Особенности: нечувствительность к выбросам; нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю.

4. Mean absolute percentage error (MAPE) — средняя абсолютная ошибка в процентах:

$begin{aligned} qquad MAPE = 1 - frac{1}{n} cdot {displaystylesum_{i=1}^{n} bigg|frac{Y_{i} - widehat{Y}_{i}}{Y_{i}}bigg|} end{aligned}$

Особенности: нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю.

5. Root Mean Square Logarithmic Error (RMSLE) — cреднеквадратичная логарифмическая ошибка, применяется, если разность между фактическим и предсказанным значениями различается на порядок и выше:

$begin{aligned} qquad RMSLE = sqrt{frac{1}{n} cdot {displaystylesum_{i=1}^{n} (ln(Y_i+1) - ln(widehat{Y_{i}}+1))^2}} = RMSEbigg(ln(Y), ln(widehat{Y})bigg) = sqrt{MSEbigg(ln(Y), ln(widehat{Y})bigg)} end{aligned}$

Особенности: нечувствительность к выбросам; смещена в сторону меньших ошибок (наказывает больше на недооценку, чем за переоценку); к значениям добавляется константа 1, так как логарифм 0 не определен.

6. $boldsymbol{R^2}$ — коэффициент детерминации:

$begin{aligned} qquad R^2 = 1 - frac{SSE}{SST} = 1 - frac{displaystylesum_{i=1}^{n} (Y_{i} - widehat{Y}_{i})^2}{displaystylesum_{i=1}^{n} (Y_{i} - overline{Y}_{i})^2} end{aligned}$

Особенность: значение $boldsymbol{R^2}$ находится в пределах [0; 1], но иногда может принимать отрицательные значения (если ошибка модели больше ошибки среднего значения).
Разумеется, приведенный перечень метрик качества аппроксимации не является исчерпывающим.

Сравнительный анализ метрик качества приведен в https://machinelearningmastery.ru/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-1-regrression-metrics-3606e25beae0/, https://machinelearningmastery.ru/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-2-regression-metrics-d4a1a9ba3d74/, https://loginom.ru/blog/quality-metrics.

Оценка ошибок и доверительных интервалов для параметров моделей аппроксимации

Инструменты аппроксимации Python позволяют получить довольно обширный набор различных данных, в том числе тех, которые нам дают возможность оценить ошибки параметров аппроксимации и построить для них доверительные интервалы. Не вдаваясь глубоко в математическую теорию вопроса, кратко разберем, как это реализовать на практике.

В общем виде доверительный интервал для параметров аппроксимации можно представить в виде , где — значение j-го параметра модели, а — стандартная ошибка этого параметра.

Для определения нам необходима матрица ковариации оценок параметров , диагональные элементы которой представляют собой дисперсию оценок параметров, то есть:

$begin{aligned} qquad sigma_j = sqrt{Sigma_{jj}}, text{ } j=overline{1,m} end{aligned}$

имеет размерность , где — число оцениваемых параметров модели аппроксимации.

Теперь разберем, как получить , используя различные инструменты аппроксимации Python:

Функция scipy.optimize.curve_fit в стандартном наборе возвращаемых данных непосредственно содержит расчетную ковариационную матрицу (The estimated covariance of popt), которая обозначается в программном коде как pcov (см. https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html). Расчетная стандартная ошибка параметров может быть определена очень просто: perr = np.sqrt(np.diag(pcov)).
Функция scipy.optimize.leastsq в стандартном наборе возвращаемых данных содержит матрицу, обратную матрице Гессе (The inverse of the Hessian) $H^{-1}$ , которая обозначается в программном коде как cov_x. Чтобы получить , необходимо умножить $H^{-1}$ на величину остаточной дисперсии

$MSE = frac{SSE}{df_E} = frac{1}{n-m-1} cdot displaystylesum_{i=1}^{n} (y_i - widehat{y}_i)^2$ :

$begin{aligned} Sigma = H^{-1} cdot MSE end{aligned}$

или в программном коде: pcov = cov_x*MSE.

Величина SSE, необходимая для расчета MSE, может быть определена в программном коде как .
Функция scipy.optimize.least_squares вместо $H^{-1}$ возвращает модифицированную матрицу Якоби (Modified Jacobian matrix) , которая обозначается в программном коде как result.jac (см. https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.least_squares.html#scipy.optimize.least_squares, https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.OptimizeResult.html#scipy.optimize.OptimizeResult). Получить $H^{-1}$ можно следующим образом:

$begin{aligned} H^{-1} = (J^T J)^{-1} end{aligned}$

или в программном коде: cov_x = np.linalg.inv(np.dot(result.jac.T, result.jac)).
Функция scipy.optimize.minimize имеет свои специфические особенности: возвращает обратную матрицу Гессе (Inverse of the objective function’s Hessian), которая обозначается в программном коде как res.hess_inv (см. https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html#scipy.optimize.minimize, https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.OptimizeResult.html#scipy.optimize.OptimizeResult), но для определения cov_x необходимо воспользоваться приближенным выражением cov_x = 2*res.hess_inv (подробнее об этом см. https://stackoverflow.com/questions/40187517/getting-covariance-matrix-of-fitted-parameters-from-scipy-optimize-least-squares).
Библиотека lmfit позволяет непосредственно в стандартном наборе возвращаемых данных получить ошибки и доверительные интервалы параметров аппроксимации.

Более подробно с вопросом можно ознакомиться здесь:

https://question-it.com/questions/9466217/poluchenie-kovariatsionnoj-matritsy-podobrannyh-parametrov-iz-metoda-scipy-optimizeleast_squares
https://stackoverflow.com/questions/40187517/getting-covariance-matrix-of-fitted-parameters-from-scipy-optimize-least-squares
https://stackoverflow.com/questions/14854339/in-scipy-how-and-why-does-curve-fit-calculate-the-covariance-of-the-parameter-es
https://stackovergo.com/ru/q/4167751/in-scipy-how-and-why-does-curvefit-calculate-the-covariance-of-the-parameter-estimates
https://math.stackexchange.com/questions/2349026/why-is-the-approximation-of-hessian-jtj-reasonable
https://mmas.github.io/least-squares-fitting-numpy-scipy
https://www.nedcharles.com/regression/Nonlinear_Least_Squares_Regression_For_Python.html

АППРОКСИМАЦИЯ ЗАВИСИМОСТЕЙ

Определим набор зависимостей, которые будем использовать для аппроксимации. В данном обзоре мы рассмотрим набор наиболее широко распространенных зависимостей, не требующих особого подхода к вычислениям. Более сложные случаи — например, зависимости с асимптотами, зависимости нелинейные по параметрам и пр. — тема для отдельного рассмотрения.

# equations
linear_func = lambda x, b0, b1: b0 + b1*x
quadratic_func = lambda x, b0, b1, b2: b0 + b1*x + b2*x**2
qubic_func = lambda x, b0, b1, b2, b3: b0 + b1*x + b2*x**2 + b3*x**3
power_func = lambda x, b0, b1: b0 * (x**b1)
exponential_type_1_func = lambda x, b0, b1: b0*np.exp(b1*x)
exponential_type_2_func = lambda x, b0, b1: b0*np.power(b1, x)
logarithmic_func = lambda x, b0, b1: b0 + b1*np.log(x)
hyperbolic_func = lambda x, b0, b1: b0 + b1/x

Далее будем собственно выполнять аппроксимацию: оценивать параметры моделей, строить графики, причем так, чтобы на графиках отображались уравнения моделей и метрики качества (по аналогии с тем, как это позволяет сделать Excel — это очень удобно), рассмотрим возможность определения ошибок и доверительных интервалов для параметров аппроксимации.

Отдельно довольно кратко остановимся на библиотеке lmfit, которая предоставляет очень широкий инструментарий для аппроксимации.

Аппроксимация с использованием scipy.optimize.leastsq

Особенности использования функции:

Реализация метода наименьших квадратов, без возможности введения ограничений на значения параметров.
Возможность выбора метода оптимизации не предусмотрена.

Данный пакет считается устаревшим по сравнению, с least_squares.

Ссылка на документацию.

from scipy.optimize import leastsq

# list of model
model_list = [
    'linear', 'quadratic',
    'qubic', 'power',
    'exponential type 1', 'exponential type 2',
    'logarithmic',
    'hyperbolic']

# model reference
models_dict = {
        'linear':             linear_func,
        'quadratic':          quadratic_func,
        'qubic':              qubic_func,
        'power':              power_func,
        'exponential type 1': exponential_type_1_func,
        'exponential type 2': exponential_type_2_func,
        'logarithmic':        logarithmic_func,
        'hyperbolic':         hyperbolic_func}

# initial values
p0_dict = {
        'linear':             [0, 0],
        'quadratic':          [0, 0, 0],
        'qubic':              [0, 0, 0, 0],
        'power':              [0, 0],
        'exponential type 1': [0, 0],
        'exponential type 2': [1, 1],
        'logarithmic':        [0, 0],
        'hyperbolic':         [0, 0]}

# titles (formulas)
formulas_dict = {
        'linear':             'y = b0 + b1*x',
        'quadratic':          'y = b0 + b1*x + b2*x^2',
        'qubic':              'y = b0 + b1*x + b2*x^2 + b3*x^3',
        'power':              'y = b0*x^b1',
        'exponential type 1': 'y = b0*exp(b1^x)',
        'exponential type 2': 'y = b0*b1^x',
        'logarithmic':        'y = b0 + b1*ln(x)',
        'hyperbolic':         'y = b0+b1/x'}

# actual data
X_fact = X1
Y_fact = Y

# function for calculating residuals
residual_func = lambda p, x, y: y - func(x, *p)

# return all optional outputs
full_output = True

# variables to save the calculation results
calculation_results_df = pd.DataFrame(columns=['func', 'p0', 'popt', 'cov_x', 'SSE', 'MSE', 'pcov', 'perr', 'Y_calc', 'error_metrics'])
error_metrics_results_df = pd.DataFrame(columns=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'])

# calculations
for func_name in model_list:
    print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')
    func = models_dict[func_name]
    calculation_results_df.loc[func_name, 'func'] = func
    p0 = p0_dict[func_name]
    print(f'p0 = {p0}')
    calculation_results_df.loc[func_name, 'p0'] = p0
    if full_output:
        (popt, cov_x, infodict, mesg, ier) = leastsq(residual_func, p0, args=(X_fact, Y_fact), full_output=full_output)
        integer_flag = f'ier = {ier}, the solution was found' if ier<=4 else f'ier = {ier}, the solution was not found'
        print(integer_flag, 'n', mesg)
        calculation_results_df.loc[func_name, 'popt'] = popt
        print(f'parameters = {popt}')
        calculation_results_df.loc[func_name, 'cov_x'] = cov_x
        print(f'cov_x = n{cov_x}')
        #SSE = (residual_func(popt, X_fact, Y_fact)**2).sum()
        SSE = (infodict['fvec']**2).sum()
        calculation_results_df.loc[func_name, 'SSE'] = SSE
        print(f'SSE = {SSE}')
        MSE = SSE / (len(Y_fact)-len(p0))
        calculation_results_df.loc[func_name, 'MSE'] = MSE
        print(f'MSE = {MSE}')
        pcov = cov_x * MSE
        calculation_results_df.loc[func_name, 'pcov'] = pcov
        print(f'pcov =n {pcov}')
        perr = np.sqrt(np.diag(pcov))
        calculation_results_df.loc[func_name, 'perr'] = perr
        print(f'perr = {perr}n') 
    else:
        popt = leastsq(residual_func, p0, args=(X_fact, Y_fact), full_output=full_output)
        calculation_results_df.loc[func_name, 'popt'] = popt
        print(f'parameters = {popt}n')
    Y_calc = func(X_fact, *popt)
    calculation_results_df.loc[func_name, 'Y_calc'] = Y_calc
    (error_metrics_dict, error_metrics_df) = regression_error_metrics(Yfact=Y_fact, Ycalc=Y_calc, model_name=func_name)
    calculation_results_df.loc[func_name, 'error_metrics'] = error_metrics_dict.values()
    error_metrics_results_df = pd.concat([error_metrics_results_df, error_metrics_df])

LINEAR MODEL: y = b0 + b1*x
p0 = [0, 0]
ier = 3, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000 and the relative error between two consecutive iterates is at 
  most 0.000000
parameters = [ 1.1850e+01 -2.1760e-03]
cov_x = 
[[ 8.7797e-02 -7.3041e-05]
 [-7.3041e-05  7.6636e-08]]
SSE = 84.42039151684142
MSE = 1.5928375757894608
pcov =
 [[ 1.3985e-01 -1.1634e-04]
 [-1.1634e-04  1.2207e-07]]
perr = [3.7396e-01 3.4938e-04]

QUADRATIC MODEL: y = b0 + b1*x + b2*x^2
p0 = [0, 0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.4343e+01 -7.0471e-03  1.8760e-06]
cov_x = 
[[ 2.8731e-01 -4.6282e-04  1.5012e-07]
 [-4.6282e-04  8.3812e-07 -2.9328e-10]
 [ 1.5012e-07 -2.9328e-10  1.1295e-13]]
SSE = 53.26102533463595
MSE = 1.0242504872045375
pcov =
 [[ 2.9428e-01 -4.7404e-04  1.5376e-07]
 [-4.7404e-04  8.5844e-07 -3.0039e-10]
 [ 1.5376e-07 -3.0039e-10  1.1569e-13]]
perr = [5.4247e-01 9.2652e-04 3.4013e-07]

QUBIC MODEL: y = b0 + b1*x + b2*x^2 + b3*x^3
p0 = [0, 0, 0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.4838e+01 -8.8040e-03  3.5207e-06 -4.1264e-10]
cov_x = 
[[ 5.7657e-01 -1.4894e-03  1.1111e-06 -2.4112e-10]
 [-1.4894e-03  4.4815e-06 -3.7039e-09  8.5573e-13]
 [ 1.1111e-06 -3.7039e-09  3.3058e-12 -8.0107e-16]
 [-2.4112e-10  8.5573e-13 -8.0107e-16  2.0099e-19]]
SSE = 52.41383349470524
MSE = 1.0277222253863771
pcov =
 [[ 5.9256e-01 -1.5307e-03  1.1419e-06 -2.4780e-10]
 [-1.5307e-03  4.6057e-06 -3.8066e-09  8.7945e-13]
 [ 1.1419e-06 -3.8066e-09  3.3974e-12 -8.2328e-16]
 [-2.4780e-10  8.7945e-13 -8.2328e-16  2.0656e-19]]
perr = [7.6978e-01 2.1461e-03 1.8432e-06 4.5449e-10]

POWER MODEL: y = b0*x^b1
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [33.4033 -0.1841]
cov_x = 
[[ 1.2667e+01 -5.7225e-02]
 [-5.7225e-02  2.6284e-04]]
SSE = 49.87968652194349
MSE = 0.9411261607913867
pcov =
 [[ 1.1922e+01 -5.3856e-02]
 [-5.3856e-02  2.4737e-04]]
perr = [3.4528 0.0157]

EXPONENTIAL TYPE 1 MODEL: y = b0*exp(b1^x)
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.2624e+01 -2.7834e-04]
cov_x = 
[[ 1.5566e-01 -1.1829e-05]
 [-1.1829e-05  1.1127e-09]]
SSE = 75.19491109027253
MSE = 1.4187719073636327
pcov =
 [[ 2.2085e-01 -1.6783e-05]
 [-1.6783e-05  1.5787e-09]]
perr = [4.6994e-01 3.9733e-05]

EXPONENTIAL TYPE 2 MODEL: y = b0*b1^x
p0 = [1, 1]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [12.6242  0.9997]
cov_x = 
[[ 1.5566e-01 -1.1826e-05]
 [-1.1826e-05  1.1121e-09]]
SSE = 75.19491108954423
MSE = 1.4187719073498912
pcov =
 [[ 2.2085e-01 -1.6778e-05]
 [-1.6778e-05  1.5778e-09]]
perr = [4.6994e-01 3.9722e-05]

LOGARITHMIC MODEL: y = b0 + b1*ln(x)
p0 = [0, 0]
ier = 3, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000 and the relative error between two consecutive iterates is at 
  most 0.000000
parameters = [23.9866 -2.1170]
cov_x = 
[[ 2.1029 -0.3106]
 [-0.3106  0.0463]]
SSE = 49.34256729321431
MSE = 0.9309918357210247
pcov =
 [[ 1.9578 -0.2891]
 [-0.2891  0.0431]]
perr = [1.3992 0.2075]

HYPERBOLIC MODEL: y = b0+b1/x
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [  9.2219 315.7336]
cov_x = 
[[ 2.2732e-02 -2.5920e+00]
 [-2.5920e+00  1.4765e+03]]
SSE = 78.69038671392151
MSE = 1.4847242776211607
pcov =
 [[ 3.3751e-02 -3.8485e+00]
 [-3.8485e+00  2.1922e+03]]
perr = [ 0.1837 46.8207]

Теперь сформируем отдельный DataFrame, в котором соберем все результаты аппроксимации — параметры моделей (, , , ), метрики качества (MSE, RMSE, MAE, MSPE, MAPE, RMSLE, ) и начальные условия (, , , ).

Для улучшения восприятия используем возможности Python по визуализации таблиц (https://pandas.pydata.org/pandas-docs/stable/user_guide/style.html):

заменим nan на «-«;
значения параметров моделей, величина которых сравнима с установленным пределом точности отображения (DecPlace), выделим цветом (orange);
для параметра установим повышенную точность отображения, а для параметров , установим экспоненциальный формат;
для метрик качества установим выделение цветом наилучшего (green) и наихудшего (red) результата.

При этом нужно обратить внимание на следующее — пользовательская функция regression_error_metrics возвращает результат как в виде DataFrame, так и в виде словаря (dict):

если мы используем данные в виде DataFrame, то необходимо откорректировать значения признаков MSPE и MAPE, так как пользовательская функция regression_error_metrics возвращает значения этих признаков в строковом формате (из-за знака ‘%’) и при определении наилучшего и наихудшего результатов могут возникнуть ошибки (значение ‘10%’ будет считаться лучшим результатом, чем ‘9%’ из-за того, что первым символом является единица), поэтому следует удалить знак ‘%’ и изменить тип данных на float;
если мы используем данные в виде словаря (dict), то подобная проблема не возникает.

result_df = pd.DataFrame(
                list(calculation_results_df.loc[:,'p0'].values),
                columns=['p0', 'p1', 'p2', 'p3'],
                index=model_list)

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'popt'].values),
                                columns=['b0', 'b1', 'b2', 'b3'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'perr'].values),
                                columns=['std(b0)', 'std(b1)', 'std(b2)', 'std(b3)'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'error_metrics'].values),
                                columns=['MSE', 'RMSE',	'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'],
                                index=model_list))

display(result_df)

# settings for displaying the DataFrame: result_df
result_df_leastsq = result_df.copy()
'''for elem in ['MSPE', 'MAPE']:
    result_df_leastsq[elem] = result_df_leastsq[elem].apply(lambda s: float(s[:-1]))'''
print('scipy.optimize.leastsq:'.upper())
display(result_df_leastsq
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))

Сформируем DataFrame, содержащий ошибки и доверительные интервалы параметров моделей аппроксимации:

result_df_with_perr = pd.DataFrame()

parameter_name_list = ['b0', 'b1', 'b2', 'b3']
result_df_with_perr[parameter_name_list] = result_df[parameter_name_list]

parameter_format_dict = {
    'b0': '{:.' + str(DecPlace) + 'f}',
    'b1': '{:.' + str(DecPlace + 3) + 'f}',
    'b2': '{:.' + str(DecPlace) + 'e}',
    'b3': '{:.' + str(DecPlace) + 'e}',
    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
    'std(b2)': '{:.' + str(DecPlace) + 'e}',
    'std(b3)': '{:.' + str(DecPlace) + 'e}'}

for parameter in parameter_name_list:
    for model in result_df.index:
        if not result_df.isna().loc[model, parameter]:
            result_df_with_perr.loc[model, parameter] = 
                str(parameter_format_dict[parameter].format(result_df.loc[model, parameter])) + 
                    ' ' + u"u00B1" + ' ' + 
                    str(parameter_format_dict[parameter].format(result_df.loc[model, 'std('+parameter+')']))
            relative_errors = abs(result_df.loc[model, 'std('+parameter+')'] / result_df.loc[model, parameter])
            result_df_with_perr.loc[model, 'error('+parameter+')'] = '{:.3%}'.format(relative_errors)

result_df_with_perr_leastsq = result_df_with_perr.copy()
print('scipy.optimize.leastsq:'.upper())
display(result_df_with_perr_leastsq)

XY_calc_df = pd.DataFrame({
    'X_fact': X_fact,
    'Y_fact': Y_fact})
for i, model in enumerate(model_list):
    XY_calc_df[model] = calculation_results_df.loc[model, 'Y_calc']
display(XY_calc_df.head(), XY_calc_df.tail())

Построим графики аппроксимации (по аналогии с Excel):

# setting colors for graphs
color_dict = {
        'linear':                      'blue',
        'quadratic':                   'darkblue',
        'qubic':                       'slateblue',
        'power':                       'magenta',
        'exponential type 1':          'cyan',
        'exponential type 2':          'black',
        'logarithmic':                 'orange',
        'inverse logarithmic':         'gold',
        'hyperbolic':                  'grey',
        'hyperbolic type 2':           'darkgrey',
        'hyperbolic type 3':           'lightgrey',
        'modified exponential type 1': 'darkcyan',
        'modified exponential type 2': 'black',
        'logistic type 1':             'green',
        'logistic type 2':             'darkgreen',
        'Gompertz':                    'brown'
        }

linewidth_dict = {
        'linear':                      2,
        'quadratic':                   2,
        'qubic':                       2,
        'power':                       2,
        'exponential type 1':          5,
        'exponential type 2':          1,
        'logarithmic':                 2,
        'inverse logarithmic':         2,
        'hyperbolic':                  2,
        'hyperbolic type 2':           2,
        'hyperbolic type 3':           2,
        'modified exponential type 1': 2,
        'modified exponential type 2': 2,
        'logistic type 1':             2,
        'logistic type 2':             2,
        'Gompertz':                    2
        }

# changing the Matplotlib settings
plt.rcParams['axes.titlesize'] = 14
plt.rcParams['legend.fontsize'] = 12
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12

# bounds of values of variables (when plotting)
Xmin = X1_min_graph
Xmax = X1_max_graph
Ymin = Y_min_graph
Ymax = Y_max_graph

# the value of the independent variable (when plotting)
nx = 100
hx = (Xmax - Xmin)/(nx - 1)
X_calc_graph = np.linspace(Xmin, Xmax, nx)

# plotting
fig, axes = plt.subplots(figsize=(420/INCH, 297/INCH))
title_figure = Title_String + 'n' + Task_Theme + 'n'
fig.suptitle(title_figure, fontsize = 16)
title_axes = 'Fuel mileage ratio'
axes.set_title(title_axes, fontsize = 18)

# actual data
sns.scatterplot(
    x=X_fact, y=Y_fact,
    label='data',
    s=75,
    color='red',
    ax=axes)

# models
for func_name in model_list:
    R2 = round(result_df.loc[func_name,'R2'], DecPlace)
    RMSE = round(result_df.loc[func_name,'RMSE'], DecPlace)
    MAE = round(result_df.loc[func_name,'MAE'], DecPlace)
    MSPE = "{:.3%}".format(result_df.loc[func_name,'MSPE'])
    MAPE = "{:.3%}".format(result_df.loc[func_name,'MAPE'])
    label = func_name + ' '+ r'$(R^2 = $' + f'{R2}' + ', ' + f'RMSE = {RMSE}' + ', ' + f'MAE = {MAE}' + ', ' + f'MSPE = {MSPE}' + ', ' + f'MAPE = {MAPE})'
    func = calculation_results_df.loc[func_name, 'func']
    popt = calculation_results_df.loc[func_name, 'popt']
    sns.lineplot(
        x=X_calc_graph, y=func(X_calc_graph, *popt),
        color=color_dict[func_name],
        linewidth=linewidth_dict[func_name],
        legend=True,
        label=label,
        ax=axes)

axes.set_xlim(Xmin, Xmax)
axes.set_ylim(Ymin, Ymax)
axes.set_xlabel(Variable_Name_X1, fontsize = 14)
axes.set_ylabel(Variable_Name_Y, fontsize = 14)
axes.legend(prop={'size': 12})

plt.show()

Аппроксимация с использованием scipy.optimize.least_squares

Особенности использования функции:

Реализация нелинейного метода наименьших квадратов, с возможностью введения ограничений на значения параметров.
Имеется возможность выбора алгоритма оптимизации:
- trf (Trust Region Reflective) — установлен по умолчанию, надежный метод, особенно подходящий для больших задач с ограничениями;
- dogbox — для небольших задач с ограничениями;
- lm (Levenberg-Marquardt algorithm) — для небольших задач без ограничений.

Ссылка на документацию.

from scipy.optimize import least_squares

# algorithm to perform minimization
methods_dict = {
        'linear':             'lm',
        'quadratic':          'lm',
        'qubic':              'lm',
        'power':              'lm',
        'exponential type 1': 'lm',
        'exponential type 2': 'lm',
        'logarithmic':        'lm',
        'hyperbolic':         'lm'}

# actual data
X_fact = X1
Y_fact = Y

# function for calculating residuals
residual_func = lambda p, x, y: y - func(x, *p)

# return all optional outputs
full_output = True

# variables to save the calculation results
calculation_results_df = pd.DataFrame(columns=['func', 'p0', 'popt', 'jac', 'hess', 'SSE', 'MSE', 'pcov', 'perr', 'Y_calc', 'error_metrics'])
error_metrics_results_df = pd.DataFrame(columns=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'])

# calculations
for func_name in model_list:
    print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')
    func = models_dict[func_name]
    calculation_results_df.loc[func_name, 'func'] = func
    p0 = p0_dict[func_name]
    print(f'p0 = {p0}')
    calculation_results_df.loc[func_name, 'p0'] = p0
    res = sci.optimize.least_squares(residual_func, p0, args=(X_fact, Y_fact), method=methods_dict[func_name])
    (popt, jac) = (res.x, res.jac)
    calculation_results_df.loc[func_name, 'popt'] = popt
    calculation_results_df.loc[func_name, 'jac'] = jac
    print(f'parameters = {popt}')
    #print(f'jac =n {jac}')
    hess = np.linalg.inv(np.dot(jac.T, jac))
    calculation_results_df.loc[func_name, 'hess'] = hess
    print(f'hess =n {hess}')
    SSE = (residual_func(popt, X_fact, Y_fact)**2).sum()
    calculation_results_df.loc[func_name, 'SSE'] = SSE
    print(f'SSE = {SSE}')
    MSE = SSE / (len(Y_fact)-len(p0))
    calculation_results_df.loc[func_name, 'MSE'] = MSE
    print(f'MSE = {MSE}')
    pcov = hess * MSE
    calculation_results_df.loc[func_name, 'pcov'] = pcov
    print(f'pcov =n {pcov}')
    perr = np.sqrt(np.diag(pcov))
    calculation_results_df.loc[func_name, 'perr'] = perr
    print(f'perr = {perr}n')
    Y_calc = func(X_fact, *popt)
    calculation_results_df.loc[func_name, 'Y_calc'] = Y_calc
    (error_metrics_dict, error_metrics_df) = regression_error_metrics(Yfact=Y_fact, Ycalc=Y_calc, model_name=func_name)
    calculation_results_df.loc[func_name, 'error_metrics'] = error_metrics_dict.values()
    error_metrics_results_df = pd.concat([error_metrics_results_df, error_metrics_df])

LINEAR MODEL: y = b0 + b1*x
p0 = [0, 0]
parameters = [ 1.1850e+01 -2.1760e-03]
hess =
 [[ 8.7797e-02 -7.3041e-05]
 [-7.3041e-05  7.6636e-08]]
SSE = 84.42039151684142
MSE = 1.5928375757894608
pcov =
 [[ 1.3985e-01 -1.1634e-04]
 [-1.1634e-04  1.2207e-07]]
perr = [3.7396e-01 3.4938e-04]

QUADRATIC MODEL: y = b0 + b1*x + b2*x^2
p0 = [0, 0, 0]
parameters = [ 1.4343e+01 -7.0471e-03  1.8760e-06]
hess =
 [[ 2.8731e-01 -4.6282e-04  1.5012e-07]
 [-4.6282e-04  8.3812e-07 -2.9328e-10]
 [ 1.5012e-07 -2.9328e-10  1.1295e-13]]
SSE = 53.26102533463595
MSE = 1.0242504872045375
pcov =
 [[ 2.9428e-01 -4.7404e-04  1.5376e-07]
 [-4.7404e-04  8.5844e-07 -3.0039e-10]
 [ 1.5376e-07 -3.0039e-10  1.1569e-13]]
perr = [5.4247e-01 9.2652e-04 3.4013e-07]

QUBIC MODEL: y = b0 + b1*x + b2*x^2 + b3*x^3
p0 = [0, 0, 0, 0]
parameters = [ 1.4838e+01 -8.8040e-03  3.5207e-06 -4.1264e-10]
hess =
 [[ 5.7657e-01 -1.4894e-03  1.1111e-06 -2.4112e-10]
 [-1.4894e-03  4.4815e-06 -3.7039e-09  8.5573e-13]
 [ 1.1111e-06 -3.7039e-09  3.3058e-12 -8.0107e-16]
 [-2.4112e-10  8.5573e-13 -8.0107e-16  2.0099e-19]]
SSE = 52.413833494705216
MSE = 1.0277222253863767
pcov =
 [[ 5.9256e-01 -1.5307e-03  1.1419e-06 -2.4780e-10]
 [-1.5307e-03  4.6057e-06 -3.8066e-09  8.7945e-13]
 [ 1.1419e-06 -3.8066e-09  3.3974e-12 -8.2328e-16]
 [-2.4780e-10  8.7945e-13 -8.2328e-16  2.0656e-19]]
perr = [7.6978e-01 2.1461e-03 1.8432e-06 4.5449e-10]

POWER MODEL: y = b0*x^b1
p0 = [0, 0]
parameters = [33.4033 -0.1841]
hess =
 [[ 1.2667e+01 -5.7226e-02]
 [-5.7226e-02  2.6284e-04]]
SSE = 49.87968652202211
MSE = 0.94112616079287
pcov =
 [[ 1.1922e+01 -5.3857e-02]
 [-5.3857e-02  2.4737e-04]]
perr = [3.4528 0.0157]

EXPONENTIAL TYPE 1 MODEL: y = b0*exp(b1^x)
p0 = [0, 0]
parameters = [ 1.2624e+01 -2.7834e-04]
hess =
 [[ 1.5566e-01 -1.1829e-05]
 [-1.1829e-05  1.1127e-09]]
SSE = 75.19491109027253
MSE = 1.4187719073636327
pcov =
 [[ 2.2085e-01 -1.6782e-05]
 [-1.6782e-05  1.5787e-09]]
perr = [4.6994e-01 3.9732e-05]

EXPONENTIAL TYPE 2 MODEL: y = b0*b1^x
p0 = [1, 1]
parameters = [12.6242  0.9997]
hess =
 [[ 1.5566e-01 -1.1825e-05]
 [-1.1825e-05  1.1121e-09]]
SSE = 75.19491108936178
MSE = 1.4187719073464486
pcov =
 [[ 2.2085e-01 -1.6778e-05]
 [-1.6778e-05  1.5778e-09]]
perr = [4.6994e-01 3.9721e-05]

LOGARITHMIC MODEL: y = b0 + b1*ln(x)
p0 = [0, 0]
parameters = [23.9866 -2.1170]
hess =
 [[ 2.1029 -0.3106]
 [-0.3106  0.0463]]
SSE = 49.342567293214316
MSE = 0.9309918357210248
pcov =
 [[ 1.9578 -0.2891]
 [-0.2891  0.0431]]
perr = [1.3992 0.2075]

HYPERBOLIC MODEL: y = b0+b1/x
p0 = [0, 0]
parameters = [  9.2219 315.7336]
hess =
 [[ 2.2732e-02 -2.5920e+00]
 [-2.5920e+00  1.4765e+03]]
SSE = 78.69038671392154
MSE = 1.484724277621161
pcov =
 [[ 3.3751e-02 -3.8485e+00]
 [-3.8485e+00  2.1922e+03]]
perr = [ 0.1837 46.8207]

По аналогии с предыдущим примером, сформируем отдельный DataFrame, в котором соберем все результаты аппроксимации, и сравним с результатами из предыдущего примера:

result_df = pd.DataFrame(
                list(calculation_results_df.loc[:,'p0'].values),
                columns=['p0', 'p1', 'p2', 'p3'],
                index=model_list)

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'popt'].values),
                                columns=['b0', 'b1', 'b2', 'b3'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'perr'].values),
                                columns=['std(b0)', 'std(b1)', 'std(b2)', 'std(b3)'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'error_metrics'].values),
                                columns=['MSE', 'RMSE',	'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'],
                                index=model_list))

#display(result_df)

# settings for displaying the DataFrame: result_df
result_df_least_squares = result_df.copy()
'''for elem in ['MSPE', 'MAPE']:
    result_df_leastsq[elem] = result_df_leastsq[elem].apply(lambda s: float(s[:-1]))'''
print('scipy.optimize.least_squares:'.upper())
display(result_df_least_squares
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))    

print('scipy.optimize.leastsq:'.upper())
display(result_df_leastsq
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))

Сформируем DataFrame, содержащий ошибки и доверительные интервалы параметров моделей аппроксимации, и сравним с результатами из предыдущего примера:

result_df_with_perr = pd.DataFrame()

parameter_name_list = ['b0', 'b1', 'b2', 'b3']
result_df_with_perr[parameter_name_list] = result_df[parameter_name_list]

parameter_format_dict = {
    'b0': '{:.' + str(DecPlace) + 'f}',
    'b1': '{:.' + str(DecPlace + 3) + 'f}',
    'b2': '{:.' + str(DecPlace) + 'e}',
    'b3': '{:.' + str(DecPlace) + 'e}',
    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
    'std(b2)': '{:.' + str(DecPlace) + 'e}',
    'std(b3)': '{:.' + str(DecPlace) + 'e}'}

for parameter in parameter_name_list:
    for model in result_df.index:
        if not result_df.isna().loc[model, parameter]:
            result_df_with_perr.loc[model, parameter] = 
                str(parameter_format_dict[parameter].format(result_df.loc[model, parameter])) + 
                    ' ' + u"u00B1" + ' ' + 
                    str(parameter_format_dict[parameter].format(result_df.loc[model, 'std('+parameter+')']))
            relative_errors = abs(result_df.loc[model, 'std('+parameter+')'] / result_df.loc[model, parameter])
            result_df_with_perr.loc[model, 'error('+parameter+')'] = '{:.3%}'.format(relative_errors)

result_df_with_perr_least_squares = result_df_with_perr.copy()
print('scipy.optimize.least_squares:'.upper())
display(result_df_with_perr_least_squares)

print('scipy.optimize.leastsq:'.upper())
display(result_df_with_perr_leastsq)

Аппроксимация с использованием scipy.optimize.curve_fit

Особенности использования функции:

Реализация нелинейного метода наименьших квадратов, с возможностью введения ограничений на значения параметров.
Имеется возможность выбора алгоритма оптимизации (trf, dogbox, lm), по аналогии с scipy.optimize.least_squares).

Ссылка на документацию.

from scipy.optimize import curve_fit

# algorithm to perform minimization
methods_dict = {
        'linear':             'lm',
        'quadratic':          'lm',
        'qubic':              'lm',
        'power':              'lm',
        'exponential type 1': 'lm',
        'exponential type 2': 'lm',
        'logarithmic':        'lm',
        'hyperbolic':         'lm'}

# actual data
X_fact = X1
Y_fact = Y

# return all optional outputs
full_output = True

# variables to save the calculation results
calculation_results_df = pd.DataFrame(columns=['func', 'p0', 'popt', 'pcov', 'perr', 'Y_calc', 'error_metrics'])
error_metrics_results_df = pd.DataFrame(columns=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'])

# calculations
for func_name in model_list:
    print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')
    func = models_dict[func_name]
    calculation_results_df.loc[func_name, 'func'] = func
    p0 = p0_dict[func_name]
    print(f'p0 = {p0}')
    calculation_results_df.loc[func_name, 'p0'] = p0
    if full_output:
        (popt, pcov, infodict, mesg, ier) = curve_fit(func, X_fact, Y_fact, p0=p0, method=methods_dict[func_name], full_output=full_output)
        integer_flag = f'ier = {ier}, the solution was found' if ier<=4 else f'ier = {ier}, the solution was not found'
        print(integer_flag, 'n', mesg)
        calculation_results_df.loc[func_name, 'popt'] = popt
        print(f'parameters = {popt}')
        calculation_results_df.loc[func_name, 'pcov'] = pcov
        print(f'pcov =n {pcov}')
        perr = np.sqrt(np.diag(pcov))
        calculation_results_df.loc[func_name, 'perr'] = perr
        print(f'perr = {perr}n') 
    else:
        (popt, pcov) = curve_fit(func, X_fact, Y_fact, p0=p0, method=methods_dict[func_name], full_output=full_output)
        calculation_results_df.loc[func_name, 'popt'] = popt
        print(f'parameters = {popt}')
        calculation_results_df.loc[func_name, 'pcov'] = pcov
        print(f'pcov =n {pcov}')
        perr = np.sqrt(np.diag(pcov))
        calculation_results_df.loc[func_name, 'perr'] = perr
        print(f'perr = {perr}n') 
    Y_calc = func(X_fact, *popt)
    calculation_results_df.loc[func_name, 'Y_calc'] = Y_calc
    (error_metrics_dict, error_metrics_df) = regression_error_metrics(Yfact=Y_fact, Ycalc=Y_calc, model_name=func_name)
    calculation_results_df.loc[func_name, 'error_metrics'] = error_metrics_dict.values()
    error_metrics_results_df = pd.concat([error_metrics_results_df, error_metrics_df])

LINEAR MODEL: y = b0 + b1*x
p0 = [0, 0]
ier = 3, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000 and the relative error between two consecutive iterates is at 
  most 0.000000
parameters = [ 1.1850e+01 -2.1760e-03]
pcov =
 [[ 1.3985e-01 -1.1634e-04]
 [-1.1634e-04  1.2207e-07]]
perr = [3.7396e-01 3.4938e-04]

QUADRATIC MODEL: y = b0 + b1*x + b2*x^2
p0 = [0, 0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.4343e+01 -7.0471e-03  1.8760e-06]
pcov =
 [[ 2.9428e-01 -4.7404e-04  1.5376e-07]
 [-4.7404e-04  8.5844e-07 -3.0039e-10]
 [ 1.5376e-07 -3.0039e-10  1.1569e-13]]
perr = [5.4247e-01 9.2652e-04 3.4013e-07]

QUBIC MODEL: y = b0 + b1*x + b2*x^2 + b3*x^3
p0 = [0, 0, 0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.4838e+01 -8.8040e-03  3.5207e-06 -4.1264e-10]
pcov =
 [[ 5.9256e-01 -1.5307e-03  1.1419e-06 -2.4780e-10]
 [-1.5307e-03  4.6057e-06 -3.8066e-09  8.7945e-13]
 [ 1.1419e-06 -3.8066e-09  3.3974e-12 -8.2328e-16]
 [-2.4780e-10  8.7945e-13 -8.2328e-16  2.0656e-19]]
perr = [7.6978e-01 2.1461e-03 1.8432e-06 4.5449e-10]

POWER MODEL: y = b0*x^b1
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [33.4033 -0.1841]
pcov =
 [[ 1.1922e+01 -5.3856e-02]
 [-5.3856e-02  2.4737e-04]]
perr = [3.4528 0.0157]

EXPONENTIAL TYPE 1 MODEL: y = b0*exp(b1^x)
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [ 1.2624e+01 -2.7834e-04]
pcov =
 [[ 2.2085e-01 -1.6783e-05]
 [-1.6783e-05  1.5787e-09]]
perr = [4.6994e-01 3.9733e-05]

EXPONENTIAL TYPE 2 MODEL: y = b0*b1^x
p0 = [1, 1]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [12.6242  0.9997]
pcov =
 [[ 2.2085e-01 -1.6778e-05]
 [-1.6778e-05  1.5778e-09]]
perr = [4.6994e-01 3.9722e-05]

LOGARITHMIC MODEL: y = b0 + b1*ln(x)
p0 = [0, 0]
ier = 3, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000 and the relative error between two consecutive iterates is at 
  most 0.000000
parameters = [23.9866 -2.1170]
pcov =
 [[ 1.9578 -0.2891]
 [-0.2891  0.0431]]
perr = [1.3992 0.2075]

HYPERBOLIC MODEL: y = b0+b1/x
p0 = [0, 0]
ier = 1, the solution was found 
 Both actual and predicted relative reductions in the sum of squares
  are at most 0.000000
parameters = [  9.2219 315.7336]
pcov =
 [[ 3.3751e-02 -3.8485e+00]
 [-3.8485e+00  2.1922e+03]]
perr = [ 0.1837 46.8207]

По аналогии с предыдущим примером, сформируем отдельный DataFrame, в котором соберем все результаты аппроксимации, и сравним с результатами из предыдущих примеров:

result_df = pd.DataFrame(
                list(calculation_results_df.loc[:,'p0'].values),
                columns=['p0', 'p1', 'p2', 'p3'],
                index=model_list)

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'popt'].values),
                                columns=['b0', 'b1', 'b2', 'b3'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'perr'].values),
                                columns=['std(b0)', 'std(b1)', 'std(b2)', 'std(b3)'],
                                index=model_list))

result_df = result_df.join(pd.DataFrame(
                                list(calculation_results_df.loc[:,'error_metrics'].values),
                                columns=['MSE', 'RMSE',	'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'],
                                index=model_list))

#display(result_df)

# settings for displaying the DataFrame: result_df
result_df_curve_fit = result_df.copy()
'''for elem in ['MSPE', 'MAPE']:
    result_df_leastsq[elem] = result_df_leastsq[elem].apply(lambda s: float(s[:-1]))'''
print('scipy.optimize.curve_fit:'.upper())
display(result_df_curve_fit
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))    

print('scipy.optimize.least_squares:'.upper())
display(result_df_least_squares
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))    

print('scipy.optimize.least_squares:'.upper())
display(result_df_leastsq
        .style
            .format(
                precision=DecPlace, na_rep='-',
                formatter={
                    'b1': '{:.' + str(DecPlace + 3) + 'f}',
                    'b2': '{:.' + str(DecPlace) + 'e}',
                    'b3': '{:.' + str(DecPlace) + 'e}',
                    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
                    'std(b2)': '{:.' + str(DecPlace) + 'e}',
                    'std(b3)': '{:.' + str(DecPlace) + 'e}'})
            .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE'])
            .highlight_max(color='green', subset='R2')
            .highlight_min(color='red', subset='R2')
            .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=['b0', 'b1', 'b2', 'b3', 'std(b0)', 'std(b1)', 'std(b2)', 'std(b3)']))

По аналогии с предыдущим примером, сформируем отдельный DataFrame, содержащий ошибки и доверительные интервалы параметров моделей аппроксимации, и сравним с результатами из предыдущих примеров:

result_df_with_perr = pd.DataFrame()

parameter_name_list = ['b0', 'b1', 'b2', 'b3']
result_df_with_perr[parameter_name_list] = result_df[parameter_name_list]

parameter_format_dict = {
    'b0': '{:.' + str(DecPlace) + 'f}',
    'b1': '{:.' + str(DecPlace + 3) + 'f}',
    'b2': '{:.' + str(DecPlace) + 'e}',
    'b3': '{:.' + str(DecPlace) + 'e}',
    'std(b1)': '{:.' + str(DecPlace + 3) + 'f}',
    'std(b2)': '{:.' + str(DecPlace) + 'e}',
    'std(b3)': '{:.' + str(DecPlace) + 'e}'}

for parameter in parameter_name_list:
    for model in result_df.index:
        if not result_df.isna().loc[model, parameter]:
            result_df_with_perr.loc[model, parameter] = 
                str(parameter_format_dict[parameter].format(result_df.loc[model, parameter])) + 
                    ' ' + u"u00B1" + ' ' + 
                    str(parameter_format_dict[parameter].format(result_df.loc[model, 'std('+parameter+')']))
            relative_errors = abs(result_df.loc[model, 'std('+parameter+')'] / result_df.loc[model, parameter])
            result_df_with_perr.loc[model, 'error('+parameter+')'] = '{:.3%}'.format(relative_errors)

result_df_with_perr_curve_fit = result_df_with_perr.copy()
print('scipy.optimize.curve_fit:'.upper())
display(result_df_with_perr_curve_fit)

print('scipy.optimize.least_squares:'.upper())
display(result_df_with_perr_least_squares)

print('scipy.optimize.leastsq:'.upper())
display(result_df_with_perr_leastsq)

Аппроксимация с использованием scipy.optimize.minimize

Особенности использования функции:

Минимизация значений скалярной функции одной или нескольких переменных; при использовании в качестве функции суммы квадратов получаем реализацию нелинейного метода наименьших квадратов.
Имеется возможность выбора широкого набора алгоритмов оптимизации (Nelder-Mead, Powell, CG, BFGS, Newton-CG, L-BFGS-B, TNC, COBYLA, SLSQP, trust-constr, dogleg, trust-ncg, trust-exact, trust-krylov, custom), получить информацию можно с помощью функции scipy.optimize.show_options (https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.show_options.html#scipy.optimize.show_options), а также есть возможность добавить пользовательский алгоритм оптимизации.

Ссылка на документацию.

Работа с данной функцией принципиально не отличается от разобранных выше, поэтому в целях экономии места в данном обзоре подробности приводить не буду; все рабочие файлы с примерами расчетов доступны в моем репозитории на GitHub (https://github.com/AANazarov/Statistical-methods).

Аппроксимация с использованием библиотеки lmfit

Библиотека lmfit — это универсальный инструмент для решения задач нелинейной оптимизации, в том числе и для аппроксимации зависимостей, представляет собой дальнейшее развитие scipy.optimize.

Особенности использования библиотеки lmfit для аппроксимации:

В качестве переменных вместо обычных чисел типа float используются объекты класса Parameter, которые обладают гораздо более обширным функционалом (https://lmfit.github.io/lmfit-py/parameters.html#lmfit.parameter.Parameter):
- для них возможно задавать границы допустимых значений и ограничения в виде алгебраических выражений;
- возможно фиксировать значения в процессе подгонки;
- после подгонки возможно получить такие атрибуты, как стандартная ошибка и коэффициенты корреляции с другими параметрами модели;
- возможно указывать размер шага для точек сетки в методе полного перебора и т.д.
Имеется возможность выбора широкого набора алгоритмов оптимизации (leastsq — default, least_squares, differential_evolution, brute, basinhopping, ampgo, nelder, lbfgsb, powell, cg, newton, cobyla, bfgs, tnc, trust-ncg, trust-exact, trust-krylov, trust-constr, dogleg, slsqp, emcee, shgo, dual_annealing) (https://lmfit.github.io/lmfit-py/fitting.html#choosing-different-fitting-methods).
Имеется возможность выбора различных целевых функций минимизации: по умолчанию — сумма квадратов остатков $sum{{r_i}^2}$ , но в случае, например, наличия выбросов может применяться negentropy — отрицательная энтропия, использующая нормальное распределение (где

$rho = exp(frac{-frac{{r_i}^2}{2}}{sqrt{2pi}})$ ),

neglogcauchy — отрицательная логарифмическая вероятность,использующая распределения Коши

$-sum{ln(frac{1+{r_i}^2}{pi})}$ ,

либо callable — функция, определенная пользователем; подробнее см. https://lmfit.github.io/lmfit-py/fitting.html#using-the-minimizer-class.
Улучшена оценка доверительных интервалов. Хотя scipy.optimize.leastsq автоматически вычисляет неопределенности и корреляции из ковариационной матрицы, точность этих оценок иногда вызывает сомнения. Чтобы помочь решить эту проблему, lmfit имеет функции явного исследования пространства параметров и определения уровней доверительной вероятности даже в самых сложных случаях.
Возможность работы с классом Model (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.Model).
Имеется набор встроенных моделей (https://lmfit.github.io/lmfit-py/builtin_models.html#builtin-models-chapter).
Для полного контроля над процессом оптимизации имеется возможность работы с объектом класса Minimizer (https://lmfit.github.io/lmfit-py/fitting.html#using-the-minimizer-class).
Имеются встроенные инструменты вывода отчетов и построения графиков.

Ссылка на документацию к библиотеке: https://lmfit.github.io/lmfit-py/

В документации к библиотеке lmfit приведено большое количество примеров, приведем здесь их описание с целью облегчения поиска полезной информации:

Fit with Data in a pandas DataFrame — аппроксимация по данным содержащимся в pandas DataFrame (https://lmfit.github.io/lmfit-py/examples/example_use_pandas.html#sphx-glr-examples-example-use-pandas-py).
Using an ExpressionModel — использование модуля ExpressionModel для построение моделей с выражениями, определенными пользователем (https://lmfit.github.io/lmfit-py/examples/example_expression_model.html#sphx-glr-examples-example-expression-model-py).
Fit Using Inequality Constraint — использование ограничений типа неравенств (https://lmfit.github.io/lmfit-py/examples/example_fit_with_inequality.html#sphx-glr-examples-example-fit-with-inequality-py).
Fit Using differential_evolution Algorithm — пример использования алгоритма Differential_evolution (https://lmfit.github.io/lmfit-py/examples/example_diffev.html#sphx-glr-examples-example-diffev-py).
Fit Using Bounds — аппроксимация с использованием ограничений параметров (https://lmfit.github.io/lmfit-py/examples/example_fit_with_bounds.html#sphx-glr-examples-example-fit-with-bounds-py).
Fit Specifying Different Reduce Function — использование различных целевых функций минимизации (https://lmfit.github.io/lmfit-py/examples/example_reduce_fcn.html#sphx-glr-examples-example-reduce-fcn-py).
Building a lmfit model with SymPy — построение модели с использованием библиотеки символьных вычислений SymPy (https://lmfit.github.io/lmfit-py/examples/example_sympy.html#sphx-glr-examples-example-sympy-py).
Fit with Algebraic Constraint — аппроксимация с использованием алгебраических ограничений (https://lmfit.github.io/lmfit-py/examples/example_fit_with_algebraic_constraint.html#sphx-glr-examples-example-fit-with-algebraic-constraint-py).
Fit Multiple Data Sets — одновременная подгонка нескольких наборов данных (https://lmfit.github.io/lmfit-py/examples/example_fit_multi_datasets.html#sphx-glr-examples-example-fit-multi-datasets-py).
Fit using the Model interface — использование класса Model (https://lmfit.github.io/lmfit-py/examples/example_Model_interface.html#sphx-glr-examples-example-model-interface-py).
Fit Specifying a Function to Compute the Jacobian — аппроксимация с указанием аналитической функции для вычисления якобиана (для ускорения вычислений) (https://lmfit.github.io/lmfit-py/examples/example_fit_with_derivfunc.html#sphx-glr-examples-example-fit-with-derivfunc-py).
Outlier detection via leave-one-out — обнаружение выбросов методом исключения одного наблюдения (https://lmfit.github.io/lmfit-py/examples/example_detect_outliers.html#sphx-glr-examples-example-detect-outliers-py).
Emcee and the Model Interface — использование алгоритма emcee (https://lmfit.github.io/lmfit-py/examples/example_emcee_Model_interface.html#sphx-glr-examples-example-emcee-model-interface-py). Алгоритм emcee может быть использован для получения апостериорного распределения вероятностей параметров, заданного набором экспериментальных данных, он исследует пространство параметров, чтобы определить распределение вероятностей для параметров, но без явной цели попытаться уточнить решение. Его не следует использовать для аппроксимации, но это полезный метод для более тщательного изучения пространства параметров вокруг решения, он позволяет получить лучшее понимание распределения вероятности для параметров; см. также https://emcee.readthedocs.io/en/stable/.
Complex Resonator Model — в примере показано, как показано, как подобрать параметры сложной модели (резонатора) с помощью lmfit.Model и определения пользовательского класса Model (https://lmfit.github.io/lmfit-py/examples/example_complex_resonator_model.html#sphx-glr-examples-example-complex-resonator-model-py).
Model Selection using lmfit and emcee — в примере показано, как можно использовать алгоритм emcee для выбора байесовской модели (https://lmfit.github.io/lmfit-py/examples/lmfit_emcee_model_selection.html#sphx-glr-examples-lmfit-emcee-model-selection-py).
Calculate Confidence Intervals — расчет доверительных интервалов (https://lmfit.github.io/lmfit-py/examples/example_confidence_interval.html#sphx-glr-examples-example-confidence-interval-py).
Fit Two Dimensional Peaks — в примере показано, как обрабатывать двумерные данные с двухмерными распределениями вероятностей (https://lmfit.github.io/lmfit-py/examples/example_two_dimensional_peak.html#sphx-glr-examples-example-two-dimensional-peak-py).
Global minimization using the brute method (a.k.a. grid search) — глобальная минимизация методом brute (он же поиск по сетке) (https://lmfit.github.io/lmfit-py/examples/example_brute.html#sphx-glr-examples-example-brute-py).

Примеры из документации (Examples from the documentation):

Cоздание и сохранение модели в файл *.sav:
- doc_model_savemodel.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_savemodel.html#sphx-glr-examples-documentation-model-savemodel-py)
- doc_model_savemodelresult.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_savemodelresult.html#sphx-glr-examples-documentation-model-savemodelresult-py)
- doc_model_savemodelresult2.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_savemodelresult2.html#sphx-glr-examples-documentation-model-savemodelresult2-py)
Загрузка модели из файла *.sav:
- doc_model_loadmodelresult.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_loadmodelresult.html#sphx-glr-examples-documentation-model-loadmodelresult-py)
- doc_model_loadmodelresult2.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_loadmodelresult2.html#sphx-glr-examples-documentation-model-loadmodelresult2-py)
- doc_model_loadmodel.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_loadmodel.html#sphx-glr-examples-documentation-model-loadmodel-py)
Создание отчетов:
- doc_fitting_withreport.py (https://lmfit.github.io/lmfit-py/examples/documentation/fitting_withreport.html#sphx-glr-examples-documentation-fitting-withreport-py)
Работа с доверительными интервалами:
- doc_confidence_basic.py (https://lmfit.github.io/lmfit-py/examples/documentation/confidence_basic.html#sphx-glr-examples-documentation-confidence-basic-py)
- построение доверительного интервала для кривой Гаусса doc_model_uncertainty.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_uncertainty.html#sphx-glr-examples-documentation-model-uncertainty-py)
- doc_confidence_advanced.py (https://lmfit.github.io/lmfit-py/examples/documentation/confidence_advanced.html#sphx-glr-examples-documentation-confidence-advanced-py)
Аппроксимация вероятностных распределений:
- распределение Гаусса — doc_model_gaussian.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_gaussian.html#sphx-glr-examples-documentation-model-gaussian-py)
- смесь распределения Гаусса и линейной зависимости — doc_model_two_components.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_two_components.html#sphx-glr-examples-documentation-model-two-components-py)
Различные опции lmfit:
- doc_model_with_nan_policy.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_with_nan_policy.html#sphx-glr-examples-documentation-model-with-nan-policy-py)
- doc_model_with_iter_callback.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_with_iter_callback.html#sphx-glr-examples-documentation-model-with-iter-callback-py)
- doc_parameters_basic.py (https://lmfit.github.io/lmfit-py/examples/documentation/parameters_basic.html#sphx-glr-examples-documentation-parameters-basic-py)
- doc_parameters_valuesdict.py (https://lmfit.github.io/lmfit-py/examples/documentation/parameters_valuesdict.html#sphx-glr-examples-documentation-parameters-valuesdict-py)
Использование различных встроенных моделей:
- ступенчатая аппроксимация doc_builtinmodels_stepmodel.py (https://lmfit.github.io/lmfit-py/examples/documentation/builtinmodels_stepmodel.html#sphx-glr-examples-documentation-builtinmodels-stepmodel-py), doc_model_composite.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_composite.html#sphx-glr-examples-documentation-model-composite-py)
- смесь двух гауссовых и экспоненциального распределения: doc_builtinmodels_nistgauss.py (https://lmfit.github.io/lmfit-py/examples/documentation/builtinmodels_nistgauss.html#sphx-glr-examples-documentation-builtinmodels-nistgauss-py), doc_builtinmodels_nistgauss2.py (https://lmfit.github.io/lmfit-py/examples/documentation/builtinmodels_nistgauss2.html#sphx-glr-examples-documentation-builtinmodels-nistgauss2-py)
- модели с пиками (распределения Гаусса и Коши-Лоренца ) doc_builtinmodels_peakmodels.py (https://lmfit.github.io/lmfit-py/examples/documentation/builtinmodels_peakmodels.html#sphx-glr-examples-documentation-builtinmodels-peakmodels-py)
- сплайны doc_builtinmodels_splinemodel.py (doc_builtinmodels_splinemodel.py)
- обзор различных возможностей (смесь распределений, дверительные интервалы, графики и т.д.) doc_model_uncertainty2.py (https://lmfit.github.io/lmfit-py/examples/documentation/model_uncertainty2.html#sphx-glr-examples-documentation-model-uncertainty2-py)
- алгортим emcee doc_fitting_emcee.py (https://lmfit.github.io/lmfit-py/examples/documentation/fitting_emcee.html#sphx-glr-examples-documentation-fitting-emcee-py)

Вначале рассмотрим различные приемы аппроксимации в lmfit:

пример 1 — аппроксимация с использованием интерфейса Model (самый простой случай);
пример 2 — аппроксимация с использованием интерфейса Model и объекта класса Parameter, расчетом доверительных интервалов;
пример 3 — аппроксимация с использованием функции minimize;
пример 4 — аппроксимация c использованием объекта класса Minimazer.

Затем рассмотрим различные частные случаи аппроксимации в lmfit:

пример 5 — аппроксимация с заданием начальных значений (initial values) (на примере экспоненциальной зависимости I типа);
пример 6 — аппроксимация c использованием встроенных моделей библиотеки lmfit;
пример 7 — аппроксимация c использованием методов глобального поиска;
пример 8 — обнаружение выбросов (outlier detection) при аппроксимации

Пример 1 — аппроксимация с использованием интерфейса Model (самый простой случай)

Для начала рассмотрим самую обычную аппроксимацию на примере линейной зависимости, для подгонки параметров модели используем метод fit класса Model.

Пояснения к расчету:

Вначале исходные данные — двумерную таблицу (X1, Y) — приводим к виду, отсортированному по возрастанию переменной X1, для того, чтобы встроенные графические возможности библиотеки lmfit корректно отображали информацию.
С помощью lmfit.Model создаем модель.
С помощью model.fit выполняем аппроксимацию (нахождение параметров). По умолчанию используется алгоритм Левенберга-Марквардта (Levenberg–Marquardt algorithm) (leastsq, least_squares).
С помощью result.fit_report выводим отчет с результатами, который содержит:
- метрики качества аппроксимации: chi-square — в данном случае сумма квадратов остатков $chi^2 = sum{{e_i}^2}$ (т.е. по сути SSE), reduced chi-square
  
  ${chi}_y^2 = frac{chi^2}{N-N_{varys}}$ и ;
- информационные критерии Акаике и Байеса;
- параметры модели и с их стандратными ошибками, относительными ошибками в % и начальными условиями (init);
- коэффициенты корреляции между параметрами C(b0, b1).
Выводим различные виды графиков:
- result.plot_fit() — обычный точечный график;
- result.plot_residuals() — график остатков;
- result.plot() — точечный график, совмещенный с графиком остатков.

import lmfit
print('{:<35}{:^0}'.format("Текущая версия модуля lmfit: ", lmfit.__version__), 'n')

# Preparation of input data
dataset_sort_df = dataset_df.loc[:, ['X1', 'Y']].sort_values(by=['X1'])
#display(dataset_sort_df)
Y_sort = np.array(dataset_sort_df['Y'])
#print(Y_sort, type(Y_sort), len(Y_sort))
X_sort = np.array(dataset_sort_df['X1'])
#print(X_sort, type(X_sort), len(X_sort))

# LINEAR MODEL
func_name = 'linear'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')
func = models_dict[func_name]
p0 = p0_dict[func_name]
model = lmfit.Model(func, independent_vars=['x'], name=func_name)
result = model.fit(Y_sort, x=X_sort, b0=p0[0], b1=p0[1])
print(result.fit_report())
result.plot_fit()
plt.show()
result.plot_residuals()
plt.show()
result.plot()
plt.show()

Текущая версия модуля lmfit:       1.1.0 

LINEAR MODEL: y = b0 + b1*x
[[Model]]
    Model(linear)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 7
    # data points      = 55
    # variables        = 2
    chi-square         = 84.4203915
    reduced chi-square = 1.59283758
    Akaike info crit   = 27.5661686
    Bayesian info crit = 31.5808350
    R-squared          = 0.42259718
[[Variables]]
    b0:  11.8501350 +/- 0.37396000 (3.16%) (init = 0)
    b1: -0.00217603 +/- 3.4938e-04 (16.06%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(b0, b1) = -0.890

Пример 2 — аппроксимация с использованием интерфейса Model и объекта класса Parameter, расчетом доверительных интервалов

Рассмотрим аппроксимацию с более широким использованием возможностей библиотеки lmfit на примере степенной зависимости:

используем объект класса Parameter для задания свойств параметров модели;
выведем дополнительные отчеты;
выполним расчет доверительного интервала (подробнее см. https://lmfit.github.io/lmfit-py/confidence.html#lmfit.conf_interval, https://lmfit.github.io/lmfit-py/examples/example_confidence_interval.html#sphx-glr-examples-example-confidence-interval-py, https://lmfit.github.io/lmfit-py/examples/documentation/confidence_advanced.html#sphx-glr-examples-documentation-confidence-advanced-py)).

Пояснения к расчету:

Исходные данные также должны быть отсортированы по возрастанию переменной X1.
Также с помощью lmfit.Model создаем модель.
С помощью model.make_params задаем свойства параметров модели (в этом примере мы просто задаем начальные значения параметров, не затрагивая прочие атрибуты — минимальные и максимальные значения, алгебраические ограничения и т.д.).
Также с помощью model.fit выполняем аппроксимацию (нахождение параметров), при этом расширим набор используемых настроек — добавим method и nan_policy (правда, значения установим по умолчанию leastsq и raise).
Также с помощью result.fit_report выводим отчет с результатами, при этом установим ограничение на коэффициент корреляции между параметрами (min_correl=0.2).
С помощью result.params.pretty_print() выведем отчет о параметрах модели.
С помощью result.ci_report() выведем отчет о границах доверительных интервалов для параметров модели.
С помощью result.eval_components и result.eval выведем расчетные значения модели: в первом случае — в виде словаря (dict), во-втором случае — в виде массива (numpy.ndarray).
С помощью result.eval_uncertainty выведем ширину доверительного интервала для расчетных значений.
По аналогии с предыдущим примером выведем графики result.plot_fit() и result.plot_residuals() с настройкой их атрибутов (размер окна, подписи осей и пр.).
Дополнительно выведем графики двух видов:
- на первом графике будут отображаться фактические данные (data), расчетные данные по модели аппроксимации (best fit) и также доверительный интервал шириной ;
- на втором графике будет отображаться остатки (residuals).

Замечание касательно расчета доверительных интервалов: для отдельных моделей lmfit может выдавать ошибку Cannot determine Confidence Intervals without sensible uncertainty estimates, в этом случае необходимо установить пакет numdifftools (https://pypi.org/project/numdifftools/).

# POWER MODEL
func_name = 'power'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

# define objective function
func = models_dict[func_name]

# initial values
p0 = p0_dict[func_name]

# create a Model
model = lmfit.Model(func,   
                    independent_vars=['x'],
                    name=func_name)

# create a set of Parameters
params = model.make_params(b0=p0[0],
                           b1=p0[1])

# calculations
result = model.fit(Y_sort, params, x=X_sort,
                   method='leastsq',
                   nan_policy='raise')

# report of the fitting results (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.ModelResult.fit_report)
print(f'result.fit_report:n{result.fit_report(min_correl=0.2)}n')

# report of parameters data (https://lmfit.github.io/lmfit-py/parameters.html#lmfit.parameter.Parameters.pretty_print)
print('result.params.pretty_print():')
result.params.pretty_print()
print('n')

# report of the confidence intervals (https://lmfit.github.io/lmfit-py/confidence.html#lmfit.ci_report)
print(f'result.ci_report:n{result.ci_report()}n')

# evaluate each component of a composite model function (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.ModelResult.eval_components)
comps = result.eval_components(x=X_sort)
print(f'result.eval_components = n{comps}n')

# evaluate the uncertainty of the model function (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.ModelResult.eval_uncertainty)
dely = result.eval_uncertainty(sigma=3)
print(f'result.eval_uncertainty(sigma=3) = n{dely}n')

# graphic (data, best-fit, uncertainty band and residuals)
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=16)

#label = func_name + ' '+ r'$(R^2 = $' + f'{R2}' + ', ' + f'RMSE = {RMSE}' + ', ' + f'MAE = {MAE}' + ', ' + f'MSPE = {MSPE}' + ', ' + f'MAPE = {MAPE})'
axes[0].set_title('data, best-fit, and uncertainty band')
sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes[0])
R2 = round(result.rsquared, DecPlace)
sns.lineplot(x=X_sort, y=result.best_fit, color='blue', linewidth=2, legend=True, label='best fit (' + r'$R^2 = $' + f'{R2})', ax=axes[0])
axes[0].fill_between(X_sort, result.best_fit-dely, result.best_fit+dely, color="grey", alpha=0.3, label=r'3-$sigma$ band')
axes[0].legend()
axes[0].set_ylabel('Y')
#axes[0].set_xlim(X1_min_graph, X1_max_graph)
#axes[0].set_ylim(Y_min_graph, Y_max_graph)

sns.scatterplot(x=X_sort, y=-result.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_xlabel('X')
axes[1].set_ylabel('residuals')
#axes[1].set_xlim(X1_min_graph, X1_max_graph)
#axes[1].set_ylim(Y_min_graph, Y_max_graph)

plt.show()

POWER MODEL: y = b0*x^b1
result.fit_report:
[[Model]]
    Model(power)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 29
    # data points      = 55
    # variables        = 2
    chi-square         = 49.8796865
    reduced chi-square = 0.94112616
    Akaike info crit   = -1.37456420
    Bayesian info crit = 2.64010217
    R-squared          = 0.65884224
[[Variables]]
    b0:  33.4032965 +/- 3.45275807 (10.34%) (init = 0)
    b1: -0.18409814 +/- 0.01572801 (8.54%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(b0, b1) = -0.992

result.params.pretty_print():
Name     Value      Min      Max   Stderr     Vary     Expr Brute_Step
b0      33.4     -inf      inf    3.453     True     None     None
b1   -0.1841     -inf      inf  0.01573     True     None     None


result.ci_report:
       99.73%    95.45%    68.27%    _BEST_    68.27%    95.45%    99.73%
 b0:  -9.61176  -6.50967  -3.33032  33.40330  +3.57568  +7.51972 +11.99711
 b1:  -0.04701  -0.03103  -0.01551  -0.18410  +0.01594  +0.03283  +0.05128

result.eval_components = 
{'power': array([17.1825, 12.2259, 11.9584, 11.2070, 11.1216, 10.7403, 10.4265,
       10.3691, 10.3104, 10.2881, 10.2818, 10.1608, 10.1608, 10.0915,
       10.0161, 10.0087,  9.9898,  9.9158,  9.8985,  9.7892,  9.7778,
        9.7755,  9.7687,  9.7574,  9.7507,  9.6757,  9.6744,  9.6691,
        9.6450,  9.5917,  9.5481,  9.4926,  9.4354,  9.4156,  9.4067,
        9.3493,  9.3306,  9.3222,  9.3222,  9.3106,  9.2345,  9.1804,
        9.1564,  9.0159,  9.0065,  8.9122,  8.8808,  8.8796,  8.8268,
        8.6752,  8.6554,  8.1915,  8.1472,  8.1083,  7.7727])}

result.eval_uncertainty(sigma=3) = 
[2.5746 0.8186 0.7464 0.5692 0.5522 0.4861 0.4464 0.4407 0.4355 0.4337
 0.4332 0.4249 0.4249 0.4213 0.4183 0.4180 0.4174 0.4158 0.4155 0.4151
 0.4151 0.4151 0.4152 0.4153 0.4154 0.4167 0.4167 0.4168 0.4174 0.4191
 0.4208 0.4234 0.4265 0.4277 0.4282 0.4320 0.4333 0.4339 0.4339 0.4348
 0.4408 0.4454 0.4476 0.4613 0.4623 0.4726 0.4762 0.4763 0.4825 0.5013
 0.5039 0.5682 0.5747 0.5804 0.6303]

Пример 3 — аппроксимация c использованием функции minimize

Про функцию minimize подробнее см. https://lmfit.github.io/lmfit-py/fitting.html#the-minimize-function.

# POWER MODEL
func_name = 'power'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

# define objective function
func = models_dict[func_name]

# initial values
p0 = p0_dict[func_name]

# create a set of Parameters
params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf)
params.add('b1', value=p0[1], min=-inf, max=inf)

# function for calculating residuals
residual_func = lambda params, x, ydata: func(x, params['b0'].value, params['b1'].value) - ydata

# calculations
result = lmfit.minimize(residual_func, params, args=(X_sort, Y_sort))
lmfit.report_fit(result)
#print(lmfit.fit_report(result))    # other type of output
best_fit = Y_sort + result.residual

POWER MODEL: y = b0*x^b1
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 29
    # data points      = 55
    # variables        = 2
    chi-square         = 49.8796865
    reduced chi-square = 0.94112616
    Akaike info crit   = -1.37456420
    Bayesian info crit = 2.64010217
[[Variables]]
    b0:  33.4032965 +/- 3.45275807 (10.34%) (init = 0)
    b1: -0.18409814 +/- 0.01572801 (8.54%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(b0, b1) = -0.992

Пример 4 — аппроксимация c использованием объекта класса Minimazer

Про класс Minimazer подробнее см. https://lmfit.github.io/lmfit-py/fitting.html#using-the-minimizer-class.

# POWER MODEL
func_name = 'power'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

# define objective function
func = models_dict[func_name]

# initial values
p0 = p0_dict[func_name]

# create a set of Parameters
params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf)
params.add('b1', value=p0[1], min=-inf, max=inf)

# function for calculating residuals
residual_func = lambda params, x, ydata: func(x, params['b0'].value, params['b1'].value) - ydata

# create Minimizer
minner = lmfit.Minimizer(residual_func, params, fcn_args=(X_sort, Y_sort), nan_policy='omit')

# calculations
result = minner.minimize()
#print(f'nfirst solve with {method_1.upper()} algorithm:')
lmfit.report_fit(result)
#print(lmfit.fit_report(result))    # other type of output
best_fit = Y_sort + result.residual
#print(best_fit)

# calculate the confidence intervals for parameters
ci, tr = lmfit.conf_interval(minner, result, sigmas=[3], trace=True)
print('nreport_ci(ci):')
lmfit.report_ci(ci)

# graphic (data, best-fit, and residuals)
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=16)

sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes[0])
sns.lineplot(x=X_sort, y=best_fit, color='blue', linewidth=2, legend=True, label='best fit', ax=axes[0])
axes[0].set_ylabel('Y')
#axes[0].set_xlim(X1_min_graph, X1_max_graph)
#axes[0].set_ylim(Y_min_graph, Y_max_graph)

sns.scatterplot(x=X_sort, y=-result.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_xlabel('X')
axes[1].set_ylabel('residuals')
#axes[1].set_xlim(X1_min_graph, X1_max_graph)
#axes[1].set_ylim(Y_min_graph, Y_max_graph)

plt.show()

POWER MODEL: y = b0*x^b1
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 29
    # data points      = 55
    # variables        = 2
    chi-square         = 49.8796865
    reduced chi-square = 0.94112616
    Akaike info crit   = -1.37456420
    Bayesian info crit = 2.64010217
[[Variables]]
    b0:  33.4032965 +/- 3.45275807 (10.34%) (init = 0)
    b1: -0.18409814 +/- 0.01572801 (8.54%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(b0, b1) = -0.992

report_ci(ci):
       99.73%    _BEST_    99.73%
 b0:  -9.61177  33.40330 +11.99711
 b1:  -0.04701  -0.18410  +0.05128

Пример 5 — аппроксимация с заданием начальных значений (initial values)

Некоторые модели при аппроксимации требуют задания начальных значений — для успешной реализации алгоритма заданием нулей или единиц в качестве p0 не обойтись. Рассмотрим аппроксимацию экспоненциальной модели I типа с заданием начальных условий, при этом воспользуемся возможностью библиотеки lmfit вывести на график зависимость с оптимальными параметрами (best fit) и зависимость с начальными параметрами (init fit) это наглядно демонстрирует, как улучшается модель в процессе поиска оптимальных параметров.

# EXPONENTIAL MODEL TYPE I: y = b0*exp(b1^x)
func_name = 'exponential type 1'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

# define objective function
func = models_dict[func_name]

# initial values
n = len(Y_sort)
(x1, x2, y1, y2) = (X_sort[0], X_sort[n-1], Y_sort[0], Y_sort[n-1])
p0_b0 = y2 * np.exp(np.log(y2/y1) * x2/(x1-x2))
p0_b1 = -np.log(y2/y1) / (x1-x2)
p0 = [p0_b0, p0_b1]
print(f'p0 = {p0}')

# create a Model
model = lmfit.Model(func,   
                    independent_vars=['x'],
                    name=func_name)

# create a set of Parameters
params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf)
params.add('b1', value=p0[1], min=-inf, max=inf)

# calculations
result = model.fit(Y_sort, params, x=X_sort,
                   method='leastsq',
                   nan_policy='raise')

# report of the fitting results (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.ModelResult.fit_report)
print(f'result.fit_report:n{result.fit_report(min_correl=0.2)}n')

# report of the confidence intervals (https://lmfit.github.io/lmfit-py/confidence.html#lmfit.ci_report)
print(f'result.ci_report:n{result.ci_report()}n')

# evaluate the uncertainty of the model function (https://lmfit.github.io/lmfit-py/model.html#lmfit.model.ModelResult.eval_uncertainty)
dely = result.eval_uncertainty(sigma=3)

# graphic (data, best-fit, uncertainty band and residuals)
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=16)

axes[0].set_title('data, init-fit, best-fit, and uncertainty band')
sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes[0])
sns.lineplot(x=X_sort, y=result.init_fit, color='cyan', linewidth=2, linestyle='dotted', legend=True, label='init fit', ax=axes[0])
R2 = round(result.rsquared, DecPlace)
sns.lineplot(x=X_sort, y=result.best_fit, color='blue', linewidth=2, legend=True, label='best fit (' + r'$R^2 = $' + f'{R2})', ax=axes[0])
axes[0].fill_between(X_sort, result.best_fit-dely, result.best_fit+dely, color="grey", alpha=0.3, label=r'3-$sigma$ band')
axes[0].legend()
axes[0].set_ylabel('Y')
#axes[0].set_xlim(X1_min_graph, X1_max_graph)
#axes[0].set_ylim(Y_min_graph, Y_max_graph)

sns.scatterplot(x=X_sort, y=-result.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_xlabel('X')
axes[1].set_ylabel('residuals')
#axes[1].set_xlim(X1_min_graph, X1_max_graph)
#axes[1].set_ylim(Y_min_graph, Y_max_graph)

plt.show()

EXPONENTIAL TYPE 1 MODEL: y = b0*exp(b1^x)
p0 = [17.037879730518267, -0.00023560415890108336]
result.fit_report:
[[Model]]
    Model(exponential type 1)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 19
    # data points      = 55
    # variables        = 2
    chi-square         = 75.1949111
    reduced chi-square = 1.41877191
    Akaike info crit   = 21.2012704
    Bayesian info crit = 25.2159368
    R-squared          = 0.48569589
[[Variables]]
    b0:  12.6241795 +/- 0.46994783 (3.72%) (init = 17.03788)
    b1: -2.7834e-04 +/- 3.9734e-05 (14.27%) (init = -0.0002356042)
[[Correlations]] (unreported correlations are < 0.200)
    C(b0, b1) = -0.899

result.ci_report:
       99.73%    95.45%    68.27%    _BEST_    68.27%    95.45%    99.73%
 b0:  -1.48083  -0.98324  -0.49401  12.62418  +0.51299  +1.06128  +1.66495
 b1:  -0.00014  -0.00009  -0.00004  -0.00028  +0.00004  +0.00009  +0.00013

Пример 6 — аппроксимация с использованием встроенных моделей библиотеки lmfit

Рассмотрим аппроксимацию с использованием встроенных моделей библиотеки lmfit. Набор этих моделей достаточно обширен (подробнее см. https://lmfit.github.io/lmfit-py/builtin_models.html,
https://lmfit.github.io/lmfit-py/examples/documentation/model_uncertainty2.html#sphx-glr-examples-documentation-model-uncertainty2-py), при этом для представляют интерес следующие модели:

линейная LinearModel;
квадратическая QuadraticModel;
полиномиальная PolynomialModel (мы рассмотрим случай m=3 — кубическую модель);
экспоненциальная ExponentialModel;
степенная PowerLawModel.

При этом необходимо учитывать, что встроенные модели в библиотеке lmfit имеют свой формализованный вид и параметры, заданные в виде служебных слов, которые нужно учитывать в программном коде (так, например, параметры линейной модели имеют названия slope и intercept):

Для экспоненциальной модели ExponentialModel мы оценим начальные значения параметров с помощью метода Model.guess (https://lmfit.github.io/lmfit-py/model.html#model-class-methods).

# list of model
model_list = ['linear', 'quadratic', 'qubic', 'power', 'exponential type 1']

# model reference
model_exponential_type_1 = lmfit.models.ExponentialModel(prefix='exponential_type_1_')
model_dict = {
        'linear':             lmfit.models.LinearModel(prefix='linear_'),
        'quadratic':          lmfit.models.QuadraticModel(prefix='quadratic_'),
        'qubic':              lmfit.models.PolynomialModel(degree=3, prefix='qubic_'),
        'power':              lmfit.models.PowerLawModel(prefix='power_'),
        'exponential type 1': model_exponential_type_1}

# create a set of Parameters
params_dict = dict()

params_linear = lmfit.Parameters()
params_linear.add('linear_intercept',    value = 0, min = -inf, max = inf)
params_linear.add('linear_slope',        value = 0, min = -inf, max = inf)
params_dict['linear'] = params_linear

params_quadratic = lmfit.Parameters()
params_quadratic.add('quadratic_a',    value = 0, min = -inf, max = inf)
params_quadratic.add('quadratic_b',    value = 0, min = -inf, max = inf)
params_quadratic.add('quadratic_c',    value = 0, min = -inf, max = inf)
params_dict['quadratic'] = params_quadratic

params_qubic = lmfit.Parameters()
params_qubic.add('qubic_c0',    value = 0, min = -inf, max = inf)
params_qubic.add('qubic_c1',    value = 0, min = -inf, max = inf)
params_qubic.add('qubic_c2',    value = 0, min = -inf, max = inf)
params_qubic.add('qubic_c3',    value = 0, min = -inf, max = inf)
params_dict['qubic'] = params_qubic

params_power = lmfit.Parameters()
params_power.add('power_amplitude',    value = 0, min = -inf, max = inf)
params_power.add('power_exponent',     value = 0, min = -inf, max = inf)
params_dict['power'] = params_power

params_exponential_type_1 = lmfit.Parameters()
#params_exponential_type_1.add('exponential_type_1_amplitude',    value = 0, min = -inf, max = inf)
#params_exponential_type_1.add('exponential_type_1_decay',        value = 0, min = -inf, max = inf)
pars_exponential_type_1 = model_exponential_type_1.guess(Y_sort, x=X_sort)
params_dict['exponential type 1'] = pars_exponential_type_1

# calculations
result_dict = dict()
for func_name in model_list:
    model = model_dict[func_name]
    result = model.fit(Y_sort, params_dict[func_name], x=X_sort)
    print(f'{func_name.upper()} MODEL:n{result.fit_report(min_correl=0.2)}n')
    result_dict[func_name] = result

# graphic 1 (various models)
fig, axes = plt.subplots(figsize=(420/INCH, 297/INCH))
#fig.suptitle(f'Model(various models)', fontsize=16)
axes.set_title('Model(various models)', fontsize=16)
sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes)
for func_name in model_list:
        result = result_dict[func_name]
        R2 = round(result.rsquared, DecPlace)
        label = func_name + ' (' + r'$R^2 = $' + f'{R2})'
        sns.lineplot(x=X_sort, y=result.best_fit, linewidth=2, color=color_dict[func_name], legend=True, label=label, ax=axes)    # the color_dict was defined earlier
plt.show()

# graphic 2 (various models)
number_models = len(model_list)
fig, axes = plt.subplots(2, number_models, figsize=(210/INCH*number_models, 297/INCH))
fig.suptitle('Model(various models)', fontsize=20)
for i, func_name in enumerate(model_list):
        ax1 = plt.subplot(2, number_models, i+1)
        ax2 = plt.subplot(2, number_models, i+1+number_models)
        ax1.set_title(f'Model({func_name})', fontsize=16)
        result = result_dict[func_name]
        dely = result.eval_uncertainty(sigma=3)
        sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=ax1)
        R2 = round(result.rsquared, DecPlace)
        label = func_name + ' (' + r'$R^2 = $' + f'{R2})'
        sns.lineplot(x=X_sort, y=result.best_fit, linewidth=2, color=color_dict[func_name], legend=True, label=label, ax=ax1)    # the color_dict was defined earlier
        ax1.fill_between(X_sort, result.best_fit-dely, result.best_fit+dely, color="grey", alpha=0.3, label=r'3-$sigma$ band')
        ax1.legend()
        ax1.set_ylabel('Y')
        sns.scatterplot(x=X_sort, y=-result.residual, ax=ax2, s=50)
        ax2.axhline(y = 0, color = 'k', linewidth = 1)
        ax2.set_xlabel('X')
        ax2.set_ylabel('residuals')
plt.show()

LINEAR MODEL:
[[Model]]
    Model(linear, prefix='linear_')
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 7
    # data points      = 55
    # variables        = 2
    chi-square         = 84.4203915
    reduced chi-square = 1.59283758
    Akaike info crit   = 27.5661686
    Bayesian info crit = 31.5808350
    R-squared          = 0.42259718
[[Variables]]
    linear_intercept:  11.8501350 +/- 0.37396000 (3.16%) (init = 0)
    linear_slope:     -0.00217603 +/- 3.4938e-04 (16.06%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(linear_intercept, linear_slope) = -0.890

QUADRATIC MODEL:
[[Model]]
    Model(parabolic, prefix='quadratic_')
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 13
    # data points      = 55
    # variables        = 3
    chi-square         = 53.2610253
    reduced chi-square = 1.02425049
    Akaike info crit   = 4.23294056
    Bayesian info crit = 10.2549401
    R-squared          = 0.63571519
[[Variables]]
    quadratic_a:  1.8760e-06 +/- 3.4013e-07 (18.13%) (init = 0)
    quadratic_b: -0.00704710 +/- 9.2652e-04 (13.15%) (init = 0)
    quadratic_c:  14.3434596 +/- 0.54247230 (3.78%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(quadratic_a, quadratic_b) = -0.953
    C(quadratic_b, quadratic_c) = -0.943
    C(quadratic_a, quadratic_c) = 0.833

QUBIC MODEL:
[[Model]]
    Model(polynomial, prefix='qubic_')
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 16
    # data points      = 55
    # variables        = 4
    chi-square         = 52.4138335
    reduced chi-square = 1.02772223
    Akaike info crit   = 5.35105531
    Bayesian info crit = 13.3803880
    R-squared          = 0.64150965
[[Variables]]
    qubic_c0:  14.8384962 +/- 0.76977661 (5.19%) (init = 0)
    qubic_c1: -0.00880398 +/- 0.00214609 (24.38%) (init = 0)
    qubic_c2:  3.5207e-06 +/- 1.8432e-06 (52.35%) (init = 0)
    qubic_c3: -4.1264e-10 +/- 4.5449e-10 (110.14%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(qubic_c2, qubic_c3) = -0.983
    C(qubic_c1, qubic_c2) = -0.962
    C(qubic_c0, qubic_c1) = -0.927
    C(qubic_c1, qubic_c3) = 0.902
    C(qubic_c0, qubic_c2) = 0.805
    C(qubic_c0, qubic_c3) = -0.708

POWER MODEL:
[[Model]]
    Model(powerlaw, prefix='power_')
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 29
    # data points      = 55
    # variables        = 2
    chi-square         = 49.8796865
    reduced chi-square = 0.94112616
    Akaike info crit   = -1.37456420
    Bayesian info crit = 2.64010217
    R-squared          = 0.65884224
[[Variables]]
    power_amplitude:  33.4032965 +/- 3.45275807 (10.34%) (init = 0)
    power_exponent:  -0.18409814 +/- 0.01572801 (8.54%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(power_amplitude, power_exponent) = -0.992

EXPONENTIAL TYPE 1 MODEL:
[[Model]]
    Model(exponential, prefix='exponential_type_1_')
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 16
    # data points      = 55
    # variables        = 2
    chi-square         = 75.1949111
    reduced chi-square = 1.41877191
    Akaike info crit   = 21.2012705
    Bayesian info crit = 25.2159368
    R-squared          = 0.48569589
[[Variables]]
    exponential_type_1_amplitude:  12.6242247 +/- 0.46996177 (3.72%) (init = 11.84731)
    exponential_type_1_decay:      3592.61300 +/- 512.762035 (14.27%) (init = 4650.427)
[[Correlations]] (unreported correlations are < 0.200)
    C(exponential_type_1_amplitude, exponential_type_1_decay) = -0.899

Пример 7 — аппроксимация с использованием методов глобального поиска

Рассмотрим более сложный случай на примере логистической зависимости I типа

$Y=frac{b_0}{1+b_1cdot e^{-b_2cdot X}}$ .

Обычно аппроксимация подобных зависимостей требует более тщательного подхода по сравнению с разобранными ранее примерами — необходимо варьировать алгоритмы, предварительно оценивать начальные точки для приближения (методом трех точек и т.д.). В этом случае эффективными могут оказаться методы глобального поиска.

В рамках данного обзора у нас нет возможности сильно углубляться в данную тему, поэтому просто проиллюстрируем возможности lmfit — проведем аппроксимацию в два этапа:

Вначале оценим параметры зависимости алгоритмом basinhopping (см. https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.basinhopping.html, https://machinelearningmastery.com/basin-hopping-optimization-in-python/).
Проверим оценку параметров алгоритмом глобальной оптимизации по сетке brute (см. https://lmfit.github.io/lmfit-py/examples/example_brute.html).

logistic_type_1_func = lambda x, b0, b1, b2: b0 / (1 + b1*np.exp(-b2*x))

# LOGISTIC MODEL TYPE I: y = b0 / (1 + b1*np.exp(-b2*x))
print('LOGISTIC MODEL TYPE I: y = b0 / (1 + b1*np.exp(-b2*x))')

# define objective function
func = logistic_type_1_func
func_name = 'logistic type 1'

# initial values
p0 = [0, 0, 0]

# create a set of Parameters
params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf, brute_step=0.01)
params.add('b1', value=p0[1], min=-inf, max=inf, brute_step=0.01)
params.add('b2', value=p0[2], min=-inf, max=inf, brute_step=0.001)

# function for calculating residuals
residual_func = lambda params, x, ydata: func(x, params['b0'].value,
                                                 params['b1'].value,
                                                 params['b2'].value
                                                 ) - ydata

# create Minimizer
minner = lmfit.Minimizer(residual_func, params, fcn_args=(X_sort, Y_sort), nan_policy='omit')

# first solve with basinhopping algorithm
method_1 = 'basinhopping'
result_1 = minner.minimize(method=method_1)
print(f'nfirst solve with {method_1.upper()} algorithm:')
lmfit.report_fit(result_1)
#print(lmfit.fit_report(result_1))
best_fit_1 = Y_sort + result_1.residual
#print(best_fit_1)

# then solve with brute algorithm using the basinhopping solution as a starting point
method_2 = 'brute'
result_2 = minner.minimize(method=method_2,
                           params=result_1.params,
                           Ns=30,
                           keep=30)
print(f'nsecond solve with {method_2.upper()} algorithm using the {method_1.upper()} solution as a starting point:')
#lmfit.report_fit(result_2)
print(lmfit.fit_report(result_2))
best_fit_2 = Y_sort + result_2.residual
#print(best_fit_2)

# calculate the confidence intervals for parameters
ci, tr = lmfit.conf_interval(minner, result_2, sigmas=[3], trace=True)
lmfit.report_ci(ci)
#print(tr)

# graphics
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=14)

axes[0].set_title('data, first fit and second fit')
sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes[0])
sns.lineplot(x=X_sort, y=best_fit_1, color='cyan', linewidth=6, legend=True, label=f'first fit ({method_1})', ax=axes[0])
sns.lineplot(x=X_sort, y=best_fit_2, color='blue', linewidth=2, legend=True, label=f'second fit ({method_2})', ax=axes[0])
axes[0].set_ylabel('Y')

sns.scatterplot(x=X_sort, y=-result_2.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_ylabel('residuals')

plt.show()

irst solve with BASINHOPPING algorithm:
[[Fit Statistics]]
    # fitting method   = basinhopping
    # function evals   = 17238
    # data points      = 55
    # variables        = 3
    chi-square         = 51.0205702
    reduced chi-square = 0.98116481
    Akaike info crit   = 1.86926364
    Bayesian info crit = 7.89126320
[[Variables]]
    b0:  7.71901123 +/- 0.45562749 (5.90%) (init = 0)
    b1: -0.53569038 +/- 0.03472051 (6.48%) (init = 0)
    b2:  0.00118052 +/- 2.6156e-04 (22.16%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(b0, b2) = 0.912
    C(b0, b1) = 0.550
    C(b1, b2) = 0.242

second solve with BRUTE algorithm using the BASINHOPPING solution as a starting point:
[[Fit Statistics]]
    # fitting method   = brute
    # function evals   = 28830
    # data points      = 55
    # variables        = 3
    chi-square         = 51.0205702
    reduced chi-square = 0.98116481
    Akaike info crit   = 1.86926364
    Bayesian info crit = 7.89126320
##  Warning: uncertainties could not be estimated:
[[Variables]]
    b0:  7.71901123 +/- 0.45562749 (5.90%) (init = 0)
    b1: -0.53569038 +/- 0.03472051 (6.48%) (init = 0)
    b2:  0.00118052 +/- 2.6156e-04 (22.16%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(b0, b2) = 0.912
    C(b0, b1) = 0.550
    C(b1, b2) = 0.242
       99.73%    _BEST_    99.73%
 b0:  -3.89422   7.71901  +1.37162
 b1:  -0.20046  -0.53569  +0.12587
 b2:  -0.00096   0.00118  +0.00149

Пример 8 — обнаружение выбросов (outlier detection) при аппроксимации

Влияние выбросов на результаты аппроксимации может быть весьма существенным и игнорировать это влияние нельзя. Не будем сейчас сильно углубляться в этот вопрос, это предмет для отдельного рассмотрения, а просто проиллюстрируем прием выявления выбросов методом исключения (см. https://lmfit.github.io/lmfit-py/examples/example_detect_outliers.html#sphx-glr-examples-example-detect-outliers-py). Этот метод очень прост и заключается в следующем: будем последовательно исключать точки из набора исходных данных, строить модель и анализировать, как влияет исключение точки на результат аппроксимации.

В качестве исходных данных рассмотрим зависимость расхода топлива (FuelFlow) от среднемесячной температуры (Temperature) из нашего датасета:

graph_scatterplot_sns(
    X2, Y,
    Xmin=X2_min_graph, Xmax=X2_max_graph,
    Ymin=Y_min_graph, Ymax=Y_max_graph,
    color='orange',
    title_figure=Title_String, title_figure_fontsize=14,
    title_axes='Dependence of FuelFlow (Y) on temperature (X2)', title_axes_fontsize=16,
    x_label=Variable_Name_X2,
    y_label=Variable_Name_Y,
    label_fontsize=14, tick_fontsize=12,
    label_legend='', label_legend_fontsize=12,
    s=80)

Подготовим исходные данные:

# Preparation of input data
dataset_sort_df = dataset_df.loc[:, ['X2', 'Y']].sort_values(by=['X2'])
display(dataset_sort_df.describe())

Y_sort = np.array(dataset_sort_df['Y'])
X_sort = np.array(dataset_sort_df['X2'])

Построим линейную модель:

# LINEAR MODEL
func_name = 'linear'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

func = models_dict[func_name]
p0 = p0_dict[func_name]

model = lmfit.Model(func,   
                    independent_vars=['x'],
                    name=func_name)

params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf)
params.add('b1', value=p0[1], min=-inf, max=inf)

result = model.fit(Y_sort, params, x=X_sort,
                   method='leastsq',
                   nan_policy='raise')

print(f'result.fit_report:n{result.fit_report(min_correl=0.2)}n')
dely = result.eval_uncertainty(sigma=3)

# graphic (data, best-fit, uncertainty band and residuals)
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=16)

axes[0].set_title('data, init-fit, best-fit, and uncertainty band')
sns.scatterplot(x=X_sort, y=Y_sort, label='data', s=50, color='red', ax=axes[0])
R2 = round(result.rsquared, DecPlace)
sns.lineplot(x=X_sort, y=result.best_fit, color='blue', linewidth=2, legend=True, label='best fit (' + r'$R^2 = $' + f'{R2})', ax=axes[0])
axes[0].fill_between(X_sort, result.best_fit-dely, result.best_fit+dely, color="grey", alpha=0.3, label=r'3-$sigma$ band')
axes[0].legend()
axes[0].set_ylabel('Y')
#axes[0].set_xlim(X1_min_graph, X1_max_graph)
axes[0].set_ylim(Y_min_graph, Y_max_graph)

sns.scatterplot(x=X_sort, y=-result.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_xlabel('X')
axes[1].set_ylabel('residuals')
#axes[1].set_xlim(X1_min_graph, X1_max_graph)
#axes[1].set_ylim(Y_min_graph, Y_max_graph)

plt.show()

LINEAR MODEL: y = b0 + b1*x
result.fit_report:
[[Model]]
    Model(linear)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 7
    # data points      = 55
    # variables        = 2
    chi-square         = 126.256130
    reduced chi-square = 2.38219113
    Akaike info crit   = 49.7038688
    Bayesian info crit = 53.7185352
    R-squared          = 0.13645691
[[Variables]]
    b0:  10.1218956 +/- 0.23996519 (2.37%) (init = 0)
    b1: -0.06161458 +/- 0.02129069 (34.55%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(b0, b1) = -0.498

График влияния на метрику качества аппроксимации — reduced chi-square

${chi}_y^2 = frac{chi^2}{N-N_{varys}}$ :

from collections import defaultdict

best_vals = defaultdict(lambda: np.zeros(X_sort.size))
stderrs = defaultdict(lambda: np.zeros(X_sort.size))
chi_sq = np.zeros_like(X_sort)

for i in range(X_sort.size):
    idx2 = np.arange(0, X_sort.size)
    idx2 = np.delete(idx2, i)
    tmp_x = X_sort[idx2]
    tmp = model.fit(Y_sort[idx2], x=tmp_x, b0=result.params['b0'], b1=result.params['b1'])
    
    chi_sq[i] = tmp.chisqr
    for p in tmp.params:
        tpar = tmp.params[p]
        best_vals[p][i] = tpar.value
        stderrs[p][i] = (tpar.stderr / result.params[p].stderr)

fig, ax = plt.subplots(figsize=(297/INCH, 210/INCH))
ax.plot(X_sort, (result.chisqr - chi_sq) / chi_sq)
ax.set_ylabel(r'Relative red. $chi^2$ change')
ax.set_xlabel('X')
ax.legend()
plt.show()

График влияния на значения параметров , и их ошибки:

fig, axs = plt.subplots(4, figsize=(297/INCH, 210/INCH*3), sharex='col')
axs[0].plot(X_sort, best_vals['b0'])
axs[0].set_ylabel('best b0')

axs[1].plot(X_sort, best_vals['b1'])
axs[1].set_ylabel('best b1')

axs[2].plot(X_sort, stderrs['b0'])
axs[2].set_ylabel('err b0 change')

axs[3].plot(X_sort, stderrs['b1'])
axs[3].set_ylabel('err b1 change')

axs[3].set_xlabel('X')
plt.show()

Видим, что выброс в интервале очень хорошо заметен на всех графиках.
Наконец, исключим выброс и построим линейную модель по очищенным данным:

mask = dataset_sort_df['Y'] < 15
dataset_sort_df_clear = dataset_sort_df[mask]
display(dataset_sort_df_clear.describe())

X_sort_clear = np.array(dataset_sort_df_clear['X2'])
Y_sort_clear = np.array(dataset_sort_df_clear['Y'])

# LINEAR MODEL
func_name = 'linear'
print(f'{func_name.upper()} MODEL: {formulas_dict[func_name]}')

func = models_dict[func_name]
p0 = p0_dict[func_name]

model = lmfit.Model(func,   
                    independent_vars=['x'],
                    name=func_name)

params = lmfit.Parameters()
params.add('b0', value=p0[0], min=-inf, max=inf)
params.add('b1', value=p0[1], min=-inf, max=inf)

result = model.fit(Y_sort_clear, params, x=X_sort_clear,
                   method='leastsq',
                   nan_policy='raise')

print(f'result.fit_report:n{result.fit_report(min_correl=0.2)}n')
dely = result.eval_uncertainty(sigma=3)

# graphic (data, best-fit, uncertainty band and residuals)
fig, axes = plt.subplots(2, 1, figsize=(297/INCH, 210/INCH))
fig.suptitle(f'Model({func_name})', fontsize=16)

axes[0].set_title('data, init-fit, best-fit, and uncertainty band')
sns.scatterplot(x=X_sort_clear, y=Y_sort_clear, label='data', s=50, color='red', ax=axes[0])
R2 = round(result.rsquared, DecPlace)
sns.lineplot(x=X_sort_clear, y=result.best_fit, color='blue', linewidth=2, legend=True, label='best fit (' + r'$R^2 = $' + f'{R2})', ax=axes[0])
axes[0].fill_between(X_sort_clear, result.best_fit-dely, result.best_fit+dely, color="grey", alpha=0.3, label=r'3-$sigma$ band')
axes[0].legend()
axes[0].set_ylabel('Y')
#axes[0].set_xlim(X1_min_graph, X1_max_graph)
axes[0].set_ylim(Y_min_graph, Y_max_graph)

sns.scatterplot(x=X_sort_clear, y=-result.residual, ax=axes[1], s=50)
axes[1].axhline(y = 0, color = 'k', linewidth = 1)
axes[1].set_xlabel('X')
axes[1].set_ylabel('residuals')
#axes[1].set_xlim(X1_min_graph, X1_max_graph)
#axes[1].set_ylim(Y_min_graph, Y_max_graph)

plt.show()

LINEAR MODEL: y = b0 + b1*x
result.fit_report:
[[Model]]
    Model(linear)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 7
    # data points      = 54
    # variables        = 2
    chi-square         = 67.8407274
    reduced chi-square = 1.30462937
    Akaike info crit   = 16.3216480
    Bayesian info crit = 20.2996161
    R-squared          = 0.28334888
[[Variables]]
    b0:  10.0379989 +/- 0.17802593 (1.77%) (init = 0)
    b1: -0.07177285 +/- 0.01582893 (22.05%) (init = 0)
[[Correlations]] (unreported correlations are < 0.200)
    C(b0, b1) = -0.488

Видим, что исключение выброса позволило улучшить качество аппроксимации с до .

Сравнительный анализ инструментов аппроксимации

Очевидно, что библиотека lmfit является наиболее совершенным инструментом аппроксимации в python, но и в то же время — наиболее сложным в освоении. Для более простых задач вполне может использоваться scipy.optimize.curve_fit.

Про быстродействие различных инструментов аппроксимации — см., например, https://mmas.github.io/least-squares-fitting-numpy-scipy.

В общем, каждый исследователь вправе сам выбирать инструменты для решения своих задач.

СОЗДАНИЕ ПОЛЬЗОВАТЕЛЬСКОЙ ФУНКЦИИ ДЛЯ АППРОКСИМАЦИИ ЗАВИСИМОСТЕЙ

Создадим пользовательскую функцию simple_approximation, которая позволит выполнять простую аппроксимацию зависимостей (по аналогии с тем, как это реализовано в MS Excel), а именно:

работать с наиболее распространенными моделями аппроксимации (линейной, квадратической, кубической, степенной, экспоненциальной, логарифмической, гиперболической);
выполнять визуализацию, в том числе нескольких моделей на одном графике;
выводить на графике уравнение моделей;
выводить на графике основные метрики качества моделей (, , );
выводить числовые значения параметров моделей и метрик качества в виде DataFrame;
выводить значения , рассчитанные по моделям, в виде DataFrame.

Разумеется, данная функция не претендует на абсолютную полноту, она предназначена только лишь для облегчения предварительных исследований. В случае необходимости расширить набор моделей и/или выводимых данных, любой исследователь сможет получить необходимый результат по аналогии с тем, как это было продемонстрировано в примерах расчетов выше.

Функция simple_approximation имеет следующие параметры:

X_in, Y_in — исходные значения переменных и ;
models_list_in — список моделей для аппроксимации (например, полный перечень models_list = [‘linear’, ‘quadratic’, ‘qubic’, ‘power’, ‘exponential’, ‘logarithmic’, ‘hyperbolic’]);
p0_dict_in=None — словарь (dict) с начальными значениями параметров (по умолчанию равны 1);
Xmin, Xmax, Ymin, Ymax — границы значений для построения графиков;
nx_in=100 — число точек, на которое разбивается область значений переменной для построения графиков;
DecPlace=4 — точность (число знаков после запятой) выводимых значений параметров и метрик качества моделей;
result_table=False, value_table_calc=False, value_table_graph=False — выводить или нет (True/False) DataFrame с параметрами моделей и метриками качества, с расчетными значениями переменной , с расчетными значениями переменной для графиков;
title_figure=None, title_figure_fontsize=16, title_axes=None, title_axes_fontsize=18 — заголовки и шрифт заголовков графиков;
x_label=None, y_label=None — наименования осей графиков;
linewidth=2 — толщина линий графиков;
label_fontsize=14, tick_fontsize=12, label_legend_fontsize=12 — заголовки и шрифт легенды;
color_list_in=None — словарь (dict), задающий цвета для графиков различных моделей (по умолчанию используется заданный в функции);
b0_formatter=None, b1_formatter=None, b2_formatter=None, b3_formatter=None — числовой формат для отображения параметров моделей (по умолчанию используется заданный в функции);
graph_size=(420/INCH, 297/INCH) — размер окна графиков;
file_name=None — имя файла для сохранения графика на диске.

Функция simple_approximation возвращает:

result_df — DataFrame с параметрами моделей и метриками качества;
value_table_calc и value_table_graph — DataFrame с расчетными значениями переменной , с расчетными значениями переменной для графиков;
выводит график аппроксимации.

def simple_approximation(
    X_in, Y_in,
    models_list_in,
    p0_dict_in=None,
    Xmin=None, Xmax=None,
    Ymin=None, Ymax=None,
    nx_in=100,
    DecPlace=4,
    result_table=False, value_table_calc=False, value_table_graph=False,
    title_figure=None, title_figure_fontsize=16,
    title_axes=None, title_axes_fontsize=18,
    x_label=None, y_label=None,
    linewidth=2,
    label_fontsize=14, tick_fontsize=12, label_legend_fontsize=12,
    color_list_in=None,
    b0_formatter=None, b1_formatter=None, b2_formatter=None, b3_formatter=None,
    graph_size=(420/INCH, 297/INCH),
    file_name=None):
    
    # Equations
    linear_func = lambda x, b0, b1: b0 + b1*x
    quadratic_func = lambda x, b0, b1, b2: b0 + b1*x + b2*x**2
    qubic_func = lambda x, b0, b1, b2, b3: b0 + b1*x + b2*x**2 + b3*x**3
    power_func = lambda x, b0, b1: b0 * x**b1
    exponential_func = lambda x, b0, b1: b0 * np.exp(b1*x)
    logarithmic_func = lambda x, b0, b1: b0 + b1*np.log(x)
    hyperbolic_func = lambda x, b0, b1: b0 + b1/x
    
    # Model reference
    p0_dict = {
        'linear':      [1, 1],
        'quadratic':   [1, 1, 1],
        'qubic':       [1, 1, 1, 1],
        'power':       [1, 1],
        'exponential': [1, 1],
        'logarithmic': [1, 1],
        'hyperbolic':  [1, 1]}
    
    models_dict = {
        'linear':      [linear_func,      p0_dict['linear']],
        'quadratic':   [quadratic_func,   p0_dict['quadratic']],
        'qubic':       [qubic_func,       p0_dict['qubic']],
        'power':       [power_func,       p0_dict['power']],
        'exponential': [exponential_func, p0_dict['exponential']],
        'logarithmic': [logarithmic_func, p0_dict['logarithmic']],
        'hyperbolic':  [hyperbolic_func,  p0_dict['hyperbolic']]}
    
    models_df = pd.DataFrame({
        'func': (
            linear_func,
            quadratic_func,
            qubic_func,
            power_func,
            exponential_func,
            logarithmic_func,
            hyperbolic_func),
        'p0': (
            p0_dict['linear'],
            p0_dict['quadratic'],
            p0_dict['qubic'],
            p0_dict['power'],
            p0_dict['exponential'],
            p0_dict['logarithmic'],
            p0_dict['hyperbolic'])},
        index=['linear', 'quadratic', 'qubic', 'power', 'exponential', 'logarithmic', 'hyperbolic'])
        
    models_dict_keys_list = list(models_dict.keys())
    models_dict_values_list = list(models_dict.values())
        
    # Initial guess for the parameters
    if p0_dict_in:
        p0_dict_in_keys_list = list(p0_dict_in.keys())
        for elem in models_dict_keys_list:
            if elem in p0_dict_in_keys_list:
                models_dict[elem][1] = p0_dict_in[elem]
            
    # Calculations
    X_fact = np.array(X_in)
    Y_fact = np.array(Y_in)
    
    nx = 100 if not(nx_in) else nx_in
    hx = (Xmax - Xmin)/(nx - 1)
    X_calc_graph = np.linspace(Xmin, Xmax, nx)
    
    parameters_list = list()
    models_list = list()
    
    error_metrics_df = pd.DataFrame(columns=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE', 'RMSLE', 'R2'])
    Y_calc_graph_df = pd.DataFrame({'X': X_calc_graph})
    Y_calc_df = pd.DataFrame({
        'X_fact': X_fact,
        'Y_fact': Y_fact})
    
    for elem in models_list_in:
        if elem in models_dict_keys_list:
            func = models_dict[elem][0]
            p0 = models_dict[elem][1]
            popt_, _ = curve_fit(func, X_fact, Y_fact, p0=p0)
            models_dict[elem].append(popt_)
            Y_calc_graph = func(X_calc_graph, *popt_)
            Y_calc = func(X_fact, *popt_)
            Y_calc_graph_df[elem] = Y_calc_graph
            Y_calc_df[elem] = Y_calc
            parameters_list.append(popt_)
            models_list.append(elem)
            (model_error_metrics, result_error_metrics) = regression_error_metrics(Yfact=Y_fact, Ycalc=Y_calc_df[elem], model_name=elem)
            error_metrics_df = pd.concat([error_metrics_df, result_error_metrics])
                
    parameters_df = pd.DataFrame(parameters_list,
                                 index=models_list)
    parameters_df = parameters_df.add_prefix('b')
    result_df = parameters_df.join(error_metrics_df)
                        
    # Legend for a linear model
    if "linear" in models_list_in:
        b0_linear = round(result_df.loc["linear", "b0"], DecPlace)
        b0_linear_str = str(b0_linear)
        b1_linear = round(result_df.loc["linear", "b1"], DecPlace)
        b1_linear_str = f' + {b1_linear}' if b1_linear > 0 else f' - {abs(b1_linear)}'
        R2_linear = round(result_df.loc["linear", "R2"], DecPlace)
        MSPE_linear = result_df.loc["linear", "MSPE"]
        MAPE_linear = result_df.loc["linear", "MAPE"]
        label_linear = 'linear: ' + r'$Y_{calc} = $' + b0_linear_str + b1_linear_str + f'{chr(183)}X' + ' ' + 
            r'$(R^2 = $' + f'{R2_linear}' + ', ' + f'MSPE = {MSPE_linear}' + ', ' + f'MAPE = {MAPE_linear})'
    
    # Legend for a quadratic model
    if "quadratic" in models_list_in:
        b0_quadratic = round(result_df.loc["quadratic", "b0"], DecPlace)
        b0_quadratic_str = str(b0_quadratic)
        b1_quadratic = result_df.loc["quadratic", "b1"]
        b1_quadratic_str = f' + {b1_quadratic:.{DecPlace}e}' if b1_quadratic > 0 else f' - {abs(b1_quadratic):.{DecPlace}e}'
        b2_quadratic = result_df.loc["quadratic", "b2"]
        b2_quadratic_str = f' + {b2_quadratic:.{DecPlace}e}' if b2_quadratic > 0 else f' - {abs(b2_quadratic):.{DecPlace}e}'
        R2_quadratic = round(result_df.loc["quadratic", "R2"], DecPlace)
        MSPE_quadratic = result_df.loc["quadratic", "MSPE"]
        MAPE_quadratic = result_df.loc["quadratic", "MAPE"]
        label_quadratic = 'quadratic: ' + r'$Y_{calc} = $' + b0_quadratic_str + b1_quadratic_str + f'{chr(183)}X' + b2_quadratic_str + f'{chr(183)}' + r'$X^2$' + ' ' + 
            r'$(R^2 = $' + f'{R2_quadratic}' + ', ' + f'MSPE = {MSPE_quadratic}' + ', ' + f'MAPE = {MAPE_quadratic})'
    
    # Legend for a qubic model
    if "qubic" in models_list_in:
        b0_qubic = round(result_df.loc["qubic", "b0"], DecPlace)
        b0_qubic_str = str(b0_qubic)
        b1_qubic = result_df.loc["qubic", "b1"]
        b1_qubic_str = f' + {b1_qubic:.{DecPlace}e}' if b1_qubic > 0 else f' - {abs(b1_qubic):.{DecPlace}e}'
        b2_qubic = result_df.loc["qubic", "b2"]
        b2_qubic_str = f' + {b2_qubic:.{DecPlace}e}' if b2_qubic > 0 else f' - {abs(b2_qubic):.{DecPlace}e}'
        b3_qubic = result_df.loc["qubic", "b3"]
        b3_qubic_str = f' + {b3_qubic:.{DecPlace}e}' if b3_qubic > 0 else f' - {abs(b3_qubic):.{DecPlace}e}'
        R2_qubic = round(result_df.loc["qubic", "R2"], DecPlace)
        MSPE_qubic = result_df.loc["qubic", "MSPE"]
        MAPE_qubic = result_df.loc["qubic", "MAPE"]
        label_qubic = 'qubic: ' + r'$Y_{calc} = $' + b0_qubic_str + b1_qubic_str + f'{chr(183)}X' + 
            b2_qubic_str + f'{chr(183)}' + r'$X^2$' + b3_qubic_str + f'{chr(183)}' + r'$X^3$' + ' ' + 
            r'$(R^2 = $' + f'{R2_qubic}' + ', ' + f'MSPE = {MSPE_qubic}' + ', ' + f'MAPE = {MAPE_qubic})'
    
    # Legend for a power model
    if "power" in models_list_in:
        b0_power = round(result_df.loc["power", "b0"], DecPlace)
        b0_power_str = str(b0_power)
        b1_power = round(result_df.loc["power", "b1"], DecPlace)
        b1_power_str = str(b1_power)
        R2_power = round(result_df.loc["power", "R2"], DecPlace)
        MSPE_power = result_df.loc["power", "MSPE"]
        MAPE_power = result_df.loc["power", "MAPE"]
        label_power = 'power: ' + r'$Y_{calc} = $' + b0_power_str + f'{chr(183)}' + r'$X$'
        for elem in b1_power_str:
            label_power = label_power + r'$^{}$'.format(elem)
        label_power = label_power  + ' ' + r'$(R^2 = $' + f'{R2_power}' + ', ' + f'MSPE = {MSPE_power}' + ', ' + f'MAPE = {MAPE_power})'
    
    # Legend for a exponential model
    if "exponential" in models_list_in:
        b0_exponential = round(result_df.loc["exponential", "b0"], DecPlace)
        b0_exponential_str = str(b0_exponential)
        b1_exponential = result_df.loc["exponential", "b1"]
        b1_exponential_str = f'{b1_exponential:.{DecPlace}e}'
        R2_exponential = round(result_df.loc["exponential", "R2"], DecPlace)
        MSPE_exponential = result_df.loc["exponential", "MSPE"]
        MAPE_exponential = result_df.loc["exponential", "MAPE"]
        label_exponential = 'exponential: ' + r'$Y_{calc} = $' + b0_exponential_str + f'{chr(183)}' + r'$e$'
        for elem in b1_exponential_str:
            label_exponential = label_exponential + r'$^{}$'.format(elem)
        label_exponential = label_exponential + r'$^{}$'.format(chr(183)) + r'$^X$' + ' ' + 
            r'$(R^2 = $' + f'{R2_exponential}' + ', ' + f'MSPE = {MSPE_exponential}' + ', ' + f'MAPE = {MAPE_exponential})'
    
    # Legend for a logarithmic model
    if "logarithmic" in models_list_in:
        b0_logarithmic = round(result_df.loc["logarithmic", "b0"], DecPlace)
        b0_logarithmic_str = str(b0_logarithmic)
        b1_logarithmic = round(result_df.loc["logarithmic", "b1"], DecPlace)
        b1_logarithmic_str = f' + {b1_logarithmic}' if b1_logarithmic > 0 else f' - {abs(b1_logarithmic)}'
        R2_logarithmic = round(result_df.loc["logarithmic", "R2"], DecPlace)
        MSPE_logarithmic = result_df.loc["logarithmic", "MSPE"]
        MAPE_logarithmic = result_df.loc["logarithmic", "MAPE"]
        label_logarithmic = 'logarithmic: ' + r'$Y_{calc} = $' + b0_logarithmic_str + b1_logarithmic_str + f'{chr(183)}ln(X)' + ' ' + 
            r'$(R^2 = $' + f'{R2_logarithmic}' + ', ' + f'MSPE = {MSPE_logarithmic}' + ', ' + f'MAPE = {MAPE_logarithmic})'
    
    # Legend for a hyperbolic model
    if "hyperbolic" in models_list_in:
        b0_hyperbolic = round(result_df.loc["hyperbolic", "b0"], DecPlace)
        b0_hyperbolic_str = str(b0_hyperbolic)
        b1_hyperbolic = round(result_df.loc["hyperbolic", "b1"], DecPlace)
        b1_hyperbolic_str = f' + {b1_hyperbolic}' if b1_hyperbolic > 0 else f' - {abs(b1_hyperbolic)}'
        R2_hyperbolic = round(result_df.loc["hyperbolic", "R2"], DecPlace)
        MSPE_hyperbolic = result_df.loc["hyperbolic", "MSPE"]
        MAPE_hyperbolic = result_df.loc["hyperbolic", "MAPE"]
        label_hyperbolic = 'hyperbolic: ' + r'$Y_{calc} = $' + b0_hyperbolic_str + b1_hyperbolic_str + f' / X' + ' ' + 
            r'$(R^2 = $' + f'{R2_hyperbolic}' + ', ' + f'MSPE = {MSPE_hyperbolic}' + ', ' + f'MAPE = {MAPE_hyperbolic})'
        
    # Legends
    label_legend_dict = {
        'linear':      label_linear if "linear" in models_list_in else '',
        'quadratic':   label_quadratic if "quadratic" in models_list_in else '',
        'qubic':       label_qubic if "qubic" in models_list_in else '',
        'power':       label_power if "power" in models_list_in else '',
        'exponential': label_exponential if "exponential" in models_list_in else '',
        'logarithmic': label_logarithmic if "logarithmic" in models_list_in else '',
        'hyperbolic':  label_hyperbolic if "hyperbolic" in models_list_in else ''}
    
    # Graphics
    color_dict = {
        'linear':      'blue',
        'quadratic':   'green',
        'qubic':       'brown',
        'power':       'magenta',
        'exponential': 'cyan',
        'logarithmic': 'orange',
        'hyperbolic':  'grey'}
    
    if not(Xmin) and not(Xmax):
        Xmin = min(X_fact)*0.99
        Xmax = max(X_fact)*1.01
    if not(Ymin) and not(Ymax):
        Ymin = min(Y_fact)*0.99
        Ymax = max(Y_fact)*1.01     
        
    fig, axes = plt.subplots(figsize=(graph_size))
    fig.suptitle(title_figure, fontsize = title_figure_fontsize)
    axes.set_title(title_axes, fontsize = title_axes_fontsize)
    
    sns.scatterplot(
        x=X_fact, y=Y_fact,
        label='data',
        s=50,
        color='red',
        ax=axes)
       
    for elem in models_list_in:
        if elem in models_dict_keys_list:
            sns.lineplot(
                x=X_calc_graph, y=Y_calc_graph_df[elem],
                color=color_dict[elem],
                linewidth=linewidth,
                legend=True,
                label=label_legend_dict[elem],
                ax=axes)

    axes.set_xlim(Xmin, Xmax)
    axes.set_ylim(Ymin, Ymax)
    axes.set_xlabel(x_label, fontsize = label_fontsize)
    axes.set_ylabel(y_label, fontsize = label_fontsize)
    axes.tick_params(labelsize = tick_fontsize)
    axes.legend(prop={'size': label_legend_fontsize})

    plt.show()
    
    if file_name:
        fig.savefig(file_name, orientation = "portrait", dpi = 300)
    
    # result output
    output_list = [result_df, Y_calc_df, Y_calc_graph_df]
    result_list = [result_table, value_table_calc, value_table_graph]
    result = list()
    for i, elem in enumerate(result_list):
        if elem:
            result.append(output_list[i])
    
    # result display
    for elem in ['MSPE', 'MAPE']:
        result_df[elem] = result_df[elem].apply(lambda s: float(s[:-1]))
    b_formatter = [b0_formatter, b1_formatter, b2_formatter, b3_formatter]
    if result_table:
        display(result_df
                .style
                    .format(
                        precision=DecPlace, na_rep='-',
                        formatter={
                            'b0': b0_formatter if b0_formatter else '{:.4f}',
                            'b1': b1_formatter if b1_formatter else '{:.4f}',
                            'b2': b2_formatter if b2_formatter else '{:.4e}',
                            'b3': b3_formatter if b3_formatter else '{:.4e}'})
                    .highlight_min(color='green', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE'])
                    .highlight_max(color='red', subset=['MSE', 'RMSE', 'MAE', 'MSPE', 'MAPE'])
                    .highlight_max(color='green', subset='R2')
                    .highlight_min(color='red', subset='R2')
                    .applymap(lambda x: 'color: orange;' if abs(x) <= 10**(-(DecPlace-1)) else None, subset=parameters_df.columns))
    
    if value_table_calc:
        display(Y_calc_df)
    if value_table_graph:
        display(Y_calc_graph_df)
                    
    return result

Выполним аппроксимацию зависимости среднемесячного расхода топлива автомобиля (л/100 км) (FuelFlow) от среднемесячного пробега (км) (Mileage):

title_figure = Title_String + 'n' + Task_Theme + 'n'
title_axes = 'Fuel mileage ratio'
    
models_list = ['linear', 'power', 'exponential', 'quadratic', 'qubic', 'logistic', 'logarithmic', 'hyperbolic']

p0_dict_in= {'exponential': [1, -0.1],
             'power': [1, -0.1]}

(result_df,
value_table_calc,
value_table_graph
) = simple_approximation(
    X1, Y,
    models_list, p0_dict_in,
    Xmin = X1_min_graph, Xmax = X1_max_graph,
    Ymin = Y_min_graph, Ymax = Y_max_graph,
    DecPlace=DecPlace,
    result_table=True, value_table_calc=True, value_table_graph=True,
    title_figure = title_figure,
    title_axes = title_axes,
    x_label=Variable_Name_X1,
    y_label=Variable_Name_Y,
    linewidth=2,
    b1_formatter='{:.' + str(DecPlace + 3) + 'f}', b2_formatter='{:.' + str(DecPlace) + 'e}', b3_formatter='{:.' + str(DecPlace) + 'e}')

Выполним аппроксимацию зависимости среднемесячного расхода топлива автомобиля (л/100 км) (FuelFlow) от срднемесячной температуры (Temperature):

models_list = ['linear', 'exponential', 'quadratic']

(result_df,
value_table_calc,
value_table_graph
) = simple_approximation(
    X_sort_clear, Y_sort_clear,
    models_list, p0_dict_in,
    Xmin = X2_min_graph, Xmax = X2_max_graph,
    Ymin = Y_min_graph, Ymax = Y_max_graph,
    DecPlace=DecPlace,
    result_table=True, value_table_calc=True, value_table_graph=True,
    title_figure = title_figure,
    title_axes = 'Dependence of FuelFlow on temperature',
    x_label=Variable_Name_X2,
    y_label=Variable_Name_Y,
    linewidth=2,
    b1_formatter='{:.' + str(DecPlace + 3) + 'f}', b2_formatter='{:.' + str(DecPlace) + 'e}', b3_formatter='{:.' + str(DecPlace) + 'e}')

Небольшой offtop — сравнение результатов расчетов с использованием различного программного обеспечения

Напоследок хочу привести данные сравнения результатов аппроксимации с помощью различных программных средств:

Python, функция scipy.optimize.curve_fit;
MS Excel;
система компьютерной алгебры Maxima (которую я настоятельно рекомендую освоить всем специалистам, выполняющим математические расчеты).

Все файлы с расчетами доступны в моем репозитории на GitHub (https://github.com/AANazarov/MyModulePython).

Итак:

Python, функция scipy.optimize.curve_fit:

Модель	Уравнение	Коэффициент
линейная	$Y=11.8501-2.1760 cdot 10^{-3} cdot X$	0.4226
квадратическая	$Y=14.3435-7.0471 cdot 10^{-3} cdot X+1.8760 cdot 10^{-6} cdot X^2$	0.6357
кубическая	$Y=14.8385-8.804 cdot 10^{-3} cdot X+3.5207 cdot 10^{-6} cdot X^2-4.1264 cdot 10^{-10} cdot X^3$	0.6415
степенная	$Y=33.4033cdot X^{-0.1841}$	0.6588
экспоненциальная I типа	$Y=12.6242cdot e^{2.783cdot 10^{-4} cdot X}$	0.4857
экспоненциальная II типа		0.4857
логарифмическая		0.6625
гиперболическая	$Y=9.2219+frac{315.7336}{X}$	0.4618

MS Excel:

Модель	Уравнение	Коэффициент
линейная		0.4226
квадратическая	$Y=14.345-0.007 cdot X+2 cdot 10^{-6} cdot X^2$	0.6359
кубическая	$Y=14.84-0.0088 cdot X+4 cdot 10^{-6} cdot X^2-4 cdot 10^{-10} cdot X^3$	0.6417
степенная	$Y=35.303cdot X^{-0.193}$	0.6582
экспоненциальная I типа	$Y=11.848cdot e^{2cdot 10^{-4} cdot X}$	0.4739
экспоненциальная II типа	—	—
логарифмическая		0.6627
гиперболическая	—	—

Maxima:

Модель	Уравнение	Коэффициент
линейная	$Y=11.85-2.1760 cdot 10^{-3} cdot X$	0.4226
квадратическая	$Y=14.343-7.0471 cdot 10^{-3} cdot X+1.8760 cdot 10^{-6} cdot X^2$	0.6357
кубическая	$Y=14.838-8.804 cdot 10^{-3} cdot X+3.5207 cdot 10^{-6} cdot X^2-4.1264 cdot 10^{-10} cdot X^3$	0.6415
степенная	$Y=33.355cdot X^{-0.18388}$	0.6588
экспоненциальная I типа	$Y=12.624cdot e^{2.7835cdot 10^{-4} cdot X}$	0.4857
экспоненциальная II типа		0.4857
логарифмическая		0.6625
гиперболическая	$Y=9.2219+frac{315.73}{X}$	0.4618

Как видим, результаты имеют незначительные отличия для степенных и экспоненциальных зависимостей. Есть над чем задуматься…

ИТОГИ

Итак, подведем итоги:

мы рассмотрели основные инструменты Python для аппроксимации зависимостей;
разобрали особенности определения ошибок и построения доверительных интервалов для параметров моделей аппроксимации;
также предложен пользовательская функция для аппроксимации простых зависимостей (по аналогии с тем, как это реализовано в Excel), облегчающая работу исследователя и уменьшающая размер программного кода.

Само собой, мы рассмотрели в рамках данного обзора далеко не все вопросы, связанные с аппроксимацией; так отдельного рассмотрения, безусловно, заслуживают следующие вопросы:

аппроксимация более сложных зависимостей (модифицированных кривых, S-образных кривых и пр.), требующих предварительной оценки начальных условий для алгоритма оптимизации;
влияние выбора алгоритма оптимизации на результат и быстройдействие;
аппроксимация с ограничениями в виде интервалов (bounds) и в виде алгебраических выражений (constraints);
более глубокое рассмотрение возможностей библиотеки lmfit для решения задач аппроксимации,

и т.д.

В общем, есть куда двигаться дальше.

Исходный код находится в моем репозитории на GitHub (https://github.com/AANazarov/Statistical-methods).

Надеюсь, данный обзор поможет специалистам DataScience в работе.

Источник

Линейная аппроксимация

Аппроксимацией (приближением) функции f(x) называется нахождение такой функции ( аппроксимирующей функции ) g(x) , которая была бы близка заданной. Критерии близости функций могут быть различные.

В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной . Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Пусть задан дискретный набор точек, называемых узлами интерполяции , а также значения функции в этих точках. Требуется построить функцию g(x) , проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi .

В качестве функции g(x) обычно выбирается полином, который называют интерполяционным полиномом .

В случае если полином един для всей области интерполяции, говорят, что интерполяция глобальная .

В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Аппроксимация линейной функцией

С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение:

Решение поставленной задачи сводится к нахождению экстремума указанной функции двух переменных. С этой целью находим частные производные функции функции по коэффициентам a и b и приравниваем их к нулю.

Решаем полученную систему уравнений

Определяем значения коэффициентов

Для вычисления коэффициентов необходимо найти следующие составляющие:

Тогда значения коэффициентов будут определены как

Пример реализации

Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

Реализация на Си

Построение графика функции

Реализация на Си

Аппроксимация с фиксированной точкой пересечения с осью y

Аппроксимация функции одной переменной

Калькулятор использует методы регрессии для аппроксимации функции одной переменной.

Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.

Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.

Аппроксимация функции одной переменной

Линейная регрессия

Коэффициент линейной парной корреляции:

Средняя ошибка аппроксимации:

Квадратичная регрессия

Система уравнений для нахождения коэффициентов a, b и c:

Коэффициент корреляции:
,
где

Средняя ошибка аппроксимации:

Кубическая регрессия

Система уравнений для нахождения коэффициентов a, b, c и d:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Степенная регрессия

Показательная регрессия

Гиперболическая регрессия

Логарифмическая регрессия

Экспоненциальная регрессия

Вывод формул

Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.

Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.

Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.

Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:

Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.

Используя формулу производной сложной функции, получим следующую систему уравнений:

Для функции вида частные производные равны:
,

Подставив производные, получим:

Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.

Как получить уравнение функции по точкам

Неверно введено число.

Точки должны быть разными.

Уравнение прямой по двум точкам

Введите координаты точек:

Количество знаков после разделителя дроби в числах:

Общее уравнение прямой:

Теория

Уравнение прямой, проходящей через две заданные точки (x₁,y₁) и (x₂,y₂), имеет вид:

или в общем виде

Т.е. получили общее уравнение прямой линии на плоскости в декартовых координатах:

источники:

http://planetcalc.ru/5992/

http://www.math.by/geometry/eqline.html

Источник

Аппроксимация линейной функцией

Пример реализации

Построение графика функции

Аппроксимация с фиксированной точкой пересечения с осью y

Линейная аппроксимация

Аппроксимация линейной функцией

Пример реализации

Построение графика функции

Аппроксимация с фиксированной точкой пересечения с осью y

Как по точкам определить функцию: Как по точкам найти функцию найти функцию по точкам Математика

Построение графиков функций — урок. Алгебра, 10 класс.

Как построить график функции

Онлайн уравнение прямой по двум точкам с подробным решением

Аппроксимация в Matlab — CodeTown.ru

Аппроксимация

МНК (Метод Наименьших Квадратов)

Примеры задач

Поделиться ссылкой:

Получить функцию по точкам. Как по точкам найти функцию

Немного матчасти

Ставим опыты

Думаем и экспериментируем

А как люди-то делают?

MS Excel

LibreOffice Calc

Highcharts , одна из самых популярных JS-библиотек для построения диаграмм

amCharts , ещё одна популярная JS-библиотека

Coreplot , самая популярная библиотека построения графиков для iOS и OS X

aChartEngine , вроде как самая популярная библиотека построения графиков для Android

Вместо заключения

Рекомендуем также

Функция поиска уравнения по таблице точек

Ответы на вопросы (FAQ)

Как найти уравнение кривой?

Как найти уравнение из набора точек?

Как найти уравнение линии?

Исходный код

Нужна помощь?

Вопросы / комментарии

Уникальный круг, проходящий через три неколлинеарных точки

Решение трех линейных уравнений с тремя неизвестными

Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) — Mathplanet

Функции: графики и пересечения

1.1: Четыре способа представления функции

Определение того, представляет ли отношение функцию

Использование обозначения функций

Представление функций с помощью таблиц

Поиск входных и выходных значений функции

Вычисление функций в алгебраических формах

Вычисление функций, выраженных в формулах

Оценка функции, заданной в табличной форме

Поиск значений функций из графика

Определение того, является ли функция однозначной

Использование теста вертикальной линии

Использование теста горизонтальной линии

Ключевые понятия

Глоссарий

Авторы и авторство

Как рассчитать уклон в точке — Видео и стенограмма урока

Нахождение уклона в точке Шаги

Дополнительная практика

Резюме урока

Линейные функции и их графики

Обзор линий графика

Как найти функцию зная только точки?

Точечная аппроксимация.

АКТУАЛЬНОСТЬ ТЕМЫ

Применение пользовательских функций

ИСХОДНЫЕ ДАННЫЕ

Сохранение данных

Визуализация

ОСНОВЫ ТЕОРИИ

Инструменты Python для аппроксимации

Основные виды моделей для аппроксимации

Оценка ошибок и доверительных интервалов для параметров моделей аппроксимации

Метрики качества аппроксимации

Оценка ошибок и доверительных интервалов для параметров моделей аппроксимации

АППРОКСИМАЦИЯ ЗАВИСИМОСТЕЙ

Аппроксимация с использованием scipy.optimize.leastsq

Аппроксимация с использованием scipy.optimize.least_squares