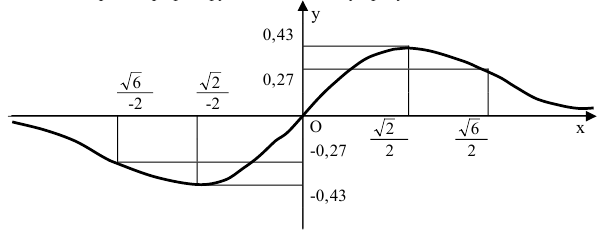
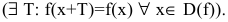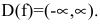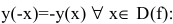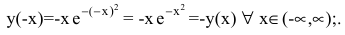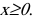Асимптоты графика функции
Часто задание на нахождение асимптот функции встречается в курсе математического анализа, в частности при решении задач на тему исследования функции. Для того, чтобы успешно ответить на вопрос: как найти асимптоты функции? необходимо уметь вычислять пределы, понимать что они собой представляют, знать основные методы решения пределов. Если всё это вы умеете на должном уровне, тогда найти асимптоты для вас не будет проблемой. Итак, что такое асимптота? Асимптота это линия, к которой бесконечно приближается ветвь графика функции. Чтобы было наглядно, посмотрите на изображения представленные ниже.
Обратите внимание, что соприкосновения между асимптотой и графиками нет, и не должно быть. Асимптота бесконечно приближается к графику функции. Давайте рассмотрим какие виды асимптоты функции бывают и как их находить, но о последнем будет рассказано далее.
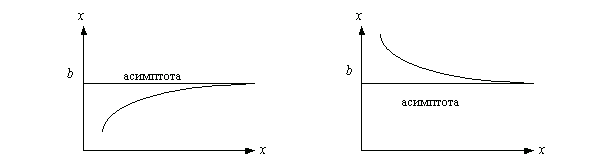
Из таблицы узнаем, что асимптоты у функции бывают трех видов: вертикальные, горизонтальные, наклонные. Каждую найти асимптоту функции нужно по своему. Для этого нужны лимиты. Сколько бывает асимптот всего у функции? Ответ: ни одной, одна, две, три… и бесконечно много. У каждой функции по разному.
Вертикальные асимптоты
Чтобы найти данный вид асимптот необходимо найти область определения заданной функции и отметить точки разрыва. В этих точках предел функции будет равен бесконечности, а это значит, что функция в этой точке бесконечно приближается к линии асимптоты.
Горизонтальные асимптоты
Необходимо устремить аргумент лимита функции к бесконечности. Если предел существует и равен числу, то горизонтальная асимптота будет найдена и равна $ y=y_0 $ как показано во втором столбце таблицы
Наклонные асимптоты
Наклонная асимптота представляется в виде $ y = kx+b $. Где $ k $ — это коэффициент наклона асимптоты. Сначала находится коэффициент $ k $, затем $ b $. Если какой либо из них равен $ infty $, тогда наклонной асимптоты нет. А если $ k = 0 $, то получаем горизонтальную асимптоту. Так что для экономии времени лучше сразу находить наклонную асимптоту, а горизонтальная проявится сама собой в случае её существования.
Примеры решений
| Пример 1 |
| Найти все асимптоты графика функции $$ f(x) = frac{5x}{3x+2} $$ |
| Решение |
|
Для начала решения найдем вертикальные асимптоты, но прежде найдем область определения функции $ f(x) $. По определению знаменатель не должен быть равен нулю. Поэтому имеем, $ 3x+2 neq 0; 3x neq -2; x neq -frac{2}{3} $. Получили точку разрыва $ x = -frac{2}{3} $. Вычислим в ней предел функции и убедимся окончательно, что вертикальная асимптота это $ x = -frac{2}{3} $. $$ limlimits_{{x rightarrow -frac{2}{3}}} frac{5x}{3x+2} = (-frac{10}{infty}) = -infty $$. Теперь найдем горизонтальные асимптоты, но прежде рассчитаем коэффициенты $ k $ и $ b $. $$ k = limlimits_{x rightarrow infty} frac{f(x)}{x} =limlimits_{x rightarrow infty} frac{5}{3x+2}=frac{5}{infty}=0 $$ Так как $ k = 0 $, то мы уже понимаем то, что наклонных асимптот нет, а есть горизонтальные. Найдем теперь коэффициент $ b $. $$ b = limlimits_{x rightarrow infty} [f(x)-kx] = limlimits_{x rightarrow infty} frac{5x}{3x+2} = frac{infty}{infty} =frac{5}{3} $$ Подставляем найденные коэффициенты в формулу $ y = kx + b $, получаем, что $ y = frac{5}{3} $ — горизонтальная асимптота. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y = frac{5}{3} $$ |
| Пример 2 |
| Найти все асимптоты графика функции $ f(x) = frac{1}{1-x} $ |
| Решение |
|
Найдем область определения данного примера, чтобы определить вертикальные асимптоты. $ 1-x neq 0; x neq 1; $. Точка разрыва $ x = 1 $, а это значит что это и есть вертикальная асимптота. Найдем для доказательства предположения предел в этой точке. $$ limlimits_{x rightarrow 1} frac{1}{1-x} = frac{1}{0} = infty $$ Приступим к поиску наклонных асимптот. $$ k = limlimits_{x rightarrow infty}frac{f(x)}{x}=limlimits_{x rightarrow infty}frac{1}{x(1-x)} = frac{1}{infty}=0 $$ $$ b =limlimits_{x rightarrow infty}[f(x)-kx]=limlimits_{x rightarrow infty}frac{1}{1-x} = frac{1}{infty}=0 $$ Итого, $ y=0 $ — горизонтальная асимптота. |
| Ответ |
| $$ y=0 $$ |
| Пример 3 |
| Найти все асимптоты графика функции $ f(x) = frac{x^3}{3x^2+5} $ |
| Решение |
|
Замечаем, что знаменатель не обращается в ноль при любом значении икса. А это значит, что нет точек разрыва и следовательно нет вертикальных асимптот. Остается найти горизонтальные асимптоты. $$ k = limlimits_{x rightarrow infty} frac{f(x)}{x} =limlimits_{x rightarrow infty}frac{x^2}{3x^2+5} =limlimits_{x rightarrow infty} frac{2x}{6x} = frac{1}{3} $$ Так как $ k $ конечное число, не равное $ 0 $ или бесконечности, то существует наклонная асимптота. Вычислим недостающее число $ b $. $$ b =limlimits_{x rightarrow infty} [f(x)-kx] =limlimits_{x rightarrow infty} [frac{x^3}{3x^2+5}-frac{x}{3}] =limlimits_{x rightarrow infty} -frac{5x}{3(3x^2+5)}= $$ $$ = -frac{5}{3}limlimits_{x rightarrow infty} frac{x}{3x^2+5} =-frac{5}{3}limlimits_{x rightarrow infty} frac{1}{6x} =-frac{5}{3}frac{1}{infty} = 0 $$ $ y =frac{1}{3}x $ — наклонная асимптота к функции с углом наклона одна третья. |
| Ответ |
| $$ y =frac{1}{3}x $$ |
| Пример 4 |
| Найти асимптоты $ f(x) = xe^{-x} $ |
| Решение |
|
Нет точек разрыва, а это значит, нет вертикальных асимптот. $$ k=limlimits_{x rightarrow infty} frac{1}{e^x} = frac{1}{infty} = 0 $$ $$ b=limlimits_{x rightarrow infty} frac{x}{e^x} =limlimits_{x rightarrow infty} frac{1}{e^x} = frac{1}{infty} = 0 $$ $ y = 0 $ — горизонтальная асимптота |
| Ответ |
| $$ y = 0 $$ |
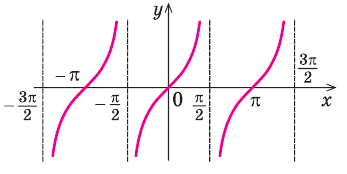
Если в задачах даются элементарные функции, то заранее известно сколько и есть ли асимптоты. Например, у параболы, кубической параболы, синусоиды вообще нет никаких. У графиков функций таких как логарифмическая или экспоненциальная есть по одной. А у функций тангенса и котангенса бесчисленное множество асимптот, но арктангенс и арккатангенс имеет по две штуки.
Во всех приведенных примерах пределы вычислялись с помощью правило Лопиталя, которое очень ускоряет процесс вычисления и создает меньше ошибок.
Если
функция f(x) не является непрерывной
в точкеx = a, то говорят, чтоf(x)
имеетразрывв этой
точке. На рисунке 1 схематически изображены
графики четырех функций, две из которых
непрерывны приx = a, а две имеют
разрыв.



разрыва функции разделяются наточки
разрыва первого и второго рода.
Говорят, что функцияf(x) имеетточку разрыва первого
родаприx = a, если в это точке
: 1.Существуют левосторонний предели
правосторонний предел;
2.Эти односторонние пределы конечны.
При этом возможно следующие два случая:
1.Левосторонний предел и правосторонний
предел равны друг другу:Такая точка называетсяточкой
устранимого разрыва. 2.Левосторонний
предел и правосторонний предел не равны
друг другу:
Такая точка называетсяточкой
конечного разрыва. Модуль разности
значений односторонних пределовназываетсяскачком функции.
Функцияf(x) имеетточку
разрыва второго родаприx = a,
если по крайней мере один из односторонних
пределов не существует или равен
бесконечности.
Асимптоты
графика функций
при
исследовании графика функции на
бесконечность, т.е. при x+
и x-,
а так же вблизи точек разрыва часто
оказывается, что график сколь угодно
близко приближается к той или иной
прямой, т.е. асимптоте.Прямая
х=х0 – вертикальная асимптота графика
функции y=f(x),
если хотя бы один из пределов
или
равен
.
Нахождение вертикальных асимптот: 1)
точки разрыва и граничные точки на
области определения 2) вычисляем
односторонний предел при х стремящимся
к этим точкам.Прямая
y=a
– горизонтальная асимптота графика
y=f(x),
при х,
если
.Прямая y=kx+b
называется наклонной асимптотой к
графику y=f(x)
при х,
если саму функцию y=f(x)
можно представить в виде f(x)=kx+b+(x),
где
.Схема нахождения:
вычисляем
,
если этот предел не существует или равен
бесконечности, то функция не имеет
наклонной асимптоты. Вычисляем,
если его нет или он бесконечен, то
асимптоты нет.
17. Комплексные числа.
Комплексным
числомбудем называть упорядоченную пару
действительных чисел,
записанную в форме
,
где—
новый объект («мнимая единица»),
для которого при вычислениях полагаем.
Первая компонента комплексного числа,
действительное число,
называется действительной частью числа,
это обозначается так:;
вторая компонента, действительное число,
называется мнимой частью числа:
.Опр.. Два комплексных числа
и
равны тогда и только тогда, когда равны
их действительные и мнимые части:.
Множество комплексных чисел неупорядочено,
т.е. для комплексных чисел не вводятся
отношения «больше» или «меньше».
Геометрически комплексное числоизображается как точка с координатами
на плоскости. Плоскость, на которой
изображаются комплексные числа,
называется комплексной плоскостью.Опр.. Суммой двух комплексных чисел
и
называется комплексное число
,
определяемое соотношением,
т.е.,
.
Это означает, что геометрически
комплексные числа складываются как
векторы на плоскости, покоординатно.Опр.Произведением двух комплексных
чисели
называется комплексное число
,
определяемое соотношением,
т.е..
Для двух комплексных чисел с нулевой
мнимой частьюи
получим
,
,
т.е. для множества комплексных чисел с
нулевой мнимой частью операции сложения
и умножения не выводят за пределы этого
множества. Отождествим каждое такое
число с действительным числом,
равным действительной части комплексного
числа, т.е. будем считать, что.
Теперь действительные числа — подмножество
множества комплексных чисел.
Далее, числа с нулевой действительной
частью, т.е. числа вида,
называютсямнимыми числами. Мнимое
число с единичной мнимой частью будем
записывать просто как:
;
квадрат этого числа, по определению
умножения, равен,
что обосновывает данное вопр.9.1.1свойство «мнимой единицы». Легко
убедиться, что операция сложения
на множестве комплексных чиселимеет свойства, аналогичным аксиомамI.1-I.4, которым
удовлетворяет операция сложения
действительных чисел (см. раздел 3.1.
Аксиомы действительных чисел):I.1.
;I.2.
;I.3. Существует такой
элемент,
чтодля
.
Этот элемент — число.I.4. Для каждого элемента
существует такой элемент
,
что.
Этот элемент — число.
Сумма чисели
называется разностью чисел
и
:
.
Прежде, чем определить операцию деления
комплексных чисел, введём понятия
сопряжённого числа и модуля комплексного
числа.Опр.. Числоназывается числом, сопряжённым к числу
.
Часто сопряжённое число обозначается
также символом.Опр.Действительное число
называется модулем комплексного числа
.
Найдём произведение сопряжённых чисел:.
Таким образом,— всегда неотрицательное действительное
число, причём.
Для нахождения частного комплексных
чиселдомножим числитель и знаменатель на
число, сопряжённое знаменателю:.

свойстваII.1.
;II.2.
;II.3. Произведение числа
на любое число
равно
;II.4. Для каждого числа
существует такое число
,
что,
;
Операции сложения и умножения подчиняется
закону дистрибутивности:III.1.
.
Операция сопряжения имеет следующие
свойства:IV..
Примеры
выполнения арифметических действий с
комплексными числами: пусть
,
.
Тогда;
;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Асимптоты кривой
Прямая линия называется асимптотой кривой y=f(x), если расстояние точки кривой до этой прямой стремится к нулю при стремлении точки к бесконечности.
Назначение сервиса. Данный сервис предназначен для нахождения асимптот к графику функции в онлайн режиме. Решение оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Оформление Word
Правила ввода функции
Примеры
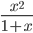
cos2(2x+π) ≡ (cos(2*x+pi))^2
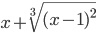
Классификация асимптот
- Вертикальные асимптоты.
- Горизонтальные асимптоты.
- Наклонные асимптоты.
Вертикальные асимптоты
Уравнение любой вертикальной прямой, то есть прямой, параллельной оси OY, имеет вид x=a.
Если прямая x=a является вертикальной асимптотой графика функции y=f(x), то очевидно, что хотя бы один из односторонних пределов 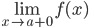
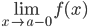
Все функции с бесконечными разрывами (разрывы второго рода) имеют вертикальные асимптоты.
Пример 1. Найти уравнение вертикальных асимптот графика функции 
Решение. Видим, что y→∞, если x→1, точнее 

Горизонтальные асимптоты
Всякая горизонтальная прямая имеет уравнение y=A.
Если прямая y=A является горизонтальной асимптотой кривой y=f(x), то 
Пример 2. Найти горизонтальные асимптоты кривой 
Решение. Найдем 
Наклонные асимптоты
Уравнения наклонных асимптот обычно ищут в виде y=kx+b. По определению асимптоты 

Разделим обе части этого равенства на x:


Теперь из (1):

Для существования наклонных асимптот необходимо существование пределов (2) и (3). Если хотя бы один из них не существует, то наклонных асимптот нет. Пределы (2) и (3) нужно находить отдельно при x→+∞ и при x→-∞, так как пределы могут быть разными (функция имеет две разные асимптоты).
Пример 4. Найти наклонные асимптоты графика функции 
Решение. По формуле (2) найдем 
Теперь найдем 
Пример 5. Найти асимптоты кривой y=(x-1)2(x+3).
Решение. Вертикальных и горизонтальных асимптот нет, так как y→∞ при x→∞. Ищем наклонные:

Таким образом, кривая асимптот не имеет.
Пример 6. Найти асимптоты кривой 
Решение. Поскольку y→∞ при x→0 и при x→4, то прямые x=0 и x=4 являются вертикальными асимптотами. Так как 

Пример 7. Построить все виды асимптот к функции
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:
Находим коэффициент k:
Находим коэффициент b:
Получаем уравнение наклонной асимптоты: y = -x
Найдем вертикальные асимптоты. Для этого определим точки разрыва:
Находим переделы в точке
— является вертикальной асимптотой.
Находим переделы в точке
— является вертикальной асимптотой.

- Понятие асимптоты
- Вертикальная асимптота
- Горизонтальная асимптота
- Наклонная асимптота
- Алгоритм исследования асимптотического поведения функции
- Примеры
п.1. Понятие асимптоты
Асимптота прямая, расстояние от которой до точки кривой стремится к нулю при удалении точки вдоль ветви кривой на бесконечность.
Различают вертикальные, горизонтальные и наклонные асимптоты.
Например:
п.2. Вертикальная асимптота
Вертикальная асимптота кривой (y=f(x)) имеет вид: (x=a)
где (a) — точка разрыва 2-го рода функции (f(x)), для которой хотя бы один односторонний предел существует и равен бесконечности.
Таким образом, практически каждой точке разрыва 2-го рода (см. §40 данного справочника) соответствует вертикальная асимптота.
Вертикальных асимптот может быть сколько угодно, в том числе, бесконечное множество (например, как у тангенса – см. §6 данного справочника).
Например:
Исследуем непрерывность функции (y=frac{1}{(x-1)(x+3)})
ОДЗ: (xne left{-3;1right})
(left{x_0=-3, x_1=1right}notin D) — точки не входят в ОДЗ, подозрительные на разрыв.
Исследуем (x_0=-3). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -3 -0}frac{1}{(x-1)(x+3)}=frac{1}{(-3-0-1)(-3-0+3)}=frac{1}{-4cdot(-0)}=+infty\ lim_{xrightarrow -3 +0}frac{1}{(x-1)(x+3)}=frac{1}{(-3+0-1)(-3+0+3)}=frac{1}{-4cdot(+0)}=-infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_0=-3) — точка разрыва 2-го рода.
Исследуем (x_1=1). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 1 -0}frac{1}{(x-1)(x+3)}=frac{1}{(1-0-1)(1-0+3)}=frac{1}{-0cdot 4}=-infty\ lim_{xrightarrow 1 +0}frac{1}{(x-1)(x+3)}=frac{1}{(1+0-1)(1+0+3)}=frac{1}{+0cdot 4}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_1=1) — точка разрыва 2-го рода.
Вывод: у функции (y=frac{1}{(x-1)(x+3)}) две точки разрыва 2-го рода (left{x_0=-3, x_1=1right}), соответственно – две вертикальные асимптоты с уравнениями (x=-3) и (x=1).
п.3. Горизонтальная асимптота
Горизонтальная асимптота кривой (y=f(x)) имеет вид: (y=b)
где (b) — конечный предел функции (f(x)) на бесконечности: (b=lim{xrightarrow pminfty}f(x), bneinfty)
Число горизонтальных асимптот не может быть больше двух.
Например:
Исследуем наличие горизонтальных асимптот у функции (y=frac{1}{(x-1)(x+3)})
Ищем предел функции на минус бесконечности: begin{gather*} lim_{xrightarrow -infty}frac{1}{(x-1)(x+3)}=frac{1}{(-infty)(-infty)}=+0 end{gather*} На минус бесконечности функция имеет конечный предел (b=0) и стремится к нему сверху (о чем свидетельствует символическая запись +0).
Ищем предел функции на плюс бесконечности: begin{gather*} lim_{xrightarrow +infty}frac{1}{(x-1)(x+3)}=frac{1}{(+infty)(+infty)}=+0 end{gather*} На плюс бесконечности функция имеет тот же конечный предел (b=0) и также стремится к нему сверху.
Вывод: у функции (y=frac{1}{(x-1)(x+3)}) одна горизонтальная асимптота (y=0). На плюс и минус бесконечности функция стремится к асимптоте сверху.
Итоговый график асимптотического поведения функции (y=frac{1}{(x-1)(x+3)}):
п.4. Наклонная асимптота
Наклонная асимптота кривой (y=f(x)) имеет вид: (y=kx+b) begin{gather*} k=lim_{xrightarrow pminfty}frac{f(x)}{x}, kne 0, kneinfty\ b=lim_{xrightarrow pminfty}(f(x)=kx) end{gather*}
Число наклонных асимптот не может быть больше двух.
Например:
Исследуем наличие наклонных асимптот у функции (y=frac{x^2+3}{x-1})
Найдем угловой коэффициент: begin{gather*} k_1=lim_{xrightarrow -infty}frac{y}{x}=lim_{xrightarrow -infty}frac{x^2+3}{x(x-1)}= lim_{xrightarrow -infty}frac{x^2+3}{x^2-x}=left[frac{infty}{infty}right]= lim_{xrightarrow -infty}frac{x^2left(1+frac{3}{x^2}right)}{x^2left(1-frac 1xright)}=\ =lim_{xrightarrow -infty}frac{1+frac{3}{x^2}}{1-frac1x}=frac{1+0}{1-0}=1\ k_2=lim_{xrightarrow +infty}frac{y}{x}=lim_{xrightarrow +infty}frac{x^2+3}{x(x-1)}=k_1=1 end{gather*} На плюс и минус бесконечности отношение функции к аргументу имеет один и тот же конечный предел (k=1).
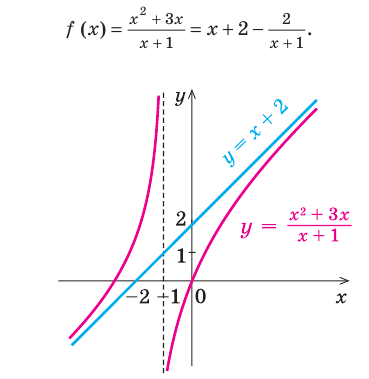
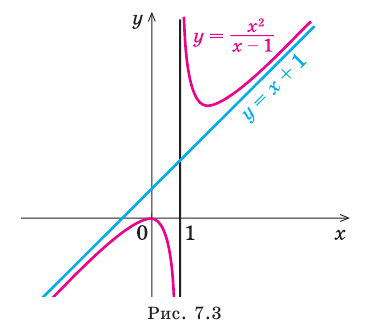
Найдем свободный член: begin{gather*} b=lim_{xrightarrow pminfty}(y-kx)=lim_{xrightarrow pminfty}left(frac{x^2+3}{x-1}-1cdot xright)= lim_{xrightarrow pminfty}left(frac{x^2+3-x(x-1)}{x-1}right)=\ =lim_{xrightarrow pminfty}frac{x+3}{x-1}=left[frac{infty}{infty}right]=lim_{xrightarrow pminfty}frac{xleft(1+frac3xright)}{xleft(1-frac1xright)}=frac{1+0}{1-0}=1 end{gather*} Вывод: у функции (y=frac{x^2+3}{x-1}) одна наклонная асимптота (y=x+1). Функция стремится к асимптоте на плюс и минус бесконечности.
Чтобы построить график асимптотического поведения, заметим, что у функции (y=frac{x^2+3}{x-1}), очевидно, есть вертикальная асимптота x=1. При этом: begin{gather*} lim_{xrightarrow -1-0}frac{x^2+3}{x-1}=-infty, lim_{xrightarrow -1+0}frac{x^2+3}{x-1}=+infty end{gather*}
График асимптотического поведения функции (y=frac{x^2+3}{x-1}):
п.5. Алгоритм исследования асимптотического поведения функции
На входе: функция (y=f(x))
Шаг 1. Поиск вертикальных асимптот
Исследовать функцию на непрерывность. Если обнаружены точки разрыва 2-го рода, у которых хотя бы один односторонний предел существует и бесконечен, сопоставить каждой такой точке вертикальную асимптоту. Если таких точек не обнаружено, вертикальных асимптот нет.
Шаг 2. Поиск горизонтальных асимптот
Найти пределы функции на плюс и минус бесконечности. Каждому конечному пределу сопоставить горизонтальную асимптоту. Если оба предела конечны и равны, у функции одна горизонтальная асимптота. Если оба предела бесконечны, горизонтальных асимптот нет.
Шаг 3. Поиск наклонных асимптот
Найти пределы отношения функции к аргументу на плюс и минус бесконечности.
Каждому конечному пределу k сопоставить наклонную асимптоту, найти b. Если только один предел конечен, у функции одна наклонная асимптота. Если оба значения k конечны и равны, и оба значения b равны, у функции одна наклонная асимптота. Если оба предела для k бесконечны, наклонных асимптот нет .
На выходе: множество всех асимптот данной функции.
п.6. Примеры
Пример 1. Исследовать асимптотическое поведение функции и построить схематический график:
a) ( y=frac{4x}{x^2-1} )
1) Вертикальные асимптоты
Точки, подозрительные на разрыв: (x=pm 1)
Односторонние пределы в точке (x=-1) begin{gather*} lim_{xrightarrow -1-0}frac{4x}{(x+1)(x-1)}=frac{4(-1-0)}{(-1-0+1)(-1-0-1)}=frac{-4}{-0cdot(-2)}=-infty\ lim_{xrightarrow -1+0}frac{4x}{(x+1)(x-1)}=frac{4(-1+0)}{(-1+0+1)(-1+0-1)}=frac{-4}{+0cdot(-2)}=+infty end{gather*} Точка (x=-1) — точка разрыва 2-го рода
Односторонние пределы в точке (x=1) begin{gather*} lim_{xrightarrow -1-0}frac{4x}{(x+1)(x-1)}=frac{4(1-0)}{(1-0+1)(1-0-1)}=frac{4}{2cdot(-0)}=-infty\ lim_{xrightarrow -1+0}frac{4x}{(x+1)(x-1)}=frac{4(1+0)}{(1+0+1)(1+0-1)}=frac{4}{2cdot(+0)}=+infty end{gather*} Точка (x=1) — точка разрыва 2-го рода
Функция имеет две вертикальные асимптоты (x=pm 1)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin{gather*} b_1=lim_{xrightarrow -infty}frac{4x}{x^2-1}=left[frac{infty}{infty}right]=lim_{xrightarrow -infty}frac{x^2cdot frac4x}{x^2(1-frac{1}{x^2})}=lim_{xrightarrow -infty}frac{frac4x}{1-frac{1}{x^2}}=frac{-0}{1}=-0\ b_2=lim_{xrightarrow +infty}frac{4x}{x^2-1}=left[frac{infty}{infty}right]=lim_{xrightarrow +infty}frac{frac4x}{1-frac{1}{x^2}}=frac{+0}{1}=+0 end{gather*} Функция имеет одну горизонтальную асимптоту (y=0). На минус бесконечности функция стремится к асимптоте снизу, не плюс бесконечности – сверху.
3) Наклонные асимптоты
Ищем угловые коэффициенты: begin{gather*} k=lim_{xrightarrow pminfty}frac{4x}{x(x^2-1)}=lim_{xrightarrow pminfty}frac{4}{x^2-1}=frac{4}{infty}=0 end{gather*} Наклонных асимптот нет.
График асимптотического поведения функции (y=frac{4x}{x^2-1})
б) ( y=e^{frac{1}{x+3}} )
1) Вертикальные асимптоты
Точка, подозрительная на разрыв: (x=-3)
Односторонние пределы: begin{gather*} lim_{xrightarrow -3-0}e^{frac{1}{x+3}}=e^{frac{1}{-3-0)+3}}=e^{frac{1}{-0}}=e^infty=0\ lim_{xrightarrow -3+0}e^{frac{1}{x+3}}=e^{frac{1}{-3+0)+3}}=e^{frac{1}{+0}}=e^{+infty}=+infty end{gather*} Точка (x=-3) — точка разрыва 2-го рода
Функция имеет одну вертикальную асимптоту (x=2)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin{gather*} b_1=lim_{xrightarrow -infty}e^{frac{1}{x+3}}=e^0=1\ b_2=lim_{xrightarrow +infty}e^{frac{1}{x+3}}=e^0=1\ b=b_1=b_2=1 end{gather*} Функция имеет одну горизонтальную асимптоту (y=1). Функция стремится к этой асимптоте на минус и плюс бесконечности.
3) Наклонные асимптоты
Ищем угловые коэффициенты: begin{gather*} k_1=lim_{xrightarrow -infty}frac{e^{frac{1}{x+3}}}{x}=frac{e^0}{-infty}=0\ k_2=lim_{xrightarrow +infty}frac{e^{frac{1}{x+3}}}{x}=frac{e^0}{+infty}=0 end{gather*} Наклонных асимптот нет.
График асимптотического поведения функции (y=e^{frac{1}{x+3}})
в) ( y=frac{x^3+x^2+x+1}{x^2-1} )
Заметим, что ( frac{x^3+x^2+x+1}{x^2-1}=frac{x^2(x+1)+(x+1)}{(x+1)(x-1)}=frac{(x^2)(x+1)}{(x+1)(x-1)}=frac{x^2+1}{x-1} ) $$ y=frac{x^3+x^2+x+1}{x^2-1}Leftrightarrow begin{cases} y=frac{x^2+1}{x-1}\ xne -1 end{cases} $$ График исходной функции совпадает с графиком функции (y=frac{x^2+1}{x-1}), из которого необходимо выколоть точку c абсциссой (x=-1).
1) Вертикальные асимптоты
Точки, подозрительные на разрыв: (x=pm 1)
Односторонние пределы в точке (x=-1) begin{gather*} lim_{xrightarrow -1-0}frac{x^3+x^2+x+1}{x^2-1}=lim_{xrightarrow -1-0}frac{x^2+1}{x-1}=frac{2}{-2}=-1\ lim_{xrightarrow -1+0}frac{x^3+x^2+x+1}{x^2-1}=lim_{xrightarrow -1-0}frac{x^2+1}{x-1}=frac{2}{-2}=-1 end{gather*} Точка (x=-1) — точка разрыва 1-го рода, устранимый разрыв («выколотая» точка).
Односторонние пределы в точке (x=1) begin{gather*} lim_{xrightarrow 1-0}frac{x^3+x^2+x+1}{x^2-1}=lim_{xrightarrow 1-0}frac{x^2+1}{x-1}=frac{2}{1-0-1}=frac{2}{-0}=-infty\ lim_{xrightarrow 1-0}frac{x^3+x^2+x+1}{x^2-1}=lim_{xrightarrow 1-0}frac{x^2+1}{x-1}=frac{2}{1+0-1}=frac{2}{+0}=+infty end{gather*} Точка (x=1) — точка разрыва 2-го рода
Функция имеет одну вертикальную асимптоту (x=1)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin{gather*} b_1=lim_{xrightarrow -infty}frac{x^2+1}{x-1}=left[frac{infty}{infty}right]=lim_{xrightarrow -infty}frac{x^2left(1+frac{1}{x^2}right)}{x^2left(frac1x-frac{1}{x^2}right)}=frac{1+0}{-0-0}=-infty\ b_2=lim_{xrightarrow +infty}frac{x^2+1}{x-1}=left[frac{infty}{infty}right]=lim_{xrightarrow +infty}frac{x^2left(1+frac{1}{x^2}right)}{x^2left(frac1x-frac{1}{x^2}right)}=frac{1+0}{0-0}=+infty end{gather*} Оба предела бесконечны.
Функция не имеет горизонтальных асимптот.
3) Наклонные асимптоты
Ищем угловые коэффициенты: begin{gather*} k_1=lim_{xrightarrow -infty}frac{x^2+1}{x(x-1)}=left[frac{infty}{infty}right]=lim_{xrightarrow -infty}frac{x^2left(1+frac{1}{x^2}right)}{x^2left(1-frac1xright)}=frac{1+0}{1-0}=1\ k_2=lim_{xrightarrow +infty}frac{x^2+1}{x(x-1)}=left[frac{infty}{infty}right]=lim_{xrightarrow +infty}frac{x^2left(1+frac{1}{x^2}right)}{x^2left(1-frac1xright)}=frac{1+0}{1-0}=1\ k=k_1=k_2=1 end{gather*} У функции есть одна наклонная асимптота с (k=1).
Ищем свободный член: begin{gather*} b=lim_{xrightarrow infty}(y-kx)= lim_{xrightarrow infty}left(frac{x^2+1}{x-1}-2right)= lim_{xrightarrow infty}frac{x^2+1-x^2+x}{x-1}= lim_{xrightarrow infty}frac{x+1}{x-1}=left[frac{infty}{infty}right]=\ =lim_{xrightarrow infty}frac{xleft(1+frac1xright)}{xleft(1-frac1xright)}=frac{1+0}{1-0}=1 end{gather*} Функция имеет одну наклонную асимптоту (y=x+1).
График асимптотического поведения функции (y=frac{x^3+x^2+x+1}{x^2-1})
г*) ( y=xe^{frac{1}{2-x}} )
1) Вертикальные асимптоты
Точка, подозрительная на разрыв: (x=2)
Односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}xe^{frac{1}{2-x}}=(2-0)e^{frac{1}{2-(2-0)}}=2e^{frac{1}{+0}}=2e^{+infty}=+infty\ lim_{xrightarrow 2+0}xe^{frac{1}{2-x}}=(2+0)e^{frac{1}{2-(2+0)}}=2e^{frac{1}{-0}}=2e^{-infty}=-infty end{gather*} Точка (x=2) — точка разрыва 2-го рода.
Функция имеет одну вертикальную асимптоту (x=2)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin{gather*} b_1=lim_{xrightarrow -infty}xe^{frac{1}{2-x}}=-inftycdot e^0=-infty\ b_2=lim_{xrightarrow +infty}xe^{frac{1}{2-x}}=+inftycdot e^0=+infty end{gather*} Оба предела бесконечны.
Функция не имеет горизонтальных асимптот.
3) Наклонные асимптоты
Ищем угловые коэффициенты: begin{gather*} k_1=lim_{xrightarrow -infty}frac{xe^{frac{1}{2-x}}}{x}=lim_{xrightarrow -infty}e^{frac{1}{2-x}}=e^0=1\ k_2=lim_{xrightarrow +infty}frac{xe^{frac{1}{2-x}}}{x}=lim_{xrightarrow +infty}e^{frac{1}{2-x}}=e^0=1\ k=k_1=k_2=1 end{gather*} У функции есть одна наклонная асимптота с (k=1).
Ищем свободный член: begin{gather*} b=lim_{xrightarrow infty}(y-kx)= lim_{xrightarrow infty}left(xe^{frac{1}{2-x}}-xright)=lim_{xrightarrow infty}xleft(e^{frac{1}{2-x}}-1right)=left[inftycdot 0right] end{gather*} Используем одно из следствий второго замечательного предела (см. §39 данного справочника): begin{gather*} lim_{xrightarrow 0}frac{e^x-1}{x}=1\ b=lim_{xrightarrow infty}xleft(e^{frac{1}{2-x}}-1right)= left[ begin{array}{l} t=frac{1}{2-x}\ trightarrow 0\ x=2-frac1t=frac{2t-1}{t} end{array} right]=\ =lim_{trightarrow 0}left(left(frac{2t-1}{t}right)(e^t-1)right)=lim_{trightarrow 0}(2t-1)cdot lim_{trightarrow 0}frac{e^t-1}{t}=-1cdot 1=-1 end{gather*} Функция имеет одну наклонную асимптоту (y=x-1).
График асимптотического поведения функции (y=xe^{frac{1}{2-x}})
Содержание:
Понятие асимптоты:
Асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
Вертикальные асимптоты

Вертикальная асимптота 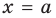
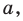
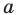
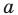
Примеры вертикальных асимптот графиков функций
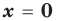
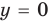
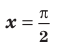
Наклонные и горизонтальные асимптоты
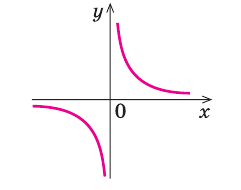
I. Если 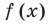
Примеры:
При 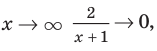
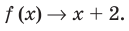
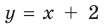
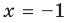
При 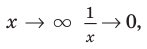
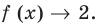
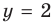
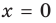
II. В общем случае уравнения наклонных и горизонтальных асимптот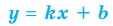
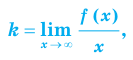
Понятие асимптоты
Если кривая 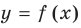
Асимптоты могут быть вертикальными, горизонтальными или наклонными.
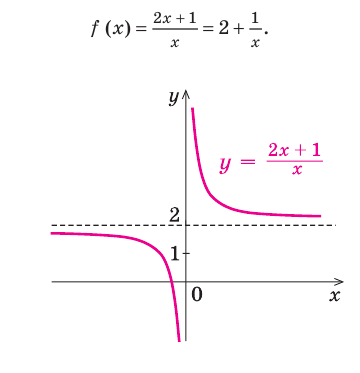
Например, для графика функции 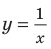
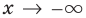
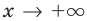
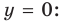
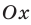
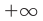
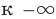
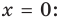
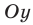
Если рассмотреть функцию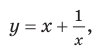
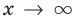
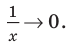
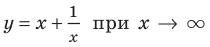
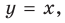
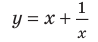
Следует отметить, что не любая кривая имеет асимптоту, поэтому не у каждого графика функции будет асимптота. Но исследование функции на наличие у ее графика асимптот позволяет уточнить свойства функции и поведение ее графика.
Вертикальные асимптоты
Если прямая 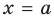
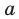

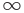
Например, у функции 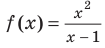
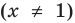

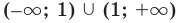

Аналогично
Таким образом, прямая 

Отметим, что не всегда в точке разрыва области определения функция будет иметь вертикальную асимптоту. Например, функция 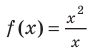
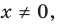
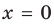
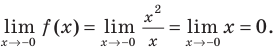
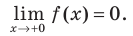
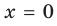
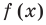
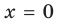
Наклонные и горизонтальные асимптоты
Наклонные и горизонтальные асимптоты довольно просто находятся для графиков дробно-рациональных функций, у которых степень числителя на единицу больше степени знаменателя (или равна степени знаменателя). Для этого достаточно выделить целую часть заданной дроби и использовать определение асимптоты.
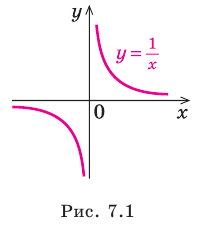
Например, еще раз рассмотрим функцию 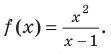
При 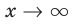
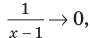
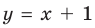
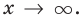
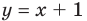
Рассмотрим, как находятся наклонные и горизонтальные асимптоты в общем случае.
Пусть наклонной (или горизонтальной) асимптотой графика функции 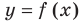

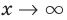
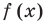
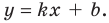
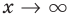
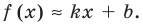
Эта равенство не нарушится, если обе его части разделить на 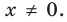
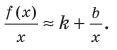
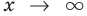
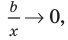
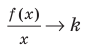
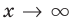
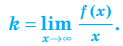
Возвращаясь к формуле (1), получаем, что при 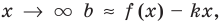
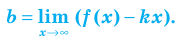
Формулы (2) и (3) дают возможность находить наклонные и горизонтальные асимптоты для графика любой функции 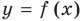
Отметим, что если у графика функции 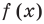
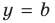
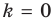
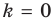
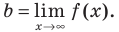
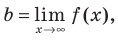
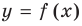
- Заказать решение задач по высшей математике
Пример:
Пользуясь общими формулами, найдите наклонную асимптоту графика функции
Решение:
Будем искать наклонную асимптоту в виде 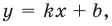
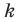
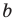
Асимптотой графика данной функции будет прямая 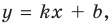
Пример:
Найдите асимптоты графика функции
Решение:
Область определения функции: 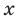
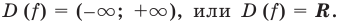
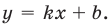
Таким образом, заданная функция имеет только горизонтальную асимптоту 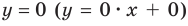
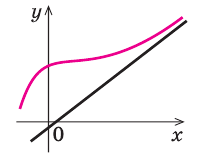
Иногда график функции 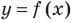
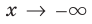
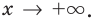
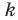
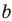
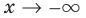
Как найти асимптоты графика функции
При исследовании поведения функции на бесконечности или вблизи точек разрыва часто оказывается, что расстояние между точками графика функции и точками некоторой прямой стремится к нулю при неограниченном удалении точек графика от начала координат. Прямая, к которой стремится кривая в бесконечно удаленной точке, называется асимптотой графика. Различают вертикальные и наклонные асимптоты. Прямая 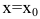
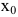
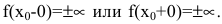
Внимание! Непрерывные на множестве действительных чисел функции вертикальных асимптот на имеют.
Для того чтобы график функции y=f(x) имел наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы
Частным случаем наклонной асимптоты (k=0) является горизонтальная асимптота.
Пример:
Найти асимптоты графика функции
Решение:
Функция 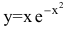
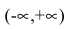
Получаем горизонтальную асимптоту y=0.
Общее исследование функции и построение графика
С помощью производной функции можно провести ее полное исследование и построить график этой функции. При этом рекомендуется использовать следующую схему.
- Найти область определения функции D(f).
- Исследовать функцию на четность
нечетность
периодичность
- Исследовать функцию на непрерывность, найти точки разрыва.
- Найти асимптоты графика функции.
- Исследовать функцию на монотонность, найти точки экстремума.
- Найти интервалы выпуклости и вогнутости, точки перегиба функции.
- Используя результаты проведенного исследования, построить график функции (можно вычислить координаты точек пересечения с осями координат).
Пример:
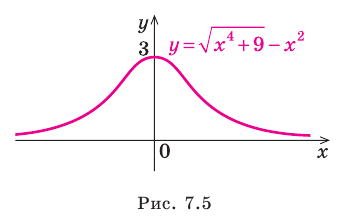
Провести полное исследование функции 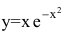
Решение:
Область определения функции — вся числовая прямая:
Функция непериодическая. Она нечетная, т.к. область определения симметрична относительно начала координат и
Следовательно, график функции симметричен относительно начала координат и достаточно исследовать функцию для
Функция непрерывна в области определения как композиция основных элементарных функций. Поскольку 
Строим график функции, используя результаты исследования.
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
- Иррациональные уравнения
- Иррациональные неравенства
- Производная в математике
- Как найти производную функции









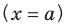
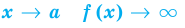
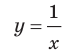
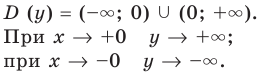
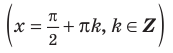
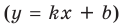
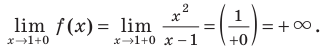
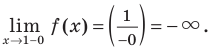
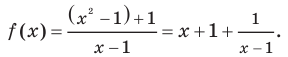
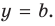
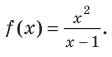
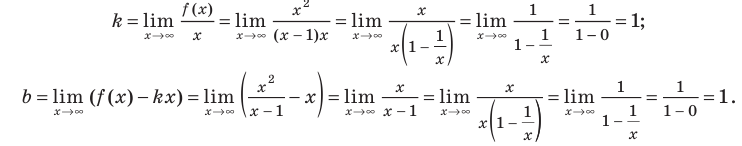
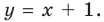
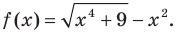
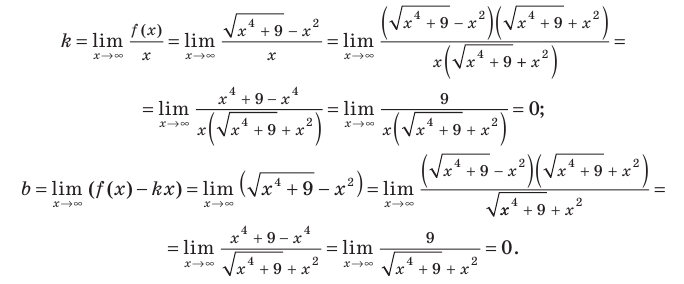
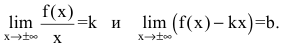
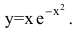
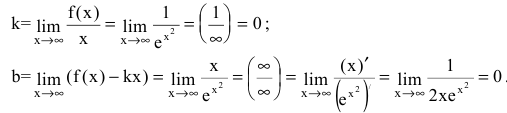
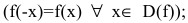 нечетность
нечетность 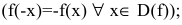 периодичность
периодичность