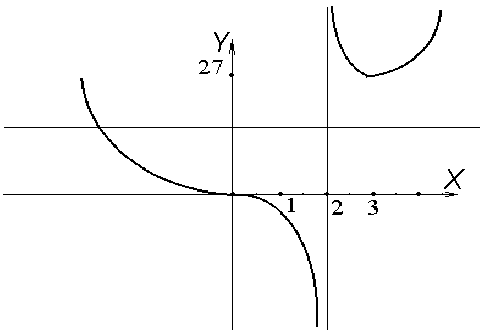Пусть функция
непрерывна в интервале
и
дифференцируема в точке.
Рассмотрим взаимное расположение
графика функции и его касательной в
точке,
уравнение которой имеет вид.
Определение1. Точканазываетсяточкой выпуклости вверх
(вниз), если,
в которой,
т.е. график функциив окрестности
лежит
ниже (выше) своей касательной в точке.
Определение 2. Если каждая точка
интервалаесть
точка выпуклости вверх (вниз) для графика
функции,
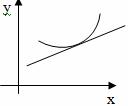
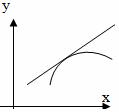
то функцияназываетсявыпуклой вверх (вниз) на
интервале(рис. 1 а,б).
а)
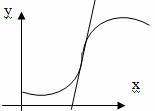
б) в)
Рис. 1
Определение3. Точканазываетсяточкой перегибаграфика
функции,
если при переходе через нее график
меняет направление выпуклости (рис. 1
в).
Исходя из приведенных определений,
достаточное условие выпуклости и
перегиба графика функции можно выразить
через первую производную (см. упр. 1).
Однако мы ограничимся следующим
утверждением.
Теорема1. Пусть функциядважды
дифференцируема в интервале.
Тогда, еслив
,
то функциявыпукла
вниз (выпукла вверх) на;
если функцияменяет знак при переходе через точку
,
то— точка перегиба.
Доказательство. Пусть— касательная к графику функции
в точке
.
Тогда по теореме Лагранжа получим
где
и точка
лежит между
и
.
Применим еще раз теорему Лагранжа к
функции
,
получим
где точка
лежит
между точкамии
.
П
точкии
лежат по одну сторону от точки
,
то.
В силу этого знак разностипри
совпадает со знаком
,
откуда и следует утверждение теоремы.
Вставка 1.
Определение4. Говорят, что прямаяявляетсявертикальной асимптотойграфика функции
,
если хотя бы одно из предельных значенийили
равно
или
Из этого определения видно, что если
есть
точка бесконечного разрыва функции,
то прямаяесть вертикальная асимптота для графика
функции.
Верно и обратное.
Определение5. Пусть,
либо,
либо.
Прямаяназываетсянаклонной асимптотойграфика функции
,
если.
Теорема2 (нахождение наклонной
асимптоты). Условиеэквивалентно паре условий
.
Доказательство. 1).
Из левого равенства получим,
из правого —,
что равносильно равенству.
-
Непосредственно из соотношения
получим
.
Вставка 2.
Вопросы и упражнения
1.Доказать утверждение:»Пусть
функциядифференцируема
в интервале.
Тогда, есливозрастает (убывает) на
,
то функциявыпукла
вниз (вверх)».
2.Доказать, что если функциянепрерывна
на интервалеи
есливыполняется неравенство
,
то функциявыпукла
вверх (вниз) на интервале.
Дать геометрическое толкование этого
неравенства.
3.Доказать неравенство.
§ 4. Примерная схема исследования графика функции
Можно порекомендовать следующую схему
исследования:
-
,
точки разрыва и их характер, вертикальные
асимптоты. -
Симметрия графика: четность, нечетность,
периодичность; точки пересечения с
осями координат. -
Наклонные асимптоты.
-
Использование первой производной:
промежутки монотонности, локальные
экстремумы. -
Использование второй производной:
интервалы выпуклости, точки перегиба,
контроль локального экстремума. -
Составление сводной таблицы.
-
Построение графика.
В случае необходимости можно определить
еще несколько точек графика.
Пример 1.Исследовать и построить
график функции.
Решение. 1),
— вертикальная асимптота.
-
График симметрией не обладает. Точки
пересечения с осями координат: (0, 0). -
наклонных асимптот нет.
-
;
при
и
при
— точка локального минимума.
-
;
при
и
при
— точка перегиба.
|
x |
y |
|
|
Эскиз |
|
|
|
– |
+ |
|
|
0 |
0 |
0 |
0 |
|
|
(0, 2) |
|
– |
– |
|
|
2 |
не опр. |
не опр. |
не опр. |
|
|
(2, 3) |
|
– |
+ |
|
|
3 |
27 |
0 |
+ |
|
|
|
|
+ |
+ |
|
Таким образом, график функции
имеет вид (рис. 2).
Рис.2
Пример 2..
Решение.1)и
определены
и непрерывны,
причем,
.
Следовательно, функцияопределена при
.
Вертикальных асимптот нет, т.к.непрерывна
как суперпозиция непрерывных функций.
2) График функции
не обладает симметрией, т.к. ее область
определения не симметрична. Точки
пересечения с осями координат: (0, 0),
(0, -2),,
.
3) Так как при
то наклонных асимптот нет.
4) при
,
приу функции
устранимый разрыв;
при
,
при
.
5) при
;
при
,
при
.
|
t |
x |
y(x) |
|
|
Эскиз |
|
|
|
|
– |
+ |
|
|
–1 |
–3 |
–2 |
0 |
+ |
|
|
(–1, 1) |
(–3, |
(–2, |
+ |
+ |
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
+ |
– |
|
Таким
образом, получим график (рис. 3).
Рис. 3
Main Content
This example describes how to analyze a simple function to find its asymptotes, maximum, minimum, and inflection point.
Define a Function
The function in this example is
f(x)=3×2+6x-1×2+x-3.
First, create the function.
syms x
num = 3*x^2 + 6*x -1;
denom = x^2 + x - 3;
f = num/denom
Plot the function by using fplot. The fplot function automatically shows vertical asymptotes.
Find Asymptotes
To find the horizontal asymptote of f mathematically, take the limit of f as x approaches positive infinity.
The limit as x approaches negative infinity is also 3. This result means the line y=3 is a horizontal asymptote to f.
To find the vertical asymptotes of f, set the denominator equal to 0 and solve it.
roots indicates that the vertical asymptotes are the lines
x=-1-132
and
x=-1+132.
Find Maximum and Minimum
You can see from the graph that f has a local maximum between the points x=–2 and x=0. It also has a local minimum between x=–6 and x=–2. To find the x-coordinates of the maximum and minimum, first take the derivative of f.
f1 =6 x+6x2+x-3-2 x+1 3 x2+6 x-1x2+x-32
To simplify this expression, enter the following.
f1 =-3 x2+16 x+17x2+x-32
Next, set the derivative equal to 0 and solve for the critical points.
crit_pts =(-133-83133-83)
As the graph of f shows, the function has a local minimum at
x1=-8-133
and a local maximum at
x1=-8+133.
Plot the maximum and minimum of f.
fplot(f) hold on plot(double(crit_pts), double(subs(f,crit_pts)),'ro') title('Maximum and Minimum of f') text(-4.8,5.5,'Local minimum') text(-2,4,'Local maximum') hold off
Find Inflection Point
To find the inflection point of f, set the second derivative equal to 0 and solve for this condition.
f2 = diff(f1);
inflec_pt = solve(f2,'MaxDegree',3);
double(inflec_pt)
ans = 3×1 complex
-5.2635 + 0.0000i
-1.3682 - 0.8511i
-1.3682 + 0.8511i
In this example, only the first element is a real number, so this is the only inflection point. MATLAB® does not always return the roots to an equation in the same order.
Instead of selecting the real root by indexing into inter_pt, identify the real root by determining which roots have a zero-valued imaginary part.
idx = imag(double(inflec_pt)) == 0; inflec_pt = inflec_pt(idx)
inflec_pt =-139 16954-2197181/3-16954-2197181/3-83
Plot the inflection point. The extra argument [-9 6] in fplot extends the range of x values in the plot so that you can see the inflection point more clearly, as the figure shows.
fplot(f,[-9 6]) hold on plot(double(inflec_pt), double(subs(f,inflec_pt)),'ro') title('Inflection Point of f') text(-7,1,'Inflection point') hold off
Интервалы выпуклости и вогнутости графика функции
С помощью онлайн-калькулятора можно найти точки перегиба и промежутки выпуклости графика функции с оформлением решения в Word. Является ли функция двух переменных f(x1,x2) выпуклой решается с помощью матрицы Гессе.
- Решение онлайн
- Видеоинструкция
Направление выпуклости графика функции. Точки перегиба
Определение: Кривая y=f(x) называется выпуклой вниз в промежутке (a; b), если она лежит выше касательной в любой точке этого промежутка.
Определение: Кривая y=f(x) называется выпуклой вверх в промежутке (a; b), если она лежит ниже касательной в любой точке этого промежутка.
Определение: Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x), характеризуется знаком ее второй производной: если в некотором промежутке f’’(x) > 0, то кривая выпукла вниз на этом промежутке; если же f’’(x) < 0, то кривая выпукла вверх на этом промежутке.
Определение: Точка графика функции y=f(x), разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции y = f(x), в которых вторая производная f’’(x) обращается в нуль или терпит разрыв.
Правило нахождения точек перегиба графика функции y = f(x)
- Найти вторую производную f’’(x).
- Найти критические точки II рода функции y=f(x), т.е. точки, в которой f’’(x) обращается в нуль или терпит разрыв.
- Исследовать знак второй производной f’’(x) в промежутка, на которые найденные критические точки делят область определения функции f(x). Если при этом критическая точка x0 разделяет промежутки выпуклости противоположных направлений, то x0 является абсциссой точки перегиба графика функции.
- Вычислить значения функции в точках перегиба.
Пример 1. Найти промежутки выпуклости и точки перегиба следующей кривой: f(x) = 6x2–x3.
Решение: Находим f ‘(x) = 12x – 3x2, f ‘’(x) = 12 – 6x.
Найдем критические точки по второй производной, решив уравнение 12-6x=0. x=2.
f(2) = 6*22 – 23 = 16
Ответ: Функция выпукла вверх при x∈(2; +∞); функция выпукла вниз при x∈(-∞; 2); точка перегиба (2;16).
Пример 2. Имеет ли точки перегиба функция: f(x)=x3-6x2+2x-1
Пример 3. Найти промежутки, на которых график функции является выпуклым и выгнутым: f(x)=x3-6x2+12x+4