Как найти тепловой эффект по энтропии

ЭЛЕМЕНТЫ ТЕРМОХИМИИ      

Термохимия – раздел химии, в котором рассматриваются тепловые явления, происходящие в процессе химических реакций.

Нужен репетитор по химии? Записывайтесь на занятия в каталоге TutorOnline!

Все химические реакции можно разделить на два типа: реакции, идущие с выделением теплоты, их называют экзотермические, и реакции, идущие с поглощением теплоты эндотермические. Критерием таких процессов является тепловой эффект реакции. 

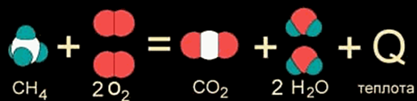
Как правило, к экзотермическим реакциям относятся реакции окисления, т.е. взаимодействия с кислородом, например сгорание метана

СН₄ + 2O₂   = СО₂ + 2Н₂О + Q   (1)

а к эндотермическим реакциям – реакции разложения. Знак Q в конце уравнения указывает на то, выделяется ли теплота в процессе реакции (+ Q) или поглощается (- Q):

СаCO₃ = СаO + CO₂ -Q   (2)

При химических процессах может выделяться или поглощаться не только тепловая, но и другие виды энергии: электрическая, световая, механическая и др.

Тепловые эффекты прямой и обратной реакций одинаковы по числу, но противоположны по знаку, например, оксид кальция (СаО) при взаимодействии с водой образует гидроксид кальция (Са(ОН)₂). Процесс сопровождается выделением большого количества теплоты:

СаО + Н₂О = Са(ОН) + 108 кДж   (3)

А реакция разложения гидроксида кальция (Са(ОН)₂) осуществляется с поглощением такого же количества теплоты извне

Са(ОН)₂ = СаО + Н₂О — 108 кДж   (4)

Если тепловой эффект реакции определяется при постоянном давлении, температуре, то он будет соответствовать стандартной энтальпии реакции, обозначаемой ∆Н, которая противоположна   по знаку величине теплового эффекта реакции. Например, если в процессе экзотермической реакции во взаимодействие вступают алюминий (Аl) и оксид железа (Fe₂O₃), то в конце уравнения это обозначится следующим образом:

2Аl + Fe₂O₃ = 2Fe + Al₂O₃ (+Q) или (-∆Н)   (5) 

А в случае эндотермической реакции значения этих тепловых величин будут иметь противоположные знаки:

С + СО₂ = 2СО (-Q) или (+∆Н)   (6)

Это объясняется тем, что выделяющаяся в процессе экзотермической реакции теплота как энергия, теряется системой (-∆Н), а при эндотермических процессах, наоборот – приобретается (+∆Н). Величина (Н) называется энтальпией системы. Часто её называют так же теплосодержанием или теплотой образования ∆Н данного вещества. В расчётах применяют справочные значения тепловых эффектов образования (или сгорания) одного моля вещества, отнесённые к 298К (25⁰С) и Р = 101,325 кПа (1 атм). Эти условия считаются стандартными и поэтому используемые значения тепловых эффектов называют стандартными теплотами образования(или сгорания) вещества и обозначают как ∆Н⁰₂₉₈. Например, тепловой эффект реакции взаимодействия графита с кислородом, выраженный через изменение энтальпии, следует записать как ∆Н⁰₂₉₈ = — 393,6 кДж, а так как при этом из простых веществ образуется 1 моль СО₂, то данный тепловой эффект является теплотой образования СО₂, выраженной в кДж/моль. Главной характеристикой топлив являются их теплоты сгорания. Тепловой эффект реакции горения одного моля вещества называется теплотой сгорания данного вещества. Следовательно, исходя из вышеприведённых положений, теплота сгорания одного моля графита (12 г) составляет 393,6 кДж/моль.

Уравнение химической реакции, в котором указан тепловой эффект, называется термохимическим уравнением.

На практике это имеет большое значение. При строительстве тепловых трасс, доменных печей, котельных и т.п. теплотопотребляющих промышленных объектов, необходимо предусмотреть или приток энергии для поддержания процессов, или наоборот, отвод избытка теплоты, чтобы не было перегрева вплоть до взрыв                                                                                                              

Расчёт теплового эффекта реакции между простыми веществами не предоставляется затруднительным. Например, для реакции образования хлористого водорода:

Н₂ + Cl₂ = 2НCl    (7)

Энергия затрачивается на разрыв двух химических связей Н–Н и Cl — Cl. При этом энергия выделяется при образовании двух химических связей Н- Cl. Значения энергий этих связей можно найти в справочных таблицах и по разности между ними определить тепловой эффект (Q) реакции (7):

 Е_Н–Н = 436 кДж/моль, Е_Cl–Cl = 240 кДж/моль,

 Е_Н–Cl = 240 кДж/моль,

 Q = 2 х 430 — ( 1 х 436 — 1 х 240 ) = 184 кДж.

Приведённая в качестве примера термохимическая реакция (7) является экзотермической. Теплоты образования простых веществ при стандартных условиях приняты равными нулю.           

Термохимические уравнения имеют особую форму записи. Они отличаются от обычных уравнений тем, что:

1). В термохимических уравнениях обязательно указывают агрегатные состояния веществ (жидкое, твёрдое, газообразное) Это связано с тем, что одна и та же реакция может иметь различный тепловой эффект в зависимости от фазового состояния вещества

2). Коэффициенты в термохимическом уравнении равны количеству веществ ( в молях), вступивших в реакцию. Например, дана реакция сгорания ацетилена:

2С₂Н₂(г) + 5О₂(г) = 4СО₂(г) + 2Н₂О (+Q)   (8)

При сгорании одного моль ацетилена С₂Н₂ выделяется 1257кДж теплоты. Поэтому, относительно одного моль С₂Н₂ необходимо все коэффициенты перед реагентами поделить на 2, тогда получим следующую запись термохимического уравнения:

С₂Н₂ + 5/2О₂ = 2СО₂ + Н₂О + 1257 кДж    (9)

Или другая тождественная запись:

С₂Н₂ + 2,5О₂ = 2СО₂ + Н₂О + 1257 кДж   (10)

Например, дано термохимическое уравнение сгорания метана:

СН₄ + 2О₂ = СО₂ + 2Н₂О + 802 кДж    (11)

Необходимо вычислить, какое количество теплоты выделится при сгорании 20 г метана?

Поскольку 1 моль метана имеет массу 16 г, а 20 г метана соответственно составляют

n = m/Mr = 20:12 = 1,25 моль,

то, составив пропорцию: при сгорании

1 моль СН₄ выделяется 802 кДж теплоты

1,25    СН₄   ———«——-Х кДж теплоты

Определим, что на сгорание 20г метана потребуется                              

Х = 1,25 х 802 / 1 = 1002,5 кДж

Приведём другой пример . Дано уравнение реакции сгорания оксида азота(+4):

4NО₂(г) + O₂(г) + 2H₂O(г) = 4НNО₃(ж) + 448 кДж   (12)

Необходимо составить термохимическое уравнение относительно сгорания одного моль оксида азота. Определить: какой объём оксида азота потребуется на образование 4258 кДж теплоты в процессе данной реакции?

Для составления термохимического уравнения относительно одного моль оксида азота(+4) необходимо все коэффициенты, стоящие перед реагентами, разделить на коэффициент, стоящий перед NО₂, т.е. на «4», тогда уравнение примет вид:

NО₂(г) + 1/4O₂(г) + 1/2H₂O(г) = НNО₃(ж) +112 кДж   (13)

В уравнении изменится количество выделяющейся теплоты, оно станет   равным 112, т.е. в четыре раза меньше, чем в приведённом уравнении. В соответствии с уравнением (13) 1 моль оксида азота(NО₂) или 22,4 л в данной реакции образует 112 кДж теплоты, а Х л соответственно 4258 кДж:                

22,4 моль NО₂ при сгорании образуют 112 кДж теплоты.

           Х л  —————-«————-4258 кДж теплоты.

            Хг = 22,4 х 4258 / 112 = 851,6 кДж

Важнейшим законом термохимии является закон Г.И.Гесса (1840): тепловой эффект реакции зависит только от начального и конечного состояния веществ и не зависит от промежуточных стадий процесса. При помощи закона Гесса можно рассчитывать такие тепловые эффекты реакции, которые измерить трудно или невозможно. Например, теплоту образования угарного газа(СО) можно вычислить, если полное сгорание углерода

С (графит) + О₂ = СО₂ (∆Н₁)   (14)

разбить на стадии:

С (графит) + 0,5О₂ = СО (∆Н₂)   (15)

СО + 0,5О₂ = СО₂ (∆Н₃)   (16)

Зная, что ∆Н₁ = -393,6 кДж/моль и ∆Н₃ = — 283,1 кДж/моль, из равенства ∆Н₁ = ∆Н₂ + ∆Н₃

находим, что ∆Н₂ = — 110,5 кДж/моль.    

В качестве другого примера можно привести образование сульфата алюминия при сгорании алюминия и серы ромбической согласно реакции:

2Al(к) + 3S(ромб) + 6О₂(г) = Al₂(SO₄)₃(к)   (17)

∆Н может быть найдена по тепловым эффектам отдельных стадий:

2Al + 1,5О₂ = Al₂O₃        ∆Н₁= -1670,2 кДж/моль   (18)

3S + 1,5О₂ = SO₃               ∆Н₂= -395,3 кДж/моль    (19)

Al₂O₃ + 3SO₃  = Al₂(SO₄)₃   ∆Н₃= -579,7 кДж/моль   (20)

Тогда ∆Н = ∆Н₁ + 3∆Н₂ + ∆Н₃  = (- 1670,2) – 3х (-395,3) – (579,7) = — 3435,8 кДж/моль.

На основании закона Гесса термохимические уравнения можно разбивать на отдельные стадии независимо от того, осуществимы они на практике или нет. Из закона Гесса вытекает важное следствие: тепловой эффект химической реакции равен сумме теплот образования получающихся веществ за вычетом суммы теплот образования исходный веществ:                                                                              

∆Н = ∑ (𝘮 ∆Н) продукты — ∑ (𝘯 ∆Н) реагенты,

где 𝘮 и 𝘯 – число молей каждого вещества в уравнении реакции. Например, теплоту сгорания ацетилена (10) можно рассчитать, зная теплоты образования  С₂Н₂ , СО₂   и Н₂О (∆Н⁰₀₂ = 0), как ∆Н⁰ = 2 ∆Н _СО2 + ∆Н_Н2О — ∆Н_С2Н2 = -2 х 393,6 — 281 — (+226,8) = -1295 кДж/моль.

НАЧАЛА ТЕРМОДИНАМИКИ

 Среди многообразия химических реакций, термохимические занимают особое положение. Если рассуждать с точки зрения эволюции жизни на Земле, то в конечном итоге, действительно, от этих процессов зависит жизнь на нашей планете. А что касается человеческой цивилизации в целом, то здесь мы имеем прямую зависимость её развития от термохимических явлений. Ведь благодаря именно данным процессам произошёл отрыв человечества в развитии от всех других видов живых организмов, населяющих нашу планету. С древнейших времён, начиная от пассивного использования огня в качестве средства для согревания и приготовления примитивной пищи, человечество пришло к активному использованию этого явления (изготовление гончарных изделий – плавка меди, железа и других металлов – паровые двигатели – двигатели внутреннего сгорания – управление ядерными реакциями)

Если можно было бы предложить создать проект монумента человеческому прогрессу, то на его фронтоне надо было бы начертать уравнение химической реакции

С + О₂ = СО₂

Именно со сгорания дров, угля, торфа начался отсчёт человеческой цивилизации. В настоящее время наше с вами существование просто немыслимо без тепловых процесов. Но кроме приведённой выше реакции существует великое множество других термодинамических процессов. Почему именно углероду дано такое предпочтение? Может быть его собрату по IV-й группе – кремнию более выгоден данный процесс?

Si + О₂ = SiО₂ 

Тем более, что кремний по массе составляет 27,6% земной коры. Это несравненно больше, чем запасы древесины и её ископаемых на нашей планете. Чего же проще? Кидай в топку кремнезём! Его ведь целая планета! Правда надо оговорить тот факт, что чистого кремния в природе не существует. В наличии только его оксид — SiО₂. Но на то и химики, чтобы придумать что-нибудь? А может быть для более сильного окислителя, чем кислород – фтору окисление углерода более выгодно термодинамически?

C + 2F₂ = СF₄

Как во всём этом разобраться? И возможно ли вообще предсказать осуществления того или иного процесса, ведь на бумаге можно написать уравнение любой химической реакции, а возможна ли она практически? Придётся начинать всё по порядку.

  Одним из самых важных и очевидных законов природы является закон сохранения энергии: энергия не возникает из ничего и не исчезает бесследно, она только переходит из одной формы в другую. Аналогичным является закон сохранения массы вещества: массы веществ вступивших в реакцию равны массам веществ, образовавшихся в процессе данной реакции.

Поэтому и при экзотермической и при эндотермической обратимых реакциях одного и того же процесса как количество затрачиваемой и расходуемой энергии равны, но противоположны по знаку, так и массы веществ распадающихся и вновь образующихся равны:

СаО + Н₂О = Са(ОН)₂ + 108 кДж

Mr=56     Mr=18          Mr=74

Са(ОН)₂ = СаО + Н₂О — 108 кДж

Mr=74          Mr=56        Mr=18

Но всё дело в том, что в приведённых выше двух реакциях уже указано, какая из них экзотермическая, а какая эндотермическая. А можно ли так, как говорится «на вскидку» по одному только уравнению реакции определить: какая это реакция? В принципе, в большинстве случаев, возможно. К экзотермическим реакциям, в основном, относятся реакции соединения и как их разновидность – реакции окисления.(8,11,12,14). А к реакциям эндотермическим, соответственно – реакции разложения (2,4). Ещё раз уточним: в большинстве случаев. Поскольку реакция окисления:

0,5N₂ + 0,5O₂ = NО  — 90 кДж

требует расхода энергии и является эндотермической, а реакция разложения нитрата натрия

2NaNO₃ = 2NaNO₂ + O₂ (+Q)

осуществляется с выделением большого количества теплоты и является экзотермической.

Значит, принцип «на вскидку» не годится. Но каким же принципом тогда следует руководствоваться в определении реакций данного типа? В приводимых выше примерах (10), (14-20) указывалось, что стандартные теплоты образования веществ (∆Н) являются справочными данными. Такие данные скрупулёзно составлялись на протяжении десятилетий для многочисленных термодинамических реакций. С этой целью использовался прибор калориметр. Именно по этим данным в настоящее время мы можем установить, какой является та или иная реакция: экзотермической или эндотермической.

  Теперь попробуем заглянуть как бы внутрь термохимической реакции. Как она начинается? Что способствует её осуществлению? В качестве примера приведём ещё раз две реакции (14) и (2):

С(графит) + О₂ = СО₂ + 393,3 кДж

СаСО₃ = СаО + СО₂  (-Q)

Представим себе, что химическими символами (С) и (О₂) будут обозначаться не элемент «углерод» и простое вещество «кислород», а дрова (или уголь, торф) и воздух (атмосфера). А в качестве соединения СаСО₃ — не карбонат кальция, а известное всем вещество: мел (или известняк). Первую реакцию будем проводить для того, чтобы нагреть печь и вскипятить чайник, а вторую – чтобы получить негашёную известь (СаО) в дальнейшем используемую для побелки садовых деревьев. Для разжигания печи приготовим щепки и, поместив сверху них дрова, зажжём огонь спичками.

Во втором случае, поместим в металлическое ведро мелко накрошенный мел, поставим на плиту и такими же действиями, как в случае разжигания огня в печи, разведём костёр под ведром.

Стоп! Тут что-то не так! Ведь мы установили, что первая реакция экзотермическая, протекает с выделением теплоты, а вторая реакция – эндотермическая, протекает с поглощением теплоты. А мы в обоих случаях разводим огонь, т.е. передаём этим процессам извне тепловую энергию. Значит, обе реакции эндотермические – идут с поглощением теплоты! Да, идут с поглощением теплоты, но это только на первом этапе. Некоторым экзотермическим реакциям требуется небольшой «толчок» — первоначальная подача энергии, а спустя некоторое время, когда загорятся дрова, процесс будет сопровождаться с выделением энергии в окружающую среду и во многие сотни, тысячи раз превзойдёт по величине первоначальное значение этой энергии. А второй процесс ка был так и останется эндотермическим. Ведь с прекращением подачи тепловой энергии мел перестанет разлагаться: реакция остановится. И всё-таки, почему в одних случаях процесс окисления (горения) является экзотермическим, а в других – эндотермическим процессом? И что является движущей силой эндотермических реакций, в ходе которых тепловая энергия поступает из окружающей среды? Ни у кого не вызывает удивление такое явление, как остывание со временем горячего чайника. Это нормально. А почему бы этому же чайнику, уже остывшему, холодному, взять, да и нагреться самому по себе? Вот это уже вызовет удивление.

Так вот, эта самая сила связана со стремлением любой системы к наиболее вероятному состоянию, характеризующимся максимальным беспорядком, называемым энтропией. Это одно из важнейших понятий в термодинамике. Энтропия обозначается символом «S». К примеру, при экзотермических реакциях, при проведении процессов плавления, кипения, переходов из жидкостей к газообразному состоянию, энтропия приобретает максимальное значение, поскольку при тепловых явлениях кинетическая энергия атомов, молекул, ионов возрастает, усиливаются беспорядочные колебания этих частиц. И наоборот, самый большой порядок в химических системах – в идеальном кристалле при температуре абсолютного нуля. Энтропия в данном случае равна нулю

Энтропия имеет численные значения, единицей её измерения является Дж/(моль ^. К); К примеру энтропия алмаза равна 2,4 Дж/(моль ^. К), пропана – 269,9 Дж/(моль ^. К). Энтропия газов значительно превышает энтропию жидких и тем более твёрдых тел. Поскольку в газообразных веществах постоянно происходит беспорядочное распределение молекул по всему объёму.

Существуют экспериментальные и теоретические методы определения энтропий различных химических соединений. Используя их, можно количественно рассчитать изменения энтропии при протекании конкретной реакции аналогично тому, как это делается для теплового эффекта реакции. Составлены специальные справочные данные, которые включают сравнительную характеристику этих величин с учётом температуры.          

Подтянуть знания по химии можно записавшись на урок к онлайн-репетиторам TutorOnline

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Область науки,
изучающей отношение между теплотой и
работой, получила название термодинамики.
Термодинамика изучает законы превращения
энергии, законы перехода одного вида
энергии в другой. Превращения энергии
подчиняются первому, второму и третьему
началам (законам) термодинамики. Причем,
если первое начало формирует законы
взаимного перехода, то второе и третье
определяет направленность превращения
энергии.

Первое начало
термодинамики представляет собой
всеобщий закон природы – закон
сохранения энергии, открытый М.В.
Ломоносовым в 1758 году. Затем он нашел
свое развитие в трудах таких ученых как
Г.И. Гесс, Д.Джоуль, Р. Майер, Г. Гельмгольц.
Наиболее общей формулировкой закона
сохранения энергии является следующая:

Общая
сумма энергии материальной системы
остается постоянной независимо от
изменений, происходящих в ней.

Математически
этот закон выражается уравнением:

 Е = const,

где Е – энергия,
 — сумма, const
– сокращенное constans –
постоянный, неизменный.

Из этого закона
следует, что энергия данной системы
не исчезает и не появляется вновь, а
только переходит из одной формы в другую
в строго эквивалентных количествах.
Это и есть современная формулировка
первого начала термодинамики.

Первое начало
термодинамики устанавливает связь
между количеством энергии, полученной
или выделенной системой в каком-либо
процессе в виде теплоты Q,
количеством произведенной или полученной
работы W и изменением
внутренней энергии системы U:

U
= W ± Q,

Внутренняя энергия
(U) является полной энергией
системы и представляет собой сумму
потенциальной и кинетической энергий
всех составляющих частей системы
(молекул, атомов, ионов и пр.) за исключением
потенциальной и кинетической энергии
самой системы, как материального тела.
Данное уравнение является математическим
выражением первого начала термодинамики.

Если процесс
изохорный, т.е. если он совершается при
постоянном объеме (V =
const), то работа не совершается,
поскольку при V = const,
V = 0
и, следовательно:

W =
-P V
= 0

Знак минус в этом
уравнении указывает на то, что система
работает против сил внешней среды. В
этом случае:

U
= Q_
,

где Q_v
— количество энергии (Дж/моль или
кал/моль), выделенной или поглощенной
системой в виде теплоты в ходе процесса
при постоянном объеме. Теплота процесса
равна изменению внутренней энергии
системы и зависит только от конечного
и начального состояния системы, т.е.

U₂
– U₁ = U
= Q_

В
реальной жизни часто встречаются
изобарные процессы, протекающие при
постоянном давлении (Р = const),
например, химические реакции, идущие
при атмосферном давлении. Изменение
внутренней энергии систе­мы в этом
случае будет равно

U
= U₂ – U₁
= W + Q_p

где Q_p
— количество энергии (Дж/моль или
кал/моль), выделенной или поглощенной
системой в виде теплоты в ходе процесса
при постоянном давлении. Поскольку в
ходе процессов, идущих при Р = const
объем системы изменяется, то работа в
таких процессах будет равна величине

W =
-P (V₂
— V₁)

Отсюда:

U₂
– U₁ = Q_p
– P(V₂
— V₁).

В результате
тепловой эффект процесса, протекающего
при Р = const
будет равен Q_p
= U₂
– U₁
+ P
(V₂
— V₁)

Q_p
= (U₂
+ PV₂)
– (U₁
+ PV₁).

Величина (U
+ PV)
обозначается буквой Н и называется
энтальпией. Энтальпия, также как
внутренняя энергия, является функцией
состояния, т.е. изменение энтальпии
(Н = H₂
– Н₁) при переходе системы из
состоя­ния 1 в состояние 2 при постоянном
давлении не зависит от пути пере­хода,
а зависит только от величин энтальпии
в конечном (2) и началь­ном (1) состояниях.
Таким образом, тепловой эффект процесса,
идущего при постоянном давлении будет
равен:

Q_p
= H₂ – Н₁ = Н

Следует отметить,
что физико-химический смысл функций
“внутренняя энергия” и “энтальпия”
одинаков. Термин “внутренняя энергия”
используется для энергетической
характеристики процессов, идущих при
V = const, а
“энтальпия” – для процессов, идущих
при P = const.
При этом для конденсированных систем
Н = U,
для газов Н ≠ U.

Первое начало
термодинамики дает только энергетическую
оценку процессов, протекающих при
постоянном объеме или постоянном
давлении, но не дает никаких указаний
о направлении процесса и предела, до
которого изучаемый процесс может идти
самопроизвольно. На эти вопросы
отвечает второе начало термодинамики
посредством новой термодинамической
функции, которая называется энтропия
и обоз­начается буквой S.

Наблюдения и опыт
показывают, что процессы, происходящие
в природе, идут в определенном направлении.
Жидкость течет от высокого уровня к
низкому, вещество диффундирует из
области большей концентрации к меньшей,
теплота переходит от тела с более высокой
температурой к телу с менее высокой и
т.д. Все эти процессы происходят
самопроизвольно. Второе начало
термодинамики гласит:

Каждая материальная
система сама по себе стремится к состоянию
термодинамического равновесия.

Таким
образом, второй закон термодинамики
ограничивает превращение энергии в
материальной системе. Клаузиус, подобно
Ломоносову, так формулирует второе
начало термодинамики: теплота
не может сама собой перейти от тела
менее нагретому к телу более нагретому.

В современной
трактовке второе начало термодинамики
звучит таким образом:

Энергия
самопроизвольно перемещается от системы
с более высоким потенциалом к системе
с более низким потенциалом энергии того
же вида, до тех пор, пока не наступит
термодинамическое равновесие.

Изменение
энтропии равно тепловому эффекту
про­цесса, деленному на абсолютную
температуру, при которой он происхо­дит,
и измеряется в
.
Для обратимых
изотермических превращений изменение
энтропии равно

∆ S
=
,

где Q_обр
– часть общего количества энергии,
выделенной системой в виде тепла. Таким
образом, если S
= 0, то процесс обратимый. Данное уравнение
является математическим выражением
второго начала термодинамики для
обратимых процессов, происходящих в
изолированной системе.

Для необратимых
химических процессов, протекающих в
изолированной системе, второе начало
термодинамики имеет следующий вид:

∆ S
>

Таким образом,
если в изолированной системе протекает
самопроизвольный (необратимый) процесс,
то S
> 0.

Процессы, для
которых

∆ S
<

самопроизвольно
осуществляться в изолированной системе
при постоянной температуре не будут.
Энтропия как критерий направленности
самопроизвольных (необратимых) процессов
может быть использована только для
характеристики процессов в изолированных
системах.

Физический смысл
энтропии сводится к характеристике
меры хаоса (беспорядка) в системе. Чем
больше изменение энтропии в системе,
тем меньше полезной работы может
совершить данная система.

Изолированная
система является идеальным случаем,
т.е. такая система не взаимодействует
с окружающей средой ни путем обмена
энергией, ни путем обмена веществом.
Реальные термодинамические системы
являются либо закрытыми (могут обмениваться
с окружающей средой энергией), либо
открытыми (могут обмениваться с окружающей
средой и энергией, и веществом). Для
указания на направленность самопроизвольного
процесса в таких системах используется
другая термодинамическая функция —
свободная энергия Гиббса (G).

Термодинамическая
функция G = H
— TS
называется свободной энергией Гиббса,
или изобарно-изотермическим потенциалом,
или полезной работой. Используется для
характеристики системы с точки зрения
совершения полезной работы, а также для
указания на направленность самопроизвольных
процессов, идущих при Р = const
и Т = const. В случае
самопроизвольных (необратимых) процессов
G <
0, Если в ре­зультате процесса G
увеличивается (G
> 0), то такой процесс идет самопроизвольно
в обратном направлении. В обратимых
процессах в момент достижения равновесия
G = 0.

Термохимия —
это раздел термодинамики, в котором
изучаются химические реакции с точки
зрения их тепловых эффектов. Рассмотрим
закрытую термодинамическую систему, в
которой происходит химическая реакция

аА + вВ = сС + dD.

В начальном
состоянии такая система имеет запас
внутренней энергии U₁,
(а) молей реагента А и (в) молей реагента
В. В конечном состоянии, т.е. после
прохождения реакции, система будет
иметь запас внутренней энергии U₂,
(с) молей продукта С и (d) молей продукте
D. Тепловым эффектом
реакции будет называться количество
энергии, которая выделяется либо
поглощается в форме тепла при
взаимодейст­вии реагентов А и В с
образованием продуктов С и D
с учетом стехиометрических коэффициентов
реакции. В зависимости от условий, в
которых будет протекать химическая
реакция (либо V = const,
либо Р = сonst), тепловым
эффектом реакции будет либо Q_v
= U,
либо Q_p
= Н.

Чтобы сравнить
между собой тепловые эффекты разных
реакций, необходимо указать точные
условия, при которых они протекают. В
термодинамике и термохимии за стандартные
условия приняты Р = 1 атм и

Т = 298ºК, при этом
вещество в этих условиях должно находиться
в наиболее устойчивом агрегатном
состоянии. Для реакций, проходящих в
стандартных условиях, изменение энтальпии
обозначается символом Н⁰_298K.

Для реакций,
протекающих в газовой фазе, было
установлено соотношение между Q_p
и Q_:

Q_p
= Q_v
+ nRT.

Это соотношение
устанавливает связь между теплотой
реакции при постоянном давлении (Q_p
или Н) и теплотой
реакции при постоянном объеме (Q_v
или U),
является следствием из закона Джоуля.
В данном уравнении n
— разность между числом молей образовавшихся
газообразных продуктов и числом
молей газообразных реагентов, т.е.
n
= n_{газовых продуктов}
– n_{газовых реагентов}.
Для реакций в конденсированных фазах
(твердых и жидких), объем которых в ходе
реакции практически не изменяется, т.е.
n
= 0, Н практи­чески
не отличается от U.
В этих случаях справедливы равенства

Q_p
= Q_v
и H
= U

Реакции, в результате
которых вещество получается из элементов,
называются реакциями образования.
Изменение энтальпии в ходе таких реакций
называется энтальпией образования
данного соединения. Не все реакции
образования можно реализовать практически.
Например, реакция

2С + 3H₂
+ 1/2O₂ = C₂H₅OH

теоретически
является реакцией образования, но
практически самопро­извольно не
идет. Реакция

С + О₂ = СО₂

тоже
является реакцией образования, но в
отличие от первой, она достаточно легко
может быть проведена практически.

Стандартной
энтальпией образования химического
соединения называется изменение
энтальпии в ходе реакции образования
1 моль данного соединения из элементов
в стандартных условиях и обозначается
сим­волом
.

В ходе реакций
образования тепловой эффект представляет
собой именно стандартную энтальпию
образования соединений, потому что
стандартная энтальпия образования
самих элементов принята рав­ной нулю
(_{(элементов)}
= 0).

Знание стандартных
энтальпий образования позволяет
рассчитать тепловой эффект любой
химической реакции (Q_p
= H)
не прибегая к экспериментальным
измерениям. Из элементов можно: 1) получить
непо­средственно продукты. Соответствующее
изменение энтальпии этой реакции будет
равно
_{(продуктов)}.
Из элементов можно: 2) получить реагенты.
Эта реакция сопровождается изменением
энтальпии
_{(реагентов)}.
И, наконец, 3) из реагентов можно получить
продукты. Изменение энтальпии в ходе
этой реакции будет равно Н.
Если эти три процесса проходили в
стандартных условиях, то термоди­намический
баланс этих реакций будет равен:

Н⁰_298K
= _{298К
(продукты)} — _{298К
(реагенты)}

Таким
образом, стандартная энтальпия химической
реакции равна разности сумм стандартных
энтальпий образования всех продуктов
и всех реаген­тов. Так записывается
математически закон Гесса.

Если из данных
исходных реагентов можно различными
путями полу­чить одни и те же конечные
продукты, то, независимо от путей
получе­ния продуктов, т.е. от вида и
количества промежуточных реакций,
суммарный тепловой эффект для всех
путей будет одним и тем же. Иначе говоря,
тепловой эффект химической реакции
не зависит от пути перехода «реагенты
— продукты», т.е. от промежуточных
реакций, а зависит только от вида и
состояния продуктов и реагентов. Это
положение было постулировано русским
ученым Г.И. Гессом в 1840 году и известно
как закон Гесса, являющийся основ­ным
законом термохимии.

Следствия из закона
Гесса:

1. Закон
   Лавуазье-Лапласа. Тепловой эффект
   реакции разложения точно равен и
   противоположен по знаку тепловому
   эффекту реакции соединения.

Пример:

Са +
О₂
= СаО + 634,71 кДж

СаО = Са +
О₂
— 634,71 кДж

Q_разл
+ (-Q_соед ) = 0.

1. Если совершаются
   две реакции, приводящие из различных
   начальных состояний к одинаковым
   конечным, то разница между тепловыми
   эффектами представляет тепловой эффект
   перехода из одного начального состояния
   в другое.

Пример:

С + О₂ = СО₂
+ 409,20 кДж (1)

СО + ½ О₂ = СО₂
+ 284,93 кДж (2)

Вычитая из (1)
уравнение (2), можно вычислит тепловой
эффект реакции сжигания углерода до
окиси углерода:

С + ½ О₂ = СО
+ 124,27 кДж

Таким образом,
можно определять тепловые эффекты таких
реакций, которые или нереализуемы, или
не могут быть проведены чисто и до конца.

1. Если совершаются
   две реакции, приводящие из одинаковых
   начальных состояний к различным
   конечным, то разница между тепловыми
   эффектами представляет тепловой эффект
   перехода из одного конечного состояния
   в другое.

Пример:

С_уг + О₂
= СО₂ + 409,20 кДж

С_гр + О₂
= СО₂ + 393,51 кДж

Таким образом,
можно рассчитать тепловой эффект
перехода от угля к графиту, который
будет равен 409,00 – 393,51=15,69 кДж/моль.

1. ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА

ТИХООКЕАНСКИЙ ГОСУДАРСТВЕНЫЙ УНИВЕРСИТЕТ
КАФЕДРА ХИМИИ
В.А. Яргаева
ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
Мультимедийные лекции по физической химии
@ В.А. Яргаева
Хабаровск
2016

2. Содержание

1. I закон термодинамики, его
применение для расчёта тепловых
эффектов.
2. II и III законы термодинамики.
Энтропия и её расчёт в различных
процессах.
3. Энергия Гиббса, энергия
Гельмгольца, их практическое
значение.

3. Библиографический список

1. Стромберг А. Г. Физическая химия / А. Г. Стромберг, Д.
П. Семченко – М.: Высш. шк., 2001. – 527 с.
2. Эткинс П. Физическая химия. В 3-х ч. Ч. 1.: Равновесная
термодинамика / П. Эткинс, Дж. де Паула. – М.: Мир, 2007.
– 494 с.
3. Евстратова К. И. Физическая и коллоидная химия / К. И.
Евстратова, Н. Н. Купина, Е. Е. Малахова. – М.: Высш.
шк., 1990. – 487 с.
4. Краткий справочник физико-химических величин / Под
ред. А. А. Равделя, А. М. Пономаревой. – СПб., 2003. – 238 с.
5. Химия – Википедия. [Электронный ресурс] – Режим
доступа: https://ru.wikipedia.org/wiki/Химия.
6. Презентации по химии. [Электронный ресурс] – Режим
доступа: https:// 900igr.net/prezentacii-po-khimii.html

4. I закон термодинамики, его применение для расчёта тепловых эффектов

1.
2.
3.
4.
5.
Основные понятия термодинамики.
I закон (начало) термодинамики.
Закон Гесса, следствия из закона.
Расчёт тепловых эффектов различных процессов.
Влияние температуры на величину теплового эффекта.

5. Предмет термодинамики

Термодинамика изучает положения и законы,
описывающие обмен энергией между изучаемой системой
и внешней средой, превращения одних форм энергии в
другие.
Химическая термодинамика применяет законы и
положения общей термодинамики к изучению
химических и физико-химических процессов, например,
определению теплового эффекта, направления
протекания процесса и др.
Термодинамика (Т/Д) базируется на трёх началах или
законах термодинамики (постулатах), установленных на
основе анализа множества экспериментальных данных.

6. Основные понятия термодинамики

Система (С.) − тело или группа тел, находящихся во
взаимосвязи и мысленно обособленных от окружающей среды.
Окружающая среда (обычно большого размера) − всё, что
находится в прямом или косвенном контакте с системой.
С. изолированная − не обменивается веществом и энергией с
окружающей средой.
С. открытая − обменивается веществом и энергией с
окружающей средой.
С. закрытая − не обменивается веществом, но обменивается
энергией с окружающей средой.
С. гомогенная − состоит из одной фазы.
С. гетерогенная − состоит из двух и более фаз.

7. Основные понятия термодинамики

Фаза − часть системы, одинаковая по составу, физическим
и химическим свойствам и отделённая от других частей
системы видимой поверхностью раздела.
Компоненты − вещества, из которых состоит система.
Состояние системы − совокупность физических и
химических свойств, характеризующих систему.
Термодинамические (Т/Д ) параметры:
T – температура;
P – давление;
V – объём;
C – состав (концентрация).

8. Основные понятия термодинамики

Т/Д параметры − характеризуют состояние системы.
Различают экстенсивные параметры (аддитивны):
m – масса; V – объём; U – внутренняя энергия и др.,
и интенсивные параметры (не обладают свойством
аддитивности, при контакте систем выравниваются):
T – температура; P – давление; C – концентрация и др.
Термодинамический (Т/Д) процесс − всякое изменение
в системе, связанное с изменением хотя бы одного
параметра.
Различают круговой, изобарный (Р = const), изохорный (V =
const), изотермический (T = const), адиабатический
(Q(теплота) = const) и др. процессы.

9. Основные понятия термодинамики

Функции состояния (U, H, S, G, A) − Т/Д функции,
значения которых зависят только от начального и
конечного состояний системы и не зависят от пути
процесса.
Стандартное состояние − при Р = 101325 Па и любой Т.
Стандартные условия − при Р = 101325 Па и Т = 298 К.
Обратимый Т/Д процесс − равновесный, протекает
бесконечно медленно, без изменений в окружающей среде.
Необратимый Т/Д процесс − неравновесный, в
результате его протекания происходят энергетические
изменения в окружающей среде.

10. I закон (начало) термодинамики (закон сохранения энергии)

— В любой изолированной системе общий запас энергии
постоянен.
— Разные формы энергии переходят друг в друга в строго
эквивалентных количествах.
— Вечный двигатель первого рода невозможен, т. е.
невозможно построить машину, которая давала бы
механическую работу без подвода энергии извне.
Теплота Q, полученная системой извне, расходуется на
изменение внутренней энергии U и работу W.
Математическая формулировка I
закона термодинамики
Q = U + W
Для физико-химических процессов:
dW = PdV или W = Р V – работа расширения
Q = U + Р V

11. I закон термодинамики

Внутренняя энергия U –
общий запас энергии
системы, которая
складывается из
кинетической и
потенциальной энергии всех
частиц системы и энергии их
взаимодействий – функция
состояния (U определить
невозможно, определяют U).
U = U2 – U1
Теплота Q и работа W не
являются функциями
состояния.
Теплота Q –
энергия,
предаваемая за
счёт
хаотического
столкновения
молекул
Работа W –
энергия,
передаваемая
за счёт
перемещения
частиц под
действием
каких-либо сил
Рис. из [2]

12. Применение I закона термодинамики

Термохимия – раздел, посвящённый изучению тепловых
эффектов химических и физико-химических процессов.
Тепловой эффект – теплота, выделяемая или
поглощаемая в результате протекания процесса.
Q = U + Р V (I закон Т/Д для физико-химических процессов)
Изохорные процессы (V = const): V= 0; Q = U;
U (изменение внутренней энергии) – изохорный тепловой
эффект.
Изобарные процессы (Р = const): H = U + PV; Q = H;
H (изменение энтальпии) – изобарный тепловой эффект.
Энтальпия Н – функция состояния, как и внутренняя энергия
характеризует общий запас энергии системы (включает энергию,
которая тратится на работу расширения).

13. Применение I закона термодинамики

В термодинамике теплота, поглощённая системой,
считается положительной, а выделенная – отрицательной!
Эндотермический
процесс
(с поглощением
теплоты)
Эндотермический процесс
CaCO3(к) → CaO(к) + CO2(г)
H = 178 кДж/моль,
U > 0; H > 0.
поглощается 178 кДж теплоты
Экзотермический
процесс
(с выделением
теплоты)
Экзотермический процесс
C(графит) + O2(г) → CO2(г)
H = – 394 кДж/моль,
U < 0; H < 0.
выделяется 394 кДж теплоты

14. Применение I закона термодинамики

Связь между изобарным и изохорным тепловыми эффектами:
H = U + Р V или H = U + nRT
(следует из уравнения Менделеева-Клапейрона Р V = nRT)
n – изменение числа моль газообразных веществ в результате
протекания реакции (процесса); R = 8,314 Дж/(моль· К).
Пример 1: Определить n в реакциях:
а) 2NO2(г) + O3(г) = O2(г) + N2O5(г);
б) CH4(г) + 2H2S(г) = CS2(ж) + 4H2(г);
в) 2CrCl3(к) + 3H2(г) =2Cr(к) + 6HCl(г).
Решение. а) n = (1 + 1) – (2 + 1) = – 1; б) n = 4 – (1 + 2) = 1;
в) n = 6 – 3 = 3.
При расчёте n число моль жидких и твёрдых веществ
не учитывают!

15. Применение I закона термодинамики

Закон Гесса
Стандартная энтальпия сложной реакции
(тепловой эффект) равна сумме
стандартных энтальпий (тепловых
эффектов) простых реакций, на которые
может быть разбита эта реакция.
Н1 = Н2 + Н3 = Н4 + Н5 + Н6
Герман Иванович
Гесс,
русский химик
(1802-1850).

16. Применение I закона термодинамики

Расчёты любого процесса основаны на свойстве
энтальпии являться функцией состояния!
1) Расчёт тепловых эффектов химических реакций r 0
или процессов, например, фазовых переходов trs 0: плавления,
испарения и др.
Для расчёта необходимы стандартные энтальпии (теплоты)
образования веществ f 0(298) – справочные величины.
f 0(298), кДж/моль – это тепловой эффект образования 1 моль вещества
из простых веществ, устойчивых при стандартных условиях
(Т = 298 К; Р = 101325 Па).
f 0 для устойчивых простых веществ принимают равной нулю.
Например, для углерода устойчивой формой считают графит.
f 0(С(графит)) = 0, но f 0(С(алмаз)) = 1,83 кДж/моль.
r 0 – стандартная энтальпия химической реакции (тепловой
эффект химической реакции при стандартном давлении и данной
температуре).

17. Применение I закона термодинамики

trs 0 – стандартная энтальпия фазового перехода (тепловой
эффект фазового перехода при стандартном давлении и данной
температуре).
Следствия из закона Гесса:
1) Тепловой эффект реакции (процесса) равен разности суммы энтальпий
(теплот) образования продуктов реакции (процесса) и суммы
энтальпий (теплот) образования исходных веществ с учётом
стехиометрических коэффициентов в уравнении реакции (процесса).
r 0 = i f 0(прод) – i f 0(исх) или
trs 0 = i f 0(кон) – i f 0(исх),
прод (кон) – продукты реакции (конечные вещества);
исх – исходные вещества;
i – стехиометрические коэффициенты в уравнении реакции (процесса).
r 0 рассчитывают, по уравнению, записанному в особой
термодинамической (термохимической) форме.

18. Применение I закона термодинамики

Особенности термодинамического уравнения:
Указываются агрегатные состояния веществ.
Допускаются дробные коэффициенты.
С термодинамическими уравнениями можно выполнять такие же
действия, как с любыми математическими уравнениями.
Для реакций, протекающих в водных растворах электролитов с участием
ионов, тепловые эффекты рассчитывают таким же способом,
используя стандартные энтальпии образования ионов в водных
растворах (справочные величины).
—
2) Тепловой эффект прямой реакции (процесса) равен тепловому эффекту
обратной реакции (процесса) с противоположным знаком
r (прямой) = – r (обратной),
trs (испарения) = – trs (конденсации),
trs (плавления) = – trs (кристаллизации).

19. Применение I закона термодинамики

Пример 2.
Определить при Т = 298 К тепловой эффект реакции разложения
воды по уравнению
2H2О(г) = 2Н2(г) + О2(г),
если известно, что для реакции
Н2(г) + 0,5О2(г) = H2О(г), r = –241,81 кДж.
Решение.
Если удвоить коэффициенты второго уравнения, то полученное
уравнение реакции
2Н2(г) + О2(г) = 2H2О(г)
отражает реакцию получения 2-х моль воды. Она является обратной для
реакции разложения 2-х моль воды. Откуда,
r (прямой) = – 2 r (обратной) = – 2· (–241,81) = 483,62 кДж.
Так как r > 0, реакция разложения воды является эндотермической,
т. е. протекает с поглощением теплоты.

20. Применение I закона термодинамики

Для реакций с участием органических веществ тепловой эффект
можно рассчитывать по стандартным энтальпиям
(теплотам) сгорания с 0 (справочные величины) – это
тепловые эффекты полного окисления 1 моль органических
соединений с образованием определённых продуктов: СО2(г), Н2О(ж),
N2(г), HCl(г), HBr(г), НI(г).
Например, с 0(C6H5О2N(ж)) представляет собой тепловой эффект
реакции
C6H5О2N(ж) + 6,25О2(г) = 6СО2(г) + 2,5Н2О(ж) + 0,5N2(г).
Из справочной таблицы с 0(C6H5О2N(ж)) = –3091,2 кДж/моль.
Расчёт тепловых реакций по теплотам сгорания проводят по формуле
r 0 = i с 0(исх) – i с 0(прод),
исх – исходные вещества; прод – продукты реакции;
i – стехиометрические коэффициенты в уравнении реакции.

21. Применение I закона термодинамики

2) Тепловые эффекты процессов растворения
Интегральная энтальпия (теплота) растворения s 0 зависит
от моляльной концентрации вещества в растворе.
s 0 ( m), кДж/моль – теплота, которая выделяется или поглощается
при растворении 1 моль вещества в таком количестве растворителя,
чтобы образовался раствор определённой моляльной концентрации
(справочная величина).
3) Расчёт тепловых эффектов процессов разбавления или
концентрирования
Для расчёта необходимы величины интегральных энтальпий (теплот)
растворения исходных и конечных растворов.
Тепловым эффектом разбавления (концентрирования) называют теплоту
, которая выделяется или поглощается при разбавлении
(концентрировании) раствора, содержащего 1 моль растворённого
вещества, от концентрации Сm(1) до концентрации Сm(2).
Раствор 1(Сm(1)) → Раствор 2(Сm(2))
= s 0(2) – s 0(1) или = m(2) – m(1).

22. Влияние температуры на тепловой эффект (уравнение Кирхгофа)

Характер влияния температуры на тепловой
эффект в соответствии с уравнением Кирхгофа
определяется знаком
изменения молярной теплоёмкости
СР (изобарной) или СV (изохорной)
в результате протекания
соответствующего процесса.
Уравнение Кирхгофа
в дифференциальной
форме
Густав Роберт
Кирхгоф,
немецкий физик
(1824-1887)

23. Анализ уравнения Кирхгофа

1) если СР > 0, то d /dТ > 0, т. е. с увеличением
температуры тепловой эффект увеличивается;
2) если СР < 0, то d /dТ < 0, т. е. с увеличением
температуры тепловой эффект уменьшается;
3) если СР = 0, то d /dТ = 0, = const, тепловой эффект
не зависит от температуры.

24. Расчёт теплового эффекта при любой температуре

Уравнение Кирхгофа
в интегральной форме
r 298 = i f 0(прод) – i f 0(исх),
СР = i СР(прод) – i СР(исх),
i – стехиометрические коэффициенты в уравнении реакции;
СР = a + bT + c’/T2 – изобарная молярная теплоёмкость для
неорганических веществ, уравнение зависимости СР от
температуры;
СР = a + bT + cT2 – изобарная молярная теплоёмкость для
органических веществ, уравнение зависимости СР от температуры;
а, b, c’, c – эмпирические коэффициенты веществ (справочные
величины в указанном интервале температур).

25. Расчёт теплового эффекта при любой температуре

Расчёт r Т с различными приближениями
Первое приближение: СР = С0Р,298;
С0Р,298 – стандартная изобарная молярная теплоёмкость
(справочная величина).
С0Р,298 = i С0Р,298(прод) – i С0Р,298(исх).
Второе приближение: СР = a + bT;
Третье приближение: СР = a + bT + c’/T2 + cT2
– наиболее точный расчёт.
а = iаi(прод) – iаi(исх).
Расчёт b, c’, c – аналогичен.
i – стехиометрические коэффициенты в уравнении
реакции.

26. Влияние температуры на тепловой эффект

Пример 3.
Определить тепловой эффект реакции
С2Н5ОН(г) + 3О2(г) = 2СО2(г) + 3Н2О(г)
при температурах 298 и 800 К.
Решение.
Для расчета r при 298 К находим справочные значения стандартных
энтальпий образования (кДж/моль) веществ-участников реакции:
f 0(С2Н5ОН(г)) = – 234,80; f 0(СО2(г)) = – 393,51;
f 0(Н2О(г)) = –241,81; для простого вещества О2 f 0(О2(г)) = 0.
r 298 = i f 0(прод) — i f 0(исх) =
(2 fH0(СО2) + 3 fH0(Н2О)) – ( fH0(С2Н5ОН) + 3 fH0(О2)) =
(2·(–393,51) + 3·(–241,81)) – ((–234,80) + 3·0) = –1277,62 кДж.
Т. к. r 298 < 0, реакция экзотермическая, протекает с выделением
теплоты.
Для расчета r при 800 К используем уравнение Кирхгофа и первое
приближение при определении СР:
СР = С0Р,298 = iС0Р,298(прод) – iС0Р,298(исх) = const.

27. Влияние температуры на тепловой эффект (уравнение Кирхгофа)

r Т = r 298 +
= r 298 + СР,298· (Т – 298).
Для расчета СР,298 выпишем справочные значения стандартных
изобарных молярных теплоёмкостей (Дж/(моль·К)) веществучастников реакции:
СР,298 (С2Н5ОН(г)) = 65,75; СР,298 (СО2(г)) = 37,11; СР,298 (О2(г)) = 29,37;
СР,298(Н2О(г)) = 33,61.
СР,298 = (2СР,298(СО2) + 3СР,298(Н2О)) – (СР,298(С2Н5ОН) + 3СР,298(О2)) =
= (2·37,11 + 3·33,61) – (65,75 + 3·29,37) = 21,19Дж/К = 0,02119 кДж/К.
Рассчитаем r Т при Т = 800 К.
r 800 = –1277,62 + 0,02119 · (800 – 298) = –1266,98 кДж.
При 800 К реакция по-прежнему – экзотермическая, но теплоты
выделится несколько меньше, чем при 298 К.

28. Качественная оценка тепловых эффектов различных процессов

С выделением теплоты ( rH < 0, trs < 0, s < 0) протекают:
– реакции горения (взаимодействие веществ с кислородом), например,
C2H4(г) + 3O2(г) = 2CO2(г) + 2H2O(г);
– реакции соединения (образование сложных веществ из более
простых), например,
2C(графит) + 3H2(г) = C2H6(г);
– процессы растворения кислот и щелочей в воде, например,
Н2SO4 + nН2O = 2Н+ ·aq + SO42− ·aq (aq — молекулы Н2O);
– процессы конденсации и кристаллизации, например,
H2O(г) = H2O(ж).
С поглощением теплоты ( rH > 0, trs > 0) протекают:
– реакции разложения (образование простых или менее сложных
веществ из более сложных), например,
CaCO3(к) = CaO(к) + СО2(г);
– процессы испарения и плавления, например,
H2O(к) = H2O(ж).

29. II и III законы термодинамики. Энтропия и её расчёт в различных процессах

1. II закон (начало) термодинамики.
2. Энтропия как критерий протекания
самопроизвольного процесса.
3. Расчёт изменения энтропии в различных процессах.
4. III закон (начало) термодинамики.

30. II закон (начало) термодинамики

I закон термодинамики позволяет определять
теплоту и работу, но не даёт ответа на вопрос: в
каком направлении и до какого предела будет
протекать самопроизвольный процесс. Ответ
на этот вопрос даёт II закон термодинамики.
Формулировка Клаузиуса (1850 г.)
— Теплота не может самопроизвольно
переходить от более холодного тела к
горячему.
Формулировка Томпсона
— Никакая совокупность процессов не
может сводиться только к превращению
теплоты в работу, тогда как
превращение работы в теплоту может
быть единственным результатом
процесса.
Рудольф Клаузиус,
немецкий физик
(1822-1888)
Томас Томпсон,
шотландский химик
(1773-1852)

31. II закон (начало) термодинамики

Формулировка Оствальда
— Невозможно создание вечного
двигателя второго рода, т. е.
невозможно построить машину,
которая превращала бы всю
теплоту в работу без передачи
части её холодильнику.
Формулировка Кельвина
— Не существует циклического
процесса, единственным
результатом которого было бы
получение теплоты от нагревателя
и полное превращение её в работу.
Вильгельм Оствальд,
немецкий физико-химик
(1853-1932)
Томсон Кельвин,
английский физик
(1824-1907)

32. II закон (начало) термодинамики

II закон термодинамики также был установлен как постулат, но в
отличие от I закона имеет более ограниченную область применения,
носит статистический характер, поэтому применим только к
системам, состоящим из большого числа частиц.
Самопроизвольными называют процессы, протекающие без
вмешательства извне (без затраты энергии)
Пример самопроизвольного процесса:
перемешивание газов
Рис. из [6]

33. II закон (начало) термодинамики

Накопленный человечеством опыт показывает, что
самопроизвольное протекание процессов в системе
возможно только в направлении выравнивания фактора
интенсивности (температуры, давления, концентрации и
т. д.). Пределом самопроизвольного протекания процесса
является достижение одинакового значения фактора
интенсивности во всех частях системы.
Но это утверждение не применимо к однородным системам,
в частности, к химическим реакциям.
Это требует введения новой функции состояния –
энтропии.
Её ввёл Р. Клаузиус (1865 г.), обозначил S.

34. II закон (начало) термодинамики

II закон (начало) термодинамики особенно наглядно
проявляется в работе тепловых машин, для которых и
был сформулирован.
В настоящее время этот закон вводят в рассмотрение путём
анализа работы тепловых машин (цикл Карно).
Второй закон термодинамики можно сформулировать
без анализа работы тепловых машин
(принцип Каратеодори).
II закон термодинамики – всеобщий закон природы, по своей
фундаментальности уступающий место только I закону
термодинамики – закону сохранения энергии!

35. II закон (начало) термодинамики

Пусть система переходит из состояния 1 в
состояние 2 с поглощением теплоты.
Предположим, что система может вернуться из
состояния 2 в состояние 1 без теплообмена
(адиабатически). В соответствии с I законом
термодинамики:
Q = U + W(1) (для прямого процесса);
0 = – U + W(2) (для обратного процесса).
В результате кругового процесса: Q = W(1) + W(2), т. е. вся теплота
должна превратиться в работу, а это невозможно согласно I закону
термодинамики.
Принцип Каратеодори: в непосредственной близости от
любого состояния имеются такие состояния, которые
недостижимы адиабатическим путём, т. е. без передачи теплоты.

36. II закон (начало) термодинамики

Из принципа Каратеодори следует утверждение о существовании новой
функции, которая связана с теплотой процесса!
II закон термодинамики – это закон о существовании и
сохранении энтропии S.
Математическое выражение
II закона термодинамики
Знак = – для обратимых Т/Д процессов;
знак > – для необратимых Т/Д процессов.
Математическое выражение
объединённого уравнения I и II
законов термодинамики

37. Энтропия как критерий самопроизвольного протекания процесса

Для изолированных систем (U = const; V = const)
теплообмен и массообмен отсутствует: Q = 0.
Для обратимых процессов: dS = 0; S = 0.
Для необратимых процессов: dS > 0; S > 0.
В изолированной системе всякий самопроизвольный
процесс протекает в направлении возрастания
энтропии:
dS > 0; S > 0; S → Smax;
при dS = 0; S = 0; S = Smax в системе – равновесие.

38. Изменение энтропии в процессах

Энтропия S – мера беспорядка (хаоса) или степень
неупорядоченности системы – функция состояния.
ТS – мера связанной энергии (не может превратиться в
полезную работу).
Всякий процесс, приводящий к увеличению
беспорядка приводит к увеличению энтропии:
— изменение агрегатного состояния т → ж → г;
— повышение температуры;
— усложнение состава вещества;
— растворение твёрдых и жидких веществ;
— в химических реакциях – увеличение числа газообразных
молекул и т. п.

39. Увеличение энтропии в процессах

Изменение агрегатного состояния
вещества: т → ж → г
и увеличение температуры
Смешивание газов

40. Статистическое обоснование II закона термодинамики

Всякая изолированная система
стремится перейти из состояния менее
вероятного в состояние более
вероятное: W → Wmax.
W – термодинамическая вероятность
(число микросостояний,
характеризующих данное
макросостояние).
Л. Больцман показал, что при
W → Wmax; S → Smax.
Уравнение Больцмана
S = k·lnW
k – постоянная Больцмана (1,38· 10−23 Дж/К)
Людвиг Больцман,
австрийский физик
(1844-1906)

41. Расчёт изменения энтропии в различных процессах

1. При фазовом превращении 1 моль вещества (Т = const;
Р = const):
Н(ф.п.) – теплота (энтальпия) фазового превращения;
Т(ф.п.) – температура фазового превращения.
2. При изменении температуры 1 моль вещества (Р = const):
3. При взаимной диффузии двух идеальных газов:
S = – R(x1lnx1 + x2lnx2)
x1, x2 – молярная доля 1-го и 2-го газа.

42. Расчёт изменения энтропии в различных процессах

4. В химических реакциях:
При Т = 298 К
rS 0298 = i S0(прод) – i S0(исх),
S2980, Дж/(моль·К) – абсолютная стандартная энтропия 1 моль
вещества (справочная величина).
При любой Т
СР = i СР(прод) – i СР(исх).
Первое приближение: СР = С0Р,298;
Второе приближение: СР = a + bT;
Третье приближение: СР = a + bT + c’/T2 + cT2 – точный расчёт.
С0Р,298 (а, b, с’, c) – стандартная изобарная молярная теплоёмкость 1 моль
вещества (эмпирические коэффициенты в уравнении для расчёта
изобарной молярной теплоёмкости вещества) – справочные величины.

43. Расчёт изменения энтропии вещества при изменении температуры

Пример 4.
Определить изменение энтропии при охлаждении 320 г моноклинной
серы от 360 0С до 25 0С.
Решение. Выпишем из справочных таблиц температуру плавления
моноклинной серы: Тпл = 119,3 0С.
При 25 0С сера находится в твёрдом (кристаллическом) состоянии,
следовательно, в интервал температур 360-25 0С попадает фазовый
переход: кристаллизация серы. При 360 0С сера находится в жидком
состоянии.
Запишем схему процессов, происходящих с серой S в интервале
температур Т1 − Т2:
Охлаждение
S(ж) →
360 0С
Кристаллизация Охлаждение
S(ж) → S(т)
→ S(т)
119,3 0С
25 0С

44. Расчёт изменения энтропии вещества при изменении температуры

Таким образом, общее изменение энтропии S при охлаждении серы в
интервале температур Т1 − Т2 складывается из изменения энтропии
S1 − при охлаждение жидкой серы; S2 − при кристаллизации серы;
S3 − при охлаждение твёрдой серы.
Для расчёта S выпишем из справочных таблиц теплоту плавления
Нпл, изобарные молярные теплоёмкости в твёрдом СР(т) и жидком
СР(ж) состояниях для моноклинной серы: Нпл = 1,446 кДж/моль;
СР(т) = 23,64 Дж/(моль∙К), СР(ж) = 35,73 Дж/(моль∙К).
Переведём массу серы в количество:
m
320
n=
=
= 10 моль.
M(S)
32
Определим теплоту кристаллизации Нкр:
Нкр = − Нпл = −1446 Дж/моль,
т. к. кристаллизация − процесс, обратный плавлению.
Переведём величины температур из 0С в К:
Т1 = 573 К; Т2 = 298 К; Тпл = Ткр= 392,3 К.

45. Расчёт изменения энтропии вещества при изменении температуры

Рассчитаем изменение энтропии в процессе охлаждения жидкой серы:
Т С
Т
392,3
S1 = ‫׬‬Т кр Р(ж)

Как правильно рассчитывать тепловой эффект реакции, изменение энтропии реакции, костанту равновесия реакции

Вычисление теплового эффекта реакции

Задача 67.
Вычислить тепловой эффект реакции: Al₂O_3(тв.) + 3SO₃ = Al₂(SO₄)_3(тв.) при условии, что она протекает в калориметрической бомбе при постоянном объеме и Т = 298 К.
Решение:
ΔН°Al₂O₃ = -1675,7 кДж/моль;
ΔН°Al₂(SO₄)₃ = -3441,8 кДж/моль;
ΔН°SO₃ = -395,8 кДж/моль 
ΔН = ?
Рассчитаем энтальпию реакции при стандартных условиях, используя следствие из закона Гесса:

ΔН_х.р. = ΔН_{обр.прод.} — ΔН_{обр.исх.}

Тогда 

ΔН°₂₉₈ = ΔH°Al₂(SO₄)₃  — (ΔH°Al₂O₃ — 3ΔH°SO₃) =
= -3441,8 — [-1675,7 + 3(-395,8)] = -578,7 кДж/моль.

Знак минус перед тепловым эффектом означает, что теплота выделяется в результате реакции.

Определение темпрературы начала протекания реакции

Задача 68.
Возможна ли реакция диссоциации углекислого газа при Т = 500 градусов цельсия? И при какой температуре эта реакция может начать протекать?
Уравнение реакции: 2CO₂ = 2CO +  O₂.
ΔH°CO₂ = -393,51  кДж/моль;      
ΔH°CO = -110,53   кДж/моль;
S°СО₂ = 213,66 Дж/(моль·К); 
S°СО = 197,55 Дж/(моль·К);
S°О₂ = 205,04 Дж/(моль·К); 
T =  500 °C = 773 K;       
∆G°₇₇₃ = ?
Решение:
Рассчитаем энтальпию реакции при стандартных условиях, используя следствие из закона Гесса, при этом учитываем, что для простых веществ стандартная теплота образования равна нулю.
Уравнение Гесса:

ΔН_х.р. = ΔН_{обр.прод}. — ΔН_{обр.исх.}

Тогда 

ΔН°₂₉₈ = 2ΔH°СО  — 2ΔH°CО₂) =
= 2(-110,53) — 2(-393,51) = 565,96 кДж/моль.

Знак плюс перед тепловым эффектом означает, что теплота поглощается в результате реакции.
Расчет энтропии будем вести по формуле Гесса:

∆S°_х.р. = ∑S°_{(обр.прод.)} — ∑S°_{(обр.исх.)}.

Подставив найденные значения энтропий в искомое уравнение, и произведя расчеты, получим:

∆S°х.р. = (2S°СО + S°O₂) — 2S°CO₂ = 
= [(2 ^. 197,55) + 205,04] — (2 ^. 213,66) = 172,82 Дж/(моль ^. К).

Теперь находим ∆G°773х.р., выражая ∆S°х.р. в кДж/(моль·К):

∆G°₇₇₃ = ΔН°₂₉₈ — Т∆S°_х.р.;
∆G°_773х.р. = [565,96 — 773(172,82 ^. 10-3)] = 432.37014 кДж/моль.

Т.к. ∆G°_773х.р. > 0, то реакция при 773 К не может протекать самостоятельно.

Рассчитаем температуру начала реакции, т.е. состояние равновесия её, получим.

В состоянии равновесия:

∆G = 0 и ∆H = T∆S.

Тогда

Т = ∆H/∆S;
Т = (565,96 кДж/моль)/(172,82 ^.10-3 кДж/моль·К) = 3274,85 K или приблизительно 3000 °С.

Причины изменения энтропии в ходе реакции

Задача 69.
Сколько тепла выделится при сгорании 50 г бензола в стандартных условиях? Подробно объясните причины изменения энтропии в ходе прямой реакции.
Решение:
m(С₆Н₆) = 50 г;
M(С6Н6) = 78,11 г/моль;
∆H°С₆Н_6(ж) = 49,03 кДж/моль;
∆H°СO_2(г) = -393,51 кДж/моль;
∆H°Н₂О_(ж) = -285,83 кДж/моль;
S°С₆Н_6(ж) = 172,8 Дж/(моль ^. K);
S°СO_2(г) = 213,67 Дж/(моль ^. K);
S°Н₂О_(ж) = 70,08 Дж/(моль ^. K);
S°O_2(г) = 205,04 Дж/(моль ^. K);
Q_p = ?
∆S° = ?
Уравнение реакции горения бензолы имеет вид:

С₆Н_6(ж) + 3,5О₂ =  2СО₂ + 3Н₂О_(ж), Q. 

Рассчитаем энтальпию реакции при стандартных условиях, используя следствие из закона Гесса, при этом учитываем, что для простых веществ стандартная теплота образования равна нулю.
Уравнение Гесса:

ΔН_х.р. = ΔН_{обр.прод.} — ΔН_{обр.исх.}

Тогда 

ΔН°₂₉₈ = 3ΔH°Н₂О_(ж) + 2∆H°СO₂ — ∆H°С₆Н_6(ж) =
= 3(-285,83) + 2(-393,51) — 49,03 = -1595,01 кДж/моль;
Q = -ΔН_х.р. = 1595,01 кДж.

Знак минус перед тепловым эффектом означает, что теплота выделяется в результате реакции.

Тогда

Q_p = [m(С₆Н₆) ^. (-ΔН_х.р.)]/M(С₆Н₆) = (50 ^. 1595,01)/78,11 = 1021 кДж.

Изменение энтропии химического процесса (ΔS°) определяется как разность сумм энтропий продуктов реакции и реагентов с учетом их стехиометрических коэффициентов в уравнении реакции. Расчет энтропии будем вести по формуле Гесса:

∆S°_х.р. = ∑S°_{(обр.прод.)} — ∑S°_{(обр.исх.).}

Подставив найденные значения энтропий в искомое уравнение, и произведя расчеты, получим:

∆S°_х.р. = [3S°Н₂О_(ж) + 2S°CO_2(г)] — [S°С₆Н_6(ж) + 3,5S°O2(г)] = 
= [(3 ^.70,08) + (2 ^. 213,67)] — [172,8 + (3,5 ^. 205,04] = -254.12 Дж/(моль ^. К).

Так как общее число молей газообразных веществ уменьшается (3,5VО₂) исходных газообразных веществ и (2VСО₂) газообразных продуктов), то система переходит из менее упорядоченного состояния в более упорядоченное, поэтому ∆S° < 0.
Если энтальпия ΔН° < 0 и энтропия ∆S°  < 0, то процесс возможен при условии, что член (ΔН°) в уравнении для энергии Гиббса (∆G =  ∆H — T∆S) больше по абсолютному значению, чем член (T∆S°); поскольку абсолютное значение члена(T∆S°) с ростом множителя (Т) увеличивается, то указанное условие будет осуществляться при достаточно низких температурах, возможно и в стандартных условиях. 

Расчет стандартной энтальпии образования оксида фосфора (V)

Задача 70.
При окислении 12,4 г фосфора выделилось 306 кДж теплоты. Рассчитайте стандартную энтальпию образования оксида фосфора (V).
Решение:
m(P) = 12,4 г;
Q = 306 кДж;
∆H = ?
Уравнение реакции имеет вид:

2Р + 5/2О₂ = Р₂О₅, Q

Из уравнения реакции вытекает, что при окислении 2 моль Р образуется 1 моль Р₂О₅, т.е. 2n(P) = n(Р₂О₅).
Рассчитаем количество окислившегося фосфора, получим:

n(P) = m(P)/M(P) = 12,4/31 = 0,4 моль.

Рассчитаем стандартную энтальпию образования оксида фосфора (V), получим:

0,4 моль : 306 кДж = 2 моль : х;
х = (306 кДж ^. 2 моль)/0,4 моль = 1530 кДж;
Q_р = 1530 кДж;
∆H = -Q_р = 11530 кДж/моль.

Расчет константы равновесия реакции (н.у.), зная значение энергии Гиббса

Задача 71.
Определите возможность протекания реакции при стандартных условиях. Если реакция возможна, то рассчитайте константу её равновесия. Как нужно изменить температуру проведения реакции, чтобы увеличить выход продуктов реакции. Дайте обоснованный ответ. Уравнение реакции имеет вид:
4HCl_(г) + O_2(г) = 2H₂O_(ж) + 2Cl_2(г).
Решение:
∆H°HC_l(г) = -92,31 кДж/моль;
∆H°H₂O_(ж) = -285,83 кДж/моль;
S°HCl_(г) = 186,79 Дж/(моль ^. К);
S°H₂O_(ж) = 70,08;
S°O_2(г) = 205,04 Дж/(моль ^. К);
S°Cl_2(г) = 222,98 Дж/(моль ^. К);
Кр = ?
Рассчитаем энтальпию реакции при стандартных условиях, используя следствие из закона Гесса, при этом учитываем, что для простых веществ стандартная теплота образования равна нулю.
Уравнение Гесса:

ΔН_х.р. = ΔН_{обр.прод.} — ΔН_{обр.исх.}

Тогда 

ΔН°₂₉₈ = 2ΔH°Н₂О_(ж) — 4∆H°HCl_(г) =
= 2(-285,83) — 4(-92,31) = -202,42 кДж/моль.

Знак минус перед тепловым эффектом означает, что теплота выделяется в результате реакции.
Согласно 3-му следствию из закона Гесса, изменение энтропии химического процесса (ΔS°) определяется как разность сумм энтропий продуктов реакции и реагентов с учетом их стехиометрических коэффициентов в уравнении реакции. Расчет энтропии будем вести по формуле Гесса:

∆S°_х.р. = ∑S°_{(обр.прод.)} — ∑S°_{(обр.исх.)}.

Подставив найденные значения энтропий в искомое уравнение, и произведя расчеты, получим:

∆S°_х.р. = [2S°Н₂О_(ж) + 2S°Cl_2(г)] — [4S°HCl_(г) + S°O_2(г)] = 
= [(2 ^. 70,08) + (2 ^. 222,98)] — [(4^. 186,79) + 205,04] = -366,08 Дж/(моль ^. К).

Отрицательное значение изменения энтропии (уменьшение энтропии) свидетельствует о невозможности осуществления указанного процесса самопроизвольно в стандартных условиях.
Теперь находим ∆G°₂₉₈, выражая ∆S°_х.р. в кДж/(моль·К):

∆G°₂₉₈ = ΔН°₂₉₈ — Т∆S°_х.р.;
∆G°₂₉₈ = [-202,42 — 298(-366,08 ^. 10^-3)] кДж/моль = -93,38816 кДж/моль.

Т.к. ∆G°_250х.р. < 0, то реакция при 298 К может протекать самостоятельно.

Рассчитаем константу равновесия реакции (н.у.) по формуле:

lgK = ∆G°₂₉₈/-5,69.

Тогда

lgK = ∆G°₂₉₈/-5,69 = -202,42/-5,69 = 35,57;
К = 3,7 ^. 10^35.

Так как процесс идес с выделением температуры, то для увеличения выхода продукта нужно понизить температуру в системе, т.е. отводить тепло.