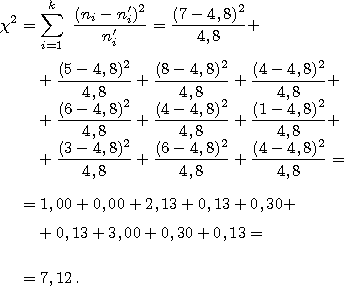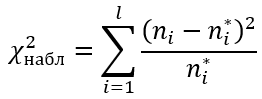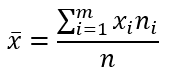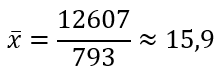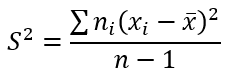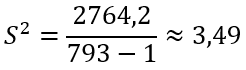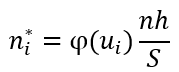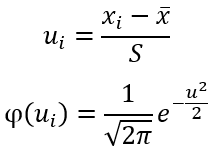Проверка гипотезы о нормальном распределении генеральной совокупности
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Проверка дискретного распределения на нормальность
Пусть
эмпирическое распределение задано в виде последовательности равноотстоящих
вариант и соответствующих им частот:
|
|
|
|
… |
|
|
|
|
|
… |
|
Требуется, используя критерий Пирсона, проверить
гипотезу о том, что генеральная совокупность
распределена нормально.
Для того,
чтобы при заданном уровне значимости
проверить гипотезу о нормальном распределении
генеральной совокупности, надо:
1. Вычислить
выборочную среднюю
и выборочное среднее квадратическое отклонение
.
2.
Вычислить теоретические частоты
где
– объем выборки,
— шаг (разность между двумя соседними
вариантами)
3. Сравнить эмпирические и теоретические частоты
с помощью критерия Пирсона. Для этого:
а)
составляют расчетную таблицу (см. пример), по которой находят наблюдаемое
значение критерия
б) по
таблице критических точек распределения
, по заданному уровню
значимости
и числу степеней свободы
(
– число групп выборки) находят критическую
точку
правосторонней критической области.
Если
– нет оснований отвергнуть гипотезу о
нормальном распределении генеральной совокупности. Если
— гипотезу отвергают.
Проверка интервального распределения на нормальность
Пусть
эмпирическое распределение задано в виде последовательности интервалов
и соответствующих им частот
.
Требуется,
используя критерий Пирсона, проверить гипотезу о том, что генеральная
совокупность
распределена нормально.
Для того,
чтобы при уровне значимости
проверить гипотезу о нормальном распределении
генеральной совокупности, надо:
1.
Вычислить выборочную среднюю
и выборочное среднее квадратическое отклонение
, причем в качестве вариант
принимают среднее арифметическое концов
интервала:
2.
Пронормировать
, то есть перейти к
случайной величине
и
вычислить концы интервалов:
причем
наименьшее значение
, то есть
полагают равным
, а наибольшее, то есть
полагают равным
.
3. Вычислить теоретические
частоты:
где
– объем выборки
– вероятности попадания
в интервалы
– функция Лапласа.
4. Сравнить эмпирические и
теоретические частоты с помощью критерия Пирсона. Для этого:
а)
составляют расчетную таблицу (см. пример), по которой находят наблюдаемое
значение критерия
б) по
таблице критических точек распределения
, по заданному уровню
значимости
и числу степеней свободы
(
– число групп выборки) находят критическую
точку
правосторонней критической области.
Если
– нет оснований отвергнуть гипотезу о
нормальном распределении генеральной совокупности. Если
— гипотезу отвергают.
Замечание.
Малочисленные частоты
следует объединить, в этом случае и
соответствующие им теоретические частоты также надо сложить. Если производилось
объединение частот, то при определении числа степеней свободы по формуле
следует в качестве
принять число групп выборки, оставшихся после
объединения частот.
Примеры решения задач
Пример 1
Используя
критерий Пирсона при уровне значимости 0,05, проверить, согласуется ли гипотеза
с нормальным распределением генеральной совокупности X с заданным эмпирическим
распределением:
| xi | -4.5 | -3.5 | -2.5 | -1.5 | -0.5 | 0.5 | 1.5 | 2.5 | 3.5 | 4.5 |
| ni | 1 | 4 | 21 | 30 | 63 | 59 | 34 | 18 | 5 | 2 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вычислим
характеристики распределения. Для этого составим расчетную таблицу.
Выборочная средняя:
Средняя
квадратов:
Выборочная
дисперсия:
Среднее квадратическое
отклонение:
Вычислим
теоретические частоты.
Вероятность
попадания в соответствующий интервал:
Теоретические
частоты:
где
-объем выборки
Составим
расчетную таблицу:
Проверим
степень согласия эмпирического и теоретического распределения по критерию
Пирсона. Объединяем малочисленные частоты (
).
Из
расчетной таблицы
Уровень
значимости
Число
степеней свободы
По
таблице критических точек распределения:
Нет
оснований отвергнуть гипотезу о нормальном распределении генеральной
совокупности.
Пример 2
Из большой партии по схеме случайной
повторной выборки было проверено 150 изделий с целью определения процента
влажности древесины, из которой изготовлены эти изделия. Получены следующие
результаты:
|
Процент влажности, xi |
11-13 |
13-15 |
15-17 |
17-19 |
19-21 |
|
Число изделий, ni |
8 |
42 |
51 |
37 |
12 |
На уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения признака (случайной величины) X, используя критерий χ2 — Пирсона.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
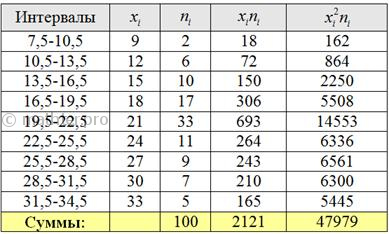
Составим расчетную таблицу
Средняя:
Средняя квадратов:
Дисперсия:
Исправленная дисперсия:
Исправленное среднее квадратическое
отклонение:
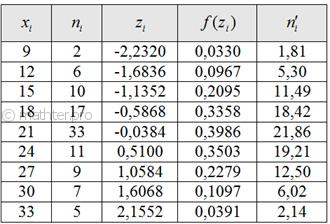
Вычислим теоретические частоты.
Составим расчетную таблицу:
Вероятность попадания в
соответствующий интервал:
, где
— функция Лапласа
Теоретические частоты:
, где
-объем выборки
Составим расчетную таблицу:
Проверим степень согласия
эмпирического и теоретического распределения по критерию Пирсона:
Из расчетной таблицы
Уровень значимости
Число степеней свободы
По таблице критических точек
распределения:
Нет оснований отвергать гипотезу о
распределении случайной величины по нормальному закону.
Задачи контрольных и самостоятельных работ
Задача 1
Выборка X
объемом n=100 задана таблицей:
|
|
0.8 | 1.1 | 1.4 | 1.7 | 2 | 2.3 | 2.6 |
|
|
5 | 13 | 25 | 25 | 19 | 10 | 3 |
1) Построить
полигон относительных частот
.
2) Вычислить
среднее выборочное
, выборочную дисперсию
и среднее квадратическое отклонение
.
3) Вычислить
теоретические частоты
. Построить график
на одном рисунке с полигоном.
4) С помощью
критерия χ2 проверить гипотезу о нормальном распределении
генеральной совокупности при уровне значимости α=0.05.
Задача 2
Построить
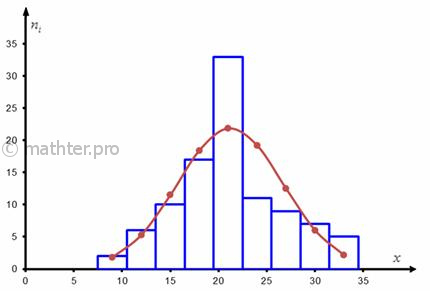
нормальную кривую по опытным данным. Рассчитать теоретические (выравнивающие) частоты
и сравнить с опытным распределением.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 3
Выборка X
объемом N=100 измерений задана таблицей:
|
|
0.6 | 1.5 | 2.4 | 3.3 | 4.2 | 5.1 | 6 |
|
|
5 | 13 | 26 | 24 | 19 | 10 | 3 |
а)
Построить полигон относительных частот
б)
вычислить среднее выборочное
, выборочную дисперсию
и среднее квадратическое отклонение
;
в) по
критерию χ2 проверить гипотезу о
нормальном распределении генеральной совокупности при уровне значимости α=0.05.
Задача 4
Для
изучения количественного признака
из генеральной совокупности извлечена выборка
объема n, имеющая данное
статистическое распределение.
а)
Построить полигон частот по данному распределению выборки.
б) Найти
выборочное среднее
, выборочное среднее
квадратическое отклонение
и исправленное среднее квадратическое
отклонение
.
в) При
данном уровне значимости
проверить по критерию Пирсона гипотезу о
нормальном распределении генеральной совокупности.
г) В
случае принятия гипотезы о нормальном распределении генеральной совокупности
найти доверительные интервалы для математического ожидания
и среднего квадратического отклонения σ при
данном уровне надежности γ=1-α; α=0.05
|
|
4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 |
|
|
5 | 9 | 15 | 19 | 20 | 16 | 10 | 6 |
Задача 5
Для выборки
объема N=100, представленной вариационным рядом
|
|
-1 | 0 | 1 | 2 | 3 | 4 | 5 |
|
|
3 | 8 | 11 | 19 | 37 | 17 | 5 |
построить
полигон относительных частот и гистограмму накопленных частот. Найти выборочное
среднее
и выборочное среднее квадратичное отклонение
. Определить доверительный интервал с
доверительной вероятностью β=0,95 для оценки математического ожидания
генеральной совокупности в предположении, что среднее квадратическое отклонение
генеральной совокупности σ равно исправленному выборочному среднему s. Проверить
гипотезу о нормальности закона распределения генеральной совокупности,
используя критерий Пирсона с уровнем значимости α=0,05.
Задача 6
Для случайной величины X составить интервальный
вариационный ряд, вычислить выборочные средние характеристики, подобрать
теоретический закон распределения, проверить его согласование с теоретическим
критерием Пирсона при α=0,05.
| 7 | 4 | 4 | 15 | 1 | 1 | 7 | 15 | 19 | 4 |
| 0 | 4 | 8 | 14 | 10 | 0 | 1 | 11 | 8 | 2 |
| 6 | 2 | 5 | 3 | 12 | 2 | 9 | 6 | 2 | 5 |
| 13 | 5 | 7 | 3 | 3 | 10 | 0 | 11 | 17 | 11 |
| 9 | 6 | 11 | 7 | 20 | 1 | 14 | 6 | 7 | 4 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Данные о
продолжительности телефонных разговоров, отобранные по схеме
собственно-случайной бесповторной выборки, приведены в таблице:
| Время, мин | 1.5-2.5 | 2.5-3.5 | 3.5-4.5 | 4.5-5.5 | 5.5-6.5 | 6.5-7.5 | 7.5-8.5 | 8.5-9.5 | 9.5-10.5 | Итого |
| Число разговоров | 3 | 4 | 9 | 14 | 37 | 12 | 8 | 8 | 5 | 100 |
Используя χ2-критерий Пирсона при уровне
значимости α=0.05 проверить гипотезу о том, что случайная величина X —
продолжительность телефонных разговоров — распределена по нормальному закону.
Построить на одном чертеже гистограмму и соответствующую нормальную кривую.
Задача 8
Распределение
случайной величины X – заработной платы сотрудников на фирме (в у.е.) –
задано в виде интервального ряда:
Найти:
. Построить теоретическое
нормальное распределение и сравнить его с эмпирическим с помощью критерия
согласия Пирсона χ2 при α=0,05.
Задача 9
Записать для выборки интервальное
распределение, построить гистограмму относительных частот. По критерию Пирсона
проверить гипотезу нормальном распределении.
| 7.81 | 3.15 | 2.27 | 32.64 | 4.72 | 5.33 | 8.51 | 7.72 | 30.23 | 20.12 |
| 9.83 | 8.33 | 9.61 | 31.83 | 8.52 | 27.22 | 27.22 | 8.43 | 15.91 | 25.46 |
| 24.82 | 26.54 | 46.73 | 17.31 | 13.05 | 53.24 | 5.23 | 18.28 | 40.93 | 17.44 |
| 32.34 | 28.26 | 9.75 | 3.72 | 8.16 | 22.91 | 0.74 | 12.97 | 12.05 | 1.53 |
| 43.15 | 45.57 | 2.02 | 32.23 | 8.67 | 4.83 | 9.12 | 6.77 | 6.48 | 19.22 |
| 36.42 | 47.81 | 40.64 | 5.45 | 0.21 | 26.51 | 17.36 | 3.62 | 15.57 | 23.21 |
| 58.73 | 62.52 | 10.15 | 38.36 | 35.55 | 6.10 | 3.04 | 4.54 | 1.95 | 5.24 |
| 64.71 | 67.63 | 1.21 | 0.81 | 2.03 | 10.17 | 5.51 | 8.35 | 43.76 | 8.74 |
| 4.72 | 17.54 | 17.32 | 29.43 | 5.91 | 6.92 | 4.72 | 16.04 | 57.54 | 15.46 |
| 13.31 | 36.45 | 3.45 | 16.15 | 15.77 | 2.43 | 14.24 | 2.25 | 15.63 | 23.72 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 10
Результаты наблюдений над случайной
величиной
оказались
лежащими на отрезке
и были
сгруппированы в 10 равновеликих интервалов. Значения
и частоты
попадания в интервалы приведены в таблице. Построить: гистограмму частот,
эмпирическую функцию распределения, найти медиану. Найти выборочное среднее
и исправленное
среднеквадратическое отклонение
. Указать 95-процентные доверительные интервалы для
. С помощью критерия Пирсона проверить гипотезу о
нормальном (с параметрами
) законе распределения (уровень значимости α=0.02
.
Задача 11
В таблице приведены результаты
измерения роста (см.) случайно отобранных 100 студентов:
|
Интервалы роста |
154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 |
|
Число студентов, |
10 | 14 | 26 | 28 | 12 | 8 | 2 |
С помощью критерия Пирсона при
уровне значимости α=0.05 проверить правдоподобие гипотезы о нормальном
распределении роста студентов.
Задача 12
При массовых стрельбах из пушек для
одинаковых общих условий были зафиксированы продольные ошибки (м) попадания
снарядов в цель:
На уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения признака (случайной величины) L, используя критерий χ2— Пирсона.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Методика вычисления теоретических частот равномерного распределения
Если проверяется
гипотеза о равномерном распределении
выборочной совокупности, теоретические
частоты определяются очень легко.
Действительно, в этом случае на каждый
разряд наблюдаемых значений должно
приходиться одинаковое число наблюдений.
Поэтому для равномерного распределения
где
—
общее число наблюдений, то есть, объем
выборки, а—
число разрядов наблюдаемых значений.
Методика вычисления теоретических частот нормального распределения
Значительно сложнее
обстоит дело в случае нормального
распределения. Один из способов нахождения
теоретических частот нормального
распределения состоит в следующем.
-
Весь интервал
наблюдаемых значений величины
делят на
частичных
интерваловодинаковой длины. Затем — находят
середины этих интервалов
и строят статистическое
распределение равноотстоящих значений
из получившегося набора значений.
-
Вычисляют выборочное
среднее значение
и выборочное
среднее квадратичное отклонение
.
-
Нормируют случайную
величину
,
то есть — переходят к случайной величине,
следующим образом:
после чего —
вычисляют границы частичных интервалов,
в пределах которых изменяются значения
:
-
Вычисляют
теоретические вероятности
попадания величины
в интервалы
по следующим формулам:
где
—
функция Лапласа, значения которой
табулированы.
-
Наконец, теоретические
частоты
находят, исходя из найденных теоретических
вероятностей:
Заметим, что теоретические частоты, в
отличие от эмпирических, могут быть
дробными. Однако их сумма должна, как
и в случае эмпирических частот, давать,
то есть, объем выборки. Этот факт можно
использовать для проверки собственных
вычислений.
Пример применения статистического критерия согласия распределений (Пирсона)
Рассмотрим пример
с распределением выборов испытуемых
из акцентированного и контрольного
списков.
В информатике
важна проблема поиска или выбора
информации. Идея примера состоит в том,
что заголовки HTML-документов можно
акцентировать, исходя из предполагаемой
поисковой фразы, таким образом, что при
прочих равных акцентированный заголовок
будет выбираться пользователями чаще,
чем неакцентированный.
Здесь мы рассмотрим
частоты выборов в двух списках:
контрольном, который состоял из десяти
неакцентированных заголовков, и
экспериментальном, содержащем десять
заголовков, акцентированных пятью
способами. После этого мы установим,
что распределение в акцентированном
случае отличается от равномерного
(тогда как в контрольном случае оно
равномерно).
Частота выборов
в контрольном списке (статистическое
распределение выборов) представлена в
следующей таблице:
|
Позиция |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Частота |
7 |
5 |
8 |
4 |
6 |
4 |
1 |
3 |
6 |
4 |
Распределение
данного ряда выборов мы подвергаем
анализу при помощи
-критерия,
для чего выдвигаем следующие статистические
гипотезы:
распределение
выборов в контрольном списке подчинено
равномерному закону;
распределение
выборов в контрольном списке отличается
от равномерного.
В целом пользователи
совершили 48 выборов (число, равное сумме
всех наблюдаемых частот). Следовательно,
если бы предпочтения пользователей
были распределены равномерно, то каждая
позиция получила бы 4,8 выбора. Это и есть
теоретическая частота
.
Вычислим эмпирическое
значение
-критерия
Пирсона:
Равномерное
распределение характеризуется двумя
параметрами — границами возможных
значений — следовательно, вычисляя
число степеней свободы, имеем:
Зададимся уровнем
значимости
и по таблице критических значений
определим.
Итак:
следовательно, на
уровне значимости
,
мы принимаем основную гипотезу:
распределение выборов в контрольном
списке подчинено равномерному закону.
Поступим так же
со второй выборкой, где испытуемые
совершали выбор из акцентированных
заголовков. Частоты этих выборов
представлены в следующей таблице:
|
Акцент |
A |
B |
C |
D |
E |
|
Частота |
4 |
4 |
7 |
11 |
22 |
Данный ряд
распределения выборов мы также подвергаем
анализу при помощи
-критерия,
для этого — выдвигаем статистические
гипотезы:
распределение
выборов в акцентированном списке
подчинено равномерному закону;
распределение
выборов в акцентированном списке
отличается от равномерного.
В данном случае
речь идет о выборе не между позициями
списка, а между различными степенями
акцентированности заголовков: от вообще
не акцентированных (акцент A)
до наиболее акцентированных (акцент
E).
В целом пользователи совершили те же
48 выборов, что и в контрольном случае.
Но на этот раз их предпочтения
распределялись не между десятью позициями
списка, а между пятью способами
акцентированности. Поэтому, если бы
предпочтения распределялись равномерно,
то каждый способ акцента получил бы 9,6
выборов. Это число — теоретическая
частота распределения выборов:
.
Снова вычисляем
эмпирическое значение критерия:
Так же как и в
предыдущем случае, учитывая, что
равномерное распределение характеризуется
двумя параметрами, вычисляем число
степеней свободы:
На уровне значимости
найдем то таблице критических значений
-критерия
Пирсона критическое значение:.
Получаем следующее неравенство:
следовательно,
основная гипотеза отвергается и
принимается альтернативная: распределение
выборов в акцентированном списке
отличается от равномерного.
Основной целью
анализа вариационных рядов является
выявление закономерности распределения,
исключая при этом влияние случайных
для данного распределения факторов.
Этого можно достичь, если увеличивать
объем исследуемой совокупности и
одновременно уменьшать интервал ряда.
При попытке изображения этих данных
графически мы получим некоторую плавную
кривую линию, которая для полигона
частот будет являться некоторым пределом.
Эту линию называют кривой распределения.
Иными словами,
кривая
распределения
есть графическое изображение в виде
непрерывной линии изменения частот в
вариационном ряду, которое функционально
связано с изменением вариант. Кривая
распределения отражает закономерность
изменения частот при отсутствии случайных
факторов. Графическое изображение
облегчает анализ рядов распределения.
Известно достаточно
много форм кривых распределения, по
которым может выравниваться вариационный
ряд, но в практике статистических
исследований наиболее часто используются
такие формы, как нормальное распределение
и распределение Пуассона.
Нормальное
распределение зависит от двух параметров:
средней арифметической
и
среднего квадратического отклонения.
Его кривая выражается уравнением

где у — ордината
кривой нормального распределения;
—
стандартизованные отклонения; е и π —
математические постоянные; x — варианты
вариационного ряда;—
их средняя величина;—
cреднее квадратическое отклонение.
Если нужно получить
теоретические частоты f’ при выравнивании
вариационного ряда по кривой нормального
распределения, то можно воспользоваться
формулой

где
—
сумма всех эмпирических частот
вариационного ряда; h — величина интервала
в группах;—
cреднее квадратическое отклонение;—
нормированное отклонение вариантов от
средней арифметической; все остальные
величины легко вычисляются по специальным
таблицам.
При помощи этой
формулы мы получаем теоретическое
(вероятностное)
распределение,
заменяя им эмпирическое
(фактическое)
распределение,
по характеру они не должны отличаться
друг от друга.
Тем не менее в ряде
случаев, если вариационный ряд представляет
собой распределение по дискретному
признаку, где при увеличении значений
признака х частоты начинают резко
уменьшаться, а средняя арифметическая,
в свою очередь, равна или близка по
значению к дисперсии (),
такой ряд выравнивается по кривой
Пуассона.
Кривую
Пуассона можно
выразить отношением
(7.8)
где Px
— вероятность наступления отдельных
значений х;
—
средняя арифметическая ряда.
При выравнивании
эмпирических данных теоретические
частоты можно определить по формуле
(7.9)
где f’ — теоретические
частоты; N — общее число единиц ряда.
Сравнивая полученные
величины теоретических частот f’ c
эмпирическими (фактическими) частотами
f, убеждаемся, что их расхождения могут
быть весьма невелики.
Объективная
характеристика соответствия теоретических
и эмпирических частот может быть получена
при помощи специальных статистических
показателей, которые называют критериями
согласия.
Для оценки близости
эмпирических и теоретических частот
применяются критерий согласия Пирсона,
критерий согласия Романовского, критерий
согласия Колмогорова.
Закон равномерного
распределения случайной величины
Закон
распределения непрерывной случайной
величины называется равномерным,
если на интервале, которому принадлежат
все возможные значения случайной
величины, плотность распределения
сохраняет постоянное значение (
f(x)
= const
при a
≤ x
≤ b,
f(x)
= 0 при x
< a,
x
> b.
Найдем
значение, которое принимает f(x)
при
Из
условия нормировки следует, что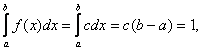
.
Вероятность
попадания равномерно распределенной
случайной величины на интервал
равна
при этом
Вид
функции распределения для нормального
закона:
Пример.
Автобусы некоторого маршрута идут с
интервалом 5 минут. Найти вероятность
того, что пришедшему на остановку
пассажиру придется ожидать автобуса
не более 2 минут.
Решение.
Время ожидания является случайной
величиной, равномерно распределенной
в интервале [0, 5]. Тогда
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
Критерий согласия Пирсона (или хи-квадрат) вычисляется по формуле:
ni – эмпирические частоты;
ni* – теоретические частоты;
l – количество интервалов (вариант)
Объем выборки по критерию Пирсона:
n>30
Теоретические частоты должны быть больше 5.
Распределение Пирсона с k степенями свободы рассчитывается по формуле:
k=l−r−1
r – число параметров предполагаемого распределения
Если предполагаемое распределение имеет нормальный закон распределения, то число степеней свободы оценивают по двум параметрам (математическое ожидание и СКО) и формула имеет вид:
k=l−3
Пример
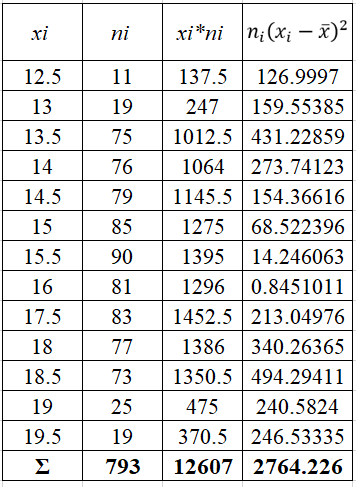
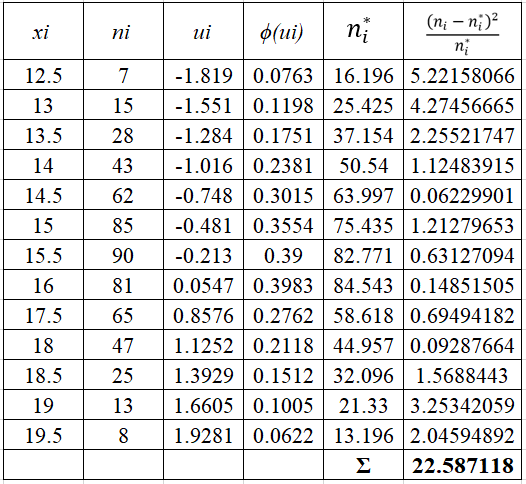
Проверить гипотезу о нормальном распределении по критерию Пирсона при уровне значимости 0,01. Дана выборка данных измерений в виде таблицы
Найдем выборочное среднее по формуле:
Отсюда
Формула выборочной исправленной дисперсии:
Тогда
Откуда получаем выборочную исправленную СКО:
Получаем параметры нормального распределения mx=15,9, σ=1,87.
Найдем теоретические частоты по формуле:
h – шаг между вариантами, h=0,5
При уровне значимости α=0,01 и число степеней свободы k=13−3=10 по таблице Пирсона найдем критическое значение:
Наблюдаемое значение критерия равно:
Ввиду того, что
следовательно, нулевую гипотезу о нормальном распределении принимаем.
14891
5.7. Критерий согласия Пирсона
Спасибо, Карл: …Всем
понятно, почему величина случайная? – По той причине, что в разных выборках мы будем получать
разные, заранее непредсказуемые эмпирические частоты.
При достаточно большом (объёме выборки) распределение этой случайной
величины близкО к распределению хи-квадрат с количеством степеней свободы , где
– количество оцениваемых параметров закона
.
Далее строится правосторонняя критическая область:
Критическое значение можно найти с помощью соответствующей
таблицы или Макета (пункт 3б).
Наблюдаемое значение критерия рассчитывается по эмпирическим и найденным теоретическим
частотам:
Если , то на уровне значимости
нет оснований
отвергать гипотезу о том, что
генеральная совокупность распределена по закону . То есть, различие между эмпирическими и теоретическими
частотами незначимо и, скорее всего, обусловлено случайными факторами (случайностью самой выборки, способом отбора,
группировки данных и т.д.)
Если , то нулевую гипотезу
отвергаем, иными словами эмпирические и теоретические частоты отличаются значимо, и это различие вряд ли
случайно.
И, наконец, коровы, которые нас уже заждались. Реалистичность фактических данных оставлю на совести автора методички
сельскохозяйственной академии:
Пример 36
По результатам выборочного исследования найдено распределение средних удоев молока в фермерском хозяйстве (литров) от
одной коровы за день:
На уровне значимости 0,05 проверить гипотезу о том, что генеральная совокупность (средний удой коров
всей фермы) распределена нормально. Построить эмпирическую гистограмму и теоретическую кривую.
…Если не любите молоко, то пусть это будет чай, сок, пиво или другой напиток, который вам нравится 
интереснее исследовать эту волшебную ферму.
Решение: на уровне значимости проверим гипотезу
о нормальном распределении генеральной совокупности против
конкурирующей гипотезы о том,
что она так НЕ распределена. Используем критерий согласия Пирсона .
Эмпирические частоты известны из предложенного интервального ряда, и
осталось найти теоретические. Для этого нужно вычислить выборочную среднюю и выборочное стандартное отклонение
. Выберем в качестве вариант
середины частичных интервалов (длина каждого интервала
) и заполним расчётную таблицу:
Вычислим выборочную среднюю: литра.
Выборочную дисперсию вычислим по формуле:
И выборочное стандартное отклонение: литра, по причине большого объёма выборки его исправлением можно пренебречь.
Теоретические частоты рассчитываются по формуле:
, где
– функция Гаусса, а
.
Входные данные известны: и
мы заполняем ещё одну расчётную таблицу:
вычисления удобно проводить в Экселе и на всякий случай я распишу 1-ю строчку:
– здесь выгодно использовать
встроенную экселевскую функцию =НОРМРАСП(-2,23; 0; 1; 0), первый аргумент которой равен текущему значению . За неимением Экселя и калькулятора
пользуйтесь стандартной таблицей, которая есть в любом учебнике по теорверу.
И, наконец, теоретическая частота: , довольно часто её округляют до целого значения, но без округления
результат всё же точнее.
Построим эмпирическую гистограмму с высотой «ступенек» и теоретическую кривую, которая проходит через точки
:
Нормальная кривая построена на основе выборочных данных (выборочной средней и стандартного отклонения), и
наилучшим образом приближает гистограмму. Дальнейшая задача состоит в том, чтобы оценить, насколько ЗНАЧИМО отличаются
эмпирические частоты (ступеньки гистограммы) от соответствующих теоретических частот (уровень коричневых
точек).
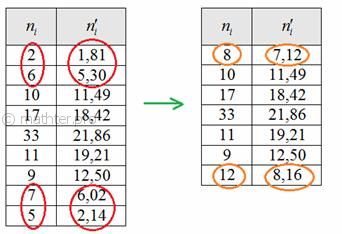
Но перед тем как сравнивать теоретические и эмпирические частоты, следует объединить интервалы с малыми (меньше пяти)
частотами. В данном случае объединяем два первых и два последних интервала, для этого суммируем частоты, обведённые красным
цветом, и получаем оранжевые результаты:
Это нужно для того, чтобы сгладить неоправданно большое расхождением между малыми частотами по краям выборки. Действие не
обязательное, но крайне желательное, ибо студентов на моей памяти из-за этого заставляли переделывать задание.
Найдём критическое значение критерия согласия Пирсона. Количество степеней свободы определяется
по формуле , где
– количество интервалов, а
– количество оцениваемых
параметров рассматриваемого закона распределения.
Так как мы объединяли интервалы, то теперь их не девять, а .
У нормального закона мы оцениваем параметра.
Пояснение: – это
оценка неизвестного генерального матоожидания, а – это оценка неизвестного генерального стандартного отклонения,
итого два оцениваемых параметра.
Таким образом, и для
уровня значимости :
Это значение можно найти по таблице критических значений распределения хи-квадрат или
с помощью Макета (Пункт 3б).
При нулевая гипотеза
отвергается, а при таких
оснований нет (заметьте, что формулировка не утверждает истинность гипотезы!):
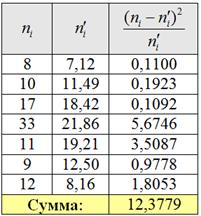
Вычислим наблюдаемое значение критерия (суть – сумму расхождений между частотами), для этого
заполним ещё одну расчётную табличку:
На всякий пожарный пример расчёта: .
В нижней строке таблицы у нас получилось готовое значение , поэтому на уровне значимости 0,05 гипотезу
о нормальном распределении генеральной
совокупности отвергаем.
Иными словами различие между эмпирическими и теоретическими частотами статистически значимо и вряд ли объяснимо
случайными факторами. При этом с вероятностью 5% мы совершили ошибку 1-го рода (то есть, ген.
совокупность на самом деле распределена нормально, но мы отвергли верную нулевую гипотезу).
Ответ: на уровне значимости 0,05 гипотезу о нормальном распределении генеральной совокупности
отвергаем
В чём может быть причина? Ведь по теореме Ляпунова, большинство коров не оказывают практически никакого влияния
на удой других коров, и поэтому распределение ген. совокупности должно быть близкО к нормальному.
Причины могут быть разными. Например, неоднородный состав совокупности (коровы разной породы), или на ферме есть
VIP-хлев, где коровы получают улучшенное питание 
влияние на остальных, в связи с чем нарушается условие теоремы Ляпунова.
Интересно отметить, что при уменьшении уровня значимости до 0,01 критическое значение , и гипотеза о нормальном распределении уже принимается.
Однако не нужно забывать, что здесь выросла -вероятность того, что мы приняли неправильную гипотезу (совершили ошибку 2-го рода). С оценкой этой вероятности можно ознакомиться в специализированной литературе
по статистике.
И, конечно, в случае сомнений имеет смысл увеличить объём выборки, чтобы провести повторное исследование.
Да, и видео по вычислениям! Хотя особой технической новизны
тут нет.
Рассмотренная задача может встретиться в более простой или более сложной формулировке. В версии-«лайт» вам предложат
готовые теоретические частоты, где остаётся только проверить гипотезу. Продвинутое же условие звучит примерно так:
На основании исследования выборки выдвинуть гипотезу о законе распределения генеральной совокупности
То есть, здесь не говорится о том, что предполагаемый закон нормальный (или какой-то другой) – этот
вопрос вам предлагается проанализировать самостоятельно.
Каким образом это можно сделать?
Во-первых, гипотезу можно выдвинуть априорно, даже не исследуя выборку. В частности, на основании упомянутой выше
теоремы Ляпунова: если каждый объект совокупности оказывается ничтожно малое влияние на всю совокупность, то её
распределение близкО к нормальному.
Это утверждение носит статус теоремы! То есть, строго доказано в теории.
Но по условию, требуют опираться на выборочные данные, и здесь есть сразу несколько признаков, чтобы «вычислить»
этот закон. Самый простой и наглядный способ – графический. Грубо говоря, чертим и смотрим. Интервальный вариационный ряд чаще
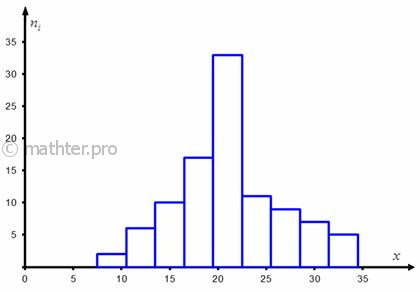
всего изображают гистограммой, возвращаемся к нашим коровам:
Построенная гистограмма по форме напоминает колоколообразный график плотности нормального распределения,
и это является веской причиной предположить, что генеральная совокупность распределена нормально. Да, здесь есть слишком
высокий средний столбик, но, возможно, это просто случайность выборки.
Если столбики примерно одинаковы по высоте, то предполагаем, что генеральная совокупность распределена равномерно. Для показательного распределениятоже будет
своя, характерная гистограмма.
В случае дискретных распределений тоже никаких проблем – строим полигон и смотрим,
на что он похож.
Следующие признаки аналитические, приведу их для нормального распределения:
1) У нормального распределения математическое ожидание совпадает с модой и
медианой. В нашем случае соответствующие выборочные показатели весьма близкИ друг к другу (матожидание оценивается выборочной средней):
(литры)
Желающие могут рассчитать моду и медиану
самостоятельно. Впрочем, желающими часто становятся поневоле, поскольку задача, которую мы рассматриваем, нередко идёт в
комплексе со всеми этими заданиями.
2) Выполнение правила «трёх» сигм. Практически все значения нормальной случайной величины находятся в
интервале . Найдём этот интервал
для нашей выборки. Матожидание «а» оценивается выборочной средней , а стандартное отклонение «сигма» – выборочным стандартным
отклонением .Таким образом, наш
эмпирический интервал:
– и в него действительно
попадают все коровы!
3) Кроме того, есть ещё коэффициенты
асимметрии и эксцесса нормального распределения, которые не вошли в этот курс
На практике в исследование желательно включить все пункты за исключением, возможно, третьего (т.к. асимметрию и
эксцесс рассчитывают далеко не всегда).
Следует отметить, что перечисленные выше предпосылки ещё не означают, что соответствующая гипотеза будет принята, в чём
мы недавно убедились. А если гипотеза и окажется принятой, то это всё равно на 100% не гарантирует нормальность распределения
(так как существует -вероятность принять неверную гипотезу (ошибка 2-го рода)).
И, конечно, задача для самостоятельного решения, передаю привет студентам Университета путей сообщения:
Пример 37
В результате проверки 500 контейнеров со стеклянными изделиями установлено, что число повреждённых изделий имеет следующее эмпирическое распределение:
( – количество
повреждённых изделий в контейнере, – количество контейнеров) …Здесь тоже представьте изделия по своему
интересу 
С помощью критерия согласия Пирсона на уровне значимости 0,05 проверить гипотезу о том, что случайная величина – число повреждённых
изделий распределена по закону
Пуассона.
Перелистываем страницу и читаем инструкцию по решению.
Все числа забиты в Эксель, придерживайтесь следующего алгоритма:
1) Находим выборочную среднюю . Это значение будет точечной
оценкой параметра «лямбда» теоретического распределения .
2) Находим значения для
. Вычисления можно проводить на
обычном калькуляторе, но удобнее использовать экселевскую функцию =ПУАССОН(i; «икс выборочное»; 0).
3) Находим теоретические частоты
4) Находим критическое значение критерия согласия Пирсона, где
. В данной задаче мы объединяем две последние варианты
ввиду их малых частот, следовательно, . Оценивается один параметр («лямбда»), поэтому
.
5) Рассчитываем наблюдаемое значение критерия .
6) Делаем вывод.
Примерный образец чистового оформления задачи в конце книги.


| Оглавление |
Предположим, что выполнено измерений некоторой случайной величины ξ :
, …,
, (4.4)
И есть основания полагать, что результаты распределены нормально с плотностью вероятности

Параметры закона распределения и σ обычно неизвестны. Вместо неизвестных параметров подставляют значения их оценок, которые вычисляют по следующим формулам:


В качестве критерия проверки выдвинутой гипотезы примем критерий согласия Пирсона (критерий согласия “хи- квадрат”)

Где – число интервалов, на которые разбито выборочное распределение,
— частоты эмпирического распределения;
– частоты теоретического распределения. Из формулы вытекает, что критерий характеризует близость эмпирического и теоретического распределений: чем меньше различаются
и
, тем меньше значение χ2.
Доказано, что при закон распределения случайной величины (4.8) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения χ2 с
степенями свободы. Число степеней свободы определяется равенством
, где
— число частичных интервалов;
– число параметров предполагаемого распределения, которые были оценены. Для нормального распределения оцениваются два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому
.
В соответствии с процедурой проверки гипотезы следует вычислить наблюдаемое значение критерия. Чтобы вычислить частоты эмпирического распределения, весь интервал наблюдаемых значений делят на частичных интервалов (бинов) точками
:
. (4.9)
определяют, подсчитав число измерений (4.4), которые попадают в
— й интервал
.
Используя теоретический закон распределения (4.5) можно рассчитать ожидаемое число Результатов измерений для каждого интервала
. Вероятность того, что результат одного измерения попадает в интервал
, равна
, (4.10)
Где – интегральный закон нормального распределения:

с параметрами
и σ связана со стандартной нормальной функцией формулой


Поскольку проводится не одно, а измерений и эти измерения независимы, то их можно рассматривать как
испытаний Бернулли, в которых “успехом” считается попадание результата измерения в интервал
. Тогда числа
вычисляются по формуле
(4.12)
(математическое ожидание числа “успехов” при испытаниях).
Для заданного уровня значимости по таблицам определяют критическое значение критерия. Сравнивая наблюдаемое и критическое значения критерия делают, вывод о соответствии экспериментальных данных предполагаемому закону распределения.
Пример 4.1. Проверить с помощью критерия χ2 при уровне значимости 0,05 гипотезу о том, что выборка объема , представленная интервальным вариационным рядом в таблице 4.4, извлечена из нормальной генеральной совокупности.
Таблица 4.4
|
Номер Интервала I |
Границы Интервала |
Частота |
|
1 |
0 – 2 |
5 |
|
2 |
2 – 4 |
11 |
|
3 |
4 –6 |
17 |
|
4 |
6 – 8 |
10 |
|
5 |
8 – 10 |
7 |
Решение. 1. Сформулируем нулевую и альтернативную гипотезы: H0 – эмпирическое распределение соответствует нормальному; H1 — эмпирическое распределение не соответствует нормальному.
Для проверки нулевой гипотезы необходимо рассчитать наблюдаемое значение критерия χ2набл по формуле (4.8) и сравнить его с критическим значением χ2кр.
2. Определим параметры предполагаемого (теоретического) нормального закона распределения.
Найдем середины интервалов и относительные частоты
. Получим следующие значения:
|
|
1 |
3 |
5 |
6 |
7 |
|
|
|
|
|
|
|
Оценку математического ожидания найдем по формуле (4.1):

Оценки дисперсии и стандартного отклонения вычислим по формулам (4.2) и (4.3):

.
3. Выполним расчет теоретических частот по формуле (4.12). Для вычисления вероятностей
по формуле (4.11) воспользуемся таблицей В Приложения со значениями нормальной стандартной функции распределения. При этом наименьшее значение, т. е.
, полагаем равным
, а наибольшее, т. е.
, полагаем равным
. Последовательно находим для интервала (-∞, 2)

;
Для интервала находим
и ;
Для интервала (4,6) соответственно :

;
Для интервала (6,8):
И ;
Для интервала вычислим

.
4. По формуле (4.8) найдем значение :

5. По таблице квантилей распределения χ2 (см. таблицу С Приложения) с числом степеней свободы находим, что χ2кр = 6,0 для
.
Поскольку (
), то можно считать, что гипотеза о нормальном распределении генеральной совокупности не противоречит опытным данным.
Порядок выполнения лабораторной работы
В данной лабораторной работе задания 1 и 2 представляют собой контрольный пример, решение которого приводится ниже. Задания 3 и 4 составляют индивидуальное задание.
Задание 1. Для выборки из 40 значений случайной величины ξ, полученной в задании 1 работы 1, оценить близость эмпирического распределения к нормальному распределению:
А) построить интервальный вариационный ряд и гистограмму частот;
Б) построить на одном графике гистограмму относительных частот и график плотности нормального распределения.
Задание 2. При уровне значимостит 0,05 проверить гипотезу о нормальном распределении генеральной совокупности с использованием χ2 — критерия как критерия согласия.
Задание 3. Для выборки нормальной случайной величины, смоделированной в задании 3 работы 1, построить, на выбор, либо гистограмму частот, либо гистограмму относительных частот.
Задание 4. Пользуясь критерием Пирсона при уровне значимости 0,01 проверить, согласуется ли с нормальным распределением статистическое распределение из задания 3 работы 1.
Выполнение задания 1.
1. Подготовьте рабочий лист в EXCEL. Для этого выполните следующее:
· перейдите на новый лист и введите в ячейку B1 название таблицы ПОСТРОЕНИЕ ГИСТОГРАММЫ;
· назовите ярлык листа Гистограмма;
· разместите в ячейках A5:B24 выборку, которая была получена при выполнении задания 1.1 лабораторной работы 1 (40 значений нормальной случайной величины с параметрами и σ=0,5 ), либо выполнив копирование значений с листа Оценки, либо повторив процедуру моделирования выборки заданного закона распределения.
Создаваемая электронная таблица представлена в таблице 4.5 в режиме вычислений и в таблице 4.6 в режиме формул.
2. Для построения интервального вариационного ряда выполните следующие действия:
2.1. Произведите расчет длины частичных интервалов в ячейках C5:G5 по указанным в ячейках формулам и комментариям так, как указано ниже.
Ячейка Значение Ячейка Значение
C5 40 C4 объем выб.
D5 =МИН(A5:B24) D4 минимум
E5 =МАКС(A5:B24) E4 максимум
F5 =1+3,32*LOG10(C5) F4 k
G5 =(E5-D5)/F5 G4 вел. инт-ла
H5 =СРЗНАЧ(A5:B24) H4 оценка мат. ож.
I5 =СТАНДОТКЛОН(A5:B24) I4 несм. станд. откл.
2.2. Разместите массив значений границ интервалов в ячейках C9:D15 (в столбце С – значения левых границ, в столбце D – значения правых границ).
Выполните это так:
· для определения левой границы первого частичного промежутка введите в ячейку С9 формулу — =$D$5-$G$5/2;
· для определения правой границы введите в ячейку D9 формулу C9+$G$5;
· поскольку левая граница последующего частичного промежутка совпадает с правой границей предыдущего введите в ячейку С10 формулу — =D9;
· перенесите автозаполнением формулу из ячейки С10 на диапазон С11:C15, а формулу из D9 – в ячейки D10:D15;
· в ячейку С8 введите текст Левый кон, в ячейку D8 – Правый кон.
3. Для построения гистограммы частот воспользуемся инструментом анализа Гистограмма. Выполните команду Сервис – Анализ данных – Гистограмма. В окне “Гистограмма” задайте параметры;
· введите в поле Входной интервал $A$5:$B$24, в поле Интервал карманов – $D$9:$D$15, в Выходной интервал – $E$8;
· установите флажок Вывод графика;
· нажмите OK.
На экране появятся выходная таблица и гистограмма. В левом столбце таблицы размещен Карман – так в MS Excel называется набор граничных значений частичных интервалов. Правый столбец содержит вычисленные значения частот.
Поместите полученную диаграмму (выделите и перетащите) так, чтобы левый верхний конец находился в ячейке J8.
4. Подготовим исходные данные для построения гистограммы относительных частот и графика плотности вероятности.
4.1. Расчет относительных частот произведите в ячейках G9:G15, для этого введите в ячейку G9 формулу =F9/$C$5 и перенесите ее на диапазон G10:G15.
4.2. При построении гистограммы используются значения плотности относительных частот. Выполните расчет этих значений в ячейках H9:H15. Введите в ячейку H9 формулу =G9/$G$5 и скопируйте ее в ячейки H10:H15. Озаглавьте столбцы: введите в G8 текст Отн. част., в H8 – Плот. отн. част.
4.3. Сформируйте в ячейках I9:I15 массив значений плотности вероятности, по которым будет построен график. Указанные значения вычислите с использованием функции НОРМРАСП в граничных точках частичных интервалов, размещенных в ячейках D9:D15. Введите в I9 формулу
=НОРМРАСП(D9;$H$5;$I$5;0)
И перенесите ее на диапазон I10:I15.
5. Как отмечалось выше, площадь гистограммы относительных частот численно равна единице. Введите для контроля правильности вычислений в ячейку G16 текст Контроль, а в ячейку H16 – формулу =СУММ(H9:H15)*$G$5.
6. Для построения гистограммы и графика выполните следующие действия:
· выделите ячейки H9:I15, в которых размещены данные;
· нажмите кнопку Мастер диаграмм, откроется окно диалога;
· выберите вкладку “Нестандартные” и вид графика График! гистограмма, нажмите кнопку Далее;
· на втором шаге построения диаграммы выберите вкладку “Ряд”. Измените текст легенды (условного обозначения для рядов данных): в разделе Ряд выделите Ряд 1, перейдите в поле Имя и введите текст Плотность вероятности, затем выделите Ряд 2 и в поле Имя Наберите Плотность отн. частот;
· введите в поле “Подписи оси Х” диапазон D9:D15 и нажмите кнопку Далее;
· оформление гистограммы на третьем шаге можно опустить (либо выполните по своему желанию);
· на четвертом шаге задайте место размещения гистограммы –Имеющийся лист И нажмите OK.
Выполнение задания 2
1. Подготовьте рабочий лист. Для этого выполните следующие действия:
· перейдите на новый лист и введите в ячейку С1 название таблицы ПРОВЕРКА ГИПОТЕЗЫ ПО КРИТЕРИЮ ПИРСОНА;
· назовите ярлык листа Крит Пирсона;
· занесите в ячейку E2 значение заданного уровня значимости 0,05, а в С2 — Уровень значимости;
· перенесите содержимое столбцов A, B, C, D, а также четвертой и пятой строк с листа Гистограмма На лист Крит Пирсона.
Создаваемая электронная таблица представлена в таблице 4.7 в режиме формул и в таблице 4.8 в режиме вычислений.
Чтобы вычислить наблюдаемое значение критерия по формуле (4.7), для каждого частичного интервала необходимо найти значения эмпирической и теоретической частот.
2. Частоту появления значений выборки в построенных частичных интервалах (эмпирическую частоту) вычислите с помощью функции ЧАСТОТА, которая возвращает распределение частот в виде вертикального массива. Эта функция подсчитывает для данного множества значений и данного множества карманов (интервалов, в математическом смысле), сколько исходных значений попадает в каждый интервал. Выполните следующие действия:
· выделите ячейки E9:E15, в которые будет введена функция ЧАСТОТА (данная функция возвращает массив, поэтому она должна задаваться в качестве формулы массива);
· нажмите кнопку Вставка функции;
· в открывшемся окне диалога “Мастер функций” выберите функцию ЧАСТОТА из категории Статистические и нажмите кнопку OK;
· укажите в поле Массив данных диапазон $A$5:$B$24, в поле Двоичный массив – $D$9:$D$15 (массив верхних границ интервалов);
· не выходя из строки формул, одновременно нажмите клавиши Ctrl+Shift+Enter;
· введите в ячейку E7 текст Эмп. частота, в D16 – Число бинов, а в E16 – формулу для подсчета числа бинов
=СЧЕТ(E9:E15).
3. Расчет теоретической частоты по формулам (4.10) и (4.12) произведите в ячейках F9:H15. Выполните следующее:
· определите значения интегральной функции распределения на правом конце для каждого частичного промежутка, для чего введите в ячейку F9 формулу =НОРМРАСП(D9;$H$5;$I$5;1)
· и перенесите ее автозаполнением на диапазон F10:F14 (в ячейку F15 введите 1, поскольку );
· вычислите вероятность того, что результат одного измерения попадет в частичный интервал, для чего введите в ячейку G9 формулу: =F9-F8
И скопируйте ее на диапазон G10:G15;
· сосчитайте теоретические частоты, введя в ячейку H9 формулу:
=$C$5*G9
и автозаполнением перенесите ее на диапазон H10:H15;
Продолжение таблицы 4.7
|
K |
Вел инт-ла |
Оценка мат ож |
Несм станд откл |
|
=1+3,32*LOG10(C5) |
=(E5-D5)/F5 |
=СРЗНАЧ(A5:B24) |
=СТАНДОТКЛОН(A5:B24) |
|
Ф р на пр конце |
Вер |
Теор частота |
|
|
=НОРМРАСП(D9;$H$5;$I$5;1) |
=F9-F8 |
=$C$5*G9 |
=(E9-H9)^2/H9 |
|
=НОРМРАСП(D10;$H$5;$I$5;1) |
=F10-F9 |
=$C$5*G10 |
=(E10-H10)^2/H10 |
|
=НОРМРАСП(D11;$H$5;$I$5;1) |
=F11-F10 |
=$C$5*G11 |
=(E11-H11)^2/H11 |
|
=НОРМРАСП(D12;$H$5;$I$5;1) |
=F12-F11 |
=$C$5*G12 |
=(E12-H12)^2/H12 |
|
=НОРМРАСП(D13;$H$5;$I$5;1) |
=F13-F12 |
=$C$5*G13 |
=(E13-H13)^2/H13 |
|
=НОРМРАСП(D14;$H$5;$I$5;1) |
=F14-F13 |
=$C$5*G14 |
=(E14-H14)^2/H14 |
|
1 |
=F15-F14 |
=$C$5*G15 |
=(E15-H15)^2/H15 |
|
Набл зн критерия |
=СУММ(I9:I15) |
||
|
Крит зн критерия |
=ХИ2ОБР($E$2;$E$16-3) |
||
Таблица 4.8
|
ПРОВЕРКА ГИПОТЕЗЫ ПО КРИТЕРИЮ ПИРСОНА |
||||||||
|
Уровень значимости |
0,05 |
|||||||
|
Вариац. ряд |
Объем выб. |
Мин. |
Макс |
K |
Вел. инт-ла |
Оценка мат ожидания |
Несм. станд. откл. |
|
|
2,522 |
3,08504 |
40 |
2,52182 |
4,951854 |
6,318839171 |
0,3845703 |
3,904166 |
0,5240692 |
|
4,06 |
4,54702 |
|||||||
|
4,475 |
3,99218 |
Левый кон. |
Правый кон. |
Эмп. частота |
Ф. р. на пр..конце |
Вер. |
Теор. частота |
|
|
2,868 |
4,18848 |
|||||||
|
4,037 |
3,80175 |
2,3295 |
2,7141 |
1 |
0,011579055 |
0,0115791 |
0,463162 |
0,622233 |
|
4,496 |
3,86077 |
2,7141 |
3,09867 |
3 |
0,062146626 |
0,0505676 |
2,022703 |
0,4721948 |
|
4,173 |
3,9781 |
3,0987 |
3,48324 |
4 |
0,210934098 |
0,1487875 |
5,951499 |
0,6398973 |
|
4,163 |
3,29599 |
3,4832 |
3,86781 |
8 |
0,472348174 |
0,2614141 |
10,45656 |
0,577121 |
|
3,786 |
4,02087 |
3,8678 |
4,25238 |
15 |
0,746798016 |
0,2744498 |
10,97799 |
1,473542 |
|
3,549 |
3,96672 |
4,2524 |
4,63695 |
7 |
0,918983001 |
0,172185 |
6,887399 |
0,0018409 |
|
3,504 |
3,92577 |
4,637 |
5,02152 |
2 |
1 |
0,081017 |
3,24068 |
0,4749888 |
|
4,547 |
4,12434 |
Число бинов |
7 |
Набл. зн. .критерия |
4,2618178 |
|||
|
4,318 |
4,30071 |
Крит. зн. критерия |
9,487729 |
|||||
|
3,047 |
4,272 |
|||||||
|
3,788 |
4,23425 |
|||||||
|
4,13 |
3,98299 |
|||||||
|
4,059 |
4,95185 |
|||||||
|
3,184 |
3,20143 |
|||||||
|
3,759 |
4,7737 |
|||||||
|
3,766 |
3,43299 |
— поясните полученные результаты, для этого в ячейку F7 введите текст Ф. р. на пр. конце, в ячейку G7 – Вер., а в H7 – Теор. частота.
4. Вычислите слагаемые критерия Пирсона, для чего введите в ячейку I9 формулу
=(E9-H9)^2/H9
И автозаполнением перенесите эту формулу в ячейки I10:I15.
5. Наблюдаемое значение критерия вычислите по формуле (4.6) в ячейке I16, для чего введите формулу =СУММ(I9:I15).
6. Критическое значение критерия “хи-квадрат” для уровня значимости 0,95 и числа степеней свободы выведите в ячейке I17, набрав формулу
=ХИ2ОБР($E$2;$E$16-3).
Функция ХИ2ОБР возвращает обратную функцию для χ2-распределения.
В ячейку H16 введите текст Набл. зн. критерия, а в H17 – Крит. зн. критерия.
Так как наблюдаемое значение критерия, равное 4,26, меньше критического значения, равного 9,49, то гипотезу о нормальном распределении генеральной совокупности не отвергаем. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, смоделированные значения случайной величины согласуются с гипотезой о распределении случайной величины с заданным законом распределения.
Подготовить отчет:
1. Название работы и задание.
2. По две распечатки таблиц, созданных при выполнении заданий 3 и 4 (одна распечатка содержит результаты вычислений, другая – сами формулы).
3. Выводы по результатам выполнения задания 4.
| < Предыдущая | Следующая > |
|---|