Фактор будущей стоимости связывает сегодняшнюю текущую (приведенную) стоимость (PV, англ. ‘present value’) денежного потока с его будущей стоимостью (FV, англ. ‘future value’). Этот коэффициент позволяет рассчитать как FV, так и PV.
Например, 5-процентная ставка приносит будущий доход в размере $105 за 1 год.
Какой должна быть текущая (первоначальная) сумма, вложенная под 5%, чтобы она выросла до $105 через 1 год?
Ответ: $100 представляют собой текущую стоимость (PV) для будущей суммы (FV) в размере $105, которая должна быть получена через 1 год, при ставке вклада 5%.
Используя будущий денежный поток, который должен быть получен в течение (N) периодов, и процентную ставку за период (r), мы можем преобразовать Формулу (2) будущей стоимости денежного потока следующим образом:
( dstl FV^N = PV (1 + r)^N )
( dstL PV = FV_N left[1 over (1 + r)^N right] ) (Формула 
или
( dstL PV = FV_N (1 + r)^{-N} )
Из Формулы 8 видно, что фактор текущей стоимости (англ. ‘present value factor’), ( (1 + r)^{-N} ) является обратной величиной фактора будущей стоимости ( (1 + r)^N ).
Пример расчета приведенной (текущей) стоимости денежного потока.
Страховая компания выпустила гарантированный инвестиционный сертификат (GIC), который гарантирует выплату $100 000 в течение 6 лет с 8-процентной прибылью.
Какую сумму страховщик должен инвестировать сегодня, чтобы через 6 лет обеспечить выплату обещанной суммы по сертификату?
Решение:
Мы можем применить Формулу 8, чтобы найти текущую (приведенную) стоимость, используя следующие данные:
(FV_N) = $100,000
(r) = 8% = 0.08
(N) = 6
( begin{aligned} dst
PV &= FV_N (1 + r)^{-N} \[1ex]
&= $100,000 [1 / (1.08)^6] \
&= $100,000(0.6301696) = $63,016.96
end{aligned} )
Можно сказать, что сегодня $63 016,96 при процентной ставке 8% эквивалентны $100 000, которые будут получены через 6 лет.
Дисконтирование сегодняшней суммы $100 000 делает будущую сумму в размере $100 000 эквивалентом $63 016,96, с учетом временной стоимости денег (TVM).
Как показывает временная линия на рисунке ниже, $100 000 дисконтированы в течение 6 полных периодов.
Текущая стоимость (PV) $100 000 в момент времени t = 6.
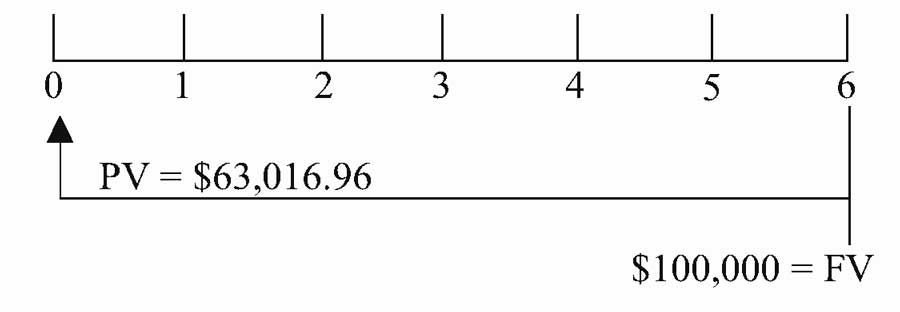
Пример прогнозирования приведенной стоимости денежного потока.
Предположим, что у вас есть ликвидный финансовый актив, который принесет вам $100 000 через 10 лет от текущей даты.
Ваша дочь планирует поступить в колледж через четыре года, и вы хотите знать, какова будет текущая (приведенная) стоимость актива к этому моменту.
С учетом 8% ставки дисконтирования, какова будет стоимость актива через 4 года от текущей даты?
Решение:
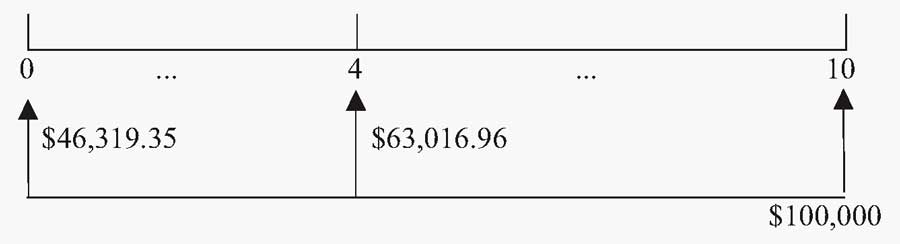
Стоимость актива ($100 000) — это текущая стоимость через 10 лет. При (t) = 4 эта сумма будет получена 6 лет спустя — см. рисунок ниже.
Связь между текущей и будущей стоимостью актива.
С помощью этой информации вы можете вычислить стоимость актива через 4 года от текущей даты, используя Формулу 8:
(FV_N) = $100,000
(r) = 8% = 0.08
(N) = 6
( begin{aligned} dst
PV &= FV_N (1 + r)^{-N} \[1ex]
&= $100,000 [1 / (1.08)^6] \
&= $100,000(0.6301696) = $63,016.96
end{aligned} )
Временная линия на рисунке выше показывает будущий платеж в размере $100 000, который должен быть получен при (t) = 10. На временной шкале также показана стоимость денежного потока при (t) = 4 и при (t) = 0.
По сравнению с суммой при (t) = 10, сумма при (t) = 4 представляет собой прогнозируемую текущую стоимость, а сумма при (t) = 0 является текущей приведенной стоимостью (на сегодняшний день).
Задачи, требующие вычисления приведенной стоимости (PV) требуют определения фактора приведенной стоимости ( (1 + r)^{-N} ).
Приведенная стоимость зависит от процентной ставки и количества периодов начисления процентов следующим образом:
- При заданной ставке дисконтирования, чем дальше в будущем будет получена сумма, тем меньше будет текущая стоимость (PV) этой суммы.
- Для одного и того же момента времени, с ростом ставки дисконтирования уменьшается текущая стоимость будущей суммы.
Расчет текущей (приведенной) стоимости с промежуточным начислением процентов.
Напомним, что проценты могут выплачиваться раз в полгода, ежеквартально, ежемесячно или даже ежедневно.
Для расчета процентных платежей, производимых более 1 раза в год, мы можем изменить формулу текущей стоимости (8).
Напомним, что (r_s) — котируемая (заявленная) процентная ставка и она равна периодической процентной ставке, умноженной на количество периодов начисления в каждом году.
В целом, если в году есть более 1 промежуточного периода начисления, мы можем выразить формулу расчета текущей стоимости (PV) как:
( dstL PV = FV_N left(1 + {r_s over m} right)^{-mN} ) (Формула 9)
где:
- (m) = количество периодов начисления в году,
- (r_s) = заявленная годовая процентная ставка,
- (N) = количество лет.
Формула 9 очень похожа на Формулу 8.
Как мы уже отмечали, фактор текущей (приведенной) стоимости и фактор будущей стоимости являются обратными значениями по отношению друг к другу. И добавление в формулу частоты начисления процентов не влияет на эту взаимозависимость между двумя факторами.
Единственное различие заключается в использовании периодической процентной ставки и соответствующего количества периодов начисления.
Следующий пример иллюстрирует Формулу 9.
Пример расчета текущей (приведенной) стоимость при ежемесячном начислении процентов.
Менеджер канадского пенсионного фонда знает, что фонд должен выполнить единовременный платеж в размере $5 млн. через 10 лет. Она планирует сегодня инвестировать некоторую сумму в гарантированный инвестиционный сертификат (GIC), чтобы эта инвестиция выросла до необходимой суммы в $5 млн.
Текущая процентная ставка по GIC составляет 6% в год, с ежемесячным начислением процентов.
Сколько она должна сегодня инвестировать в GIC?
Решение:
Используя Формулу 9, чтобы находим требуемую приведенную стоимость:
(FV_N) = $5,000,000
(r_s) = 6% = 0.06
(m) = 12
(r_s/m) = 0.06/12 = 0.005
(N) = 10
(mN) = 12(10) = 120
( begin{aligned} dst
PV &=FV_N left(1 + {r_s over m} right)^{-mN} \[1ex]
&= $5,000,000 (1.005)^{-120} \
&= $5,000,000 (0.549633) \
&= $2,748,163.67
end{aligned} )
При применении Формулы 9 мы используем периодическую ставку (в данном случае, месячную ставку) и соответствующее количество периодов с ежемесячным начислением процентов (в данном случае 10 лет ежемесячных начислений или 120 периодов).
Расскажем простыми словами, что это такое NPV (Net Present Value). Покажем формулы и методы расчета чистой приведенной стоимости всех денежных потоков инвестиционного проекта с помощью ставки дисконтирования.
Откройте счет
в БКС Мир Инвестиций
Зачем нужно считать NPV (Net Present Value)
NPV (чистая приведенная стоимость) — это метод, который позволяет вычислить ожидаемую доходность с учетом изменения ценности денежных потоков (дисконтирования).
Финансовый показатель нужен для того, чтобы сопоставить будущую прибыль с текущими вложениями. Таким образом можно оценить, стоит ли инвестировать в тот или иной проект, окупятся ли вложенные средства и насколько вероятен риск убытков. Также с помощью NPV сравнивают инвестиционные проекты, чтобы выявить из них более привлекательный по критерию прибыльности.
Преимущества и недостатки подсчета чистой приведенной стоимости
Главное преимущество NPV состоит в том, что с помощью показателя можно произвести оценку инвестиционной привлекательности проекта. При расчетах допустимо учитывать дополнительные составляющие: срок жизни проекта и распределение денежных потоков во времени. Также одним из плюсов NPV является возможность складывать показатели различных проектов.
Основные недостатки NPV — это сложность расчетов и относительно низкая достоверность. Если говорить об ожидаемой прибыли, которую планирует получить инвестор, то показатель может отразить ее некорректно. Все дело в ряде факторов, влияющих на точность расчетов: например, ставка дисконтирования имеет свойство меняться, как и показатель инфляции. Эти риски можно принимать во внимание при проведении расчетов, но вместе с ними возрастает и сложность вычислений.
На практике организации чаще используют другой показатель для оценки проектов — IRR (внутренняя норма доходности). Он позволяет определить максимальную ставку кредита, которая позволительна для того, чтобы инвестиционный проект не был убыточным.
Формула расчета
Рассмотрим формулу, по которой можно рассчитать NPV:
где:
n — временной отрезок, за который производится расчет;
Pk — денежный поток за выбранный интервал времени;
i — ставка дисконтирования;
IC — капитал, вложенный на этапе первоначальных инвестиций.
Денежные потоки инвестиционного проекта
Денежные потоки — это разница между доходами и расходами компании или проекта.
Одним из самых сложных пунктов при расчете NPV является учет всей массы денежных потоков. Для этого необходимо соотнести размер первоначально вложенного капитала, а также ожидаемую прибыль и планируемые расходы в будущем.
Сложность состоит в том, что при подсчете денежных потоков следует учесть множество нюансов: экономическую ситуацию, наличие спроса, если ваш инвестиционный проект связан с производством, конкурентную составляющую и так далее.
Также необходимо произвести расчеты, которые связаны с потенциальными операционными расходами. В свою очередь, они напрямую зависят от ряда факторов: размера заработной платы сотрудников, занятых в проекте, стоимости сырьевого обеспечения, динамики курсов валют и других показателей.
Ставка дисконтирования простыми словами
Ставка дисконтирования — это инструмент для прогнозирования, который позволяет оценить доходность будущих инвестиций. При этом полученный результат выражается в текущей стоимостной величине.
Если говорить простыми словами, то ставка дисконтирования позволяет рассчитать стоимость будущего дохода по меркам настоящего времени. Это эталонная величина, которая используется для приведения будущих денежных потоков к одному знаменателю. Например, чтобы оценить, стоит ли инвестировать финансовые средства в тот или иной инструмент и какой доход он принесет в будущем по отношению к настоящему моменту.
Как рассчитать NPV
Рассмотрим, как рассчитать чистую приведенную стоимость, на примере. Допустим, капитал, инвестированный в качестве стартовых вложений, составит 500 тысяч рублей. Временной интервал, за который будут производиться вычисления, — 1 год. Также необходимо определить ставку дисконтирования: в нашем примере она будет равна 10% (показатель рассчитывается как коэффициент, поэтому его значение мы определим как 0,1). Дополнительно следует предположить, какой размер денежных поступлений планируется: например: 300 тысяч рублей.
300 000 ₽ / (1+0,1) – 500 000 ₽ = –227 273 ₽
В итоге мы получили число, которые выражает чистую прибыль за годовой период. Так как ниже нуля, то данный инвестиционный проект можно назвать убыточным на выбранном отрезке времени. Но если мы увеличим количество таких периодов, то получит другое значение.
Рассчитаем NPV за 3 года, учитывая, что в каждом из них ставка дисконтирования будет уменьшаться.
300 000 ₽ / (1+0,1) + 300 000 ₽ / (1+0,1)² + 300 000 ₽ / (1+0,1)³ + 300 000 ₽ / (1+0,1)⁴ – 500 000 ₽ = 518 952 ₽
Сумма, полученная в результаты вычислений, положительная, а это означает, что по прошествии трех лет данный инвестиционный проект окупится и будет приносить прибыль.
Пример расчета в MS Excel
Для быстроты и удобства можно также применить инструмент таблицы в MS Excel. Этот метод позволит не производить вычисления самостоятельно и поможет избежать возможных ошибок, возможных при расчетах вручную. Для начала заполните все поля таблицы необходимыми данными.
Затем используйте ЧПС — специальную функцию для вычисления NPV. Для этого в ячейку B10 необходимо добавить формулу, приведенную на картинке ниже.
Таблица произведет расчеты самостоятельно, и вы увидите результат в ячейке B10.
Полученная сумма в нашем примере отрицательное. Это значит, что инвестиционный проект невыгоден и не окупиться за 3 года.
Популярные ошибки при расчете
Игнорирование сопутствующих расходов
Допустим, инвестор планирует приобрести оборудование для производства автомобильных деталей и продавать их по определенной стоимости. В этом случае необходимо учесть расходы на износ и амортизацию оборудования, а это — дополнительные деньги в качестве трат. Если не учесть их при вычислении, NPV будет ошибочным;
Завышенные ожидания от проекта
При расчете NPV следует опираться на реалистичные прогнозы, ведь доходность зависит от множества факторов. Недальновидно ожидать, что приток пользователей вашего проекта будет динамично расти, а вместе с ним и размер прибыли. Ведь у каждого бизнеса есть периоды простоя: например, из-за фактора сезонности;
Некорректное значение ставки дисконтирования
Для расчета показателя используется ряд методов, каждый из которых учитывает различные исходные данные. Спустя некоторое количество времени значения могут меняться (например, уровень инфляции), соответственно, рассчитанная ранее чистая приведенная стоимость станет неактуальной.
Выводы для инвестора
Метод чистой приведенной стоимости используется, чтобы рассчитать ожидаемую доходность инвестиционного проекта и сроки его окупаемости;
Для вычисления NPV понадобится учесть ряд показателей: стартовый капитал, вложенный в проект в качестве персональных инвестиций, ставку. дисконтирования, временной отрезок и денежные потоки за выбранный период;
Для более корректного результата необходимо включить в расчете все предполагаемые риски, с которыми можно столкнуться в ходе проекта.
Инвестируйте из любой точки мира, покупайте и продавайте валюту по выгодному курсу, пользуйтесь умными подсказками и качественной аналитикой.
Приложение БКС Мир инвестиций
Отсканируйте QR-код и скачайте приложение
Прогноз цены: как применять технический и фундаментальный анализ рынка
Как составить личный финансовый план. Пошаговая инструкция
Приведенная стоимость (PV) относится к приведенной стоимости всех будущих притоков денежных средств в компанию в течение определенного периода времени, тогда как чистая приведенная стоимость (NPV) представляет собой стоимость, полученную путем вычета приведенной стоимости всех оттоков денежных средств компании из текущая стоимость общего денежного притока компании.
Оглавление
- Разница между PV и NPV
- Что такое текущая стоимость (PV)?
- Что такое чистая приведенная стоимость (NPV)?
- Инфографика PV и NPV
- Ключевое отличие
- Сравнительная таблица PV и NPV
- Заключение
- Рекомендуемые статьи
Что такое текущая стоимость (PV)?
PV или Текущая стоимость представляет собой сумму всех будущих денежных потоков, дисконтированных с определенной нормой прибыли. Текущая стоимость также известна как дисконтированная стоимость, и она помогает определить справедливую стоимость будущих доходов или обязательств. Расчет приведенной стоимости является очень важным понятием в финансах, а также используется при расчете стоимости компании. Это понятие также важно при определении цены облигации, ставок спот, стоимости аннуитетов, а также для расчета пенсионных обязательств. Расчет текущей стоимости помогает определить, сколько вам нужно для достижения будущей цели, такой как покупка дома или оплата обучения. Это также поможет вам рассчитать, следует ли вам покупать автомобиль на EMI или платить по ипотеке.
Текущая стоимость рассчитывается по уравнению:
Текущая стоимость = FV / (1 + r)n
где
- FV – это будущая стоимость
- r — требуемая норма прибыли, n — количество периодов.
Чем выше ставка, тем ниже доходность. Это связано с тем, что денежные потоки дисконтируются по более высокой ставке.
Мы хотим узнать текущую стоимость 100 долларов через год, из которых ставка дисконтирования составляет 10%.
- Текущая стоимость = 100/(1+10%)1 = 91 доллар.
Что такое чистая приведенная стоимость (NPV)?
NPVNPVЧистая приведенная стоимость (NPV) оценивает прибыльность проекта и представляет собой разницу между приведенной стоимостью притока денежных средств и приведенной стоимостью оттока денежных средств за период времени проекта. Если разница положительна, проект прибыльный; в противном случае это не .Читать далее, или чистая приведенная стоимость, представляет собой сумму всех приведенных стоимостей серии платежей и будущих денежных потоков. NPV обеспечивает метод сравнения продуктов, денежные потоки которых распределены по годам. Эта концепция может использоваться в кредитах, выплатах, инвестициях и многих других приложениях. Чистая приведенная стоимость представляет собой разницу между сегодняшними ожидаемыми денежными потоками и сегодняшней стоимостью денежных инвестиций. Денежные инвестиции Денежные инвестиции — это инвестиции в краткосрочные инструменты или сберегательный счет, как правило, на 90 дней или менее, которые обычно имеют низкую процентную ставку или доход с высокой доходностью. сравнительно низкий уровень риска по сравнению с другими формами инвестирования.Подробнее.
Это также важная концепция в составлении бюджета капиталовложений. Это сложный и всеобъемлющий способ расчета и понимания финансовой жизнеспособности проекта. Эта концепция включает в себя множество других финансовых концепций, таких как денежные потоки, требуемый доход (средневзвешенная стоимость капитала), конечная стоимость. Это значение является постоянным значением с этого момента. подробнее, временная стоимость денегВременная стоимость денегПринцип временной стоимости денег (TVM) утверждает, что деньги, полученные в настоящем, имеют более высокую ценность, чем деньги, полученные в будущем, потому что деньги, полученные сейчас, можно инвестировать и использовать для создания денежных потоков в будущем. предприятие в будущем в форме процентов или от будущего прироста инвестиций и реинвестирования. Читать далее, а также ликвидационная стоимостьСпасательная стоимостьСпасательная стоимость или ликвидационная стоимость — это оценочная стоимость актива после окончания срока его полезного использования. Например, если оборудование компании имеет срок службы 5 лет и по истечении этого срока оценивается всего в 5000 долларов, ликвидационная стоимость составит 5000 долларов.Подробнее
Положительная приведенная стоимость означает, что компания получает больше доходов, чем расходов, и получает прибыль. Считается, что если компания оценивает, что проект имеет положительную чистую текущую стоимость, то проект считается прибыльным, а проект с отрицательными денежными потокамиОтрицательный денежный потокОтрицательный денежный поток относится к ситуации, когда денежные расходы компании больше чем генерация денежных средств в конкретный рассматриваемый период. Это означает, что общий приток денежных средств от различных рассматриваемых видов деятельности меньше общего оттока за тот же период. Читать далее предполагается убыточным.
Чистую текущую стоимость можно рассчитать по формуле.
Где R1 = чистый денежный поток в первом периоде, R2 = чистый денежный поток во втором периоде, R3 = чистый денежный поток в третьем периоде и i = ставка дисконтирования.
Предположим, что компания покупает машину за 1000 долларов, которая генерирует денежные потоки в размере 600 долларов в первый год, 550 долларов во второй год, 400 долларов в третий год и 100 долларов в четвертый год. Рассчитайте чистую текущую стоимостьНастоящая стоимостьНастоящая стоимость (PV) — это сегодняшняя стоимость денег, которую вы ожидаете получить от будущих доходов. Он рассчитывается как сумма будущих доходов от инвестиций, дисконтированных по определенной ставке ожидаемой доходности. подробнее при условии, что ставка дисконтирования составляет 15%.
- чистая приведенная стоимость = [ $600/(1+15)1 + $550/(1+15)2 + $400/(1+15)3 + $100/(1+15)4 ] – 1000 долларов
- Чистая приведенная стоимость = 257,8 долл. США
Инфографика PV и NPV
Ключевое отличие
- Приведенная стоимость или PV — это сумма всех будущих притоков денежных средств по определенной ставке. С другой стороны, чистая приведенная стоимость представляет собой разницу между денежными потоками, полученными в разные периоды, и первоначальными инвестициями, необходимыми для финансирования.
- Текущая стоимость помогает в принятии инвестиционных решений для автомобилей или для расчета стоимости обязательств, инвестиционных решений, связанных с облигациями, спотовыми ставкамиСпотовые ставкиСпотовая ставка — это денежная ставка, по которой происходит немедленная сделка и/или расчет между покупателем и продавцом. . Эту ставку можно рассматривать для любых и всех видов продуктов, распространенных на рынке, от потребительских товаров до недвижимости и рынков капитала. Он дает непосредственную стоимость продукта, с которым осуществляется сделка. Подробнее и т. д. С другой стороны, чистая текущая стоимость в основном используется компаниями при оценке решений по бюджетированию капиталовложений. Здесь важно отметить, что предполагается, что каждый проект с положительной чистой приведенной стоимостью является прибыльным. Для компании, которая имеет неограниченные источники денежных средств, она может принимать только такие решения; такой сценарий невозможен в реальном мире. Проекты с самым высоким NPV выбираются компанией вместе с другими показателями, такими как IRR (внутренняя норма доходности), PB (период окупаемости), DPB (дисконтированный период окупаемости) Дисконтированный период окупаемости , основанный на временной стоимости денег. Он определяет ожидаемый доход от предлагаемой возможности капитальных вложений. Он добавляет дисконтирование к первоначальному определению периода окупаемости, что значительно повышает точность результата. Подробнее)
- Расчет приведенной стоимости — это просто дисконтирование будущего денежного потока на требуемую норму прибыли за требуемый период. Однако чистая приведенная стоимость является более сложной и учитывает денежные потоки в разные периоды.
- Чистая текущая стоимость помогает в расчете прибыльности, в то время как текущая стоимость не помогает в расчете создания богатства или прибыльности.
- Чистая приведенная стоимость учитывает первоначальные инвестиции, необходимые для расчета чистой цифры, в то время как приведенная стоимость учитывает только денежный поток.
- Очень важно понимать концепцию Приведенной стоимости; однако концепция чистой приведенной стоимости является более всеобъемлющей и сложной.
Сравнительная таблица PV и NPV
ОсноваПриведенная стоимостьЧистая приведенная стоимостьОпределениеТекущая стоимость рассчитывает дисконтированные денежные потоки всех доходов, которые, по оценкам, будут получены в проекте. Чистая приведенная стоимость рассчитывает, насколько прибыльным является проект после расчета необходимых первоначальных инвестиций.МераОн измеряет стоимость будущих денежных потоков сегодня. Он измеряет стоимость проекта. Должна ли компания браться за проект или нетСоздание богатстваТекущая стоимость дает абсолютное число и не измеряет созданное дополнительное богатство. NPV рассчитывает дополнительное богатство, созданное путем расчета прибыльности проекта.ПринятиеМетод PV прост и понятен широкой публике и может использоваться в их повседневном процессе принятия решений. Чистая приведенная стоимость используется в основном бизнес-менеджерами и помогает в составлении бюджета капиталовложений. Составление бюджета капиталовложений — это процесс планирования долгосрочных инвестиций, который определяет являются ли проекты плодотворными для бизнеса и принесут ли требуемую отдачу в последующие годы или нет. Это необходимо, потому что капитальные затраты требуют значительного количества средств. Читать далее решений.Денежный потокPV рассчитывает текущую стоимость притока денежных средств, которая генерируется за определенный период. NPV выбивает приток денежных средств с оттоком денежных средств для принятия решения.
Заключение
Приведенная стоимость является ступенькой к пониманию концепции чистой приведенной стоимости. Применение обеих этих концепций очень важно в процессе принятия решений для человека и компании. Однако другие концепции, наряду с этими двумя, помогут инвестору или бизнес-менеджеру принимать более обоснованные решения.
Рекомендуемые статьи
Это было руководство по сравнению NPV и PV (текущей стоимости и чистой приведенной стоимости). Здесь мы обсуждаем основную разницу между NPV (чистая приведенная стоимость) и PV (текущая стоимость), а также инфографику и сравнительную таблицу. Вы также можете ознакомиться со следующими статьями –
- NPV против IRR
- ЧПС в Excel
- NPV против XNPV
- Оценка дисконтированных денежных потоков
In economics and finance, present value (PV), also known as present discounted value, is the value of an expected income stream determined as of the date of valuation. The present value is usually less than the future value because money has interest-earning potential, a characteristic referred to as the time value of money, except during times of zero- or negative interest rates, when the present value will be equal or more than the future value.[1] Time value can be described with the simplified phrase, «A dollar today is worth more than a dollar tomorrow». Here, ‘worth more’ means that its value is greater than tomorrow. A dollar today is worth more than a dollar tomorrow because the dollar can be invested and earn a day’s worth of interest, making the total accumulate to a value more than a dollar by tomorrow. Interest can be compared to rent.[2] Just as rent is paid to a landlord by a tenant without the ownership of the asset being transferred, interest is paid to a lender by a borrower who gains access to the money for a time before paying it back. By letting the borrower have access to the money, the lender has sacrificed the exchange value of this money, and is compensated for it in the form of interest. The initial amount of borrowed funds (the present value) is less than the total amount of money paid to the lender.
Present value calculations, and similarly future value calculations, are used to value loans, mortgages, annuities, sinking funds, perpetuities, bonds, and more. These calculations are used to make comparisons between cash flows that don’t occur at simultaneous times,[1] since time and dates must be consistent in order to make comparisons between values. When deciding between projects in which to invest, the choice can be made by comparing respective present values of such projects by means of discounting the expected income streams at the corresponding project interest rate, or rate of return. The project with the highest present value, i.e. that is most valuable today, should be chosen.
Background[edit]
If offered a choice between $100 today or $100 in one year, and there is a positive real interest rate throughout the year, a rational person will choose $100 today. This is described by economists as time preference. Time preference can be measured by auctioning off a risk free security—like a US Treasury bill. If a $100 note with a zero coupon, payable in one year, sells for $80 now, then $80 is the present value of the note that will be worth $100 a year from now. This is because money can be put in a bank account or any other (safe) investment that will return interest in the future.
An investor who has some money has two options: to spend it right now or to save it. But the financial compensation for saving it (and not spending it) is that the money value will accrue through the compound interest that he or she will receive from a borrower (the bank account in which he has the money deposited).
Therefore, to evaluate the real value of an amount of money today after a given period of time, economic agents compound the amount of money at a given (interest) rate. Most actuarial calculations use the risk-free interest rate which corresponds to the minimum guaranteed rate provided by a bank’s saving account for example, assuming no risk of default by the bank to return the money to the account holder on time. To compare the change in purchasing power, the real interest rate (nominal interest rate minus inflation rate) should be used.
The operation of evaluating a present value into the future value is called a capitalization (how much will $100 today be worth in 5 years?). The reverse operation—evaluating the present value of a future amount of money—is called a discounting (how much will $100 received in 5 years—at a lottery for example—be worth today?).
It follows that if one has to choose between receiving $100 today and $100 in one year, the rational decision is to choose the $100 today. If the money is to be received in one year and assuming the savings account interest rate is 5%, the person has to be offered at least $105 in one year so that the two options are equivalent (either receiving $100 today or receiving $105 in one year). This is because if $100 is deposited in a savings account, the value will be $105 after one year, again assuming no risk of losing the initial amount through bank default.
Interest rates[edit]
Interest is the additional amount of money gained between the beginning and the end of a time period. Interest represents the time value of money, and can be thought of as rent that is required of a borrower in order to use money from a lender.[2][3] For example, when an individual takes out a bank loan, the individual is charged interest. Alternatively, when an individual deposits money into a bank, the money earns interest. In this case, the bank is the borrower of the funds and is responsible for crediting interest to the account holder. Similarly, when an individual invests in a company (through corporate bonds, or through stock), the company is borrowing funds, and must pay interest to the individual (in the form of coupon payments, dividends, or stock price appreciation).[1]
The interest rate is the change, expressed as a percentage, in the amount of money during one compounding period. A compounding period is the length of time that must transpire before interest is credited, or added to the total.[2] For example, interest that is compounded annually is credited once a year, and the compounding period is one year. Interest that is compounded quarterly is credited four times a year, and the compounding period is three months. A compounding period can be any length of time, but some common periods are annually, semiannually, quarterly, monthly, daily, and even continuously.
There are several types and terms associated with interest rates:
- Compound interest, interest that increases exponentially over subsequent periods,
- Simple interest, additive interest that does not increase
- Effective interest rate, the effective equivalent compared to multiple compound interest periods
- Nominal annual interest, the simple annual interest rate of multiple interest periods
- Discount rate, an inverse interest rate when performing calculations in reverse
- Continuously compounded interest, the mathematical limit of an interest rate with a period of zero time.
- Real interest rate, which accounts for inflation.
Calculation[edit]
The operation of evaluating a present sum of money some time in the future is called a capitalization (how much will 100 today be worth in five years?). The reverse operation—evaluating the present value of a future amount of money—is called discounting (how much will 100 received in five years be worth today?).[3]
Spreadsheets commonly offer functions to compute present value. In Microsoft Excel, there are present value functions for single payments — «=NPV(…)», and series of equal, periodic payments — «=PV(…)». Programs will calculate present value flexibly for any cash flow and interest rate, or for a schedule of different interest rates at different times.
Present value of a lump sum[edit]
The most commonly applied model of present valuation uses compound interest. The standard formula is:
Where 
is the future amount of money that must be discounted, 
is the number of compounding periods between the present date and the date where the sum is worth , 
is the interest rate for one compounding period (the end of a compounding period is when interest is applied, for example, annually, semiannually, quarterly, monthly, daily). The interest rate, , is given as a percentage, but expressed as a decimal in this formula.
Often, 
is referred to as the Present Value Factor [2]
This is also found from the formula for the future value with negative time.
For example, if you are to receive $1000 in five years, and the effective annual interest rate during this period is 10% (or 0.10), then the present value of this amount is
The interpretation is that for an effective annual interest rate of 10%, an individual would be indifferent to receiving $1000 in five years, or $620.92 today.[1]
The purchasing power in today’s money of an amount of money, years into the future, can be computed with the same formula, where in this case is an assumed future inflation rate.
If we are using lower discount rate(i ), then it allows the present values in the discount future to have higher values.
Net present value of a stream of cash flows[edit]
A cash flow is an amount of money that is either paid out or received, differentiated by a negative or positive sign, at the end of a period. Conventionally, cash flows that are received are denoted with a positive sign (total cash has increased) and cash flows that are paid out are denoted with a negative sign (total cash has decreased). The cash flow for a period represents the net change in money of that period.[3] Calculating the net present value, 
, of a stream of cash flows consists of discounting each cash flow to the present, using the present value factor and the appropriate number of compounding periods, and combining these values.[1]
For example, if a stream of cash flows consists of +$100 at the end of period one, -$50 at the end of period two, and +$35 at the end of period three, and the interest rate per compounding period is 5% (0.05) then the present value of these three Cash Flows are:
- respectively
Thus the net present value would be:
There are a few considerations to be made.
- The periods might not be consecutive. If this is the case, the exponents will change to reflect the appropriate number of periods
- The interest rates per period might not be the same. The cash flow must be discounted using the interest rate for the appropriate period: if the interest rate changes, the sum must be discounted to the period where the change occurs using the second interest rate, then discounted back to the present using the first interest rate.[2] For example, if the cash flow for period one is $100, and $200 for period two, and the interest rate for the first period is 5%, and 10% for the second, then the net present value would be:
- The interest rate must necessarily coincide with the payment period. If not, either the payment period or the interest rate must be modified. For example, if the interest rate given is the effective annual interest rate, but cash flows are received (and/or paid) quarterly, the interest rate per quarter must be computed. This can be done by converting effective annual interest rate, , to nominal annual interest rate compounded quarterly:
- [2]
Here, 
is the nominal annual interest rate, compounded quarterly, and the interest rate per quarter is 
Present value of an annuity[edit]
Many financial arrangements (including bonds, other loans, leases, salaries, membership dues, annuities including annuity-immediate and annuity-due, straight-line depreciation charges) stipulate structured payment schedules; payments of the same amount at regular time intervals. Such an arrangement is called an annuity. The expressions for the present value of such payments are summations of geometric series.
There are two types of annuities: an annuity-immediate and annuity-due. For an annuity immediate, payments are received (or paid) at the end of each period, at times 1 through , while for an annuity due, payments are received (or paid) at the beginning of each period, at times 0 through 
.[3] This subtle difference must be accounted for when calculating the present value.
An annuity due is an annuity immediate with one more interest-earning period. Thus, the two present values differ by a factor of 
:
- [2]
The present value of an annuity immediate is the value at time 0 of the stream of cash flows:
![PV=sum _{{k=1}}^{{n}}{frac {C}{(1+i)^{{k}}}}=Cleft[{frac {1-(1+i)^{{-n}}}{i}}right],qquad (1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/a066ae37c39918d2d70ded42d528b3fdd4d62f56)
where:
- = number of periods,
- = amount of cash flows,
- = effective periodic interest rate or rate of return.
An approximation for annuity and loan calculations[edit]
The above formula (1) for annuity immediate calculations offers little insight for the average user and requires the use of some form of computing machinery. There is an approximation which is less intimidating, easier to compute and offers some insight for the non-specialist. It is given by [4]
Where, as above, C is annuity payment, PV is principal, n is number of payments, starting at end of first period, and i is interest rate per period. Equivalently C is the periodic loan repayment for a loan of PV extending over n periods at interest rate, i. The formula is valid (for positive n, i) for ni≤3. For completeness, for ni≥3 the approximation is 
.
The formula can, under some circumstances, reduce the calculation to one of mental arithmetic alone. For example, what are the (approximate) loan repayments for a loan of PV = $10,000 repaid annually for n = ten years at 15% interest (i = 0.15)? The applicable approximate formula is C ≈ 10,000*(1/10 + (2/3) 0.15) = 10,000*(0.1+0.1) = 10,000*0.2 = $2000 pa by mental arithmetic alone. The true answer is $1993, very close.
The overall approximation is accurate to within ±6% (for all n≥1) for interest rates 0≤i≤0.20 and within ±10% for interest rates 0.20≤i≤0.40. It is, however, intended only for «rough» calculations.
Present value of a perpetuity[edit]
A perpetuity refers to periodic payments, receivable indefinitely, although few such instruments exist. The present value of a perpetuity can be calculated by taking the limit of the above formula as n approaches infinity.
Formula (2) can also be found by subtracting from (1) the present value of a perpetuity delayed n periods, or directly by summing the present value of the payments
which form a geometric series.
Again there is a distinction between a perpetuity immediate – when payments received at the end of the period – and a perpetuity due – payment received at the beginning of a period. And similarly to annuity calculations, a perpetuity due and a perpetuity immediate differ by a factor of :
- [2]
PV of a bond[edit]
- See: Bond valuation #Present value approach
A corporation issues a bond, an interest earning debt security, to an investor to raise funds.[3] The bond has a face value, 
, coupon rate, 
, and maturity date which in turn yields the number of periods until the debt matures and must be repaid. A bondholder will receive coupon payments semiannually (unless otherwise specified) in the amount of 
, until the bond matures, at which point the bondholder will receive the final coupon payment and the face value of a bond, 
.
The present value of a bond is the purchase price.[2]
The purchase price can be computed as:
![PV=left[sum _{{k=1}}^{{n}}Fr(1+i)^{{-k}}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ded6592018770a0310beed7f91db0372ad6426b3)
The purchase price is equal to the bond’s face value if the coupon rate is equal to the current interest rate of the market, and in this case, the bond is said to be sold ‘at par’. If the coupon rate is less than the market interest rate, the purchase price will be less than the bond’s face value, and the bond is said to have been sold ‘at a discount’, or below par. Finally, if the coupon rate is greater than the market interest rate, the purchase price will be greater than the bond’s face value, and the bond is said to have been sold ‘at a premium’, or above par.[3]
Technical details[edit]
Present value is additive. The present value of a bundle of cash flows is the sum of each one’s present value. See time value of money for further discussion.
These calculations must be applied carefully, as there are underlying assumptions:
- That it is not necessary to account for price inflation, or alternatively, that the cost of inflation is incorporated into the interest rate; see Inflation-indexed bond.
- That the likelihood of receiving the payments is high — or, alternatively, that the default risk is incorporated into the interest rate; see Corporate bond #Risk analysis.
(In fact, the present value of a cashflow at a constant interest rate is mathematically one point in the Laplace transform of that cashflow, evaluated with the transform variable (usually denoted «s») equal to the interest rate. The full Laplace transform is the curve of all present values, plotted as a function of interest rate. For discrete time, where payments are separated by large time periods, the transform reduces to a sum, but when payments are ongoing on an almost continual basis, the mathematics of continuous functions can be used as an approximation.)
Variants/approaches[edit]
There are mainly two flavors of Present Value. Whenever there will be uncertainties in both timing and amount of the cash flows, the expected present value approach will often be the appropriate technique. With Present Value under uncertainty, future dividends are replaced by their conditional expectation.
- Traditional Present Value Approach – in this approach a single set of estimated cash flows and a single interest rate (commensurate with the risk, typically a weighted average of cost components) will be used to estimate the fair value.
- Expected Present Value Approach – in this approach multiple cash flows scenarios with different/expected probabilities and a credit-adjusted risk free rate are used to estimate the fair value.
Choice of interest rate[edit]
The interest rate used is the risk-free interest rate if there are no risks involved in the project. The rate of return from the project must equal or exceed this rate of return or it would be better to invest the capital in these risk free assets. If there are risks involved in an investment this can be reflected through the use of a risk premium. The risk premium required can be found by comparing the project with the rate of return required from other projects with similar risks. Thus it is possible for investors to take account of any uncertainty involved in various investments.
Present value method of valuation[edit]
An investor, the lender of money, must decide the financial project in which to invest their money, and present value offers one method of deciding.[1]
A financial project requires an initial outlay of money, such as the price of stock or the price of a corporate bond. The project claims to return the initial outlay, as well as some surplus (for example, interest, or future cash flows). An investor can decide which project to invest in by calculating each projects’ present value (using the same interest rate for each calculation) and then comparing them. The project with the smallest present value – the least initial outlay – will be chosen because it offers the same return as the other projects for the least amount of money.[2]
Years’ purchase[edit]
The traditional method of valuing future income streams as a present capital sum is to multiply the average expected annual cash-flow by a multiple, known as «years’ purchase». For example, in selling to a third party a property leased to a tenant under a 99-year lease at a rent of $10,000 per annum, a deal might be struck at «20 years’ purchase», which would value the lease at 20 * $10,000, i.e. $200,000. This equates to a present value discounted in perpetuity at 5%. For a riskier investment the purchaser would demand to pay a lower number of years’ purchase. This was the method used for example by the English crown in setting re-sale prices for manors seized at the Dissolution of the Monasteries in the early 16th century. The standard usage was 20 years’ purchase.[5]
See also[edit]
- Capital budgeting
- Derivative (finance)
- Lifetime value
- Liquidation
- Net present value
References[edit]
- ^ a b c d e f Moyer, Charles; William Kretlow; James McGuigan (2011). Contemporary Financial Management (12 ed.). Winsted: South-Western Publishing Co. pp. 147–498. ISBN 9780538479172.
- ^ a b c d e f g h i j Broverman, Samuel (2010). Mathematics of Investment and Credit. Winsted: ACTEX Publishers. pp. 4–229. ISBN 9781566987677.
- ^ a b c d e f Ross, Stephen; Randolph W. Westerfield; Bradford D. Jordan (2010). Fundamentals of Corporate Finance (9 ed.). New York: McGraw-Hill. pp. 145–287. ISBN 9780077246129.
- ^ Swingler, D. N., (2014), «A Rule of Thumb approximation for time value of money calculations», Journal of Personal Finance, Vol. 13,Issue 2, pp.57-61
- ^ Youings, Joyce, «Devon Monastic Lands: Calendar of Particulars for Grants 1536–1558», Devon & Cornwall Record Society, New Series, Vol.1, 1955
Further reading[edit]
- Henderson, David R. (2008). «Present Value». Concise Encyclopedia of Economics (2nd ed.). Indianapolis: Library of Economics and Liberty. ISBN 978-0865976658. OCLC 237794267.
Инвестирование – это способ получения стабильного дохода путем вложения денег в бизнес, финансовые проекты, расширения уже функционирующего предприятия. Не ошибиться в выборе объекта вложения капитала позволяет расчет NPV. Разберем, что это за показатель, зачем он нужен, как рассчитывается и многие другие сопутствующие вопросы.
Что такое NPV
NPV (Net Present Value) или чистая приведенная стоимость – это показатель, для оценки экономической эффективности инвестиционных проектов. Он позволяет оценить разницу между совокупными текущими денежными поступлениями и затратами на инвестиционный проект с учетом стоимости денег в данный момент времени.
NPV показывает, сколько денег вы заработаете или потеряете в результате инвестирования в проект с учетом времени и стоимости денег в будущем. Если NPV положительный, то инвестиция считается эффективной, а если отрицательный, то неэффективной.
В русскоязычном варианте можно встретить три альтернативных термина, которые имеют некоторые отличия:
- Чистая приведенная стоимость (ЧПС). Это один из основных инструментов оценки бизнес-проектов. Стоит отметить, что ЧПС применяют для определения потенциальной прибыли компании, принимая во внимание различные аспекты, в том числе фактические затраты на проект, налоговые платежи, расходы по оплате кредитования производства.
Это показатель, который рассматривает все фактические и последующие денежные потоки, а также ставку дисконтирования, чтобы определить, насколько ценный может быть проект.
В основе расчета ЧПС лежит формула, которая учитывает все денежные потоки, производимые проектом. Для расчета ЧПС используется ставка дисконтирования, которая отражает стоимость капитала, затраченного на инвестиционный сценарий. - Чистый дисконтированный доход (ЧДД) – другой термин, который применяется для обозначения ЧПС. Он делает акцент на том, что значения сначала подвергаются дисконтированию, а после складываются. С помощью ЧДД можно рассчитать размер прибыли, которую можно получить от финансового проекта, учитывая время и затраты.
- Чистая текущая стоимость (ЧТС) – третий термин, который применяется для обозначения ЧПС. Он отражает текущую стоимость всей суммы денежных потоков, связанных с инвестиционным проектом. Это показатель, который учитывает стоимость денег в нынешнее время, а не в будущем.
Стоит отметить, что расчет ЧДД возможен за любой отрезок времени, например, за 5, 7 или более лет. Все зависит от потребности и целей компании.
Простыми словами, «Net Present Value» – это метод определения финансовой целесообразности инвестиционного проекта. Он позволяет определить, будет ли проект давать доход или убыток в определенный год в будущем. Для этого NPV анализирует все поступления финансов и расходы, а также применяет дисконтирование для приведения дальнейших денежных потоков к текущей стоимости. Более высокое полученное значение NPV означает более выгодный сценарий. NPV может быть использован для сравнения разных направлений инвестирования и выбора наиболее прибыльной. Однако, при расчетах нужно учитывать ряд факторов, таких как инфляция, продолжительность, точность прогнозов поступлений и расходов и т.д.
Зачем нужно считать NPV
Главный фактор в современном бизнесе – финансовая успешность. Инвесторы и менеджеры сталкиваются с постоянной необходимостью принимать решения о вложении определенной суммы денег в различные программы и бизнесы, чтобы получить максимальную отдачу от своих инвестиций. Именно здесь важную роль играет понимание концепции Net Present Value (NPV) – показателя, который выражает современную стоимость денежных потоков и дает оценку эффективности деятельности компании.
Существует несколько целей, для которых используют расчет NPV:
- Определение размера первоначальных вложений. Это имеет значение для инвесторов, которые хотят понимать, сколько средств им будет нужно для старта и какие затраты потребуются на каждом этапе реализации. Расчет NPV помогает определить размер инвестиций, который нужно внести, чтобы достичь желаемых показателей. Кроме того, NPV также дает возможность оценить, насколько эффективно использованы вложенные средства.
- Вычисление сроков окупаемости. Эта цель также очень важна для инвесторов, которые хотят знать, сколько времени требуется, чтобы проект начал приносить прибыль и начал окупаться. Расчет NPV может помочь определить срок его окупаемости, что позволит вкладчикам принимать обоснованные решения и планировать свои дальнейшие действия.
- Оценка размеров дохода, требуемого для окупаемости. Эта цель связана с поиском необходимого уровня доходности, который должен быть достигнут, чтобы инвесторы могли окупить свои инвестиции. Расчет NPV обеспечивает возможность оценить размеры дохода, необходимые для достижения желаемой точки окупаемости. Кроме того, это также помогает вкладчикам оценить, как изменение финансовых параметров программы может повлиять на ее доходность.
- Доходность у конкурентов. Определяет, какой уровень доходности необходим для того, чтобы проект стал конкурентоспособным на рынке. Если вложенные ресурсы приводят к меньшей отдаче, чем у других компаний, то это может негативно сказаться на финансовом положении компании. Поэтому, при проектировании и разработке новых программ, нужно использовать этот фактор и стремиться к тому, чтобы доходность была не менее, чем у других участников данного рынка.
Расчет NPV является одним из главных инструментов для оценки финансовой эффективности планов и принятия решений об инвестировании. Он нужен для определения размера первоначальных вложений, вычисления сроков окупаемости, оценки необходимого дохода для окупаемости и сравнения отдачи от инвестиций с конкурентами. Все эти цели важны для бизнеса и помогают инвесторам и руководству компании принимать обоснованные решения в области инвестирования и развития бизнеса.
Как рассчитать NPV
Чтобы рассчитать NPV, требуется определить все поступления и расходы проекта на каждый год, затем дисконтировать каждый годовой поток денежных средств на основе соответствующей ставки, которая обычно равна стоимости капитала компании или другой альтернативной инвестиции. Затем суммируются все дисконтированные потоки денег за каждый год и вычитается начальный капитал, который был вложен в проект. Полученное значение и будет являться NPV.
Формула расчета чистой приведенной стоимости выглядит следующим образом:
Где:
n — отрезок времени, за который производится расчет;
Pk — денежный поток (cash flow) за данный временной интервал;
i — ставка дисконтирования;
IC — вложенный капитал на этапе первоначальных инвестиций.
По этой формуле можно рассчитать текущую стоимость предстоящих денежных потоков и оценить экономическую целесообразность для инвестора. Для расчета NPV нужно определить сумму намеченных денежных потоков, сроки их получения, а также оценить стоимость капитала. Результат расчета NPV может показать, является ли проект прибыльным или убыточным, а также какая величина доходности может ожидаться в будущем.
Цифры для расчета NPV инвестиционного проекта
Расчет NPV является важным инструментом для оценки инвестиционных программ, чтобы, решить стоит ли инвестировать в проект, и какие будут ожидаемые доходы. Для расчета NPV нужно знать некоторые входные данные, которые мы рассмотрим в этой статье.
Список цифр для расчета NPV:
- Размер первоначальных вложений (Initial Investment) – сумма денег, которой достаточно вложить в проект в начале.
- Продолжительность проекта (Project Life) – количество лет, в течение которых проект будет действовать.
- Доходы от проекта (Cash Flows) — денежные потоки, которые будут получены от проекта в течение его продолжительности.
- Ставка дисконта (Discount Rate) — процентная ставка, которую инвестор использует для расчета текущей цены последующих денежных потоков.
Точный расчет является главным фактором для принятия правильного решения об инвестировании в проект. Для этого нужна достоверная информация и умение работать с формулой чистого дисконтированного дохода.
Использование данного метода позволяет инвесторам снизить риски инвестирования и увеличить вероятность успешного завершения проекта. Грамотная оценка инвестиционного проекта позволяет на начальном этапе получить представление о доходности организации в будущем.
Пример расчета NPV в Excel
Расчет величины чистого дисконтированного дохода в Excel можно выполнить с помощью следующих двух способов.
-
Первый способ заключается в создании таблицы, в которой в верхней части по периодам записываются суммы инвестиций, расходов и доходов по проекту. Затем необходимо рассчитать чистый денежный поток и выбрать один из способов расчета NPV.
Способ предполагает занесение значения i для проекта по периодам. Затем формула разбивается на блоки и последовательно рассчитывается до получения конечного показателя. Этот метод подходит, если необходимо видеть промежуточные показатели и, если ставка дисконтирования различается в различные периоды.
-
Второй способ включает использование встроенной формулы Excel, которая называется ЧПС и находится в блоке финансовых формул. Значит для этого нужно заполнить поля со значениями ставки и диапазона суммирования значений чистого денежного потока по периодам.
Давайте рассмотрим пример с использованием встроенной формулы, поскольку первый способ не так удобен и чаще рассчитывают NPV с помощью формулы.
Предположим, у нас есть определенный инвестиционный проект стоимостью 1000000 руб., который будет приносить 250000 рублей прибыли в течение 5 лет. Стоимость капитала для этого проекта составляет 10%. Чтобы сделать расчеты необходимо:
-
В Excel создайте таблицу и введите данные о затратах и доходах по проекту для каждого года в отдельной строке.
-
Следующим шагом рассчитайте чистый денежный поток проекта. Для этого вычитайте расходы (стоимость проекта) из доходов по проекту для каждого года:
Год 1: 250000 — 1000000 = -750000
Год 2: 250000 — 0 = 250000
Год 3: 250000 — 0 = 250000
Год 4: 250000 — 0 = 250000
Год 5: 250000 — 0 = 250000
-
Выберите ячейку, в которую вы хотите поместить результат NPV, далее введите формулу в таком виде: =NPV (ставка дисконтирования, диапазон чистого денежного потока).
В качестве примера, =NPV (10%,B2:B6)
Здесь ставка составляет 10%, а диапазон чистого денежного потока находится в ячейках B2:B6.
-
Нажмите Enter, чтобы завершить формулу. Excel рассчитает NPV финансового проекта.
В нашем примере NPV составляет примерно 45 366 рублей. Это говорит о том, что проект может принести положительный чистый денежный поток при условии, что стоимость капитала составляет 10%. Если ставка была бы выше, проект мог бы получить отрицательный NPV и не был бы рентабельным.
-
Анализ результата расчета NPV
После расчета NPV следует проанализировать полученные материалы. Самым главным критерием для оценки рентабельности проекта является итоговый показатель. Возможны три варианта:
- Если показатель положительный, то это означает, что инвестиционный проект является доходным и его стоит реализовывать. Более высокое значение — выше потенциальная доходность проекта.
- Если результат отрицательный, значит, что инвестиционный проект нецелесообразен и его не стоит реализовывать. В этом случае необходимо пересмотреть параметры проекта или отказаться от его реализации.
- Если же NPV 0, то это означает, что инвестиционный проект не дает ни прибыли, ни убытков. В таком случае нужно пересмотреть параметры проекта или можно принять решение о его реализации, исходя из других факторов, как пример, социальной значимости проекта.
Кроме того, следует помнить и о других факторах, таких как срок окупаемости проекта, объем инвестиций, потенциальный рост доходов и риски проекта. Все эти факторы необходимо проанализировать для принятия правильного решения о реализации инвестиционного проекта.
Ставка дисконтирования простыми словами
Ставка дисконтирования – это процентная ставка, которая используется для приведения грядущих денежных потоков в нынешнее время. Это означает, что денежные потоки, получаемые в будущем, должны быть пересчитаны на сегодняшний день с учетом их стоимости в будущем. В течении времени ставка дисконтирования, как и инфляция может меняться. Нужно не забывать учитывать эти риски.
Также необходимо учитывать коэффициент дисконтирования – значение, которое определяет денежные вложения необходимые для получения определенного дохода в будущем.
Выполнить расчет ставки дисконтирования можно просуммировав следующие факторы:
- инфляция;
- ключевая ставка Центробанка;
- премия за риск.
Существуют и другие методы расчета, например:
- CAPM – модель оценки капитальных активов. Этот инструмент чаще всего применяется в процессе инвестирования в ценные бумаги крупных корпораций.
- Метод кумулятивного построения. Для получения итогового показателя необходимо просуммировать безрисковую ставку дохода и надбавки за риск инвестирования в выбранное предприятие.
Ставка дисконтирования используется для расчета стоимости предстоящих денежных потоков на основе их текущей стоимости. Чем выше ставка, тем меньше стоит будущий денежный поток в данное время, а чем ниже ставка дисконтирования, тем он стоит больше сегодня. В бизнесе этот показатель используется для оценки проектов и определения их целесообразности на основе ожидаемой прибыли.
Преимущества и недостатки NPV
Преимущества и недостатки чистой приведенной стоимости – это важные аспекты, которые нужно знать при использовании данного инвестиционного инструмента, чтобы менеджмент был максимально эффективным.
|
Преимущества |
Недостатки |
|
|
Несмотря на эти ограничения, NPV все еще является одним из главных инструментов для оценки инвестиционных планов и принятия решений о вложении капитала.
Трудности и ошибки при расчете NPV
Несмотря на то, что NPV – это простой и эффективный инструмент для оценки привлекательности финансовых программ, при его расчете могут возникать некоторые трудности и ошибки. Ниже приведены некоторые из них.
- Неправильный выбор периода расчета. Неверное определение периода, на который производится расчет NPV, может привести к неправильным результатам. Обычно период выбирается равным жизненному циклу инвестиционного проекта.
- Неправильное определение начальных инвестиций. Начальные инвестиции должны включать все расходы, связанные с запуском проекта, включая приобретение оборудования, аренду помещения, оплату труда персонала, маркетинг и рекламу и т.д.
- Ошибочное определение потоков денежных средств. Важно точно определить все потоки денежных средств, включая доходы от продаж, затраты на обслуживание, налоги и т.д. Если какие-то потоки денежных средств упустить, то расчет NPV будет неправильным.
- Неправильный выбор ставки дисконтирования. Эта ошибка может привести к неправильному расчету NPV. Ставку следует выбирать, исходя из уровня риска инвестиционного проекта.
- Игнорирование инфляции. Инфляция может существенно повлиять на реальную стоимость инвестиционного бизнес-плана. В процессе расчетов следует использовать эти данные, чтобы получить более точный результат.
- Завышенные ожидания. Это происходит, когда ожидания относительно прибыли или успеха не соответствуют реальности. К примеру, если предположить, что продукт будет давать огромную прибыль без учета рисков или недостатков, это может стать причиной убытков. Поэтому необходимо оценивать потенциальный доход проекта с реалистической точки зрения, учитывая возможные риски и факторы, которые могут повлиять на его успех.
- Игнорирование сопутствующих расходов может привести к искажению результатов. Например, если инвестор планирует открыть ресторан, то помимо инвестиций в оборудование и персонал, необходимо учесть такие расходы, как аренда помещения, коммунальные платежи, закупка продуктов и т.д. Если не учесть эти расходы, то оценка рентабельности может быть завышенной, что приведет к неверным решениям в инвестировании. Поэтому при расчете NPV необходимо учитывать все сопутствующие расходы, которые могут повлиять на итоговую доходность.
В целом, при правильном подходе к расчету NPV и учете всех необходимых параметров, можно получить достоверное восприятие привлекательности инвестиционного плана.
Часто задаваемые вопросы
В этой статье также нужно затронуть следующие часто задаваемые вопросы.
NPV (чистая приведенная стоимость NPV) и IRR (внутренняя норма доходности) – это два метода анализа доходности инвестиционного плана. Главная разница между ними заключается в том, что NPV вычисляет денежный поток на основе заданной ставки дисконтирования, тогда как IRR определяет ту ставку, при которой NPV будет равен нулю, т.е. точку безубыточности.
Другими словами, NPV предполагает, что инвесторы могут использовать заранее заданную ставку дисконтирования для анализа потока денежных средств, а IRR позволяет инвестору вычислить сколько процентов доходности может принести предприятие.
В отличие от NPV, IRR может иметь несколько значений, что может привести к затруднениям при интерпретации результатов. NPV, в свою очередь, не имеет такого недостатка и может дать точный прогноз доходности при известной ставке дисконтирования.
Это два разных показателя оценивания инвестиционных инициатив. NPV оценивает текущую стоимость потоков денежных средств, на основе стоимости капитала, и показывает, принесет ли проект прибыль или убыток.
Период окупаемости, с другой стороны, измеряет, сколько времени нужно для полной окупаемости. Однако не учитывается сумма прибыли, которую проект может принести в долгосрочной перспективе, а только показывает, сколько лет или месяцев потребуется для того, чтобы инвестиции начали окупаться.
Хорошая чистая приведенная или дисконтированная стоимость означает, что проект приносит положительную прибыль, а стоимость будущих денежных потоков превышает изначальные инвестиции. В общем случае, чем выше показатель, тем более выгоден проект. Однако, пороговое значение для нахождения «хорошей» NPV может быть различным в зависимости от индустрии и рисков.
Ставка дисконтирования показывает, какая стоимость будущих денежных потоков будет иметь сегодняшнюю стоимость. Если ставка дисконтирования выше, то будущие денежные потоки будут иметь меньшую сегодняшнюю стоимость и, следовательно, ниже NPV. Если же она ниже, то будущие денежные потоки будут иметь большую сегодняшнюю стоимость и, следовательно, выше NPV проекта. Таким образом, высокая ставка дисконтирования снижает чистую приведенную стоимость, а — повышает ее.
Можно рассмотреть несколько возможных вариантов использования денег:
- Потратить на текущие нужды: купить товары, оплатить счета, питание, развлечения и т.д.
- Сохранить на счете в банке для будущих потребностей и возможных непредвиденных расходов.
- Инвестировать в ценные бумаги, недвижимость или другие активы для получения дополнительного дохода в будущем.
- Отложить деньги на пенсию, например, в пенсионный фонд или инвестировать в долгосрочные финансовые продукты для получения стабильного дохода после выхода на пенсию.
- Пожертвовать на благотворительность или инвестировать в социально ответственные программы.
Заключение
Мы определили, что чистая дисконтированная стоимость является одним из ключевых инструментов для оценки финансовой целесообразности инвестиционных проектов. Она позволяет оценить приведенную стоимость денежных потоков, с учетом их сроков и стоимости капитала. При расчетах необходимо учитывать реалистичные прогнозы и не игнорировать сопутствующие расходы, чтобы получить точные и полезные результаты. Кроме того, необходимо учитывать зависимость показателя от ставки дисконтирования, чтобы понимать, как изменения ставки могут повлиять на результаты. В целом, использование NPV является весомым инструментом для принятия взвешенных финансовых решений.
Алексей Ефремов
Финансовый консультант
Все статьи автора
Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter