Загрузить PDF
Загрузить PDF
Если вы умеете вычислять угловые коэффициенты (тангенс угла наклона) прямых, то на основании этих коэффициентов можно узнать другие параметры. Например, выяснить, параллельны ли прямые или же перпендикулярны, найти их точку пересечения и многие другие величины. Вычисление углового коэффициента — довольно простая задача. Прочитайте эту статью, чтобы узнать, как это сделать.
-
1
Угловой коэффициент (тангенс угла наклона) определяется как отношение изменения координаты «у» к изменению координаты «х».
Реклама
-
1
Рассмотрите любую прямую линию. Убедитесь, что линия прямая, так как угловой коэффициент вычисляется только для прямых линий.
-
2
Выберите любые две точки, лежащие на прямой. Запишите их координаты в виде (х,у). Не имеет значения, какие точки вы выберете (главное, чтобы они были разными и лежали на одной прямой).
-
3
Дайте обозначение выбранным точкам. Не имеет значения, какую из них вы обозначите первой, а какую – второй (главное — на протяжении всего процесса вычисления строго придерживаться выбранного обозначения). Координаты первой точки запишем как x1 и y1, а координаты второй точки как x2 и y2.
-
4
Подставьте координаты точек в формулу для вычисления углового коэффициента, приведенную выше.
-
5
Вычтите две координаты «у».
-
6
Вычтите две координаты «х».
-
7
Разделите результат разности координат «у» на результат разности координат «х». Сократите дробь, если возможно.
-
8
Проверьте полученный результат.
- Прямые, идущие вверх слева направо, всегда имеют положительный угловой коэффициент (даже если это дробь).
- Прямые, идущие вниз слева направо, всегда имеют отрицательный угловой коэффициент (даже если это дробь).
Реклама
Пример
- Дана прямая с точками A и B, лежащими на ней.
- Координаты точек: A(-2,0) и B(0,-2)
- (y2-y1): -2-0=-2; Изменение координаты «у» = -2
- (x2-x1): 0-(-2)=2; Изменение координаты «х» = 2
- Угловой коэффициент данной прямой равен -1.
Советы
- Как только вы обозначили координаты точек на прямой через (х1,у1) и (у1,у2), не меняйте эти обозначения, или вы получите неверный ответ.
- Вы нашли «m» в линейном уравнении вида y=mx+b, где «у» — координата «у», «m» – угловой коэффициент, «х» — координата «х», «b» – смещение прямой по оси Y (или значение координаты «у» при х=0).
- Для получения ответов на возникающие вопросы прочитайте школьный учебник или обратитесь к учителю.
Реклама
Предупреждения
- Не путайте формулу для вычисления углового коэффициента (тангенса угла наклона) прямой с любой другой формулой, например, с формулой для вычисления расстояния или формулой для вычисления средней точки.
Реклама
Что вам понадобится
- Миллиметровка (возможно).
- Координатная плоскость или прямая с координатами двух точек, лежащих на ней.
- Формула для вычисления углового коэффициента (тангенса угла наклона) прямой.
- Карандаш, бумага, линейка, калькулятор.
- Прямая.
- Координаты «х».
- Координаты «у».
Об этой статье
Эту страницу просматривали 103 403 раза.
Была ли эта статья полезной?
Задание. Найти тангенс угла между кривыми $y=x^2-1$ и
$y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.
Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:
$$begin{array}{c}
left{begin{array}{l}
y_{1}=x^{2}-1 \
y_{2}=x^{3}-1
end{array} Rightarrow x^{2}-1=x^{3}-1 Rightarrow x^{3}-x^{2}=0 Rightarrowright. \
Rightarrow x_{1,2}=0, x_{3}=1
end{array}$$
Таким образом, искомая точка $x=1$.
Далее находим производные заданных функций в найденной точке:
$$begin{array}{c}
y_{1}^{prime}=left(x^{2}-1right)^{prime}=left(x^{2}right)^{prime}-(1)^{prime}=2 x-0=2 x, y_{1}^{prime}(1)=2 \
y_{2}^{prime}=left(x^{3}-1right)^{prime}=left(x^{3}right)^{prime}-(1)^{prime}=3 x^{2}-0=3 x^{2}, y_{2}^{prime}(1)=3
end{array}$$
Итак, искомый тангенс:
$$operatorname{tg} phi=frac{3-2}{1+2 cdot 3}=frac{1}{7}$$
Ответ. $operatorname{tg} phi=frac{1}{7}$
Для
построения профиля необходимо вычислить
элементы кривой: Т –
тангенс,
К – кривая, Д – домер, Б – биссектриса.
Элементы кривой
вычисляются по формулам:
Тангенс
; Кривая
;
Домер
; Биссектриса
,
где R
– радиус
кривой, м;
– угол
поворота трассы.
Пример вычисления
элементов кривой.
В
примере вершина угла поворота пк 4 + 33,
угол поворота
= 43
26
и радиус кривой R
= 150 м.
Тангенс
м;
Кривая
м;
Домер
м;
Биссектриса
м.
2.7 Вычисление пикетажного значения главных точек кривой
Главные
точки кривой – это начало кривой (НК),
середина кривой (СК) и конец кривой (КК).
Пикетажное значение показывает расстояние
от начала трассы (НТ) до соответствующей
точки.
Вычисление
пикетажного значения главных точек
кривой выполняется по формулам:
пк НК = пк ВУ – Т;
пкКК = пкНК + К;
пкСК = пкНК +0,5К
Контроль: пкКК =
пкВУ + Т – Д;
пкКК = пкСК +0,5К.
Пример вычисления
пикетажных значений главных точек
кривой.
По
приведенным исходным данным пикетажные
значения главных точек кривой принимают
значения:
пк НК = пк ВУ – Т =
пк 4+33 – 59,74 = 3+73,26
пкКК
= пкНК + К = 373,26 + 113,65 = 486,91
пкСК
= пкНК +0,5К = пк 3+73,26 + 0,5
113,65 = 430,08
Контроль:
пкКК
= пкВУ + Т – Д = пк 4 +33 +59,74 – 5,83 = 486,91
пкКК
= пкСК +0,5К = 430,08 + 0,5
113,65 = 486,90
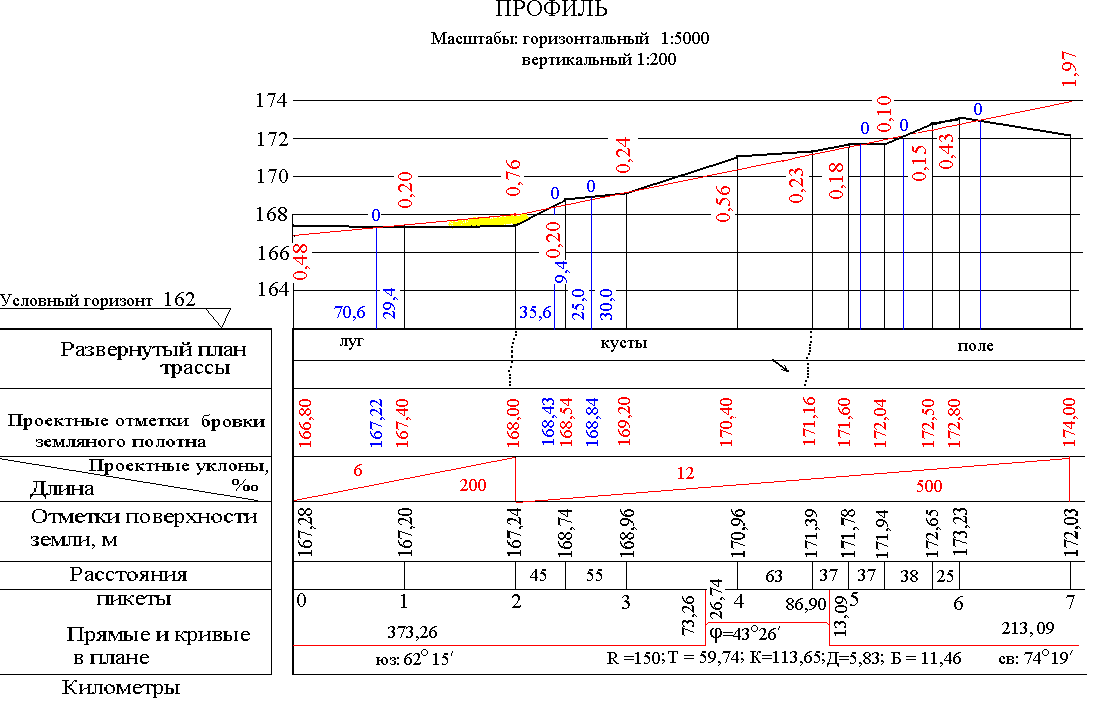
2.8 Построение продольного профиля
Профиль строится
на миллиметровой бумаге формата А3.
Масштаб для построения продольного
профиля по горизонтали и вертикали
различный. Для обеспечения наглядности
обычно вертикальный масштаб в 10 раз
крупнее горизонтального. В индивидуальном
задании указываются масштабы для
построения профиля. Профиль строится
с использованием специальной таблицы
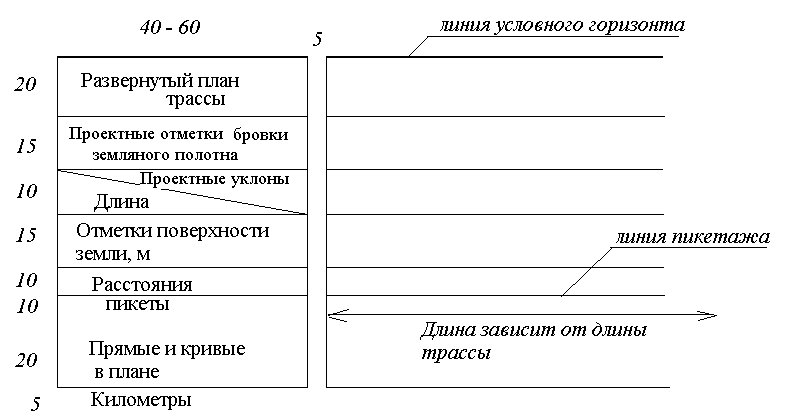
– сетки профиля. Ее размеры (в мм) и графы
приведены на рис.
7.
Рис 7. Сетка профиля
Профиль располагается
выше сетки профиля. При его построении
это необходимо учесть. Общий вид профиля
приведен на рис. 9.
Построение профиля
начинается с графы «Расстояния».
В этой графе указываются пикетные и
плюсовые точки. С учетом горизонтального
масштаба строятся полные пикеты по 100
м. В графе они отмечаются вертикальными
линиями. Если между пикетами есть
плюсовые точки, они также наносятся в
эту графу и подписываются расстояния
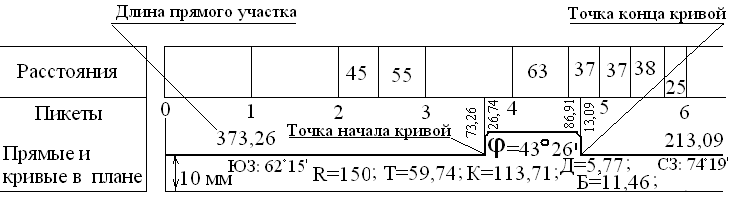
между ними (рис. 8).
Рис. 8. Заполнение
графы «Расстояния» и «Пикеты»
В примере, между
пикетами 5 и 6 расположены две плюсовые
точки: +37 и +75. Расстояния подписываются
37и38(75 – 37 = 38 м) и25(100 – 75
м). Сумма отрезков 37 + 38 + 25 = 100 м (Рис.8).
Затем заполняется
графа «Пикеты».
В этой графе подписываются пикеты около
вертикальных линий, начиная с пикета 0
(пк0) (рис. 8).
Графа «Развернутый
план трассы»
заполняется по данным пикетажа
(пикетажной книжки). По середине графы
проводится ось дороги условно развернутая
в прямую линию. Вдоль линии наносится
план местности, прилегающий к трассе и
все объекты, которые находятся в полосе
25 м влево и вправо от оси трассы,
показываются границы между угодьями и
строения. В точках, соответствующих
вершинам углов поворота показывается
направление поворота трассы (вправо
или влево). Вместо условных знаков
допускается писать соответствующее
название: «луг», «лес» и т. д. (рис. 10).
Рис. 10. Заполнение
графы «Развернутый план трассы»
Графа «Прямые
и кривые в плане»
заполняется по результатам вычисления
пикетажных значений главных точек
кривых (Рис.11). В графе проводится прямая
линия на расстоянии 10 мм от нижней
границы. По пикетажному значению точки
«Начало кривой» она наносится на профиль
с учетом горизонтального масштаба на
линии пикетажа. От линии пикетажа
опускается перпендикуляр на ось дороги,
которая проводится вдоль графы. До точки
«Начало кривой» трасса показывается
прямой линией. Аналогично показывается
точка «Конец кривой». От нее трасса так
же показывается прямой. Между точками
«Начало кривой» и «Конец кривой» ось
дороги прерывается и кривая показывается
скобой. Если поворот правый, то скоба
направлена вверх, если поворот левый,
то скоба обращена вниз.
Рис. 11. Заполнение
графы «Прямые и кривые в плане»
Вдоль перпендикуляров
от пикетажной линии до оси дороги у
точек «Начало кривой» и «Конец кривой»
подписываются расстояния от заднего
пикета до точки и от точки до переднего
пикета.
Внутри кривой
выписываются угол поворота трассы ,
радиус R,
тангенс Т, кривая К, домер Д, биссектриса
Б.
Над
серединой каждой прямой вставки
записывают ее длину, а под ней дирекционный
угол или румб. Начальное направление
трассы выдается в задании. После поворота
трассы направление меняется. Ориентирующий
угол вычисляется по формулам зависимости
дирекционного угла и румба. В нашем
примере применяется формула второй
четверти:
пк0-НК
= r
+ 180
= 6215
+ 180
= 24215;
КК-ПК7
= пк0-НК
+
= 43
26
= 285
41.
r
= 360
– 285
41
= 7419(сз).
Графа «Отметки
земли»
заполняется из «Ведомости геометрического
нивелирования». Отметки выписываются
к соответствующим пикетам и плюсовым
точкам с точностью 0,01 м.
ВНИМАНИЕ: «иксовые»
точки в построении не участвуют и их
отметки не
выписываются (рис.
2).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти тангенс угла наклона касательной
Геометрический смысл производной первого порядка функции F(х) представляет собой касательную прямую к ее графику, проходящую через заданную точку кривой и совпадающую с ней в этой точке. Причем значение производной в данной точке х0 является угловым коэффициентом или иначе – тангенсом угла наклона касательной прямой k = tg a = F`(х0). Вычисление данного коэффициента – одна из наиболее распространенных задач теории функций.

Инструкция
Запишите заданную функцию F(x), например F(x) = (x³ + 15х +26). Если в задаче явно указана точка, через которую проводится касательная, например, ее координата х0 = -2, можно обойтись без построения графика функции и дополнительных прямых на декартовой системе ОХY. Найдите производную первого порядка от заданной функции F`(x). В рассматриваемом примере F`(x) = (3x² + 15). Подставьте заданное значение аргумента х0 в производную функции и вычислите ее значение: F`(-2) = (3(-2)² + 15) = 27. Таким образом, вы нашли tg a = 27.
При рассмотрении задачи, где требуется определить тангенс угла наклона касательной к графику функции в точке пересечения этого графика с осью абсцисс, вам понадобится сначала найти числовое значение координат точки пересечения функции с ОХ. Для наглядности лучше всего выполнить построение графика функции на двухмерной плоскости ОХY.
Задайте координатный ряд для абсцисс, например, от -5 до 5 с шагом 1. Подставляя в функцию значения х, вычислите соответствующие им ординаты у и отложите на координатной плоскости полученные точки (х, у). Соедините точки плавной линией. Вы увидите на выполненном графике место пересечения функцией оси абсцисс. Ордината функции в данной точке равна нулю. Найдите численное значение соответствующего ей аргумента. Для этого заданную функцию, например F(x) = (4x² — 16), приравняйте к нулю. Решите полученное уравнение с одной переменной и вычислите х: 4x² — 16 = 0, x² = 4, х = 2. Таким образом, согласно условию задачи, тангенс угла наклона касательной к графику функции необходимо найти в точке с координатой х0 = 2.
Аналогично описанному ранее способу определите производную функции: F`(x) = 8*x. Затем вычислите ее значение в точке с х0 = 2, что соответствует точке пересечения исходной функции с ОХ. Подставьте полученное значение в производную функции и вычислите тангенс угла наклона касательной: tg a = F`(2) = 16.
При нахождении углового коэффициента в точке пересечения графика функции с осью ординат (ОY) выполните аналогичные действия. Только координату искомой точки х0 сразу следует принять равной нулю.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Угловой коэффициент касательной как тангенс угла наклона
(blacktriangleright) Если уравнение прямой задано в виде ({color{royalblue}{y=kx+b ;}}), то число (k) называется угловым коэффициентом.
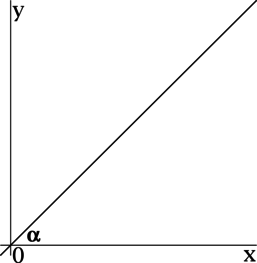
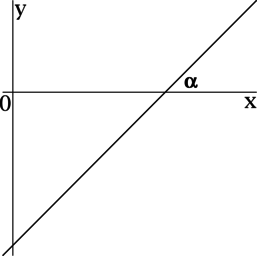
(blacktriangleright) Угол (alpha) наклона прямой – это угол между этой прямой и положительным направлением оси (Ox) ((0leqslant
alpha< 180^circ)), лежащий в верхней полуплоскости.
(blacktriangleright) Основная формула. Угловой коэффициент прямой (y=kx+b) равен тангенсу угла наклона этой прямой:
[{large{color{royalblue}{k=mathrm{tg}, alpha}}}]
Т.к. касательная к графику некоторой функции — это и есть прямая, то для нее верны все эти утверждения.
Если (alpha<90^circ), то (k>0);
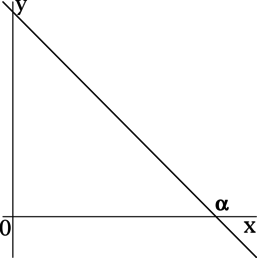
если (alpha>90^circ), то (k<0);
если (alpha=0^circ), то (k=0) (уравнение прямой имеет вид (y=b) и она параллельна оси (Ox));
если (alpha=90^circ), то уравнение прямой имеет вид (x=a) и она перпендикулярна оси (Ox).
Задание
1
#685
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = x), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = x) коэффициент (k) равен (1), то (mathrm{tg}, alpha = 1).
Ответ: 1
Задание
2
#686
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = 2x — 3), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = 2x — 3) коэффициент (k) равен (2), то (mathrm{tg}, alpha = 2).
Ответ: 2
Задание
3
#687
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = -x + 2), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = -x + 2) коэффициент (k) равен (-1), то (mathrm{tg}, alpha = -1).
Ответ: -1
Задание
4
#688
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx + 77), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = 12).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx + 77) и положительным направлением оси (Ox) равен (12), то (k = mathrm{tg}, alpha = 12).
Ответ: 12
Задание
5
#689
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx + 0,2), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = -3,3).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx + 0,2) и положительным направлением оси (Ox) равен (-3,3), то (k = mathrm{tg}, alpha = -3,3).
Ответ: -3,3
Задание
6
#690
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = 0).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx) и положительным направлением оси (Ox) равен (0), то (k = mathrm{tg}, alpha = 0).
Ответ: 0
Задание
7
#693
Уровень задания: Легче ЕГЭ
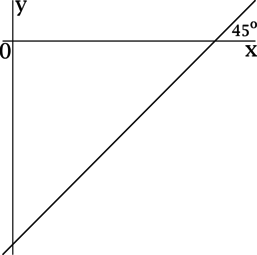
Прямая (y = kx — 2016) образует угол (45^{circ}) с положительным направлением оси (Ox). Найдите (k).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как угол между прямой (y = kx — 2016) и положительным направлением оси (Ox) равен (dfrac{pi}{4}), то (k = mathrm{tg}, dfrac{pi}{4} = 1).
Ответ: 1
Теме «Угловой коэффициент касательной как тангенс угла наклона» в аттестационном экзамене отводится сразу несколько заданий. В зависимости от их условия, от выпускника может требоваться как полный ответ, так и краткий. При подготовке к сдаче ЕГЭ по математике ученику обязательно стоит повторить задачи, в которых требуется вычислить угловой коэффициент касательной.
Сделать это вам поможет образовательный портал «Школково». Наши специалисты подготовили и представили теоретический и практический материал максимально доступно. Ознакомившись с ним, выпускники с любым уровнем подготовки смогут успешно решать задачи, связанные с производными, в которых требуется найти тангенс угла наклона касательной.
Основные моменты
Для нахождения правильного и рационального решения подобных заданий в ЕГЭ необходимо вспомнить базовое определение: производная представляет собой скорость изменения функции; она равна тангенсу угла наклона касательной, проведенной к графику функции в определенной точке. Не менее важно выполнить чертеж. Он позволит найти правильное решение задач ЕГЭ на производную, в которых требуется вычислить тангенс угла наклона касательной. Для наглядности лучше всего выполнить построение графика на плоскости ОХY.
Если вы уже ознакомились с базовым материалом на тему производной и готовы приступить к решению задач на вычисление тангенса угла наклона касательной, подобных заданиям ЕГЭ, сделать это можно в режиме онлайн. Для каждого задания, например, задач на тему «Связь производной со скоростью и ускорением тела», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут попрактиковаться в выполнении задач различного уровня сложности. В случае необходимости упражнение можно сохранить в разделе «Избранное», чтобы потом обсудить решение с преподавателем.

УСТАЛ? Просто отдохни