|
Как найти тангенс угла, если известен косинус? Как найти котангенс угла, если известен косинус? Итак, читаем внимательно условие вопроса, и вспоминаем, чему нас учили в школе, у нас есть косинус угла, и этого окажется вполне достаточным для того, чтобы мы выполнили задание автора вопроса и нашли тангенс и котангенс данного угла. Вспоминаем, что мы можем найти, зная косинус, конечно-же, мы сразу можем найти синус, это очень легко, и в этом нам поможет вот это волшебное тождество и то, что из него следует, — формула для нахождения синуса: Теперь, зная чему равен синус угла, через косинус, проще простого решать дальше по известным формулам для нахождения тангенса и котангенса, просто подставляя в них эти формулы для синуса, которые я разместила выше: система выбрала этот ответ лучшим Ксарфакс 5 лет назад Для того, чтобы найти тангенс и котангенс через косинус, достаточно вспомнить тригонометрические формулы: tgα = sinα / cosα. ctgα = cosα / sinα. Так как косинус известен, то синус можно найти из основного тригонометрического тождества: sin²α + cos²α = 1. sinα = √(1 — cos²α), если угол α находится в 1 и 2 четверти. sinα = — √(1 — cos²α), если угол α находится в 3 и 4 четверти. Таким образом: tgα = ± √(1 — cos²α) / cosα. ctgα = ± cosα / √(1 — cos²α). Так как произведение тангенса и котангенса = 1, то ctgα также можно найти из формулы: ctgα = 1 / tgα. Пример Косинус угла α равен 0,94, при этом α находится в 1 четверти (0 < α < 90). Нужно найти тангенс и котангенс. Воспользуемся формулой: tgα = √(1 — cos²α) / cosα. В первой четверти синус и косинус больше 0, поэтому тангенс и котангенс также будут положительными. tgα ≈ 0,34 / 0,94 ≈ 0,36. Соответственно ctgα ≈ 1 / 0,36 ≈ 2,78. Лара Изюминка 6 месяцев назад В школе изучают следующую тригонометрическую формулу: Косинус в квадрате альфа равно единица разделить на сумму единицы и тангенса в квадрате альфа. Из этой формулы легко выразить тангенс в квадрате альфа. Он очевидно равен 1 деленная на косинус в квадрате альфа и из этой дроби нужно вычесть один, а можно еще преобразовать как на картинке. Ну, а для того чтобы выразить котангенс, нужно вспомнить , что произведение тангенса и котангенса равно единице, тогда просто меняем числитель и знаменатель местами и получается формула для нахождения котангенса через косинус. Ну, а знак тангенса и котангенса определяем по той четверти, в которой находится угол. Если это первая и третья четверти, то плюс, иначе минус. bezdelnik 5 лет назад tg а = Sin a/Cos a. Чтобы выразить тангенс через косинус осталось выразить синус через косинус. Для этого воспользуемся основной тригонометрической формулой (Sin a)^2 +/(Cos a)^2 = 1. Тогда (Sin a)^2 = 1 — (Cos a)^2, Sin a = √(1 — (Cos a)^2), а tg = √(1 — (Cos a)^2)/Cos a. Например, при а= 60 градусов Cos 60° = 0,5, tg = √(1 — 0,25)/0,5 = √(0,75)/0,5 = √(3*0,25)/0,5 = (0,5*√3)/0,5 = √3 = 1,732… . ctg a = Cos a/Sin a, то-есть величина обратная tg а, и при а = 60° ctg 60° = 1/√3 = √3/3 = 0,57735… . 127771 3 года назад Первым делом стоит вспомнить определение тангенса и котангенса, а именно: То есть получаются следующие формулы: tg(x) = sin(x) / cos(x) ctg(x) = cos(x) / sin(x) Из условия задачи нам известен косинус, значит нам нужно будет найти синус. Для этого есть такая формула: sin^2(x) + cos^2(x) = 1 Значит: sin^2(x) = 1 — cos^2(x) sin(x) = √(1 — (Cos a)^2) Теперь у нас есть значения синуса и косинуса, которые можно будет подставить в следующие формулы: Rafail 5 лет назад Наверное все помнят основное тождество тригонометрии: sin^2(x)+cos^2(x)=1. Почему-то также чётко я запомнил следующие простые формулы: tg^2(x)+1=sec^2(x) и ctg^2(x)+1=cosec^2(x). Ну и три определения: sec(x)=1/cos(x), cosec(x)=1/sin(x) и ctg(x)=1/tg(x). Теперь осталось выбрать нужные и применить. Допустим, cos(x)=(√3)/2, тогда sec(x)=2/√3, sec^2(x)=4/3, tg^2(x)=1/3, tg(x)=1/√3, ctg(x)=√3. Зайцевана 5 лет назад Пусть cosa = 1/2, тогда tga^2 = 1/(cosa)^2-1, (tga)^2 =1/0,25 — 1 = 3, tga =корень квадратный из 3, (со знаком + или — в зависимости в какой четверти находится а). ctga = 1/корень из 3. Синус, косинус, тангенс и котангенс угла — это тригонометрические функции. Можно сказать, что все они связаны между собой. Часто для нахождения одной из этих функций при условии, что известна другая, приходится вспоминать основные тригонометрические равенства или тождества, а также определение самих этих понятий. Зная все перечисленное выше, несложно выразить одну функцию через другую. Тангенс угла — это отношение синуса этого угла к его косинусу. Котангенс угла — это отношение косинуса угла к его синусу. Нам известен косинус, из основного тригонометрического тождества ( sin²α + cos²α = 1 ) выразим синус: sinα = √(1 — cos²α) для α из 1 и 2 четвертей, sinα = -√(1 — cos²α) для α из 3 и 4 четвертей. Подставив формулу для синуса угла в формулу тангенса и котангенса, получим формулы для вычисления значений этих функций: tgα = ± √(1 — cos²α) / cosα, ctgα = ± cosα / √(1 — cos²α). Котангенс, впрочем, можно вычислить путем попроще, вспомнив, что тангенс и котангенс — функции обратные, то есть ctgα = 1 / tgα. Подставляем в формулу значение тангенса и вычисляем котангенс. Если вам требуется найти тангенс и котангенс при помощи косинуса, то вам предстоит воспользоваться определенной тригонометрической формулой: при которой вы сможете отыскать синус из данной формулы, при том, что мы имеем известный косинус. Получившаяся формула выглядит таким образом: Теперь, нам следует подставить значение синуса в формулу вычисления тангенса, а именно речь идет о : Теперь подставим аналогичную формулу через косинус для котангенса: TheSun 3 года назад Для нахождения тангенса и котангенса через косинус необходимо воспользоваться приведенной ниже тригонометрической формулой: Находим синус из формулы указанной выше (при условии, что косинус нам известен), получается: Подставляем в формулу вычисления тангенса значение синуса: tg? = sin? / cos? = ± ?(1 — cos??) / cos?. Теперь аналогично для котангенса через косинус. ctg? = cos? / sin? = ± cos? / ?(1 — cos??). Все функции мы знаем из курса тригонометрии, и в это же время проходят и алгоритм нахождения тангенса/котангенса через косинус. Ну как следует из вопроса косинус нам известен. Если нет, то находим по формулам — Имея на руках значения двух вводных — синуса и косинуса, далее еще проще действовать по формулам нахождения тангенса и котангенса. Знаете ответ? |
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi
Как найти тангенс фи, если известен косинус фи формула:
- tg φ = (√(1-cos²φ))/cos φ
Калькулятор онлайн — косинус в тангенс
cos φ:
tg φ:
Поделиться в соц сетях:
Популярные сообщения из этого блога
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о «Использование сердечного индекса Руфье в медико-спортивном контроле». Проба Руфье — представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор — онлайн tg φ: cos φ: ± Поделиться в соц сетях:
НП
Наталья Посаднева
Из тождества известно что синус в квадрате + косинус в квадрате= 1
Можно из этой формулы вычислить синус, синус= Корень квадратный 1-косинус в квадрате.
После этого находим тангенс)) )
Думаю поняли меня)))
Используйте наш онлайн конвертер для быстрого и простого перевода значения косинуса фи в тангенс фи. Наш инструмент позволяет точно и быстро рассчитать тангенс угла, используя заданные значения косинуса. Получите точный результат в считанные секунды, без необходимости использовать сложные математические формулы. Бесплатный и доступный для использования в любое время!
Калькулятор коэффициент мощности cos fi в tg fi
Как найти тангенс фи, если известен косинус фи формула:
- tg φ = (√(1-cos²φ))/cos φ
Калькулятор онлайн — косинус в тангенс
cos φ:
tg φ:
Поделиться в соц сетях:
Как найти тангенс, если известен косинус
Понятие тангенса является одним из основных в тригонометрии. Оно обозначает некую тригонометрическую функцию, которая является периодической, но не непрерывной в области определения, как синус и косинус. И имеет разрывы в точках (+,-)Пи*n+Пи/2, где n — это период функции. В России он обозначается как tg(x). Его можно представить через любую тригонометрическую функцию, так как все они тесно взаимосвязаны между собой.

Вам понадобится
- Учебник по тригонометрии.
Инструкция
Для того, чтобы выразить тангенс угла через синус, нужно вспомнить геометрическое определение тангенса. Итак, тангенсом острого угла в прямоугольном треугольнике, называют отношение противолежащего катета к прилежащему.
С другой стороны, рассмотрите декартову систему координат, на которой начерчена единичная окружность с радиусом R=1, и центром О в начале координат. Примите поворот против часовой стрелки, как положительный, а в обратную сторону отрицательный.
Отметьте некую точку M на окружности. Из нее опустите перпендикуляр на ось Ох, назовите ее точкой N. Получился треугольник OMN, у которого угол ONM является прямым.
Теперь рассмотрите острый угол MON, по определению синуса и косинуса острого угла в прямоугольном треугольнике
sin(MON) = MN/OM, cos(MON) = ON/OM. Тогда MN= sin(MON)*OM, а ON = cos(MON)*OM.
Вернувшись к геометрическому определению тангенса (tg(MON) = MN/ON), подставьте полученные выше выражения. Тогда:
tg(MON) = sin(MON)*OM/cos(MON)*OM, сократите OM, тогда tg(MON) = sin(MON)/cos(MON).
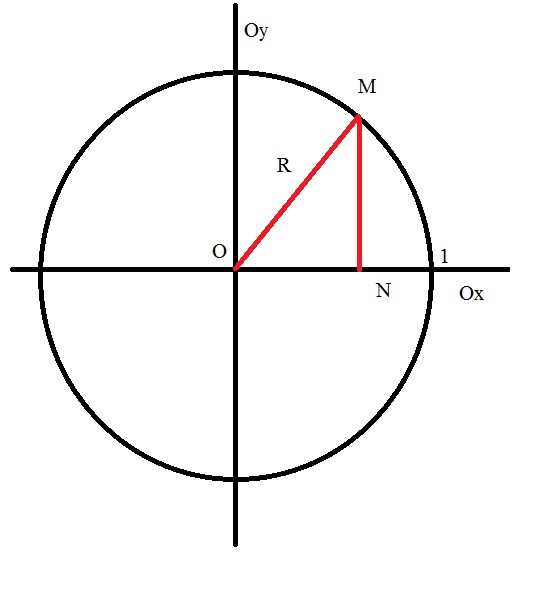
Из основного тригонометрического тождества (sin^2(x)+cos^2(x)=1) выразите косинус, через синус: cos(x)=(1-sin^2(x))^0,5 Подставьте это выражение в полученное на шаге 5. Тогда tg(MON) = sin(MON)/(1-sin^2(MON))^0,5.
Иногда существует потребность в вычисление тангенса двойного и половинчатого угла. Тут тоже выведены соотношения:tg(x/2) = (1-cos(x))/sin(x) = (1-(1-sin^2(x))^0,5)/sin(x);tg(2x) = 2*tg(x)/(1-tg^2(x)) = 2*sin(x)/(1-sin^2(x))^0,5/(1-sin(x)/(1-sin^2(x))^0,5)^2) =
= 2*sin(x)/(1-sin^2(x))^0,5/(1-sin^2(x)/(1-sin^2(x)).
Также возможно выразить квадрат тангенса через двойной угол косинуса, либо синус. tg^2(x) = (1-cos(2x))/(1+cos(2x)) = (1-1+2*sin^2(x))/(1+1-2*sin^2(x)) = (sin^2(x))/(1-sin^2(x)).
Обратите внимание
Обратите внимание на области допустимых значений при решение уравнений и неравенств.
Полезный совет
Знание наизусть основных тождеств, поможет быстро переходить от одних тригонометрических функций к другим.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.













