|
Как найти тангенс угла, если известен косинус? Как найти котангенс угла, если известен косинус? Итак, читаем внимательно условие вопроса, и вспоминаем, чему нас учили в школе, у нас есть косинус угла, и этого окажется вполне достаточным для того, чтобы мы выполнили задание автора вопроса и нашли тангенс и котангенс данного угла. Вспоминаем, что мы можем найти, зная косинус, конечно-же, мы сразу можем найти синус, это очень легко, и в этом нам поможет вот это волшебное тождество и то, что из него следует, — формула для нахождения синуса: Теперь, зная чему равен синус угла, через косинус, проще простого решать дальше по известным формулам для нахождения тангенса и котангенса, просто подставляя в них эти формулы для синуса, которые я разместила выше: система выбрала этот ответ лучшим Ксарфакс 5 лет назад Для того, чтобы найти тангенс и котангенс через косинус, достаточно вспомнить тригонометрические формулы: tgα = sinα / cosα. ctgα = cosα / sinα. Так как косинус известен, то синус можно найти из основного тригонометрического тождества: sin²α + cos²α = 1. sinα = √(1 — cos²α), если угол α находится в 1 и 2 четверти. sinα = — √(1 — cos²α), если угол α находится в 3 и 4 четверти. Таким образом: tgα = ± √(1 — cos²α) / cosα. ctgα = ± cosα / √(1 — cos²α). Так как произведение тангенса и котангенса = 1, то ctgα также можно найти из формулы: ctgα = 1 / tgα. Пример Косинус угла α равен 0,94, при этом α находится в 1 четверти (0 < α < 90). Нужно найти тангенс и котангенс. Воспользуемся формулой: tgα = √(1 — cos²α) / cosα. В первой четверти синус и косинус больше 0, поэтому тангенс и котангенс также будут положительными. tgα ≈ 0,34 / 0,94 ≈ 0,36. Соответственно ctgα ≈ 1 / 0,36 ≈ 2,78. Лара Изюминка 6 месяцев назад В школе изучают следующую тригонометрическую формулу: Косинус в квадрате альфа равно единица разделить на сумму единицы и тангенса в квадрате альфа. Из этой формулы легко выразить тангенс в квадрате альфа. Он очевидно равен 1 деленная на косинус в квадрате альфа и из этой дроби нужно вычесть один, а можно еще преобразовать как на картинке. Ну, а для того чтобы выразить котангенс, нужно вспомнить , что произведение тангенса и котангенса равно единице, тогда просто меняем числитель и знаменатель местами и получается формула для нахождения котангенса через косинус. Ну, а знак тангенса и котангенса определяем по той четверти, в которой находится угол. Если это первая и третья четверти, то плюс, иначе минус. bezdelnik 5 лет назад tg а = Sin a/Cos a. Чтобы выразить тангенс через косинус осталось выразить синус через косинус. Для этого воспользуемся основной тригонометрической формулой (Sin a)^2 +/(Cos a)^2 = 1. Тогда (Sin a)^2 = 1 — (Cos a)^2, Sin a = √(1 — (Cos a)^2), а tg = √(1 — (Cos a)^2)/Cos a. Например, при а= 60 градусов Cos 60° = 0,5, tg = √(1 — 0,25)/0,5 = √(0,75)/0,5 = √(3*0,25)/0,5 = (0,5*√3)/0,5 = √3 = 1,732… . ctg a = Cos a/Sin a, то-есть величина обратная tg а, и при а = 60° ctg 60° = 1/√3 = √3/3 = 0,57735… . 127771 3 года назад Первым делом стоит вспомнить определение тангенса и котангенса, а именно: То есть получаются следующие формулы: tg(x) = sin(x) / cos(x) ctg(x) = cos(x) / sin(x) Из условия задачи нам известен косинус, значит нам нужно будет найти синус. Для этого есть такая формула: sin^2(x) + cos^2(x) = 1 Значит: sin^2(x) = 1 — cos^2(x) sin(x) = √(1 — (Cos a)^2) Теперь у нас есть значения синуса и косинуса, которые можно будет подставить в следующие формулы: Rafail 5 лет назад Наверное все помнят основное тождество тригонометрии: sin^2(x)+cos^2(x)=1. Почему-то также чётко я запомнил следующие простые формулы: tg^2(x)+1=sec^2(x) и ctg^2(x)+1=cosec^2(x). Ну и три определения: sec(x)=1/cos(x), cosec(x)=1/sin(x) и ctg(x)=1/tg(x). Теперь осталось выбрать нужные и применить. Допустим, cos(x)=(√3)/2, тогда sec(x)=2/√3, sec^2(x)=4/3, tg^2(x)=1/3, tg(x)=1/√3, ctg(x)=√3. Зайцевана 5 лет назад Пусть cosa = 1/2, тогда tga^2 = 1/(cosa)^2-1, (tga)^2 =1/0,25 — 1 = 3, tga =корень квадратный из 3, (со знаком + или — в зависимости в какой четверти находится а). ctga = 1/корень из 3. Синус, косинус, тангенс и котангенс угла — это тригонометрические функции. Можно сказать, что все они связаны между собой. Часто для нахождения одной из этих функций при условии, что известна другая, приходится вспоминать основные тригонометрические равенства или тождества, а также определение самих этих понятий. Зная все перечисленное выше, несложно выразить одну функцию через другую. Тангенс угла — это отношение синуса этого угла к его косинусу. Котангенс угла — это отношение косинуса угла к его синусу. Нам известен косинус, из основного тригонометрического тождества ( sin²α + cos²α = 1 ) выразим синус: sinα = √(1 — cos²α) для α из 1 и 2 четвертей, sinα = -√(1 — cos²α) для α из 3 и 4 четвертей. Подставив формулу для синуса угла в формулу тангенса и котангенса, получим формулы для вычисления значений этих функций: tgα = ± √(1 — cos²α) / cosα, ctgα = ± cosα / √(1 — cos²α). Котангенс, впрочем, можно вычислить путем попроще, вспомнив, что тангенс и котангенс — функции обратные, то есть ctgα = 1 / tgα. Подставляем в формулу значение тангенса и вычисляем котангенс. Если вам требуется найти тангенс и котангенс при помощи косинуса, то вам предстоит воспользоваться определенной тригонометрической формулой: при которой вы сможете отыскать синус из данной формулы, при том, что мы имеем известный косинус. Получившаяся формула выглядит таким образом: Теперь, нам следует подставить значение синуса в формулу вычисления тангенса, а именно речь идет о : Теперь подставим аналогичную формулу через косинус для котангенса: TheSun 3 года назад Для нахождения тангенса и котангенса через косинус необходимо воспользоваться приведенной ниже тригонометрической формулой: Находим синус из формулы указанной выше (при условии, что косинус нам известен), получается: Подставляем в формулу вычисления тангенса значение синуса: tg? = sin? / cos? = ± ?(1 — cos??) / cos?. Теперь аналогично для котангенса через косинус. ctg? = cos? / sin? = ± cos? / ?(1 — cos??). Все функции мы знаем из курса тригонометрии, и в это же время проходят и алгоритм нахождения тангенса/котангенса через косинус. Ну как следует из вопроса косинус нам известен. Если нет, то находим по формулам — Имея на руках значения двух вводных — синуса и косинуса, далее еще проще действовать по формулам нахождения тангенса и котангенса. Знаете ответ? |
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi
Как найти тангенс фи, если известен косинус фи формула:
- tg φ = (√(1-cos²φ))/cos φ
Калькулятор онлайн — косинус в тангенс
cos φ:
tg φ:
Поделиться в соц сетях:
Популярные сообщения из этого блога
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о «Использование сердечного индекса Руфье в медико-спортивном контроле». Проба Руфье — представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор — онлайн tg φ: cos φ: ± Поделиться в соц сетях:
Используйте наш онлайн конвертер для быстрого и простого перевода значения косинуса фи в тангенс фи. Наш инструмент позволяет точно и быстро рассчитать тангенс угла, используя заданные значения косинуса. Получите точный результат в считанные секунды, без необходимости использовать сложные математические формулы. Бесплатный и доступный для использования в любое время!
Калькулятор коэффициент мощности cos fi в tg fi
Как найти тангенс фи, если известен косинус фи формула:
- tg φ = (√(1-cos²φ))/cos φ
Калькулятор онлайн — косинус в тангенс
cos φ:
tg φ:
Поделиться в соц сетях:
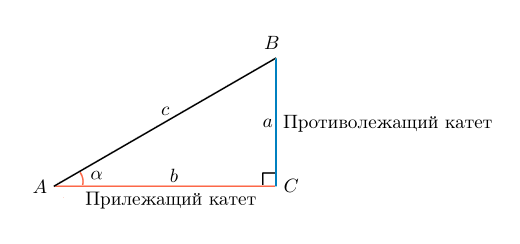
Тангенсом угла в прямоугольном треугольнике называют отношение противолежащего катета к прилежащему.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: тангенс угла — это отношение дальнего от рассматриваемого угла катета к ближнему катету.
В случае с рисунком, описанным выше: tgα=abtgalpha=frac{a}{b}
Тангенс можно найти напрямую пользуясь данной формулой, а можно и через тригонометрические тождества. Разберем подробнее задачи.
В прямоугольном треугольнике катеты равны 6 см6text{ см} и 8 см8text{ см}. Найдите тангенс угла, близлежащего к меньшей стороне.
Решение
a=8a=8
b=6b=6
tgα=ab=86≈1.33tgalpha=frac{a}{b}=frac{8}{6}approx1.33
Ответ
1.331.33
Формулу:
tgα=abtgalpha=frac{a}{b}
Можно записать в следующем виде:
tgα=sinαcosαtgalpha=frac{sinalpha}{cosalpha}
Проверим истинность данного выражения. Подставим вместо синуса и косинуса их определения:
tgα=sinαcosα=acbc=abtgalpha=frac{sinalpha}{cosalpha}=frac{frac{a}{c}}{frac{b}{c}}=frac{a}{b}
Получили первичное равенство, значит выражение для тангенса через отношение синуса к косинусу верно.
Решим задачу, пользуясь этой формулой.
По условию задачи известен косинус угла, равный 32frac{sqrt{3}}{2} и синус того же угла, равный 12frac{1}{2}. Найдите тангенс данного угла.
Решение
cosα=32cosalpha=frac{sqrt{3}}{2}
sinα=12sinalpha=frac{1}{2}
tgα=sinαcosα=1232=13tgalpha=frac{sinalpha}{cosalpha}=frac{frac{1}{2}}{frac{sqrt{3}}{2}}=frac{1}{sqrt{3}}
Ответ
13frac{1}{sqrt{3}}
Еще одно тождество помогает решить задачи, связанные с тангенсом:
1+tg2α=1cos2α1+tg^2alpha=frac{1}{cos^2alpha}
Оно появляется путем деление каждого слагаемого основного тождества тригонометрии на квадрат косинуса.
Известен квадрат косинуса угла в прямоугольном треугольнике, равный 0.80.8. Нужно найти тангенс этого угла.
Решение
cos2α=0.8cos^2alpha=0.8
1+tg2α=1cos2α1+tg^2alpha=frac{1}{cos^2alpha}
1+tg2α=10.81+tg^2alpha=frac{1}{0.8}
1+tg2α=1.251+tg^2alpha=1.25
tg2α=0.25tg^2alpha=0.25
tgα=0.25tgalpha=sqrt{0.25}
tgα=0.5tgalpha=0.5
Ответ
0.50.5
У вас есть трудности с вычислением тангенса? Можете заказать задачу по математике у наших экспертов!
Тест по теме “Вычисление тангенса”
Как найти тангенс через косинус
Косинус, как и синус, относят к «прямым» тригонометрическим функциям. Тангенс (вместе с котангенсом) причисляют к другой паре, называемой «производными». Существует несколько определений этих функций, которые делают возможным нахождение тангенса заданного угла по известному значению косинуса от этой же величины.
Вычтите из единицы частное от деления единицы на возведенное в квадрат значение косинуса заданного угла, а из результата извлеките квадратный корень — это и будет значение тангенса от угла, выраженное через его косинус: tg(α)=√(1-1/(cos(α))²). При этом обратите внимание на то, что в формуле косинус стоит в знаменателе дроби. Невозможность деления на ноль исключает использование этого выражения для углов, равных 90°, а также отличающихся от этой величины на числа, кратные 180° (270°, 450°, -90° и т.д.).
Существует и альтернативный способ вычисления тангенса по известному значению косинуса. Его можно применять, если не установлено ограничение на использование других тригонометрических функций. Для реализации этого способа сначала определите величину угла по известному значению косинуса — это можно сделать с помощью функции арккосинус. Затем просто рассчитайте тангенс для угла полученной величины. В общем виде этот алгоритм можно записать так: tg(α)=tg(arccos(cos(α))).
Есть и еще более экзотический вариант с использованием определения косинуса и тангенса через острые углы прямоугольного треугольника. Косинусу в таком определении соответствует отношение длины прилежащего к рассматриваемому углу катета к длине гипотенузы. Зная значение косинуса можно подобрать соответствующие ему длины этих двух сторон. Например, если cos(α)=0,5, то прилежащий катет можно принять равным 10см, а гипотенузу — 20см. Конкретные числа здесь значения не имеют — одинаковое и правильное решение вы получите с любыми значениями, имеющими такое же соотношение. Затем по теореме Пифагора определите длину недостающей стороны — противолежащего катета. Она будет равна квадратному корню из разницы между длинами возведенных в квадрат гипотенузы и известного катета: √(20²-10²)=√300. Тангенсу по определению соответствует отношение длин противолежащего и прилежащего катетов (√300/10) — рассчитайте его и получите значение тангенса, найденное с использованием классического определения косинуса.