Таблица ТАНГЕНСОВ для углов от 0° до 360° градусов
ТАНГЕНС (Tg α) острого угла в прямоугольном треугольнике равняется отношение противолежащего катета к прилежащему катету.
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| tg α (Тангенс) | 0 | 1/√3 | 1 | √3 | — | 0 | — | 0 |
Малая таблица значений тригонометрических функций (в радианах и градусах)
| Угол в градусах | tg (Тангенс) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0524 |
| 4° | 0.0699 |
| 5° | 0.0875 |
| 6° | 0.1051 |
| 7° | 0.1228 |
| 8° | 0.1405 |
| 9° | 0.1584 |
| 10° | 0.1763 |
| 11° | 0.1944 |
| 12° | 0.2126 |
| 13° | 0.2309 |
| 14° | 0.2493 |
| 15° | 0.2679 |
| 16° | 0.2867 |
| 17° | 0.3057 |
| 18° | 0.3249 |
| 19° | 0.3443 |
| 20° | 0.364 |
| 21° | 0.3839 |
| 22° | 0.404 |
| 23° | 0.4245 |
| 24° | 0.4452 |
| 25° | 0.4663 |
| 26° | 0.4877 |
| 27° | 0.5095 |
| 28° | 0.5317 |
| 29° | 0.5543 |
| 30° | 0.5774 |
| 31° | 0.6009 |
| 32° | 0.6249 |
| 33° | 0.6494 |
| 34° | 0.6745 |
| 35° | 0.7002 |
| 36° | 0.7265 |
| 37° | 0.7536 |
| 38° | 0.7813 |
| 39° | 0.8098 |
| 40° | 0.8391 |
| 41° | 0.8693 |
| 42° | 0.9004 |
| 43° | 0.9325 |
| 44° | 0.9657 |
| 45° | 1 |
| 46° | 1.0355 |
| 47° | 1.0724 |
| 48° | 1.1106 |
| 49° | 1.1504 |
| 50° | 1.1918 |
| 51° | 1.2349 |
| 52° | 1.2799 |
| 53° | 1.327 |
| 54° | 1.3764 |
| 55° | 1.4281 |
| 56° | 1.4826 |
| 57° | 1.5399 |
| 58° | 1.6003 |
| 59° | 1.6643 |
| 60° | 1.7321 |
| 61° | 1.804 |
| 62° | 1.8807 |
| 63° | 1.9626 |
| 64° | 2.0503 |
| 65° | 2.1445 |
| 66° | 2.246 |
| 67° | 2.3559 |
| 68° | 2.4751 |
| 69° | 2.6051 |
| 70° | 2.7475 |
| 71° | 2.9042 |
| 72° | 3.0777 |
| 73° | 3.2709 |
| 74° | 3.4874 |
| 75° | 3.7321 |
| 76° | 4.0108 |
| 77° | 4.3315 |
| 78° | 4.7046 |
| 79° | 5.1446 |
| 80° | 5.6713 |
| 81° | 6.3138 |
| 82° | 7.1154 |
| 83° | 8.1443 |
| 84° | 9.5144 |
| 85° | 11.4301 |
| 86° | 14.3007 |
| 87° | 19.0811 |
| 88° | 28.6363 |
| 89° | 57.29 |
| 90° | ∞ |
Полная таблица тангенсов для углов от 0° до 360°
| Угол | tg (Тангенс) |
|---|---|
| 91° | -57.29 |
| 92° | -28.6363 |
| 93° | -19.0811 |
| 94° | -14.3007 |
| 95° | -11.4301 |
| 96° | -9.5144 |
| 97° | -8.1443 |
| 98° | -7.1154 |
| 99° | -6.3138 |
| 100° | -5.6713 |
| 101° | -5.1446 |
| 102° | -4.7046 |
| 103° | -4.3315 |
| 104° | -4.0108 |
| 105° | -3.7321 |
| 106° | -3.4874 |
| 107° | -3.2709 |
| 108° | -3.0777 |
| 109° | -2.9042 |
| 110° | -2.7475 |
| 111° | -2.6051 |
| 112° | -2.4751 |
| 113° | -2.3559 |
| 114° | -2.246 |
| 115° | -2.1445 |
| 116° | -2.0503 |
| 117° | -1.9626 |
| 118° | -1.8807 |
| 119° | -1.804 |
| 120° | -1.7321 |
| 121° | -1.6643 |
| 122° | -1.6003 |
| 123° | -1.5399 |
| 124° | -1.4826 |
| 125° | -1.4281 |
| 126° | -1.3764 |
| 127° | -1.327 |
| 128° | -1.2799 |
| 129° | -1.2349 |
| 130° | -1.1918 |
| 131° | -1.1504 |
| 132° | -1.1106 |
| 133° | -1.0724 |
| 134° | -1.0355 |
| 135° | -1 |
| 136° | -0.9657 |
| 137° | -0.9325 |
| 138° | -0.9004 |
| 139° | -0.8693 |
| 140° | -0.8391 |
| 141° | -0.8098 |
| 142° | -0.7813 |
| 143° | -0.7536 |
| 144° | -0.7265 |
| 145° | -0.7002 |
| 146° | -0.6745 |
| 147° | -0.6494 |
| 148° | -0.6249 |
| 149° | -0.6009 |
| 150° | -0.5774 |
| 151° | -0.5543 |
| 152° | -0.5317 |
| 153° | -0.5095 |
| 154° | -0.4877 |
| 155° | -0.4663 |
| 156° | -0.4452 |
| 157° | -0.4245 |
| 158° | -0.404 |
| 159° | -0.3839 |
| 160° | -0.364 |
| 161° | -0.3443 |
| 162° | -0.3249 |
| 163° | -0.3057 |
| 164° | -0.2867 |
| 165° | -0.2679 |
| 166° | -0.2493 |
| 167° | -0.2309 |
| 168° | -0.2126 |
| 169° | -0.1944 |
| 170° | -0.1763 |
| 171° | -0.1584 |
| 172° | -0.1405 |
| 173° | -0.1228 |
| 174° | -0.1051 |
| 175° | -0.0875 |
| 176° | -0.0699 |
| 177° | -0.0524 |
| 178° | -0.0349 |
| 179° | -0.0175 |
| 180° | 0 |
Таблица тангенсов для углов от 91° до 180°
| Угол | tg (Тангенс) |
|---|---|
| 181° | 0.0175 |
| 182° | 0.0349 |
| 183° | 0.0524 |
| 184° | 0.0699 |
| 185° | 0.0875 |
| 186° | 0.1051 |
| 187° | 0.1228 |
| 188° | 0.1405 |
| 189° | 0.1584 |
| 190° | 0.1763 |
| 191° | 0.1944 |
| 192° | 0.2126 |
| 193° | 0.2309 |
| 194° | 0.2493 |
| 195° | 0.2679 |
| 196° | 0.2867 |
| 197° | 0.3057 |
| 198° | 0.3249 |
| 199° | 0.3443 |
| 200° | 0.364 |
| 201° | 0.3839 |
| 202° | 0.404 |
| 203° | 0.4245 |
| 204° | 0.4452 |
| 205° | 0.4663 |
| 206° | 0.4877 |
| 207° | 0.5095 |
| 208° | 0.5317 |
| 209° | 0.5543 |
| 210° | 0.5774 |
| 211° | 0.6009 |
| 212° | 0.6249 |
| 213° | 0.6494 |
| 214° | 0.6745 |
| 215° | 0.7002 |
| 216° | 0.7265 |
| 217° | 0.7536 |
| 218° | 0.7813 |
| 219° | 0.8098 |
| 220° | 0.8391 |
| 221° | 0.8693 |
| 222° | 0.9004 |
| 223° | 0.9325 |
| 224° | 0.9657 |
| 225° | 1 |
| 226° | 1.0355 |
| 227° | 1.0724 |
| 228° | 1.1106 |
| 229° | 1.1504 |
| 230° | 1.1918 |
| 231° | 1.2349 |
| 232° | 1.2799 |
| 233° | 1.327 |
| 234° | 1.3764 |
| 235° | 1.4281 |
| 236° | 1.4826 |
| 237° | 1.5399 |
| 238° | 1.6003 |
| 239° | 1.6643 |
| 240° | 1.7321 |
| 241° | 1.804 |
| 242° | 1.8807 |
| 243° | 1.9626 |
| 244° | 2.0503 |
| 245° | 2.1445 |
| 246° | 2.246 |
| 247° | 2.3559 |
| 248° | 2.4751 |
| 249° | 2.6051 |
| 250° | 2.7475 |
| 251° | 2.9042 |
| 252° | 3.0777 |
| 253° | 3.2709 |
| 254° | 3.4874 |
| 255° | 3.7321 |
| 256° | 4.0108 |
| 257° | 4.3315 |
| 258° | 4.7046 |
| 259° | 5.1446 |
| 260° | 5.6713 |
| 261° | 6.3138 |
| 262° | 7.1154 |
| 263° | 8.1443 |
| 264° | 9.5144 |
| 265° | 11.4301 |
| 266° | 14.3007 |
| 267° | 19.0811 |
| 268° | 28.6363 |
| 269° | 57.29 |
| 270° | ∞ |
Таблица тангенсов для углов от 181° до 270°
| Угол | tg (Тангенс) |
|---|---|
| 271° | -57.29 |
| 272° | -28.6363 |
| 273° | -19.0811 |
| 274° | -14.3007 |
| 275° | -11.4301 |
| 276° | -9.5144 |
| 277° | -8.1443 |
| 278° | -7.1154 |
| 279° | -6.3138 |
| 280° | -5.6713 |
| 281° | -5.1446 |
| 282° | -4.7046 |
| 283° | -4.3315 |
| 284° | -4.0108 |
| 285° | -3.7321 |
| 286° | -3.4874 |
| 287° | -3.2709 |
| 288° | -3.0777 |
| 289° | -2.9042 |
| 290° | -2.7475 |
| 291° | -2.6051 |
| 292° | -2.4751 |
| 293° | -2.3559 |
| 294° | -2.246 |
| 295° | -2.1445 |
| 296° | -2.0503 |
| 297° | -1.9626 |
| 298° | -1.8807 |
| 299° | -1.804 |
| 300° | -1.7321 |
| 301° | -1.6643 |
| 302° | -1.6003 |
| 303° | -1.5399 |
| 304° | -1.4826 |
| 305° | -1.4281 |
| 306° | -1.3764 |
| 307° | -1.327 |
| 308° | -1.2799 |
| 309° | -1.2349 |
| 310° | -1.1918 |
| 311° | -1.1504 |
| 312° | -1.1106 |
| 313° | -1.0724 |
| 314° | -1.0355 |
| 315° | -1 |
| 316° | -0.9657 |
| 317° | -0.9325 |
| 318° | -0.9004 |
| 319° | -0.8693 |
| 320° | -0.8391 |
| 321° | -0.8098 |
| 322° | -0.7813 |
| 323° | -0.7536 |
| 324° | -0.7265 |
| 325° | -0.7002 |
| 326° | -0.6745 |
| 327° | -0.6494 |
| 328° | -0.6249 |
| 329° | -0.6009 |
| 330° | -0.5774 |
| 331° | -0.5543 |
| 332° | -0.5317 |
| 333° | -0.5095 |
| 334° | -0.4877 |
| 335° | -0.4663 |
| 336° | -0.4452 |
| 337° | -0.4245 |
| 338° | -0.404 |
| 339° | -0.3839 |
| 340° | -0.364 |
| 341° | -0.3443 |
| 342° | -0.3249 |
| 343° | -0.3057 |
| 344° | -0.2867 |
| 345° | -0.2679 |
| 346° | -0.2493 |
| 347° | -0.2309 |
| 348° | -0.2126 |
| 349° | -0.1944 |
| 350° | -0.1763 |
| 351° | -0.1584 |
| 352° | -0.1405 |
| 353° | -0.1228 |
| 354° | -0.1051 |
| 355° | -0.0875 |
| 356° | -0.0699 |
| 357° | -0.0524 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Таблица тангенсов для углов от 271° до 360°
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Чему равен тангенс 30? …
— Ищем в таблице соответствующее значение. Правильный ответ: 0.5774
Значения тангенса и котангенса на тригонометрическом круге
В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.
Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.
Где же на тригонометрическом круге оси тангенсов и котангенсов?
Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).
Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).
На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?
Я думаю, вы легко сообразите и сами. 
Собственно, картинка за себя сама говорит.
Если не очень все же понятно, разберем примеры:
Пример 1.
Вычислить
Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что
Ответ:
Пример 2.
Вычислить
Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.
не существует.
Ответ: не существует
Пример 3.
Вычислить
Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .
Так значит,
Ответ:
Пример 4.
Вычислить
Поэтому от точки (именно там будет ) откладываем против часовой стрелки .
Выходим на ось котангенсов, получаем, что
Ответ:
Пример 5.
Вычислить
Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что
Ответ:
Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Тригонометрический круг со всеми значениями
Тригонометрический круг один из основных элементов геометрии для решения уравнений с синусом, косинусом, тангенсом и котангенсом.
Каково определение данного термина, как строить данный круг, как определить четверть в тригонометрии, как узнать углы в построенном тригонометрическом круге — об этом и многом другом расскажем далее.
Тригонометрическая окружность
Тригонометрическим видом числовой окружности в математике является круг, имеющий одинарный радиус с центром в начале координатной плоскости. Как правило, она образована пространством из формул синуса с косинусом, тангенсом и котангенсом на системе координат.
Назначение такой сферы с n-мерным пространством в том, что благодаря ей могут быть описаны тригонометрические функции. Выглядит она просто: круг, внутри которого находится система координат и множественные прямоугольного вида треугольники, образованные из этой окружности по тригонометрическим функциям.
Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике
Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты две стороны треугольника, которые прилегают к углу 90°, а третья гипотенуза, она всегда длиннее катетов.
Синусом называется отношение одного из катетов к гипотенузе, косинусом отношение другого катета к ней, а тангенсом отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.
Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).
Построение единичной окружности
Построение единичной окружности сводится к ее прорисовке с единичным радиусом в центре системы координат. Затем для построения нужно отсчитать углы и, двигаясь против часовой стрелки, обойти по целому кругу, проставляя соответствующие им линии координаты.
Начинается построение после черчения круга и установки точки в его центре с размещения системы координат ОХ. Точкой О сверху оси координат является синус, а Х косинус. Соответственно они являются абсциссой и ординатой. Затем нужно провести измерения ∠. Они проводятся градусами и радианами.
Сделать перевод этих показателей просто полный круг равен двум пи радиан. Угол от нуля против часовой стрелки идет со знаком +, а ∠ от 0 по часовой стрелке со знаком -. Положительные и отрицательные значения синуса с косинусом повторяются каждый оборот круга.
Углы на тригонометрическом круге
Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.
Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три 360°. Как пользоваться этой информацией?
Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.
Измеряются углы в радианах:
- от 0 до 90° значения углов от 0 до ∏/2,
- от 90 до 180° значения углов от ∏/2 до ∏,
- от 180 до 270° от ∏ до 3*∏/2,
- последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.
Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.
Перевод углов из градусов в радианы
Углы возможно измерить в градусах либо радианах. Требуется осознавать связь между обоими значениями. Эта взаимосвязь выражена в тригонометрии с помощью специальной формулы. Благодаря пониманию связи, можно научиться оперативным образом управлять углами и переходить от градусов к радианам обратно.
Для того чтобы точно узнать, чему равен один радиан, можно воспользоваться следующей формулой:
1 рад. = 180 / ∏ = 180 / 3,1416 = 57,2956
В конечном итоге, 1 радиан равен 57°, а в 1 градусе 0,0175 радиан:
1 градус = (∏ /180) рад. = 3,1416 / 180 рад. = 0,0175 рад.
Косинус, синус, тангенс, котангенс на тригонометрической окружности
Косинус с синусом, тангенсом и котангенсом на тригонометрической окружности функции углов альфа от 0 до 360 градусов. Каждая функция обладает положительным или отрицательным значением в зависимости от того, какая величина у угла. Они символизируют отношения к прямоугольным треугольникам, образованным в круге.
Заключение
В целом, тригонометрическая окружность – единичная окружность, необходимая для решения соответствующих задач и описания функций. Она состоит из многих составляющих, запомнить которые нужно обязательно для правильного решения последующих задач.
http://tvercult.ru/nauka/trigonometricheskiy-krug-so-vsemi-znacheniyami
henlesesoni759
Вопрос по математике:
Ребята помогите пожалуйста! 1)Вычислить с помощью формулы приведения: а)tg405°;б)cos420°;в)sin7п/4;г)sin11п/3.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
lexththind55
Tg(405)=tg(360+45)=tg 45=1
cos(420)=cos(360+60)=cos(60)=0.5
sin(7п/4)=sin(2п-п/4)=sin (-п/4)=-√2/2
sin(11п/3)=sin(4п-п/3)=sin(-п/3)=-√3/2
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
Таблица тангенсов, найти тангенс угла
Тангенс угла – одна из основных тригонометрических функций. Представляет собой соотношение катетов прямоугольного треугольника. То есть, tg(А)=ВС/АС, где ВС – противолежащий к углу (А) катет, АС – прилежащий катет.
Зачем необходимо знать тангенс угла? Такие данные имеют вполне практическое применение: в геодезии, мореходстве, авиации. Зная одну из сторон треугольника и угол, можно легко получить все остальные данные, используя тригонометрические тождества. Все расчеты легко производить с помощью онлайн-калькулятора на нашем сайте. Данные указаны в таблице тангенсов.
Для практического использования подходят не только таблицы Брадиса. Все тригонометрические функции вычисляются посредством калькулятора. Найдите красивое решение для вашей задачи.
Таблица тангенсов от 0° — 360°
|
|
|
|
|
|
|
|
|
|
Вам помог этот калькулятор?
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
НЕТ
tg(0°)=tg(360°)=0 точная, но чуть более сложная таблица ( с точностью до 1′) здесь.
|
Углы |
Углы |
Углы |
Углы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
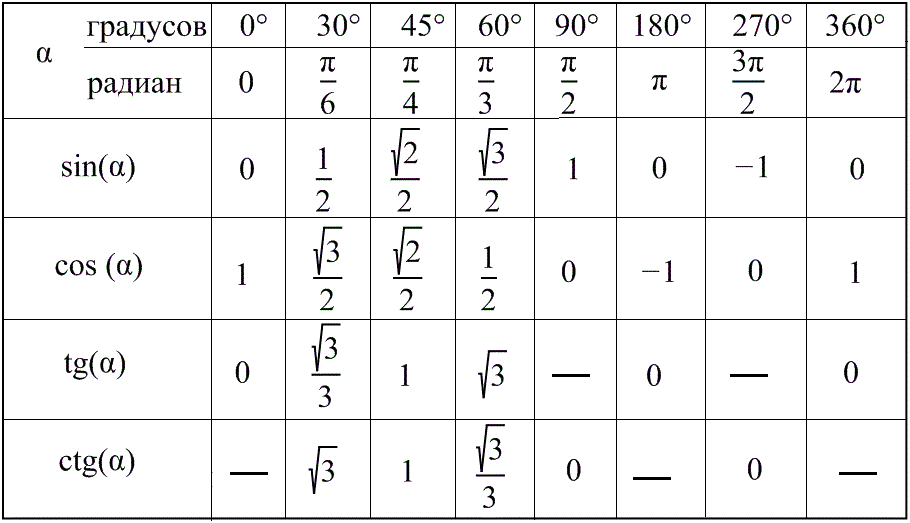
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций
Доп. Инфо:
- Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов.
- Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов.
- Таблица синусов, она-же косинусов точная.
- Таблица тангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
- Таблица котангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg
- Таблица тангенсов, она же котангенсов точная.
- Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций. - Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
- Определение и численные соотношения между единицами измерения углов в РФ.
Тысячные, угловые градусы, минуты, секунды, радианы, обороты. - Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.
Тангенс угла. Таблица тангенсов.
Тангенс угла через градусы, минуты и секунды
Тангенс угла через десятичную запись угла
Определение тангенса
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
tg(α) = sin(α)/cos(α)
tg(α) = 1/ctg(α)
Таблица тангенсов в радианах
tg(0°) = 0tg(π/12) = tg(15°) = 0.2679491924tg(π/6) = tg(30°) = 0.5773502692tg(π/4) = tg(45°) = 1tg(π/3) = tg(60°) = 1.732050808tg(5π/12) = tg(75°) = 3.732050808tg(π/2) = tg(90°) = ∞tg(7π/12) = tg(105°) = -3.732050808tg(2π/3) = tg(120°) = -1.732050808tg(3π/4) = tg(135°) = -1tg(5π/6) = tg(150°) = -0.5773502692tg(11π/12) = tg(165°) = -0.2679491924tg(π) = tg(180°) = 0tg(13π/12) = tg(195°) = 0.2679491924tg(7π/6) = tg(210°) = 0.5773502692tg(5π/4) = tg(225°) = 1tg(4π/3) = tg(240°) = 1.732050808tg(17π/12) = tg(255°) = 3.732050808tg(3π/2) = tg(270°) = ∞tg(19π/12) = tg(285°) = -3.732050808tg(5π/3) = tg(300°) = -1.732050808tg(7π/4) = tg(315°) = -1tg(11π/6) = tg(330°) = -0.5773502692tg(23π/12) = tg(345°) = -0.2679491924
Таблица Брадиса тангенсы
| tg(0) = 0 | tg(120) = -1.732050808 | tg(240) = 1.732050808 |
| tg(1) = 0.01745506493 | tg(121) = -1.664279482 | tg(241) = 1.804047755 |
| tg(2) = 0.03492076949 | tg(122) = -1.600334529 | tg(242) = 1.880726465 |
| tg(3) = 0.05240777928 | tg(123) = -1.539864964 | tg(243) = 1.962610506 |
| tg(4) = 0.06992681194 | tg(124) = -1.482560969 | tg(244) = 2.050303842 |
| tg(5) = 0.08748866353 | tg(125) = -1.428148007 | tg(245) = 2.144506921 |
| tg(6) = 0.1051042353 | tg(126) = -1.37638192 | tg(246) = 2.246036774 |
| tg(7) = 0.1227845609 | tg(127) = -1.327044822 | tg(247) = 2.355852366 |
| tg(8) = 0.1405408347 | tg(128) = -1.279941632 | tg(248) = 2.475086853 |
| tg(9) = 0.1583844403 | tg(129) = -1.234897157 | tg(249) = 2.605089065 |
| tg(10) = 0.1763269807 | tg(130) = -1.191753593 | tg(250) = 2.747477419 |
| tg(11) = 0.1943803091 | tg(131) = -1.150368407 | tg(251) = 2.904210878 |
| tg(12) = 0.2125565617 | tg(132) = -1.110612515 | tg(252) = 3.077683537 |
| tg(13) = 0.2308681911 | tg(133) = -1.07236871 | tg(253) = 3.270852618 |
| tg(14) = 0.2493280028 | tg(134) = -1.035530314 | tg(254) = 3.487414444 |
| tg(15) = 0.2679491924 | tg(135) = -1 | tg(255) = 3.732050808 |
| tg(16) = 0.2867453858 | tg(136) = -0.9656887748 | tg(256) = 4.010780934 |
| tg(17) = 0.3057306815 | tg(137) = -0.9325150861 | tg(257) = 4.331475874 |
| tg(18) = 0.3249196962 | tg(138) = -0.9004040443 | tg(258) = 4.704630109 |
| tg(19) = 0.3443276133 | tg(139) = -0.8692867378 | tg(259) = 5.144554016 |
| tg(20) = 0.3639702343 | tg(140) = -0.8390996312 | tg(260) = 5.67128182 |
| tg(21) = 0.383864035 | tg(141) = -0.8097840332 | tg(261) = 6.313751515 |
| tg(22) = 0.4040262258 | tg(142) = -0.7812856265 | tg(262) = 7.115369722 |
| tg(23) = 0.4244748162 | tg(143) = -0.7535540501 | tg(263) = 8.144346428 |
| tg(24) = 0.4452286853 | tg(144) = -0.726542528 | tg(264) = 9.514364454 |
| tg(25) = 0.4663076582 | tg(145) = -0.7002075382 | tg(265) = 11.4300523 |
| tg(26) = 0.4877325886 | tg(146) = -0.6745085168 | tg(266) = 14.30066626 |
| tg(27) = 0.5095254495 | tg(147) = -0.6494075932 | tg(267) = 19.08113669 |
| tg(28) = 0.5317094317 | tg(148) = -0.6248693519 | tg(268) = 28.63625328 |
| tg(29) = 0.5543090515 | tg(149) = -0.600860619 | tg(269) = 57.28996163 |
| tg(30) = 0.5773502692 | tg(150) = -0.5773502692 | tg(270) = ∞ |
| tg(31) = 0.600860619 | tg(151) = -0.5543090515 | tg(271) = -57.28996163 |
| tg(32) = 0.6248693519 | tg(152) = -0.5317094317 | tg(272) = -28.63625328 |
| tg(33) = 0.6494075932 | tg(153) = -0.5095254495 | tg(273) = -19.08113669 |
| tg(34) = 0.6745085168 | tg(154) = -0.4877325886 | tg(274) = -14.30066626 |
| tg(35) = 0.7002075382 | tg(155) = -0.4663076582 | tg(275) = -11.4300523 |
| tg(36) = 0.726542528 | tg(156) = -0.4452286853 | tg(276) = -9.514364454 |
| tg(37) = 0.7535540501 | tg(157) = -0.4244748162 | tg(277) = -8.144346428 |
| tg(38) = 0.7812856265 | tg(158) = -0.4040262258 | tg(278) = -7.115369722 |
| tg(39) = 0.8097840332 | tg(159) = -0.383864035 | tg(279) = -6.313751515 |
| tg(40) = 0.8390996312 | tg(160) = -0.3639702343 | tg(280) = -5.67128182 |
| tg(41) = 0.8692867378 | tg(161) = -0.3443276133 | tg(281) = -5.144554016 |
| tg(42) = 0.9004040443 | tg(162) = -0.3249196962 | tg(282) = -4.704630109 |
| tg(43) = 0.9325150861 | tg(163) = -0.3057306815 | tg(283) = -4.331475874 |
| tg(44) = 0.9656887748 | tg(164) = -0.2867453858 | tg(284) = -4.010780934 |
| tg(45) = 1 | tg(165) = -0.2679491924 | tg(285) = -3.732050808 |
| tg(46) = 1.035530314 | tg(166) = -0.2493280028 | tg(286) = -3.487414444 |
| tg(47) = 1.07236871 | tg(167) = -0.2308681911 | tg(287) = -3.270852618 |
| tg(48) = 1.110612515 | tg(168) = -0.2125565617 | tg(288) = -3.077683537 |
| tg(49) = 1.150368407 | tg(169) = -0.1943803091 | tg(289) = -2.904210878 |
| tg(50) = 1.191753593 | tg(170) = -0.1763269807 | tg(290) = -2.747477419 |
| tg(51) = 1.234897157 | tg(171) = -0.1583844403 | tg(291) = -2.605089065 |
| tg(52) = 1.279941632 | tg(172) = -0.1405408347 | tg(292) = -2.475086853 |
| tg(53) = 1.327044822 | tg(173) = -0.1227845609 | tg(293) = -2.355852366 |
| tg(54) = 1.37638192 | tg(174) = -0.1051042353 | tg(294) = -2.246036774 |
| tg(55) = 1.428148007 | tg(175) = -0.08748866353 | tg(295) = -2.144506921 |
| tg(56) = 1.482560969 | tg(176) = -0.06992681194 | tg(296) = -2.050303842 |
| tg(57) = 1.539864964 | tg(177) = -0.05240777928 | tg(297) = -1.962610506 |
| tg(58) = 1.600334529 | tg(178) = -0.03492076949 | tg(298) = -1.880726465 |
| tg(59) = 1.664279482 | tg(179) = -0.01745506493 | tg(299) = -1.804047755 |
| tg(60) = 1.732050808 | tg(180) = 0 | tg(300) = -1.732050808 |
| tg(61) = 1.804047755 | tg(181) = 0.01745506493 | tg(301) = -1.664279482 |
| tg(62) = 1.880726465 | tg(182) = 0.03492076949 | tg(302) = -1.600334529 |
| tg(63) = 1.962610506 | tg(183) = 0.05240777928 | tg(303) = -1.539864964 |
| tg(64) = 2.050303842 | tg(184) = 0.06992681194 | tg(304) = -1.482560969 |
| tg(65) = 2.144506921 | tg(185) = 0.08748866353 | tg(305) = -1.428148007 |
| tg(66) = 2.246036774 | tg(186) = 0.1051042353 | tg(306) = -1.37638192 |
| tg(67) = 2.355852366 | tg(187) = 0.1227845609 | tg(307) = -1.327044822 |
| tg(68) = 2.475086853 | tg(188) = 0.1405408347 | tg(308) = -1.279941632 |
| tg(69) = 2.605089065 | tg(189) = 0.1583844403 | tg(309) = -1.234897157 |
| tg(70) = 2.747477419 | tg(190) = 0.1763269807 | tg(310) = -1.191753593 |
| tg(71) = 2.904210878 | tg(191) = 0.1943803091 | tg(311) = -1.150368407 |
| tg(72) = 3.077683537 | tg(192) = 0.2125565617 | tg(312) = -1.110612515 |
| tg(73) = 3.270852618 | tg(193) = 0.2308681911 | tg(313) = -1.07236871 |
| tg(74) = 3.487414444 | tg(194) = 0.2493280028 | tg(314) = -1.035530314 |
| tg(75) = 3.732050808 | tg(195) = 0.2679491924 | tg(315) = -1 |
| tg(76) = 4.010780934 | tg(196) = 0.2867453858 | tg(316) = -0.9656887748 |
| tg(77) = 4.331475874 | tg(197) = 0.3057306815 | tg(317) = -0.9325150861 |
| tg(78) = 4.704630109 | tg(198) = 0.3249196962 | tg(318) = -0.9004040443 |
| tg(79) = 5.144554016 | tg(199) = 0.3443276133 | tg(319) = -0.8692867378 |
| tg(80) = 5.67128182 | tg(200) = 0.3639702343 | tg(320) = -0.8390996312 |
| tg(81) = 6.313751515 | tg(201) = 0.383864035 | tg(321) = -0.8097840332 |
| tg(82) = 7.115369722 | tg(202) = 0.4040262258 | tg(322) = -0.7812856265 |
| tg(83) = 8.144346428 | tg(203) = 0.4244748162 | tg(323) = -0.7535540501 |
| tg(84) = 9.514364454 | tg(204) = 0.4452286853 | tg(324) = -0.726542528 |
| tg(85) = 11.4300523 | tg(205) = 0.4663076582 | tg(325) = -0.7002075382 |
| tg(86) = 14.30066626 | tg(206) = 0.4877325886 | tg(326) = -0.6745085168 |
| tg(87) = 19.08113669 | tg(207) = 0.5095254495 | tg(327) = -0.6494075932 |
| tg(88) = 28.63625328 | tg(208) = 0.5317094317 | tg(328) = -0.6248693519 |
| tg(89) = 57.28996163 | tg(209) = 0.5543090515 | tg(329) = -0.600860619 |
| tg(90) = ∞ | tg(210) = 0.5773502692 | tg(330) = -0.5773502692 |
| tg(91) = -57.28996163 | tg(211) = 0.600860619 | tg(331) = -0.5543090515 |
| tg(92) = -28.63625328 | tg(212) = 0.6248693519 | tg(332) = -0.5317094317 |
| tg(93) = -19.08113669 | tg(213) = 0.6494075932 | tg(333) = -0.5095254495 |
| tg(94) = -14.30066626 | tg(214) = 0.6745085168 | tg(334) = -0.4877325886 |
| tg(95) = -11.4300523 | tg(215) = 0.7002075382 | tg(335) = -0.4663076582 |
| tg(96) = -9.514364454 | tg(216) = 0.726542528 | tg(336) = -0.4452286853 |
| tg(97) = -8.144346428 | tg(217) = 0.7535540501 | tg(337) = -0.4244748162 |
| tg(98) = -7.115369722 | tg(218) = 0.7812856265 | tg(338) = -0.4040262258 |
| tg(99) = -6.313751515 | tg(219) = 0.8097840332 | tg(339) = -0.383864035 |
| tg(100) = -5.67128182 | tg(220) = 0.8390996312 | tg(340) = -0.3639702343 |
| tg(101) = -5.144554016 | tg(221) = 0.8692867378 | tg(341) = -0.3443276133 |
| tg(102) = -4.704630109 | tg(222) = 0.9004040443 | tg(342) = -0.3249196962 |
| tg(103) = -4.331475874 | tg(223) = 0.9325150861 | tg(343) = -0.3057306815 |
| tg(104) = -4.010780934 | tg(224) = 0.9656887748 | tg(344) = -0.2867453858 |
| tg(105) = -3.732050808 | tg(225) = 1 | tg(345) = -0.2679491924 |
| tg(106) = -3.487414444 | tg(226) = 1.035530314 | tg(346) = -0.2493280028 |
| tg(107) = -3.270852618 | tg(227) = 1.07236871 | tg(347) = -0.2308681911 |
| tg(108) = -3.077683537 | tg(228) = 1.110612515 | tg(348) = -0.2125565617 |
| tg(109) = -2.904210878 | tg(229) = 1.150368407 | tg(349) = -0.1943803091 |
| tg(110) = -2.747477419 | tg(230) = 1.191753593 | tg(350) = -0.1763269807 |
| tg(111) = -2.605089065 | tg(231) = 1.234897157 | tg(351) = -0.1583844403 |
| tg(112) = -2.475086853 | tg(232) = 1.279941632 | tg(352) = -0.1405408347 |
| tg(113) = -2.355852366 | tg(233) = 1.327044822 | tg(353) = -0.1227845609 |
| tg(114) = -2.246036774 | tg(234) = 1.37638192 | tg(354) = -0.1051042353 |
| tg(115) = -2.144506921 | tg(235) = 1.428148007 | tg(355) = -0.08748866353 |
| tg(116) = -2.050303842 | tg(236) = 1.482560969 | tg(356) = -0.06992681194 |
| tg(117) = -1.962610506 | tg(237) = 1.539864964 | tg(357) = -0.05240777928 |
| tg(118) = -1.880726465 | tg(238) = 1.600334529 | tg(358) = -0.03492076949 |
| tg(119) = -1.804047755 | tg(239) = 1.664279482 | tg(359) = -0.01745506493 |
Похожие калькуляторы