Понятие температуры – одно из важнейших в молекулярной физике.
Температура — это физическая величина, которая характеризует степень нагретости тел.
Беспорядочное хаотическое движение молекул называется тепловым движением.
Кинетическая энергия теплового движения растет с возрастанием температуры. При низких температурах средняя кинетическая энергия молекулы может оказаться небольшой. В этом случае молекулы конденсируются в жидкое или твердое вещество; при этом среднее расстояние между молекулами будет приблизительно равно диаметру молекулы. При повышении температуры средняя кинетическая энергия молекулы становится больше, молекулы разлетаются, и образуется газообразное вещество.
Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты.
Рассмотрим пример. Если положить нагретый металл на лед, то лед начнет плавится, а металл – охлаждаться до тех пор, пока температуры тел не станут одинаковыми. При контакте между двумя телами разной температуры происходит теплообмен, в результате которого энергия металла уменьшается, а энергия льда увеличивается.
Энергия при теплообмене всегда передается от тела с более высокой температурой к телу с более низкой температурой. В конце концов, наступает состояние системы тел, при котором теплообмен между телами системы будет отсутствовать. Такое состояние называют тепловым равновесием.
Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными.
Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии. Возможность введения понятия температуры следует из опыта и носит название нулевого закона термодинамики.
Тела, находящиеся в тепловом равновесии, имеют одинаковые температуры.
Для измерения температур чаще всего используют свойство жидкости изменять объем при нагревании (и охлаждении).
Прибор, с помощью которого измеряется температура, называется термометр.
Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину, характеризующую свойство вещества (например, длина ртутного или спиртового столбика). В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании). Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении.
Обыкновенный жидкостный термометр состоит из небольшого стеклянного резервуара, к которому присоединена стеклянная трубка с узким внутренним каналом. Резервуар и часть трубки наполнены ртутью. Температуру среды, в которую погружен термометр определяют по положению верхнего уровня ртути в трубке. Деления на шкале условились наносить следующим образом. Цифру 0 ставят в том месте шкалы, где устанавливается уровень столбика жидкости, когда термометр опущен в тающий снег (лед), цифру 100 – в том месте, где устанавливается уровень столбика жидкости, когда термометр погружен в пары воды, кипящей при нормальном давлении (105 Па). Расстояние между этими отметками делят на 100 равных частей, называемых градусами. Такой способ деления шкалы введен Цельсием. Градус по шкале Цельсия обозначают ºС.
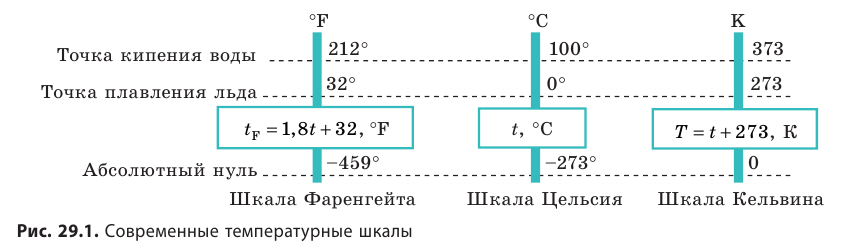
По температурной шкале Цельсия точке плавления льда приписывается температура 0 °С, а точке кипения воды – 100 °С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0 °С и 100 °С принимается равным 1 °С.
В ряде стран (США) широко используется шкала Фаренгейта (TF), в которой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Следовательно,
Ртутные термометры применяют для измерения температуры в области от -30 ºС до +800 ºС. Наряду с жидкостными ртутными и спиртовыми термометрами применяются электрические и газовые термометры.
Электрический термометр – термосопротивление – в нем используется зависимость сопротивления металла от температуры.
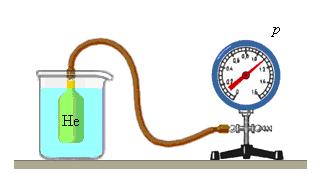
Особое место в физике занимают газовые термометр, в которых термометрическим веществом является разреженный газ (гелий, воздух) в сосуде неизменного объема (V = const), а термометрической величиной – давление газа p. Опыт показывает, что давление газа (при V = const) растет с ростом температуры, измеренной по шкале Цельсия.
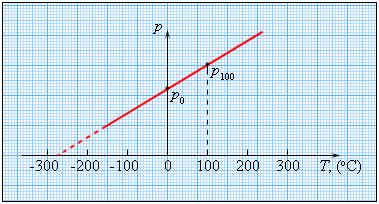
Чтобы проградуировать газовый термометр постоянного объема, можно измерить давление при двух значениях температуры (например, 0 °C и 100 °C), нанести точки p0 и p100 на график, а затем провести между ними прямую линию. Используя полученный таким образом калибровочный график, можно определять температуры, соответствующие другим значениям давления.
Газовые термометры громоздки и неудобны для практического применения: они используются в качестве прецизионного стандарта для калибровки других термометров.
Показания термометров, заполненных различными термометрическими телами, обычно несколько различаются. Чтобы точное определение температуры не зависело от вещества, заполняющего термометр, вводится термодинамическая шкала температур.
Чтобы её ввести, рассмотрим, как зависит давление газа от температуры, когда его масса и объём остаются постоянными.
Термодинамическая шкала температур. Абсолютный нуль.
Возьмем закрытый сосуд с газом, и будем нагревать его, первоначально поместив в тающий лед. Температуру газа t определим с помощью термометра, а давление p манометром. С увеличением температуры газа его давление будет возрастать. Такую зависимость нашел французский физик Шарль. График зависимости p от t, построенный на основании такого опыта, имеет вид прямой линии.
Если продолжить график в область низких давлений, можно определить некоторую «гипотетическую» температуру, при которой давление газа стало бы равным нулю. Опыт показывает, что эта температура равна –273,15 °С и не зависит от свойств газа. Невозможно на опыте получить путем охлаждения газ в состоянии с нулевым давлением, так как при очень низких температурах все газы переходят в жидкие или твердые состояния. Давление идеального газа определяется ударами хаотически движущихся молекул о стенки сосуда. Значит, уменьшение давления при охлаждении газа объясняется уменьшением средней энергии поступательного движения молекул газа Е; давление газа будет равно нулю, когда станет равна нулю энергия поступательного движения молекул.
Английский физик У. Кельвин (Томсон) выдвинул идею о том, что полученное значение абсолютного нуля соответствует прекращению поступательного движения молекул всех веществ. Температуры ниже абсолютного нуля в природе быть не может. Это предельная температура при которой давление идеального газа равно нулю.
Температуру, при которой должно прекратиться поступательное движение молекул, называют абсолютным нулем (или нулем Кельвина).
Кельвин в 1848 г. предложил использовать точку нулевого давления газа для построения новой температурной шкалы –термодинамической шкалы температур (шкала Кельвина). За начало отсчета по этой шкале принята температура абсолютного нуля.
В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой К.
Размер градуса кельвина определяют так, чтобы он совпадал с градусом Цельсия, т.е 1К соответствует 1ºС.
Температура, отсчитанная по термодинамической шкале температур, обозначается Т. Её называют абсолютной температурой илитермодинамической температурой.
Температурная шкала Кельвина называется абсолютной шкалой температур. Она оказывается наиболее удобной при построении физических теорий.
Кроме точки нулевого давления газа, которая называется абсолютным нулем температуры, достаточно принять еще одну фиксированную опорную точку. В шкале Кельвина в качестве такой точки используется температура тройной точки воды (0,01 °С), в которой в тепловом равновесии находятся все три фазы – лед, вода и пар. По шкале Кельвина температура тройной точки принимается равной 273,16 К.
Связь между абсолютной температурой и температурой по шкале Цельсия выражается формулой Т = 273,16 + t , где t – температура в градусах Цельсия.
Чаще пользуются приближенной формулой Т = 273 + t и t = Т – 273
Абсолютная температура не может быть отрицательной.
Температура газа – мера средней кинетической энергии движения молекул.
В опытах Шарлем была найдена зависимость p от t. Эта же зависимость будет и между р и Т: т.е. между р и Т прямопропорциональная зависимость.
С одной стороны, давление газа прямопропорционально его температуре, с другой стороны, мы уже знаем, что давление газа прямопропорционально средней кинетической энергии поступательного движения молекул Е (p = 2/3*E*n ). Значит, Е прямопропорциональна Т.
Немецкий ученый Больцман предложил ввести коэффициент пропорциональности (3/2)k в зависимость Е от Т
Е = (3/2)kТ
Из этой формулы следует, что среднее значение кинетической энергии поступательного движения молекул не зависит от природы газа, а определяется только его температурой.
Так как Е = m*v2/2, то m*v2/2 = (3/2)kТ
откуда средняя квадратичная скорость молекул газа
Постоянная величина k называется постоянная Больцмана.
В СИ она имеет значение k = 1,38*10-23 Дж/К
Если подставить значение Е в формулу p = 2/3*E*n , то получим p = 2/3*(3/2)kТ* n, сократив, получим p = n* k*Т
Давление газа не зависит от его природы, а определяется только концентрацией молекул n и температурой газа Т.
Соотношение p = 2/3*E*n устанавливает связь между микроскопическими (значения определяются с помощью расчетов) и макроскопическими (значения можно определить по показаниям приборов) параметрами газа, поэтому его принято называть основным уравнением молекулярно – кинетической теории газов.
Идеальный газ — газ, удовлетворяющий трем условиям:
- Молекулы — материальные точки.
- Потенциальная энергия взаимодействия молекул пренебрежительно мала.
- Столкновения между молекулами являются абсолютно упругими.
Реальный газ с малой плотностью можно считать идеальным газом.
Измерение температуры
Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.
Обозначение температуры
- По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 oC).
- По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).
Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:
∆t = ∆T
При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:
T = t + 273
Если особо важна точность, следует использовать более точную формулу:
T = t + 273,15
Пример №1. Температура воды равна oC. Определить температуру воды в Кельвинах.
T = t + 273 = 2 + 273 = 275 (К)
Основное уравнение МКТ идеального газа
Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).
Основное уравнение МКТ
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
p=23n−Ek
p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.
Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:
|
p=13m0n−v2 |
m0— масса одной молекулы газа; n — концентрация молекул газа; −v2 — среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2 |
|
p=13ρ−v2 |
ρ — плотность газа |
|
p=nkT |
k — постоянная Больцмана (k = 1,38∙10–3 Дж/кг) T — температура газа по шкале Кельвина |
Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?
Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:
Следствия из основного уравнения МКТ идеального газа
Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):
v=√3kTm0=√3RTM
R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:
R=NAk=8,31 Дж/К·моль
Температура — мера кинетической энергии молекул идеального газа:
−Ek=32kT
T=2−Ek3k
Полная энергия поступательного движения молекул газа определяется формулой:
E=N−Ek
Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?
Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:
Следовательно:
Составим систему уравнений:
Отсюда:
Задание EF19012

Алгоритм решения
1.Указать, в каких координатах построен график.
2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
T=2−Ek3
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
νR=p1V1T1=p2V2T2
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
Ответ:
• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.
• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17560
Первоначальное давление газа в сосуде равнялось р1. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р2 газа в сосуде стало равным
Ответ:
а) 13p1
б) 2p1
в) 23p1
г) 43p1
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для состояний 1 и 2.
4.Выразить искомую величину.
Решение
Исходные данные:
• Начальное давление: p0.
• Начальная концентрация молекул: n1 = 3n.
• Конечная концентрация молекул: n2 = n.
• Начальная средняя энергия хаотичного движения молекул: Ek1 = Ek.
• Конечная средняя энергия хаотичного движения молекул: Ek2 = 2Ek.
Основное уравнение МКТ:
p=23n−Ek
Составим уравнения для начального и конечного состояний:
p1=23n1−Ek1=233n−Ek=2n−Ek
p2=23n2−Ek2=23n2−Ek=43n−Ek
Отсюда:
n−Ek=p12=3p24
p2=4p16=23p1
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18416
Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Концентрации кислорода и водорода в сосуде равны. Следовательно, n1 = n2 = n.
• Давление кислорода вдвое выше давления водорода. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n−Ek1
p2=23n2−Ek2 или p=23n−Ek2
Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:
−Ek1=3pn
−Ek2=3p2n
Поделим уравнения друг на друга и получим:
−Ek1−Ek2=3pn·2n3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18824
В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение концентрации молекул аргона к концентрации молекул неона.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.
• Давление аргона в 2 раза больше давления неона. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n1−Ek
p2=23n2−Ek2 или p=23n2−Ek
Выразим концентрации молекул газа из каждого уравнения:
n1=3p−Ek
n2=3p2−Ek
Поделим уравнения друг на друга и получим:
n1n2=3p−Ek·2−Ek3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 10.9k
Перевод из градусов Цельсия в градусы Кельвина .
В системе СИ температура измеряется в градусах Кельвина
Шкала Цельсия и шкала Кельвина связаны простым соотношением:
(T=t+273 )
(T) — температура в градусах Кельвина
(t) — температура в градусах Цельсия
Задача 1.(Перевод из градусов Цельсия в градусы Кельвина)
Температура воздуха на улице (t=0^0C ).
Какова температура этого воздуха в градусах Кельвина?
Показать ответ
Показать решение
Видеорешение
Задача 2.(Перевод из градусов Цельсия в градусы Кельвина)
Температура воздуха на улице (t=1^0C ).
Какова температура этого воздуха в градусах Кельвина?
Показать ответ
Показать решение
Видеорешение
Задача 3.(Перевод из градусов Цельсия в градусы Кельвина)
Температура воздуха на улице (t=2^0C ).
Какова температура этого воздуха в градусах Кельвина?
Показать ответ
Показать решение
Видеорешение
Задача 4.(Перевод из градусов Цельсия в градусы Кельвина)
Температура воздуха в помещении (t=27^0C ).
Какова температура этого воздуха в градусах Кельвина?
Показать ответ
Показать решение
Видеорешение
Задача 5.(Перевод из градусов Цельсия в градусы Кельвина)
Температура газа в баллоне составляет (t=140^0C ).
Какова температура этого газа в градусах Кельвина?
Показать ответ
Показать решение
Видеорешение
Задача 6.(Перевод из градусов Цельсия в градусы Кельвина)
Температура гелия в воздушном шарике, принесенном с мороза составляет (t=-23^0C ).
Какова температура этого гелия в градусах Кельвина?
Показать ответ
Показать решение
Видеорешение
Задача 7.(Перевод из градусов Цельсия в градусы Кельвина)
Самая низкая температура на земле была зафиксирована в Арктике и составила (t=-90^0C )
Найти значение этой температуры в в градусах Кельвина.
Показать ответ
Показать решение
Видеорешение
Задача 8.(Перевод из градусов Цельсия в градусы Кельвина)
В лабораторных условиях была получена температура (t=-273^0C )
Найти значение этой температуры в в градусах Кельвина.
Показать ответ
Показать решение
Видеорешение
Задача 9.(Перевод из градусов Кельвина в градусы Цельсия)
Температура газовой смеси в камере сгорания составила (T=1600 K)
Найти значение этой температуры в в градусах Цельсия.
Показать ответ
Показать решение
Видеорешение
Задача 10.(Перевод из градусов Кельвина в градусы Цельсия)
Температура углекислого газа равна 273 Кельвина
Найти значение этой температуры в в градусах Цельсия.
Показать ответ
Показать решение
Видеорешение
Задача 11.(Перевод из градусов Кельвина в градусы Цельсия)
Температура сжатого воздуха в баллоне равна 300 Кельвинов
Найти значение этой температуры в в градусах Цельсия.
Показать ответ
Показать решение
Видеорешение
Задача 12.
Температура газа увеличилась на 1 Кельвин
На сколько градусов Цельсия увеличилась температура?
Показать ответ
Показать решение
Видеорешение
Уравнение состояния газа

Среднее расстояние, пробегаемое молекулами между двумя последовательными столкновениями, называется длиной свободного пробега. Она зависит от плотности, давления и температуры газа. При атмосферном давлении и температуре 0° С длина свободного пробега молекул воздуха имеет порядок 10-6 —10-5 см. Рис. 2, а дает примерный характер пути, проводимого одной молекулой газа при увеличении его в 106 раз.
По мере разрежения газа в сосуде длина свободного пробега молекул увеличивается и при высокой степени разрежения может достигать нескольких сантиметров и даже десятков сантиметров. Если длина пробега молекул становится больше размеров сосуда, т. е. молекулы пробегают от стенки до стенки без столкновения, считают, что в сосуде образовался вакуум.
Уравнение состояния идеального газа
Газ, в котором среднее расстояние между молекулами значительно превышает их размеры и поэтому силами притяжения между молекулами, а также объемом, который они занимают, можно пренебречь, называется идеальным газом. Эти допущения значительно облегчают установление соотношения между тремя основными величинами, характеризующими состояние газа: давлением р, объемом V и температурой Т
Взаимосвязь между этими величинами описывается так называемым уравнением состояния газа. Это уравнение обобщает три основных закона, установленных Бойлем — Мариоттом, Шарлем и Гей-Люссаком, и имеет теоретическое обоснование в кинетической теории газов. Напомним, что для данной массы идеального газа:
- При постоянной температуре Т = const давление р изменяется обратно пропорционально объему V газа: р1/р2 = V2/V1 (закон Бойля — Мариотта);
- При неизменном объеме V =const давление р изменяется обратно пропорционально температур пропорционально температуре Т газа: р1/р2 = Т2/Т1 (закон Шарля);
- При постоянном давлении p =const объем V газа изменяется прямо пропорционально температуре Т газа:
V1/V2 = Т2/Т1 (закон Гей-Люссака).
Из этих законов следует, что при одновременном изменении объема и температуры давление р будет изменяться прямо пропорционально температуре Т и обратно пропорционально объему V газа:
p=R’(T/V)
или
pV/T = R’
где R’ — есть некоторая постоянная.
Это и есть уравнение состояния идеального газа. Оно показывает, что при изменении состояния данной массы газа произведение давления на объем, деленное на абсолютную температуру, остается постоянным.
Следовательно, для одной и той же массы идеального газа, находящейся в различных условиях, характеризующихся давлениями р1 и р2, объемами V1 и V2 и абсолютными температурами Т1 и Т2, выполняется соотношение:
p1V1/T1 = p2V2/T2
Уравнение состояния газа позволяет произвести приведение объема какой-либо массы газа к нормальным условиям, т. е., зная объем V при заданном давлении р и температуре t (или Т=273 + t), найти объем газа V0 при нормальных условиях: давлении p0=760 мм рт. ст. и температуре t = 0° С (T = 273° К). Действительно:
pV/T = p0V0/T0
или
pV/273 + t = 760V0/273,
откуда
V0 = V(273p/(760(273 + t))
Если уравнение состояния идеального газа отнести к одной грамм-молекуле газа (объем ее обозначим Vμ и соответствующую постоянную R), то получим:
PVμ = RT.
Это выражение называется уравнением Клапейрона — Менделеева.
При одинаковых давлениях и температурах в равных объемах различных идеальных газов содержится одинаковое число молекул (закон Авогадро). Если при этом учесть, что в грамм-молекуле любого газа содержится постоянное число молекул (NA = 6,023•1023 1/моль), то отсюда следует, что объемы грамм-молекул идеальных газов при одинаковых давлениях и температурах равны между собой. При нормальных условиях этот объем составляет: Vμ0 = 22 400 см3/моль.
В связи с этим постоянная R должна иметь одинаковую величину для всех газов независимо от их природы. Она называется универсальной газовой постоянной и может быть вычислена с помощью уравнения состояния газа при нормальных условиях (давление р0=1,012Vμ106 дин/см2 и температура T0=273° К):
R = p0Vμ0/T0 = (1,012 • 106 • 22400)/273 = 8,32 • 107 эрг/(град•моль) = 8,2 дж(град•моль)
Для практических целей удобнее объем V газа выражать в литрах, на моль и давление р0 в атмосферах, тогда:
R = (1 • 22,4)/273 = 0,082 л•ат/(град•моль).
Уравнение Клапейрона — Менделеева
Уравнение Клапейрона — Менделеева можно применить и к любой массе М газа. При тех же давлении р и температуре Т объем Vm массы М граммов газа и массы одной грамм-молекулы относятся как масса М и молекулярный вес μ газа:
Vм/Vμ = M/μ или Vм = (М/μ)Vμ
Умножая обе части этого выражения на отношение p/V, получим:
pVм/Т = (М/μ)р(Vμ/T), но pVμ/T = R
следовательно,
pVм = (M/μ)RT.
Статья на тему Уравнение состояния газа
Содержание:
Температура:
Перед тем как, например, пойти на пляж, многие интересуются прогнозом погоды. И если ожидается температура воздуха 10 °С, то, скорее всего, планы будут изменены. А стоит ли отказываться от прогулки, если прогнозируется температура 300 К (кельвинов)? И что на самом деле вкладывают физики в понятие «температура»?
Что такое температура
Эксперименты показывают, что макроскопическая система может переходить из одного состояния в другое. Например, если в морозный день занести в комнату шарик, наполненный гелием, то гелий в шарике будет нагреваться и при этом будут изменяться давление, объем и некоторые другие параметры газа. После того как шарик пробудет в комнате некоторое время, изменения прекратятся. Один из постулатов молекулярной физики и термодинамики — его еще называют нулевое начало термодинамики — гласит: любое макроскопическое тело или система тел при неизменных внешних условиях самопроизвольно переходит в термодинамическое равновесное состояние (состояние теплового равновесия), после достижения которого все части системы имеют одинаковую температуру. Нулевое начало термодинамики фактически вводит и определяет понятие температуры.
Температура — физическая величина, характеризующая состояние теплового равновесия макроскопической системы.
Состояние теплового равновесия — это такое состояние макроскопической системы, при котором все макроскопические параметры системы остаются неизменными сколь угодно долго.
В состоянии теплового равновесия все части системы имеют одинаковую температуру; другие макроскопические параметры неизменны, но могут быть разными. Вспомните пример с шариком: после того как установится тепловое равновесие, температура окружающего воздуха и температура гелия в шарике будут одинаковыми, а давление, плотность и объем — разными.
Как работают термометры
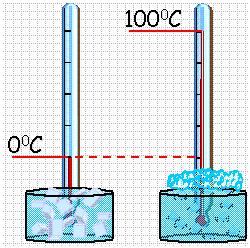
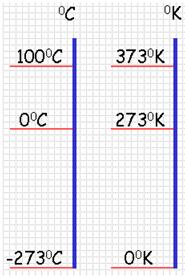
Температура — это физическая величина, и ее можно измерять. Для этого нужно установить шкалу температур. Самые распространенные температурные шкалы — шкалы Цельсия, Кельвина, Фаренгейта (рис. 29.1).
Построение шкалы температур начинается с выбора реперных (опорных) точек, которые должны быть однозначно связаны с какими-либо физическими процессами, которые легко воспроизвести. Например, за нулевую точку температурной шкалы Цельсия принята температура таяния льда при нормальном атмосферном давлении ( t = 0 °С). Температуре кипения воды при нормальном атмосферном давлении приписывают значение t =100 °С. Единица температуры по шкале Цельсия — градус Цельсия: 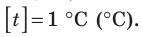
Рис. 29.2. различные виды термометров: а — жидкостный (принцип действия: изменение объема жидкости при изменении температуры); б — термометр сопротивления (изменение электрического сопротивления проводника при изменении температуры); в — биметаллический деформационный (изменение длин двух разных металлических пластин при изменении температуры)
Приборы для измерения температуры — термометры (рис. 29.2). Основные части любого термометра — термометрическое тело (ртуть или спирт в жидкостном термометре, биметаллическая пластина в металлическом деформационном термометре и т. д.) и шкала. Если термометрическое тело привести в контакт с телом, температуру которого нужно измерить, система придет в неравновесное состояние. При переходе в равновесное состояние будут изменяться некоторые параметры термометрического тела (объем, сопротивление и т. п.). Зная, как эти параметры зависят от температуры, определяют температуру тела.
Обратите внимание!
- Термометр фиксирует собственную температуру, равную температуре тела, с которым термометр находится в термодинамическом равновесии.
- Термометрическое тело не должно быть массивным, иначе оно существенно изменит температуру тела, с которым контактирует.
Температура и средняя кинетическая энергия молекул
То, что температура тела должна быть связана с кинетической энергией его молекул, следует из простых соображений. Например, с увеличением температуры увеличивается скорость движения броуновских частиц, ускоряется диффузия, повышается давление газа, а это значит, что молекулы движутся быстрее и их кинетическая энергия становится больше. Можно предположить: если газы находятся в состоянии теплового равновесия, средние кинетические энергии молекул этих газов одинаковы. Но как это доказать, ведь непосредственно измерить эти энергии невозможно?
Обратимся к основному уравнению МКТ идеального газа: 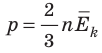
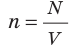
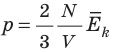
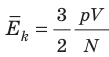
Таким образом, чтобы экспериментально убедиться в равенстве средних кинетических энергий молекул различных газов при одинаковой температуре, нужно измерить объемы (V), давления (p) и массы (m) газов и, зная их молярную массу (M), найти число молекул каждого газа (N) по формуле 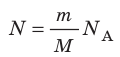
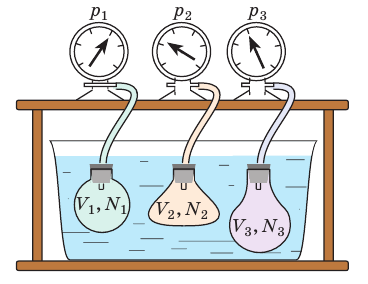
Чтобы обеспечить одинаковую температуру, можно, например, погрузить баллоны с различными газами в сосуд с водой и дождаться состояния теплового равновесия (рис. 29.3).
Рис. 29.3. опыт, позволяющий установить связь между температурой и средней кинетической энергией поступательного движения молекул газа. Газы в сосудах находятся в состоянии теплового равновесия со средой, а следовательно, и друг с другом
Эксперименты показывают, что для всех газов в состоянии теплового равновесия отношение 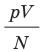
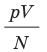
Например, при температуре 0 °С (сосуды с газами погрузили в тающий лед) 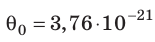
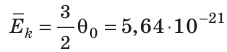
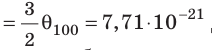
Абсолютная шкала температур
Понятно, что в джоулях представлять температуру неудобно (прежде всего потому, что значения θ очень малы), к тому же неудобно полностью отказываться от шкалы Цельсия. В 1848 г. английский физик Уильям Томсон (лорд Кельвин) (1824–1907) предложил абсолютную шкалу температур (сейчас ее называют шкалой Кельвина).
Температуру Т, измеренную по шкале кельвина, называют абсолютной температурой.
Единица абсолютной температуры — кельвин — основная единица СИ: [T] = 1 К (К).
Шкала Кельвина построена следующим образом:
- изменение температуры по шкале Кельвина равно изменению температуры по шкале Цельсия: ∆ = T t ∆ , то есть цена деления шкалы Кельвина равна цене деления шкалы Цельсия: 1 °С = 1 К; температуры, измеренные по шкалам Кельвина и Цельсия, связаны соотношениями:
- температура по шкале Кельвина связана с величиной
соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа:
- абсолютная температура имеет глубокий физический смысл: средняя кинетическая энергия поступательного движения молекул идеального газа прямо пропорциональна абсолютной температуре:
(1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (
). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.
Абсолютный нижний предел температуры, при котором движение молекул и атомов должно прекратиться, называют абсолютным нулем температуры. Давление p газа полностью определяется его абсолютной температурой T и концентрацией n молекул газа: p=nkT (2).
Выводы:
- Физическая величина, характеризующая состояние теплового равновесия макроскопической системы, называется температурой. Абсолютный нижний предел температуры, при котором движение молекул и атомов должно прекратиться, называют абсолютным нулем температуры. Шкала, за нулевую точку которой взят абсолютный нуль температуры, называется абсолютной шкалой температур (шкалой Кельвина). Единица абсолютной температуры — кельвин (К) — основная единица СИ. Температуры по шкале Кельвина и Цельсия связаны соотношением: T=t + 273; t=T – 273.
- Средняя кинетическая энергия поступательного движения молекул идеального газа прямо пропорциональна абсолютной температуре, а давление газа определяется абсолютной температурой и концентрацией молекул газа:
— постоянная Больцмана.
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Твердые тела и их свойства в физике
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
- Уравнение состояния идеального газа

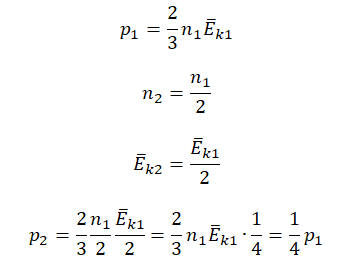
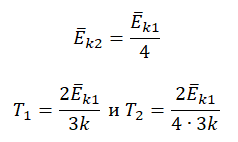
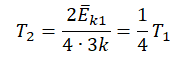
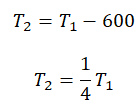
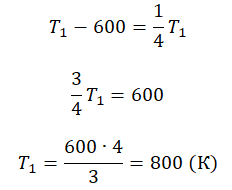


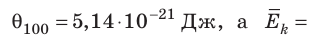
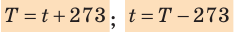
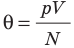 соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа:
соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа: 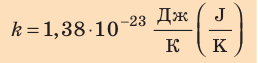
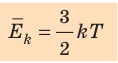 (1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (
(1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (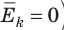 ). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.
). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.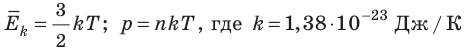 — постоянная Больцмана.
— постоянная Больцмана.