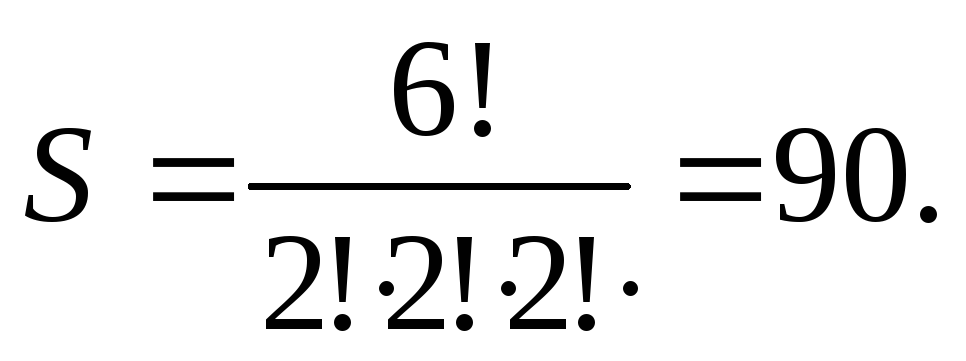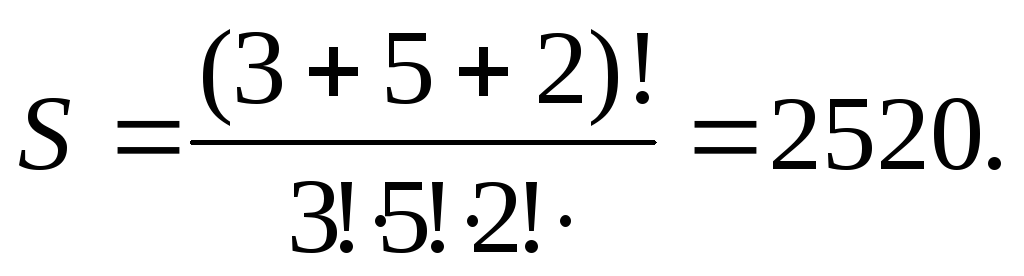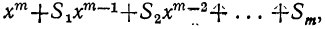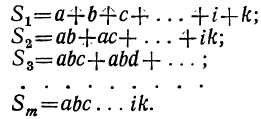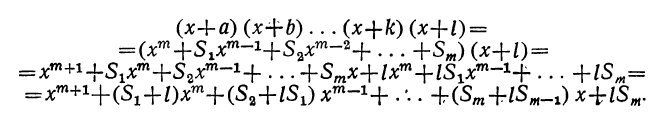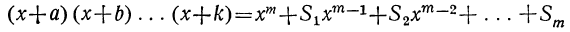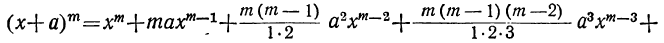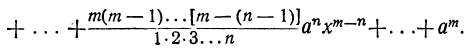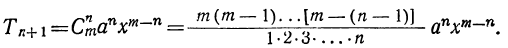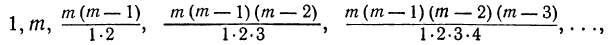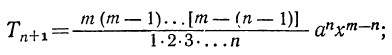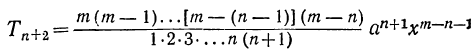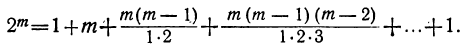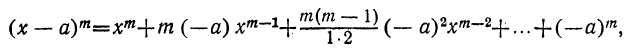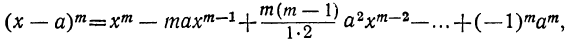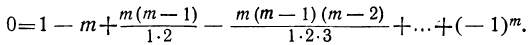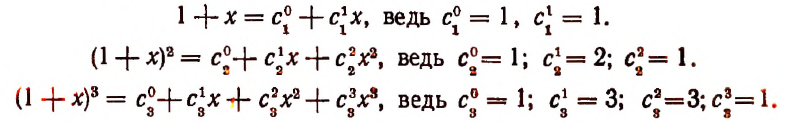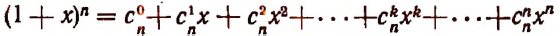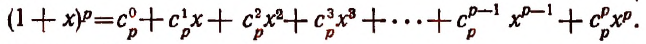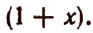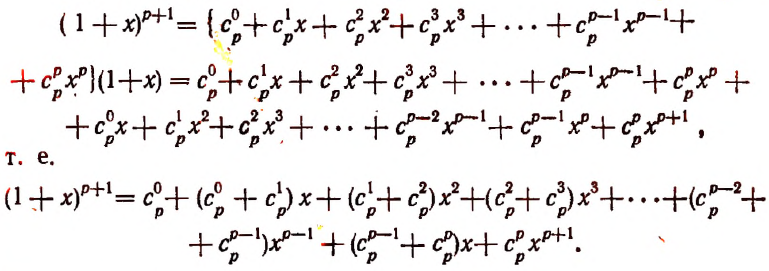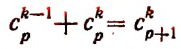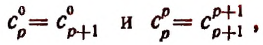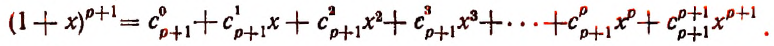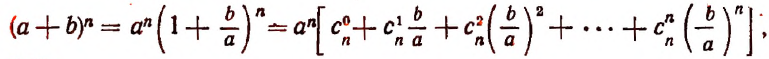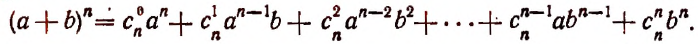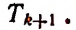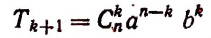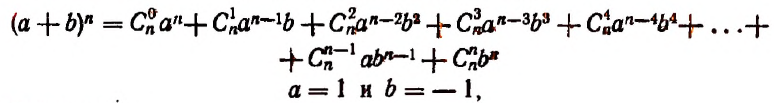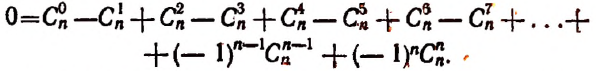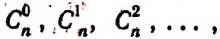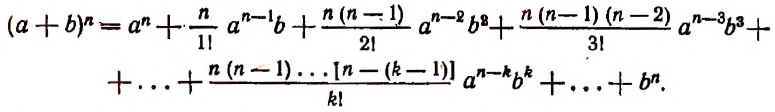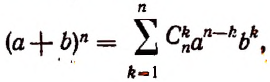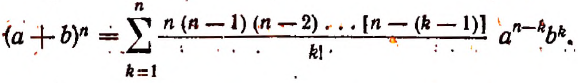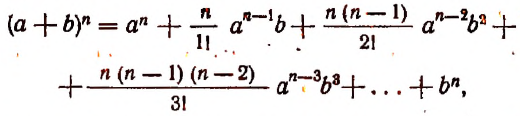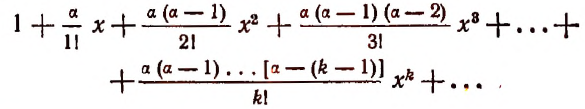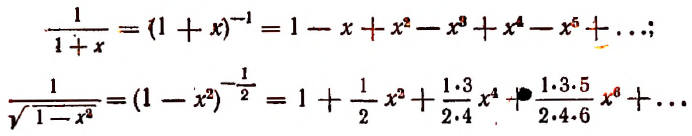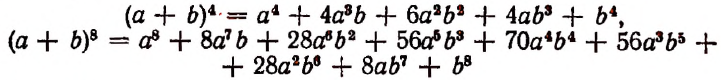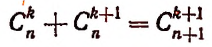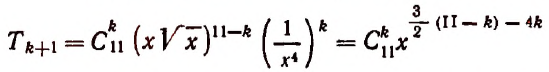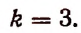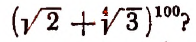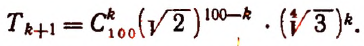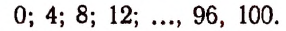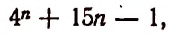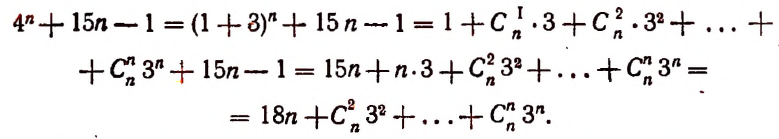Как найти сумму всех биномиальных коэффициентов - Avtoru.top

Пусть
множество,
состоящее изэлементов. Любое подмножество(включая и пустое подмножество), содержащееэлементов, называетсясочетаниемпоэлементов из
(или комбинацией поэлементов из₎,
при этом, разумеется,,
т.е.

сочетанияминазывают комбинации,
составленные изnразличных элементов поmэлементам. Сочетания считаются различными,
если их состав отличаются друг от друга
хотя бы одним элементом.

Теорема 2. Число сочетаний из n
элементов по m
определяется равенством:

(3)
.

Доказательство.Пустьзаданное
множество, состоящее изэлементов,—
какое либо подмножество,
содержащееэлементов. Составим всевозможные
перестановки из элементов,
получимразличных строк длиной.
Если указанную операцию произвести с
каждымэлементным
подмножеством множества,
то получим всегоразличных строк длиной.
Естественно, таким способом должны
получиться без исключения все строки

длиной
без
повторений, которые можно составить из
элементов множества.
Поскольку, по теореме 1, число таких
строкто имеем равенство,
из которого следует доказательство
теоремы.Подчеркнем, что
числа размещений, перестановок и
сочетаний связаны равенствами

т.е.
с учетом равенство (2) получаем (3). В
частности,

Далее,
рассмотрим несколько примеров на
применение комбинаторных понятий.

Пример 7. Сколько трехзначных
чисел можно составить из цифр 1, 2, 3, если
каждая цифра входит в изображение числа
только один раз?

Решение: Искомое число трехзначных
чисел:

Выпишите
самостоятельно эти наборы чисел.

Пример 8. Сколько можно составить
сигналов из 6 флажков различного цвета,
взятых

по 2?

Решение: Искомое число сигналов

Пример 9. Сколькими способами
можно выбрать две детали из ящика,
содержащего 10 деталей?

Решение: Искомое число способов.

Пример 10. Какое количество партий
сыграли 8 шахматистов, встречаясь с
каждым партнером только один раз.

Решение. В данной задаче набор
пар несущественен.

Двухэлементное
множество можно упорядочить только
2!=2 способами (число
перестановок). Следовательно, общее
число партий (пар) будет в 2! меньше, чем
число размещений.
Поэтому, общее число партий равно.

Решение этой задачи можно изящно
иллюстрировать геометрически (см.
Рис.4). Рассмотрим выпуклый восьмиугольник
.
С каждой любой вершины восьмиугольника
можно провести к другим вершинам семь
отрезков, т.е. количество встреч партий
шахматистов с другими партнерами равно
числу отрезков, соединяющих с остальными.
Общее число вершин (шахматистов) равно
8, а так как отрезкиАВиВАи т.д.
являются равными, то различных отрезков
(партий) будет равно.

Задания. 1.Эту же задачу решите, с
помощью турнирной таблицу встреч.

Бином Ньютона. Пустьитакие величины, для которых имеет место
равенство.
Из школьного курса известны алгебраические
тождества:

Продолжая, этот процесс, т.е. пользуясь
равенствами
можно написать следующее равенство:

Данное равенство называется
формулой бинома Ньютона. При этом мы
воспользовались равенствами:
=1.
Неотрицательные целые числа(обычно называют их биномиальными
коэффициентами) определены равенствами:

если
ипри остальных значениях.
Напомним, что принято 0!=1.

В
частности, имеют место равенства:

Обычно
формула бинома Ньютона доказывается
методом математической индукции с
учетом равенств:

Основные свойства бинома Ньютона.

1. В разложении
содержитсяслагаемых.

2. Показатель степени параметра
убывает отnдо 0,
напротив, показатель степенивозрастает от 0 до n,
в любом случае сумма показателей
степени величин (параметров)иравнаn – показателю
степени бинома.

3. Биномиальные коэффициенты, равноудаленные
от концов разложения, равны между собой,
т.е.
А также верно и другое разложение

(1)

4. Для биномиальных коэффициентов
верно равенство

Некоторые непосредственные выводы.

5. Из общей формулы (1) непосредственно
выводятся следующие равенства:

а. Если сумма чисел,
то имеет место равенство

В
дальнейшем это равенство играет важную
роль в теории вероятностей.

в. Если
,
то сумма биномиальных коэффициентов
равно,
т.е. верна формула

с. Если
,
то сумма биномиальных коэффициентов
всегда равна нулю.

В частности, полагая
,
получим равенство

Формулу
(1) можно переписать в виде:

6. Биномиальные коэффициенты сначала
возрастают, а затем, убывают. При этом:

— если показатель степени бинома
четный, то биномиальный коэффициент
среднего слагаемого разложения
наибольший;

— если же показатель степени бинома
нечетный, то биномиальные коэффициенты
двух средних слагаемых равны между
собой и являются наибольшими;

— на основании свойства 4.биномиальные
коэффициентымогут быть вычислены с помощью так
называемого «треугольника Паскаля»

В этих «треугольных» таблицах
легко заметить, что каждое число, кроме
крайних единиц, является суммой двух
вышерасположенных чисел.

7. Поскольку биномиальный коэффициент
начинается с нулевого члена, то в общем
виде принято ()
– ое слагаемоесчитать
–
им членом разложения, и обозначается:

Задача 1. Для выражениянайти
шестое слагаемое.

Решение.Нужно воспользоваться
биномиальной формулой, когда.

Ответ.
.

Задача 2..Найдите наибольший член
разложения

Решение.Для решения этой задачи
необходимо выяснить для каких
выполняется неравенства:

Рассмотрим отношение

Отсюда
следует, что при

т.е.,
при
коэффициенты убывают. Значит, для номеранаибольший
член разложения бинома и он же будетдесятым слагаемым

Задача 3. Найти член разложения,
не содержащий положительной степени(т.е. найти слагаемое содержащее).

Решение. Так как,тогда выписывая показатель степени,
после несложных упрощений получим:

Следовательно, четвёртый
член разложения (он же пятое
слагаемое) является
решением задачи.

Ниже предложим некоторые сведения из
теории арифметических функций.

Упражнения:
А. Докажите,
что

1.
При
любом простом

биномиальные
коэффициенты
делятся
на число
.

2.
Докажите
тождества:

,
еслилюбое
нечётное простое число..

В.
Дополнительные сведения. Пусть
—
каноническое представление натурального
числа,
определим классическую функцию Мебиусас помощью комбинаторных коэффициентов

равенством:

(**)

Докажите, что

1. Для
любых взаимно простых натуральных

,
(свойство
мультипликативности)

2.(свойство ортогональности)

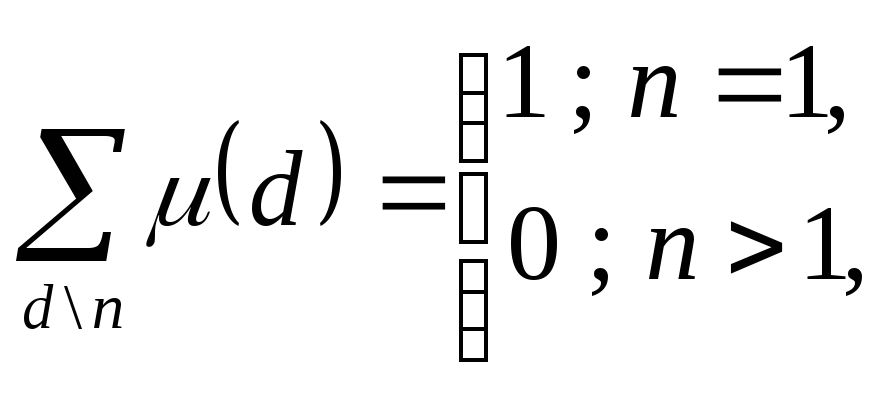
где
суммирование ведётся по всем положительным
целым делителям числа
.

3.
Вычислите функцию

Примечание.
Классическая
функция Мебиуса определяется несколько
иначе. По этому поводу можно обратиться,
например, к известным учебникам по
теории чисел
[3;4].
Определение
(**) предложенное здесь выгодно по
многим причинам. Во – первых, функция
определена одной формулой, во – вторых,
легко определяются различные обобщения
(речь идёт о функциях

которая
равна 0 или 1, смотря по тому, делится
или не делится число
натую степень числа,
а также других арифметических функций,
связанные с функцией Мебиуса). Подробные
сведения о функции Мебиуса и её свойства
можно найти в учебниках по теории чисел
[3;4].

Читателям
интересующихся более обстоятельно
этими вопросами, рекомендуем обратиться
к фундаментальным источникам по
аналитической теории чисел [5-7].

Рассмотрим ещё
одну тематику,
обобщающую
понятие размещения.

8.
Размещения данного состава. Полиномиальная
формула.

Начнём со следующей
простой задачи

.
Состав строки.
Размещение
данного состава. Рассмотрим
наборы (строки)
и.
Очевидно, что они различны, но имеют
один и тот же «состав»
— в каждую из них входят три буквы
и две буквы.
Далее, уточним понятиесостава
строки.
Пусть
некоторое
членное
множество,
строка длиной,
составленная из элементов множества.
Тогда каждому номеруиз совокупностибудет
соответствовать число
указывающее, на количество участия
элементовв строке
.
Выписывая по порядку эти числа, получаем
новую строку,
которую и называют составом строки.

Например, если
и
,
то строкаимеет следующий состав.
Следовательно, в строкеэлементучаствует три раза, элементне участвует, элементучаствует два раза, элементучаствует один раз. Две строки, имеющие
один и тот же состав, могут отличаться
друг от друга лишь порядков элементов.
Их называютразмещениями
с повторениями данного состава.

Рассмотрим следующую
комбинаторную задачу:
найти
число размещений, имеющий данный состав
.

Приведём
основное утверждение о числе составов

Теорема
3.
Количество

—
различных
последовательностей (составов),
составленных из элементов
,
в которых
каждый элемент
встречается

раз
(равно

(4)
.

Доказательство.
Обозначим
количество
составов указанных в формулировке
теоремы 1 буквой
.
А так же, положим.
Введём в рассмотрениепроизвольных
различных элементов:

.
Для любой исходной последовательности

строим различные перестановки из
указанных
элементов, заменяя элементы по следующему
правилу. На тех местах исходной
последовательности, где стояло одно и
то же(этот элемент встречалсяраз), записываем какой-нибудь перестановку
изэлементов
.
Согласно
равенству (2) такое действие для одного
можно осуществлять в точностиразличными способами. Проделав такое
действие для каждого(),
мы получим некоторую перестановку изиз указанных выше элементов. На основании
формулы умножения (см. пункт)
для любой последовательности строки
получим всего указанным способом
различных перестановок из
элементов. Для различных исходных
последовательностей вышеуказанным
способом мы, естественно, получаем
различные перестановки из взятыхэлементов.
При этом любая из выбранныхэлементов может быть получена этим
способом, если в качестве начальной
последовательности выбрать ту строку,
которая образуется в результате замены
всех элементов
во
взятой перестановке одним элементом
для кахдого.
Таким образом, с учётом равенства (2)
получаем:,
следовательно,

И с учётом нашего
обозначения
,
теорема доказана.

Пример 1. Количество
различных 6 — значных натуральных чисел,
которые можно записать с помощью цифр
1,2,3 так, чтобы каждая цифра встречалась
в записи по два раза, равно:

Пример 2. В
наличии имеются книги трёх наименований,
причём имеется три экземпляра книг
одного наименования, пять экземпляров
другого и два экземпляра третьего.
Количество различных размещений этих
книг на одной полке составляет:

Если в наличии
имеются книги
различных наименований, причём поэкземпляров книг каждого наименования,
то всеэкземпляров
книг могут быть размещены на полке

способами.

Пример 3. В
одном ряду шахматной доски располагаются:
1 король, 1
ферз, 2 слона, 2 коня, 2 ладьи. Количество
всевозможных расположения этих фигур
в одном ряду равно:

.
Полиномиальная формула. Обобщением
формулы Бинома Ньютона является так
называемая полиномиальная формула,
которую приведём без доказательства.

Пусть
любые
числа (или произвольные комутативные
объекты). Имеет место

следующее утверждение

Теорема 4.
Справедлива
полиномиальная формула

(4)

где
суммирование распространяется на
всевозможные целые числа
,
для которых

Следствие.

1) Для
случая
,
получаем формулу

(5)

2) Для случая
имеет
место равенство

Задания:
1. На
основании равенство (5) проверьте
тождество

2.
Пусть
,
тогда при целомсправедливо
неравенство

Это
известное неравенство Бернулли.

Указание.
Используйте
метод математической индукции.

В
завершении этого раздела сформулируем
известную формулу Стирлинга без
доказательства.

где
основание
натурального логарифма. Эта формула
обычно применяется при больших значениях.
В частности, из неё вытекает, чтос точностью доприближается выражением

Другими
словами, справедливо (с учётом свойства
логарифмической функции) неравенство

Источник

Бином Ньютона и треугольник Паскаля

18 декабря 2021

Сегодня мы детально разберём Бином Ньютона. Это формула, по которой можно раскрыть скобки ${{left( a+b right)}^{n}}$ и получить готовый многочлен. Сама формула выглядит так:

[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]

где $C_{n}^{k}$ — биноминальные коэффициенты (они же — «число сочетаний из $n$ по $k$»), которые считаются по формуле

[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]

Вот и всё. На этом можно было бы закончить, но есть одно но: большинство начинающих учеников не понимают эту формулу, не умеют пользоваться её, а уж чтобы доказать её — об этом даже речи не идёт.

Сегодня мы всё это исправим. Вы узнаете буквально всё, что нужно знать про Бином Ньютона:

Постановка задачи — в чём вообще проблема?
Формула бинома Ньютона — что значат все эти значки?
Знак суммы — чрезвычайно полезный материал для всех, кто хочет понять математику.
Биноминальные коэффициенты — минутка комбинаторики.
Треугольник Паскаля — лайфхак для быстрых вычислений.
Доказательство Бинома Ньютона — для тех, кто хочет познать Истину.:)

Материала много, но всё будет максимально понятно и — главное — чрезвычайно полезно. Погнали!

1. Постановка задачи

Итак, мы хотим быстро раскрывать скобки в конструкциях вида ${{left( a+b right)}^{n}}$. Начнём с того, что мы и так знаем. Например:

[{{left( a+b right)}^{1}}=a+b]

Спасибо, кэп. Теперь вспомним формулы сокращённого умножения. Квадрат суммы:

[{{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}]

И куб суммы:

[{{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}]

Видим, что с ростом степени растёт и количество слагаемых-одночленов: их всегда на одно больше, чем степень. Но это не проблема. Проблема в другом: у этих одночленов появляются некие коэффициенты, принцип вычисления которых не ясен. Пока не ясен…

Именно для нахождения этих коэффициентов придумали бином Ньютона.

2. Бином Ньютона

Пусть $nin mathbb{N}$. Тогда верно равенство

[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]

где $sum{left( … right)}$ — краткая запись суммы, $C_{n}^{k}$ — биноминальный коэффициент, который считается по формуле

[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]

В этой формуле прекрасно всё. Одних пугает знак суммы. Другие не понимают, что за $C_{n}^{k}$ такое (ещё раз: это объект из мира комбинаторики, читается «число сочетаний из $n$ по $k$»). Третьи более-менее понимают, о чём речь, но применить эту формулу на практике не могут.

Сегодня мы решим все эти проблемы. Начнём со знака суммы.

3. Знак суммы

Знак суммы — это краткая запись суммы нескольких однотипных слагаемых:

[sumlimits_{k=a}^{k=b}{fleft( k right)}]

Формула $fleft( k right)$ задаёт общий вид однотипных слагаемых, а нижний и верхний индексы $k=a$ и $k=b$ (сверху вместо $k=b$ обычно пишут просто $b$) определяют диапазон значений, которые «пробегает» $k$ и которые нужно подставить в $fleft( k right)$. Например:

[sumlimits_{k=3}^{5}{2k}=2cdot 3+2cdot 4+2cdot 5]

Более привычный формат:

[sumlimits_{k=1}^{n}{fleft( k right)=fleft( 1 right)+fleft( 2 right)+…+fleft( n right)}]

То же самое с индексами:

[sumlimits_{k=1}^{n}{{{a}_{k}}={{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}]

Обратите внимание: если $k$ пробегает значения от $k=a$ до $k=b$, то всего таких слагаемых будет ровно $b-a+1$:

[sumlimits_{k=a}^{b}{fleft( k right)=underbrace{fleft( a right)+fleft( a+1 right)+ldots +fleft( b right)}_{b-a+1text{ слагаемых!}}}]

Кроме того, полезно потренироваться и с обратным переходом — от полной записи к краткой:

[frac{1}{1}+frac{1}{3}+frac{1}{5}+frac{1}{7}+frac{1}{9}=sumlimits_{n=1}^{5}{frac{1}{2n-1}}]

[frac{2}{3}+frac{4}{9}+frac{6}{27}+frac{8}{81}=sumlimits_{n=1}^{4}{frac{2n}{{{3}^{n}}}}]

В приложении к уроку — куча задач для самостоятельной тренировки.

Но вернёмся к биному Ньютона. Распишем его без знака суммы:

[begin{align} {{left( a+b right)}^{n}} & =C_{n}^{0}cdot {{a}^{n}}{{b}^{0}}+C_{n}^{1}cdot {{a}^{n-1}}{{b}^{1}}+ \ & +ldots +C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}+ldots + \ & +C_{n}^{n-1}cdot {{a}^{1}}{{b}^{n-1}}+C_{n}^{n}cdot {{a}^{0}}{{b}^{n}} end{align}]

В целом, всё понятно: степени буквы $a$ уменьшаются с ${{a}^{n}}$ до ${{a}^{0}}$; одновременно степени буквы $b$ растут с ${{b}^{0}}$ до ${{b}^{n}}$. Сумма степеней этих букв в каждом одночлене равна $n$. Но что такое $C_{n}^{k}$?

4. Биноминальные коэффициенты

Немного комбинаторики.

Определение. Число сочетаний из $n$ по $k$ — это число способов, которыми можно выбрать $k$ элементов среди $n$ элементов, если порядок выбора не имеет значения. Обозначается $C_{n}^{k}$ и считается по формуле

[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]

Обратите внимание: в числителе и знаменателе стоят факториалы. Стандартное определение: $n!$ — это произведение всех чисел от единицы до $n$:

[n!=1cdot 2cdot 3cdot …cdot n]

У факториалов много интересных свойств. Чуть позже мы рассмотрим их и даже введём более корректное определение самого факториала. А пока просто потренируемся считать биноминальные коэффициенты.

Пример. На пруду плавают 5 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?

Очевидно, порядок кормления уток неважен. Покормить сначала утку №1, а затем №2 — это то же самое, что покормить сначала утку №2, затем №1. Результат один и тот же: накормлены лишь эти две утки, а остальные три — нет. Поэтому считаем $C_{5}^{2}$:

[begin{align} C_{5}^{2} & =frac{5!}{2!cdot 3!} \ & =frac{5cdot 4cdot 3cdot 2cdot 1}{2cdot 1cdot 3cdot 2cdot 1}= \ & =10 end{align}]

Вот и всё. Однако при больших $n$ и $k$ посчитать число сочетаний напрямую становится затруднительно. Тут на помощь приходит сокращение дробей.

Пример. На пруду 150 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?

Порядок вновь неважен, просто уток стало больше. Поэтому считаем $C_{150}^{2}$:

[begin{align} C_{150}^{2} & =frac{150!}{2!cdot 148!}= \ & =frac{150cdot 149cdot 148cdot …cdot 1}{2cdot 1cdot 148cdot …cdot 1}= \ & =frac{150cdot 149}{2cdot 1}= \ & =11175 end{align}]

Видим, что факториалы образуют «длинные хвосты» в числителе и знаменателе, которые легко сокращаются. Однако для корректной работы с биномом Ньютона нам потребуется расширить определение факториала.

4.1. Новое определение факториала

Стандартное определение мы уже привели выше:

[n!=1cdot 2cdot 3cdot …cdot n,quad nin mathbb{N}]

Но как посчитать, например, факториал нуля? И как сокращать «длинные хвосты», не расписывая факториалы? Здесь нам поможет более грамотное определение.

Определение. Пусть $nin mathbb{N}bigcup left{ 0 right}$ — целое неотрицательное число. Тогда факториал считается по формуле:

[n!=left{ begin{align} & 1,quad n=0 \ & ncdot left( n-1 right)!,quad n gt 0 \ end{align} right.]

В частности, $0!=1$ по определению.

Простейшие коэффициенты:

[begin{align} C_{n}^{0} & =frac{n!}{0!left( n-0 right)!}=frac{n!}{1cdot n!}=1; \ C_{n}^{1} & =frac{n!}{1!left( n-1 right)!}=frac{ncdot left( n-1 right)!}{1cdot left( n-1 right)!}=n; \ end{align}]

А вот ещё парочка весёлых примеров:

[begin{align} C_{7}^{3} & =frac{7cdot 6cdot 5cdot 4cdot ldots cdot 1}{3cdot 2cdot 1cdot 4cdot ldots cdot 1}=35 \ C_{8}^{2} & =frac{8cdot 7cdot 6cdot ldots cdot 1}{2cdot 1cdot 6cdot ldots cdot 1}=28 \ C_{64}^{3} & =frac{64cdot 63cdot 62cdot 61cdot ldots cdot 1}{3cdot 2cdot 1cdot 61cdot ldots cdot 1}= \ & =41664 end{align}]

5. Треугольник Паскаля

Посчитаем бином Ньютона для $n=0$, $n=1$, $n=2$, $n=3$:

[begin{align} & {{left( a+b right)}^{0}}=1 \ & {{left( a+b right)}^{1}}=1cdot a+1cdot b \ & {{left( a+b right)}^{2}}=1cdot {{a}^{2}}+2cdot ab+1cdot {{b}^{2}} \ & {{left( a+b right)}^{3}}=1cdot {{a}^{3}}+3cdot {{a}^{2}}b+3cdot a{{b}^{2}}+1cdot {{b}^{3}} \ end{align}]

Составим таблицу:

[begin{matrix} 1 \ 1quad 1 \ 1quad 2quad 1 \ 1quad 3quad 3quad 1 \ 1quad 4quad 6quad 4quad 1 \ end{matrix}]

Получили треугольник, который в народе называют «Треугольник Паскаля»: по бокам единицы, а внутри каждое число равно сумме двух ближайших, стоящих этажом выше:

[begin{align} & 3=1+2 \ & 4=1+3 \ & 6=3+3 \ end{align}]

И это не случайность. Перед нами важнейшее свойство биноминальных коэффициентов, которое мы оформим в виде теоремы и докажем.

Теорема. Биноминальные коэффициенты вычисляются по формуле

[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]

Доказывается напролом.

Распишем доказательство детально:

[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!}]

[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!} \ end{align}]

Заметим, что по определению факториала

[begin{align} & left( k+1 right)!=left( k+1 right)cdot k! \ & left( n-k right)!=left( n-k right)cdot left( n-k-1 right)! end{align}]

Поэтому знаменатели биноминальных коэффициентов можно переписать:

[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)left( n-k-1 right)!}+frac{n!}{left( k+1 right)k!left( n-k-1 right)!}]

[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{n!}{k!left( n-k right)left( n-k-1 right)!}+ \ & +frac{n!}{left( k+1 right)k!left( n-k-1 right)!} end{align}]

Приведём к общему знаменателю:

[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} end{align}]

[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ = & frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}=frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} \ end{align}]

Окончательно получим:

[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( n+1 right)!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)!}{left( k+1 right)!left( n+1-left( k+1 right) right)!}= \ & = C_{n+1}^{k+1} end{align}]

Теорема доказана. Теперь мы знаем, как формируется треугольник Паскаля. Осталось доказать сам Бином Ньютона.

6. Доказательство Бинома Ньютона

Итак, нужно доказать, что

[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]

где $C_{n}^{k}$ — биноминальные коэффициенты с теми чудесными свойствами, которые мы рассмотрели и доказали выше.

Будем доказывать по индукции.

6.1. База индукции

Рассмотрим $n=1$. Формула Бинома Ньютона для него:

[begin{align} {{left( a+b right)}^{1}} & =sumlimits_{k=0}^{1}{C_{1}^{k}{{a}^{1-k}}{{b}^{k}}}= \ & =C_{1}^{0}{{a}^{1}}{{b}^{0}}+C_{1}^{1}{{a}^{0}}{{b}^{1}}= \ & =a+bend{align}]

Очевидно, для $n=1$ формула верна. Переходим к индуктивному предположению.

6.2. Индуктивное предположение

Пусть Бином Ньютона верен для некоторого $n=t$:

[{{left( a+b right)}^{t}}=sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}]

Используя этот факт, докажем верность и для $n=t+1$, т.е. выполним индуктивный переход.

6.3. Индуктивный переход

Докажем, что бином Ньютона верен для $n=t+1$:

[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]

Для этого сначала заметим, что

[{{left( a+b right)}^{t+1}}={{left( a+b right)}^{t}}cdot left( a+b right)]

Однако согласно индуктивному предположению, ${{left( a+b right)}^{t}}$ допускает разложение по Биному Ньютона, поэтому

[begin{align} left( a+b right)cdot {{left( a+b right)}^{t}} & =left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} end{align}]

[begin{align} & left( a+b right)cdot {{left( a+b right)}^{t}}= \ = & left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} \ end{align}]

Запишем отдельно первое слагаемое первой суммы и учтём, что $C_{t}^{0}=C_{t+1}^{0}=1$:

[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} & = C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ & = C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} end{align}]

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}= \ = & C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]

И последнее слагаемое последней второй суммы и учтём, что $C_{t}^{t}=C_{t+1}^{t+1}=1$:

[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} end{align}]

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Сейчас будет самая нетривиальная операция. Меняем индекс суммирования в последней сумме: выполняем подстановку $k=m-1$. При этом меняются и пределы суммирования:

[left[ begin{align} k & =m-1 \ k & =0Rightarrow m=1 \ k & =t-1Rightarrow m=t \ k+1 & =m \ t-k & =t+1-m \ end{align} right]]

В итоге последняя сумма перепишется так:

[sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]

[begin{align} & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ = & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Объединяем суммы вместе:

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+ \ + & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Заметим, что два знака суммы различаются лишь названием индекса и биноминальными коэффициентами. Всё остальное — диапазоны суммирования, степени буквы $a$ и буквы $b$ — всё идеально совпадает и никак не меняется, если написать вместо $k$ индекс $m$ или наоборот.

Такие суммы можно записать под единым знаком:

[C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]

[begin{align} & C_{t+1}^{0}cdot {{a}^{t+1}}+ \ + & sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+ \ + & C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]

Выражение под знаком суммы легко раскладывается на множители:

[begin{align} C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} & =left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ & =C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} end{align}]

[begin{align} & C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} \ end{align}]

Здесь в последнем шаге мы использовали свойство биноминальных коэффициентов, доказанное выше:

[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]

Или, что то же самое

[C_{n}^{k-1}+C_{n}^{k}=C_{n+1}^{k}]

Таким образом, всю сумму можно переписать более компактно, а затем внести под знак суммы первое и последнее слагаемое:

[ C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]

[begin{align} C_{t+1}^{0}cdot {{a}^{t+1}} & +sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ & =sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]

Сопоставляя исходное выражение и конечное, получим

[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]

Именно это и требовалось доказать. Следовательно, исходная формула Бинома Ньютона верна.

Смотрите также:

Схема Горнера
Теорема Безу и корни многочленов
Знаки тригонометрических функций
Уравнение касательной к графику функции
Как представить обычную дробь в виде десятичной
Сложные задачи B2 на проценты: вычисление полной стоимости

Источник

Формула бинома Ньютона
- Свойства формулы бинома Ньютона
- Применение формулы бинома к многочлену
Вывод формулы бинома ньютона
Свойства разложения бинома
Свойства биномиальных коэффициентов
Арифметический треугольник, или треугольник паскаля
Примеры с решением на Бином Ньютона
Дополнение к Бином Ньютону

Произведение биномов, отличающихся только вторыми членами. Обыкновенным умножением находим:
(x+α) (x+b)=x²+ax+bx+ab=x²+(a+b) x+ab;
(x+a) (x+b) (x+c) = [x²+(a+b) x+ab] (x+c) =
= x³+(a+b) x2+abx+cx²+(ac+bc) x+abc=
= x³ + (a+b+c) x²+(ab+ac+bc) x+abc.

Подобно этому найдём:
(x+a) (х+b) (х+с) (x+d) = x⁴+(a +b+c+d) x³+
+ (ab+ac+ ad+bc+bd+cd) x²+(abc+abd+acd+bcd) x+abcd.

Рассматривая эти произведения, замечаем, что все они составлены по одному и тому же закону, а именно:

Произведение составляет многочлен, расположенный по убывающим степеням буквы х.

Показатель первого члена равен числу перемножаемых биномов; показатели при х в следующих членах убывают на 1; последний член не содержит х (содержит его в нулевой степени).

Коэффициент первого члена есть 1; коэффициент второго члена есть сумма всех вторых членов перемножаемых биномов; коэффициент третьего члена есть сумма всех произведений вторых членов, взятых по два; коэффициент четвёртого члена есть сумма всех произведений вторых членов, взятых по три. Последний член есть произведение всех вторых членов.

Докажем, что этот закон применим к произведению какого угодно числа биномов. Для этого предварительно убедимся, что если он верен для произведения m биномов:
(x+a) (x+b) (х+с) … (x+k),
то при этом предположении будет верен и для произведения (m+1) биномов:
(x+a) (x+b) (x+c) . .. (x+k) (х+l).

Итак, допустим, что верно следующее равенство:
(x+α) (x+b) (х+с)… (x+k) =
где для краткости мы положим:

Умножим обе части допущенного равенства на бином x+l:

Рассматривая это новое произведение, убеждаемся, что оно подчиняется такому же закону, какой мы предположили верным для m биномов. Действительно, во-первых, этому закону следуют показатели буквы х; во-вторых, ему же следуют и коэффициенты, так как коэффициент второго члена S+l есть сумма всех вторых членов перемножаемых биномов, включая сюда и l; коэффициент третьего члена S₂+lS₁ есть сумма парных произведений всех вторых членов, включая сюда и l, и т. д.; наконец, 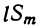есть произведение всех вторых членов: abc… kl.

Мы видели, что закон этот верен для произведения двух, трёх и четырёх биномов; следовательно, по доказанному теперь, он должен быть верен и для произведения 4+1, т. е. для произведения пяти биномов, если же он верен для произведения пяти биномов, то он верен и для произведения 5+1, т. е. для произведения шести биномов, и т. д.

Изложенное рассуждение представляет так называемое „доказательство от m к m+1“. Оно называется также „математической индукцией» (или „совершенной индукцией»). Заметим, что в предыдущих главах этой книги неоднократно представлялся случай применить доказательство от m к m + 1 . Мы этого не делали только ради простоты изложения.

Формула бинома Ньютона

Предположим, что в доказанном нами равенстве

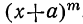
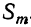
все вторые члены биномов одинаковы, т. е. что a=b=c= … =k. Тогда левая часть будет степень бинома . Посмотрим, во что обратятся коэффициенты S₁, S₂, …, .

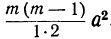
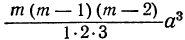
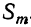
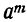
Коэффициент S₁, равный a+b+c+ … +k, обратится в та. Коэффициент S₂, равный ab+ac+ad+ …. обратится в число α², повторённое столько раз, сколько можно составить сочетаний из m элементов по 2, т. е. обратится в . Коэффициент S₃, равный abc+abd+…, обратится в число а³, повторённое столько раз, сколько можно составить сочетаний из т элементов по 3, т. е. и т. д. Наконец, коэффициент , равный abc...k, обратится в . Таким образом, мы получим:

Это равенство известно как формула бинома Ньютона, причём многочлен, стоящий в правой части формулы, называется разложением бинома. Рассмотрим особенности этого многочлена.

Свойства формулы бинома Ньютона

Из этих свойств мы укажем следующие 10:

1) Показатели буквы х уменьшаются на 1 от первого члена к последнему, причём в первом члене показатель х равен показателю степени бинома, а в последнем он есть 0; наоборот, показатели буквы а увеличиваются на 1 от первого члена к последнему, причём в первом члене показатель при а есть 0; а в последнем он равен показателю степени бинома. Вследствие этого сумма показателей при х и а в каждом члене одна и та же, а именно: она равна показателю степени бинома.

2) Число всех членов разложения есть m+1, так как разложение содержит все степени а от 0 до m включительно.

3) Коэффициенты равны: у первого члена — единице, у второго члена — показателю степени бинома, у третьего члена — числу сочетаний из m элементов по 2, у четвёртого члена — числу сочетаний из m элементов по 3; вообще коэффициент (n+1)-ro члена есть число сочетаний из m элементов по n. Наконец, коэффициент последнего члена равен числу сочетаний из т элементов по m, т. е. 1.

Заметим, что эти коэффициенты называются биномиальными.

4) Обозначая каждый член разложения буквой T с цифрой внизу, указывающей номер места этого члена в разложении, т. е. первый член T₁, второй член T₂ и т. д., мы можем написать:

Эта формула выражает общий член разложения, так как из неё мы можем получить все члены (кроме первого), подставляя на место n числа: 1, 2, 3,…. m.

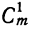
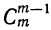
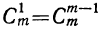
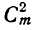
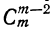
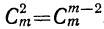
5) Коэффициент первого члена от начала разложения равен единице, коэффициент первого члена от конца тоже равен единице. Коэффициент второго члена от начала есть m, т. е. ; коэффициент второго члена от конца есть ; но так как , то эти коэффициенты одинаковы. Коэффициент третьего члена от начала есть , а третьего члена от конца есть ; но , поэтому и эти коэффициенты одинаковы и т. д. Значит:

Коэффициенты членов, одинаково удалённых от концов разложения, равны между собой.

6) Рассматривая биномиальные коэффициенты:

мы замечаем, что при переходе от одного коэффициента к следующему числители умножаются на числа, всё меньшие и меньшие (на m—1, на m — 2, на m — 3 и т. д.), а знаменатели умножаются на числа, всё большие и большие (на 2, на 3, на 4 и т. д.). Вследствие этого коэффициенты сначала возрастают (пока множители в числителе остаются большими соответственных множителей в знаменателе), а затем убывают. Так как коэффициенты членов, равно отстоящих от концов разложения, одинаковы, то наибольший коэффициент должен находиться посередине разложения. При этом, если число всех членов разложения нечётное (что бывает при чётном показателе бинома), то посередине будет один член с наибольшим коэффициентом; если же число всех членов чётное (что бывает при нечётном показателе бинома), то посередине должны быть два члена с одинаковыми наибольшими коэффициентами. Например:
(х+α)⁴=x⁴+4αx³+6α²x²+4α³x+α⁴;
(x+α)⁵=x⁵+5αx⁴+10α²x3+10α³x²+5α⁴x+α⁵∙

7) Из сравнения двух рядом стоящих членов:

заключаем, что:

Для получения коэффициента следующего члена достаточно умножить коэффициент предыдущего члена на показатель буквы х в этом члене и разделить на число членов, предшествующих определяемому.

Пользуясь этим свойством, можно сразу писать, например, (x+a)⁷=x⁷+7ax⁶+…

Теперь берём 7, умножаем его на 6 и делим на 2, получаем 21: (x+a)⁷=x⁷+7ax⁶+21a²x⁵+… .

Теперь берём 21, умножаем на 5 и делим на 3, получаем 35:
(x+a)⁷ =х⁷+7ax⁶+21a²x⁵+35a³x⁴+….

Теперь уже выписаны члены до середины ряда, остальные получим, основываясь на свойстве пятом:
(х+а)⁷ =х⁷-7αx⁶+21α²x⁵+35α³x⁴+35α⁴x³+21α⁵x²+7α⁶x+α⁷.

Сумма всех биномиальных коэффициентов равна . Действительно, положив в формуле бинома x=a=1, получим:

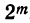
Например, сумма коэффициентов в разложении (х+a)⁷ равна
1+7+21+35+35 +21+7+1 = 128=2⁷.

9) Заменив в формуле бинома а на — а, получим:

т. е.

следовательно, знаки + и — чередуются.

10) Если в последнем равенстве положим x=α =1, то найдём:

Сумма биномиальных коэффициентов, стоящих на нечётных местах, равна сумме биномиальных коэффициентов, стоящих на чётных местах.

Применение формулы бинома к многочлену

Формула бинома Ньютона позволяет возвышать в степень многочлен. Так:
(α+ b+c)⁴ = [(а+b)+с]⁴= (a+b)⁴+4c (а+b)³+6c² (а+b)²+4c³ (a+b)+c⁴.

Разложив (a+b)⁴, (a+b)³, (а+b)², окончательно получим:
(a+b+с)⁴=a⁴+4a³b+ 6a²b²+ 4ab³+ b⁴ +4a³c+12a²bc+
+12ab²c+4b³c+6a²c²+12abc²+6b²c²+ 4ac³ + 4bc³+с⁴.

Вывод формулы бинома ньютона

Очевидно, что

Возникает вопрос, будет ли закономерность, наблюдаемая в этих формулах, обладать общностью, т. е. будет ли справедливой формула

при всяком натуральном значении n?

Воспользуемся методом полной индукции. Допустим, что формула верна для произвольно взятого натурального числа р, т. е. предположим справедливым следующее равенство:

Умножим обе части этого предполагаемого равенства на

Тогда получим:

Пользуясь формулой

и приняв во внимание, что

получим окончательно:

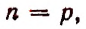
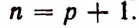
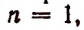
Из предположения, что формула верна при мы пришли к тому, что формула оказалась верной и при Но поскольку, кроме того, формула верна при то она должна быть верна и при любом натуральном значении n.

Теперь легко получить разложение и для

Действительно,

или

Последняя формула и называется формулой бинома Ньютона. Ее правая часть называется разложением степени бинома.

Числа называются биномиальными коэффициентами.

Свойства разложения бинома

В разложении бинома содержится членов на один больше, чем показатель степени бинома.

Все члены разложения имеют относительно букв а и b одно и то же измерение, равное показателю степени бинома. (Измерением одночлена относительно букв а и b называется сумма показателей степеней этих букв, входящих в этот одночлен.)

Поскольку все члены разложения имеют одинаковое измерение относительно букв а и b, то это разложение является однородным многочленом относительно букв а и b (см. стр. 450).

В разложении показатель степени буквы а последовательно понижается на единицу, начиная с показателя n, а показатель степени буквы b последовательно повышается на единицу, начиная с показателя, равного нулю.

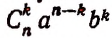
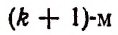
Член разложения является членом разложения и обозначается символом

Формула

называется формулой общего члена разложения, так как, давая букве k целые значения от 0 до n, мы можем получить из нее любой член разложения.

Теперь напишем разложение для выражения

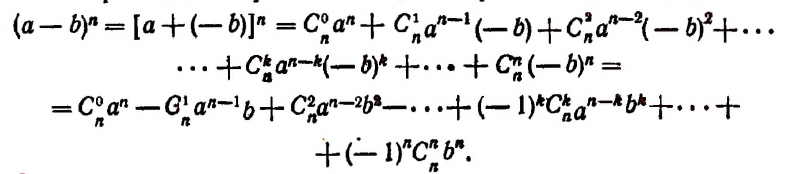
Здесь

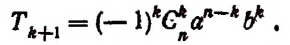
Свойства биномиальных коэффициентов

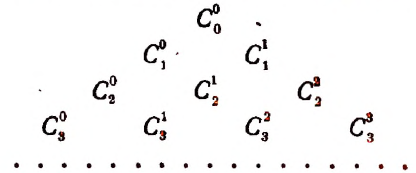
1. Биномиальные коэффициенты, равноудаленные от начала и конца разложения, равны между собой. Действительно, по первому свойству числа сочетаний имеем:

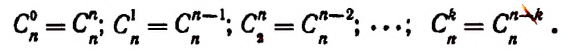
2. Сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома.

Доказательство:

Положим, в формуле бинома

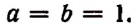
Тогда получим:

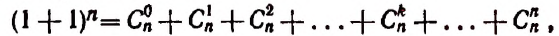
или

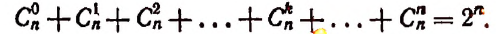
3. Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме, биномиальных коэффициентов, стоящих на нечетных местах.

Доказательство:

Полагая в тождестве

получим:

Перенеся все отрицательные члены в левую часть, получим:

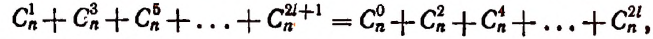
что и требовалось доказать.

Если вместо биномиальных коэффициентов подставить их значения, то формула бином Ньютона примет вид:

Формулу бинома Ньютона принято записывать ради краткости в следующем символическом виде:

или

Читателю может показаться непонятным, почему столь элементарная формула

где n — целое положительное число, носит имя великого ученого Ньютона, тем более что эта формула была известна до Ньютона. Например, ее знал Аль-Каши (XV век) и она встречается в трудах Паскаля. Объясняется это тем, что именно Ньютоном была обобщена эта формула для любого действительного показателя.

Ньютон впервые показал, что выражение

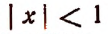
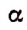
где и — любое действительное число, равняется сумме следующего сходящегося, ряда:

Например, если 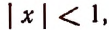то

Арифметический треугольник, или треугольник паскаля

Написанная ниже таблица

называется треугольником Паскаля *.

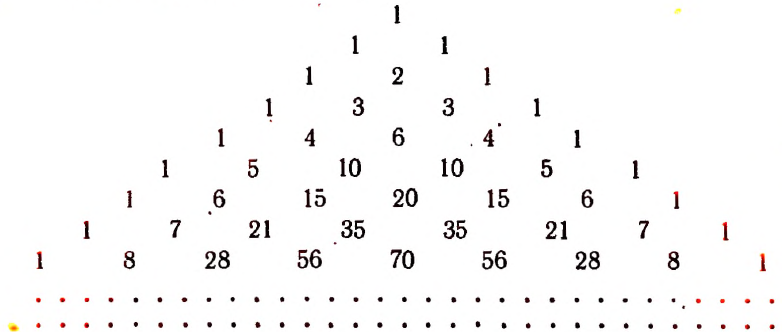
По боковым сторонам этой таблицы стоят единицы, внутри же стоят числа, получающиеся сложением двух соответствующих чисел предыдущей строки. Например, число 21 в 8-й строке получается сложением стоящих над ним чисел 6 и 15.

строка этой таблицы дает биномиальные коэффициенты разложения n-й степени бинома. Например:

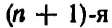
и так далее.

Треугольник Паскаля получается из следующей таблицы:

в силу того, что

(см. стр. 662).

Треугольник Паскаля приведен в книге Паскаля «Трактат об арифметическом треугольнике», изданной после его смерти в 1665 году.

Примеры с решением на Бином Ньютона

1. В разложении 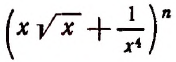коэффициент третьего члена на 44 больше коэффициента второго члена. Найти свободный член, т. е. член разложения, не зависящий от x (членом, не зависящим от х, будет тот, который содержит х в нулевой степени).

Решение:

Отсюда

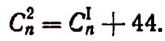
Приравняв показатель степени буквы х к нулю, получим:

Отсюда

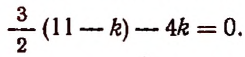
Искомым свободным членом будет четвертый, и он будет равен т. е. 165.

2. Сколько рациональных членов содержится в разложении

Решение:

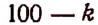
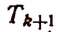
Для рациональности члена разложения необходимо, чтобы число k было кратно четырем. Но тогда будет числом четным и будет числом рациональным.

Число k может принимать целые значения 0, 1, 2….. 100. Среди этих чисел кратными четырем будут

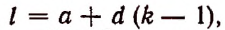
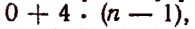
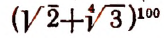
Пользуясь формулой получим: или Следовательно, в разложении рациональных членов будет 26.

3. Доказать, что значение выражения

где n — натуральное число, делится на 9.

Доказательство:

Каждое слагаемое последней суммы делится на 9, следовательно, и вся эта сумма, т. е. значение выражения 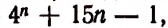делится на 9, что и требовалось доказать.

Дополнение к Бином Ньютону

Смотрите также:

Решение задач по финансовой математике

Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Источник

Содержание

Бином Ньютона

Бином

Задача. Для произвольных вещественных чисел $ a,b_{} $ и натурального $ n_{} $
выписать разложение выражения $ (a+b)^{n} $ по степеням $ a_{} $ и $ b_{} $.

Из школьного курса алгебры известны эти разложения для малых $ n_{} $:
$$
begin{array}{lccccccccc}
(a+b)= & &&& a&+&b , , \
(a+b)^2= & & &a^2 &+&2ab &+&b^2 , , \
(a+b)^3= & &a^3 &+&3a^2b &+& 3ab^2 &+& b^3 , , \
(a+b)^4= &a^4 &+& 4a^3b &+&6a^2b^2 &+&4ab^3 &+& b^4 , .
end{array}
$$

Выражение
$$
C_n^m = frac{n!}{m!, (n-m)!}= frac{n(n-1)times dots times (n-m+1)}
{1cdot 2 times dots times m}
$$
при $ min{0,dots,n} $ и $ 0! = 1 $ называется биномиальным коэффициентом. В западной литературе принято обозначение $ {n choose m} $.

Пример.

$$ C_n^0=C_n^n=1, C_n^{1}=C_n^{n-1}=n,
C_n^2=C_n^{n-2}= frac{n(n-1)}{2}, C_{17}^5=frac{17cdot 16cdot 15 cdot 14 cdot 13}{2cdot 3 cdot 4 cdot 5} =6188 .
$$

Теорема 1. Для любых натуральных $ n_{} $ и $ m_{} $ справедливы следующие
формулы:
$$
{mathbf a}) C_n^m=C_n^{n-m} , quad
{mathbf b}) C_n^m + C_n^{m+1}=C_{n+1}^{m+1} .
$$

Теорема 2. Имеет место формула бинома Ньютона

$$
(a+b)^n=sum_{m=0}^n C_n^m a^{n-m}b^m =
$$
$$=C_n^0a^{n}+C_n^1a^{n-1}b+C_n^2a^{n-2}b^2+dots+
C_n^m a^{n-m}b^m+dots+C_n^nb^{n} .
$$

Доказательство ведется индукцией по $ n_{} $. Для $ n=1,2_{} $ формула справедлива.
Предположим, что она справедлива для степени $ n_{} $, докажем ее справедивость для
степени $ n_{}+1 $, т.е. докажем, что в разложении $ (a+b)^{n+1} $ по степеням
$ a_{} $ и $ b_{} $ коэффициент при $ a^{n-m}b^{m+1} $ равен $ C_{n+1}^{m+1} $.
$$(a+b)^{n+1}=(a+b)^{n}(a+b)=$$
$$
begin{array}{rrrrrrrr}
=&a^{n+1}+&C_n^1a^{n}b+&C_n^2a^{n-1}b^2+&dots+
&C_n^m a^{n-m+1}b^m+&C_n^{m+1} a^{n-m}b^{m+1}+&dots + \
&+&a^{n}b+&C_n^1a^{n-1}b^2+&dots
&+ &C_n^{m} a^{n-m}b^{m+1}+&dots =\
=&a^{n+1}+&C_{n+1}^1a^{n}b+
&C_{n+1}^2a^{n-1}b^2+&dots &+&C_{n+1}^{m+1} a^{n-m}b^{m+1}+&dots
end{array}
$$
Последнее равенство следует из пункта $ {mathbf b}) $ теоремы 1.

♦

Для малых значений показателя $ n_{} $ вычисления биномиальных коэффициентов
удобно производить по следующей схеме.

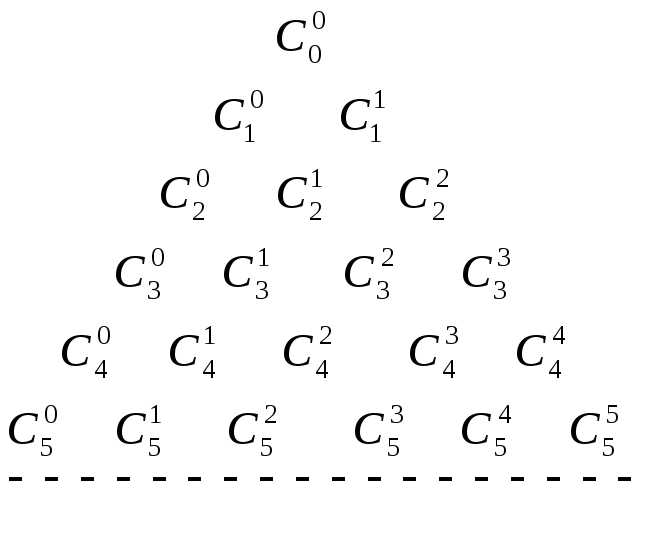
Треугольник Паскаля.

$$
begin{array}{l|cccccccccccccccc}
&&&&&&&&1 \
n=1&&&&&&& 1 && 1 \
n=2&&&&&& 1 && 2 && 1 \
n=3&&&&&1 && 3 && 3 && 1 \
n=4&&&&1 && 4 && 6 && 4 && 1 \
n=5&&&1 && 5 && 10 && 10 && 5 && 1 \
n=6&&1 && 6 && 15 && 20 && 15 && 6 && 1 \
n=7&1 && 7 && 21 && 35 && 35 && 21 && 7 && 1 \
dots& dots && && && dots && && &&
end{array}
$$
Правила формирования его просты: на сторонах треугольника ставится $ 1_{} $, а элемент каждой строки получается суммированием двух стоящих над ним в предыдущей строке.
Обоснование этой схемы, очевидно, следует из формул теоремы 1.

Обобщение

Теорема. Выражение $ (a_1+a_2+dots+a_K)^n $ при $ Kge 3 $ раскладывается по степеням чисел $ a_1,a_2,dots,a_K $ с помощью
обобщения биномиальных коэффициентов — так называемых мультиномиальных
коэффициентов¹⁾:

$$(a_1+a_2+dots+a_K)^n=sum_{n_{_1}+n_{_2}+dots+n_{_K}=n}frac{n!}{n_1!, n_2!
times dots times n_K!}
a_1^{n_1}a_2^{n_2}times dots times a_K^{n_K} ,$$
где суммирование идет по всем различным наборам $ (n_{1},n_2,dots,n_K) $
неотрицательных целых индексов, удовлетворяющих ограничению
$$n_1+n_2+dots+n_K=n .$$

Доказательство приведем для случая $ K=3 $. Выражение $ (a_1+a_2+a_3)^n $ можно представить в виде бинома
$$ (a_1+a_2+a_3)^n=left( (a_1+a_2)+a_3 right)^n= $$
$$ C_n^0 (a_1+a_2)^n+ C_n^1 (a_1+a_2)^{n-1}a_3+dots+
C_n^{n_{_3}} (a_1+a_2)^{n-n_3}a_3^{n_3}+dots+C_n^na_3^n . $$
Все возможные слагаемые (мономы) полного разложения, содержащие сомножителем $ a_3^{n_3} $, присутствуют в слагаемом $ C_n^{n_{_3}} (a_1+a_2)^{n-n_{_3}}a_3^{n_{_3}} $. Если нас интересует конкретное слагаемое, содержащее $ a_1^{n-n_{_2}}a_2^{n_{_2}}a_3^{n_3} $, то коэффициент при этом слагаемом вычислится с помощью биномиального разложения, т.е. он равен
$$ C_n^{n_{_3}}C_{n-n_{_3}}^{n_2}=frac{n!}{n_3!(n-n_3)!}frac{(n-n_3)!}{n_2!(n-n_3-n_2)!}=frac{n!}{(n-n_3-n_2)! n_2! n_3!} . $$

♦

Пример.

$$ (a+b+c)^3=a^3+3,a^2b+3,a^2c+3,ab^2+6,abc+3,ac^2+b^3+3,b^2c+3,bc^2+c^3 . $$

Непосредственное доказательство того, что мультиномиальные коэффициенты — числа целые (т.е. что число $ n_{}! $ делится нацело на $ n_1!, n_2! times dots times n_K! $ при
$ n_1+ n_2+ dots + n_K = n $)

☞

ЗДЕСЬ.

Суммы биномиальных коэффициентов

$$ sum_{j=0}^n C_n^j =C_n^0+C_n^1+C_n^2+dots+C_n^n = 2^n . $$
$$ sum_{j=0}^n (-1)^jC_n^j = C_n^0-C_n^1+C_n^2-dots+(-1)^nC_n^n = 0 . $$
$$ sum_{j=2}^n C_j^2= C_2^2+C_3^2+dots+C_n^2= frac{(n-1)n(n+1)}{6}=C_{n+1}^3 . $$
$$ sum_{m=0}^n C_{ell+m-1}^{ell-1}=C_{ell-1}^{ell-1}+C_{ell}^{ell-1}+C_{ell+1}^{ell-1}+dots+C_{n+ell-1}^{ell-1} = C_{n+ell}^{ell} , . $$
Формулы Вандермонда:
$$ sum_{j=0}^n (C_n^j)^2 = (C_n^0)^2+(C_n^1)^2+(C_n^2)^2+dots+(C_n^n)^2 = C_{2n}^n ; $$
$$ sum_{j=0}^k C_n^jC_m^{k-j}=C_n^0C_m^k+C_n^1C_m^{k-1}+dots+C_n^{k-1}C_m^1+C_n^kC_m^0=C_{m+n}^k .$$
Связь с числами Фибоначчи:
$$ sum_{j=0}^{lfloor n/2 rfloor} C_{n-j}^j = C_n^0+C_{n-1}^1+C_{n-2}^2+dots
= F_n .
$$
Здесь $ lfloor rfloor $ — целая часть числа. Идея доказательства

☞

ЗДЕСЬ.

Пример.
$$C_8^0+C_7^1+C_6^2+C_5^3+C_4^4=34=F_8 . $$

Связь с числами Каталана:
$$ C_{2n-2}^{n-1}-C_{2n-2}^{n}=C_{n-1} , . $$

Задачи

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Given a positive integer n, the task is to find the sum of binomial coefficient i.e
ⁿC₀ + ⁿC₁ + ⁿC₂ + ……. + ⁿC_n-1 + ⁿC_n
Examples:

Input : n = 4
Output : 16
⁴C₀ + ⁴C₁ + ⁴C₂ + ⁴C₃ + ⁴C₄
= 1 + 4 + 6 + 4 + 1
= 16

Input : n = 5
Output : 32

Method 1 (Brute Force):
The idea is to evaluate each binomial coefficient term i.e ⁿC_r, where 0 <= r <= n and calculate the sum of all the terms.
Below is the implementation of this approach:

C++

#include <bits/stdc++.h>

using namespace std;

int binomialCoeffSum(int n)

{

int C[n + 1][n + 1];

for (int i = 0; i <= n; i++) {

for (int j = 0; j <= min(i, n); j++) {

if (j == 0 || j == i)

C[i][j] = 1;

else

C[i][j] = C[i - 1][j - 1] + C[i - 1][j];

}

int sum = 0;

for (int i = 0; i <= n; i++)

sum += C[n][i];

return sum;

}

int main()

{

int n = 4;

printf("%d", binomialCoeffSum(n));

return 0;

}

Java

class GFG {

static int binomialCoeffSum(int n)

{

int C[][] = new int[n + 1][n + 1];

for (int i = 0; i <= n; i++)

{

for (int j = 0; j <= Math.min(i, n); j++)

{

if (j == 0 || j == i)

C[i][j] = 1;

else

C[i][j] = C[i - 1][j - 1] +

C[i - 1][j];

}

int sum = 0;

for (int i = 0; i <= n; i++)

sum += C[n][i];

return sum;

}

public static void main(String[] args)

{

int n = 4;

System.out.println(binomialCoeffSum(n));

}

Python3

import math

def binomialCoeffSum( n):

C = [[0]*(n+2) for i in range(0,n+2)]

for i in range(0,n+1):

for j in range(0, min(i, n)+1):

if (j == 0 or j == i):

C[i][j] = 1

else:

C[i][j] = C[i - 1][j - 1] + C[i - 1][j]

sum = 0

for i in range(0,n+1):

sum += C[n][i]

return sum

n = 4

print(binomialCoeffSum(n))

C#

using System;

class GFG {

static int binomialCoeffSum(int n)

{

int[, ] C = new int[n + 1, n + 1];

for (int i = 0; i <= n; i++)

{

for (int j = 0; j <= Math.Min(i, n); j++)

{

if (j == 0 || j == i)

C[i, j] = 1;

else

C[i, j] = C[i - 1, j - 1] + C[i - 1, j];

}

int sum = 0;

for (int i = 0; i <= n; i++)

sum += C[n, i];

return sum;

}

public static void Main()

{

int n = 4;

Console.WriteLine(binomialCoeffSum(n));

}

PHP

<?php

function binomialCoeffSum($n)

{

$C[$n + 1][$n + 1] = array(0);

for ($i = 0; $i <= $n; $i++)

{

for ($j = 0;

$j <= min($i, $n); $j++)

{

if ($j == 0 || $j == $i)

$C[$i][$j] = 1;

else

$C[$i][$j] = $C[$i - 1][$j - 1] +

$C[$i - 1][$j];

}

$sum = 0;

for ($i = 0; $i <= $n; $i++)

$sum += $C[$n][$i];

return $sum;

}

$n = 4;

echo binomialCoeffSum($n);

?>

Javascript

<script>

function binomialCoeffSum(n)

{

let C = new Array(n + 1);

for (var i = 0; i < C.length; i++) {

C[i] = new Array(2);

}

for (let i = 0; i <= n; i++)

{

for (let j = 0; j <= Math.min(i, n); j++)

{

if (j == 0 || j == i)

C[i][j] = 1;

else

C[i][j] = C[i - 1][j - 1] +

C[i - 1][j];

}

let sum = 0;

for (let i = 0; i <= n; i++)

sum += C[n][i];

return sum;

}

let n = 4;

document.write(binomialCoeffSum(n));

</script>

Output:

Method 2 (Using Formula):

This can be proved in 2 ways.
First Proof: Using Principle of induction.

For basic step, n = 0
LHS = ⁰C₀ = (0!)/(0! * 0!) = 1/1 = 1.
RHS= 2⁰ = 1.
LHS = RHS
For induction step:
Let k be an integer such that k > 0 and for all r, 0 <= r <= k, where r belong to integers,
the formula stand true.
Therefore,
^kC₀ + ^kC₁ + ^kC₂ + ……. + ^kC_k-1 + ^kC_k = 2^k
Now, we have to prove for n = k + 1,
^k+1C₀ + ^k+1C₁ + ^k+1C₂ + ……. + ^k+1C_k + ^k+1C_k+1 = 2^k+1
LHS = ^k+1C₀ + ^k+1C₁ + ^k+1C₂ + ……. + ^k+1C_k + ^k+1C_k+1
(Using ⁿC₀ = 0 and ⁿ⁺¹C_r = ⁿC_r + ⁿC_r-1)
= 1 + ^kC₀ + ^kC₁ + ^kC₁ + ^kC₂ + …… + ^kC_k-1 + ^kC_k + 1
= ^kC₀ + ^kC₀ + ^kC₁ + ^kC₁ + …… + ^kC_k-1 + ^kC_k-1 + ^kC_k + ^kC_k
= 2 X ∑ ⁿC_r
= 2 X 2^k
= 2^k+1
= RHS

Second Proof: Using Binomial theorem expansion

Binomial expansion state,
(x + y)ⁿ = ⁿC₀ xⁿ y⁰ + ⁿC₁ x^n-1 y¹ + ⁿC₂ x^n-2 y² + ……… + ⁿC_n-1 x¹ y^n-1 + ⁿC_n x⁰ yⁿ
Put x = 1, y = 1
(1 + 1)ⁿ = ⁿC₀ 1ⁿ 1⁰ + ⁿC₁ x^n-1 1¹ + ⁿC₂ 1^n-2 1² + ……… + ⁿC_n-1 1¹ 1^n-1 + ⁿC_n 1⁰ 1ⁿ
2ⁿ = ⁿC₀ + ⁿC₁ + ⁿC₂ + ……. + ⁿC_n-1 + ⁿC_n

Below is implementation of this approach:

C++

#include <bits/stdc++.h>

using namespace std;

int binomialCoeffSum(int n)

{

return (1 << n);

}

int main()

{

int n = 4;

printf("%d", binomialCoeffSum(n));

return 0;

}

Java

import java.io.*;

class GFG

{

static int binomialCoeffSum(int n)

{

return (1 << n);

}

public static void main (String[] args)

{

int n = 4;

System.out.println(binomialCoeffSum(n));

}

Python3

import math

def binomialCoeffSum( n):

return (1 << n);

n = 4

print(binomialCoeffSum(n))

C#

using System;

class GFG {

static int binomialCoeffSum(int n)

{

return (1 << n);

}

static public void Main()

{

int n = 4;

Console.WriteLine(binomialCoeffSum(n));

}

PHP

<?php

function binomialCoeffSum($n)

{

return (1 << $n);

}

$n = 4;

echo binomialCoeffSum($n);

?>

Javascript

<script>

function binomialCoeffSum(n)

{

return (1 << n);

}

let n = 4;

document.write(binomialCoeffSum(n));

</script>

Output:

Last Updated :
30 Apr, 2021

Like Article

Save Article

Источник

Бином Ньютона и треугольник Паскаля

1. Постановка задачи

2. Бином Ньютона

3. Знак суммы

4. Биноминальные коэффициенты

4.1. Новое определение факториала

5. Треугольник Паскаля

6. Доказательство Бинома Ньютона

6.1. База индукции

6.2. Индуктивное предположение

6.3. Индуктивный переход

Формула бинома Ньютона

Свойства формулы бинома Ньютона

Применение формулы бинома к многочлену

Вывод формулы бинома ньютона

Свойства разложения бинома

Свойства биномиальных коэффициентов

Арифметический треугольник, или треугольник паскаля

Примеры с решением на Бином Ньютона

Дополнение к Бином Ньютону

Содержание

Бином Ньютона

Бином

Обобщение

Суммы биномиальных коэффициентов

Задачи

C++

Java

Python3

C#

PHP

Javascript

C++

Java

Python3

C#

PHP

Javascript

Не пропустите также: