Формулы тангенса суммы и разности углов устанавливают соотношение между тангенсом общей суммы или разности аргументов и тангенсами отдельных аргументов — слагаемых.
При всех допустимых значениях аргументов справедливы формулы:
тангенса суммы аргументов:
tg(α+β)=tgα+tgβ1−tgα⋅tgβ
; (1)
тангенса разности аргументов:
tg(α−β)=tgα−tgβ1+tgα⋅tgβ
. (2)
Оговорка о допустимых значениях аргументов означает, что все тангенсы имеют смысл, т. е. выполняются условия:
, для формулы (1),
α−β≠π2+πm,m∈ℤ
, для формулы (2).
Эти формулы очень важны и широко применяются не только в математике, но и в физике — особенно в радиотехнике.
Вывод формул естественным образом получается из определения функции тангенса и использования уже известных формул синуса и косинуса суммы и разности аргументов.
Докажем формулу тангенса суммы аргументов. Имеем:
.
Разделим каждое из слагаемых числителя и знаменателя на
cosα⋅cosβ
,
учитывая, что значение дроби от этого не изменится и что
cosα⋅cosβ≠0
из принятых выше условий
для допустимых значений аргументов, т. е.
α≠π2+πk,β≠π2+πnk,n∈ℤ
. Тогда:
tg(α+β)=sin(α+β)cos(α+β)=sinα⋅cosβ+cosα⋅sinβcosα⋅cosβ−sinα⋅sinβ=sinα⋅cosβcosα⋅cosβ+cosα⋅sinβcosα⋅cosβcosα⋅cosβcosα⋅cosβ−sinα⋅sinβcosα⋅cosβ=tgα+tgβ1−tgα⋅tgβ
— что и требовалось доказать.
Аналогично доказывается формула тангенса разности аргументов:
tg(α−β)=sin(α−β)cos(α−β)=sinα⋅cosβ−cosα⋅sinβcosα⋅cosβ+sinα⋅sinβ=sinα⋅cosβcosα⋅cosβ−cosα⋅sinβcosα⋅cosβcosα⋅cosβcosα⋅cosβ+sinα⋅sinβcosα⋅cosβ=tgα−tgβ1+tgα⋅tgβ.
Сумма тангенсов
ОПРЕДЕЛЕНИЕ
Сумма тангенсов двух углов (
alpha
) и (
beta
) равна отношению синуса суммы (
alpha+beta
) к произведению косинусов этих углов:
(
operatorname{tg} alpha+operatorname{tg} beta=frac{sin (alpha+beta)}{cos alpha cdot cos beta}
)
Примеры решения задач
ПРИМЕР 1
Проверить, что (
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=2
)
Применим формулу суммы тангенсов
(
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=frac{sin left(15^{circ}+60^{circ}right)}{cos 15^{circ} cos 60^{circ}}=frac{sin 75^{circ}}{cos 15^{circ} cos 60^{circ}}
)
Представим (
cos 15^{circ}
) в (
cos 15^{circ}=cos left(90^{circ}-75^{circ}right)=sin 75^{circ}
) и подставим в предыдущее равенство: (
frac{sin 75^{circ}}{cos 15^{circ} cos 60^{circ}}=frac{sin 75^{circ}}{sin 75^{circ} cos 60^{circ}}=frac{1}{cos 60^{circ}}=2
)
т.е.
(
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=2
)
ПРИМЕР 2
Найти значение выражения (
operatorname{tg}^{3 pi}+operatorname{tg} frac{pi}{8}
)
Представим сумму разность в виде
(
operatorname{tg} frac{3 pi}{8}+operatorname{tg} frac{pi}{8}=frac{sin left(frac{3 pi}{8}+frac{pi}{8}right)}{cos frac{3 pi}{8} cdot cos frac{pi}{8}}=frac{sin frac{pi}{2}}{frac{1}{2}left(cos frac{pi}{4}+cos frac{pi}{2}right)}=frac{1}{frac{1}{2}left(frac{sqrt{2}}{2}+0right)}=frac{4}{sqrt{2}}=2 sqrt{2}
)
(
operatorname{tg} frac{3 pi}{8}+operatorname{tg} frac{pi}{8}=2 sqrt{2}
)
Ниже в табличном виде представлены формулы сумм основных тригонометрических функций.
Содержание
- Прямые и производные функции: sin, cos, tg, ctg
- Обратные функции: arcsin, arccos, arctg, arcctg
Прямые и производные функции: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg).
| Действие | Формула |
| Сумма синусов |  |
| Сумма косинусов |  |
| Сумма тангенсов | tg α + tg β = sin (α + β) / cos α cos β |
| Сумма котангенсов | ctg α + ctg β = sin (α + β) / sin α sin β |
microexcel.ru
Обратные функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).
| Действие | Формула |
| Сумма арксинусов |
 |
| Сумма арккосинусов |
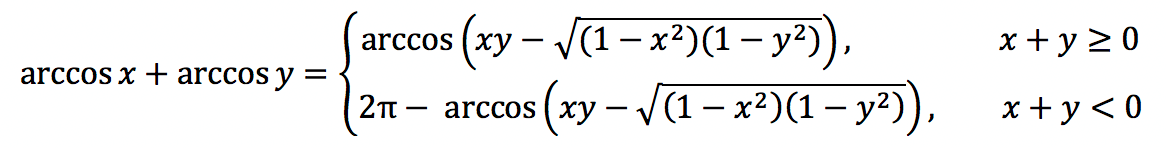 |
| Сумма арктангенсов |
 |
| Сумма арккотангенсов |
 |
microexcel.ru
