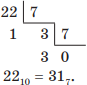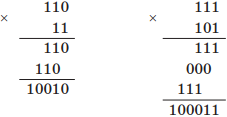Информатика, 10 класс. Урок № 9.
Тема урока — Арифметические операции в позиционных системах счисления
Урок посвящен теме «Арифметические операции в позиционных системах счисления»». В ходе урока школьники научатся складывать, вычитать, умножать и делить в разных позиционных системах счисления.
Ключевые слова:
— позиционные системы счисления,
— арифметические операции в системе счисления с основанием q,
— таблица сложения,
— таблица умножения.
Учебник:
— Информатика. 10 класс: учебник / Л. Л. Босова, А. Ю. Босова. — М.: БИНОМ. Лаборатория знаний, 2016. — 288 с.
— Математические основы информатики: учебное пособие / Е. В. Андреева, Л. Л Босова, И. Н. Фалина — М.: БИНОМ. Лаборатория знаний, 2008. — 328 с.
Мы продолжаем изучать позиционные системы счисления. Вы узнали, что позиционные системы счисления бывают разные: десятичная, двоичная, восьмеричная и шестнадцатеричная. Вы научились переводить числа из одной системы счисления в другую. Но зачем нам с вами это надо? Конечно для того, чтобы производить расчеты. С 1 класса нас учат производить расчеты в десятичной системе счисления. А как вы думаете, можно ли производить расчеты в произвольной позиционной системе счисления? И зачем это нужно?
Двоичная система счисления издавна была предметом пристального внимания многих ученых. Первый кто заговорил о двоичном кодировании, был Лейбниц Готфрид Вильгельм. Он написал трактат «Expication de l’Arithmetique Binary» — об использовании двоичной системы счисления в вычислительных машинах. В рукописи на латинском языке, написанной в марте 1679 года, Лейбниц разъясняет, как выполнять вычисление в двоичной системе, в частности умножение, а позже в общих чертах разрабатывает проект вычислительной машины, работающей в двоичной системе счисления. Вот что он пишет: « Вычисления такого рода можно было бы выполнять и на машине». Эти слова подчеркивают универсальность алфавита, состоящего из двух символов.
Все позиционные системы счисления “одинаковы”, а именно, во всех них выполняются арифметические операции по одним и тем же правилам:
— справедливы одни и те же законы арифметики: коммутативный (переместительный), ассоциативный (сочетательный), дистрибутивный (распределительный);
— справедливы правила сложения, вычитания, умножения и деления столбиком.
Мы узнаем на уроке:
- как строить таблицы сложения и умножения в заданной позиционной системе счисления;
- как выполнять сложение, умножение, вычитание и деление чисел, записанных в двоичной, восьмеричной и шестнадцатеричной системах счисления;
- как подсчитывать количество единиц в двоичной записи числа, являющегося результатом суммирования или вычитания степеней двойки.
Арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления.
Рассмотрим сложение.

Чтобы в системе счисления с основанием q получить сумму S двух чисел A и B, надо просуммировать образующие их цифры по разрядам i справа налево:
- если ai + bi < q, то si = ai + bi,
старший (i + 1)-й разряд не изменяется - если ai + bi ≥ q, то si = ai + bi – q,
старший (i + 1)-й разряд увеличивается на 1
Можно составить таблицу сложения:

Давайте рассмотрим правило сложения на примере в двоичной системе счисления
Это мы рассмотрели сложение в двоичной системе счисления, а теперь сложим два числа в троичной, восьмеричной и шестнадцатеричной системе счисления.

— 1 + 2 = 3 ≥ 3
записываем 3 – 3 = 0 под 1-м разрядом,
а 2-й разряд увеличиваем на 1
— 1 + 2 = 3 ≥ 3
записываем 3 – 3 = 0 под 2-м разрядом,
а 3-й разряд увеличиваем на 1
— 1 + 1 + 2 = 4 ≥ 3
записываем 4 – 3 = 1 под 3-м разрядом,
а 4-й разряд увеличиваем на 1
— 1 + 1 = 2 < 3
записываем 2 под 4-м разрядом
Сложим в восьмеричной и шестнадцатеричной системе счисления.
Теперь разберём вычитание в системах счисления с основанием q.
Чтобы в системе счисления с основанием q получить разность R двух чисел A и B, надо вычислить разности образующих их цифр по разрядам i справа налево:
— если ai ≥ bi, то ri = ai – bi,
старший (i + 1)-й разряд не изменяется
— если a i < b i , то ri = q + ai – bi ,
старший (i + 1)-й разряд уменьшается на 1
Рассмотрим правило вычитания в двоичной системе счисления на примере.
Рассмотрим правило вычитания в троичной системе счисления, где q=3
- 1 ≥ 0
записываем 1 – 0 = 1 под 1-м разрядом - 0 < 1
записываем 3 + 0 – 1 = 2 под 2-м разрядом,
делая заем в 3-м разряде - 0 < 2
записываем 3 + 0 – 2 = 1 под 3-м разрядом,
делая заем в 4-м разряде - 0 = 0
записываем 0 под 4-м разрядом - 0 < 1
записываем 3 + 0 – 1 = 2 под 5-м разрядом,
делая заем в 6-м разряде
В восьмеричной и шестнадцатеричной системе выполним вычитание.
Как же выполняется умножение чисел в системе счисления с основанием q? Если мы рассмотрим таблицы умножения в двоичной, троичной, восьмеричной и шестнадцатеричной системах счисления, то увидим, что алгоритм умножения точно такой же, как и в десятичной системе.
Чтобы в системе счисления q получить произведение M многозначного числа A и однозначного числа b, надо вычислить произведения b и цифр числа A по разрядам i:
- если ai · b <q, то mi = ai · b,
старший (i + 1)-й разряд не изменяется - если ai · b ≥ q, то mi = ai · b mod q,
старший (i + 1)-й разряд увеличивается на ai · b div q
Рассмотрим примеры:
— 2 · 2 = 4 ≥ 3
записываем 4 mod 3 = 1 под 1-м разрядом,
2-й разряд увеличиваем на 4 div 3 = 1
— 1 · 2 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 2-м разрядом,
3-й разряд увеличиваем на 3 div 3 = 1
— 2 · 2 + 1 = 3 ≥ 3
записываем 5 mod 3 = 2 под 3-м разрядом,
4-й разряд увеличиваем на 5 div 3 = 1
— 2 · 1 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 4-м разрядом
и в 5-й разряд записываем 3 div 3 = 1
По этому алгоритму выполним умножение в других системах счисления.
Умножение многозначного числа на многозначное число выполняется столбиком. При этом два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце). Посмотрим пример в двоичной системе счисления.
Деление нельзя свести к поразрядным операциям над цифрами, составляющими число. Деление чисел в системе счисления с произвольным основанием q выполняется так же, как и в десятичной системе счисления. А значит, нам понадобятся правила умножения и вычитания чисел в системе счисления с основанием q. Давайте разберем деление в двоичной системе.
И попробуем поделить в восьмеричной системе счисления.
В числе 2338 поместится 2 ∙ 738 = 1668
В числе 4568 поместится 5 ∙ 738 = 4478
В числе 738 поместится 1 ∙ 738 = 738
Теперь мы знаем, как производится арифметика в двоичной системе счисления. Используя таблицы, мы можем решить любой пример.
Давайте рассмотрим пример:
Задание 1. Найдём количество единиц в двоичной записи числа, являющегося результатом десятичного выражения
24000 + 42016 + 22018 – 8600 + 6
Решение:
Представим все операнды исходного выражения в виде степеней двойки:
Исходное выражение 24000 + 42016 + 22018 – 8600 + 6
примет вид 24000 + 24032 + 22018 – 21800 + 22 + 21
Перепишем выражение в порядке убывания степеней: 24032 + 24000 + 22018 – 21800 + 22 + 21
Для работы с десятичными числами вида 2n полезно иметь в виду следующие закономерности в их двоичной записи:
21 = 10 = 1 + 1; 22 = 100 = 11 + 1; 23 = 1000 = 111 + 1; …
В общем виде
Для натуральных n и m таких, что n > m, получаем:
Эти соотношения позволят подсчитать количество «1» в выражении без вычислений. Двоичные представления чисел 24032 и 24000 внесут в двоичное представление суммы по одной «1». Разность 22018 – 21800 в двоичной записи представляет собой цепочку из 218 единиц и следующих за ними 1800 нулей. Слагаемые 22 и 21 дают ещё 2 единицы.
Так как в задаче надо найти единицы, то получаем:
Итого: 1 + 1 + 218 + 1 + 1 = 222.
Давайте разберем еще одну задачу.
Найдём количество цифр в восьмеричной записи числа, являющегося результатом десятичного выражения: 2299 + 2298 + 2297 + 2296.
Решение:
Двоичное представление исходного числа имеет вид:
Всего в этой записи 300 двоичных символов. При переводе двоичного числа в восьмеричную систему счисления каждая триада исходного числа заменяется восьмеричной цифрой. Следовательно, восьмеричное представление исходного числа состоит из 100 цифр.
Ответ: 100 цифр
Итак, сегодня вы узнали, что арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления. Если необходимо вычислить значение арифметического выражения, операнды которого представлены в различных системах счисления, можно:
- все операнды представить в привычной нам десятичной системе счисления;
- вычислить результат выражения в десятичной системе счисления;
- перевести результат в требуемую систему счисления.
Для работы с десятичными числами вида 2n, полезно иметь ввиду следующие закономерности в их двоичной записи:
Для натуральных n и m таких, что n > m, получаем:
Тренировочный модуль.
1 задание
Выберите выражения, значения которых одинаковые.
Возьми карандаш и подчеркни результат сложения
145 + 325
225 1035 435 1015
Реши кросснамбер
По вертикали:
1. Найди сумму и запиши в двоичной системе счисления 1538 + F916
3. Найди произведение и запиши в двоичной системе счисления 1223 * 112
6. Выполни операцию деления 100100002 / 11002
7. Реши пример, ответ запиши в десятичной системе счисления (5648 + 2348) * C16
По горизонтали:
2. Разность двоичных чисел 11001100 — 11111
4. Найти разность 1678 – 568
5. Выполнить операцию деления 416128 / 128
8. Найти разность 12E16 – 7916 ответ запиши в десятичной системе счисления
Проверь себя:
Этот калькулятор умеет осуществлять простейшие арифметические операции над числами. Причем числа могут быть введены в разных системах счисления.
Вам необходимо определиться сколько чисел вам необходимо посчитать и выбрать это количество в графе количество чисел.
Далее Вам необходимо ввести каждое число и выбрать его систему счисления. Если в указанном списке Вы не нашли нужной СС, то выберите пункт другая и введите числом основание вашей системы счисления.
После ввода всех чисел и выбора арифметических операций нажмите кнопку рассчитать.
17
Практическое
занятие № 2
Арифметические операции с числами в позиционных системах счисления
Рассмотрим основные
арифметические операции: сложение,
вычитание, умножение и деление.
Правила выполнения этих операций в
десятичной системе хорошо известны —
это сложение, вычитание, умножение
столбиком и деление углом.
Эти правила применимы и ко всем другим
позиционным системам счисления. Только
надо пользоваться особыми таблицами
сложения и умножения для каждой системы.
1. Сложение
Таблицы сложения
легко составить, используя правила
счета.
|
Сложение |
Сложение |
|
Сложение |
При сложении
цифры суммируются по разрядам, и если
при этом возникает избыток, то он
переносится влево.
Пример
1. Сложим
числа 15 и 6 в различных системах счисления.
|
Шестнадцатеричная:F16+616 |
Ответ: 15+6 Проверка. 101012 258 1516 |
Пример
2. Сложим
числа 15, 7 и 3.
-
Шестнадцатеричная:
F16+716+316Ответ:
15+7+3 = 2510
= 110012
= 318
= 1916.Проверка:
110012
= 24
+ 23
+ 20
= 16+8+1=25,318
= 3 .
81
+ 1 .
80
= 24 + 1 = 25,1916
= 1 .
161
+ 9 .
160
= 16+9 = 25.
Пример 3.
Сложим числа
141,5 и 59,75.
Ответ: 141,5 + 59,75 = 201,2510
= 11001001,012
= 311,28
= C9,416
Проверка. Преобразуем
полученные суммы к десятичному виду:
11001001,012
= 27
+ 26
+ 23
+ 20
+ 2-2
= 201,25
311,28
= 3 .
82
+ 1 .
81
+ 1 .
80
+ 2 .
8-1
= 201,25
C9,416
= 12 .
161
+ 9 .
160
+ 4 .
16-1
= 201,25
2. Вычитание
|
Вычитание в
заем |
Вычитание в
Заем единицы из |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вычитание в
|
Заем
единицы из
старшего разряда
Пример
4.
Вычтем
единицу из чисел 102,
108
и 1016
Пример
5. Вычтем
единицу из чисел 1002,
1008
и 10016.
Пример
6.
Вычтем
число 59,75 из числа 201,25.

Ответ: 201,2510
— 59,7510
= 141,510
= 10001101,12
= 215,48
= 8D,816.
Проверка. Преобразуем
полученные разности к десятичному виду:
10001101,12
= 27
+ 23
+ 22
+ 20
+ 2-1
= 141,5;
215,48
= 2 .
82
+ 1 .
81
+ 5 .
80
+ 4 .
8-1
= 141,5;
8D,816
= 8 .
161
+ D .
160
+ 8 .
16-1
= 141,5.
Соседние файлы в папке Задачи
- #
- #
- #
Представление числовой информации. Сложение и умножение в разных системах счисления
Представление числовой информации с помощью систем счисления
Для представления информации в компьютере используется двоичный код, алфавит которого состоит из двух цифр — 0 и 1. Каждая цифра машинного двоичного кода несет количество информации, равное одному биту.
Система счисления — это система записи чисел с помощью определенного набора цифр.
Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.
Позиционной является десятичная система счисления. Например, в числе 999 цифра «9» в зависимости от позиции означает 9, 90, 900.
Римская система счисления является непозиционной. Например, значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.
Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.
Количество различных цифр, употребляемых в позиционной системе счисления, называется ее основанием.
Развернутая форма числа — это запись, которая представляет собой сумму произведений цифр числа на значение позиций.
Например: 8527 = 8 ⋅ 103 + 5 ⋅ 102 + 2 ⋅ 101 + 7 ⋅ 100.
Развернутая форма записи чисел произвольной системы счисления имеет вид
$∑↙{i=n-1}↖{-m}a_iq^i$,
где $X$ — число;
$a$ — цифры численной записи, соответствующие разрядам;
$i$ — индекс;
$m$ — количество разрядов числа дробной части;
$n$ — количество разрядов числа целой части;
$q$ — основание системы счисления.
Например, запишем развернутую форму десятичного числа $327.46$:
$n=3, m=2, q=10.$
$X=∑↙{i=2}↖{-2}a_iq^i=a_2·10^2+a_1·10^1+a_0·10^0+a_{-1}·10^{-1}+a_{-2}·10^{-2}=3·10^2+2·10^1+7·10^0+4·10^{-1}+6·10^{-2}$
Если основание используемой системы счисления больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение: В — двоичная система, О — восмеричная, Н — шестнадцатиричная.
Например, если в двенадцатеричной системе счисления 10 = А, а 11 = В, то число 7А,5В12 можно расписать так:
7А,5В12 = В ⋅ 12-2 + 5 ⋅ 2-1 + А ⋅ 120 + 7 ⋅ 121.
В шестнадцатеричной системе счисления 16 цифр, обозначаемых 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует следующим числам десятеричной системы счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Примеры чисел: 17D,ECH; F12AH.
Перевод чисел в позиционных системах счисления
Перевод чисел из произвольной системы счисления в десятичную
Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:
11012 = 1 ⋅ 23 + 1 ⋅ 22 + 0 ⋅ 21 + 1 ⋅ 20 = 1310;
17D,ECH = 12 ⋅ 16–2 + 14 ⋅ 16–1 + 13 ⋅ 160 + 7 ⋅ 161 + 1 ⋅ 162 = 381,921875.
Перевод чисел из десятичной системы счисления в заданную
Для преобразования целого числа десятичной системы счисления в число любой другой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.
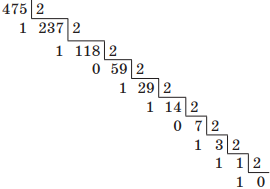
Например, переведем десятичное число 475 в двоичную систему счисления. Для этого будем последовательно выполнять деление нацело на основание новой системы счисления, т. е. на 2:
Читая остатки от деления снизу вверх, получим 111011011.
Проверка:
1 ⋅ 28 + 1 ⋅ 27 + 1 ⋅ 26 + 0 ⋅ 25 + 1 ⋅ 24 + 1 ⋅ 23 + 0 ⋅ 22 + 1 ⋅ 21 + 1 ⋅ 20 = 1 + 2 + 8 + 16 + 64 + 128 + 256 = 47510.
Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют умножение на основание системы счисления, пока дробная часть произведения не будет равна нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.
Например, переведем десятичную дробь 0,37510 в двоичную систему счисления:
Полученный результат — 0,0112.
Не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части.
Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно
Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны 8 вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита информации (8 = 2І; І = 3).
Таким образом, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.
Например:
1234,7778 = 001 010 011 100,111 111 1112 = 1 010 011 100,111 111 1112;
12345678 = 001 010 011 100 101 110 1112 = 1 010 011 100 101 110 1112.
При переводе двоичного числа в восьмеричную систему счисления нужно каждую триаду двоичных цифр заменить восьмеричной цифрой. При этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.
Например:
11001112 = 001 100 1112 = 1478;
11,10012 = 011,100 1002 = 3,448;
110,01112 = 110,011 1002 = 6,348.
Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. для каждого разряда числа возможны 16 вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита информации (16 = 2І; І = 4).
Таким образом, для перевода двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры и преобразовать каждую группу в шестнадцатеричную цифру.
Например:
11001112 = 0110 01112 = 6716;
11,10012 = 0011,10012 = 3,916;
110,01110012 = 0110,0111 00102 = 65,7216.
Для перевода шестнадцатеричного числа в двоичный код необходимо каждую цифру этого числа представить четверкой двоичных цифр.
Например:
1234,AB7716 = 0001 0010 0011 0100,1010 1011 0111 01112 = 1 0010 0011 0100,1010 1011 0111 01112;
CE456716 = 1100 1110 0100 0101 0110 01112.
При переводе числа из одной произвольной системы счисления в другую нужно выполнить промежуточное преобразование в десятичное число. При переходе из восьмеричного счисления в шестнадцатеричное и обратно используется вспомогательный двоичный код числа.
Например, переведем троичное число 2113 в семеричную систему счисления. Для этого сначала преобразуем число 2113 в десятичное, записав его развернутую форму:
2113 = 2 ⋅ 32 + 1 ⋅ 31 + 1 ⋅ 30 = 18 + 3 + 1 = 2210.
Затем переведем десятичное число 2210 в семеричную систему счисления делением нацело на основание новой системы счисления, т. е. на 7:
Итак, 2113 = 317.
Примеры решения задач
Пример 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Указать это основание.
Решение. Обозначим искомое основание п. По правилу записи чисел в позиционных системах счисления 1210 = 110n = 0 ·n0 + 1 · n1 + 1 · n2. Составим уравнение: n2 + n = 12 . Найдем натуральный корень уравнения (отрицательный корень не подходит, т. к. основание системы счисления, по определению, натуральное число большее единицы): n = 3 . Проверим полученный ответ: 1103 = 0· 30 + 1 · 31 + 1 · 32 = 0 + 3 + 9 = 12 .
Ответ: 3.
Пример 2. Указать через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
Решение. Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления. 22 — 4 = 18. Найдем делители числа 18. Это числа 2, 3, 6, 9, 18. Числа 2 и 3 не подходят, т. к. в системах счисления с основаниями 2 и 3 нет цифры 4. Значит, искомыми основаниями являются числа 6, 9 и 18. Проверим полученный результат, записав число 22 в указанных системах счисления: 2210 = 346 = 249 = 1418.
Ответ: 6, 9, 18.
Пример 3. Указать через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ записать в десятичной системе счисления.
Решение. Для удобства воспользуемся восьмеричной системой счисления. 1012 = 58. Тогда число х можно представить как x = 5 · 80 + a1 · 81 + a2 · 82 + a3 · 83 + … , где a1, a2, a3, … — цифры восьмеричной системы. Искомые числа не должны превосходить 25, поэтому разложение нужно ограничить двумя первыми слагаемыми ( 82 > 25), т. е. такие числа должны иметь представление x = 5 + a1 · 8. Поскольку x ≤ 25 , допустимыми значениями a1 будут 0, 1, 2. Подставив эти значения в выражение для х, получим искомые числа:
a1 = 0; x = 5 + 0 · 8 = 5;.
a1=1; x = 5 + 1 · 8 = 13;.
a1 = 2; x = 5 + 2 · 8 = 21;.
Выполним проверку:
510 = 1012;
1310 = 11012;
2110 = 101012.
Ответ: 5, 13, 21.
Арифметические операции в позиционных системах счисления
Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 – 0 = 0 | 0 ⋅ 0 = 0 |
| 0 + 1 = 1 | 1 – 0 = 1 | 0 ⋅ 1 = 0 |
| 1 + 0 = 1 | 1 – 1 = 0 | 1 ⋅ 0 = 0 |
| 1 + 1 = 10 | 10 – 1 = 1 | 1 ⋅ 1 = 1 |
Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.
Пример выполнения сложения: сложим двоичные числа 111 и 101, 10101 и 1111:
Пример выполнения вычитания: вычтем двоичные числа 10001 – 101 и 11011 – 1101:
Пример выполнения умножения: умножим двоичные числа 110 и 11, 111 и 101:
Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.
Например, выполним сложение восьмеричных чисел 368 и 158, а также вычитание шестнадцатеричных чисел 9С16 и 6716:
При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему.
Представление чисел в компьютере
Формат с фиксированной запятой
В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.
Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно
1 ⋅ 27 + 1 ⋅ 26 + 1 ⋅ 25 + 1 ⋅ 24 + 1 ⋅ 23 + 1 ⋅ 22 + 1 ⋅ 21 + 1 ⋅ 20 = 25510.
Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.
Для п-разрядного представления диапазон будет составлять от 0 до 2n – 1.
Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.
Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2n − |А|.
Алгоритм получения дополнительного кода отрицательного числа:
1. Записать прямой код числа в п двоичных разрядах.
2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)
3. Прибавить единицу к полученному обратному коду.
Например, получим дополнительный код числа –201410 для шестнадцатиразрядного представления:
| Прямой код | Двоичный код числа 201410 со знаковым разрядом | 1000011111011110 |
| Обратный код | Инвертирование (исключая знаковый разряд) | 1111100000100001 |
| Прибавление единицы | 1111100000100001 + 0000000000000001 | |
| Дополнительный код | 1111100000100010 |
При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.
Например:
1) Найдем разность 1310 – 1210 для восьмибитного представления. Представим заданные числа в двоичной системе счисления:
1310 = 11012 и 1210 = 11002.
Запишем прямой, обратный и дополнительный коды для числа –1210 и прямой код для числа 1310 в восьми битах:
| 1310 | –1210 | |
| Прямой код | 00001101 | 10001100 |
| Обратный код | — | 11110011 |
| Дополнительный код | — | 11110100 |
Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):
Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.
2) Найдем разность 810 – 1310 для восьмибитного представления.
Запишем прямой, обратный и дополнительный коды для числа –1310 и прямой код для числа 810 в восьми битах:
| 810 | –1310 | |
| Прямой код | 00001000 | 10001101 |
| Обратный код | — | 11110010 |
| Дополнительный код | — | 11110011 |
Вычитание заменим сложением:
В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:
11111011 – 00000001 = 11111010.
Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –510.
Так как при п-разрядном представлении отрицательного числа А в дополнительном коде старший разряд выделяется для хранения знака числа, минимальное отрицательное число равно: А = –2n–1, а максимальное: |А| = 2n–1 или А = –2n–1 – 1.
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно
А = –231 = –214748364810.
Максимальное положительное число равно
А = 231 – 1 = 214748364710.
Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.
Сергей Андреевич Дремук
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Система счисления – это способ записи чисел с помощью письменных знаков.
Операция сложения в разных системах счисления
Операция сложения в десятичной системе счисления давно известна каждому школьнику. Большие числа удобно суммировать в столбик. Например:
Рисунок 1. Сложение в столбик. Автор24 — интернет-биржа студенческих работ
Основное, что нужно помнить это разрядность систем счисления. Необходимо освежить в памяти алфавит системы счисления и все операции окажутся лёгкими и простыми.
Сложение в двоичной системе счисления выполняется абсолютно аналогично десятичной системе. Рассмотрим конкретный пример:
Рисунок 2. Сложение в столбик. Автор24 — интернет-биржа студенческих работ
Самое основное — это нужно помнить, что в двоичной системе счисления используются всего два значения, а именно нуль и единица. Это означает, что сложение двух единиц даёт в сумме нуль в текущем разряде и единицу переноса в следующий разряд. В приведённом выше примере действия выполняются в следующем порядке:
- Операция сложения начинается с младшего разряда, то есть справ налево. Нуль плюс нуль равен нулю, то есть пишем нуль в младшем разряде и выполняем переход на следующий разряд.
- Суммируем один плюс один, получаем два. Но это основание системы счисления, поэтому в этом разряде пишем ноль, а единица переносится в следующий разряд.
- В данном разряде нужно сложить три единицы, что в сумме даёт тройку, что также недопустимо. Вычитаем из трёх основание системы счисления, то есть два и получаем единицу. То есть в данном разряде пишется единица и единица переносится в следующий разряд.
- Суммируем две единицы и снова сумма равна двум, что означает запись нуля в данном разряде и перенос единицы в следующий разряд.
- Получаем итоговый результат: 10100.
«Системы счисления и арифметические операции в них» 👇
Далее рассмотрим операцию сложения в восьмеричной системе счисления. Рассмотрим конкретный пример:
Рисунок 3. Сложение в столбик. Автор24 — интернет-биржа студенческих работ
Действия выполняются в следующем порядке:
- Выполняем суммирование младших разрядов, то есть четыре плюс три равняется семи.
- Далее выполняется суммирование следующего разряда, а именно пять плюс четыре равно девяти. Вычитаем из девяти основание системы счисления, то есть восемь, и получаем единицу в этом разряде и единицу переноса в следующий.
- Выполняем суммирование текущего разряда, три плюс семь равно одиннадцати. Вычитаем основание восемь, результат равен трём и единица переноса в следующий разряд.
- Суммируем шесть и один, что даёт в итоге семь.
- Итоговый результат получается 7317.
Рассмотрим конкретный пример сложения в шестнадцатеричной системе счисления:
Рисунок 4. Сложение в столбик. Автор24 — интернет-биржа студенческих работ
- Выполняем суммирование младших разрядов, то есть два плюс один равняется трём.
- Суммируем следующий разряд, то есть пять плюс девять равно четырнадцати. Согласно алфавиту шестнадцатеричной системы счисления это символ Е.
- Суммируем символ С, который означает двенадцать, и восемь, что в итоге равно двадцати. Вычитаем из двадцати основание системы счисления, то есть шестнадцать. Получаем четыре и единицу переноса в следующий разряд.
- Суммируем две единицы, получаем двойку.
- Получаем итоговый результат 24Е3.
Операция вычитания в разных системах счисления
Рассмотрим конкретный пример операции вычитания в десятичной системе счисления:
Рисунок 5. Вычитание в столбик. Автор24 — интернет-биржа студенческих работ
- Выполняем вычитание младших разрядов, то есть три минус один равно двум.
- Выполняем вычитание в следующем разрядом, от двух отнимаем нуль, получаем два.
- Необходимо из четырёх вычесть восемь. Выполняем заимствование единицы из старшего разряда и отнимаем от четырнадцати восемь. Результат равен шести.
- Поскольку было заимствование единицы, то из пяти вычитаем единицу и получаем четвёрку.
- Итоговый результат: 4622.
Рассмотрим пример вычитания в двоичной системе счисления:
Рисунок 6. Вычитание в столбик. Автор24 — интернет-биржа студенческих работ
- Выполняем вычитание младших разрядов, один минус один равно нулю.
- Вычитаем из единицы нуль, в итоге получаем единицу.
- Поскольку нуль меньше единицы, то выполняем заимствование единицы из старшего разряда и вычитаем из двойки единицу, Итогом будет единица.
- Итоговый результат: 110.
Рассмотрим пример вычитания в восьмеричной системе счисления:
Рисунок 7. Вычитание в столбик. Автор24 — интернет-биржа студенческих работ
- Выполняем вычитание из четырёх тройки, получаем единицу.
- Вычитаем из пяти нуль, итогом будет нуль.
- Нельзя из трёх вычесть семь, поэтому выполняем заимствование из старшего разряда. Вычитаем из одиннадцати семь и получаем в итоге четыре.
- Поскольку было заимствование единицы, то вычитаем из шести единицу и получаем пять.
- Итоговый результат: 5451.
Рассмотрим пример вычитания в шестнадцатеричной системе счисления:
Рисунок 8. Вычитание в столбик. Автор24 — интернет-биржа студенческих работ
- Выполняем вычитание из четырёх три и получаем один.
- Из пяти вычитаем нуль и получаем в итоге пять.
- Далее необходимо из трёх вычесть семь, что недопустимо и поэтому заимствуем единицу из старшего разряда. Вычитаем из девятнадцати семь и получаем двенадцать, что в шестнадцатеричной системе обозначается символом С.
- Так как была заимствована единица, то из шести вычитаем единицу. Итог равен пяти.
- Итоговый результат равен 5С51.
Операция умножения в разных системах счисления
Рассмотрим пример умножения в восьмеричной системе счисления:
Рисунок 9. Умножение в столбик. Автор24 — интернет-биржа студенческих работ
- Умножаем младшие разряды, то есть пять на четыре, получаем двадцать. Число двадцать равно два по восемь (основание системы счисления) плюс четыре. То есть в данном разряде пишем четыре, а двойку переносим в следующий разряд. Выполняем это действие для остальных разрядов, в итоге получаем 40234.
- Умножаем на нуль, что в итоге дает четыре нуля.
- Выполняем по аналогии умножение на семь. Результатом будет число 55164.
- Выполняем суммирование всех произведений, что даёт 5556634. Это и есть итоговый результат умножения.
Рассмотрим пример умножения в шестнадцатеричной системе счисления:
Рисунок 10. Умножение в столбик. Автор24 — интернет-биржа студенческих работ
- Выполняем умножение на младший разряд. Пять умножаем на четыре, получаем двадцать, что равно шестнадцати плюс четыре. Четыре пишется в данном разряде, единица переносится в следующий разряд.
- Аналогичные процедуры выполняются дальше, итог будет А334.
- Умножаем остальные разряды и затем всё суммируем.
- Итоговый результат будет 169В974.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме