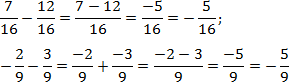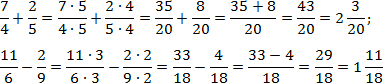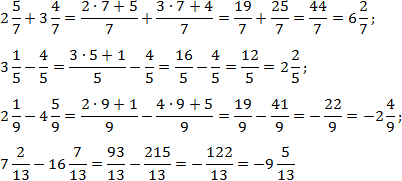Отрицательные дроби
- Сложение и вычитание
- Умножение и деление
Отрицательные дроби — это дроби, числитель или знаменатель которых является отрицательным числом.
Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:
-2 : 7 и 2 : (-7),
каждое из них равно отрицательному числу
Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:
| -2 : 7 | = | -2 | и | 2 : (-7) | = | 2 | . |
| 7 | -7 |
Следовательно, при записи отрицательных дробей знак минус
можно ставить перед дробью, перед числителем или перед знаменателем:
| — | 2 | = | -2 | = | 2 | . |
| 7 | 7 | -7 |
Сложение и вычитание
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.
Пример.
| — | 2 | + (- | 1 | ) | . |
| 5 | 4 |
Приведём дроби к общему знаменателю:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | . |
| 5 | 4 | 20 | 20 |
Теперь сложим числители дробей по правилам сложения рациональных чисел:
| -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 | 20 | 20 |
Таким образом:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | = |
| 5 | 4 | 20 | 20 |
| = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 |
Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.
Пример.
| — | 5 | — (- | 11 | ) = | — | 5 | + (+ | 11 | ) = |
| 12 | 12 | 12 | 12 |
| = | — | 5 | + | 11 | = | -5 + 11 | = | 6 | . |
| 12 | 12 | 12 | 12 |
Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.
Умножение и деление
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.
Пример.
| — | 2 | · (- | 4 | ) = | -2 | · | -4 | = | -2 · (-4) | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить сразу, отбросив оба минуса:
| — | 2 | · (- | 4 | ) = | 2 | · | 4 | = | 2 · 4 | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
При умножении отрицательной дроби на положительную результат будет отрицательным.
Пример.
| — | 2 | · | 4 | = | — | 2 · 4 | = | — | 8 | . |
| 3 | 5 | 3 · 5 | 15 |
К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:
| 4 | · (- | 2 | ) = | — | 4 · 2 | = | — | 8 | . |
| 5 | 3 | 5 · 3 | 15 |
То есть при умножении положительной дроби на отрицательную результат будет отрицательным.
Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
Пример.
| — | 2 | : (- | 4 | ) = | -2 | : | -4 | = |
| 3 | 5 | 3 | 5 |
| = | -2 · 5 | = | -10 | = | 10 | . |
| 3 · (-4) | -12 | 12 |
Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.
Отрицательные дроби складываются и вычитаются также как и отрицательные числа, только по правилам сложения дробей. Мы можете добавлять только половинки к половинкам, четверти к четвертям или десятые к десятым и так далее. Вычитание отрицательных дробей следует тем же правилам. Для того чтобы сложить или вычесть две дроби нам нужно привести их к общему знаменателю. Если дробь отрицательная мы можем знак минус поставить в числитель и наоборот. Ниже расписано сложение (-frac{7}{6}+frac{5}{7}):
При сложении двух отрицательных дробей результат будет отрицательным. Когда мы вычитаем две отрицательные дроби, то мы к первой отрицательной дроби прибавляем положительную вторую, так как минус на минус дает плюс.
Рассмотрим сложение и вычитание следующих отрицательных дробей.
Задача 1. Вычислите (frac{1}{4}+(-frac{3}{10})-(-frac{1}{2}).).
Приводим к наименьшему общему знаменателю:
(frac{1}{4}+(-frac{3}{10})-(-frac{1}{2})=frac{5-3*2+10}{20}=frac{9}{20})
Ответ: (frac{9}{20}).
. Вычислите (frac{1}{7}-(-frac{5}{6})-(-frac{1}{3})).
. Приводим к наименьшему общему знаменателю:
(frac{6-35+14}{42}=-frac{15}{42}=-frac{5}{14})
(-frac{5}{14}).
. Вычислите (frac{1}{4}+frac{5}{3}-(-frac{1}{12})).
. Приводим к наименьшему общему знаменателю:
(frac{3+20+1}{12}=frac{24}{12}=2.)
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Negative fractions are like any other fraction, except that they have a preceding negative (-) sign. The process of adding and subtracting negative fractions can be straightforward, if you keep in mind two things. A negative fraction added to another negative fraction will result in a negative fraction as result. A negative fraction subtracted from another is the same thing as adding the positive complement of that fraction.
- 1/4 + (-3/10) — 1/4 — (-3/10)
Make the denominators (the bottom of the fraction) the same, if they are not already. You can only add halves to halves or quarters to quarters or tenths to tenths and so on. Subtraction of negative fractions follows the same method.
Thus, if the negative fractions you are adding do not have the same denominator, you can make it so.
-1/2, for example, can be written as -2/4, -3/6, -4/8, et cetera. In each case, the number at the top is always half the number at the bottom. These fractions all mean half of a quantity.
Consider the adding and subtracting of the following negative fractions.
The first example is the addition of negative three-tenths to negative one-fourth. The second is the subtraction of negative three-tenths from negative one-fourth.
Method: You cannot add one-fourths to three-tenths until you express both of them to a uniform standard, so that you have a common point of reference with which you can work. You can only add like to like, or subtract like from like. More like being able to compare apples to oranges only when you at least call them both pieces of fruit.
You need a common denominator. This will be the lowest number that the two denominators 4 and 10 will divide into. This will be 20.
Keep the fraction equivalent using this common denominator: 20.
(- 1/4) becomes (- 5/20), because 5 is a quarter of 20.
(- 3/10) becomes (- 6/20). The denominator increased 2 times, so the numerator, the top part, has to double also, to keep the fraction the same.
Now that a common denominator has been found, and the negative fractions expressed in terms of this new denominator, the negative fractions can then be added or subtracted.
When adding negative fractions, add as per normal. Then stick the negative sign to your answer.
When subtracting negative fractions, you are, in effect, adding the positive complement of the negative fraction you are subtracting, because subtracting a negative number or fraction is the same as adding the positive of that negative fraction or number. The two consecutive negative signs «cancel out» to give a positive sign.
Adding the negative fractions: (- 1/4) + (- 3/10) = — 5/20 + — 6/20 = — (11/20)
When subtracting: (- 1/4) — (- 3/10) = — 5/20 — (- 6/20) = — 5/20 + 6/20 (two consecutive minus signs become a + sign) = 1/20.
Сумма отрицательных дробей, одинаковые знаменатели
1. Сумма чисел с одинаковыми знаками (целые числа до 10)
| Вычисли: a) 1 + 6 = 7 b) −3 + (−1) = -4 |
2. Сумма отрицательных дробей, одинаковые знаменатели
3. Алгебраическая сумма двух десятичных дробей (десятые)
4. Сумма чисел с одинаковыми знаками (десятичные дроби)
| a) 2,6 + 0,14 = 2,74 b) −1,5 + (−2,6) = -4,1 |
5. Алгебраическая сумма двух обыкновенных дробей, одинаковые знаменатели

|
6. Алгебраическая сумма двух смешанных чисел, одинаковые знаменатели
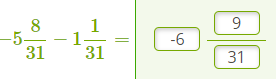
|
7. Алгебраическая сумма двух дробей с разными знаменателями
8. Сумма отрицательных смешанных чисел, разные знаменатели
9. Обыкновенная дробь и десятичная
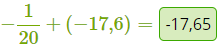
|
10. Алгебраическая сумма, шесть десятичных дробей (десятые, сотые, тысячные)
11. Значение буквенного выражения (целые числа)
12. Значение выражения (обыкновенные и десятичные дроби)
13. Уравнение (десятичные дроби)
| −87,9+(−t) =2,3. Ответ: t= -90,2 |
| −t=2,3+87,9 |
14. Значение буквенного выражения (десятичные дроби)
15. Составление выражения, значение выражения (смешанные числа)
16. Уравнение (десятичные дроби и смешанные числа)
Сложение и вычитание дробей
30 июля 2011
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Задача. Найдите значение выражения:
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:
Как видите, ничего сложного: просто складываем или вычитаем числители — и все.
Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.
Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!
Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
Разберем все это на конкретных примерах:
Задача. Найдите значение выражения:
В первом случае все просто, а во втором внесем минусы в числители дробей:
Что делать, если знаменатели разные
Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю», поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:
Задача. Найдите значение выражения:
В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.
Что делать, если у дроби есть целая часть
Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.
Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:
- Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
- Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
- Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.
Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:
Задача. Найдите значение выражения:
Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.
Резюме: общая схема вычислений
В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:
- Если в одной или нескольких дробях выделена целая часть, переведите эти дроби в неправильные;
- Приведите все дроби к общему знаменателю любым удобным для вас способом (если, конечно, этого не сделали составители задач);
- Сложите или вычтите полученные числа по правилам сложения и вычитания дробей с одинаковыми знаменателями;
- Если возможно, сократите полученный результат. Если дробь оказалась неправильной, выделите целую часть.
Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.
Смотрите также:
- Тест к уроку «Сложение и вычитание дробей» (легкий)
- Приведение дробей к общему знаменателю
- Тест к уроку «Десятичные дроби» (1 вариант)
- Метод узлов в задаче B5
- Задача B5: площадь кольца
- Сфера, вписанная в куб