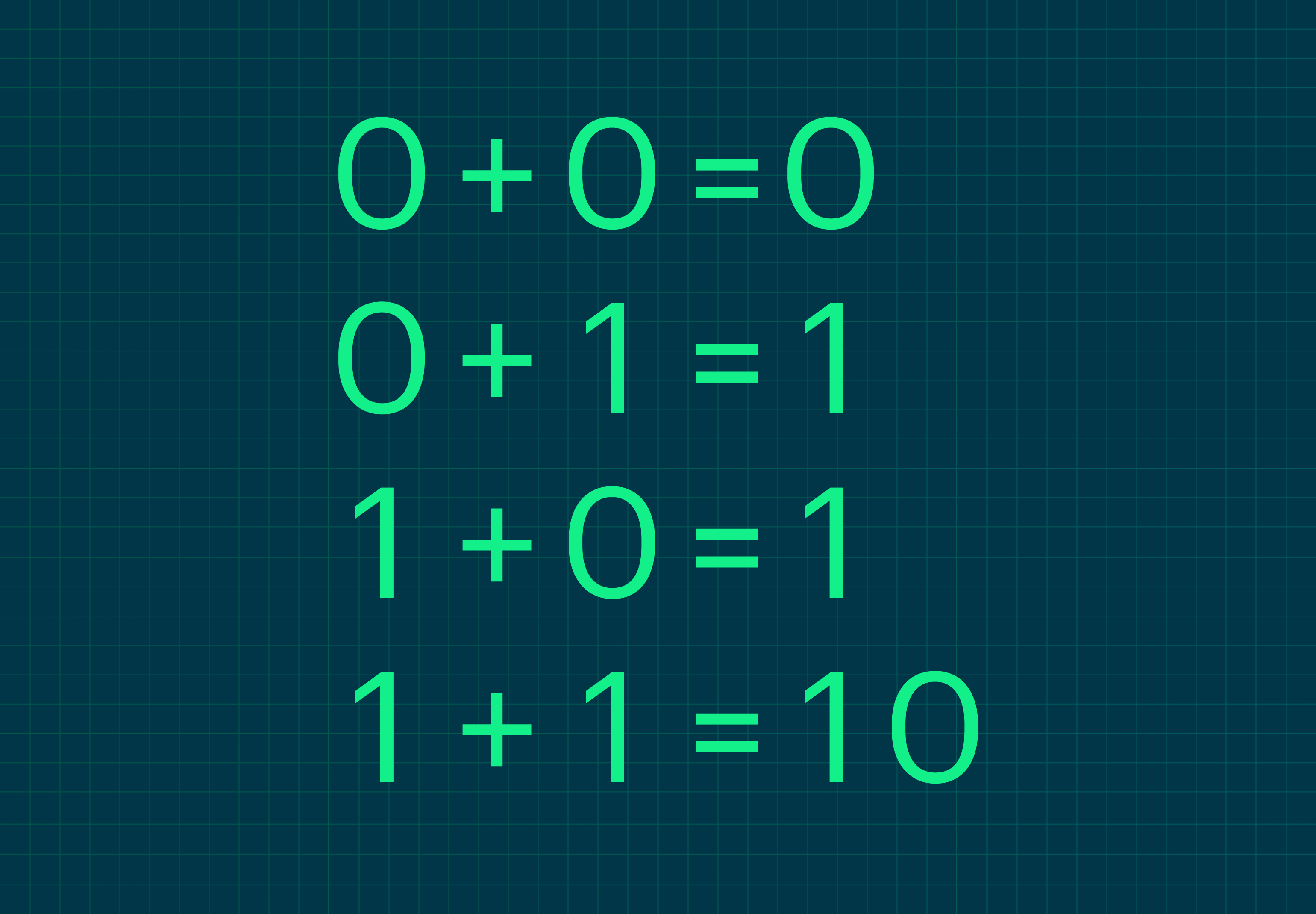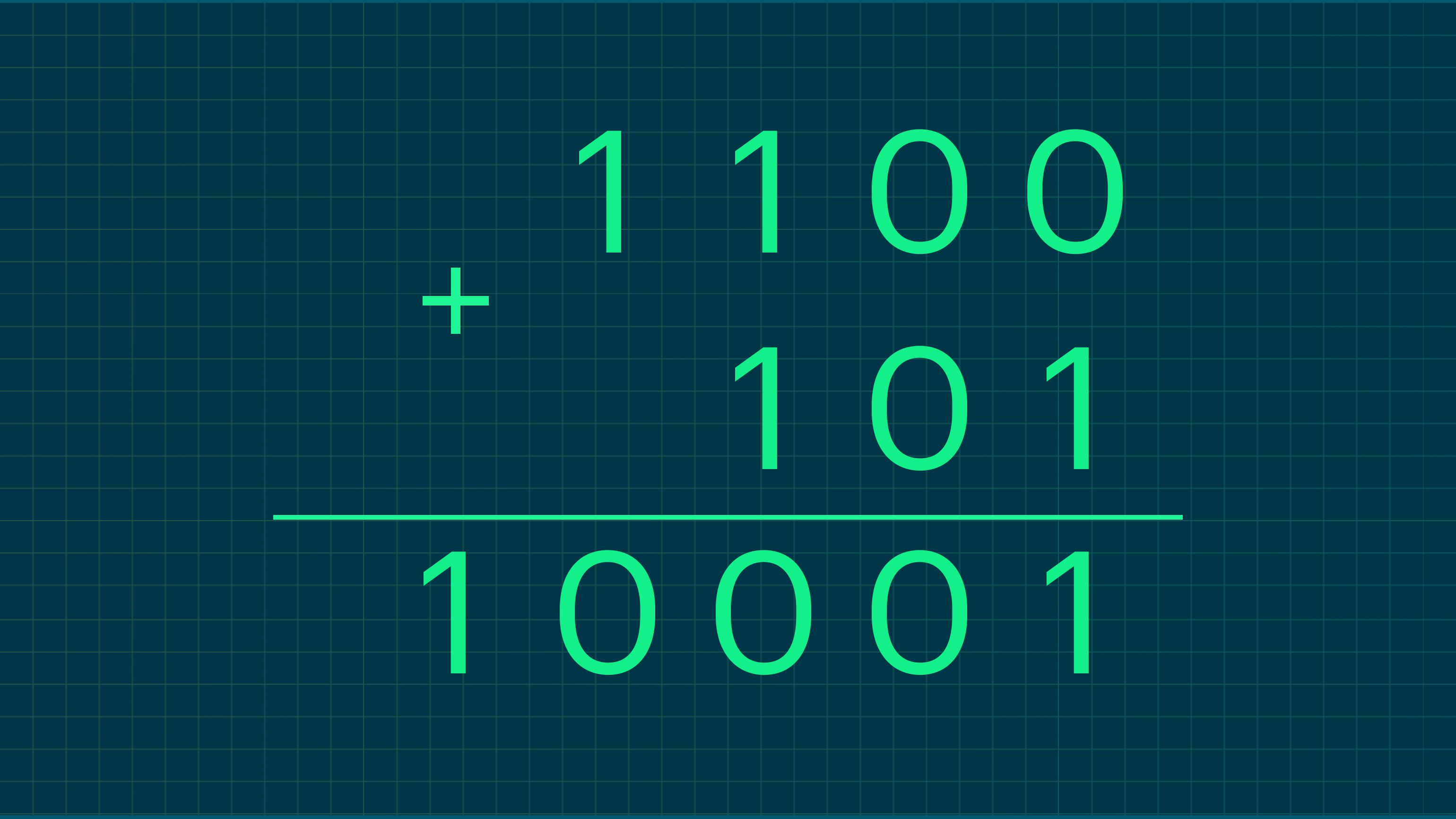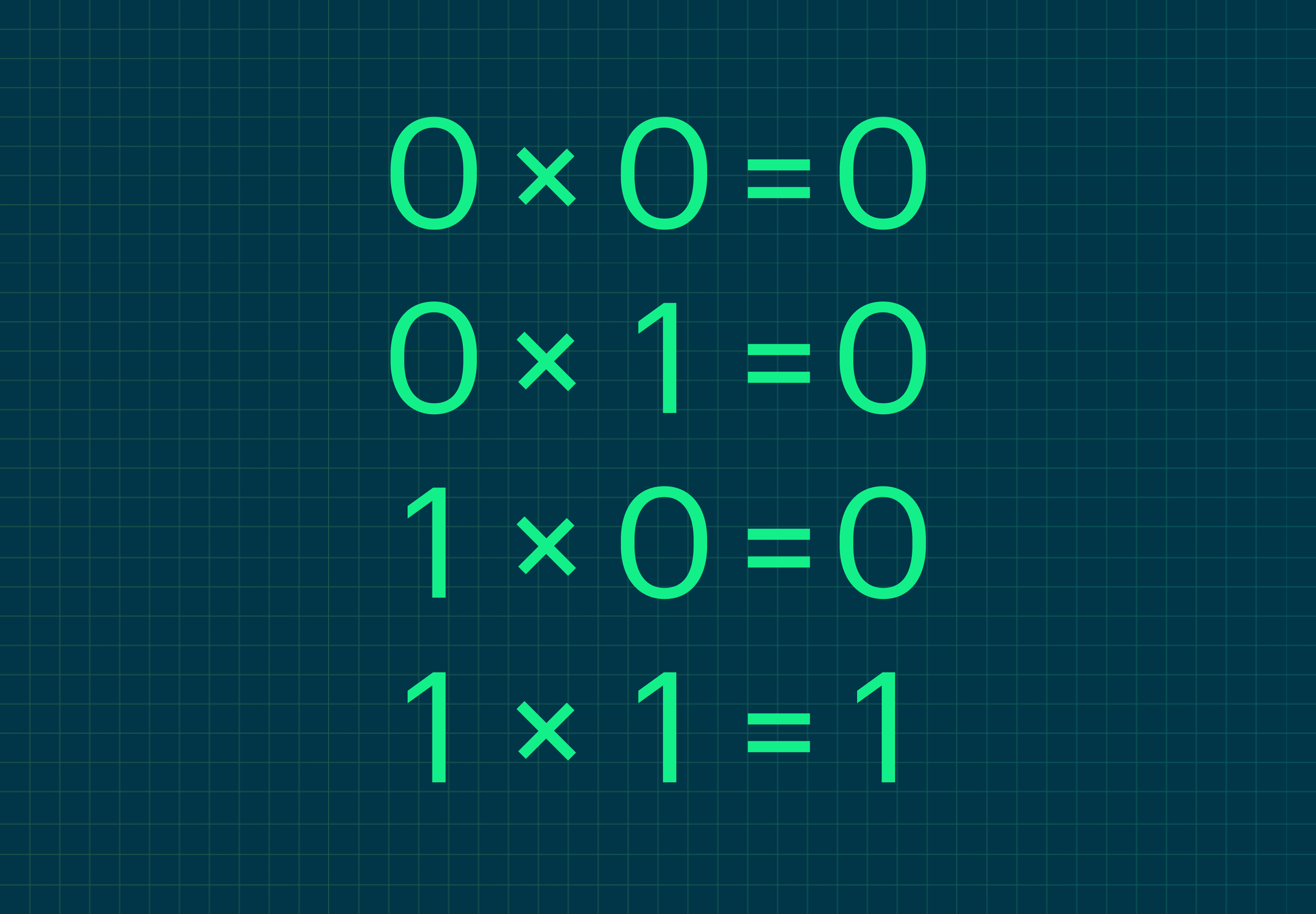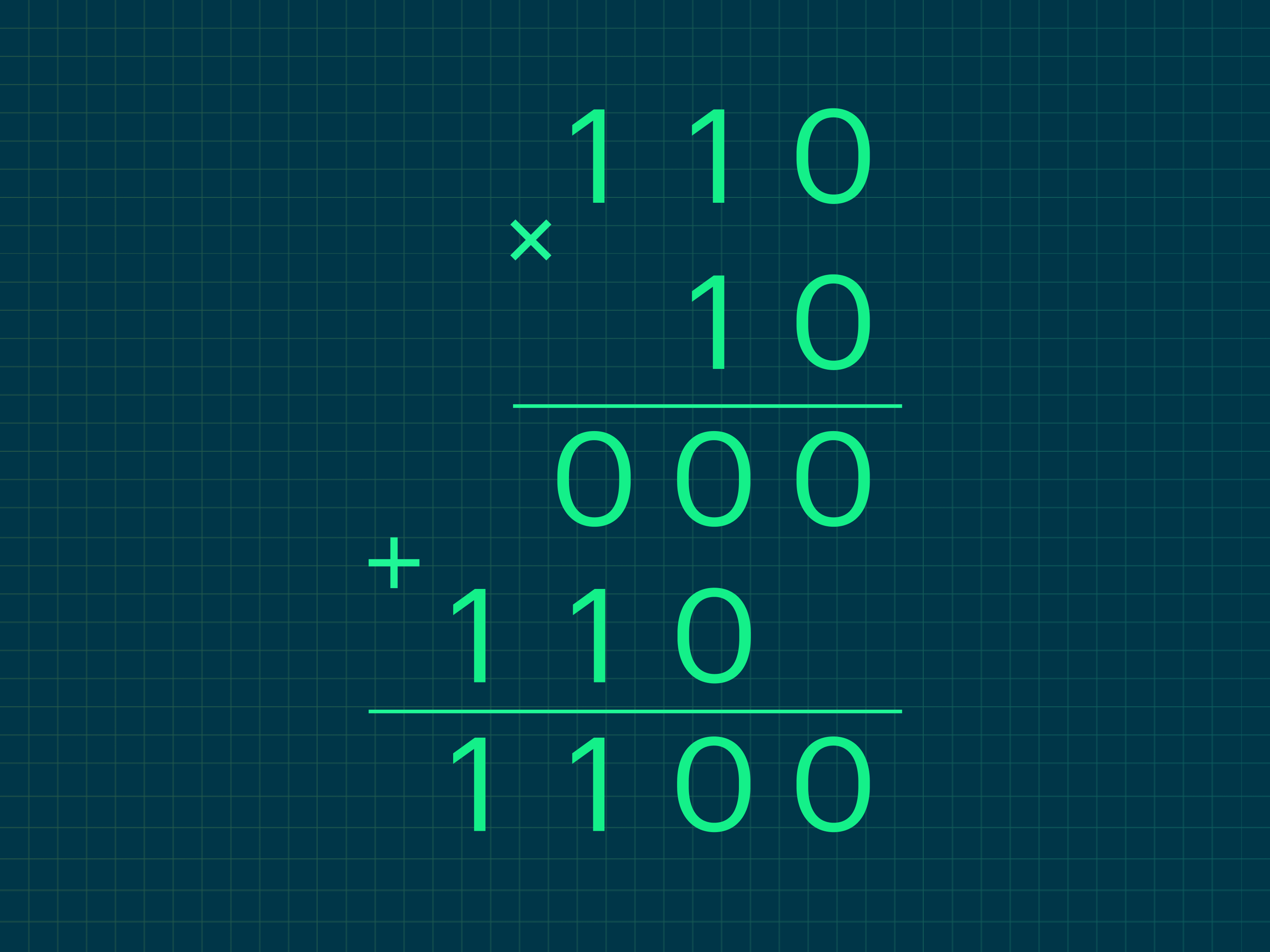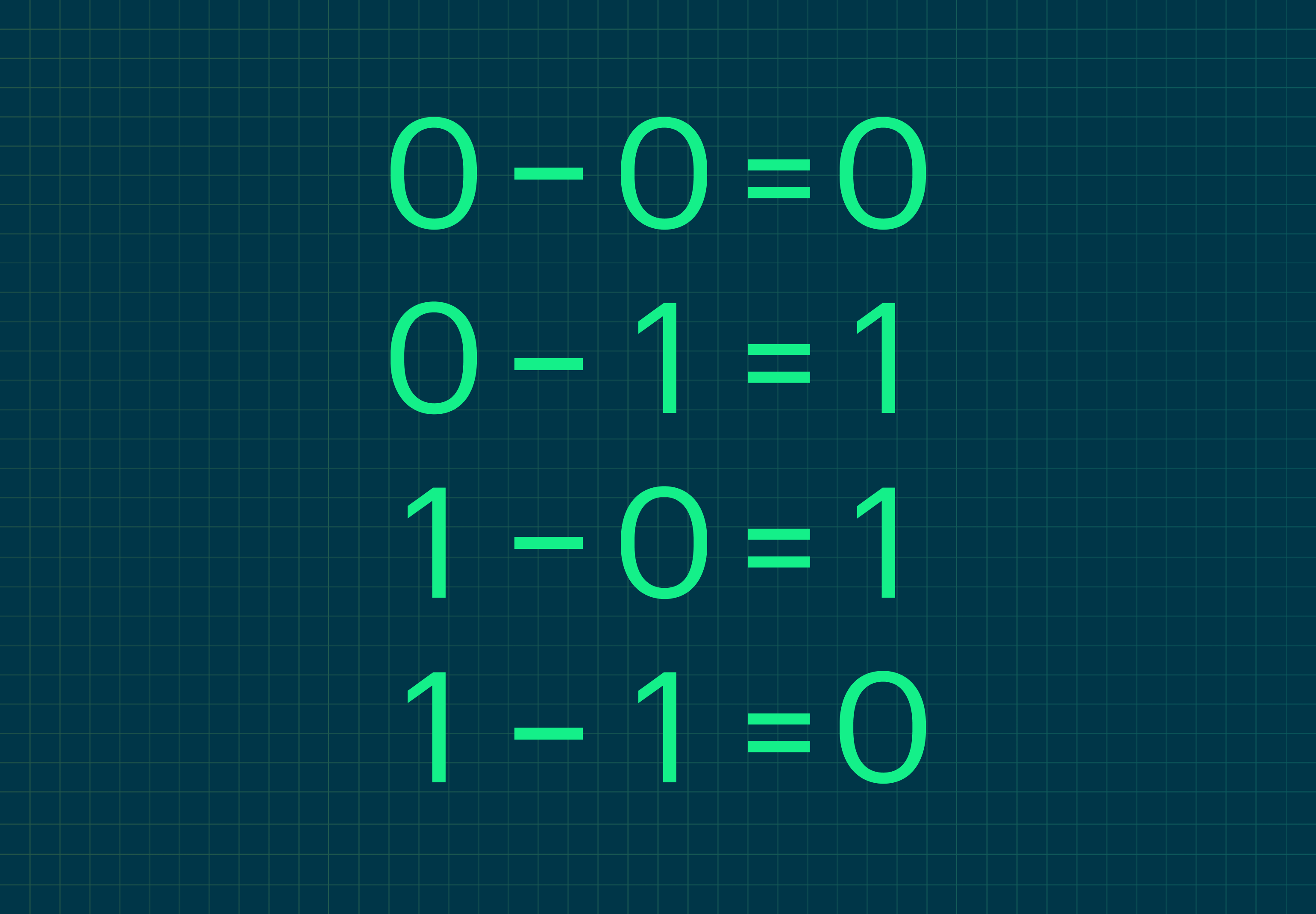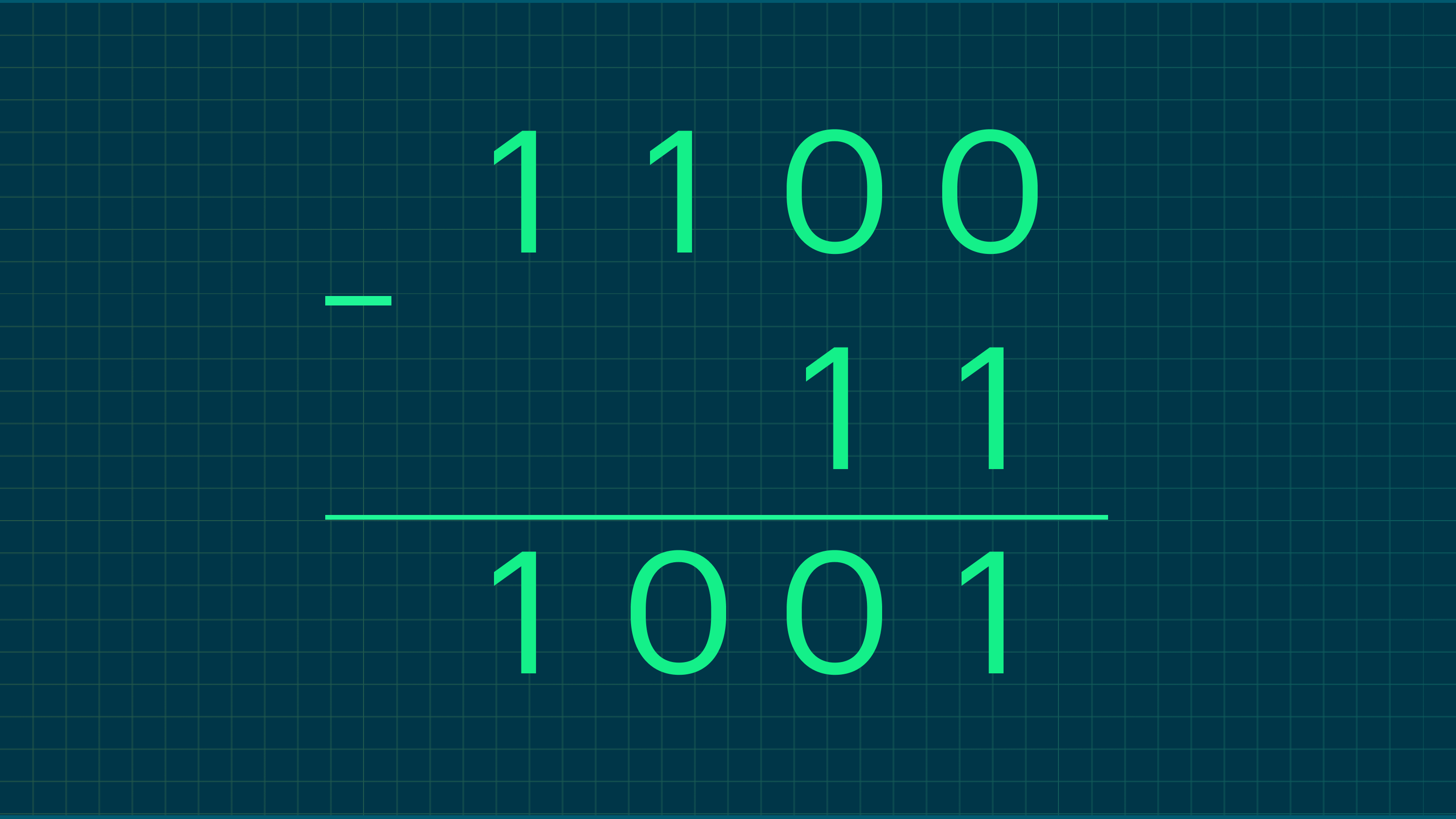Как найти сумму двух чисел в информатике - Avtoru.top

program z1;

var a,b;

begin

writeln(‘введите a’); readln (a);

writeln(‘введите b’); readln (b);

Writeln(a+b);

end.

program – по-английски «программа», пишется в самом начале кода, после чего идет название программы латиницей и точка с запятой

var-переменные программы

в Паскале означает величину, которая в процессе программы может изменять свое значение

begin-начало тела программы

вместо writeln можно также писать write,на ваше усмотрение.

Когда вы пишете write,числа пишутся в одну строку.Например:34,504

С помощью writeln числа пишутся в две строки.

Вот так:

34

504

end.- конец программы.после end ВСЕГДА ставится точка.

begin и end. означают открытие операторных скобок,а также их закрытие.

удачи.

Источник

Формулировка задания: Найти сумму двух чисел и записать результат в двоичной системе счисления.

Задание входит в ЕГЭ по информатике для 11 класса под номером 1 (Различные системы счисления).

Рассмотрим, как решаются подобные задания на примере.

Пример задания:

Найти сумму двух чисел и записать результат в двоичной системе счисления: X=110111₂, Y=135₈

11010100₂
10100100₂
10010011₂
10010100₂

Решение:

Переведем второе число в двоичную систему и выполним сложение:

135₈ = 001 011 101₂ = 1011101₂

В результате получилось число 10010100₂. Таким образом, правильным является ответ номер 4.

Ответ: 4

Источник

#статьи

27 фев 2023
0

Двоичная арифметика: сложение, умножение, вычитание, деление бинарных чисел

Учимся складывать, вычитать, умножать и делить двоичные числа — работаем с фундаментальными законами современной цифровой электроники.

Иллюстрация: Катя Павловская для Skillbox Media

Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.

Мы привыкли считать всё в десятичной системе, потому что у нас 10 пальцев — и это удобно. Но если бы у нас было больше пальцев, например 12, то система могла бы быть двенадцатиричной и мы бы воспринимали её как обычную.

Когда дело доходит до двоичной системы счисления, сложно вот так сразу переключиться на её арифметику — хотя, казалось бы, принципы такие же, как для десятичной. Ведь там есть все привычные операции: сложение, вычитание, умножение, деление. Единственное отличие: в двоичных числах используются всего две цифры — ноль и единица.

Давайте избавимся от страха и наконец узнаем, как проводить знакомые нам математические операции в двоичной системе.

Правила сложения двоичных чисел похожи на привычные нам: сложение происходит поразрядно справа налево, при этом важно помнить о переносе чисел в новый разряд.

В десятичной системе у нас всего 10 цифр: от 0 до 9. Когда мы складываем 1 и 9, у нас получается переполнение, так как больше 9 в одном разряде нельзя записать. Поэтому мы переносим единицу в следующий, получаем 10.

Двоичная система работает аналогично: чтобы понять, как складывать числа, нужно помнить об этом переполнении. Всего в двоичной системе две цифры — 0 и 1. Если сложить 1 и 1, мы получим переполнение, а значит, единица пойдёт в следующий разряд, результатом станет 10 (только не «десять», а «один-ноль»).

Если представить правила сложения двоичных чисел в общем виде, получим такую таблицу:

Изображение: Skillbox Media

Но лучше разобраться на примерах.

Пример 1. Давайте сложим 1100 и 101.

Изображение: Skillbox Media

Рассмотрим пример подробнее. Как мы уже упоминали ранее, сложение происходит справа налево. Разряды считаются тоже справа налево:

Первый: 0 + 1 = 1.
Второй: 0 + 0 = 0.
Третий: 1 + 1 = 10 — переполнение, единица переходит в следующий разряд.
Четвёртый: 1 + 0 + 1 = 10 — добавляем единицу из прошлого разряда, получаем переполнение, единица переходит в следующий разряд.
Пятый: 0 + 0 + 1 = 1 — единица пришла из предыдущего разряда.

Пример 2. Сложим 1111 и 111.

Изображение: Skillbox Media

Теперь поразрядно:

Первый: 1 + 1 = 0 — единица переходит в следующий разряд.
Второй: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
Третий: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
Четвёртый: 1 + 0 + 1 = 0 — единица переходит в следующий разряд.
Пятый: 0 + 0 + 1 = 1.

Вроде бы пока несложно. Так что попробуйте сами сложить 1101 и 1011, чтобы закрепить знания.

Ответ

1101 + 1011 = 11000.

Умножение в двоичной системе, как в десятичной, основано на сложении — и умении считать в столбик.

Сведём в таблицу правила умножения двоичных чисел:

Изображение: Skillbox Media

Давайте теперь посмотрим на реальных примерах, как правильно умножать двоичные числа.

Пример 1. Умножим 110 на 10.

Изображение: Skillbox Media

Здесь мы воспользуемся привычным школьным «столбиком»: сначала умножаем верхнее число, 110, на 0, затем на 1, а потом складываем полученные два и получаем результат.

По сути, если мы умножаем число на ноль, то оно превращается в ноль, а если на единицу — остаётся неизменным, но сдвигается на число разрядов, равное номеру разряда этой единицы, как в обычном умножении:

110 × 0 = 000;
110 × 1 = 110.

Сдвигаем 110 на один разряд влево и складываем результаты промежуточных умножений:

000 + 1100 = 1100.

Мы получили 1100, потому что сместили результат умножения 110 × 1 на один разряд влево, а затем добавили один 0 справа — как в обычном умножении.

Пример 2. Давайте теперь умножим 101 на 101.

Изображение: Skillbox Media

Не пугайтесь, что у нас получилось три числа, которые нужно сложить: правила остаются теми же. Ещё можно приписывать дополнительные нули туда, где находится пустое пространство — это поможет не запутаться.

Разберём пошагово:

101 × 1 = 101;
101 × 0 = 000;
101 × 1 = 101.

Снова сдвигаем влево промежуточные результаты и складываем:

101 + 0000 + 10100 = 11001.

Попробуйте сами умножить 1101 на 111.

Ответ

1011011.

Правила двоичного вычитания тоже ничем не отличаются от десятичного. Мы также вычитаем поразрядно и, если нужно, занимаем единицу из старшего разряда.

Таблица вычитания выглядит так:

Изображение: Skillbox Media

Заметьте, что 0 − 1 = 1. Это всё потому, что мы занимаем единицу из старшего разряда и получаем 10, или 2 в десятичной системе, а если вычесть из 10 число 1, получим 1 (ведь 2 − 1 = 1).

Перейдём к примерам, чтобы понять, как вычитать одно число из другого.

Пример 1. Вычтем из 1100 число 11.

Изображение: Skillbox Media

Разберём подробнее поразрядно:

Первый: 0 − 1 = 1 — занимаем единицу из старшего разряда.
Второй: 1 − 1 = 0 — так как отсюда заняли единицу, но у нас её не было, мы взяли её из следующего разряда и вычли единицу из этого.
Третий: 0 − 0 = 0 — из этого разряда единица ушла в первый.
Четвёртый: 1 − 0 = 1 — здесь всё нормально.

Всё то же знакомое нам вычитание.

Пример 2. Вычтем из 1011 число 101.

Изображение: Skillbox Media

Тот же алгоритм по разрядам:

Первый: 1 − 1 = 0.
Второй: 1 − 0 = 1.
Третий: 0 − 1 = 1 — заняли единицу из следующего разряда.
Четвёртый: 0 − 0 = 0 — отдали единицу в предыдущий разряд.

Кажется, что всё несложно. Попробуйте теперь сами вычесть из 11010 число 1111.

Ответ

1011.

Вы удивитесь, но правила деления двоичных чисел похожи на деление десятичных. Рисуем привычный «столбик», умножаем, вычитаем, получаем результат.

Таблицы тут нет, потому что она бессмысленна — давайте сразу на примерах разбирать, как делить двоичные числа.

Пример 1. Поделить 1100 на 10.

Изображение: Skillbox Media

У нас есть только два варианта: умножить делитель на 1 или на 0. Поэтому алгоритм будет таким:

Смотрим на делимое, видим, что первые две его цифры — 11. Умножаем делитель на 1 и вычитаем из 11 число 10.
Получили 1, дописываем справа следующую по порядку цифру — 0. Теперь 10 равно делителю, значит, тоже умножаем его на 1 и вычитаем.
Получаем 0. Но у нас ещё остался один 0 у делимого — дописываем его справа от полученного 0.
Число 0 меньше, чем 10, поэтому умножаем делитель на 0. Получаем конечный ответ — 110.

Пример 2. Поделить 10010 на 110.

Изображение: Skillbox Media

Пошаговый алгоритм:

Первые три числа делимого меньше, чем делитель — значит, умножаем делитель на 0 и вычитаем. Получаем 100.
Дописываем 1 справа от 100, видим, что 1001 больше, чем 110, поэтому умножаем делитель на 1 и вычитаем его из 1001. Получаем 11.
Дописываем 0 справа. Полученное 110 равно делителю, поэтому тоже умножаем его на 1, получаем конечный результат.

Попробуйте сами теперь поделить 10100 на 100.

Ответ

101.

Двоичная арифметика во многом похожа на десятичную: мы так же можем складывать, вычитать, делить и умножать числа столбиком. Правда, в двоичной системе всего две цифры: 0 и 1 — поэтому привычные математические операции в ней могут показаться немного странными. К счастью, в основе двоичной арифметики лежат простые принципы, которые нужно запомнить.

Научитесь: Профессия Python-разработчик
Узнать больше

Источник

4.2. Задача «Сумма двух чисел»

Рассмотрим совсем простую задачу.

Входные данные: Целые числа $a$ и $b$ на одной строке (разделённые пробелом).
Выходные данные: Сумма $a$ и $b$.
Ограничения: $0 le a, b le 9$.
Пример

Ввод	Вывод
9 7	16

Ограничение по времени (с): 1 секунда
Ограничение по памяти: 512 Mb.

Поскольку задача решается в одно действие, шаг Спроектировать алгоритм мы пропустим и перейдём сразу к псевдокоду.

SumOfTwoDigits(a, b):
    return a + b

Так как псевдокод не уточняет ввод $a$ и $b$, ниже мы приводим решения для языков C++, Java и Python3, а также рекомендации по компиляции и реализации. Вы можете скопировать и вставить код в файл, скомпилировать, запустить и протестировать с разными данными, а затем сдать исходный файл в систему проверки. Разумеется, мы рассчитываем, что вы знакомы с основами одного из языков программирования, который используется в нашей системе тестирования: C++, Python3, Java.

`C++`

#include <iostream>

int sum_of_digits(int first, int second) {
    return first + second;
}

int main() {
    int a = 0;
    int b = 0;
    std::cin >> a;
    std::cin >> b;
    std::cout << sum_of_digits(a, b);
    return 0;
}

`Java`

import java.util.Scanner;

class SumOfTwoDigits {
    static int sumOfTwoDigits(int first_digit, int second_digit) {
        return first_digit + second_digit;
    }

    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        int a = s.nextInt();
        int b = s.nextInt();
        System.out.println(sumOfTwoDigits(a, b));
    }
}

`Python3`

def sum_of_digits(first_digit, second_digit):
    return first_digit + second_digit

if __name__ == '__main__':
    a, b = map(int, input().split())
    print(sum_of_digits(a, b))

Ваша цель — реализовать алгоритм, который дает верный результат с ограничениями по времени и памяти и при любом вводе. Нет необходимости проверять, что входные данные соответствуют ограничениям: например, в задаче Сумма двух чисел вам не нужно следить за тем, чтобы целые числа $a$ и $b$ действительно были однозначными числами (это гарантировано).

Глава прочитана

Задачи

0 / 0 задач выполнено Перейти

Перейти к главам

Практические задания с автоматической проверкой

Сформулируем чеклист решения алгоритмической задачи: от разбора условия до анализа вердикта системы проверки.

Задача «Максимальное произведение»

Без ошибок практически невозможно написать программу. В этой главе мы рассмотрим подробнее, как их искать. А заодно поговорим о том, как подбирать корректные входные данные, чтобы проверить работоспособность алгоритма во всех сценариях.

Источник

Информатика, 10 класс. Урок № 9.

Тема урока — Арифметические операции в позиционных системах счисления

Урок посвящен теме «Арифметические операции в позиционных системах счисления»». В ходе урока школьники научатся складывать, вычитать, умножать и делить в разных позиционных системах счисления.

Ключевые слова:

— позиционные системы счисления,

— арифметические операции в системе счисления с основанием q,

— таблица сложения,

— таблица умножения.

Учебник:

— Информатика. 10 класс: учебник / Л. Л. Босова, А. Ю. Босова. — М.: БИНОМ. Лаборатория знаний, 2016. — 288 с.

— Математические основы информатики: учебное пособие / Е. В. Андреева, Л. Л Босова, И. Н. Фалина — М.: БИНОМ. Лаборатория знаний, 2008. — 328 с.

Мы продолжаем изучать позиционные системы счисления. Вы узнали, что позиционные системы счисления бывают разные: десятичная, двоичная, восьмеричная и шестнадцатеричная. Вы научились переводить числа из одной системы счисления в другую. Но зачем нам с вами это надо? Конечно для того, чтобы производить расчеты. С 1 класса нас учат производить расчеты в десятичной системе счисления. А как вы думаете, можно ли производить расчеты в произвольной позиционной системе счисления? И зачем это нужно?

Двоичная система счисления издавна была предметом пристального внимания многих ученых. Первый кто заговорил о двоичном кодировании, был Лейбниц Готфрид Вильгельм. Он написал трактат «Expication de l’Arithmetique Binary» — об использовании двоичной системы счисления в вычислительных машинах. В рукописи на латинском языке, написанной в марте 1679 года, Лейбниц разъясняет, как выполнять вычисление в двоичной системе, в частности умножение, а позже в общих чертах разрабатывает проект вычислительной машины, работающей в двоичной системе счисления. Вот что он пишет: « Вычисления такого рода можно было бы выполнять и на машине». Эти слова подчеркивают универсальность алфавита, состоящего из двух символов.

Все позиционные системы счисления “одинаковы”, а именно, во всех них выполняются арифметические операции по одним и тем же правилам:

— справедливы одни и те же законы арифметики: коммутативный (переместительный), ассоциативный (сочетательный), дистрибутивный (распределительный);

— справедливы правила сложения, вычитания, умножения и деления столбиком.

Мы узнаем на уроке:

как строить таблицы сложения и умножения в заданной позиционной системе счисления;
как выполнять сложение, умножение, вычитание и деление чисел, записанных в двоичной, восьмеричной и шестнадцатеричной системах счисления;
как подсчитывать количество единиц в двоичной записи числа, являющегося результатом суммирования или вычитания степеней двойки.

Арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления.

Рассмотрим сложение.

Чтобы в системе счисления с основанием q получить сумму S двух чисел A и B, надо просуммировать образующие их цифры по разрядам i справа налево:

если a_i + b_i < q, то s_i = a_i + b_i,
старший (i + 1)-й разряд не изменяется
если a_i + b_i≥ q, то s_i = a_i + b_i– q,
старший (i + 1)-й разряд увеличивается на 1

Можно составить таблицу сложения:

Давайте рассмотрим правило сложения на примере в двоичной системе счисления

Это мы рассмотрели сложение в двоичной системе счисления, а теперь сложим два числа в троичной, восьмеричной и шестнадцатеричной системе счисления.

— 1 + 2 = 3 ≥ 3
записываем 3 – 3 = 0 под 1-м разрядом,
а 2-й разряд увеличиваем на 1

— 1 + 2 = 3 ≥ 3
записываем 3 – 3 = 0 под 2-м разрядом,
а 3-й разряд увеличиваем на 1

— 1 + 1 + 2 = 4 ≥ 3
записываем 4 – 3 = 1 под 3-м разрядом,
а 4-й разряд увеличиваем на 1

— 1 + 1 = 2 < 3
записываем 2 под 4-м разрядом

Сложим в восьмеричной и шестнадцатеричной системе счисления.

Теперь разберём вычитание в системах счисления с основанием q.

Чтобы в системе счисления с основанием q получить разность R двух чисел A и B, надо вычислить разности образующих их цифр по разрядам i справа налево:

— если a_i ≥ b_i, то r_i = a_i – b_i,
старший (i + 1)-й разряд не изменяется

— если a _i < b _i, то r_i = q + a_i – b_i,

старший (i + 1)-й разряд уменьшается на 1

Рассмотрим правило вычитания в двоичной системе счисления на примере.

Рассмотрим правило вычитания в троичной системе счисления, где q=3

1 ≥ 0
записываем 1 – 0 = 1 под 1-м разрядом
0 < 1
записываем 3 + 0 – 1 = 2 под 2-м разрядом,
делая заем в 3-м разряде
0 < 2
записываем 3 + 0 – 2 = 1 под 3-м разрядом,
делая заем в 4-м разряде
0 = 0
записываем 0 под 4-м разрядом
0 < 1
записываем 3 + 0 – 1 = 2 под 5-м разрядом,
делая заем в 6-м разряде

В восьмеричной и шестнадцатеричной системе выполним вычитание.

Как же выполняется умножение чисел в системе счисления с основанием q? Если мы рассмотрим таблицы умножения в двоичной, троичной, восьмеричной и шестнадцатеричной системах счисления, то увидим, что алгоритм умножения точно такой же, как и в десятичной системе.

Чтобы в системе счисления q получить произведение M многозначного числа A и однозначного числа b, надо вычислить произведения b и цифр числа A по разрядам i:

если a_i · b <q, то m_i = a_i · b,
старший (i + 1)-й разряд не изменяется
если a_i · b ≥ q, то m_i = a_i · b mod q,
старший (i + 1)-й разряд увеличивается на a_i · b div q

Рассмотрим примеры:

— 2 · 2 = 4 ≥ 3
записываем 4 mod 3 = 1 под 1-м разрядом,
2-й разряд увеличиваем на 4 div 3 = 1

— 1 · 2 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 2-м разрядом,
3-й разряд увеличиваем на 3 div 3 = 1

— 2 · 2 + 1 = 3 ≥ 3
записываем 5 mod 3 = 2 под 3-м разрядом,
4-й разряд увеличиваем на 5 div 3 = 1

— 2 · 1 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 4-м разрядом
и в 5-й разряд записываем 3 div 3 = 1

По этому алгоритму выполним умножение в других системах счисления.

Умножение многозначного числа на многозначное число выполняется столбиком. При этом два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце). Посмотрим пример в двоичной системе счисления.

Деление нельзя свести к поразрядным операциям над цифрами, составляющими число. Деление чисел в системе счисления с произвольным основанием q выполняется так же, как и в десятичной системе счисления. А значит, нам понадобятся правила умножения и вычитания чисел в системе счисления с основанием q. Давайте разберем деление в двоичной системе.

И попробуем поделить в восьмеричной системе счисления.

В числе 233₈ поместится 2 ∙ 73₈ = 166₈

В числе 456₈ поместится 5 ∙ 73₈ = 447₈

В числе 73₈ поместится 1 ∙ 73₈ = 73₈

Теперь мы знаем, как производится арифметика в двоичной системе счисления. Используя таблицы, мы можем решить любой пример.

Давайте рассмотрим пример:

Задание 1. Найдём количество единиц в двоичной записи числа, являющегося результатом десятичного выражения

2⁴⁰⁰⁰+4²⁰¹⁶+ 2²⁰¹⁸– 8⁶⁰⁰+ 6

Решение:

Представим все операнды исходного выражения в виде степеней двойки:

Исходное выражение 2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ – 8⁶⁰⁰ + 6

примет вид 2⁴⁰⁰⁰ + 2⁴⁰³² + 2²⁰¹⁸ – 2¹⁸⁰⁰ + 2²+ 2¹

Перепишем выражение в порядке убывания степеней: 2⁴⁰³² + 2⁴⁰⁰⁰ + 2²⁰¹⁸ – 2¹⁸⁰⁰ + 2² + 2¹

Для работы с десятичными числами вида 2ⁿ полезно иметь в виду следующие закономерности в их двоичной записи:

2¹ = 10 = 1 + 1; 2² = 100 = 11 + 1; 2³ = 1000 = 111 + 1; …

В общем виде

Для натуральных n и m таких, что n > m, получаем:

Эти соотношения позволят подсчитать количество «1» в выражении без вычислений. Двоичные представления чисел 2⁴⁰³² и 2⁴⁰⁰⁰ внесут в двоичное представление суммы по одной «1». Разность 2²⁰¹⁸ – 2¹⁸⁰⁰ в двоичной записи представляет собой цепочку из 218 единиц и следующих за ними 1800 нулей. Слагаемые 2²и 2¹ дают ещё 2 единицы.

Так как в задаче надо найти единицы, то получаем:

Итого: 1 + 1 + 218 + 1 + 1 = 222.

Давайте разберем еще одну задачу.

Найдём количество цифр в восьмеричной записи числа, являющегося результатом десятичного выражения: 2²⁹⁹+ 2²⁹⁸ + 2²⁹⁷ + 2²⁹⁶.

Решение:

Двоичное представление исходного числа имеет вид:

Всего в этой записи 300 двоичных символов. При переводе двоичного числа в восьмеричную систему счисления каждая триада исходного числа заменяется восьмеричной цифрой. Следовательно, восьмеричное представление исходного числа состоит из 100 цифр.

Ответ: 100 цифр

Итак, сегодня вы узнали, что арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления. Если необходимо вычислить значение арифметического выражения, операнды которого представлены в различных системах счисления, можно: